The Effect of Rotation on Gas Storage in Nanoporous Materials
Abstract
:1. Introduction
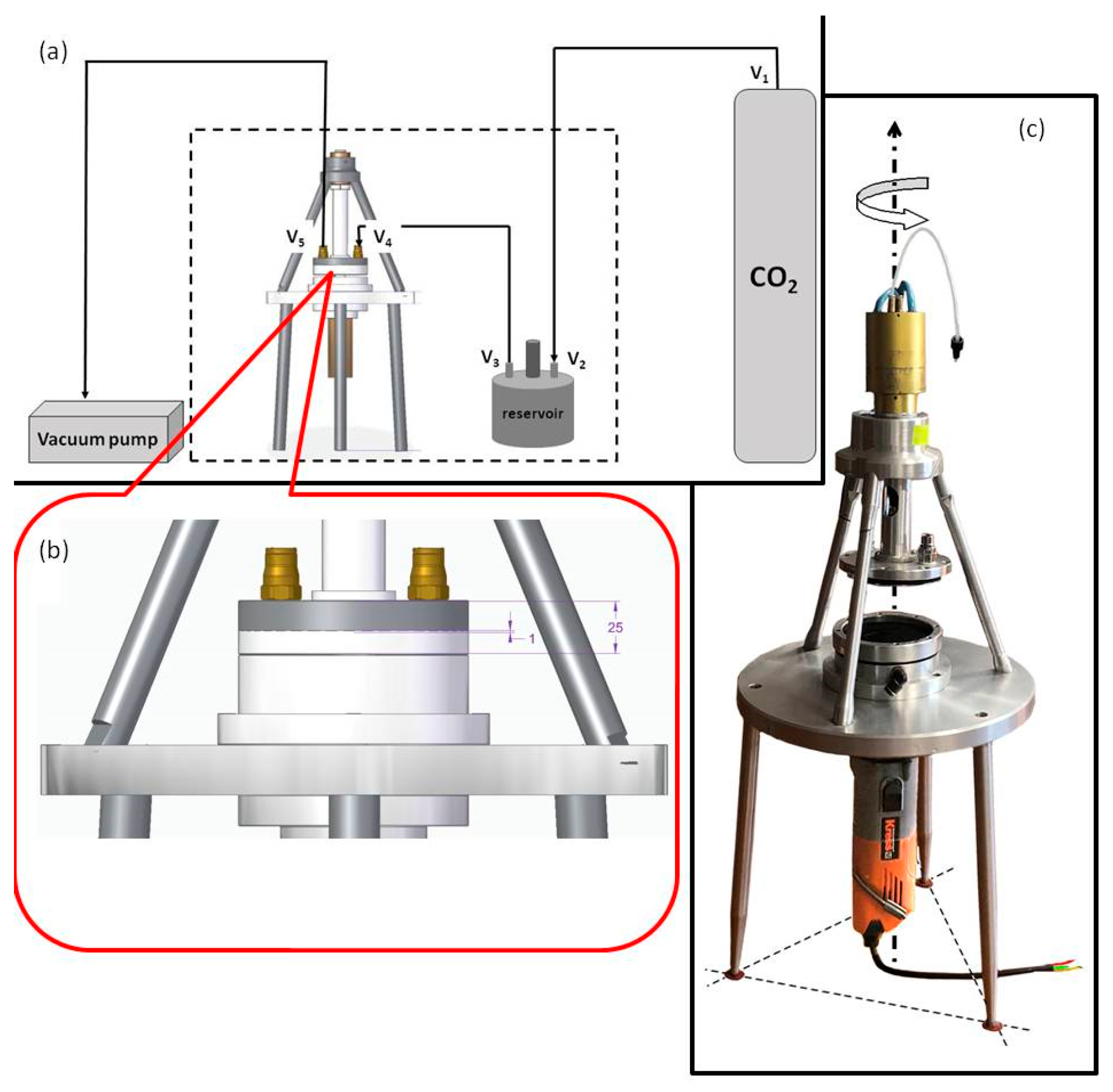
2. Experimental Details
2.1. Adsorption Isotherms
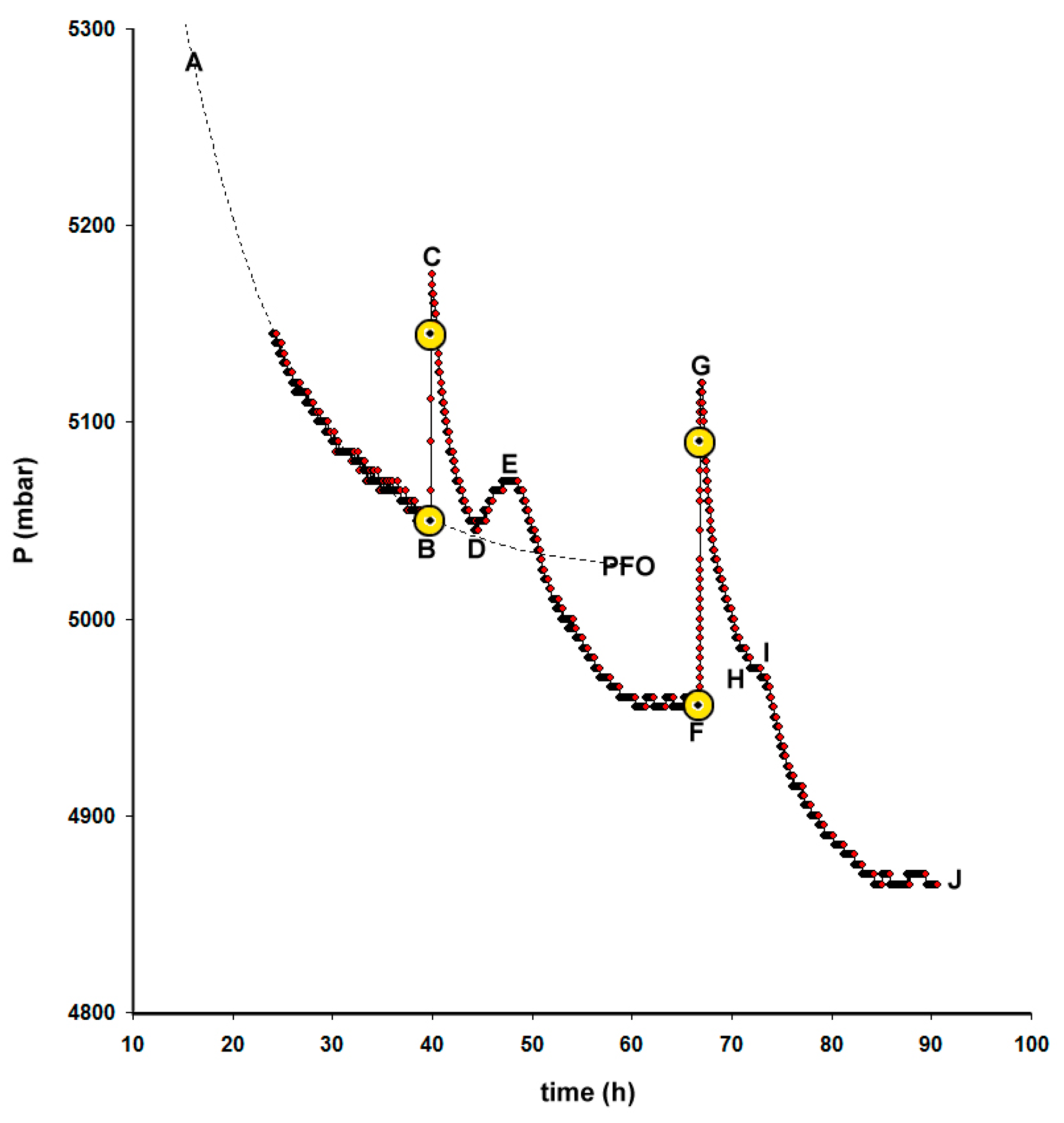
2.2. Adsorption Kinetics
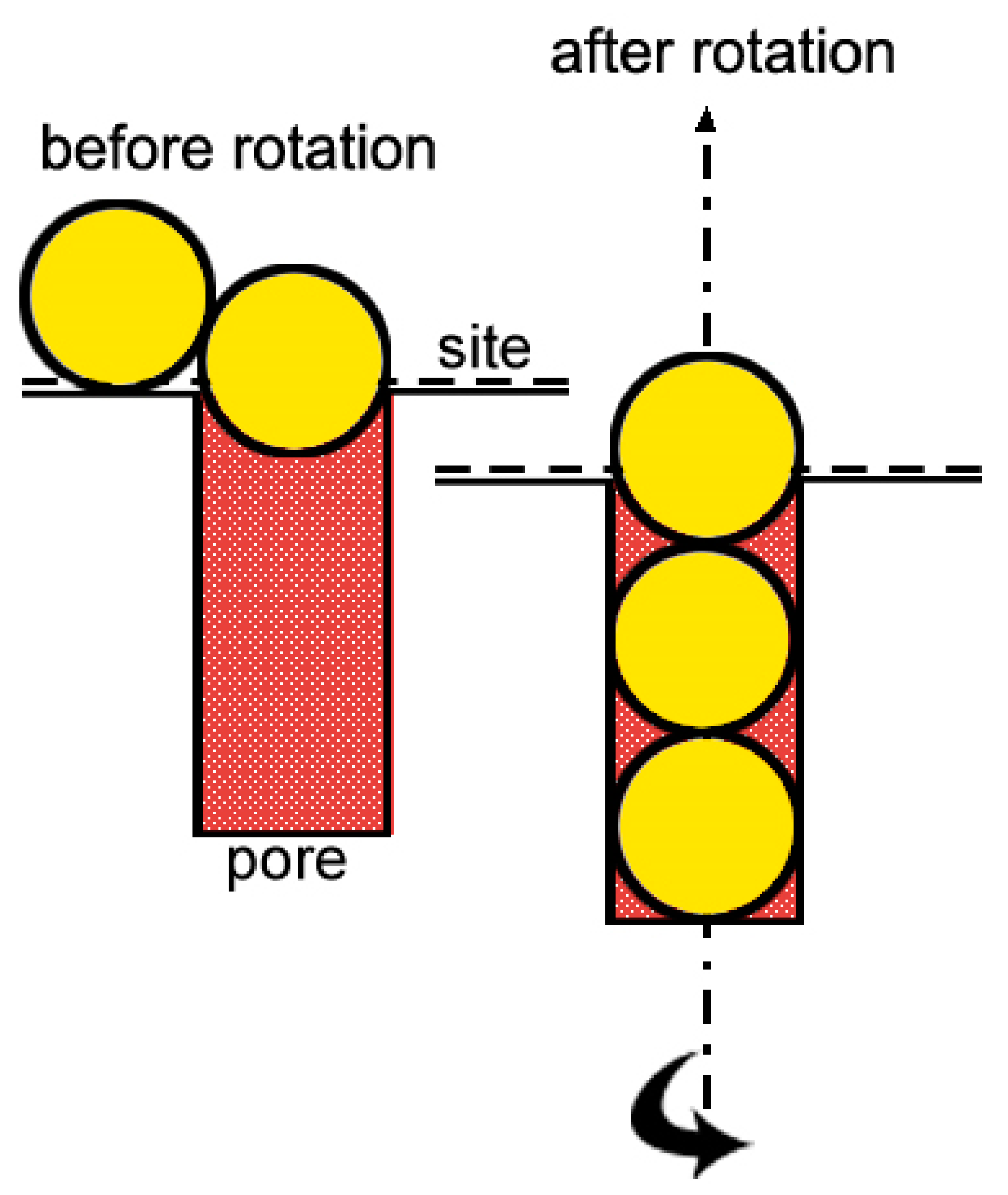
2.3. Adsorption Isotherms under Rotation
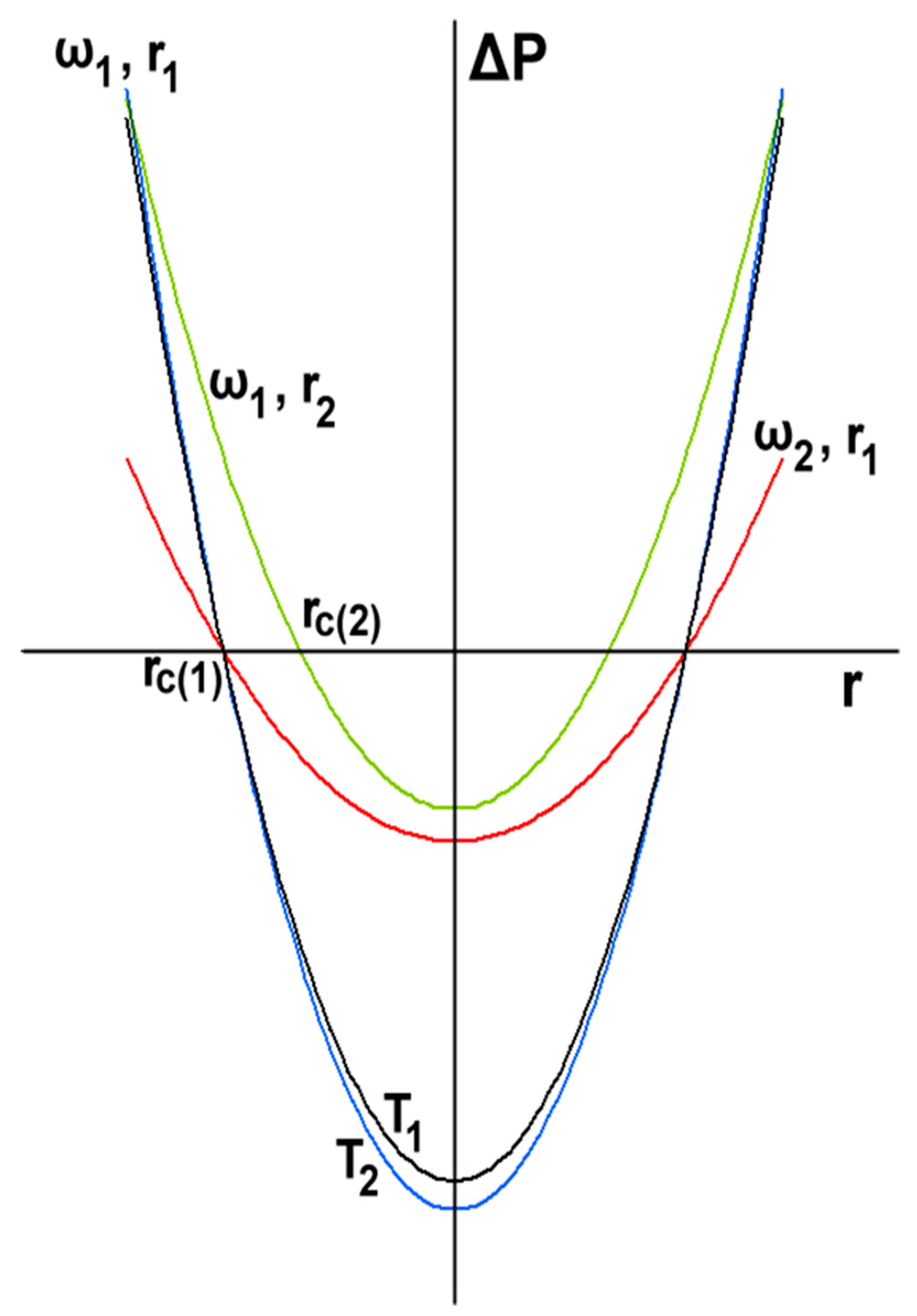
3. Kinetics
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Yue, M.; Lambert, H.; Pahon, E.; Roche, R.; Jemei, S.; Hissel, D. Hydrogen energy systems: A critical review of technologies, applications, trends and challenges. Renew. Sustain. Energy Rev. 2021, 146, 111180. [Google Scholar] [CrossRef]
- Bahman, N.; Al-Khalifa, M.; Al Baharna, S.; Abdulmohsen, Z.; Khan, E. Review of carbon capture and storage technologies in selected industries: Potentials and challenges. Rev. Environ. Sci. Bio/Technol. 2023, 22, 451–470. [Google Scholar] [CrossRef]
- Dixit, F.; Zimmermann, K.; Alamoudi, M.; Abkar, L.; Barbeau, B.; Mohseni, M.; Kandasubramanian, B.; Smith, K. Application of MXenes for air purification, gas separation and storage: A review. Renew. Sustain. Energy Rev. 2022, 164, 112527. [Google Scholar] [CrossRef]
- Ghazvini, M.F.; Vahedi, M.; Nobar, S.N.; Sabouri, F. Investigation of the MOF adsorbents and the gas adsorptive separation mechanisms. J. Environ. Chem. Eng. 2021, 9, 104790. [Google Scholar] [CrossRef]
- Tarkowski, R.; Uliasz-Misiak, B.; Tarkowski, P. Storage of hydrogen; natural gas, and carbon dioxide—Geological and legal conditions. Int. J. Hydrogen Energy 2021, 46, 20010–20022. [Google Scholar] [CrossRef]
- Yuan, B.; Wu, X.; Chen, Y.; Huang, J.; Luo, H.; Deng, S. Adsorption of CO2, CH4, and N2 on Ordered Mesoporous Carbon: Approach for Greenhouse Gases Capture and Biogas Upgrading. Environ. Sci. Technol. 2013, 47, 5474–5480. [Google Scholar] [CrossRef]
- Diwan, A.D.; Harke, S.N.; Panche, A.N. Application of proteomics in shrimp and shrimp aquaculture. Comp. Biochem. Physiol. Part D Genom. Proteom. 2022, 43, 101015. [Google Scholar] [CrossRef] [PubMed]
- Madejski, P.; Chmiel, K.; Subramanian, N.; Kuś, T. Methods and techniques for CO2 capture: Review of potential solutions and applications in modern energy technologies. Energies 2022, 15, 887. [Google Scholar] [CrossRef]
- Moussa, M.; Bader, N.; Querejeta, N.; Durán, I.; Pevida, C.; Ouederni, A. Toward sustainable hydrogen storage and carbon dioxide capture in post-combustion conditions. J. Environ. Chem. Eng. 2017, 5, 1628–1637. [Google Scholar] [CrossRef]
- Zhu, X.; Xie, W.; Wu, J.; Miao, Y.; Xiang, C.; Chen, C.; Ge, B.; Gan, Z.; Yang, F.; Zhang, M.; et al. Recent advances in direct air capture by adsorption. Chem. Soc. Rev. 2022, 51, 6574–6651. [Google Scholar] [CrossRef] [PubMed]
- de Queiroz Fernandes Araújo, O.; de Medeiros, J.L. Carbon capture and storage technologies: Present scenario and drivers of innovation. Curr. Opin. Chem. Eng. 2017, 17, 22–34. [Google Scholar] [CrossRef]
- Ma, S. Gas storage in porous metal–organic frameworks for clean energy applications. Chem. Commun. 2010, 46, 44–53. [Google Scholar] [CrossRef]
- Deegan, M.M.; Lorzing, G.R.; Korman, K.J.; Rowland, C.A.; Dworzak, M.R.; Antonio, A.M.; Bloch, E.D. Hydrogen Storage in Porous Cages. ACS Mater. Au 2023, 3, 66–74. [Google Scholar] [CrossRef]
- Lee, S.-Y.; Lee, J.-H.; Kim, Y.-H.; Kim, J.-W.; Lee, K.-J.; Park, S.-J. Recent Progress Using Solid-State Materials for Hydrogen Storage: A Short Review. Processes 2022, 10, 304. [Google Scholar] [CrossRef]
- Ding, M.; Liu, X.; Ma, P.; Yao, J. Porous materials for capture and catalytic conversion of CO2 at low concentration. Coord. Chem. Rev. 2022, 465, 214576. [Google Scholar] [CrossRef]
- Berenguer-Murcia, Á.; Marco-Lozar, J.P.; Cazorla-Amorós, D. Hydrogen storage in porous materials: Status, milestones, and challenges. Chem. Rec. 2018, 18, 900–912. [Google Scholar] [CrossRef] [PubMed]
- Heinemann, N.; Alcalde, J.; Miocic, J.M.; Hangx, S.J.T.; Kallmeyer, J.; Ostertag-Henning, C.; Hassanpouryouzband, A.; Thaysen, E.M.; Strobel, G.J.; Schmidt-Hattenberger, C. Enabling large-scale hydrogen storage in porous media–the scientific challenges. Energy Environ. Sci. 2021, 14, 853–864. [Google Scholar] [CrossRef]
- Marco-Lozar, J.P.; Kunowsky, M.; Suarez-Garcia, F.; Carruthers, J.D.; Linares-Solano, A. Activated carbon monoliths for gas storage at room temperature. Energy Environ. Sci. 2012, 5, 9833–9842. [Google Scholar] [CrossRef]
- Zhang, W.J.; Rabiei, S.; Bagreev, A.; Zhuang, M.S.; Rasouli, F. Study of NO adsorption on activated carbons. Appl. Catal. B Environ. 2008, 83, 63–71. [Google Scholar] [CrossRef]
- Feroldi, M.; Neves, A.C.; Borba, C.E.; Alves, H.J. Methane storage in activated carbon at low pressure under different temperatures and flow rates of charge. J. Clean. Prod. 2018, 172, 921–926. [Google Scholar] [CrossRef]
- Strizhenov, E.M.; Shkolin, A.V.; Chugaev, S.S.; Men’shchikov, I.E.; Solovtsova, O.V.; Shiryaev, A.A.; Nickolsky, M.S. Adsorbed natural gas storage facility based on activated carbon of wood waste origin. Adsorption 2022, 29, 291–307. [Google Scholar] [CrossRef]
- Conte, G.; Policicchio, A.; De Luca, O.; Rudolf, P.; Desiderio, G.; Agostino, R.G. Copper-doped activated carbon from amorphous cellulose for hydrogen, methane and carbon dioxide storage. Int. J. Hydrogen Energy 2022, 47, 18384–18395. [Google Scholar] [CrossRef]
- Kusdhany, M.I.M.; Ma, Z.; Mufundirwa, A.; Li, H.-W.; Sasaki, K.; Hayashi, A.; Lyth, S.M. Hydrogen and carbon dioxide uptake on scalable and inexpensive microporous carbon foams. Microporous Mesoporous Mater. 2022, 343, 112141. [Google Scholar] [CrossRef]
- Luo, L.; Chen, T.; Li, Z.; Zhang, Z.; Zhao, W.; Fan, M. Heteroatom self-doped activated biocarbons from fir bark and their excellent performance for carbon dioxide adsorption. J. CO2 Util. 2018, 25, 89–98. [Google Scholar] [CrossRef]
- Peredo-Mancilla, D.; Hort, C.; Jeguirim, M.; Ghimbeu, C.M.; Limousy, L.; Bessieres, D. Experimental Determination of the CH4 and CO2 Pure Gas Adsorption Isotherms on Different Activated Carbons. J. Chem. Eng. Data 2018, 63, 3027–3034. [Google Scholar] [CrossRef]
- Zhang, C.; Song, W.; Ma, Q.; Xie, L.; Zhang, X.; Guo, H. Enhancement of CO2 Capture on Biomass-Based Carbon from Black Locust by KOH Activation and Ammonia Modification. Energy Fuels 2016, 30, 4181–4190. [Google Scholar] [CrossRef]
- Cui, H.; Shi, J.; Xu, J.; Yan, N.; Liu, Y. Direct synthesis of N, S co-doped porous carbons using novel organic potassium salts as activators for efficient CO2 adsorption. Fuel 2023, 342, 127824. [Google Scholar] [CrossRef]
- Neumann, K.; Gladyszewski, K.; Groß, K.; Qammar, H.; Wenzel, D.; Górak, A.; Skiborowski, M. A guide on the industrial application of rotating packed beds. Chem. Eng. Res. Des. 2018, 134, 443–462. [Google Scholar] [CrossRef]
- Sang, L.; Luo, Y.; Chu, G.-W.; Liu, Y.-Z.; Liu, X.-Z.; Chen, J.-F. Modeling and experimental studies of mass transfer in the cavity zone of a rotating packed bed. Chem. Eng. Sci. 2017, 170, 355–364. [Google Scholar] [CrossRef]
- Guo, Z.; Sun, Z.; Zhang, N.; Cao, X.; Ding, M. Mean porosity variations in packed bed of monosized spheres with small tube-to-particle diameter ratios. Powder Technol. 2019, 354, 842–853. [Google Scholar] [CrossRef]
- Dolamore, F.; Fee, C.; Dimartino, S. Modelling ordered packed beds of spheres: The importance of bed orientation and the influence of tortuosity on dispersion. J. Chromatogr. A 2018, 1532, 150–160. [Google Scholar] [CrossRef]
- Geyko, V.I. Reduced Compressibility and an Inverse Problem for a Spinning Gas. Phys. Rev. Lett. 2013, 110, 150604. [Google Scholar] [CrossRef]
- Liu, H.-S.; Lin, C.-C.; Wu, S.-C.; Hsu, H.-W. Characteristics of a rotating packed bed. Ind. Eng. Chem. Res. 1996, 35, 3590–3596. [Google Scholar] [CrossRef]
- Zhang, J.; Burke, N.; Zhang, S.; Liu, K.; Pervukhina, M. Thermodynamic analysis of molecular simulations of CO2 and CH4 adsorption in FAU zeolites. Chem. Eng. Sci. 2014, 113, 54–61. [Google Scholar] [CrossRef]
- Kosheleva, R.I.; Karapantsios, T.D.; Kostoglou, M.; Mitropoulos, A.C. Thermodynamic analysis of the effect of rotation on gas adsorption. J. Non-Equilib. Thermodyn. 2023, 48, 403–416. [Google Scholar] [CrossRef]
- Guo, Q.; Zhao, Y.; Qi, G.; Liu, Y. Performance and Mechanism of Gas-Solid Adsorption in a Rotating Adsorption Bed. Chem. Eng. Technol. 2022, 45, 844–852. [Google Scholar] [CrossRef]
- Kosheleva, R.I.; Karapantsios, T.D.; Kostoglou, M.; Mitropoulos, A.C. A novel device for in situ study of gas adsorption under rotation. Rev. Sci. Instrum. 2021, 92, 45106. [Google Scholar] [CrossRef] [PubMed]
- Azizian, S. Chapter 6—Adsorption isotherms and kinetics. In Adsorption: Fundamental Processes and Applications; Ghaedi, M., Ed.; Elsevier: Amsterdam, The Netherlands, 2021; pp. 445–509. [Google Scholar] [CrossRef]
- Bénard, P. 10—Carbon nanostructures for hydrogen storage. In Solid-State Hydrogen Storage: Materials and Chemistry; Woodhead Publishing Series in Electronic and Optical Materials; Woodhead Publishing: Sawston, UK, 2008; pp. 261–287. [Google Scholar] [CrossRef]
- Guo, Q.; Liu, Y.; Qi, G. Application of high-gravity technology NaOH-modified activated carbon in rotating packed bed (RPB) to adsorb toluene. J. Nanoparticle Res. 2019, 21, 175. [Google Scholar] [CrossRef]



| Adsorbents | qmax mmol/g | T °C | P Bar | Ref. |
|---|---|---|---|---|
| Cellulosic AC doped with Cu | 48 | 25 | 15 | [22] |
| Carbon foam | 15.2 | 0 | 5 | [23] |
| Chemically activated AC from olive stone | 10 | 50 | 1 | [9] |
| Modified AC from fir bark | 7l | 0 | 1 | [24] |
| AC Norit RX * | 2.5 | 30 | 5 | [25] |
| AC from black locust activated with KOH | 5.05 | 25 | 1 | [26] |
| AC doped with N,S and activated with potassium salts | 3.04–3.99 | 25 | 1 | [27] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mitropoulos, A.C.; Kosheleva, R.I.; Kostoglou, M.; Karapantsios, T.D. The Effect of Rotation on Gas Storage in Nanoporous Materials. Separations 2024, 11, 72. https://doi.org/10.3390/separations11030072
Mitropoulos AC, Kosheleva RI, Kostoglou M, Karapantsios TD. The Effect of Rotation on Gas Storage in Nanoporous Materials. Separations. 2024; 11(3):72. https://doi.org/10.3390/separations11030072
Chicago/Turabian StyleMitropoulos, Athanasios Ch., Ramonna I. Kosheleva, Margaritis Kostoglou, and Thodoris D. Karapantsios. 2024. "The Effect of Rotation on Gas Storage in Nanoporous Materials" Separations 11, no. 3: 72. https://doi.org/10.3390/separations11030072
APA StyleMitropoulos, A. C., Kosheleva, R. I., Kostoglou, M., & Karapantsios, T. D. (2024). The Effect of Rotation on Gas Storage in Nanoporous Materials. Separations, 11(3), 72. https://doi.org/10.3390/separations11030072









