Tuning the Inlet Flow Pattern of Cyclones for Boosted Particle Rotation Behaviors with High Purification Performances of Oily Sludge
Abstract
1. Introduction
2. Materials and Methods
2.1. Numerical Simulation Experiments
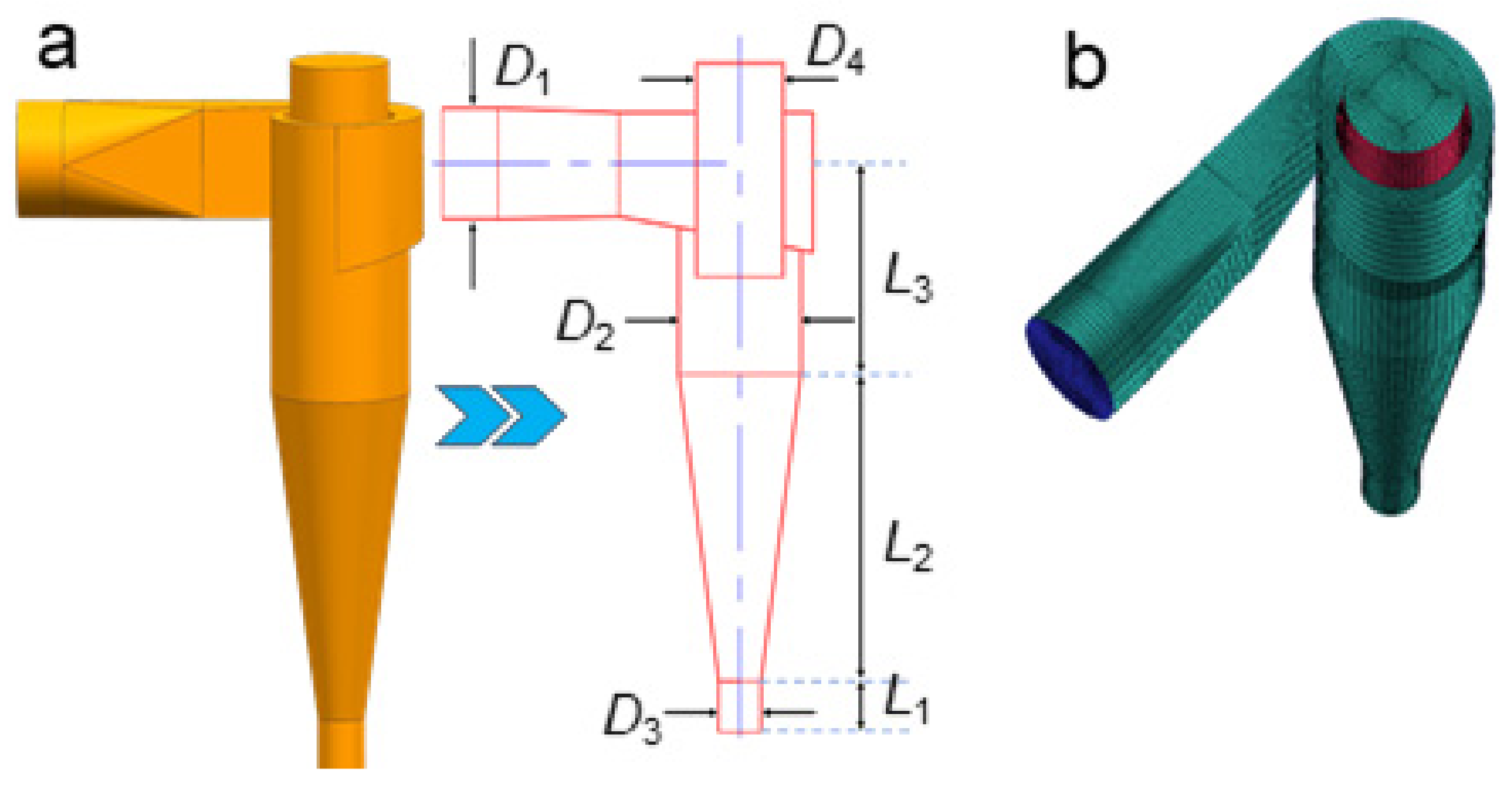
2.1.1. Cyclone Model
2.1.2. Computational Equation
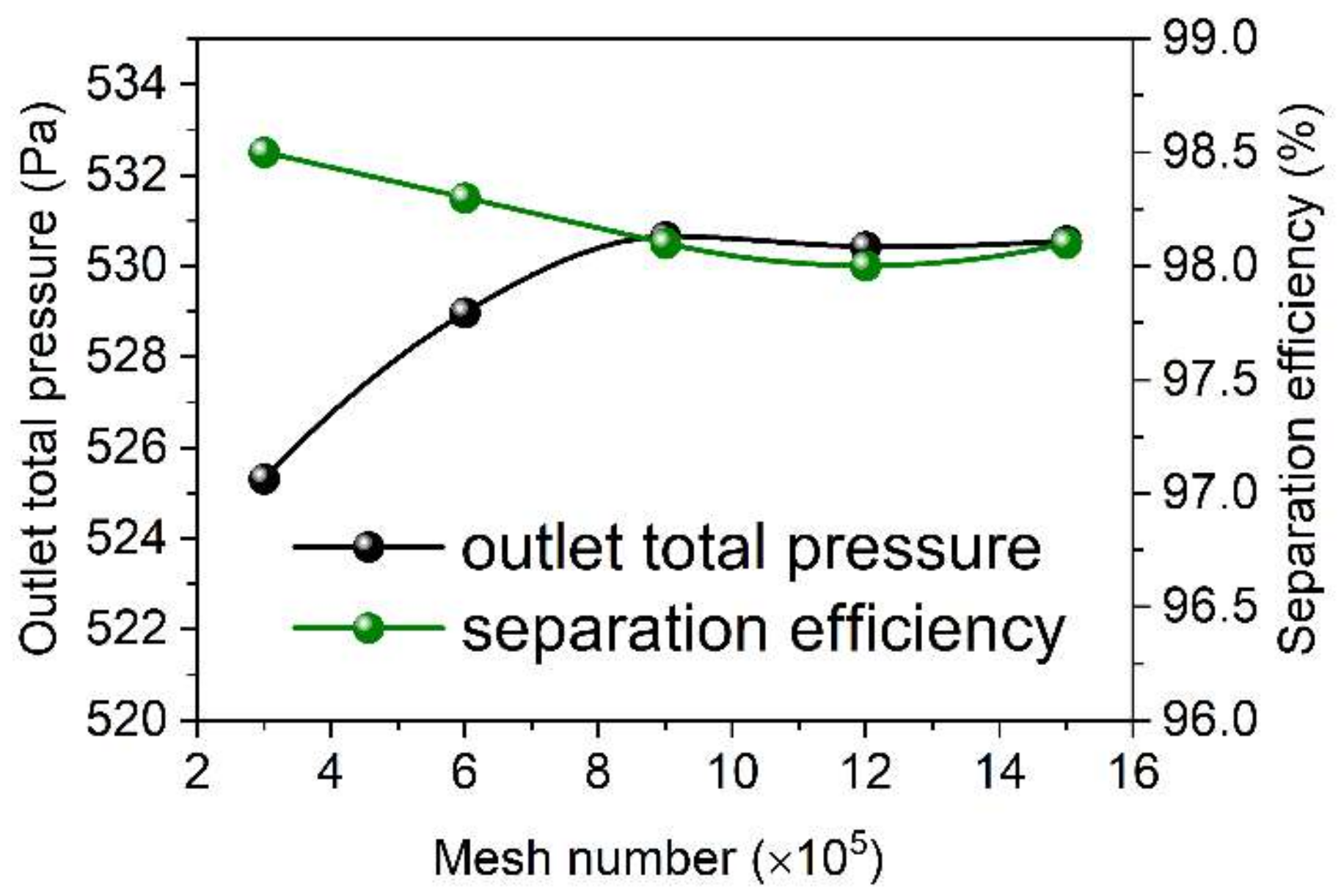
2.1.3. Boundary Conditions and Simulation Setting
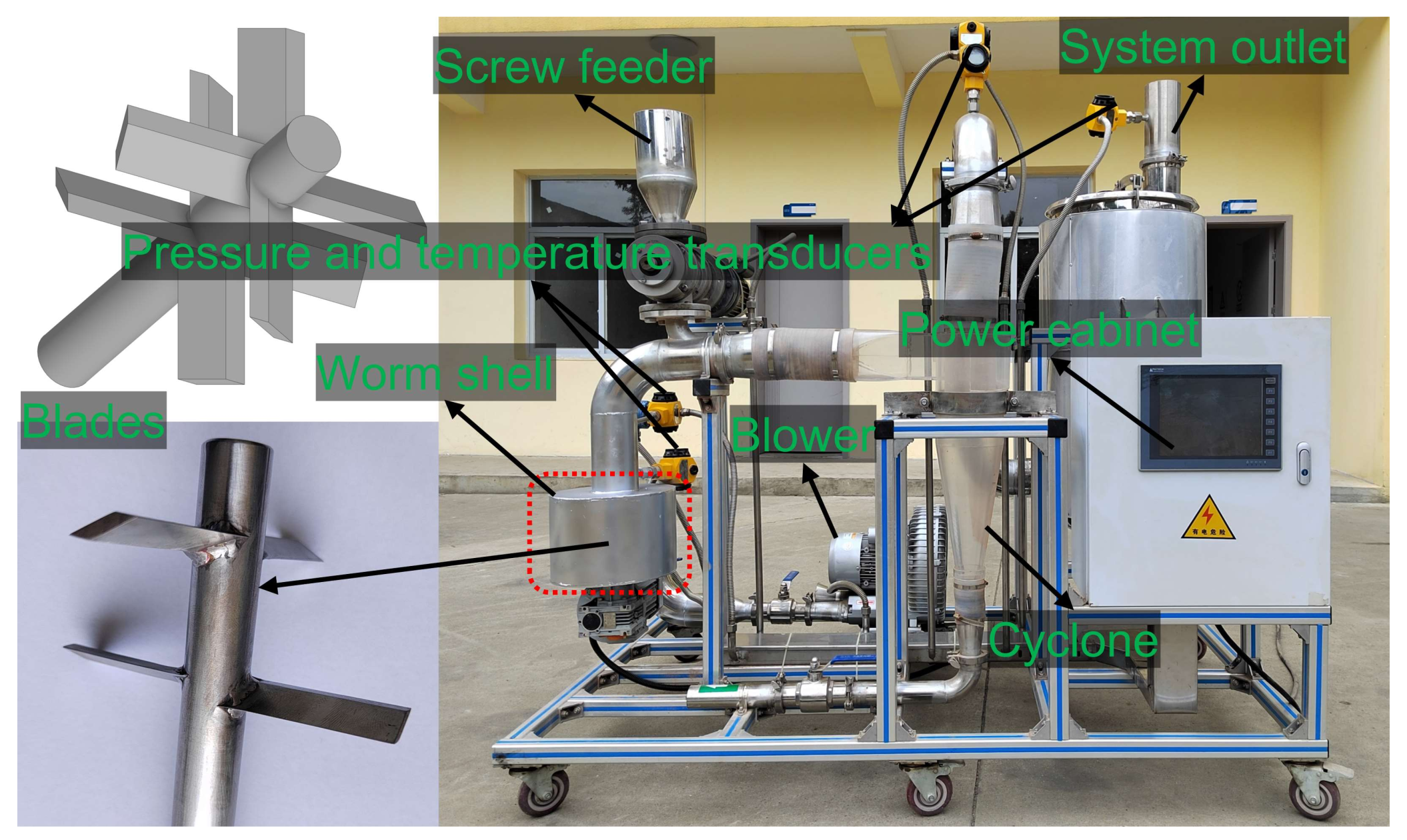
2.2. Cyclone Separation of Oily Sludges
3. Results and Discussion
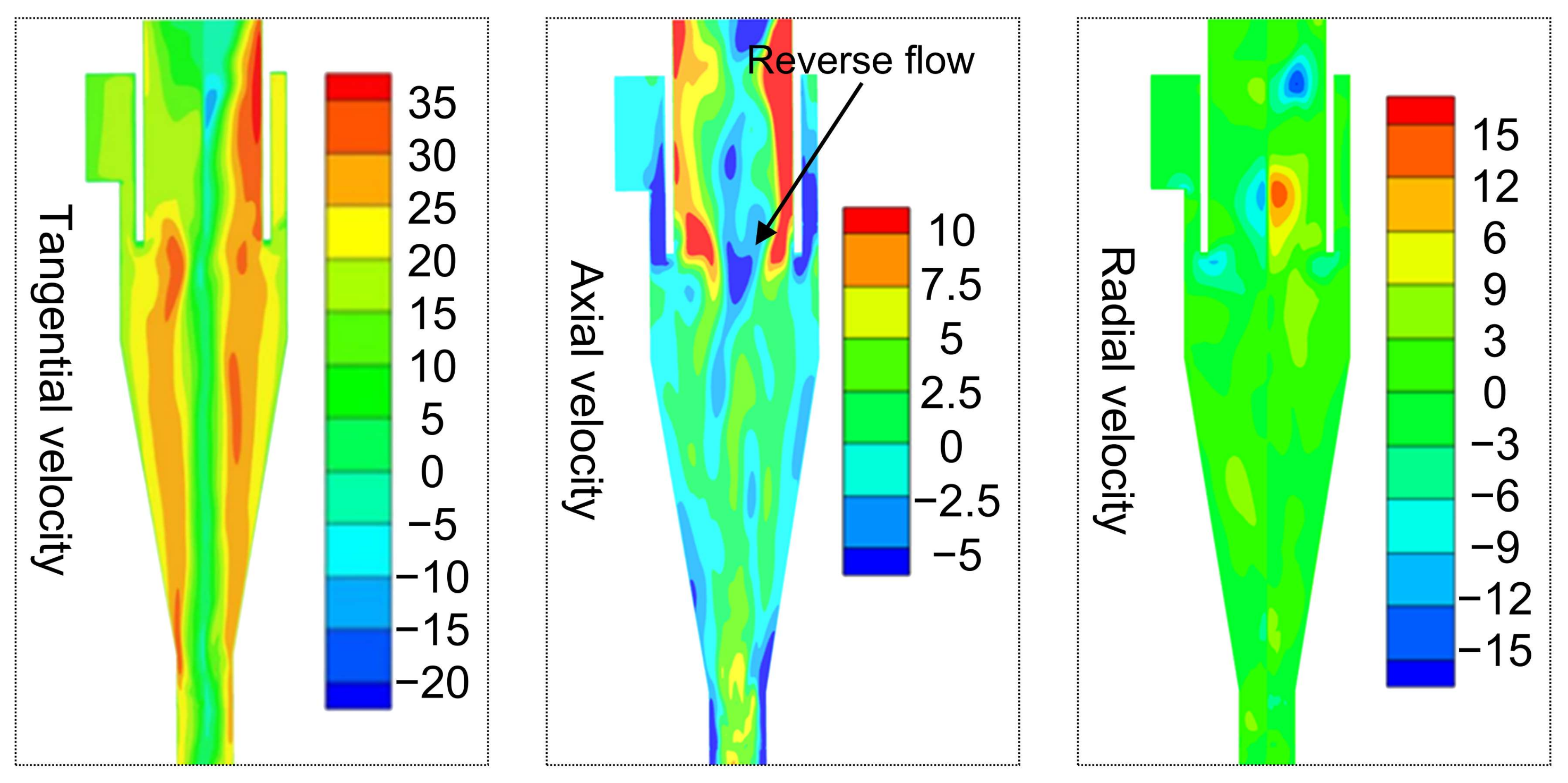
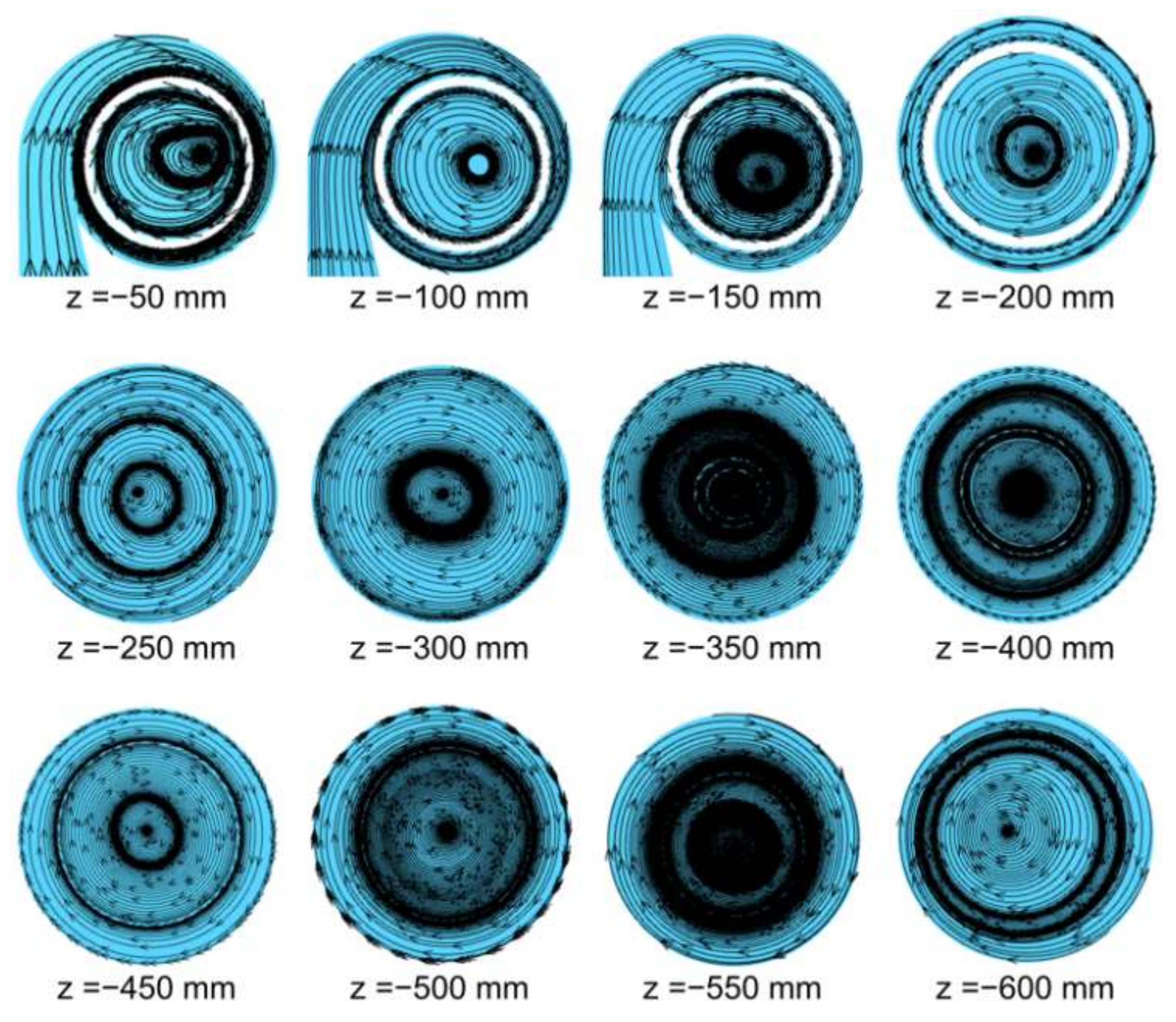
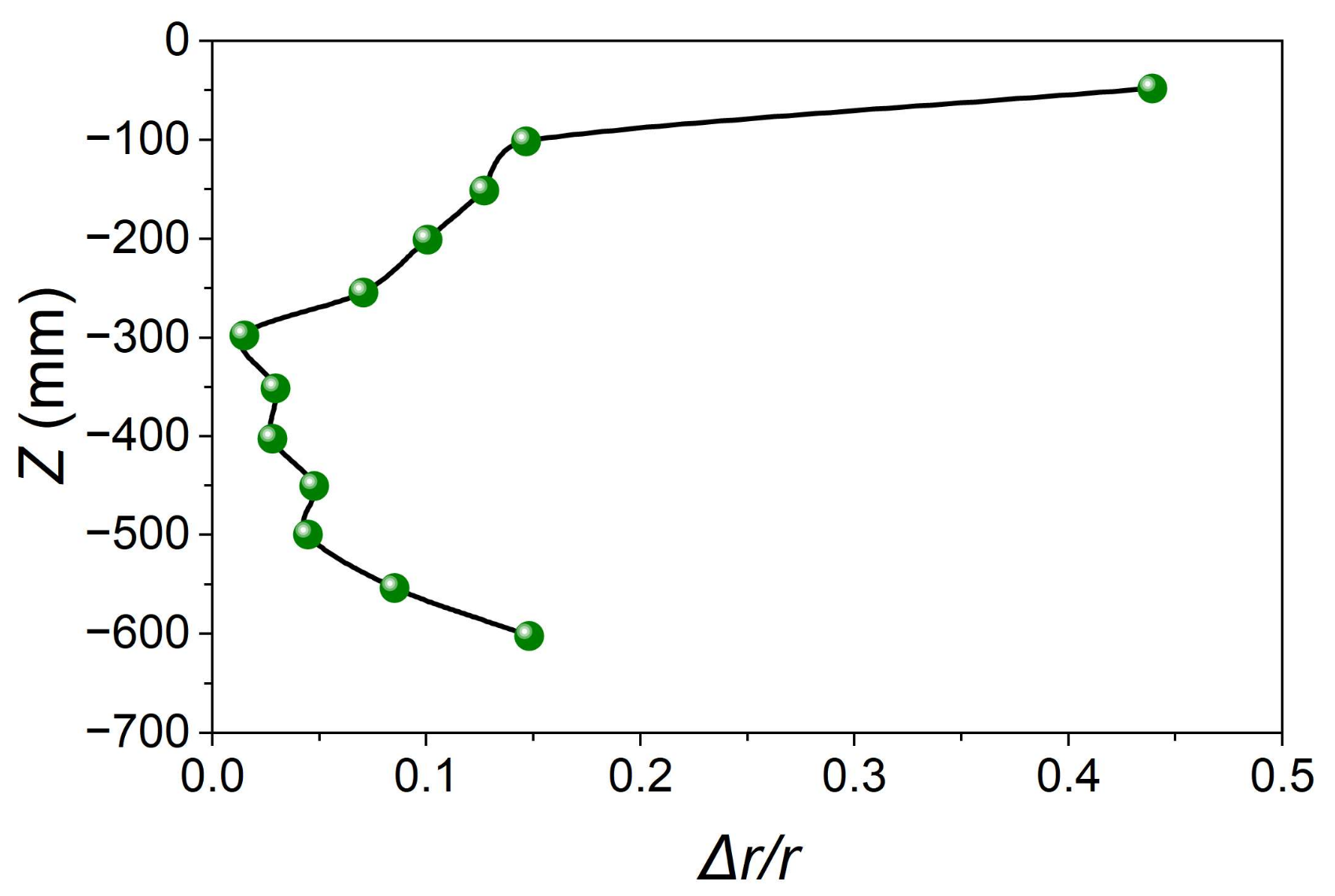
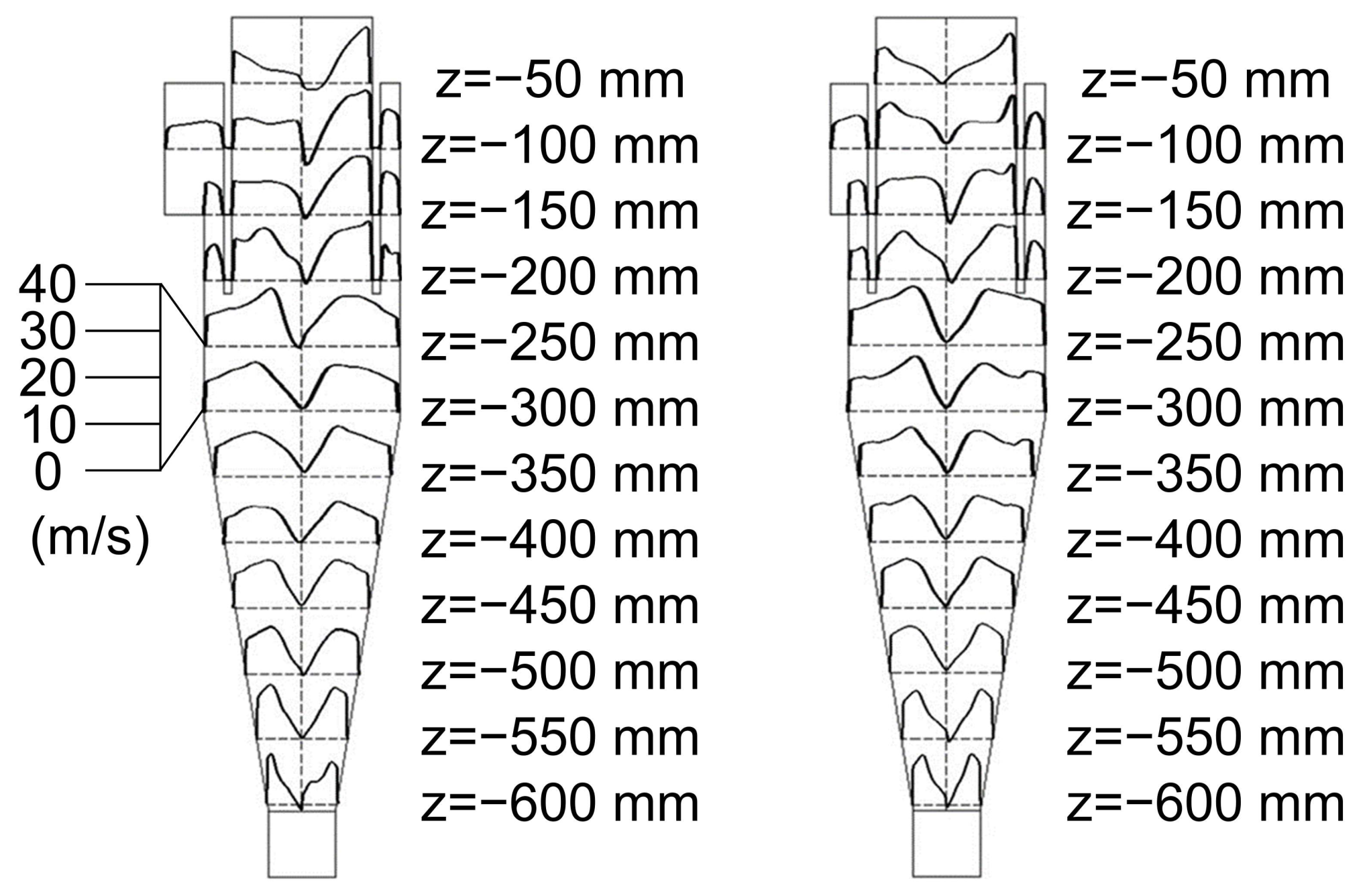
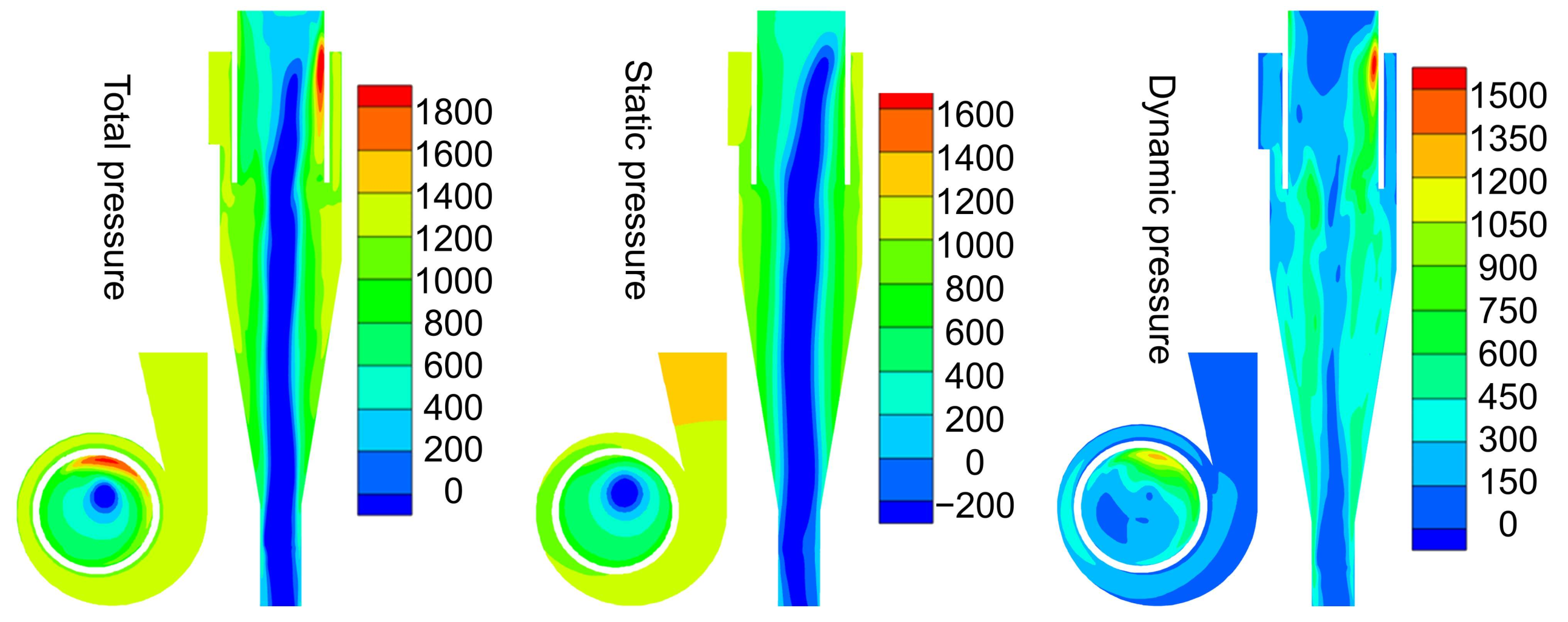
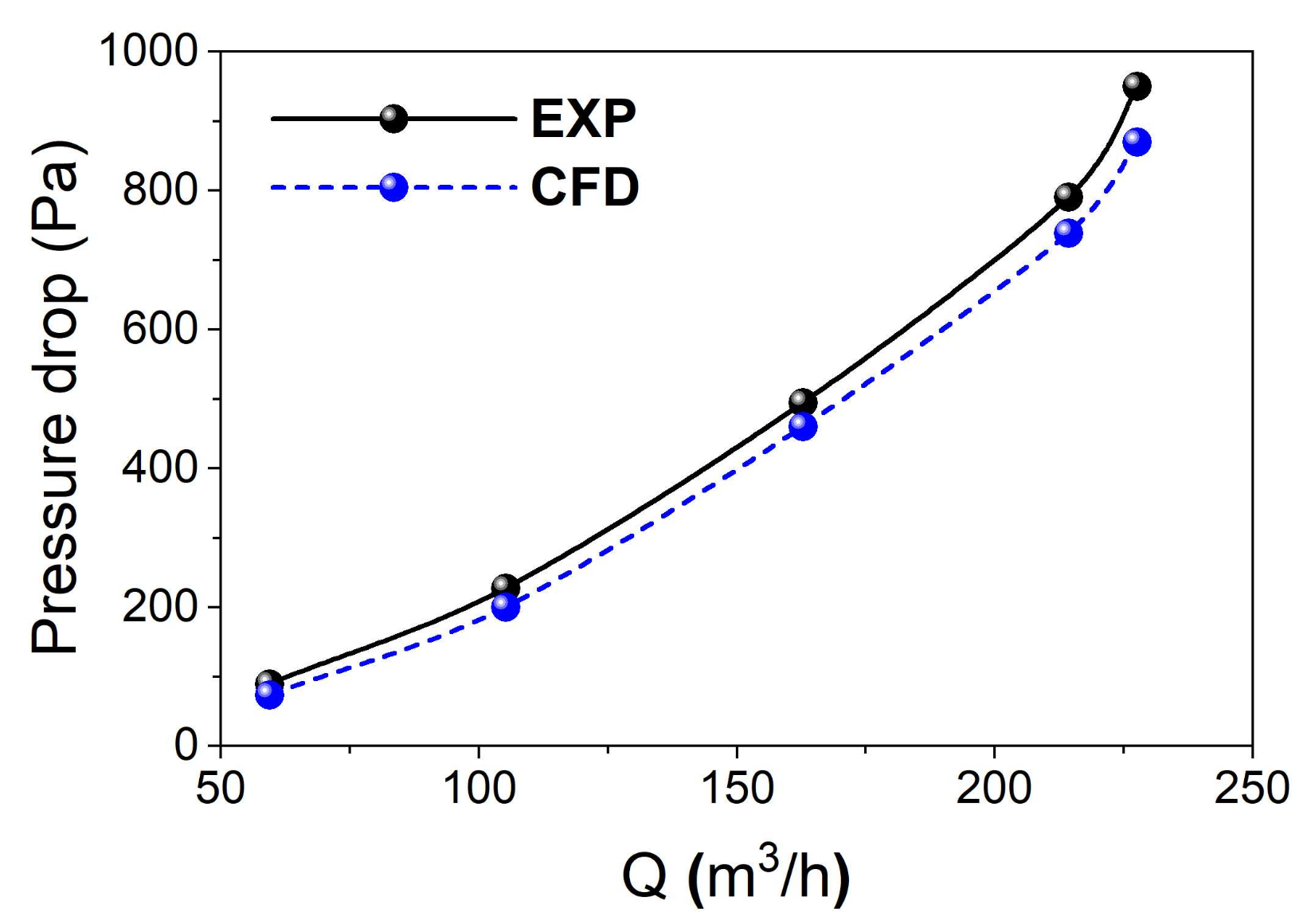
3.1. Numerical Simulation
3.2. The Separation Results of Oily Sludge by Cyclone
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Geometrical Parameters | Symbol | Value |
|---|---|---|
| Inlet diameter | D1 | D1/D1 = 1.0 |
| Cylinder diameter | D2 | D2/D1 = 1.5 |
| Circular cone bottom diameter | D3 | D3/D1 = 0.5 |
| Outlet diameter | D4 | D4/D1 = 1.0 |
| Length of collector | L1 | L1/D1 = 0.5 |
| Length of circular cone | L2 | L2/D1 = 2.8 |
| Length of cylinder | L3 | L3/D1 = 1.9 |
| Instrument | Model | Range | Accuracy | Error |
|---|---|---|---|---|
| Blower | RB-61D-A2 | 0–270 m3 h−1 0–22 kPa | - - | - - |
| Gas flow meter | JY-BS-100 | 0–300 m3 h−1 | 1% | ±3.0 |
| Pressure sensors | GG10-G15 | 0–30 kPa | 0.2% | ±0.06 |
| Temperature sensor | WTZP-EM2B | 0–100 °C | 0.2% | ±0.2 |
| Z (mm) | Δr | r | Δr/r |
|---|---|---|---|
| −50 | 23.42008 | 53.5 | 0.437758 |
| −100 | 11.00691 | 75 | 0.146759 |
| −150 | 9.481034 | 75 | 0.126414 |
| −200 | 7.50733 | 75 | 0.100098 |
| −250 | 5.27731 | 75 | 0.070364 |
| −300 | 1.103676 | 75 | 0.014716 |
| −350 | 1.984943 | 67.5 | 0.029407 |
| −400 | 1.581139 | 59.3 | 0.026663 |
| −450 | 2.300011 | 51 | 0.045098 |
| −500 | 1.868154 | 42.8 | 0.043648 |
| −550 | 2.906888 | 34.5 | 0.084258 |
| −600 | 3.88125 | 26.3 | 0.147576 |
References
- Noh, S.; Heo, J.; Woo, S.; Kim, S.; Ock, M.; Kim, Y.; Yook, S. Performance improvement of a cyclone separator using multiple subsidiary cyclones. Powder Technol. 2018, 338, 145–152. [Google Scholar] [CrossRef]
- Misiulia, D.; Andersson, A.G.; Lundström, T.S. Computational Investigation of an Industrial Cyclone Separator with Helical-Roof Inlet. Chem. Eng. Technol. 2015, 38, 1425–1434. [Google Scholar] [CrossRef]
- Wang, Z.; Sun, G.; Jiao, Y. Experimental study of large-scale single and double inlet cyclone separators with two types of vortex finder. Chem. Eng. Process. Process Intensif. 2020, 158, 108188. [Google Scholar] [CrossRef]
- Elsayed, K. Design of a novel gas cyclone vortex finder using the adjoint method. Sep. Purif. Technol. 2015, 142, 274–286. [Google Scholar] [CrossRef]
- Hoffmann, A.C.; de Jonge, R.; Arends, H.; Hanrats, C. Evidence of the ‘natural vortex length’ and its effect on the separation efficiency of gas cyclones. Filtr. Sep. 1995, 32, 799–804. [Google Scholar] [CrossRef]
- Hoffmann, A.C.; Peng, W.; Dries, H.; Regelink, M.; Foo, K.-K. Effect of Pressure Recovery Vanes on the Performance of a Swirl Tube, with Emphasis on the Flow Pattern and Separation Efficiency. Energy Fuels 2006, 20, 1691–1697. [Google Scholar] [CrossRef]
- Gao, Z.; Wang, J.; Liu, Z.; Wei, Y.; Wang, J.; Mao, Y. Effects of different inlet structures on the flow field of cyclone separators. Powder Technol. 2020, 372, 519–531. [Google Scholar] [CrossRef]
- Ma, L.; Shen, Q.; Li, J.; Zhang, Y.; Wu, J.; Wang, H. Efficient gas-liquid cyclone device for recycled hydrogen in a hydrogenation unit. Chem. Eng. Technol. 2014, 37, 1072–1078. [Google Scholar] [CrossRef]
- Wang, L.; Xie, C.; Wang, Z.; Chen, K. Optimization analysis and Field application of gas-liquid cyclone separator based on CFX. Adv. Mech. Eng. 2022, 14, 1–15. [Google Scholar] [CrossRef]
- Wang, Q.; Chen, J.; Wang, C.; Ji, Y.; Shang, C.; Zhang, M.; Shi, Y.; Ding, G. Design and performance study of a two-stage inline gas-liquid cyclone separator with large range of inlet gas volume fraction. J. Pet. Sci. Eng. 2023, 220, 111218. [Google Scholar] [CrossRef]
- Nakhaei, M.; Lu, B.; Tian, Y.; Wang, W.; Dam-Johansen, K.; Wu, H. CFD modeling of gas–solid cyclone separators at ambient and elevated temperatures. Processes 2020, 8, 228. [Google Scholar] [CrossRef]
- Chu, K.W.; Wang, B.; Yu, A.B.; Vince, A. Particle scale modelling of the multiphase flow in a dense medium cyclone: Effect of vortex finder outlet pressure. Miner. Eng. 2012, 31, 46–58. [Google Scholar] [CrossRef]
- Mazyan, W.I.; Ahmadi, A.; Ahmed, H.; Hoorfar, M. Increasing efficiency of natural gas cyclones through addition of tangential chambers. J. Aerosol Sci. 2017, 110, 36–42. [Google Scholar] [CrossRef]
- Ko, M.S.; Chen, Y.L.; Wei, P.S. Recycling of municipal solid waste incinerator fly ash by using hydrocyclone separation. Waste Manag 2013, 33, 615–620. [Google Scholar] [CrossRef]
- Vieira, L.G.M.; Damasceno, J.J.R.; Barrozo, M.A.S. Improvement of hydrocyclone separation performance by incorporating a conical filtering wall. Chem. Eng. Process. Process Intensif. 2010, 49, 460–467. [Google Scholar] [CrossRef]
- Senfter, T.; Neuner, T.; Bachmann, C.; Berger, M.; Mayerl, C.; Kofler, T.; Kraxner, M.; Pillei, M. An Empirical Study on the Upcycling of Glass Bottles into Hydrocyclone Separators. Separations 2024, 11, 230. [Google Scholar] [CrossRef]
- Qian, P.; Ma, J.; Liu, Y.; Yang, X.; Zhang, Y.; Wang, H. Concentration distribution of droplets in a liquid-liquid hydrocyclone and its application. Chem. Eng. Technol. 2016, 39, 953–959. [Google Scholar] [CrossRef]
- Nascimento, M.R.M.; Bicalho, I.C.; Mognon, J.L.; Ataíde, C.H.; Duarte, C.R. Performance of a new geometry of deoiling hydrocyclones: Experiments and numerical simulations. Chem. Eng. Technol. 2013, 36, 98–108. [Google Scholar] [CrossRef]
- Elsayed, K.; Lacor, C. Optimization of the cyclone separator geometry for minimum pressure drop using mathematical models and CFD simulations. Chem. Eng. Sci. 2010, 65, 6048–6058. [Google Scholar] [CrossRef]
- Elsayed, K. Optimization of the cyclone separator geometry for minimum pressure drop using Co-Kriging. Powder Technol. 2015, 269, 409–424. [Google Scholar] [CrossRef]
- Chen, J.; Yang, B.; Jiang, Z.A.; Wang, Y. Effect of external cyclone diameter on performance of a two-stage cyclone separator. ACS Omega 2019, 4, 13603–13616. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Li, J.-P.; Zhang, Y.-H.; Wang, H.-L. High-speed particle rotation for coating oil removal by hydrocyclone. Sep. Purif. Technol. 2017, 177, 263–271. [Google Scholar] [CrossRef]
- Wang, H.; Fu, P.; Li, J.; Huang, Y.; Zhao, Y.; Jiang, L.; Fang, X.; Yang, T.; Huang, Z.; Huang, C. Separation-and-Recovery Technology for Organic Waste Liquid with a High Concentration of Inorganic Particles. Engineering 2018, 4, 406–415. [Google Scholar] [CrossRef]
- Xiong, Z.; Wang, Y.; Gu, X.; Yang, Y.; Shang, J. A Study on the Erosion Mechanism of an Axial Cyclone Separator for Gas Purification. Separations 2022, 9, 409. [Google Scholar] [CrossRef]
- Kang, I.; Seo, W.; Im, S.; Kim, K. Cyclone Shapes for Sand and Microplastic Separation: Efficiency and Reynolds Number Relationships. Separations 2024, 11, 222. [Google Scholar] [CrossRef]
- Hoekstra, A.J.; Derksen, J.J.; Van Den Akker, H.E.A. An experimental and numerical study of turbulent swirling flow in gas cyclones. Chem. Eng. Sci. 1999, 54, 2055–2065. [Google Scholar] [CrossRef]
- Wasilewski, M.; Brar, L.S. Effect of the inlet duct angle on the performance of cyclone separators. Sep. Purif. Technol. 2019, 213, 19–33. [Google Scholar] [CrossRef]
- Wasilewski, M. Analysis of the effects of temperature and the share of solid and gas phases on the process of separation in a cyclone suspension preheater. Sep. Purif. Technol. 2016, 168, 114–123. [Google Scholar] [CrossRef]
- Wasilewski, M.; Duda, J. Multicriteria optimisation of first-stage cyclones in the clinker burning system by means of numerical modelling and experimental research. Powder Technol. 2016, 289, 143–158. [Google Scholar] [CrossRef]
- Morsi, S.A.; Alexander, A.J. An investigation of particle trajectories in two-phase flow systems. J. Fluid Mech. 1972, 55, 193–208. [Google Scholar] [CrossRef]
- Haider, A.; Levenspiel, O. Drag coefficient and terminal velocity of spherical and nonspherical particles. Powder Technol. 1989, 58, 63–70. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, R.; Zheng, W.; Shi, B. Tuning the Inlet Flow Pattern of Cyclones for Boosted Particle Rotation Behaviors with High Purification Performances of Oily Sludge. Separations 2025, 12, 31. https://doi.org/10.3390/separations12020031
Ye R, Zheng W, Shi B. Tuning the Inlet Flow Pattern of Cyclones for Boosted Particle Rotation Behaviors with High Purification Performances of Oily Sludge. Separations. 2025; 12(2):31. https://doi.org/10.3390/separations12020031
Chicago/Turabian StyleYe, Rui, Wan Zheng, and Bi Shi. 2025. "Tuning the Inlet Flow Pattern of Cyclones for Boosted Particle Rotation Behaviors with High Purification Performances of Oily Sludge" Separations 12, no. 2: 31. https://doi.org/10.3390/separations12020031
APA StyleYe, R., Zheng, W., & Shi, B. (2025). Tuning the Inlet Flow Pattern of Cyclones for Boosted Particle Rotation Behaviors with High Purification Performances of Oily Sludge. Separations, 12(2), 31. https://doi.org/10.3390/separations12020031






