Maximal Product of Graphs under Vague Environment

Abstract

Graph models are found everywhere in natural and human made structures, including process dynamics in physical, biological and social systems. The product of graphs are appropriately used in several combinatorial applications and in the formation of different structural models. In this paper, we present a new product of graphs, namely, maximal product of two vague graphs. Then we describe certain concepts, including strongly, completely, regularity and connectedness on a maximal product of vague graphs. Further, we consider some results of edge regular and totally edge regular in a maximal product of vague graphs. Finally, we present an application for optimization of the biomass based on a maximal product of vague graphs.

1. Introduction

In the real world, there are data values that are uncertainly specified in many applications, for instance sensor information. The fuzzy set theory [1] has been introduced to handle this vagueness by extending the concept of belonging to a set. In a fuzzy set, each element is essentially associated with a point value selected in the range of units [0, 1], indicated as the quality of belonging membership grade of the set. Klement and Mesiar [2] reviewed some generalizations of fuzzy sets with two- or three-dimensional lattices of truth values and study their relationship. A vague set introduced by Gau and Buehrer [3] is a further extension of a fuzzy set. Instead of using point-based membership as in fuzzy set, interval-based membership is used in a vague set and to describe the boundaries of the membership degree, a true-membership function and a false membership function are used. Belonging to intervals in vague sets is more expressive to capture data inaccuracy. In literature, the notions of intuitionistic fuzzy set and vague set are considered isomorphic. Deng et al. [4] presented the distance between vague sets with applications in decision making. Wang [5] developed vague parameterized vague soft sets and provide its applications in decision-making.

A graph is a useful tool for describing decision problems in a diagram format. Using this tool, decision objects and their relationship are represented by vertices and edges, respectively. Rosenfeld [6] introduced the fuzzy graphs by providing a fuzzy analogue of several basic graph-theoretic concepts. Ramakrishna [7] originally developed the concept of vague graphs and discussed their prominent characteristics. The vague models are more and more flexible, and practical as compared to the crisp and fuzzy models. The notion of vague hypergraphs was defined by Akram et al. [8]. Later, Akram et al. introduced many new concepts under vague environment, such as Cayley vague graphs [9], types of vague cycles and vague trees [10], regularity in vague intersection graphs and vague line graphs [11], and certain types of vague graphs [12] and so forth. Borzooei and Rashmanlou [13,14] investigated domination in vague graphs and degree of vertices in vague graphs. Nowadays, extended fuzzy graph theory is a hot research area. Recently, many researchers discussed the graph theoretical concepts in generalized fuzzy environment, such as Pythagorean fuzzy graphs (PFG) [15], complex Pythagorean fuzzy graphs [16], rough fuzzy graphs [17] and q-rung orthopair fuzzy graphs [18] along with its decision making applications.

Product operations on graphs play a very important role in graph theory. Many scholars discussed product operations on various generalized fuzzy graphs. Mordeson and Peng [19] defined some of these product operations on fuzzy graphs. Subsequently, utilizing these operations, the degree of the vertices is obtained from two fuzzy graphs in Reference [20]. Gong and Wang [21] have defined some operations on the product fuzzy hypergraphs. Sahoo and Pal [22] presented some operations on intuitionistic fuzzy graph (IFG) products and calculated the vertex degree in the IFGs. Rashmanlou et al. [23] proposed product operations over a range of values fuzzy graphs, that is, interval-valued fuzzy graphs and discussed the degree of a vertex in fuzzy graphs with interval values. Recently, Naz et al. [15] studied some of the PFG operations, the vertex degree and the vertex total degree in the PFG. However, the maximal operations on products with vague graphs were not sought. Therefore, in this paper, we will focus on this topic. We present new product of graphs, namely, maximal product of two vague graphs. Then we describe certain concepts, including strongly, completely, regularity and connectedness on maximal product of vague graphs. Fuhrer, we consider some results of edge regular and totally edge regular in maximal product of vague graphs. Finally, we present an application for optimization of the biomass based on maximal product of vague graphs.

2. Maximal Products of Vague Graphs

In this section we introduce the concept of maximal product of two vague graphs. Then we get some results on strong and complete maximal product of two vague graphs.

Definition 1

([3]). A vague set A is a pair $(t_A,f_A)$, where $t_A$ and $f_A$ are fuzzy sets on finite non-empty set X and we called them by true and false membership functions, respectively, such that for all $x\in X$, $(t_A\left(x\right)+f_A\left(x\right))\in [0,1]$.

Definition 2

([7]). Let X and Y be ordinary finite non-empty sets. We call a vague relation to be a vague subset of $X\times Y$, that is, an expression R defined by:

$$R=\{<(x,y),t_R(x,y),f_R(x,y)>|x\in X,y\in Y\},$$

where $t_R:X\times Y⟶[0,1]$, $f_R:X\times Y⟶[0,1]$, which satisfies the condition $0\le t_R(x,y)+f_R(x,y)\le 1$, for all $(x,y)\in X\times Y$.

Definition 3

([7]). A vague graph on a non-empty set V is a pair $G=(A,B)$, where $A=(t_A,f_A)$ is a vague set on V and $B=(t_B,f_B)$ is a vague relation on V such that

$$\begin{array}{c}\hfill t_B(x,y)\le min(t_A\left(x\right),t_A\left(y\right)),f_B(x,y)\ge max(f_A\left(x\right),f_A\left(y\right))\end{array}$$

(1)

for all x, $y\in V.$ Note that B is called vague relation on A.

Definition 4

([7]). Let $G^{*}=(V,E)$ be a simple graph and $G=(A,B)$ be a vague graph on $G^{*}$. Then a vague graph G is called:

• Strong if for every edge$(x,y)\in E$,

  $$\begin{array}{c}\hfill t_B(x,y)=t_A\left(x\right)\wedge t_A\left(y\right),f_B(x,y)=f_A\left(x\right)\vee f_A\left(y\right)\end{array}$$

  (2)
• Complete vague graph, if for every$x,y\in V$,

  $$\begin{array}{c}\hfill t_B(x,y)=t_A\left(x\right)\wedge t_A\left(y\right),f_B(x,y)=f_A\left(x\right)\vee f_A\left(y\right)\end{array}$$

  (3)

Definition 5.

Let$G_1=(A_1,B_1)$and$G_2=(A_2,B_2)$be two vague graphs on simple graphs$G_1^{*}=(V_1,E_1)$and$G_2^{*}=(V_2,E_2)$, respectively. Define$G^{*}=(V,E)$, where$V=V_1\times V_2$and

$$E=\left\{((x_1,y_1),(x_2,y_2))\right|x_1=x_2,(y_1,y_2)\in E_2\}\cup \left\{((x_1,y_1),(x_2,y_2))\right|y_1=y_2,(x_1,x_2)\in E_1\}$$

and we define vague graph$G=(A,B)$on$G^{*}$, for all$(x_1,y_1)\in V_1\times V_2$by

$$\begin{array}{c}\hfill t_A(x_1,y_1)=t_{A_1}\left(x_1\right)\vee t_{A_2}\left(y_1\right),f_A(x_1,y_1)=f_{A_1}\left(x_1\right)\wedge f_{A_2}\left(y_1\right)\end{array}$$

(4)

and for all$((x_1,y_1),(x_2,y_2))\in E_1\times E_2$by

$$\begin{array}{c}{t}_B((x_1,y_1),(x_2,y_2))=\left\{\begin{array}{cc}{t}_{A_1}\left(x_1\right)\vee t_{B_2}(y_1,y_2),\hfill & if{x}_1=x_2,(y_1,y_2)\in E_2\hfill \\ t_{B_1}(x_1,x_2)\vee t_{A_2}\left(y_1\right),\hfill & if{y}_1=y_2,(x_1,x_2)\in E_1\hfill \end{array}\right.\end{array}$$

(5)

$$\begin{array}{c}{f}_B((x_1,y_1),(x_2,y_2))=\left\{\begin{array}{cc}{f}_{A_1}\left(x_1\right)\wedge f_{B_2}(y_1,y_2),\hfill & if{x}_1=x_2,(y_1,y_2)\in E_2\hfill \\ f_{B_1}(x_1,x_2)\wedge f_{A_2}\left(y_1\right),\hfill & if{y}_1=y_2,(x_1,x_2)\in E_1.\hfill \end{array}\right.\end{array}$$

(6)

Then$G=(A,B)$is called the maximal product of two vague graphs$G_1$and$G_2$and denoted by$G=G_1{\ast }_M{G}_2$,$A=A_1{\ast }_M{A}_2$and$B=B_1{\ast }_M{B}_2$.

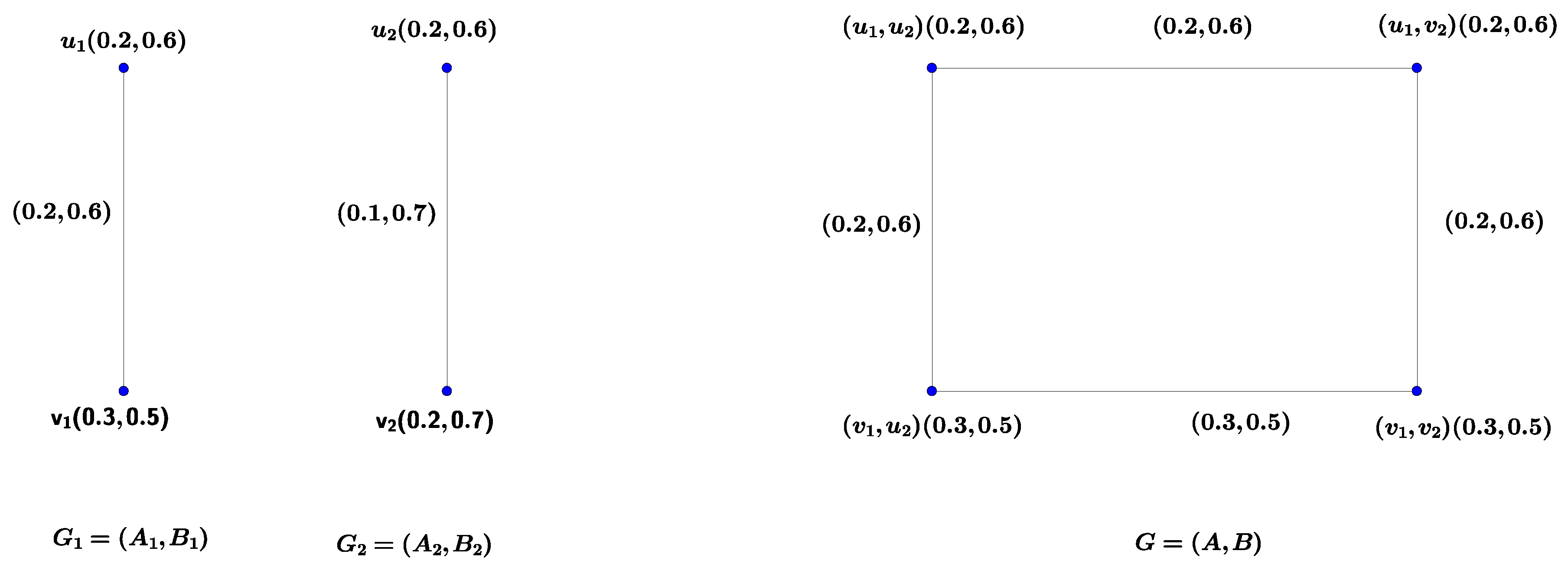
Example 1.

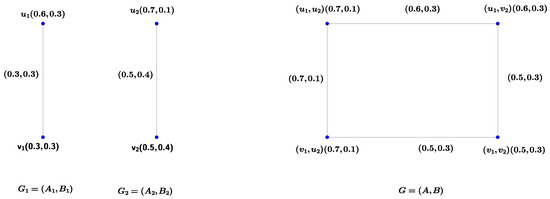
Consider the vague graphs$G_1$and$G_2$as in Figure 1. In the right side of following figures, we can see that the maximal product of two vague graphs$G_1$and$G_2$, that is$G=G_1{\ast }_M{G}_2$.

Figure 1. Vague graphs $G_1$, $G_2$ and G.

Proposition 1.

Maximal product of two vague graphs$G_1$and$G_2$, is a vague graph.

Proof. 

Let $G_1=(A_1,B_1)$ and $G_2=(A_2,B_2)$ be two vague graphs on simple graphs $G_1^{\ast }=(V_1,E_1)$ and $G_2^{\ast }=(V_2,E_2)$, respectively. Then by Definition 5, we have two cases:

Case (i): If $x_1=x_2$ and $(y_1,y_2)\in E_2$, then we have

$$\begin{array}{ccc}\hfill t_B((x_1,y_1),(x_2,y_2))& =& t_{A_1}\left(x_1\right)\vee t_{B_2}(y_1,y_2)\hfill \\ & \le & t_{A_1}\left(x_1\right)\vee (t_{A_2}\left(y_1\right)\wedge t_{A_2}\left(y_2\right))\hfill \\ & =& (t_{A_1}\left(x_1\right)\vee t_{A_2}\left(y_1\right))\wedge (t_{A_1}\left(x_1\right)\vee t_{A_2}\left(y_2\right))\hfill \\ & =& t_A(x_1,y_1)\wedge t_A(x_2,y_2),\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill f_B((x_1,y_1),(x_2,y_2))& =& f_{A_1}\left(x_1\right)\wedge f_{B_2}(y_1,y_2)\hfill \\ & \ge & f_{A_1}\left(x_1\right)\wedge (f_{A_2}\left(y_1\right)\vee f_{A_2}\left(y_2\right))\hfill \\ & =& (f_{A_1}\left(x_1\right)\wedge f_{A_2}\left(y_1\right))\vee (f_{A_1}\left(x_1\right)\wedge f_{A_2}\left(y_2\right))\hfill \\ & =& f_A(x_1,y_1)\vee f_A(x_1,y_2)\hfill \\ & =& f_A(x_1,y_1)\vee f_A(x_2,y_2).\hfill \end{array}$$

Hence in this case we have

$$t_B((x_1,y_1),(x_2,y_2))\le t_A(x_1,y_1)\wedge t_A(x_2,y_2)$$

$$f_B((x_1,y_1),(x_2,y_2))\ge f_A(x_1,y_1)\vee f_A(x_2,y_2).$$

Case (ii): The proof is similar to the proof of case (i), by the some modification.

Therefore, $G=(A,B)$ is a vague graph. □

Theorem 1.

The maximal product of two strong vague graphs is a strong vague graphs.

Proof. 

Let $G_1=(A_1,B_1)$ and $G_2=(A_2,B_2)$ be two strong vague graphs on simple graphs $G_1^{\ast }=(V_1,E_1)$ and $G_2^{\ast }=(V_2,E_2)$, respectively, and $G=(A,B)$ be the maximal product of $G_1$ and $G_2$. Then by Proposition 1, G is a vague graph. Now we have two cases:

Case (i): If $x_1=x_2$ and $(y_1,y_2)\in E_2$, then we have

$$\begin{array}{ccc}\hfill t_B((x_1,y_1),(x_2,y_2))& =& t_{A_1}\left(x_1\right)\vee t_{B_2}(y_1,y_2)\hfill \\ & =& t_{A_1}\left(x_1\right)\vee (t_{A_2}\left(y_1\right)\wedge t_{A_2}\left(y_2\right))\hfill \\ & =& (t_{A_1}\left(x_1\right)\vee t_{A_2}\left(y_1\right))\wedge (t_{A_1}\left(x_1\right)\vee t_{A_2}\left(y_2\right))\hfill \\ & =& t_A(x_1,y_1)\wedge t_A(x_2,y_2)\hfill \end{array}$$

by the similar way $f_B((x_1,y_1),(x_2,y_2))=f_A(x_1,y_1)\vee f_A(x_2,y_2)$.

Case (ii): The proof is similar to the proof of case (i), by some modifications.

Thus for all edge in the maximal product $G=(A,B)$, we have

$$t_B((x_1,y_1),(x_2,y_2))=t_A(x_1,y_1)\wedge t_A(x_2,y_2)$$

and

$$f_B((x_1,y_1),(x_2,y_2))=f_A(x_1,y_1)\vee f_A(x_2,y_2).$$

Hence G is a strong vague graph. □

Remark 1.

If maximal product of two vague graphs$G_1$and$G_2$is a strong vague graph, then$G_1$and$G_2$need not to be strong vague graphs, in general.

Example 2.

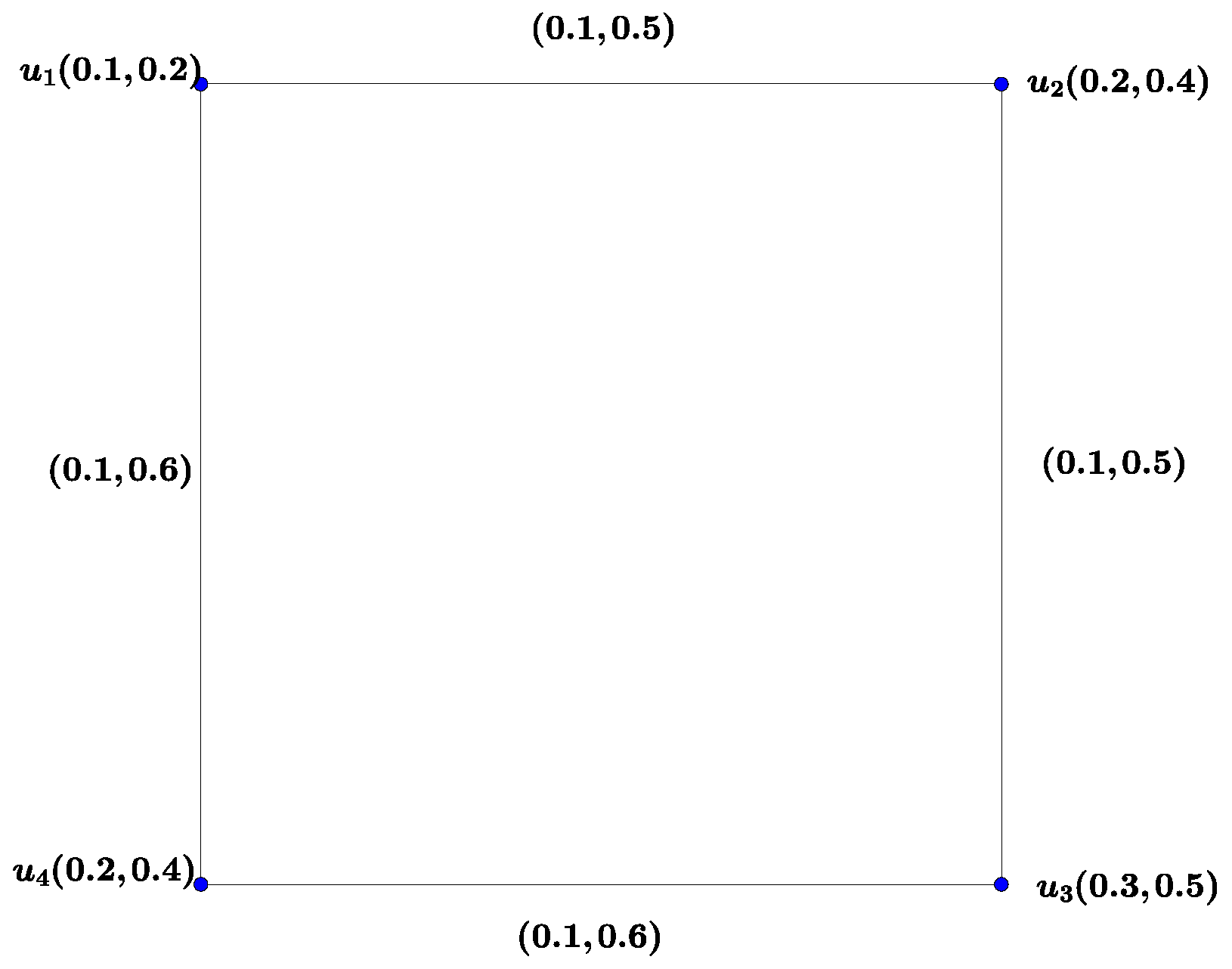
Consider the vague graphs$G_1$,$G_2$and$G=G_1{\ast }_M{G}_2$, by the Figure 2.

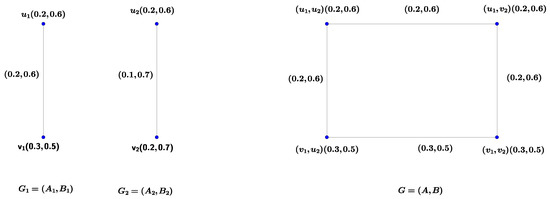
Figure 2. Vague graphs $G_1$, $G_2$ and G.

Then$G_1$and G are strong vague graphs, but$G_2$is not a strong vague graph. Since,$t_{B_2}(u_2,v_2)=0.1$, but$t_{A_2}\left(u_2\right)\wedge t_{A_2}\left(v_2\right)=0.2\wedge 0.2=0.2$. Hence$t_{B_2}(u_2,v_2)\ne t_{A_2}\left(u_2\right)\wedge t_{A_2}\left(v_2\right)$.

Theorem 2.

The maximal product of two connected vague graphs is a connected vague graph.

Proof. 

Let $G_1=(A_1,B_1)$ and $G_2=(A_2,B_2)$ be two connected vague graphs on simple graphs $G_1^{\ast }=(V_1,E_1)$ and $G_2^{\ast }=(V_2,E_2)$, respectively, where $V_1=\{x_1,x_2,\dots ,x_k\}$ and $V_2=\{y_1,y_2,\dots ,y_s\}$. Then $t_{B_1}^{\infty }(x_i,x_j)>0$, for all $x_i,x_j\in V_1$ and $t_{B_2}^{\infty }(y_i,y_j)>0$, for all $y_i,y_j\in V_2$ (or $f_{B_1}^{\infty }(x_i,x_j)<1$, for all $x_i,x_j\in V_1$ and $f_{B_2}^{\infty }(y_i,y_j)<1$, for all $y_i,y_j\in V_2$). The maximal product of $G_1=(A_1,B_1)$ and $G_2=(A_2,B_2)$ can be taken as $G=(A,B)$. Now consider the ${}^{\prime }{k}^{\prime }$ subgraphs of G with the vertex sets $\{(x_i,y_1),(x_i,y_2),\dots ,(x_i,y_s)\}$, for $i=1,2,\dots ,k$. Each of these subgraphs of G is connected, since the $x_i$’s are the same and since $G_2$ is connected, each $y_i$ is adjacent to at least one of the vertices in $V_2$. Also since $G_1$ is connected, each $x_i$ is adjacent to at least one of the vertices in $V_1$. Hence there exists at least one edge between any pair of the above ${}^{\prime }{k}^{\prime }$ subgraphs. Thus we have $t_B^{\infty }((x_i,y_j),\left(x_m{y}_n\right))>0$ (or $f_B^{\infty }((x_i,y_j),\left(x_m{y}_n\right))<1$), for all $((x_i,y_j),\left(x_m{y}_n\right))\in E$. Hence, G is a connected vague graph. □

Remark 2.

Maximal product of two complete vague graphs is not a complete vague graphs, in general. Because we do not include the case$(x_1,x_2)\in E_1$and$(y_1,y_2)\in E_2$in the definition of the maximal product of vague graphs. Since every complete vague graph is strong, we have the maximal product of two complete vague graph is a strong vague graph.

Definition 6.

Let$G_1=(A_1,B_1)$and$G_2=(A_2,B_2)$be two vague graphs on simple graphs$G_1^{\ast }=(V_1,E_1)$and$G_2^{\ast }=(V_2,E_2)$, respectively, where$x_i,x_k\in V_1$and$y_j,y_l\in V_2$,$i,k,j,l=1,2,\dots ,n$. The degree of any vertex in the maximal product of the vague graphs$G_1=(A_1,B_1)$and$G_2=(A_2,B_2)$is defined by,$d_{G_1{\ast }_M{G}_2}(x_i,y_j)=(k_1,k_2)$, where

$$\begin{array}{c}\hfill {\displaystyle k_1=\sum _{x_i=x_k,(y_j,y_l)\in E_2}{t}_{A_1}\left(x_i\right)\vee t_{B_2}(y_j,y_l)+\sum _{(x_i,x_k)\in E_1,y_j=y_l}{t}_{B_1}(x_i,x_k)\vee t_{A_2}\left(y_j\right)}\end{array}$$

(7)

$$\begin{array}{c}\hfill {\displaystyle k_2=\sum _{x_i=x_k,(y_j,y_l)\in E_2}{f}_{A_1}\left(x_i\right)\wedge f_{B_2}(y_j,y_l)+\sum _{(x_i,x_k)\in E_1,y_j=y_l}{f}_{B_1}(x_i,x_k)\wedge f_{A_2}\left(y_j\right).}\end{array}$$

(8)

Example 3.

Consider the vague graphs in Example 2. Then

$$\begin{array}{c}{d}_{G_1{\ast }_M{G}_2}(u_1,u_2)=(0.2+0.2,0.6+0.6)=(0.4,1.2),\hfill \\ d_{G_1{\ast }_M{G}_2}(v_1,u_2)=(0.3+0.2,0.5+0.6)=(0.5,1.1),\hfill \\ d_{G_1{\ast }_M{G}_2}(v_1,v_2)=(0.2+0.3,0.6+0.5)=(0.5,1.1),\hfill \\ d_{G_1{\ast }_M{G}_2}(u_1,v_2)=(0.2+0.2,0.6+0.6)=(0.4,1.2).\hfill \end{array}$$

Definition 7.

Let$G_1=(A_1,B_1)$and$G_2=(A_2,B_2)$be two vague graphs on simple graphs$G_1^{\ast }=(V_1,E_1)$and$G_2^{\ast }=(V_2,E_2)$, respectively. Then, the maximal product of$G_1$and$G_2$, that is$G=G_1{\ast }_M{G}_2$, is called$(k_1,k_2)$-regular if$d_{G_1{\ast }_M{G}_2}(u,v)=(k_1,k_2)$, for all$(u,v)\in V_1\times V_2$. In this case, G is called regular vague graph (of degree$(k_1,k_2)$).

Example 4.

Consider two vague graphs$G_1$and$G_2$and maximal product vague graph$G=G_1{\ast }_M{G}_2$as in Figure 3.

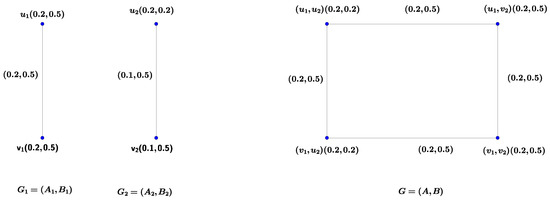
Figure 3. Vague graphs $G_1$, $G_2$ and G.

Hence$G=G_1{\ast }_M{G}_2$is a regular vague graph of degree$(0.4,1)$.

Note. If $G_1$ and $G_2$ are two regular vague graphs, then the maximal product of $G_1$ and $G_2$ is not a regular vague graph, in general.

Example 5.

Consider regular vague graphs$G_1$and$G_2$and maximal product vague graph$G=G_1{\ast }_M{G}_2$as in Figure 4.

Figure 4. Vague graphs $G_1$, $G_2$ and G.

Since$d_{G_1{\ast }_M{G}_2}(u_1,u_2)=(0.2+0.3,0.5+0.4)=(0.5,0.9)$, but$d_{G_1{\ast }_M{G}_2}(v_1,v_2)=(0.2+0.2,0.4+0.5)=(0.4,0.9)$. Then$G_1{\ast }_M{G}_2$is not regular.

Definition 8.

Let$G=(A,B)$be a vague graph on simple graph$G^{\ast }=(V,E)$. If$G^{\ast }$is a regular graph, then G is said to be partially regular vague graph. If G is both regular and partially regular vague graph, then G is said to be a full regular vague graph.

Example 6.

Consider the vague graphs$G_1$,$G_2$and$G=G_1{\ast }_M{G}_2$as Example 4. Since$G^{\ast }$is a regular graph, so G is a partially regular vague graph. Hence G is a full regular vague graph.

Definition 9.

Let G be the maximal product of two vague graphs$G_1$and$G_2$. Then the degree of an edge$(x_i,x_j)\in E$is defined as

$$\begin{array}{c}\hfill d_{G_1{\ast }_M{G}_2}(x_i,x_j)=(d_t(x_i,x_j),d_f(x_i,x_j))=(l_1,l_2)\end{array}$$

(9)

where

$$\begin{array}{c}\hfill {\displaystyle l_1=\sum _{(x_i,x_k)\in E,k\ne j}{t}_B(x_i,x_k)+\sum _{(x_k,x_j)\in E,k\ne i}{t}_B(x_k,x_j)}\end{array}$$

(10)

$$\begin{array}{c}\hfill {\displaystyle l_2=\sum _{(x_i,x_k)\in E,k\ne j}{f}_B(x_i,x_k)+\sum _{(x_k,x_j)\in E,k\ne i}{f}_B(x_k,x_j).}\end{array}$$

(11)

Moreover, the total degree of an edge$(x_i,x_j)\in E$is defined as

$$\begin{array}{c}\hfill t{d}_{G_1{\ast }_M{G}_2}(x_i,x_j)=(t{d}_t(x_i,x_j),t{d}_f(x_i,x_j))=(t_1,t_2)\end{array}$$

(12)

where

$$\begin{array}{c}\hfill {\displaystyle t_1=\sum _{(x_i,x_k)\in E,k\ne j}{t}_B(x_i,x_k)+\sum _{(x_k,x_j)\in E,k\ne i}{t}_B(x_k,x_j)+t_B(x_i,x_j)}\end{array}$$

(13)

$$\begin{array}{c}\hfill {\displaystyle t_2=\sum _{(x_i,x_k)\in E,k\ne j}{f}_B(x_i,x_k)+\sum _{(x_k,x_j)\in E,k\ne i}{f}_B\left(x_k{x}_j\right)+f_B(x_i,x_j).}\end{array}$$

(14)

Example 7.

Consider the vague graphs$G_1$,$G_2$and the maximal product$G_1{\ast }_M{G}_2=(A,B)$in Example 5. Then

$$\begin{array}{ccc}\hfill d_{G_1{\ast }_M{G}_2}\left((u_1,u_2),(u_1,v_2)\right)& =& (d_t\left((u_1,u_2),(u_1,v_2)\right),d_f\left((u_1,u_2),(u_1,v_2)\right))\hfill \\ & =& (0.3+0.2,0.4+0.5)=(0.5,0.9),\hfill \end{array}$$

$$\begin{array}{ccc}\hfill d_{G_1{\ast }_M{G}_2}\left((u_1,u_2),(v_1,u_2)\right)& =& (d_t\left((u_1,u_2),(v_1,u_2)\right),d_f\left((u_1,u_2),(v_1,u_2)\right))\hfill \\ & =& (0.2+0.2,0.5+0.4)=(0.4,0.9),\hfill \end{array}$$

$$\begin{array}{ccc}\hfill d_{G_1{\ast }_M{G}_2}\left((u_1,v_2),(v_1,v_2)\right)& =& (d_t\left((u_1,v_2),(v_1,v_2)\right),d_f\left((u_1,v_2),(v_1,v_2)\right))\hfill \\ & =& (0.2+0.2,0.5+0.4)=(0.4,0.9),\hfill \end{array}$$

$$\begin{array}{ccc}\hfill d_{G_1{\ast }_M{G}_2}\left((v_1,v_2),(v_1,u_2)\right)& =& (d_t\left((v_1,v_2),(v_1,u_2)\right),d_f\left((v_1,v_2),(v_1,u_2)\right))\hfill \\ & =& (0.2+0.3,0.5+0.4)=(0.5,0.9),\hfill \end{array}$$

$$\begin{array}{ccc}\hfill t{d}_{G_1{\ast }_M{G}_2}\left((u_1,u_2),(u_1,v_2)\right)& =& (t{d}_t\left((u_1,u_2),(u_1,v_2)\right),t{d}_f\left((u_1,u_2),(u_1,v_2)\right))\hfill \\ & =& (0.5+0.2,0.9+0.5)=(0.7,1.4),\hfill \end{array}$$

$$\begin{array}{ccc}\hfill t{d}_{G_1{\ast }_M{G}_2}\left((u_1,u_2),(v_1,u_2)\right)& =& (t{d}_t\left((u_1,u_2),(v_1,u_2)\right),t{d}_f\left((u_1,u_2),(v_1,u_2)\right))\hfill \\ & =& (0.4+0.3,0.9+0.4)=(0.7,1.3),\hfill \end{array}$$

$$\begin{array}{ccc}\hfill t{d}_{G_1{\ast }_M{G}_2}\left((u_1,v_2),(v_1,v_2)\right)& =& (t{d}_t\left((u_1,v_2),(v_1,v_2)\right),t{d}_f\left((u_1,v_2),(v_1,v_2)\right))\hfill \\ & =& (0.4+0.2,0.9+0.5)=(0.6,1.4),\hfill \end{array}$$

$$\begin{array}{ccc}\hfill t{d}_{G_1{\ast }_M{G}_2}\left((v_1,v_2),(v_1,u_2)\right)& =& (t{d}_t\left((v_1,v_2),(v_1,u_2)\right),t{d}_f\left((v_1,v_2),(v_1,u_2)\right))\hfill \\ & =& (0.5+0.2,0.9+0.4)=(0.7,1.3).\hfill \end{array}$$

Theorem 3.

Let$G_1$and$G_2$be two vague graphs and$G^{\ast }=(V,E)$be the finite underlying crisp graph of$G=G_1{\ast }_M{G}_2$, which is a cycle. Then the summation of degree of all vertices in$G_1{\ast }_M{G}_2$is equal to the summation of degree of all edges in$G_1{\ast }_M{G}_2$, that is:

$$\begin{array}{c}\hfill {\displaystyle \sum _{(x_i,y_j)\in V}{d}_{G_1{\ast }_M{G}_2}(x_i,y_j)=\sum _{((x_i,y_j),(x_i^{\prime },y_j^{\prime }))\in E}{d}_{G_1{\ast }_M{G}_2}((x_i,y_j),(x_i^{\prime },y_j^{\prime })),}\end{array}$$

(15)

where$1\le i\le j\le n$.

Proof. 

Let $G=G_1{\ast }_M{G}_2=(A,B)$ be a vague graph and $G^{\ast }$ be the simple graph of G which is a cycle, that is $G^{\ast }:h_{11}{h}_{12}{h}_{13}\dots h_{1j}\dots h_{ij}\dots h_{i1}{h}_{11}$ for all $h_{ij}:=(x_i,y_j)\in V$, where $i\le j\le n$. Then

$${\displaystyle \sum _{i,j=1}^n{d}_{G_1{\ast }_M{G}_2}((x_i,y_j),(x_i^{\prime },y_j^{\prime }))=(\sum _{i,j=1}^n{d}_t((x_i,y_j),(x_i^{\prime },y_j^{\prime })),\sum _{i,j=1}^n{d}_f((x_i,y_j),(x_i^{\prime },y_j^{\prime })))=(l_1,l_2).}$$

Now we have

$$\begin{array}{ccc}\hfill l_1& =& {\displaystyle \sum _{i,j=1}^n{d}_t((x_i,y_j),(x_i^{\prime },y_j^{\prime }))}\hfill \\ & =& d_t((x_1,y_1),(x_1,y_2))+d_t((x_1,y_2),(x_1,y_3))+\dots +d_t((x_1,y_{n-1}),(x_1{y}_n))\hfill \\ & & +d_t((x_1,y_n)(x_n,y_n))+d_t((x_n,y_n)(x_{n-1},y_n))+\dots +d_t((x_1,y_n)(x_1,y_1))\hfill \\ & =& d_t(x_1,y_1)+d_t(x_1,y_2)-2t_B((x_1,y_1),(x_1,y_2))+d_t(x_1,y_2)+d_t(x_1,y_3)\hfill \\ & & -2t_B((x_1,y_2),(x_1,y_3))+\dots +d_t(x_1{y}_n)+d_t(x_1{y}_1)-2t_B((x_1{y}_n),(x_1{y}_1))\hfill \\ & =& 2d_t(x_1,y_1)+2d_t(x_1,y_2)+\dots +2d_t(x_1,y_n)-2(t_B((x_1,y_1),(x_1,y_2))\hfill \\ & & +t_B((x_1,y_2),(x_1,y_3))+t_B((x_1{y}_n),(x_1{y}_1)))\hfill \\ & =& {\displaystyle 2\sum _{(x_i,y_j)\in V}{d}_t(x_i,y_j)-2\sum _{i=1}^n{t}_B((x_i,y_j),(x_i^{\prime },y_j^{\prime }))}\hfill \\ & =& {\displaystyle \sum _{(x_i,y_j)\in V}{d}_t(x_i,y_j)+2\sum _{i=1}^n{t}_B((x_i,y_j),(x_i^{\prime },y_j^{\prime }))-2\sum _{i=1}^n{t}_B((x_i,y_j),(x_i^{\prime },y_j^{\prime }))}\hfill \\ & =& {\displaystyle \sum _{(x_i,y_j)\in V}{d}_t(x_i,y_j).}\hfill \end{array}$$

Similarly,

$${\displaystyle l_2=\sum _{i,j=1}^n{d}_f((x_i,y_j),(x_i^{\prime },y_j^{\prime }))=\sum _{(x_i,y_j)\in V}{d}_f(x_i,y_j).}$$

Hence,

$${\displaystyle \sum _{i,j=1}^n{d}_{G_1{\ast }_M{G}_2}((x_i,y_j),(x_i^{\prime },y_j^{\prime }))=(\sum _{(x_i,y_j)\in V}{d}_t(x_i,y_j),\sum _{(x_i,y_j)\in V}{d}_f(x_i,y_j))=\sum _{(x_i,y_j)\in V}{d}_{G_1{\ast }_M{G}_2}(x_i,y_j).}$$

 □

Remark 3.

Let$G_1$and$G_2$be two vague graphs and$G=G_1{\ast }_M{G}_2=(A,B)$with simple graph$G^{\ast }$. Then

$$\begin{array}{cc}& {\displaystyle \sum _{((x_i,y_j),(x_i^{\prime },y_j^{\prime }))\in E}{d}_{G_1{\ast }_M{G}_2}((x_i,y_j),(x_i^{\prime },y_j^{\prime }))}\hfill \\ =& {\displaystyle (\sum _{((x_i,y_j),(x_i^{\prime },y_j^{\prime }))\in E}{d}_{G_1^{\ast }{\ast }_M{G}_2^{\ast }}((x_i,y_j),(x_i^{\prime },y_j^{\prime }))t_B((x_i,y_j),(x_i^{\prime },y_j^{\prime })),}\hfill \\ & {\displaystyle \sum _{((x_i,y_j),(x_i^{\prime },y_j^{\prime }))\in E}{d}_{G_1^{\ast }{\ast }_M{G}_2^{\ast }}((x_i,y_j),(x_i^{\prime },y_j^{\prime }))f_B((x_i,y_j),(x_i^{\prime },y_j^{\prime }))),}\hfill \end{array}$$

where

$$\begin{array}{c}\hfill d_{G_1^{\ast }{\ast }_M{G}_2^{\ast }}((x_i,y_j),(x_i^{\prime },y_j^{\prime }))=d_{G_1^{\ast }{\ast }_M{G}_2^{\ast }}(x_i,y_j)+d_{G_1^{\ast }{\ast }_M{G}_2^{\ast }}(x_i^{\prime },y_j^{\prime })-2\end{array}$$

(16)

for all$((x_i,y_j),(x_i^{\prime },y_j^{\prime }))\in E$.

Definition 10.

Let$G_1$and$G_2$be a vague graphs and$G=G_1{\ast }_M{G}_2=(A,B)$. If each edge in vague graph$G_1{\ast }_M{G}_2=(A,B)$has the same degree$(l_1,l_2)$, then$G_1{\ast }_M{G}_2=(A,B)$is said to be an$(l_1,l_2)$-edge regular vague graph. Moreover if each edge in vague graph$G_1{\ast }_M{G}_2=(A,B)$has the same total degree$(t_1,t_2)$, then$G_1{\ast }_M{G}_2=(A,B)$is said to be a$(t_1,t_2)$-totally edge regular vague graph.

Example 8.

Consider the vague graph$G_1$,$G_2$and G as in Example 4. Then G is an$(0.4,1)$-edge regular vague graph and G is a$(0.6,1.5)$-totally edge regular.

Example 9.

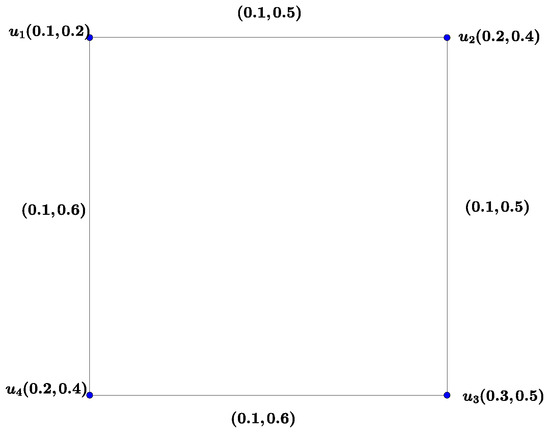
Consider the vague graph$G_1{\ast }_M{G}_2=(A,B)$as in Figure 5.

Figure 5. Vague graph G.

Then

$$d_{G_1{\ast }_M{G}_2}(u_1,u_2)=d_{G_1{\ast }_M{G}_2}(u_2,u_3)=d_{G_1{\ast }_M{G}_2}(u_3,u_4)=d_{G_1{\ast }_M{G}_2}(u_4,u_1)=(0.2,1.1).$$

So$G_1{\ast }_M{G}_2$is an$(0.2,1.1)$-edge regular vague graph, but is not an totally edge regular vague graph.

Theorem 4.

Let$G_1$and$G_2$be two vague graphs,$G=G_1{\ast }_M{G}_2=(A,B)$and$G^{\ast }$be the simple graph of G. If$G^{\ast }$is k-regular, then the summation of degree of all edges in G, is as follows:

$$\begin{array}{c}\hfill {\displaystyle \sum _{((x_i,y_j),(x_i^{\prime },y_j^{\prime }))\in E}(d_G)((x_i,y_j),(x_i^{\prime },y_j^{\prime }))=((k-1)\sum _{(x_i,y_j)\in V}{d}_t(x_i,y_j),(k-1)\sum _{(x_i,y_j)\in V}{d}_f(x_i,y_j)).}\end{array}$$

(17)

Proof. 

By Remark 3, we have

$$\begin{array}{cc}& {\displaystyle \sum _{((x_i,y_j),(x_i^{\prime },y_j^{\prime }))\in E}{d}_G((x_i,y_j),(x_i^{\prime },y_j^{\prime }))}\hfill \\ \hfill =& {\displaystyle (\sum _{((x_i,y_j),(x_i^{\prime },y_j^{\prime }))\in E}{d}_{G^{\ast }}((x_i,y_j),(x_i^{\prime },y_j^{\prime }))t_B((x_i,y_j),(x_i^{\prime },y_j^{\prime })),}\hfill \\ & {\displaystyle \sum _{((x_i,y_j),(x_i^{\prime },y_j^{\prime }))\in E}{d}_{G^{\ast }}((x_i,y_j),(x_i^{\prime },y_j^{\prime }))f_B((x_i,y_j),(x_i^{\prime },y_j^{\prime })))}\hfill \\ \hfill =& {\displaystyle (\sum _{((x_i,y_j),(x_i^{\prime },y_j^{\prime }))\in E}(d_{G^{\ast }}(x_i,y_j)+d_{G^{\ast }}(x_i^{\prime },y_j^{\prime })-2)t_B((x_i,y_j),(x_i^{\prime },y_j^{\prime })),}\hfill \\ & {\displaystyle \sum _{((x_i,y_j),(x_i^{\prime },y_j^{\prime }))\in E}(d_{G^{\ast }}(x_i,y_j)+d_{G^{\ast }}(x_i^{\prime },y_j^{\prime })-2)f_B((x_i,y_j),(x_i^{\prime },y_j^{\prime }))).}\hfill \end{array}$$

Since $G^{\ast }$ is a regular crisp graph, $d_{G^{\ast }}(x_i,y_j)=k$, for all $(x_i,y_j)\in V$ and so we have

$$\begin{array}{ccc}\hfill {\displaystyle \sum _{((x_i,y_j),(x_i^{\prime },y_j^{\prime }))\in E}{d}_G((x_i,y_j),(x_i^{\prime },y_j^{\prime }))}& =& {\displaystyle ((k+k-2)\sum _{((x_i,y_j),(x_i^{\prime },y_j^{\prime }))\in E}{t}_B((x_i,y_j),(x_i^{\prime },y_j^{\prime })),}\hfill \\ & & {\displaystyle (k+k-2)\sum _{((x_i,y_j),(x_i^{\prime },y_j^{\prime }))\in E}{f}_B((x_i,y_j),(x_i^{\prime },y_j^{\prime }))).}\hfill \end{array}$$

Hence

$$\begin{array}{ccc}\hfill {\displaystyle \sum _{((x_i,y_j),(x_i^{\prime },y_j^{\prime }))\in E}{d}_G((x_i,y_j),(x_i^{\prime },y_j^{\prime }))}& =& {\displaystyle (2(k-1)\sum _{((x_i,y_j),(x_i^{\prime },y_j^{\prime }))\in E}{t}_B((x_i,y_j),(x_i^{\prime },y_j^{\prime })),}\hfill \\ & & {\displaystyle 2(k-1)\sum _{((x_i,y_j),(x_i^{\prime },y_j^{\prime }))\in E}{f}_B((x_i,y_j),(x_i^{\prime },y_j^{\prime }))).}\hfill \end{array}$$

So

$$\begin{array}{ccc}\hfill {\displaystyle \sum _{((x_i,y_j),(x_i^{\prime },y_j^{\prime }))\in E}(d_G)((x_i,y_j),(x_i^{\prime },y_j^{\prime }))}& =& {\displaystyle ((k-1)\sum _{(x_i,y_j)\in V}{d}_t(x_i,y_j)(k-1)\sum _{(x_i,y_j)\in V}{d}_f(x_i,y_j)).}\hfill \end{array}$$

 □

Theorem 5.

Let$G_1$and$G_2$be two vague graphs,$G=G_1{\ast }_M{G}_2=(A,B)$and$G^{\ast }$be the simple graph of G. Then the summation of total degree of all edges in G is as follows:

$$\begin{array}{cc}& {\displaystyle \sum _{((x_i,y_j),(x_i^{\prime },y_j^{\prime }))\in E}t{d}_G((x_i,y_j),(x_i^{\prime },y_j^{\prime }))}\hfill \\ \hfill =& {\displaystyle (\sum _{((x_i,y_j),(x_i^{\prime },y_j^{\prime }))\in E}(d_{G^{\ast }})((x_i,y_j),(x_i^{\prime },y_j^{\prime }))t_B((x_i,y_j),(x_i^{\prime },y_j^{\prime }))}\hfill \\ \hfill +& {\displaystyle \sum _{((x_i,y_j),(x_i^{\prime },y_j^{\prime }))\in E}{t}_B((x_i,y_j),(x_i^{\prime },y_j^{\prime })),}\hfill \\ & {\displaystyle \sum _{((x_i,y_j),(x_i^{\prime },y_j^{\prime }))\in E}(d_{G^{\ast }})((x_i,y_j),(x_i^{\prime },y_j^{\prime }))f_B((x_i,y_j),(x_i^{\prime },y_j^{\prime }))}\hfill \\ \hfill +& {\displaystyle \sum _{((x_i,y_j),(x_i^{\prime },y_j^{\prime }))\in E}{f}_B((x_i,y_j),(x_i^{\prime },y_j^{\prime }))).}\hfill \end{array}$$

Proof. 

By definition of total edge degree of G, we have

$$\begin{array}{cc}& {\displaystyle \sum _{((x_i,y_j),(x_i^{\prime },y_j^{\prime }))\in E}(t{d}_G)((x_i,y_j),(x_i^{\prime },y_j^{\prime }))}\hfill \\ & {\displaystyle =(\sum _{((x_i,y_j),(x_i^{\prime },y_j^{\prime }))\in E}t{d}_t((x_i,y_j),(x_i^{\prime },y_j^{\prime })),\sum _{((x_i,y_j),(x_i^{\prime },y_j^{\prime }))\in E}t{d}_f((x_i,y_j),(x_i^{\prime },y_j^{\prime })))}\hfill \\ & {\displaystyle =(\sum _{((x_i,y_j),(x_i^{\prime },y_j^{\prime }))\in E}(d_t((x_i,y_j),(x_i^{\prime },y_j^{\prime }))+t_B((x_i,y_j),(x_i^{\prime },y_j^{\prime }))),}\hfill \\ & {\displaystyle \sum _{((x_i,y_j),(x_i^{\prime },y_j^{\prime }))\in E}(d_f((x_i,y_j),(x_i^{\prime },y_j^{\prime }))+f_B((x_i,y_j),(x_i^{\prime },y_j^{\prime })))}\hfill \\ =& {\displaystyle (\sum _{((x_i,y_j),(x_i^{\prime },y_j^{\prime }))\in E}{d}_t((x_i,y_j),(x_i^{\prime },y_j^{\prime }))+\sum _{((x_i,y_j),(x_i^{\prime },y_j^{\prime }))\in E}{t}_B((x_i,y_j),(x_i^{\prime },y_j^{\prime })),}\hfill \\ & {\displaystyle \sum _{((x_i,y_j),(x_i^{\prime },y_j^{\prime }))\in E}{d}_f((x_i,y_j),(x_i^{\prime },y_j^{\prime }))+\sum _{((x_i,y_j),(x_i^{\prime },y_j^{\prime }))\in E}{f}_B((x_i,y_j),(x_i^{\prime },y_j^{\prime }))).}\hfill \end{array}$$

By Remark 3, we get

$$\begin{array}{c}{\displaystyle \sum _{((x_i,y_j),(x_i^{\prime },y_j^{\prime }))\in E}(t{d}_G)((x_i,y_j),(x_i^{\prime },y_j^{\prime }))}\hfill \\ {\displaystyle =\sum _{((x_i,y_j),(x_i^{\prime },y_j^{\prime }))\in E}(d_{G^{\ast }})((x_i,y_j),(x_i^{\prime },y_j^{\prime }))t_B((x_i,y_j),(x_i^{\prime },y_j^{\prime }))}\hfill \\ {\displaystyle +\sum _{((x_i,y_j),(x_i^{\prime },y_j^{\prime }))\in E}{t}_B((x_i,y_j),(x_i^{\prime },y_j^{\prime })),}\hfill \\ {\displaystyle \sum _{((x_i,y_j),(x_i^{\prime },y_j^{\prime }))\in E}(d_{G^{\ast }})((x_i,y_j),(x_i^{\prime },y_j^{\prime }))f_B((x_i,y_j),(x_i^{\prime },y_j^{\prime }))}\hfill \\ {\displaystyle +\sum _{((x_i,y_j),(x_i^{\prime },y_j^{\prime }))\in E}{f}_B((x_i,y_j),(x_i^{\prime },y_j^{\prime }))).}\hfill \end{array}$$

 □

Theorem 6.

Let$G_1=(A_1,B_1)$and$G_2=(A_2,B_2)$be two vague graphs on simple graphs$G_1^{\ast }=(V_1,E_1)$and$G_2^{\ast }=(V_2,E_2)$, respectively./ Then$(t_B,f_B)$of

$G=G_1{\ast }_M{G}_2$is a constant function if and only if the following are equivalent:

(i)

G is an edge regular vague graph.

(ii)

G is a totally edge regular vague graph.

Proof. 

Assume that $(t_B,f_B)$ of $G=G_1{\ast }_M{G}_2$ is a constant function. Then

$$t_B((x_i,y_j),(x_i^{\prime },y_j^{\prime }))=c_1,f_B((x_i,y_j),(x_i^{\prime },y_j^{\prime }))=c_2$$

for every $((x_i,y_j),(x_i^{\prime },y_j^{\prime }))\in E$, where $c_1$ and $c_2$ are constants. Let G be an $(l_1,l_2)$-edge regular vague graph. Then, for all $((x_i,y_j),(x_i^{\prime },y_j^{\prime }))\in E$,

$d_G((x_i,y_j),(x_i^{\prime },y_j^{\prime }))=(l_1,l_2)$ and

$$\begin{array}{cc}\hfill t{d}_G((x_i,y_j),(x_i^{\prime },y_j^{\prime }))& =(d_t((x_i,y_j),(x_i^{\prime },y_j^{\prime }))+t_B((x_i,y_j),(x_i^{\prime },y_j^{\prime })),d_f((x_i,y_j),(x_i^{\prime },y_j^{\prime }))+f_B((x_i,y_j),(x_i^{\prime },y_j^{\prime })))\hfill \\ & =(l_1+c_1,l_2+c_2)\hfill \end{array}$$

for all $((x_i,y_j),(x_i^{\prime },y_j^{\prime }))\in E$. Then G is a totally edge regular. Now, let G be a $(t_1,t_2)$-totally edge regular vague graph. Then $(t{d}_G)((x_i,y_j),(x_i^{\prime },y_j^{\prime }))=(t_1,t_2)$, for all $((x_i,y_j),(x_i^{\prime },y_j^{\prime }))\in E$. So we have

$$\begin{array}{cc}\hfill (t{d}_G)((x_i,y_j),(x_i^{\prime },y_j^{\prime }))& =(d_t((x_i,y_j),(x_i^{\prime },y_j^{\prime }))+t_B((x_i,y_j),(x_i^{\prime },y_j^{\prime })),\hfill \\ & d_f((x_i,y_j),(x_i^{\prime },y_j^{\prime }))+f_B((x_i,y_j),(x_i^{\prime },y_j^{\prime }))).\hfill \\ & =(t_1,t_2).\hfill \end{array}$$

Hence

$$\begin{array}{ccc}\hfill (d_t((x_i,y_j),(x_i^{\prime },y_j^{\prime })),d_f((x_i,y_j),(x_i^{\prime },y_j^{\prime })))& =& (t_1-t_B((x_i,y_j),(x_i^{\prime },y_j^{\prime })),t_2-f_B((x_i,y_j),(x_i^{\prime },y_j^{\prime })))\hfill \\ & =& (t_1-c_1,t_2-c_2).\hfill \end{array}$$

Then G is a $(t_1-c_1,t_2-c_2)$ edge regular vague graph.

Conversely, assume that (i) and (ii) are equivalent. We have to prove that $(t_B,f_B)$ is a constant function. Suppose that $(t_B,f_B)$ is not a constant function. Then $t_B((x_i,y_j),(x_i^{\prime },y_j^{\prime }))\ne t_B((x_r,y_s),(x_r^{\prime },y_s^{\prime }))$ and $f_B((x_i,y_j),(x_i^{\prime },y_j^{\prime }))\ne f_B((x_r,y_s),(x_r^{\prime },y_s^{\prime }))$, for at least one pair of $((x_i,y_j),(x_i^{\prime },y_j^{\prime })),((x_r,y_s),(x_r^{\prime },y_s^{\prime }))\in E$. Let G be an $(l_1,l_2)$ edge regular vague graph. Then

$$(d_G)((x_i,y_j),(x_i^{\prime },y_j^{\prime }))=d_G((x_r,y_s),(x_r^{\prime },y_s^{\prime }))=(l_1,l_2)$$

Hence for all $((x_i,y_j),(x_i^{\prime },y_j^{\prime }))\in E$ and for all $((x_r,y_s),(x_r^{\prime },y_s^{\prime }))\in E$,

$$\begin{array}{cc}& (t{d}_G)((x_i,y_j),(x_i^{\prime },y_j^{\prime }))\hfill \\ =& (d_t((x_i,y_j),(x_i^{\prime },y_j^{\prime }))+t_B((x_i,y_j),(x_i^{\prime },y_j^{\prime })),d_f((x_i,y_j),(x_i^{\prime },y_j^{\prime }))+f_B((x_i,y_j),(x_i^{\prime },y_j^{\prime })))\hfill \\ =& (l_1+t_B((x_i,y_j),(x_i^{\prime },y_j^{\prime })),l_2+f_B((x_i,y_j),(x_i^{\prime },y_j^{\prime }))),\hfill \end{array}$$

and

$$\begin{array}{cc}& (t{d}_G)((x_r,y_s),(x_r^{\prime },y_s^{\prime }))\hfill \\ =& (d_t((x_r,y_s),(x_r^{\prime },y_s^{\prime }))+t_B((x_r,y_s),(x_r^{\prime },y_s^{\prime })),d_f((x_r,y_s),(x_r^{\prime },y_s^{\prime }))+f_B((x_r,y_s),(x_r^{\prime },y_s^{\prime })))\hfill \\ =& (l_1+t_B((x_r,y_s),(x_r^{\prime },y_s^{\prime })),l_2+f_B((x_r,y_s),(x_r^{\prime },y_s^{\prime }))).\hfill \end{array}$$

Since

$$t_B((x_i,y_j),(x_i^{\prime },y_j^{\prime }))\ne t_B((x_r,y_s),(x_r^{\prime },y_s^{\prime }))$$

and

$$f_B((x_i,y_j),(x_i^{\prime },y_j^{\prime }))\ne f_B((x_r,y_s),(x_r^{\prime },y_s^{\prime }))$$

we have

$$(t{d}_G)((x_i,y_j),(x_i^{\prime },y_j^{\prime }))\ne (t{d}_G)((x_r,y_s),(x_r^{\prime },y_s^{\prime })).$$

Hence G is not a totally edge regular, that is a contradiction to our assumption. Therefore $(t_B,f_B)$ is a constant function. Similarly, we can show that $(t_B,f_B)$ is a constant function, when G is a totally edge regular vague graph. □

3. Application

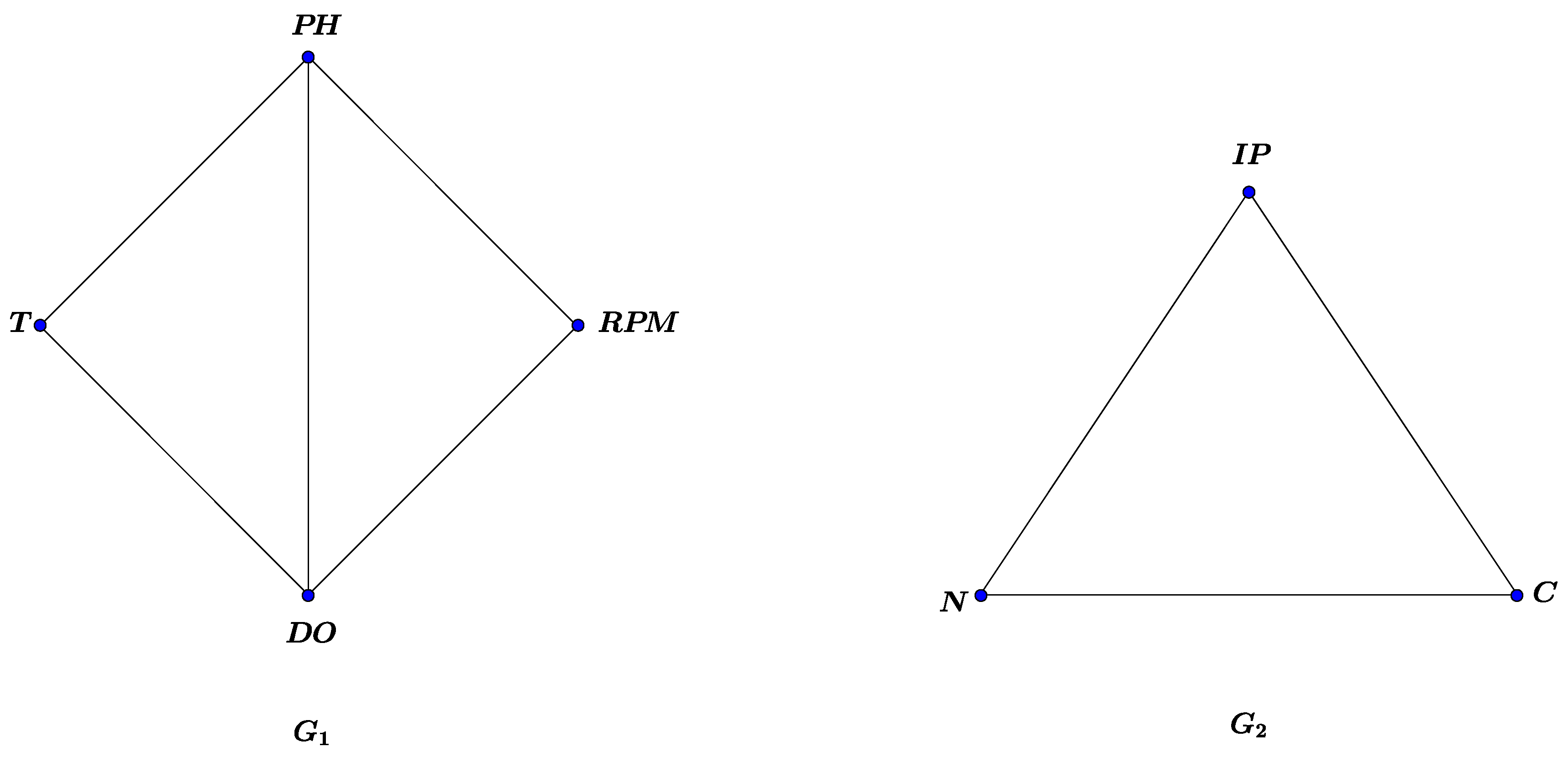
In this section, we express application of maximal product of two vague graphs. To this end we want to optimize the production of bacterial biomass. One of the most commonly used bacteria in genetic engineering is Escherichia coli. Many high-efficiency proteins are expressed in Escherichia coli using genetic engineering technologies. The recombinant protein is a protein that has been added to the genetic engineering by virtue of its genetic engineering. For this purpose, in order to produce recombinant proteins in the research laboratory, bacteria are grown in liquid medium containing essential nutrients. E. Coli is able to produce a large amount of biomass and consequently, increase the production of the desired protein in a nutrient-rich medium. It should be noted that biomass is, in fact, a degradable source composed of living organisms. Cultivation conditions are divided into two biological and physical categories. Biological sources for bacterial growth medium include carbon source, nitrogen source and Percentage of inoculum pre-culture. Physical conditions set by the device include Potential of hydrogen, temperature, dissolved oxygens, revolutions per minute and finally, the optimization of bacterial culture conditions leads to maximizing the production efficiency of large quantities of the product (recombinant proteins), which ultimately results in increased economic efficiency. According to studies by Hosseini et al. [24], the optimal conditions for bacterial cultivation were reported as follows: due to the differences in these parameters, the optical absorption of bacterial culture medium at a wavelength of 600 nm is considered to be consistent with all the parameters. Our goal is to model this problem using vague graphs. Now in Figure 6, we assume $G_1=(A_1,B_1)$ is the vague graph of the physical conditions and $G_2=(A_2,B_2)$ is the vague graph of the biological conditions where $A_1=\{$potential of hidrogen, temperature, dissolved oxygene, revolutions per minute} as shown in Table 1, and $A_2=\{$carbon source, nitrogen source, percentage of inoculum pre-culture}. Also $t_A$ is the intensity of optical absorption of the optimum conditions, $f_A$ the intensity of optical absorption under common conditions, $t_B$ is the term of the mass in grams in optimal conditions and $f_B$ in terms of mass gram in the optimal. By direct calculations, degree of vertices in vague graphs $G_1$ and $G_2$ are given in Table 2 and Table 3, and degree of edges in vague graphs $G_1$ and $G_2$ are given in Table 4 and Table 5.

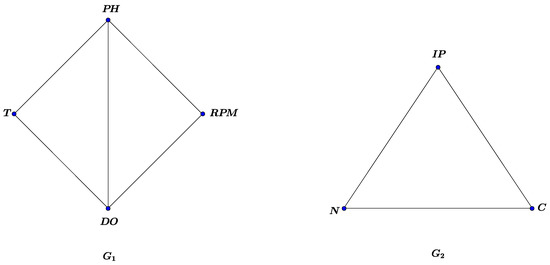
Figure 6. Vague graphs $G_1$ and $G_2$.

Table 1. Biological terms.

Name	Abbreviation
Potential of Hidrogen	PH
Temperature	T
Dissolved oxygene	DO
Revolutions Per Minute	RPM
Carbon source	C
Nitrogen source	N
Percentage of inoculum pre-culture	IP

Table 2. Degree of vertices in vague graph $G_1$.

${\mathit{G}}_1$	PH	T	RPM	DO
($t_{A_1},f_{A_1}$)	($0.99,0.0$)	($0.55,0.44$)	($0.53,0.46$)	($1,0$)

Table 3. Degree of vertices in vague graph $G_2$.

${\mathit{G}}_2$	C	N	IP
($t_{A_2},f_{A_2}$)	($0.53,0.46$)	($0.54,0.45$)	($0.50,0.49$)

Table 4. Degree of edges in vague graph $G_1$.

${\mathit{G}}_1$	(T, PH)	(RPM, PH)	(DO, PH)
($t_{B_1},f_{B_1}$)	($0.55,0.44$)	($0.51,0.48$)	($0.59,0.40$)
${\mathit{G}}_{\mathbf{1}}$	(DO, RPM)	(T, DO)
($t_{B_1},f_{B_1}$)	($0.46,0.53$)	($0.52,0.47$)

Table 5. Degree of edges in vague graph $G_2$.

${\mathit{G}}_2$	(C, IP)	(N, IP)	(N, C)
($t_{B_2},f_{B_2}$)	($0.46,0.53$)	($0.46,0.53$)	($0.53,0.46$)

Now we consider the vague graph $G_1{\ast }_M{G}_2=(A,B)$ as follows (see Table 6 and Table 7):

Table 6. Degree of vertices in vague graph $G_1{\ast }_M{G}_2$.

${\mathit{G}}_{\mathbf{1}}{\ast }_{\mathit{M}}{\mathit{G}}_{\mathbf{2}}$	(PH, N)	(PH, C)	(PH, IP)
($t_A,f_A$)	($0.99,0$)	($0.99,0$)	($0.99,0$)
${\mathit{G}}_{\mathbf{1}}{\ast }_{\mathit{v}}{\mathit{G}}_{\mathbf{2}}$	(RPM, N)	(RPM, C)	(RPM, IP)
($t_A,f_A$)	($0.53,0.46$)	($0.54,0.45$)	($0.53,0.46$)
${\mathit{G}}_{\mathbf{1}}{\ast }_{\mathit{M}}{\mathit{G}}_{\mathbf{2}}$	(T, N)	(T, C)	(T, IP)
($t_A,f_A$)	($0.55,0.44$)	($0.55,0.44$)	($0.55,0.44$)
${\mathit{G}}_{\mathbf{1}}{\ast }_{\mathit{v}}{\mathit{G}}_{\mathbf{2}}$	(DO, N)	(DO, C)	(DO, IP)
($t_A,f_A$)	($1,0$)	($1,0$)	($1,0$)

Table 7. Degree of edges in vague graph $G_1{\ast }_M{G}_2$.

${\mathit{G}}_{\mathbf{1}}{\ast }_{\mathit{M}}{\mathit{G}}_{\mathbf{2}}$	((PH, N), (PH, C))	((PH, N), (PH, IP))
$(t_B,f_B)$	$(0.99,0)$	$(0.99,0)$
${\mathit{G}}_{\mathbf{1}}{\ast }_{\mathit{M}}{\mathit{G}}_{\mathbf{2}}$	((PH, C), (PH, IP))	((PH, IP), (DO, IP))
$(t_B,f_B)$	$(0.99,0)$	$(0.59,0.40)$
${\mathit{G}}_{\mathbf{1}}{\ast }_{\mathit{M}}{\mathit{G}}_{\mathbf{2}}$	((PH, IP), (DO, IP))	((PH, IP), (T, IP))
$(t_B,f_B)$	$(0.59,0.40)$	$(0.55,0.44)$
${\mathit{G}}_{\mathbf{1}}{\ast }_{\mathit{M}}{\mathit{G}}_{\mathbf{2}}$	((T, N), (T, IP))	((T, C), (T, IP))
$(t_B,f_B)$	$(0.55,0.44)$	$(0.55,0.44)$
${\mathit{G}}_{\mathbf{1}}{\ast }_{\mathit{M}}{\mathit{G}}_{\mathbf{2}}$	((DO, C), (DO, IP))	((DO, C), (DO, N))
$(t_B,f_B)$	$(1,0)$	$(1,0)$
${\mathit{G}}_{\mathbf{1}}{\ast }_{\mathit{M}}{\mathit{G}}_{\mathbf{2}}$	((RPM, C), (RPM, N))	((RPM, C), (RPM, IP))
$(t_B,f_B)$	$(0.53,0.46)$	$(0.53,0.46)$
${\mathit{G}}_{\mathbf{1}}{\ast }_{\mathit{M}}{\mathit{G}}_{\mathbf{2}}$	((PH, C), (DO, C))	((T, N), (DO, N))
$(t_B,f_B)$	$(0.59,0.40)$	$(0.54,0.45)$
${\mathit{G}}_{\mathbf{1}}{\ast }_{\mathit{M}}{\mathit{G}}_{\mathbf{2}}$	((PH, N), (T, N))	((PH, N), (RPM, N))
$(t_B,f_B)$	$(0.55,0.44)$	$(0.54,0.45)$
${\mathit{G}}_{\mathbf{1}}{\ast }_{\mathit{M}}{\mathit{G}}_{\mathbf{2}}$	((PH, C), (RPM, C))	((PH, C), (T, C))
$(t_B,f_B)$	$(0.53,0.46)$	$(0.55,0.44)$
${\mathit{G}}_{\mathbf{1}}{\ast }_{\mathit{M}}{\mathit{G}}_{\mathbf{2}}$	((PH, IP), (RPM, IP))	((T, N), (T, C))
$(t_B,f_B)$	$(0.51,0.48)$	$(0.55,0.44)$
${\mathit{G}}_{\mathbf{1}}{\ast }_{\mathit{M}}{\mathit{G}}_{\mathbf{2}}$	((T, C), (DO, C))	((T, IP), (DO, IP))
$(t_B,f_B)$	$(0.53,0.46)$	$(0.52,0.47)$
${\mathit{G}}_{\mathbf{1}}{\ast }_{\mathit{M}}{\mathit{G}}_{\mathbf{2}}$	((DO, N), (RPM, N))	((DO, N), (DO, IP))
$(t_B,f_B)$	$(0.54,0.45)$	$(1,0)$
${\mathit{G}}_{\mathbf{1}}{\ast }_{\mathit{M}}{\mathit{G}}_{\mathbf{2}}$	((RPM, N), (RPM, IP))	((PH, N), (DO, N))
$(t_B,f_B)$	$(0.53,0.46)$	$(0.59,0.40)$
${\mathit{G}}_{\mathbf{1}}{\ast }_{\mathit{M}}{\mathit{G}}_{\mathbf{2}}$	((RPM, N), (RPM, IP))	((DO, C), (RPM, C))
$(t_B,f_B)$	$(0.53,0.46)$	$(0.53,0.46)$
${\mathit{G}}_{\mathbf{1}}{\ast }_{\mathit{M}}{\mathit{G}}_{\mathbf{2}}$	((DO, IP), (RPM, IP))
($t_B,f_B$)	($0.50,0.49$)

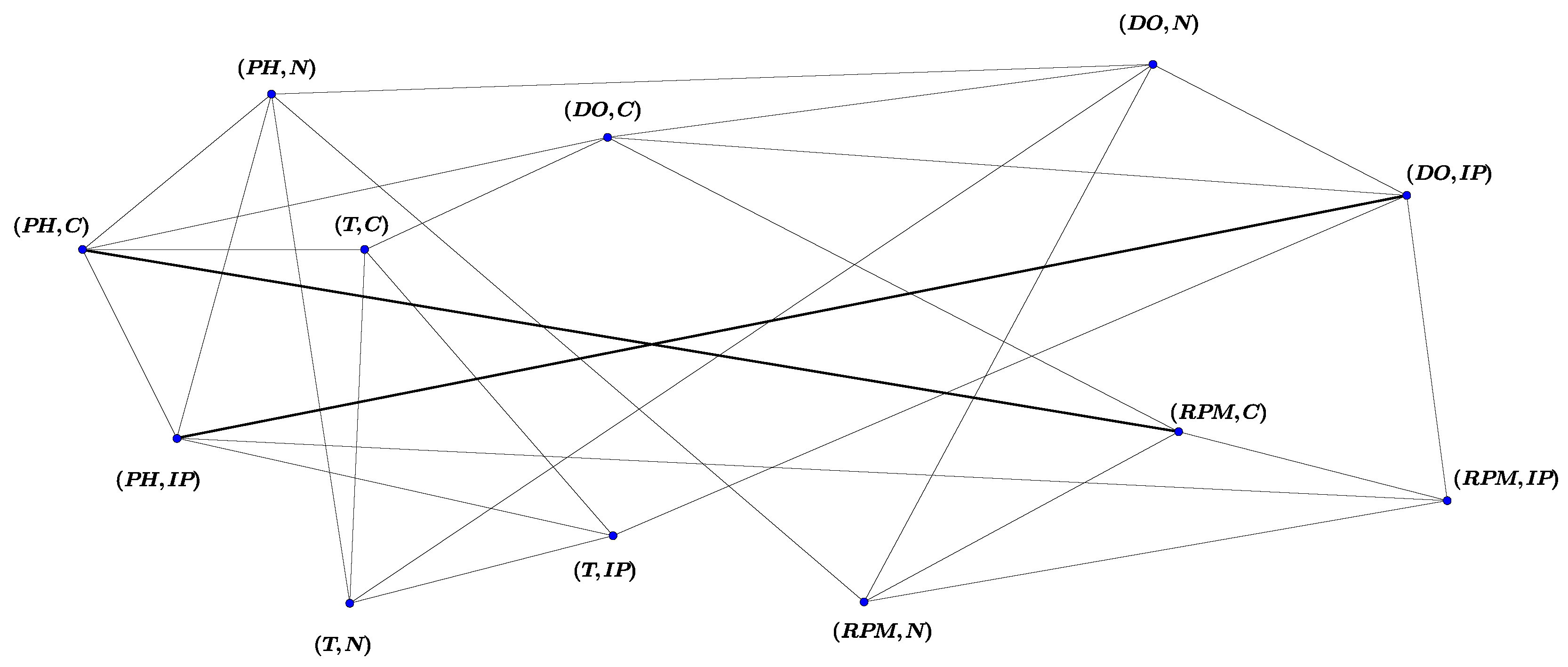
The results of the Table 6 are matched with the results of experiments. So that, due to the increasing growth of bacteria, in the presence of optimized sources of $(DO,N)$, $(DO,C)$ and $(DO,IP)$ intensity of absorption measured by the spectrophotometer is the highest number in optimal condition and lowest number in optical ordinary condition. Based on the results of Table 6, the high values of obtained biomass from simultaneous use of optimal nitrogen source, optimal carbon source, Percentage of inoculum pre-culture and optimal dissolved oxygen in erlenmeyer in laboratory condition match with the obtained biomass using of maximal product $G_1{\ast }_M{G}_2$. Although, in this case, low values of biomass in common condition have the same terms of mass gram in both laboratory condition and Table 6. So that by Table 7, the biomass obtained from $((DO,C),(DO,IP))$, $((DO,C),(DO,N))$ and $((DO,N),(DO,IP))$ in optimal conditions, compared to all other investigated optimal mode, have the highest terms of mass gram. Likewise biomass obtained from $((DO,C),(DO,IP))$, $((DO,C),(DO,N))$ and $((DO,N),(DO,IP))$ in common conditions, compared to all other investigated optimal mode, have the lowest terms of mass gram. Hence the results of Table 7 are matched with the results of experiments. Vague graph $G_1{\ast }_M{G}_2$ is shown in Figure 7.

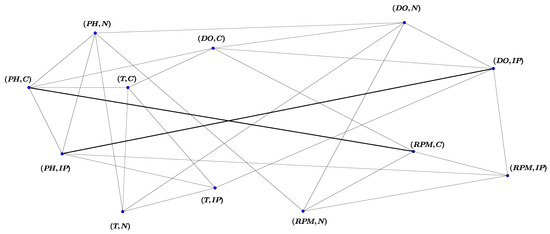
Figure 7. Vague graph $G_1{\ast }_M{G}_2$.

Therefore, we conclude that the mathematical modeling of this laboratory research using a maximized multiplication graph is a good tool for predicting laboratory samples for optimal biomass production and a suitable link between biotechnology and fuzzy mathematics can be established.

4. Conclusions

Graph theory is an important area in mathematics which is used to represent networks of communication, data organization, computational devices and the flow of computation. We have presented the concept of maximal products of two vague graphs. We have illustrated that the operation maximal products of two vague graphs is not commutative. Then we describe certain concepts, including strongly, completely, regularity and connectedness on maximal product of vague graphs. Fuhrer, we consider some results of edge regular and totally edge regular in maximal product of vague graphs. Finally, we have considered an application of this operator. In future, we shall focus on (1) Hesitant Pythagorean fuzzy graphs; (2) Interval-valued Pythagorean fuzzy graphs; and (3) Vague graphs under Hamacher aggregation operator.