The Minimum Lindley Lomax Distribution: Properties and Applications
Abstract
:1. Introduction
2. Structural Properties
2.1. Quantile Function
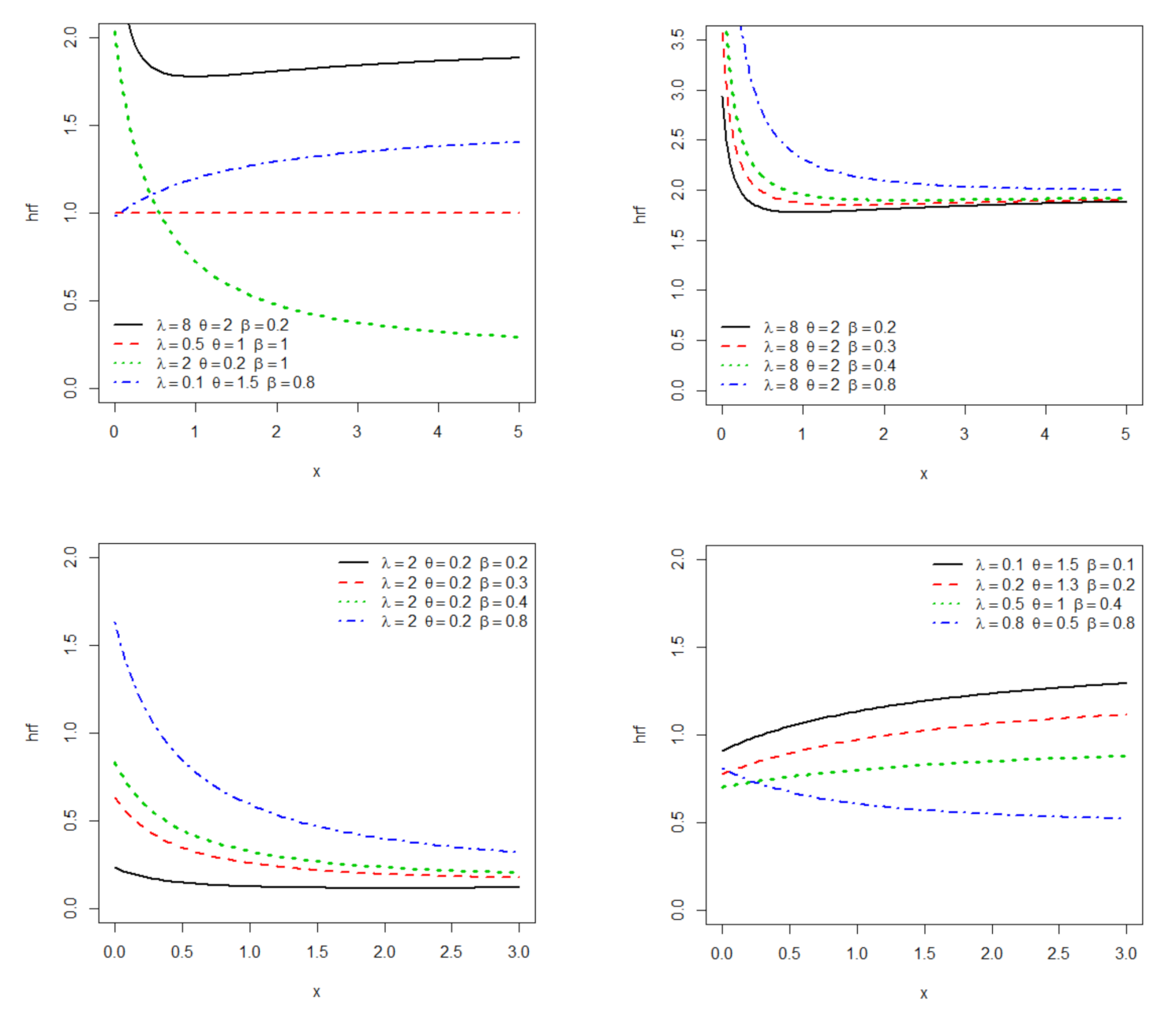
2.2. The Shape of the minLLx Distribution
2.3. Moments and Moment Generating Function
2.4. Probability Weighted Moments
2.5. Order Statistics
2.6. Rényi Entropy
2.7. Stochastic Dominance
2.8. Stress Strength Model
3. Characterization Results
3.1. Characterizations on the Basis of Two Truncated Moments
3.2. Characterizations on the Basis of Conditional Expectation of Certain Functions of an Arbitrary Variable
4. Maximum Likelihood Estimation
5. Simulation Study
- Set the values for n, λ, θ, and β, as well as the starting value of.
- Develop .
- Update each time via the Newton−Raphson’s methodology, as shown below.
- If where is very small tolerance limit, then store as a variate from minLLX distribution.
- If , fix and then proceed to step III.
- In order to develop , steps II-V are repeated times.
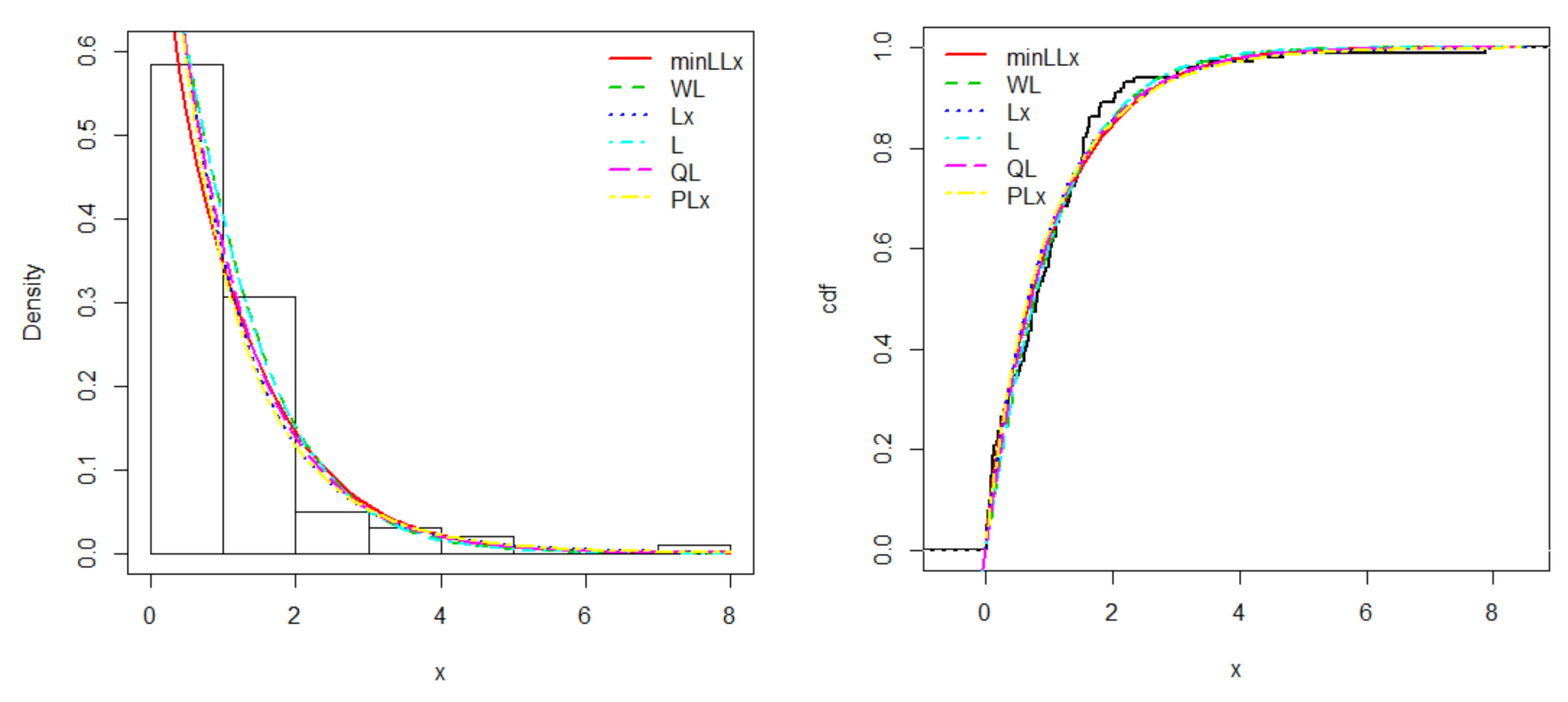
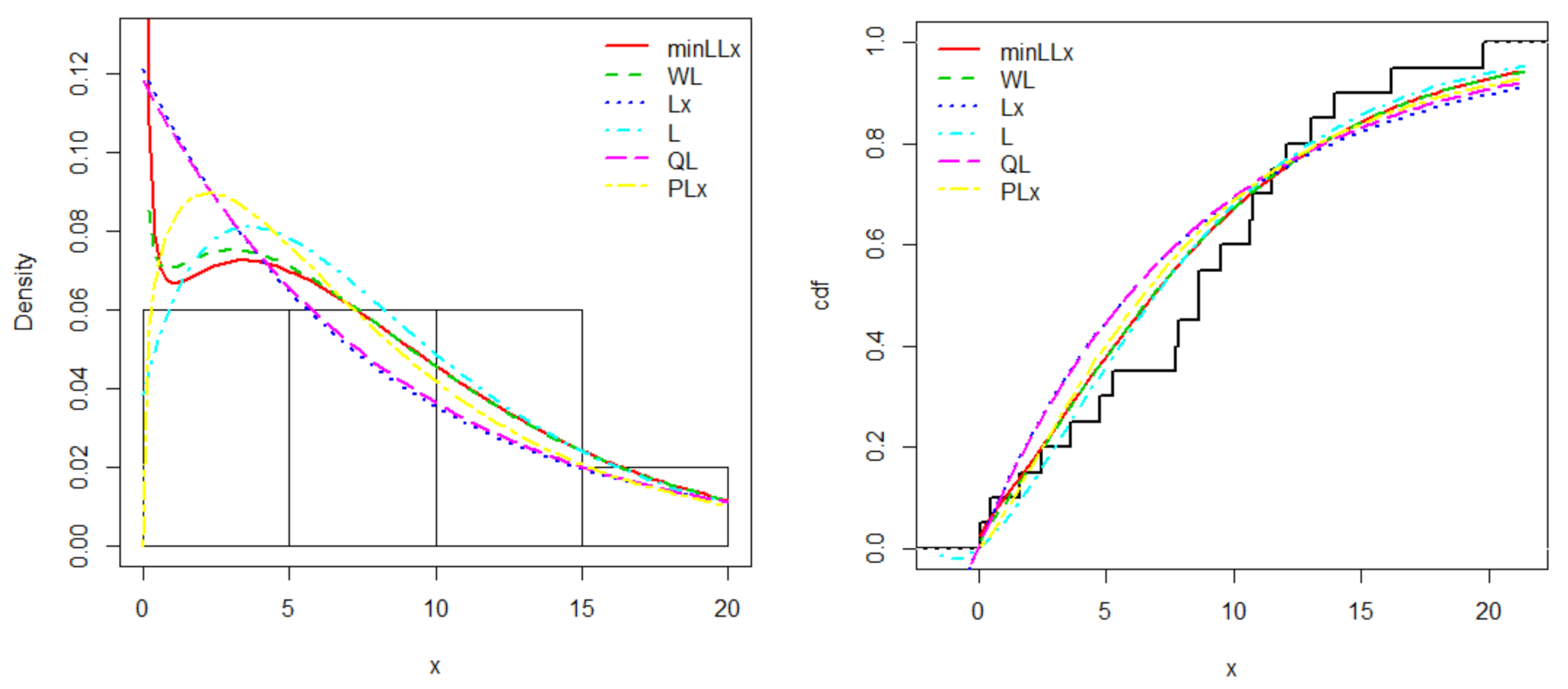
6. Applications
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix B
References
- Tahir, M.H.; Nadarajah, S. Parameter induction in continuous univariate distributions: Well-established G families. Ann. Braz. Acad. Sci. 2015, 87, 539–568. [Google Scholar] [CrossRef] [PubMed]
- Tahir, M.H.; Cordeiro, G.M. Compounding of distributions: A survey and new generalized classes. J. Stat. Distrib. Appl. 2016, 3, 13. [Google Scholar] [CrossRef] [Green Version]
- Cordeiro, G.M.; Ortega, E.; Lemonte, A.J. The exponential–Weibull lifetime distribution. J. Stat. Comput. Simul. 2013, 84, 2592–2606. [Google Scholar] [CrossRef]
- Ghitany, M.E.; Atieh, B.; Nadarajah, S. Lindley distribution and its application. Math. Comput. Simul. 2008, 78, 493–506. [Google Scholar] [CrossRef]
- Ramos, P.; Louzada, F. The generalized weighted Lindley distribution: Properties, estimation, and applications. Cogent Math. 2016, 3, 1256022. [Google Scholar] [CrossRef]
- Singh, S.K.; Singh, U.; Sharma, V.K. Estimation and prediction for Type-I hybrid censored data from generalized Lindley distribution. J. Stat. Manag. Syst. 2016, 19, 367–396. [Google Scholar] [CrossRef]
- Oguntunde, P.E.; Khaleel, M.A.; Ahmed, M.T.; Adejumo, A.O.; Odetunmibi, O. A New Generalization of the Lomax Distribution with Increasing, Decreasing, and Constant Failure Rate. Model. Simul. Eng. 2017, 2017, 6043169. [Google Scholar] [CrossRef] [Green Version]
- Wei, S.; Wang, C.; Li, Z. Bayes estimation of Lomax distribution parameter in the composite LINEX loss of symmetry. J. Interdiscip. Math. 2017, 20, 1277–1287. [Google Scholar] [CrossRef]
- Elgarhy, M.; Sharma, V.K.; ElBatal, I. Transmuted Kumaraswamy Lindley distribution with application. J. Stat. Manag. Syst. 2018, 21, 1083–1104. [Google Scholar] [CrossRef]
- David, H.A.; Nagaraja, H. Order Statistics, 3rd ed.; Wiley: New York, NY, USA, 2003. [Google Scholar]
- Shaked, M.; Shanthikumar, J.G. Stochastic Orders; Wiley: New York, NY, USA, 2007. [Google Scholar]
- Glanzel, W. Some consequences of a characterization theorem based on truncated moments. J. Theor. Appl. Stat. 1990, 21, 613–618. [Google Scholar] [CrossRef]
- Glanzel, W. A Characterization Theorem Based on Truncated Moments and its Application to Some Distribution Families. In Mathematical Statistics and Probability Theory; Springer: Dordrecht, The Netherlands, 1987; pp. 75–84. [Google Scholar] [CrossRef]
- Hamedani, G.G. On Certain Generalized Gamma Convolution Distribution II; Technical Report No. 484, MSCS; Marquette University: Milwaukee, WI, USA, 2013. [Google Scholar]
- Andrews, D.F.; Herzberg, A.M. Data: A Collection of Problems from Many Fields for the Student and Research Worker (Springer Series in Statistics); Springer: New York, NY, USA, 1985. [Google Scholar]
- Barlow, R.E.; Toland, R.H.; Freeman, T. A Bayesian analysis of stress-rupture life of Kevlar 49/epoxy spherical pressure vessels. In Proceedings of the Canadian Conference in Applied Statistics, Dwivedi, T.D., Ed. Marcel Dekker: New York, NY, USA, 1984. [Google Scholar]
- Cooray, K.; Ananda, M.M.A. A Generalization of the Half-Normal Distribution with Applications to Lifetime Data. Commun. Stat. Theory Methods 2008, 37, 1323–1337. [Google Scholar] [CrossRef]
- Al-Aqtash, R.; Lee, C.; Famoye, F. Gumbel-Weibull distribution: Properties and applications. J. Mod. Appl. Stat. Methods 2014, 13, 201–225. [Google Scholar] [CrossRef]
- Murthy, D.N.P.; Xie, M.; Jiang, R. Weibull Models; Wiley: New York, NY, USA, 2004. [Google Scholar]
- Asgharzadeh, A.; Nadarajah, S.; Sharafi, F. Weibull Lindley distribution. REVSTAT Stat. J. 2018, 16, 87–113. [Google Scholar]
- Shanker, R.; Mishra, A. A quasi Lindley distribution. Afr. J. Math. Comput. Sci. Res. 2013, 6, 64–71. [Google Scholar]
- Rady, E.-H.A.; Hassanein, W.A.; Elhaddad, T.A. The power Lomax distribution with an application to bladder cancer data. SpringerPlus 2016, 5, 1838. [Google Scholar] [CrossRef] [PubMed] [Green Version]

| 1.126862 | 0.3661565 | 0.9344674 | 0.164529 | |
| 1.406321 | 0.2563243 | 1.76341 | 0.1045506 | |
| 1.896405 | 0.2028995 | 5.733562 | 0.07738473 | |
| 2.72086 | 0.172917 | 28.11525 | 0.06041124 | |
| Variance | 0.1365036 | 0.1222537 | 0.890181 | 0.07748082 |
| S.D | 0.369464 | 0.349648 | 0.9434941 | 0.2783538 |
| Skewness | 1.137115 | 1.563494 | 2.448468 | 2.289103 |
| Kurtosis | 1.375744 | 1.731832 | 0.84139 | 1.526684 |
| n | Para | Init. | MLE | Bias | MSE | 95% CI | 99% CI | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| CPs | LB | UB | CPs | LB | UB | ||||||
| 50 | 1.5 | 2.554 | 1.054 | 1.250 | 0.99 | 2.451 | 2.657 | 1.00 | 2.448 | 2.793 | |
| 0.85 | 1.763 | 0.913 | 0.857 | 0.96 | 1.746 | 1.797 | 0.99 | 1.719 | 1.808 | ||
| 0.72 | 1.334 | 0.614 | 0.889 | 0.92 | 1.309 | 1.395 | 0.97 | 1.288 | 1.443 | ||
| 100 | 1.5 | 2.527 | 1.027 | 1.137 | 0.94 | 2.471 | 2.583 | 0.97 | 2.454 | 2.601 | |
| 0.85 | 1.667 | 0.817 | 0.698 | 0.97 | 1.656 | 1.781 | 0.98 | 1.637 | 1.798 | ||
| 0.72 | 1.227 | 0.507 | 0.733 | 0.95 | 1.215 | 1.266 | 0.96 | 1.202 | 1.291 | ||
| 200 | 1.5 | 2.495 | 0.995 | 1.024 | 0. 90 | 2.469 | 2.521 | 0.98 | 2.520 | 2.599 | |
| 0.85 | 1.601 | 0.751 | 0.583 | 0.97 | 1.586 | 1.625 | 0.95 | 1.547 | 1.643 | ||
| 0.72 | 1.111 | 0.391 | 0.526 | 0.95 | 1.084 | 1.159 | 0.94 | 1.005 | 1.187 | ||
| 300 | 1.5 | 1.738 | 0.238 | 0.556 | 0.94 | 1.721 | 1.755 | 1.00 | 1.727 | 1.779 | |
| 0.85 | 1.229 | 0.379 | 0.273 | 0.96 | 1.189 | 1.242 | 0.97 | 1.147 | 1.267 | ||
| 0.72 | 0.997 | 0.277 | 0.377 | 0.95 | 0.979 | 1.015 | 0.97 | 0.958 | 1.093 | ||
| 500 | 1.5 | 1.712 | 0.212 | 0.484 | 0.96 | 1.701 | 1.723 | 0.98 | 1.694 | 1.754 | |
| 0.85 | 1.003 | 0.153 | 0.097 | 0.94 | 0.985 | 1.036 | 0.98 | 0.970 | 1.088 | ||
| 0.72 | 0.837 | 0.117 | 0.114 | 0.96 | 0.826 | 0.877 | 0.99 | 0.811 | 0.893 | ||
| n | Para | Init. | MLE | Bias | MSE | 95% CI | 99% CI | ||||
| CPs | LB | UB | CPs | LB | UB | ||||||
| 50 | 2.4 | 3.807 | 1.407 | 2.230 | 0.90 | 3.648 | 3.966 | 0.97 | 3.466 | 3.886 | |
| 0.5 | 1.128 | 0.628 | 0.604 | 0.98 | 0.932 | 1.324 | 0.94 | 0.87 | 1.386 | ||
| 0.5 | 0.981 | 0.481 | 0.481 | 0.96 | 0.785 | 1.177 | 0.96 | 0.723 | 1.239 | ||
| 100 | 2.4 | 3.595 | 1.195 | 1.678 | 0.97 | 3.719 | 3.870 | 0.98 | 3.454 | 3.627 | |
| 0.5 | 0.967 | 0.467 | 0.398 | 0.94 | 0.575 | 1.359 | 0.99 | 0.451 | 1.483 | ||
| 0.5 | 0.864 | 0.364 | 0.382 | 0.97 | 0.472 | 1.256 | 0.98 | 0.348 | 1.38 | ||
| 200 | 2.4 | 2.753 | 0.353 | 1.888 | 0.94 | 2.721 | 2.786 | 0.99 | 2.503 | 2.597 | |
| 0.5 | 0.881 | 0.381 | 0.395 | 0.96 | 0.691 | 1.071 | 0.96 | 0.631 | 1.131 | ||
| 0.5 | 0.722 | 0.222 | 0.199 | 0.97 | 0.532 | 0.912 | 0.97 | 0.472 | 0.972 | ||
| 300 | 2.4 | 2.532 | 0.132 | 0.833 | 0.95 | 2.705 | 2.762 | 1.00 | 2.499 | 2.569 | |
| 0.5 | 0.646 | 0.146 | 0.271 | 0.96 | 0.42452 | 0.867 | 0.98 | 0.354 | 0.938 | ||
| 0.5 | 0.637 | 0.137 | 0.269 | 0.97 | 0.415 | 0.858 | 0.99 | 0.345 | 0.929 | ||
| 500 | 2.4 | 2.518 | 0.118 | 0.270 | 0.96 | 2.506 | 2.531 | 1.00 | 2.537 | 2.577 | |
| 0.5 | 0.557 | 0.057 | 0.253 | 0.95 | 0.5276 | 0.586 | 0.99 | 0.518 | 0.596 | ||
| 0.5 | 0.597 | 0.097 | 0.259 | 0.96 | 0.5676 | 0.626 | 1.00 | 0.558 | 0.636 | ||
| n | Para | Init. | MLE | Bias | MSE | 95% CI | 99% CI | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| CPs | LB | UB | CPs | LB | UB | ||||||
| 50 | 2.4 | 3.551 | 1.151 | 1.575 | 0.90 | 3.648 | 3.966 | 1.00 | 3.466 | 3.886 | |
| 0.15 | 0.667 | 0.517 | 0.477 | 0.99 | 0.471 | 0.863 | 0.94 | 0.409 | 0.925 | ||
| 1.5 | 2.778 | 1.278 | 1.883 | 0.92 | 2.582 | 2.974 | 0.97 | 2.52 | 3.036 | ||
| 100 | 2.4 | 3.295 | 0.895 | 1.051 | 0.98 | 3.719 | 3.870 | 0.96 | 3.454 | 3.627 | |
| 0.15 | 0.546 | 0.396 | 0.337 | 0.97 | 0.154 | 0.938 | 0.98 | 0.03 | 1.062 | ||
| 1.5 | 2.337 | 0.837 | 0.951 | 0.94 | 1.945 | 2.729 | 0.99 | 1.821 | 2.853 | ||
| 200 | 2.4 | 3.016 | 0.616 | 0.629 | 0.96 | 2.721 | 2.786 | 0.95 | 2.503 | 2.597 | |
| 0.15 | 0.881 | 0.731 | 0.784 | 0.96 | 0.691 | 1.071 | 0.97 | 0.631 | 1.131 | ||
| 1.5 | 1.836 | 0.336 | 0.263 | 0.95 | 1.646 | 2.026 | 0.97 | 1.586 | 2.086 | ||
| 300 | 2.4 | 2.842 | 0.442 | 0.345 | 0.97 | 2.705 | 2.762 | 0.98 | 2.499 | 2.569 | |
| 0.15 | 0.646 | 0.496 | 0.496 | 0.96 | 0.425 | 0.867 | 0.99 | 0.354 | 0.938 | ||
| 1.5 | 1.772 | 0.272 | 0.324 | 0.95 | 1.551 | 1.993 | 0.97 | 1.480 | 2.064 | ||
| 500 | 2.4 | 2.537 | 0.137 | 0.27 | 0.95 | 2.506 | 2.531 | 0.98 | 2.537 | 2.577 | |
| 0.15 | 0.557 | 0.407 | 0.416 | 0.96 | 0.5276 | 0.5864 | 0.99 | 0.5183 | 0.5957 | ||
| 1.5 | 1.606 | 0.106 | 0.261 | 0.95 | 1.5766 | 1.6354 | 0.98 | 1.5673 | 1.6447 | ||
| n | Para | Init. | MLE | Bias | MSE | 95% CI | 99% CI | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| CPs | LB | UB | CPs | LB | UB | ||||||
| 50 | 2.4 | 3.851 | 1.451 | 2.355 | 0.99 | 3.648 | 3.966 | 1.00 | 3.466 | 3.886 | |
| 0.15 | 0.767 | 0.617 | 0.631 | 0.93 | 0.571 | 0.963 | 0.94 | 0.509 | 1.025 | ||
| 3.5 | 4.708 | 1.208 | 1.709 | 0.98 | 4.512 | 4.904 | 0.92 | 4.45 | 4.966 | ||
| 100 | 2.4 | 3.529 | 1.129 | 1.525 | 0.98 | 3.719 | 3.870 | 0.98 | 3.454 | 3.627 | |
| 0.15 | 0.665 | 0.515 | 0.515 | 0.97 | 0.273 | 1.057 | 0.95 | 0.149 | 1.181 | ||
| 3.5 | 4.553 | 1.053 | 1.359 | 0.96 | 4.161 | 4.945 | 0.93 | 4.037 | 5.069 | ||
| 200 | 2.4 | 3.119 | 0.719 | 0.767 | 0.98 | 2.721 | 2.786 | 0.94 | 2.503 | 2.597 | |
| 0.15 | 0.498 | 0.348 | 0.371 | 0.97 | 0.308 | 0.688 | 0.98 | 0.248 | 0.748 | ||
| 3.5 | 4.078 | 0.578 | 0.584 | 0.96 | 3.888 | 4.268 | 0.99 | 3.828 | 4.328 | ||
| 300 | 2.4 | 2.728 | 0.328 | 0.358 | 0.96 | 2.705 | 2.762 | 0.98 | 2.499 | 2.569 | |
| 0.15 | 0.367 | 0.217 | 0.297 | 0.97 | 0.146 | 0.588 | 0.99 | 0.075 | 0.659 | ||
| 3.5 | 3.876 | 0.376 | 0.391 | 0.94 | 3.655 | 4.097 | 0.98 | 3.584 | 4.168 | ||
| 500 | 2.4 | 2.643 | 0.243 | 0.209 | 0.96 | 2.506 | 2.531 | 0.99 | 2.537 | 2.577 | |
| 0.15 | 0.268 | 0.118 | 0.164 | 0.95 | 0.2386 | 0.2974 | 0.98 | 0.2293 | 0.3067 | ||
| 3.5 | 3.711 | 0.211 | 0.195 | 0.95 | 3.6816 | 3.7404 | 1.00 | 3.6723 | 3.7497 | ||
| Distribution | ML Estimates with SEs | |||||
|---|---|---|---|---|---|---|
| minLLx | 29.1543 (24.5461) | 1.1967 (0.1353) | 0.0565 (0.0444) | - | - | - |
| WL | - | - | - | 54.8909 (46.5022) | 0.1262 (0.0029) | 1.3776 (0.1066) |
| Lx | - | 0.0649 (0.0730) | - | 16.0324 (11.8945) | - | - |
| L | - | --- | - | 1.3848 (0.1068) | - | - |
| QL | - | 16.2215 (18.4297) | - | 1.0312 (0.1876) | - | - |
| PLx | - | - | 49.8009 (55.9286) | - | 0.9381 (0.0842) | 48.6282 (64.3737) |
| Distribution | Goodness-of-Fit Statistics | ||||||
|---|---|---|---|---|---|---|---|
| −LL | A* | W* | KS | p-Value | AIC | BIC | |
| minLLx | 101.7467 | 0.73166 | 0.1174 | 0.0751 | 0.6188 | 209.4934 | 217.3388 |
| WL | 103.7773 | 0.8412 | 0.1372 | 0.1069 | 0.1985 | 213.5547 | 221.4001 |
| Lx | 103.2335 | 1.1543 | 0.2082 | 0.0836 | 0.4803 | 210.4669 | 215.6972 |
| L | 104.6558 | 0.8349 | 0.1377 | 0.1062 | 0.2046 | 211.3115 | 213.9267 |
| QL | 103.5036 | 1.0226 | 0.1796 | 0.0892 | 0.3968 | 211.0071 | 216.2374 |
| PLx | 102.9973 | 1.1376 | 0.2044 | 0.0912 | 0.3694 | 211.9947 | 219.8400 |
| Distribution | ML Estimates with SEs | |||||
|---|---|---|---|---|---|---|
| minLLx | 23.2537 (6.2332) | 0.2000 (0.0357) | 0.0176 (0.0242) | - | - | - |
| WL | - | - | - | 0.5063 (0.2646) | 0.0022 (0.0049) | 0.1936 (0.0376) |
| Lx | - | 0.0063 (0.0050) | - | 19.2257 (15.1770) | - | - |
| L | - | - | - | 0.2161 (0.0344) | - | - |
| QL | - | 12.7561 (8.1217) | - | 0.1276 (0.0188) | - | - |
| PLx | - | - | 5.1542 (4.2880) | --- | 1.2999 (0.2549) | 77.2599 (64.2934) |
| Distribution | Goodness-of-Fit Statistics | ||||||
|---|---|---|---|---|---|---|---|
| −LL | A* | W* | KS | p-Value | AIC | BIC | |
| minLLx | 60.4860 | 0.4993 | 0.0891 | 0.2013 | 0.3319 | 126.1758 | 129.0630 |
| WL | 60.8537 | 0.5622 | 0.0992 | 0.2051 | 0.3237 | 127.7075 | 128.2906 |
| Lx | 62.9558 | 0.9314 | 0.1602 | 0.2484 | 0.1422 | 129.9117 | 131.9032 |
| L | 61.3791 | 0.6909 | 0.1203 | 0.2022 | 0.3298 | 126.9583 | 129.7541 |
| QL | 62.6023 | 0.8804 | 0.1514 | 0.2493 | 0.1396 | 129.2046 | 131.1960 |
| PLx | 62.5202 | 0.9067 | 0.1561 | 0.2315 | 2000 | 131.0405 | 134.0277 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, S.; Hamedani, G.G.; Reyad, H.M.; Jamal, F.; Shafiq, S.; Othman, S. The Minimum Lindley Lomax Distribution: Properties and Applications. Math. Comput. Appl. 2022, 27, 16. https://doi.org/10.3390/mca27010016
Khan S, Hamedani GG, Reyad HM, Jamal F, Shafiq S, Othman S. The Minimum Lindley Lomax Distribution: Properties and Applications. Mathematical and Computational Applications. 2022; 27(1):16. https://doi.org/10.3390/mca27010016
Chicago/Turabian StyleKhan, Sadaf, Gholamhossein G. Hamedani, Hesham Mohamed Reyad, Farrukh Jamal, Shakaiba Shafiq, and Soha Othman. 2022. "The Minimum Lindley Lomax Distribution: Properties and Applications" Mathematical and Computational Applications 27, no. 1: 16. https://doi.org/10.3390/mca27010016
APA StyleKhan, S., Hamedani, G. G., Reyad, H. M., Jamal, F., Shafiq, S., & Othman, S. (2022). The Minimum Lindley Lomax Distribution: Properties and Applications. Mathematical and Computational Applications, 27(1), 16. https://doi.org/10.3390/mca27010016








