Controllability Criteria for Nonlinear Impulsive Fractional Differential Systems with Distributed Delays in Controls

Abstract

We establish a class of nonlinear fractional differential systems with distributed time delays in the controls and impulse effects. We discuss the controllability criteria for both linear and nonlinear systems. The main results required a suitable Gramian matrix defined by the Mittag–Leffler function, using the standard Laplace transform and Schauder fixed-point techniques. Further, we provide an illustrative example supported by graphical representations to show the validity of the obtained abstract results.

1. Introduction

Fractional calculus has become a topic of growing interest in Applied Mathematics because of its potential to model many physical phenomena; in fact, it has become a subject of significant interest to many researchers, scientists and engineers, since it applies to a wide range of applications in physics, mathematics and engineering; see, for instance [1,2,3,4,5,6,7,8,9,10,11]. Concerning different applications and mathematical models, the literature contains, among many others, reaction–diffusion problems [12], neural networks [13], a COVID-19 model [14] and an anomalous transport model [15].

A delay differential equation is a differential equation where the time derivatives at the current time depend on the solution and possibly its derivatives at previous times. Instead of a simple initial condition, an initial history function needs to be specified. Fractional differential equations with delays have recently played a significant role in modelling in many areas of science. Appropriately, fractional differential equations are further considered to be alternative models to nonlinear differential equations. For more details, see the monographs of Kilbas et al. [16], Miller and Ross [17], and Podlubny [18]. Mathematical models for systems with distributed delays in the controls occur in the study of agricultural economics and population dynamics [19,20].

On the other hand, it is noted that controllability is one of the most important qualitative behaviours of a dynamical structure. Based on this fact, we can infer that it is possible to steer any initial state of the system to any final state in some finite time using an admissible control. Moreover, controllability outcomes can be acquired by using non-identical techniques, for which the fixed point theory is the most powerful tool [21]. Therefore, the fusion of fractional-order derivatives and integrals in control theory lead to better results than integer order approaches. Recently, Balachandran et al. [22] proved the relative controllability of fractional dynamical systems with distributed delays in the controls. In [23], the authors established some analysis for the stability and controllability of a fractional damped differential system with non-instantaneous impulses supported by numerical treatments. Furthermore, the dynamics of developing processes is frequently subjected to immediate changes such as shocks, harvesting or natural disasters, and so on. These types of short-term performances are regularly treated as having acted instantaneously or in the form of impulses. Zhang et al. [24] proved the controllability of an impulsive fractional differential equation with a state delay. Very recently, in [25], the authors proved in a relative controllability analysis fractional order differential equations with multiple time delays. For further works, the readers may refer to [26,27,28,29]. Motivated by the above statements and extending the results of [22,25], in this work, we are concerned with the problem of controllability of impulsive fractional differential systems with distributed delays in controls.

$$\begin{array}{ccc}\hfill {}^C{D}^{\alpha }x(t)& =& \mathfrak{A}x(t)+Kx(t-\tau )+{\int }_{-h}^0{d}_{\tau }\mathfrak{B}(t,\tau )u(t+\tau )+f(t,x(t),x(t-h),u(t-\tau )),\hfill \\ & & t\in [0,T]-\{t_1,t_2,\dots ,t_k\},\hfill \\ \hfill \mathsf{\Delta }x(t_i)& =& x(t_i^{+})-x(t_i^{-})=I_i(x(t_i)),i=1,2,\dots ,k,\hfill \\ \hfill x(t)& =& \phi (t),t\in [-\tau ,0],\hfill \end{array}$$

(1)

where ${}^C{D}^{\alpha }$ represents the Caputo fractional derivative of order $\alpha$, $0<\alpha <1$ and $\mathfrak{A}\in {\mathbb{R}}^{n\times n}$ denotes a constant matrix, $x\in {\mathbb{R}}^n$ is the state variable and the third integral term is in the Lebesgue–Stieltjes sense with respect to $\tau$. Let $f,k$ and $h>0$ be given. The control input $u:[-h,T]\to {\mathbb{R}}^m$ for all $t\in J$, and $u_t$ denotes the function on $[-h,0]$, defined by $u_t(s)=u(t+s)$ for $s\in [-h,0)$. $\mathfrak{B}(t,\tau )$ is an $n\times m$ dimensional matrix continuous in t for fixed $\tau$ and is of bounded variation in $\tau$ on $[-h,0)$ for each $t\in J$ and continuous from left in $\tau$ on the interval. $(-h,0)$, $\varphi \in C([-\tau ,0],{\mathbb{R}}^n)$ is the initial state function, where $C([-\tau ,0],{\mathbb{R}}^n)$ denotes the space of all continuous functions mapping the interval $[-\tau ,0]$ into ${\mathbb{R}}^n;I_i:{\mathbb{R}}^n\to {\mathbb{R}}^n$ is continuous for $i=1,2,\dots ,k$, and

$$\begin{array}{c}\hfill x(t_i^{+})=\underset{\epsilon \to 0^{+}}{lim}x(t_i+\epsilon ),\\ \hfill x(t_i^{-})=\underset{\epsilon \to 0^{-}}{lim}x(t_i+\epsilon ),\end{array}$$

(2)

represent the right and left limits of $x(t)$ at $t=t_i$ and the discontinuous points

$$\begin{array}{c}\hfill t_1<t_2<\dots <t_i<\dots <t_k,\end{array}$$

where $0=t_0<\tau <t_1,t_k<t_{k+1}=T<+\infty$, and $x(t_i)=x(t_i^{-})$, which implies that the solution of the system (1) is left continuous at $t_i$.

The notable contributions of our work is as follows:

• Nonlinear impulsive fractional differential systems with distributed delays in controls are considered.
• The solution representation is formulated via an unsymmetric Fubini’s theorem.
• The controllability of the linear system is proved by using the controllability Gramian operator.
• The controllability of the nonlinear system is investigated by employing the Schauder fixed-point theorem.
• Numerical treatments are given using MATLAB.

Our paper is organized as follows. In Section 2, we present some basic definitions and preliminary facts, which will be used in order to obtain our desired results. In Section 3, we state and prove the main results of this work. In Section 4, an example is given to illustrate the effectiveness and validity of our controllability results. Finally, we conclude our results and suggest new directions in Section 5.

2. Preliminaries

Throughout the paper, $C_P([0,T],{\mathbb{R}}^n)$ denotes the space of all piecewise left-continuous functions mapping the interval $[0,T]$ into ${\mathbb{R}}^n$.

Definition 1 ([18]).

The Caputo fractional derivative of order $\alpha >0$, $n-1<\alpha <n$ is defined as

$$\begin{array}{c}\hfill {(}^C{D}_{0+}^{\alpha }f)(t)=\frac{1}{\mathsf{\Gamma }(n-\alpha )}{\int }_0^t{(t-s)}^{n-\alpha -1}{f}^{(n)}(s)ds,\end{array}$$

where the function $f(t)$ has absolutely continuous derivatives up to order $(n-1)$. If $0<\alpha <1$, then

$$\begin{array}{ccc}\hfill {(}^C{D}_{0+}^{\alpha }f)(t)& =& \frac{1}{\mathsf{\Gamma }(1-\alpha )}{\int }_0^t\frac{f^{{}^{\prime }}(s)}{{(t-s)}^{\alpha }}ds.\hfill \end{array}$$

Definition 2 ([18]).

The Mittag–Leffler function in two parameters is defined as

$$\begin{array}{c}\hfill E_{\alpha ,\beta }(z)=\sum _{k=0}^{\infty }\frac{z^k}{\mathsf{\Gamma }(k\alpha +\beta )},for\alpha ,\beta >0,\end{array}$$

so that $z\in \mathbb{C}$, $\mathbb{C}$ denotes the complex plane. The general Mittag–Leffler function satisfies

$$\begin{array}{c}\hfill {\int }_0^{\infty }{e}^{-t}{t}^{\beta -1}{E}_{\alpha ,\beta }(t^{\alpha }z)dt=\frac{1}{1-z},for\left|z\right|<1.\end{array}$$

The linear fractional delay differential system without impulses is considered as follows.

$$\begin{array}{ccc}\hfill {}^C{D}^{\alpha }x(t)& =& \mathfrak{A}x(t)+Kx(t-\tau )+{\int }_{-h}^0{d}_{\tau }\mathfrak{B}(t,\tau )u(t+\tau ),t\in [0,T],\hfill \\ \hfill x(t)& =& \phi (t),t\in [-\tau ,0].\hfill \end{array}$$

(3)

The nonlinear fractional delay differential system without impulses is considered as follows.

$$\begin{array}{ccc}\hfill {}^C{D}^{\alpha }x(t)& =& \mathfrak{A}x(t)+Kx(t-\tau )+{\int }_{-h}^0{d}_{\tau }\mathfrak{B}(t,\tau )u(t+\tau )+f(t,x(t),x(t-\tau ),u(t)),t\in [0,T],\hfill \\ \hfill x(t)& =& \phi (t),t\in [-\tau ,0].\hfill \end{array}$$

(4)

Lemma 1.

For $0<\alpha <1$, if $f:[0,T]\to {\mathbb{R}}^n$ is continuous and exponentially bounded, then the solution of the system (3) can be represented as

$$\begin{array}{ccc}\hfill x(t)& =& \varphi (0)+{\int }_0^t{(t-s)}^{\alpha -1}{E}_{\alpha ,\alpha }(\mathfrak{A}{(t-s)}^{\alpha })[\mathfrak{A}\varphi (0)+Kx(s-\tau )]ds\hfill \\ & & +{\int }_{-h}^{0}d{\mathfrak{B}}_{\tau }[{\int }_{\tau }^0{(t-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }(\mathfrak{A}{(t-(s-\tau ))}^{\alpha })\mathfrak{B}(s-\tau ,\tau )u_0(s)ds]\hfill \\ & & +{\int }_0^t[{\int }_{-h}^0{(t-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }(\mathfrak{A}{(t-(s-\tau ))}^{\alpha })d_{\tau }{\mathfrak{B}}_t(s-\tau ,\tau )u(s)ds,t\in [0,T],\hfill \end{array}$$

$$\begin{array}{c}\hfill where{\mathfrak{B}}_t(s,\tau )=\left\{\begin{array}{c}\mathfrak{B}(s,\tau ),s\le t,\hfill \\ 0,s>t,\hfill \end{array}\right.\end{array}$$

$$\begin{array}{ccc}\hfill andx(t)& =& \phi (t),t\in [-\tau ,0].\hfill \end{array}$$

Proof. 

Let $t\in [0,T]$, employing the Laplace transform with respect to t on both sides of system (3), the result is

$$\begin{array}{ccc}\hfill s^{\alpha }L[x(t)]-s^{\alpha -1}\varphi (0)& =& \mathfrak{A}L[x(t)]+L[Kx(t-\tau )+{\int }_{-h}^0{d}_{\tau }\mathfrak{B}(t,\tau )u(t+\tau )],\hfill \\ \hfill L[x(t)]& =& {(s^{\alpha }I-\mathfrak{A})}^{-1}{s}^{\alpha -1}\varphi (0)+{(s^{\alpha }I-\mathfrak{A})}^{-1}L[Kx(t-\tau )+{\int }_{-h}^0{d}_{\tau }\mathfrak{B}(t,\tau )u(t+\tau )],\hfill \\ \hfill L[x(t)]& =& L[\varphi (0)]+{(s^{\alpha }I-\mathfrak{A})}^{-1}L[\mathfrak{A}\varphi (0)+Kx(t-\tau )+{\int }_{-h}^0{d}_{\tau }\mathfrak{B}(t,\tau )u(t+\tau )],\hfill \\ & =& L[\varphi (0)]+L[t^{\alpha -1}{E}_{\alpha ,\alpha }(\mathfrak{A}{t}^{\alpha })]L[\mathfrak{A}\varphi (0)+Kx(t-\tau )\hfill \\ & & +{\int }_{-h}^0{d}_{\tau }\mathfrak{B}(t,\tau )u(t+\tau )].\hfill \end{array}$$

(5)

Applying the convolution theorem of the Laplace transform to (5), we get

$$\begin{array}{ccc}\hfill L[x(t)]& =& L[\varphi (0)]+L[t^{\alpha -1}{E}_{\alpha ,\alpha }(\mathfrak{A}{t}^{\alpha })][\mathfrak{A}\varphi (0)+Kx(t-\tau )+{\int }_{-h}^0{d}_{\tau }\mathfrak{B}(t,\tau )u(t+\tau )].\hfill \end{array}$$

Employing the inverse Laplace transform, then we have

$$\begin{array}{ccc}\hfill x(t)& =& \varphi (0)+{\int }_0^t{(t-s)}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(t-s)}^{\alpha }][\mathfrak{A}\varphi (0)+Kx(s-\tau )]ds\hfill \\ & & +{\int }_0^t{(t-s)}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(t-s)}^{\alpha }][{\int }_{-h}^0{d}_{\tau }\mathfrak{B}(s,\tau )u(s+\tau )]ds.\hfill \end{array}$$

Using the well-known result of the unsymmetric Fubini theorem [30] and the change of order of the integration to the last term, we have

$$\begin{array}{ccc}\hfill x(t)& =& \varphi (0)+{\int }_0^t{(t-s)}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(t-s)}^{\alpha }][\mathfrak{A}\varphi (0)+Kx(s-\tau )]ds\hfill \\ & & +{\int }_{-h}^{0}d{\mathfrak{B}}_{\tau }[{\int }_0^t{(t-s)}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(t-s)}^{\alpha }]u(s+\tau )\mathfrak{B}(s,\tau )ds]\hfill \\ & =& \varphi (0)+{\int }_0^t{(t-s)}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(t-s)}^{\alpha }][\mathfrak{A}\varphi (0)+Kx(s-\tau )]ds\hfill \\ & & +{\int }_{-h}^{0}d{\mathfrak{B}}_{\tau }[{\int }_{\tau }^0{(t-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(t-(s-\tau ))}^{\alpha }]\mathfrak{B}(s-\tau ,\tau )u_0(s)ds]\hfill \\ & & +{\int }_{-h}^{0}d{\mathfrak{B}}_{\tau }[{\int }_0^{t+\tau }{(t-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(t-(s-\tau ))}^{\alpha }]\mathfrak{B}(s-\tau ,\tau )u(s)ds]\hfill \\ & =& \varphi (0)+{\int }_0^t{(t-s)}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(t-s)}^{\alpha }][\mathfrak{A}\varphi (0)+Kx(s-\tau )]ds\hfill \\ & & +{\int }_{-h}^{0}d{\mathfrak{B}}_{\tau }[{\int }_{\tau }^0{(t-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(t-(s-\tau ))}^{\alpha }]\mathfrak{B}(s-\tau ,\tau )u_0(s)ds]\hfill \\ & & +{\int }_0^t[{\int }_{-h}^0{(t-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(t-(s-\tau ))}^{\alpha }]d_{\tau }{\mathfrak{B}}_t(s-\tau ,\tau ))u(s)ds,\hfill \end{array}$$

where

$$\begin{array}{c}\hfill {\mathfrak{B}}_t(s,\tau )=\left\{\begin{array}{c}\mathfrak{B}(s,\tau ),s\le t,\hfill \\ 0,s>t,\hfill \end{array}\right.\end{array}$$

and $d{\mathfrak{B}}_{\tau }$ denotes the integration of the Lebesgue–Stieltjes sense with respect to the variable $\tau$ in the function $\mathfrak{B}(t,\tau )$, hence the proof. □

Lemma 2.

For $0<\alpha <1$, the solution representation of the nonlinear structure (4) is

$$\begin{array}{ccc}\hfill x(t)& =& \varphi (0)+{\int }_0^t{(t-s)}^{\alpha -1}{E}_{\alpha ,\alpha }(\mathfrak{A}{(t-s)}^{\alpha })[\mathfrak{A}\varphi (0)+Kx(s-\tau )+f(s,x(s),x(s-h),u(s))]ds,\hfill \\ & & +{\int }_{-h}^{0}d{\mathfrak{B}}_{\tau }[{\int }_{\tau }^0{(t-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }(\mathfrak{A}{(t-(s-\tau ))}^{\alpha })\mathfrak{B}(s-\tau ,\tau )u_0(s)ds],\hfill \\ & & +{\int }_0^t[{\int }_{-h}^0{(t-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }(\mathfrak{A}{(t-(s-\tau ))}^{\alpha })d_{\tau }{\mathfrak{B}}_t(s-\tau ,\tau )]u(s)ds,t\in [0,T],\hfill \end{array}$$

(6)

where

$$\begin{array}{c}\hfill {\mathfrak{B}}_t(s,\tau )=\left\{\begin{array}{c}\mathfrak{B}(s,\tau ),s\le t,\hfill \\ 0,s>t,\hfill \end{array}\right.\end{array}$$

$$\begin{array}{ccc}\hfill andx(t)& =& \phi (t),t\in [-\tau ,0].\hfill \end{array}$$

Proof. 

The proof is similar to Lemma 1. Hence, it is eliminated. □

Lemma 3.

Let $0<\alpha <1$ and $u\in C_p([0,T],{\mathbb{R}}^m)$ then the solution of structure (1) is as follows.

For $t\in [-\tau ,0],$ $x(t)=\phi (t),$

For $t\in [0,t_1),$

$$\begin{array}{ccc}\hfill x(t)& =& \varphi (0)+{\int }_0^t{(t-s)}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(t-s)}^{\alpha }][\mathfrak{A}\varphi (0)+Kx(s-\tau ))]ds,\hfill \\ & & +{\int }_{-h}^{0}d{\mathfrak{B}}_{\tau }[{\int }_{\tau }^0{(t-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(t-(s-\tau ))}^{\alpha }]\mathfrak{B}(s-\tau ,\tau )u_0(s)ds],\hfill \\ & & +{\int }_0^t[{\int }_{-h}^0{(t-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(t-(s-\tau ))}^{\alpha }]d_{\tau }{\mathfrak{B}}_t(s-\tau ,\tau ))u(s)ds.\hfill \end{array}$$

(7)

For $t\in (t_1,t_2),$

$$\begin{array}{ccc}\hfill x(t)& =& \varphi (0)+I_1(x(t_1^{-}))+{\int }_0^t{(t-s)}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(t-s)}^{\alpha }][\mathfrak{A}\varphi (0)+Kx(s-\tau )]ds,\hfill \\ & & +{\int }_{-h}^{0}d{\mathfrak{B}}_{\tau }[{\int }_{\tau }^0{(t-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(t-(s-\tau ))}^{\alpha }]\mathfrak{B}(s-\tau ,\tau )u_0(s)ds],\hfill \\ & & +{\int }_0^t[{\int }_{-h}^0{(t-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(t-(s-\tau ))}^{\alpha }]d_{\tau }{\mathfrak{B}}_t(s-\tau ,\tau ))u(s)ds.\hfill \end{array}$$

(8)

For $t\in (t_i,T],i=1,2,\dots ,k$,

$$\begin{array}{ccc}\hfill x(t)& =& \varphi (0)+\sum _{j=1}^i{I}_j(x(t_j^{-})+{\int }_0^t{(t-s)}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(t-s)}^{\alpha }][\mathfrak{A}\varphi (0)+Kx(s-\tau )]ds,\hfill \end{array}$$

$$\begin{array}{ccc}& & +{\int }_{-h}^{0}d{\mathfrak{B}}_{\tau }[{\int }_{\tau }^0{(t-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(t-(s-\tau ))}^{\alpha }]\mathfrak{B}(s-\tau ,\tau )u_0(s)ds],\hfill \\ & & +{\int }_0^t[{\int }_{-h}^0{(t-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(t-(s-\tau ))}^{\alpha }]d_{\tau }{\mathfrak{B}}_t(s-\tau ,\tau ))u(s)ds.\hfill \end{array}$$

(9)

Proof. 

For $t\in [-\tau ,0]$, the proof is obvious. For $t\in [0,t_1)$, by Lemma 2,

$$\begin{array}{ccc}\hfill x(t)& =& \varphi (0)+{\int }_0^t{(t-s)}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(t-s)}^{\alpha }][\mathfrak{A}\varphi (0)+Kx(s-\tau )]ds\hfill \\ & & +{\int }_{-h}^{0}d{\mathfrak{B}}_{\tau }[{\int }_{\tau }^0{(t-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(t-(s-\tau ))}^{\alpha }]\mathfrak{B}(s-\tau ,\tau )u_0(s)ds]\hfill \\ & & +{\int }_0^t[{\int }_{-h}^0{(t-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(t-(s-\tau ))}^{\alpha }]d_{\tau }{\mathfrak{B}}_t(s-\tau ,\tau ))u(s)ds.\hfill \\ \hfill x(t_1)& =& \varphi (0)+{\int }_0^{t_1}{(t_1-s)}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(t_1-s)}^{\alpha }][\mathfrak{A}\varphi (0)+Kx(s-\tau )]ds\hfill \\ & & +{\int }_{-h}^{0}d{\mathfrak{B}}_{\tau }[{\int }_{\tau }^0{(t_1-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(t_1-(s-\tau ))}^{\alpha }]\mathfrak{B}(s-\tau ,\tau )u_0(s)ds]\hfill \\ & & +{\int }_0^{t_1}[{\int }_{-h}^0{(t_1-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(t_1-(s-\tau ))}^{\alpha }]d_{\tau }{\mathfrak{B}}_{t_1}(s-\tau ,\tau ))u(s)ds.\hfill \end{array}$$

If $t\in (t_1,t_2)$, using (7), we have

$$\begin{array}{ccc}\hfill x(t)& =& x(t_1^{+})-{\int }_0^{t_1}{(t_1-s)}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(t_1-s)}^{\alpha }][\mathfrak{A}\varphi (0)+Kx(s-\tau )]ds\hfill \\ & & +{\int }_{-h}^{0}d{\mathfrak{B}}_{\tau }[{\int }_{\tau }^0{(t_1-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(t_1-(s-\tau ))}^{\alpha }]\mathfrak{B}(s-\tau ,\tau )u_0(s)ds]\hfill \\ & & +{\int }_0^{t_1}[{\int }_{-h}^0{(t_1-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(t_1-(s-\tau ))}^{\alpha }]d_{\tau }{\mathfrak{B}}_{t_1}(s-\tau ,\tau ))u(s)ds\hfill \\ & & +{\int }_0^t{(t-s)}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(t-s)}^{\alpha }][\mathfrak{A}\varphi (0)+Kx(s-\tau )]ds+{\int }_{-h}^{0}d{\mathfrak{B}}_{\tau }[{\int }_{\tau }^0{(t-(s-\tau ))}^{\alpha -1}\hfill \\ & & \times E_{\alpha ,\alpha }[\mathfrak{A}{(t-(s-\tau ))}^{\alpha }]\mathfrak{B}(s-\tau ,\tau )u_0(s)ds]+{\int }_0^t[{\int }_{-h}^0{(t-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(t-(s-\tau ))}^{\alpha }]\hfill \\ & & \times d_{\tau }{\mathfrak{B}}_t(s-\tau ,\tau ))u(s)ds.\hfill \\ \hfill x(t)& =& x(t_1^{-})+I_1(x(t_1^{-}))-{\int }_0^{t_1}{(t_1-s)}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(t_1-s)}^{\alpha }][\mathfrak{A}\varphi (0)+Kx(s-\tau )]ds\hfill \\ & & +{\int }_{-h}^{0}d{\mathfrak{B}}_{\tau }[{\int }_{\tau }^0{(t_1-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(t_1-(s-\tau ))}^{\alpha }]\mathfrak{B}(s-\tau ,\tau )u_0(s)ds]\hfill \\ & & +{\int }_0^{t_1}[{\int }_{-h}^0{(t_1-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(t_1-(s-\tau ))}^{\alpha }]d_{\tau }{\mathfrak{B}}_{t_1}(s-\tau ,\tau ))u(s)ds\hfill \\ & & +{\int }_0^t{(t-s)}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(t-s)}^{\alpha }][\mathfrak{A}\varphi (0)+Kx(s-\tau )]ds+{\int }_{-h}^{0}d{\mathfrak{B}}_{\tau }[{\int }_{\tau }^0{(t-(s-\tau ))}^{\alpha -1}\hfill \\ & & \times E_{\alpha ,\alpha }[\mathfrak{A}{(t-(s-\tau ))}^{\alpha }]\mathfrak{B}(s-\tau ,\tau )u_0(s)ds]+{\int }_0^t[{\int }_{-h}^0{(t-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(t-(s-\tau ))}^{\alpha }]\hfill \\ & & \times d_{\tau }{\mathfrak{B}}_t(s-\tau ,\tau ))u(s)ds\hfill \\ \hfill x(t)& =& \varphi (0)+I_1(x(t_1^{-}))+{\int }_0^t{(t-s)}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(t-s)}^{\alpha }][\mathfrak{A}\varphi (0)+Kx(s-\tau )]ds\hfill \end{array}$$

$$\begin{array}{ccc}& & +{\int }_{-h}^{0}d{\mathfrak{B}}_{\tau }[{\int }_{\tau }^0{(t-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(t-(s-\tau ))}^{\alpha }]\mathfrak{B}(s-\tau ,\tau )u_0(s)ds]\hfill \\ & & +{\int }_0^t[{\int }_{-h}^0{(t-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(t-(s-\tau ))}^{\alpha }]d_{\tau }{\mathfrak{B}}_t(s-\tau ,\tau ))u(s)ds.\hfill \end{array}$$

If $t\in (t_2,t_3)$, then

$$\begin{array}{ccc}\hfill x(t)& =& x(t_2^{+})-{\int }_0^{t_2}{(t_2-s)}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(t_2-s)}^{\alpha }][\mathfrak{A}\varphi (0)+Kx(s-\tau )]ds\hfill \\ & & +{\int }_{-h}^{0}d{\mathfrak{B}}_{\tau }[{\int }_{\tau }^0{(t_2-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(t_2-(s-\tau ))}^{\alpha }]\mathfrak{B}(s-\tau ,\tau )u_0(s)ds]\hfill \\ & & +{\int }_0^{t_2}[{\int }_{-h}^0{(t_2-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(t_2-(s-\tau ))}^{\alpha }]d_{\tau }{\mathfrak{B}}_{t_2}(s-\tau ,\tau ))u(s)ds\hfill \\ & & +{\int }_0^t{(t-s)}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(t-s)}^{\alpha }][\mathfrak{A}\varphi (0)+Kx(s-\tau )]ds\hfill \\ & & +{\int }_{-h}^{0}d{\mathfrak{B}}_{\tau }[{\int }_{\tau }^0{(t-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(t-(s-\tau ))}^{\alpha }]\mathfrak{B}(s-\tau ,\tau )u_0(s)ds]\hfill \\ & & +{\int }_0^t[{\int }_{-h}^0{(t-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(t-(s-\tau ))}^{\alpha }]d_{\tau }{\mathfrak{B}}_t(s-\tau ,\tau ))u(s)ds.\hfill \\ \hfill x(t)& =& \varphi (0)+\sum _{j=1}^2{I}_j(x(t_j^{-}))+{\int }_0^t{(t-s)}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(t-s)}^{\alpha }][\mathfrak{A}\varphi (0)+Kx(s-\tau )]ds\hfill \\ & & +{\int }_{-h}^{0}d{\mathfrak{B}}_{\tau }[{\int }_{\tau }^0{(t-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(t-(s-\tau ))}^{\alpha }]\mathfrak{B}(s-\tau ,\tau )u_0(s)ds]\hfill \\ & & +{\int }_0^t[{\int }_{-h}^0{(t-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(t-(s-\tau ))}^{\alpha }]d_{\tau }{\mathfrak{B}}_t(s-\tau ,\tau ))u(s)ds.\hfill \end{array}$$

If $t\in (t_i,T](i=1,2,\dots ,k)$, using similar reasoning, we get

$$\begin{array}{ccc}\hfill x(t)& =& \varphi (0)+\sum _{j=1}^i{I}_j(x(t_j^{-}))+{\int }_0^t{(t-s)}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(t-s)}^{\alpha }][\mathfrak{A}\varphi (0)+Kx(s-\tau )]ds\hfill \\ & & +{\int }_{-h}^{0}d{\mathfrak{B}}_{\tau }[{\int }_{\tau }^0{(t-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(t-(s-\tau ))}^{\alpha }]\mathfrak{B}(s-\tau ,\tau )u_0(s)ds]\hfill \\ & & +{\int }_0^t[{\int }_{-h}^0{(t-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(t-(s-\tau ))}^{\alpha }]d_{\tau }{\mathfrak{B}}_t(s-\tau ,\tau ))u(s)ds.\hfill \end{array}$$

The proof is complete. □

3. Controllability Results

In this section, we prove the controllability result of the labelled system.

Definition 3.

System (1) is called controllable on $[0,w](w\in (0,T]);$ for any initial function, $\phi \in C([-\tau ,0],{\mathbb{R}}^n)$, and any state, $x_w\in {\mathbb{R}}^n$, there exists a control input $u(t)\in C_p([0,w],{\mathbb{R}}^m),$ so that the corresponding solution of (1) satisfies $x(w)=x_w$.

Theorem 1.

Structure (1) is controllable on $[0,w]$ if and only if the Gramian matrix

$$\begin{array}{c}\hfill W_C[0,w]={\int }_0^{w}G(w-s)G^{\ast }(w,s)ds,\end{array}$$

(10)

is nonsingular for some $w\in [0,T]$, where

$$\begin{array}{c}\hfill G(w,s)={\int }_{-h}^0{(w-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(t-(s-\tau ))}^{\alpha }]d_{\tau }{\mathfrak{B}}_w(s-\tau ,\tau )\end{array}$$

and ∗ denotes the matrix transpose.

Proof. 

Assume that $W[0,w]$ is nonsingular, then $W^{-1}[0,w]$ is well defined. If $\phi \in C([-\tau ,0],{\mathbb{R}}^n)$, let $w\in [0,t_1]$ the control function is

$$\begin{array}{ccc}\hfill u(t)& =& G^{\ast }(w,t)W^{-1}[0,w][x_w-\varphi (0)-{\int }_0^w{(w-s)}^{\alpha -1}{E}_{\alpha ,\alpha }(\mathfrak{A}{(w-s)}^{\alpha })[\mathfrak{A}\varphi (0)+Kx(s-\tau )]ds,\hfill \\ & & -{\int }_{-h}^{0}d{\mathfrak{B}}_{\tau }[{\int }_{\tau }^0{(w-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }\mathfrak{A}{(w-(s-\tau ))}^{\alpha }\mathfrak{B}(s-\tau ,\tau )u_0(s)ds]].\hfill \end{array}$$

(11)

By substituting $t=w$ in (7) and inserting (11), we get

$$\begin{array}{ccc}\hfill x(w)& =& \varphi (0)+{\int }_0^w{(w-s)}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(w-s)}^{\alpha }][\mathfrak{A}\varphi (0)+Kx(s-\tau ))]ds\hfill \\ & & +{\int }_{-h}^{0}d{\mathfrak{B}}_{\tau }[{\int }_{\tau }^0{(w-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(w-(s-\tau ))}^{\alpha }]\mathfrak{B}(s-\tau ,\tau )u_0(s)ds]\hfill \\ & & +{\int }_0^{w}G(w,s)G^{\ast }(w,s)W^{-1}[0,w][x_w-\varphi (0)-{\int }_0^w{(w-s)}^{\alpha -1}{E}_{\alpha ,\alpha }(\mathfrak{A}{(w-s)}^{\alpha })\hfill \\ & & \times [\mathfrak{A}\varphi (0)+Kx(s-\tau )]ds-{\int }_{-h}^{0}d{\mathfrak{B}}_{\tau }[{\int }_{\tau }^0{(w-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }\mathfrak{A}{(w-(s-\tau ))}^{\alpha }\hfill \\ & & \times \mathfrak{B}(s-\tau ,\tau )u_0(s)ds]]d\tau .\hfill \\ \hfill x(w)& =& x_w.\hfill \end{array}$$

Thus, system (1) is controllable on $[0,w],w\in [0,t_1]$. For $w\in (t_1,t_2]$, we take the control function as

$$\begin{array}{ccc}\hfill u(t)& =& G^{\ast }(w,t)W^{-1}[0,w][x_w-\varphi (0)-I_1(x(t_1^{-}))-{\int }_0^w{(w-s)}^{\alpha -1}{E}_{\alpha ,\alpha }(\mathfrak{A}{(w-s)}^{\alpha })\hfill \\ & & \times [\mathfrak{A}\varphi (0)+Kx(s-\tau )]ds-{\int }_{-h}^{0}d{\mathfrak{B}}_{\tau }[{\int }_{\tau }^0{(w-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }\mathfrak{A}{(w-(s-\tau ))}^{\alpha }\hfill \\ & & \mathfrak{B}(s-\tau ,\tau )u_0(s)ds]].\hfill \end{array}$$

(12)

By substituting $t=w$ in (8) and inserting (12), we get

$$\begin{array}{ccc}\hfill x(w)& =& \varphi (0)+I_1(x(t_1^{-}))+{\int }_0^w{(w-s)}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(w-s)}^{\alpha }][\mathfrak{A}\varphi (0)+Kx(s-\tau ))]ds\hfill \\ & & +{\int }_{-h}^{0}d{\mathfrak{B}}_{\tau }[{\int }_{\tau }^0{(w-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(w-(s-\tau ))}^{\alpha }]\mathfrak{B}(s-\tau ,\tau )u_0(s)ds]\hfill \\ & & +{\int }_0^{w}G(w,s)G^{\ast }(w,s)W^{-1}[0,w][x_w-\varphi (0)-{\int }_0^w{(w-s)}^{\alpha -1}{E}_{\alpha ,\alpha }(\mathfrak{A}{(w-s)}^{\alpha })\hfill \\ & & [\mathfrak{A}\varphi (0)+Kx(s-\tau )]ds-{\int }_{-h}^{0}d{\mathfrak{B}}_{\tau }[{\int }_{\tau }^0{(w-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }\mathfrak{A}{(w-(s-\tau ))}^{\alpha }\hfill \\ & & \times \mathfrak{B}(s-\tau ,\tau )u_0(s)ds]]d\tau .\hfill \\ \hfill x(w)=x_w.\end{array}$$

Hence, system (1) is controllable on $[0,w],w\in [t_1,t_2]$. For $w\in (t_i,t_{i+1}],i=1,2,\dots ,k$, the control function, u, is defined by

$$\begin{array}{ccc}\hfill u(t)& =& G^{\ast }(w,t)W^{-1}[0,w][x_w-\varphi (0)-\sum _{j=1}^i{I}_j(x(t_j^{-}))-{\int }_0^w{(w-s)}^{\alpha -1}{E}_{\alpha ,\alpha }(\mathfrak{A}{(w-s)}^{\alpha })\hfill \\ & & \times [\mathfrak{A}\varphi (0)+Kx(s-\tau )]ds-{\int }_{-h}^{0}d{\mathfrak{B}}_{\tau }[{\int }_{\tau }^0{(w-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }\hfill \\ & & \times \mathfrak{A}{(w-(s-\tau ))}^{\alpha }\mathfrak{B}(s-\tau ,\tau )u_0(s)ds]].\hfill \end{array}$$

(13)

By substituting $t=w$ in (9) and installing the result in (13), similar reasoning gives $x(w)=x_w$. Hence, structure (1) is controllable on $[0,w]$.

Conversely, assume that $W[0,w]$ is singular, If $w\in (t_i,t_{i+1}],i=1,2,\dots ,k$, there is a vector $z_0\ne 0$, such that $z_0^{\ast }W[0,w]z_0=0$. That is,

$$\begin{array}{c}\hfill z_0^{\ast }{\int }_0^{w}G(w,s)G^{\ast }(W,s)z_{0}ds=0,\\ \hfill z_0^{\ast }G(w,s)=0,on[0,w].\end{array}$$

Because structure (1) is controllable, there exist control inputs, $u_1(t) \mathrm{and} u_2(t)$, so that

$$\begin{array}{ccc}\hfill x(w)& =& \varphi (0)+\sum _{j=1}^i{I}_j(x(t_j^{-}))+{\int }_0^w{(w-s)}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(w-s)}^{\alpha }][\mathfrak{A}\varphi (0)+Kx(s-\tau )]ds\hfill \\ & & +{\int }_{-h}^{0}d{\mathfrak{B}}_{\tau }[{\int }_{\tau }^0{(w-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(w-(s-\tau ))}^{\alpha }]\mathfrak{B}(s-\tau ,\tau )u_0(s)ds]\hfill \\ & & +{\int }_0^w[{\int }_{-h}^0{(w-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(w-(s-\tau ))}^{\alpha }]d_{\tau }{\mathfrak{B}}_w(s-\tau ,\tau ))u_1(s)ds.\hfill \end{array}$$

(14)

$$\begin{array}{ccc}\hfill z_0& =& \varphi (0)+\sum _{j=1}^i{I}_j(x(t_j^{-}))+{\int }_0^w{(w-s)}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(w-s)}^{\alpha }][\mathfrak{A}\varphi (0)+Kx(s-\tau )]ds\hfill \\ & & +{\int }_{-h}^{0}d{\mathfrak{B}}_{\tau }[{\int }_{\tau }^0{(w-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(w-(s-\tau ))}^{\alpha }]\mathfrak{B}(s-\tau ,\tau )u_0(s)ds]\hfill \\ & & +{\int }_0^w[{\int }_{-h}^0{(w-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(w-(s-\tau ))}^{\alpha }]d_{\tau }{\mathfrak{B}}_w(s-\tau ,\tau ))u_2(s)ds.\hfill \end{array}$$

(15)

By combining (14) and (15), we get

$$\begin{array}{c}\hfill z_0-{\int }_0^w[{\int }_{-h}^0{(w-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(w-(s-\tau ))}^{\alpha }]d_{\tau }{\mathfrak{B}}_w(s-\tau ,\tau ))(u_2(s)-u_1(s))ds=0.\end{array}$$

(16)

By multiplying $z_0^{\ast }$ on both sides of (16), we get

$$\begin{array}{c}\hfill z_0^{\ast }{z}_0-{\int }_0^w{z}_0^{\ast }G(w,s)[u_2(s)-u_1(s)]ds=0.\end{array}$$

According to $z_0^{\ast }G(w,s)=0$, we have $z_0^{\ast }{z}_0=0$. Thus, $z_0=0$. This is a contradiction to $z_0\ne 0$, hence the proof. □

Definition 4.

Systems (3) or (4) are said to be completely controllable on $[0,w](w\in [0,T]);$ for any initial function, $\phi \in C([-\tau ,0],{\mathbb{R}}^n)$, and any state, $x_w\in {\mathbb{R}}^n$, there exists a control input $u(t)$, so that the corresponding solutions of (3) or (4) satisfy $x(w)=x_w$.

Theorem 2.

System (3) is completely controllable on $[0,w]$ if and only if W is nonsingular for some $w\in [0,T]$.

Proof. 

Assume that W is nonsingular. Let $\varphi (t)$ be continuous on $[-\tau ,0]$, and let $x_w\in {\mathbb{R}}^n$. The control function u can be taken as

$$\begin{array}{ccc}\hfill u(t)& =& G^{\ast }(w,t)W^{-1}[0,w][x_w-\varphi (0)-{\int }_0^w{(w-s)}^{\alpha -1}{E}_{\alpha ,\alpha }(\mathfrak{A}{(w-s)}^{\alpha })[\mathfrak{A}\varphi (0)+Kx(s-\tau )]ds\hfill \\ & & -{\int }_{-h}^{0}d{\mathfrak{B}}_{\tau }[{\int }_{\tau }^0{(w-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }\mathfrak{A}{(w-(s-\tau ))}^{\alpha }\mathfrak{B}(s-\tau ,\tau )u_0(s)ds]],\hfill \end{array}$$

(17)

where

$$\begin{array}{c}\hfill G(w,s)={\int }_{-h}^0{(w-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }[\mathfrak{A}{(t-(s-\tau ))}^{\alpha }]d_{\tau }{\mathfrak{B}}_w(s-\tau ,\tau ).\end{array}$$

By substituting $t=w$ in the solution of (7), we get

$$\begin{array}{ccc}\hfill x(w)& =& \varphi (0)+{\int }_0^w{(w-s)}^{\alpha -1}{E}_{\alpha ,\alpha }(\mathfrak{A}{(w-s)}^{\alpha })[\mathfrak{A}\varphi (0)+Kx(s-\tau )]ds\hfill \\ & & +{\int }_{-h}^{0}d{\mathfrak{B}}_{\tau }[{\int }_{\tau }^0{(w-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }(A{(w-(s-\tau ))}^{\alpha })\mathfrak{B}(s-\tau ,\tau )u_0(s)ds]\hfill \\ & & +{\int }_0^w[{\int }_{-h}^0{(w-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }(\mathfrak{A}{(w-(s-\tau ))}^{\alpha })d_{\tau }{\mathfrak{B}}_w(s-\tau ,\tau )]u(s)ds.\hfill \end{array}$$

(18)

and, using (17) in (18), we have

$$\begin{array}{ccc}\hfill x(w)& =& \varphi (0)+{\int }_0^w{(w-s)}^{\alpha -1}{E}_{\alpha ,\alpha }(\mathfrak{A}{(w-s)}^{\alpha })[\mathfrak{A}\varphi (0)+Kx(s-\tau )]ds\hfill \\ & & +{\int }_{-h}^{0}d{\mathfrak{B}}_{\tau }[{\int }_{\tau }^0{(w-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }(\mathfrak{A}{(w-(s-\tau ))}^{\alpha })\mathfrak{B}(s-\tau ,\tau )u_0(s)ds]\hfill \\ & & +{\int }_0^{w}G(w,s)G^{\ast }(w,s)W^{-1}[0,w][x_w-\varphi (0)-{\int }_0^w{(w-s)}^{\alpha -1}{E}_{\alpha ,\alpha }(\mathfrak{A}{(w-s)}^{\alpha })\hfill \\ & & \times [\mathfrak{A}\varphi (0)+Kx(s-\tau )]ds-{\int }_{-h}^{0}d{\mathfrak{B}}_{\tau }[{\int }_{\tau }^0{(w-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }\hfill \\ & & \times \mathfrak{A}{(w-(s-\tau ))}^{\alpha }\mathfrak{B}(s-\tau ,\tau )u_0(s)ds]]d\tau .\hfill \\ \hfill x(w)& =& x_w.\hfill \end{array}$$

Now, we assume that W is singular. There exists a non-zero, z, so that $z^{\ast }Wz=0$. That is, $Z^{\ast }{\int }_0^{w}G(w,s)G^{\ast }(w,s)zds=0$. $z^{\ast }G(w,s)=0on[0,w],w\in [0,T]$. Take $\varphi =0$ and the terminal point, $x_w=z$. Since the system is controllable, there exists a control, $u(t)$, on J that steers the response to $x_w=z$ at $t=w$, that is, $x(w)=z$. From $\varphi =0,x(w,\varphi )=0$, and $z^{\ast }z\ne 0$ for $z\ne 0$. On the other hand,

$$\begin{array}{ccc}\hfill z& =& x(w)=\varphi (0)+{\int }_0^w{(w-s)}^{\alpha -1}{E}_{\alpha ,\alpha }(\mathfrak{A}{(w-s)}^{\alpha })[\mathfrak{A}\varphi (0)+Kx(s-\tau )]ds\hfill \\ & & +{\int }_{-h}^{0}d{\mathfrak{B}}_{\tau }[{\int }_{\tau }^0{(w-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }(\mathfrak{A}{(w-(s-\tau ))}^{\alpha })\mathfrak{B}(s-\tau ,\tau )u_0(s)ds]\hfill \\ & & +{\int }_0^w[{\int }_{-h}^0{(w-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }(\mathfrak{A}{(w-(s-\tau ))}^{\alpha })d_{\tau }{\mathfrak{B}}_w(s-\tau ,\tau )]u(s)ds,\hfill \end{array}$$

hence

$$\begin{array}{ccc}\hfill z^{\ast }z& =& {\int }_0^w{z}^{\ast }G(w,s)u(s)ds+z^{\ast }{\int }_{-h}^{0}d{\mathfrak{B}}_{\tau }[{\int }_{\tau }^0{(w-(s-\tau ))}^{\alpha -1}\hfill \\ & & \times E_{\alpha ,\alpha }(\mathfrak{A}{(w-(s-\tau ))}^{\alpha })\mathfrak{B}(s-\tau ,\tau )u_0(s)ds].\hfill \end{array}$$

Therefore, $z^{\ast }z=0$, which yields a contradiction that $z\ne 0$. Hence, W is nonsingular, hence the proof. □

Theorem 3.

Let the continuous function, f, satisfy the condition $lim\left|p\right|\to \infty \frac{|f(t,p)|}{\left|p\right|}=0$ uniformly in $t\in J$, and suppose that the system, (3), is completely controllable on J. Then, the system (4) is completely controllable on J. Here $p=(x,z,u)\in {\mathbb{R}}^n\times {\mathbb{R}}^n\times {\mathbb{R}}^m$, and let $\left|p\right|=\left|x\right|+\left|z\right|+\left|u\right|$.

Proof. 

Let $\varphi (t)$ be continuous on $[-\tau ,0]$, and let $x_w\in {\mathbb{R}}^n$. Let Q be the Banach space of all the continuous functions $(x,u):[-\tau ,w]\times [-\tau ,w]\to {\mathbb{R}}^n\times {\mathbb{R}}^m$, with the norm $\Vert (x,u)\Vert =\Vert x\Vert +\Vert u\Vert$, where $\Vert x(t)\Vert =\{sup|x(t)|fort\in [-\tau ,w]\}$ and $\Vert u\Vert =\left\{sup\right|u(t)|fort\in [0,w]\}$. The operator $\mathsf{\Psi }:Q\to Q$ is defined by $\mathsf{\Psi }(x,u)=(z,v)$, where

$$\begin{array}{ccc}\hfill v(t)& =& G^{\ast }(w,t)W^{-1}[0,w][x_w-\varphi (0)-{\int }_0^w{(w-s)}^{\alpha -1}{E}_{\alpha ,\alpha }(\mathfrak{A}{(w-s)}^{\alpha })[\mathfrak{A}\varphi (0)+Kx(s-\tau )]ds\hfill \\ & & -{\int }_{-h}^{0}d{\mathfrak{B}}_{\tau }[{\int }_{\tau }^0{(w-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }\mathfrak{A}{(w-(s-\tau ))}^{\alpha }\mathfrak{B}(s-\tau ,\tau )u_0(s)ds]].\hfill \\ \hfill z(t)& =& \varphi (0)+{\int }_0^w{(w-s)}^{\alpha -1}{E}_{\alpha ,\alpha }(\mathfrak{A}{(w-s)}^{\alpha })[\mathfrak{A}\varphi (0)+Kx(s-\tau )]ds\hfill \\ & & +{\int }_{-h}^{0}d{\mathfrak{B}}_{\tau }[{\int }_{\tau }^0{(w-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }(\mathfrak{A}{(w-(s-\tau ))}^{\alpha })\mathfrak{B}(s-\tau ,\tau )u_0(s)ds]\hfill \\ & & +{\int }_0^w[{\int }_{-h}^0{(w-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }(\mathfrak{A}{(w-(s-\tau ))}^{\alpha })d_{\tau }{\mathfrak{B}}_w(s-\tau ,\tau )]u(s)ds,\hfill \end{array}$$

for $t\in J$ and $z(t)=\varphi (t),t\in [-\tau ,0]$. Let

$$\begin{array}{cc}\hfill a_1& =sup\Vert \varphi (0)\Vert ,a_2=sup\Vert Kx(s-\tau )\Vert ,\hfill \\ \hfill a_3& =sup\Vert E_{\alpha ,\alpha }(\mathfrak{A}{(w-s)}^{\alpha })\Vert ,a_4=sup\Vert E_{\alpha ,\alpha }(\mathfrak{A}{(w-(s-\tau ))}^{\alpha })\Vert ,\hfill \\ \hfill a_5& =\Vert {\int }_{\tau }^0{(w-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }\mathfrak{A}{(w-(s-\tau ))}^{\alpha }\mathfrak{B}(s-\tau ,\tau )u_0(s)ds\Vert ,\hfill \\ \hfill a_6& =sup\Vert G^{\ast }(w,t)\Vert ,a_7=W^{-1}[0,w],\hfill \\ \hfill a& =max\{a_{4}w\Vert G(w,s)\Vert ,1\},d_1=a_6{a}_7[|x_w+a_1+a_5|],d_2=8(a_1+a_5),\hfill \\ \hfill c_1& =8a_3{a}_6{a}_7{w}^{\alpha }{\alpha }^{-1}(a_1+a_2),c_2=8a_3(a_1+a_2)w^{\alpha }{\alpha }^{-1}\hfill \end{array}$$

$$\begin{array}{cc}\hfill e_1& =8a_3{a}_6{a}_7{w}^{\alpha }{\alpha }^{-1},e_2=8a_3{w}^{\alpha }{\alpha }^{-1},\hfill \\ \hfill c& =max\{c_1,c_2\},d=max\{d_1,d_2\},e=max\{e_1,e_2\},\hfill \\ \hfill sup\left|f\right|& =sups\in J\left\{\right|f(s,x(s),x(s-\tau ),u(s))\left|\right\}.\hfill \end{array}$$

Then,

$$\begin{array}{ccc}\hfill |v(t)|& \le & \Vert G^{\ast }(w,t)\Vert |W^{-1}[0,w]|[x_w+a_1+a_5]+\Vert G^{\ast }(w,t)\Vert |W^{-1}[0,w]|a_3{w}^{\alpha }{\alpha }^{-1}[a_1+a_2]\hfill \\ & & +\Vert G^{\ast }(w,t)\Vert |W^{-1}[0,w]|a_3{w}^{\alpha }{\alpha }^{-1}sup\left|f\right|.\hfill \\ \hfill |u(t)|& \le & \frac{d_1}{8a}+\frac{c_1}{8a}+\frac{e_1}{8a}sup\left|f\right|\hfill \\ & \le & \frac{1}{8a}(d+c+esup|f|).\hfill \\ \hfill |z(t)|& \le & (a_1+a_5)+a_4{\int }_0^t\Vert G(t,s)\Vert \Vert u(s)\Vert ds+a_3{\int }_0^t{(t-s)}^{\alpha -1}sup\left|f\right|ds\hfill \\ & & +a_3{\int }_0^t{(t-s)}^{\alpha -1}(a_1+a_2)ds\hfill \\ & \le & \frac{d}{8}+\frac{1}{8}[d+c+esup|f|]+\frac{e}{8}sup\left|f\right|\hfill \\ & \le & \frac{d}{4}+\frac{c}{8}+\frac{e}{4}sup\left|f\right|.\hfill \end{array}$$

We make the following assumption about the function f, as in [31]. Letting c and d be each pair of the positive constants, there exists a positive constant, r, so that, if $|(x,u)|\le r$, then

$$\begin{array}{c}\hfill c|f(t,p)|+d\le r,\mathrm{for}\mathrm{all}t\in J,\end{array}$$

(19)

then, any $r_1$, as long as $r<r_1$, will also satisfy (19). Let r be chosen so that (19) is satisfied and ${sup}_{-1\le t\le 0}\left|\varphi (t)\right|\le \frac{r}{4}$. Therefore, if $\Vert x\Vert \le \frac{r}{4}$ and $\Vert u\Vert \le \frac{r}{4}$, then $|x(s)|+|x(s-h)|+|u(s)|\le r,s\in J$. It follows that $d+c+esup\left|f\right|\le r,fors\in J$. Therefore, $\left|v(t)\right|\le \frac{r}{8a}forallt\in J$ and, hence, $\Vert v(t)\Vert \le \frac{r}{8a}$, we have $\Vert z\Vert \le \frac{r}{4}$. Thus, if $Q(r)=\{(x,v)\in Q:\Vert x\Vert \le \frac{r}{4}$ and $\Vert u\Vert \le \frac{r}{4}\}$, then $\mathsf{\Psi }$ maps $Q(r)$ into itself. The operator $\mathsf{\Psi }$ is continuous since f is continuous. Let $M_0$ be a bounded subset of Q. Consider a sequence, $(z_j,v_j)$, contained in $\mathsf{\Psi }(M)$; let $(z_j,v_j)=\mathsf{\Psi }(x_j,u_j),forsome(x_j,u_j)\in M_0,forj=1,2,\dots$. Hence, $v_j(t)$ is an equicontinuous and uniformly bounded sequence on $[0,w]$. $\mathsf{\Psi }(M_0)$ is sequentially compact; hence, the closure is sequentially compact. Thus, $\mathsf{\Psi }$ is completely continuous. Since $Q(r)$ is closed, bounded and convex, using the Schauder fixed-point theorem, $\mathsf{\Psi }$ has a fixed point $(x,u)\in Q(r)$, so that $(z,v)=\mathsf{\Psi }(x,u)=(x,u)$.

Therefore,

$$\begin{array}{ccc}\hfill x(t)& =& \varphi (0)+{\int }_0^t{(t-s)}^{\alpha -1}{E}_{\alpha ,\alpha }(\mathfrak{A}{(t-s)}^{\alpha })[\mathfrak{A}\varphi (0)+Kx(s-\tau )+f(s,x(s),x(s-h),u(s))]ds\hfill \\ & & +{\int }_{-h}^{0}d{\mathfrak{B}}_{\tau }[{\int }_{\tau }^0{(t-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }(\mathfrak{A}{(t-(s-\tau ))}^{\alpha })\mathfrak{B}(s-\tau ,\tau )u_0(s)ds]\hfill \\ & & +{\int }_0^t[{\int }_{-h}^0{(t-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }(\mathfrak{A}{(t-(s-\tau ))}^{\alpha })d_{\tau }{\mathfrak{B}}_t(s-\tau ,\tau )u(s)ds,t\in [0,T]=J,\hfill \end{array}$$

where

$$\begin{array}{c}\hfill {\mathfrak{B}}_t(s,\tau )=\left\{\begin{array}{c}\mathfrak{B}(s,\tau ),s\le t,\hfill \\ 0,s>t,\hfill \end{array}\right.\end{array}$$

$$\begin{array}{ccc}\hfill x(t)& =& \phi (t),t\in [-\tau ,0].\hfill \end{array}$$

Therefore, $x(t)$ is the solution to the system, and

$$\begin{array}{ccc}\hfill x(w)& =& \varphi (0)+{\int }_0^w{(w-s)}^{\alpha -1}{E}_{\alpha ,\alpha }(\mathfrak{A}{(w-s)}^{\alpha })[\mathfrak{A}\varphi (0)+Kx(s-\tau )]ds\hfill \\ & & +{\int }_{-h}^{0}d{\mathfrak{B}}_{\tau }[{\int }_{\tau }^0{(w-(s-\tau ))}^{\alpha -1}{E}_{\alpha ,\alpha }(\mathfrak{A}{(w-(s-\tau ))}^{\alpha })\mathfrak{B}(s-\tau ,\tau )u_0(s)ds]\hfill \\ & & +{\int }_0^{w}G(w,s)G^{\ast }(w,s)W^{-1}[0,w][x_w-\varphi (0)-{\int }_0^w{(w-s)}^{\alpha -1}\hfill \\ & & \times E_{\alpha ,\alpha }(\mathfrak{A}{(w-s)}^{\alpha })[\mathfrak{A}\varphi (0)+Kx(s-\tau )]ds-{\int }_{-h}^{0}d{\mathfrak{B}}_{\tau }[{\int }_{\tau }^0{(w-(s-\tau ))}^{\alpha -1}\hfill \\ & & \times E_{\alpha ,\alpha }\mathfrak{A}{(w-(s-\tau ))}^{\alpha }\mathfrak{B}(s-\tau ,\tau )u_0(s)ds]]d\tau .\hfill \\ \hfill x(w)& =& x_w.\hfill \end{array}$$

Hence, the system (4) is completely controllable. □

4. Example

Consider the following linear fractional dynamical system:

$$\begin{array}{ccc}\hfill {}^C{D}^{\frac{1}{2}}{x}_1(t)& =& x_2(t)+{\int }_{-1}^0{e}^{\tau }[sint{u}_1(t+\tau )+cost{u}_2(t+\tau )]d\tau ,\hfill \\ \hfill {}^C{D}^{\frac{1}{2}}{x}_2(t)& =& -x_1(t)+{\int }_{-1}^0{e}^{\tau }[-cost{u}_1(t+\tau )+sint{u}_2(t+\tau )]d\tau ,\hfill \\ \hfill x(t)& =& 1,-1\le t\le 0,\hfill \end{array}$$

(20)

for $t\in [0,3]$ and $\alpha =\frac{1}{2}$. Here,

$$\begin{array}{c}\hfill \mathfrak{A}=\left(\begin{array}{cc}0& 1\\ -1& 0\end{array}\right),\mathfrak{B}(t,\tau )=\left(\begin{array}{cc}{e}^{\tau }sint& e^{\tau }cost\\ -e^{\tau }cost& e^{\tau }sint\end{array}\right),x(t)=\left(\begin{array}{c}{x}_1(t)\\ x_2(t)\end{array}\right)\end{array}$$

and

$$\begin{array}{c}\hfill E_{\frac{1}{2}}(\mathfrak{A}{t}^{\frac{1}{2}})=\left(\begin{array}{cc}\sum _{j=0}^{\infty }\frac{{(-1)}^j{t}^j}{\mathsf{\Gamma }(1+j)}& \sum _{j=0}^{\infty }\frac{{(-1)}^j{t}^{(2j+1)/2}}{\mathsf{\Gamma }(1+(2j+1)/2)}\\ \sum _{j=0}^{\infty }\frac{{(-1)}^j{t}^{(2j+1)/2}}{\mathsf{\Gamma }(1+(2j+1)/2)}& \sum _{j=0}^{\infty }\frac{{(-1)}^j{t}^j}{\mathsf{\Gamma }(1+j)}\end{array}\right).\end{array}$$

Further,

$$\begin{array}{c}\hfill E_{\frac{1}{2},\frac{1}{2}}(\mathfrak{A}{(3-(s-\tau ))}^{\frac{1}{2}})=\left(\begin{array}{ccc}\sum _{j=0}^{\infty }\frac{{(-1)}^j{(3-(s-\tau ))}^j}{\mathsf{\Gamma }(1+j)}& \sum _{j=0}^{\infty }\frac{{(-1)}^j{(3-(s-\tau ))}^{(2j+1)/2}}{\mathsf{\Gamma }[1+(2j+1)/2]}& \\ -\sum _{j=0}^{\infty }\frac{{(-1)}^j{(3-(s-\tau ))}^{(2j+1)/2}}{\mathsf{\Gamma }[1+(2j+1)/2]}& \sum _{j=0}^{\infty }\frac{{(-1)}^j{(3-(s-\tau ))}^j}{\mathsf{\Gamma }(1+j)}\end{array}\right)\end{array}$$

and

$$\begin{array}{c}\hfill (3-{(s-\tau )}^{-\frac{1}{2}})E_{\frac{1}{2},\frac{1}{2}}(\mathfrak{A}{(3-(s-\tau ))}^{\frac{1}{2}})=\left(\begin{array}{cc}{sin}_{\frac{1}{2}}(t)& {cos}_{\frac{1}{2}}(t)\\ -{cos}_{\frac{1}{2}}(t)& {sin}_{\frac{1}{2}}(t)\end{array}\right),\end{array}$$

where

$$\begin{array}{ccc}\hfill {cos}_{\frac{1}{2}}(t)& =& \sum _{j=0}^{\infty }\frac{{(-1)}^j{(3-(s-\tau ))}^{-(2j+1)/2}}{\mathsf{\Gamma }[(2j+1)/2]},\hfill \\ \hfill {sin}_{\frac{1}{2}}(t)& =& \sum _{j=0}^{\infty }\frac{{(-1)}^j{(3-(s-\tau ))}^{(j+1)-1}}{\mathsf{\Gamma }(j+1)}.\hfill \end{array}$$

Also,

$$\begin{array}{ccc}\hfill G(3,s)& =& {\int }_{-1}^0{(3-(s-\tau ))}^{-\frac{1}{2}}{E}_{\frac{1}{2},\frac{1}{2}}(\mathfrak{A}{(3-(s-\tau ))}^{\frac{1}{2}})d_{\tau }{\mathfrak{B}}_3(s-\tau ,\tau )\hfill \\ & =& \left(\begin{array}{cc}p(s)& q(s)\\ -q(s)& p(s)\end{array}\right),\hfill \end{array}$$

such that,

$$\begin{array}{ccc}\hfill p(s)& =& {\int }_{-1}^0{e}^{\tau }[{sin}_{\alpha }(3-(s-\tau ))sin(s-\tau )-{cos}_{\frac{1}{2}}(3-(s-\tau ))cos(s-\tau )]d\tau ,\hfill \\ \hfill q(s)& =& {\int }_{-1}^0{e}^{\tau }[{cos}_{\frac{1}{2}}(3-(s-\tau ))sin(s-\tau )-{sin}_{\frac{1}{2}}(3-(s-\tau ))cos(s-\tau )]d\tau .\hfill \end{array}$$

Using matrix calculation,

$$\begin{array}{ccc}\hfill W(0,3)& =& {\int }_0^{3}G(3,s)G^{\ast }(3,s)ds\hfill \\ & =& {\int }_0^3[p^2(s)+q^2(s)]\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)ds\hfill \\ & =& \left(\begin{array}{cc}84.6306& 40.9686\\ 200.6702& 84.6306\end{array}\right),\hfill \\ \hfill W^{-1}(0,3)& =& \left(\begin{array}{cc}-0.0799& 0.0387\\ 0.1895& -0.0799\end{array}\right).\hfill \end{array}$$

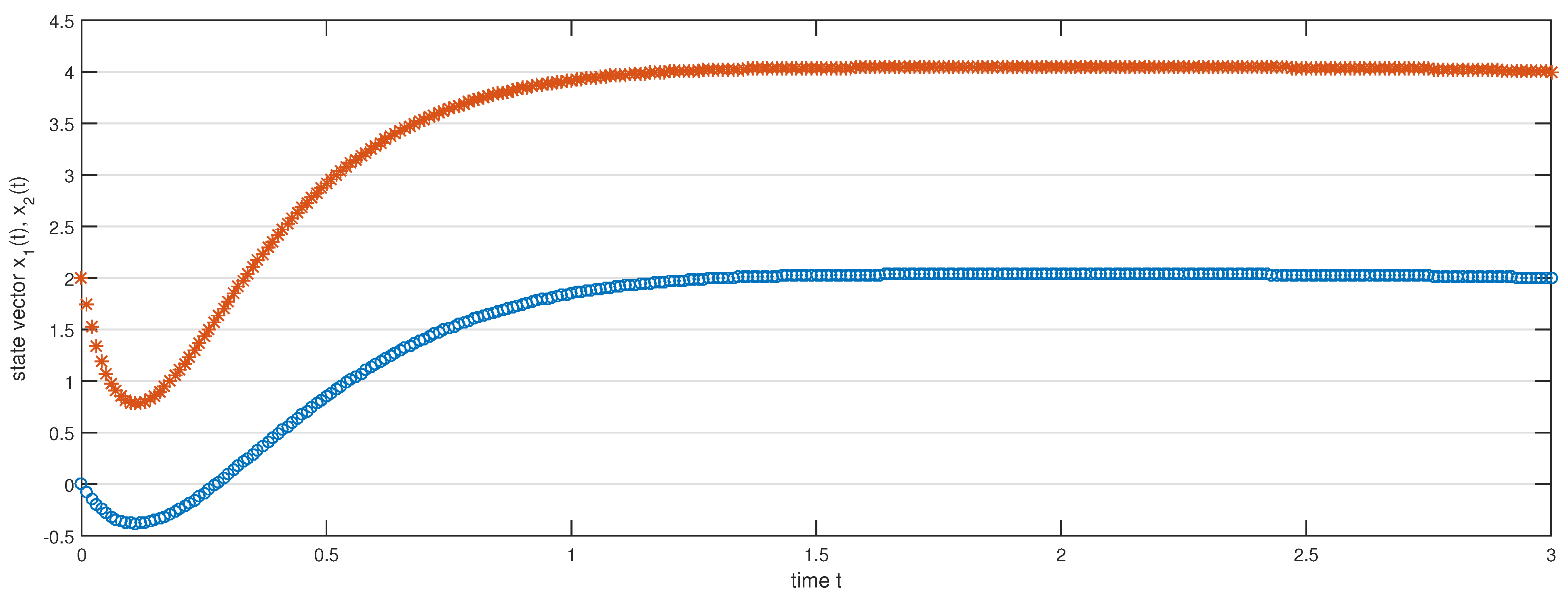
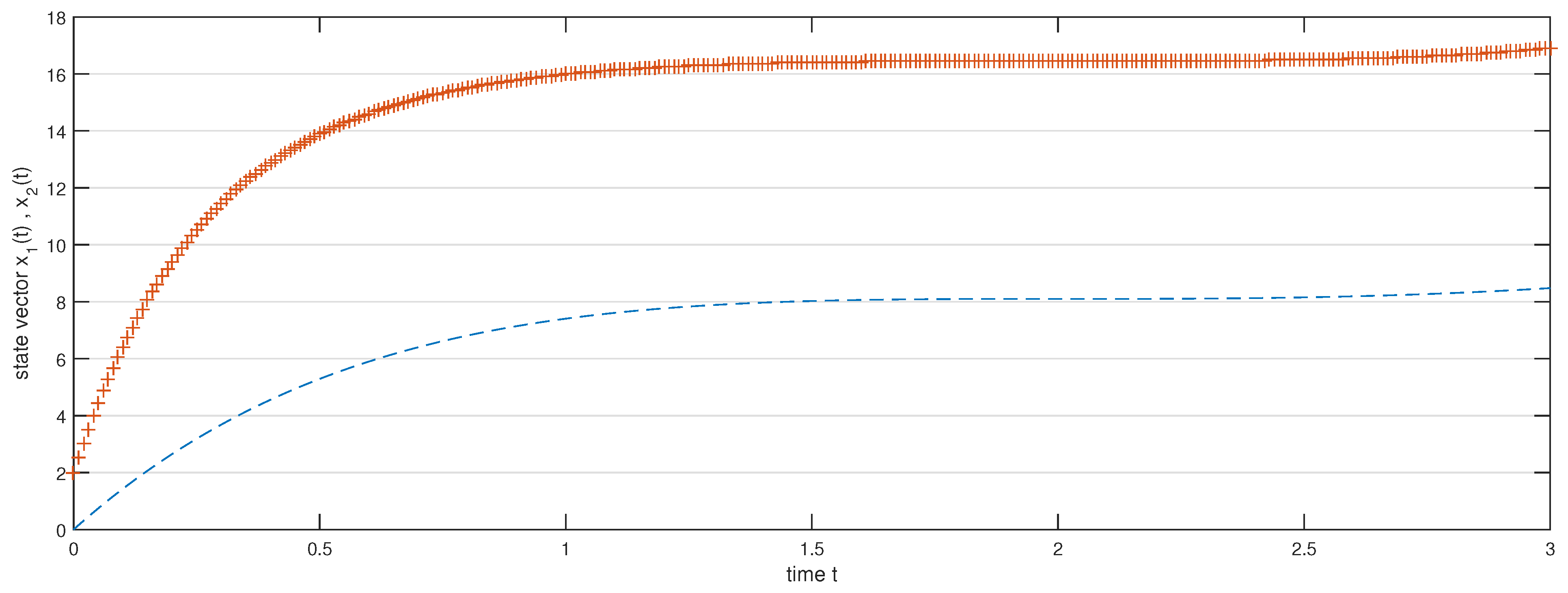
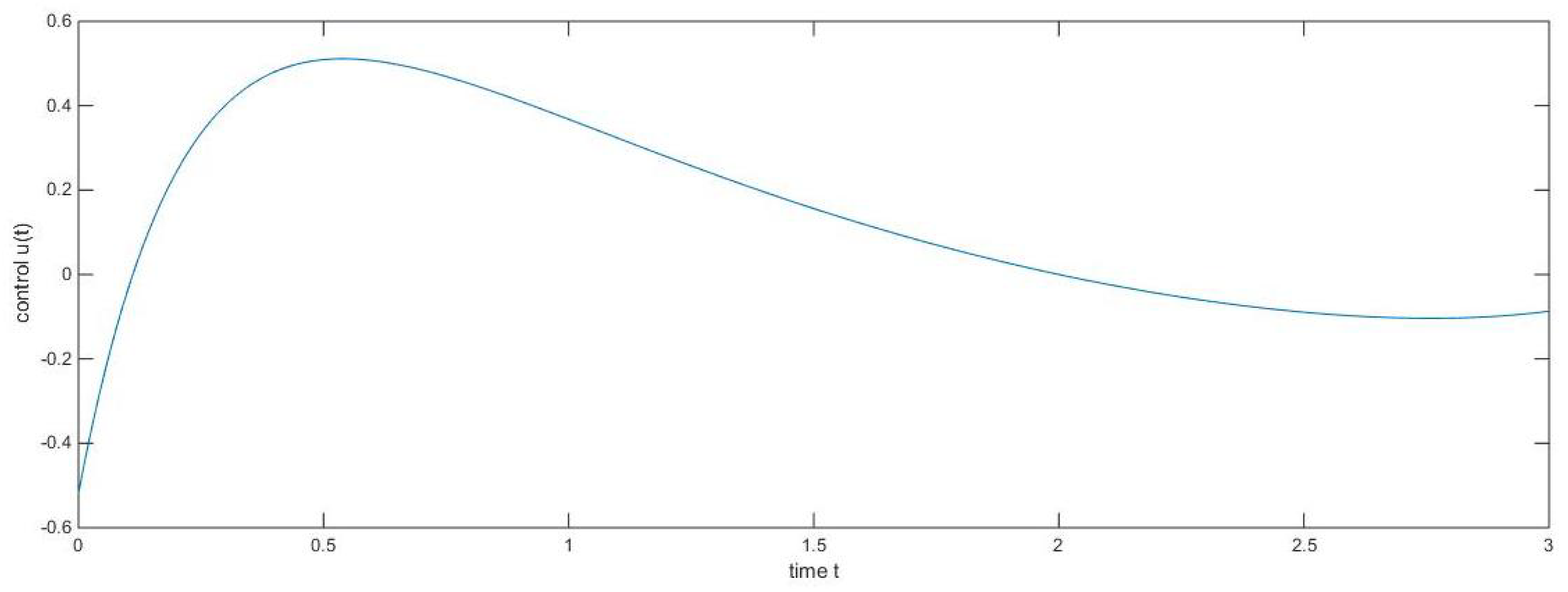
Hence, by Theorem 2, the fractional system (20) is completely controllable on $[0,3]$. Based on our chosen values, we have drawn diagrams for the state function with control Figure 1, the state function without control Figure 2 and the steering control function Figure 3 respectively.

Figure 1. State with control function steers initial state $x(0)={(0,2)}^T$ to final state $x(2)={(2,4)}^T$.

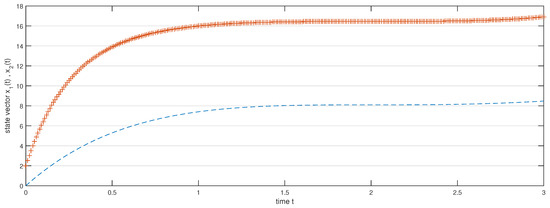
Figure 2. State vectors without control function.

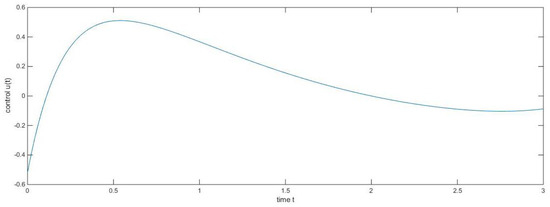
Figure 3. The steering control function.

Remark 1.

Consider the following nonlinear impulsive fractional dynamical system

$$\begin{array}{ccc}\hfill {}^C{D}^{\frac{2}{3}}{x}_1(t)& =& x_2(t)+{\int }_{-1}^0{e}^{\tau }[sint{u}_1(t+\tau )+cost{u}_2(t+\tau )]d\tau +\frac{10x_1(t)}{1+x_1^2(t)+x_2^2(t)},\hfill \\ \hfill {}^C{D}^{\frac{2}{3}}{x}_2(t)& =& -x_1(t)+{\int }_{-1}^0{e}^{\tau }[-cost{u}_1(t+\tau )+sint{u}_2(t+\tau )]d\tau +\frac{x_2(t)}{1+x_1^2(t)+t},\hfill \\ \hfill {\mathsf{\Delta }x|}_{t=\frac{1}{2}}& =& \frac{|x({\frac{1}{2}}^{-})|}{8+|x({\frac{1}{2}}^{-}|)},\hfill \\ \hfill x(t)& =& 1,-1\le t\le 0.\hfill \end{array}$$

(21)

Under appropriate choices and by following the previous techniques, Theorem 3 can be applied to guarantee the controllability result of the fractional system (21), and hence the diagrams can be also associated.

5. Conclusions

We investigated the concept of controllability criteria for nonlinear fractional differential systems with state delays and distributed delays in the controls with impulsive perturbations. We used the unsymmetric Fubini’s theorem with the change of order of integration, and also, by effecting the notion of Mittag–Leffler’s matrix function, we find the solution representation for the considered system. Further, by applying the controllability Gramian matrix, we studied the controllability results for the system addressed in the preliminary section. Moreover, we have given a numerical example that justifies the exactness of the obtained theoretical results in our main results. As further directions to be considered in our future projects, we intend to combine the above analysis with the topics of differential inclusion, fractional discreet calculus and variable order derivatives.