A Generalized Finite Difference Scheme for Multiphase Flow
Abstract
1. Introduction
2. Materials and Methods
2.1. Incompressible General Finite Difference Method
2.2. Multiphase Model
2.3. Time Integration Scheme
2.4. Pressure Poisson Equation
2.5. Reimann Solver Pressure Correction
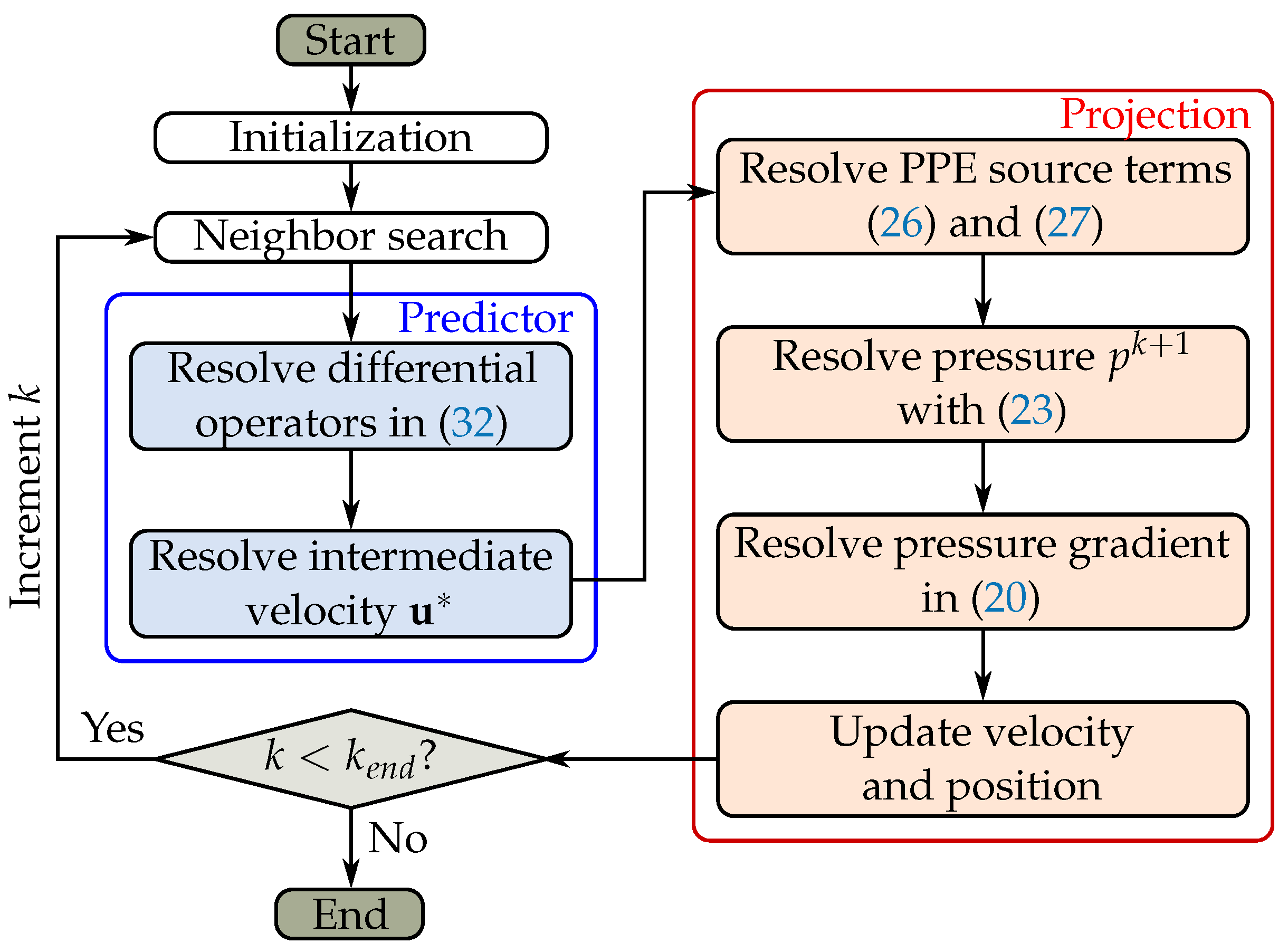
2.6. Solver Overview
3. Results and Discussion
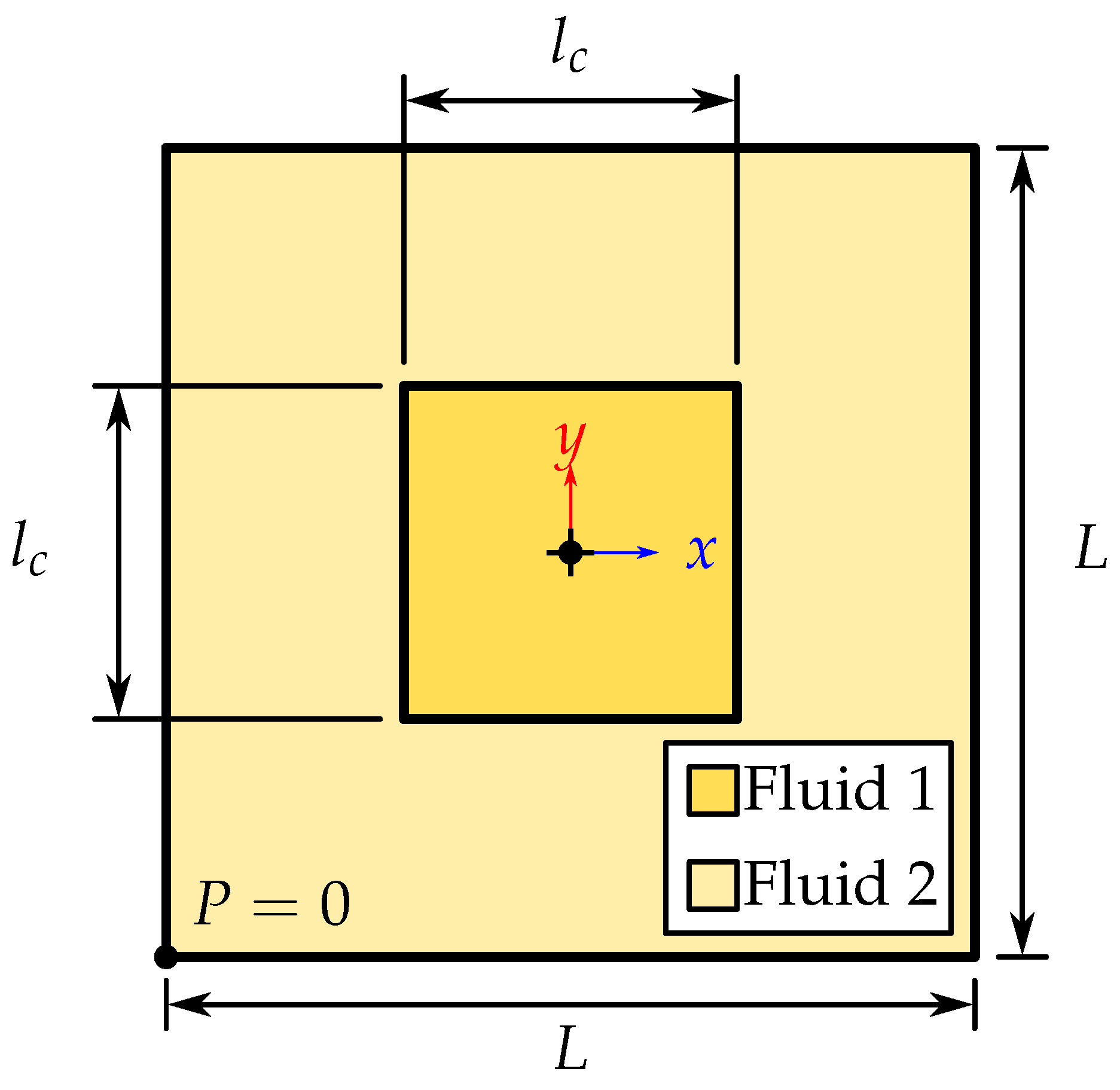
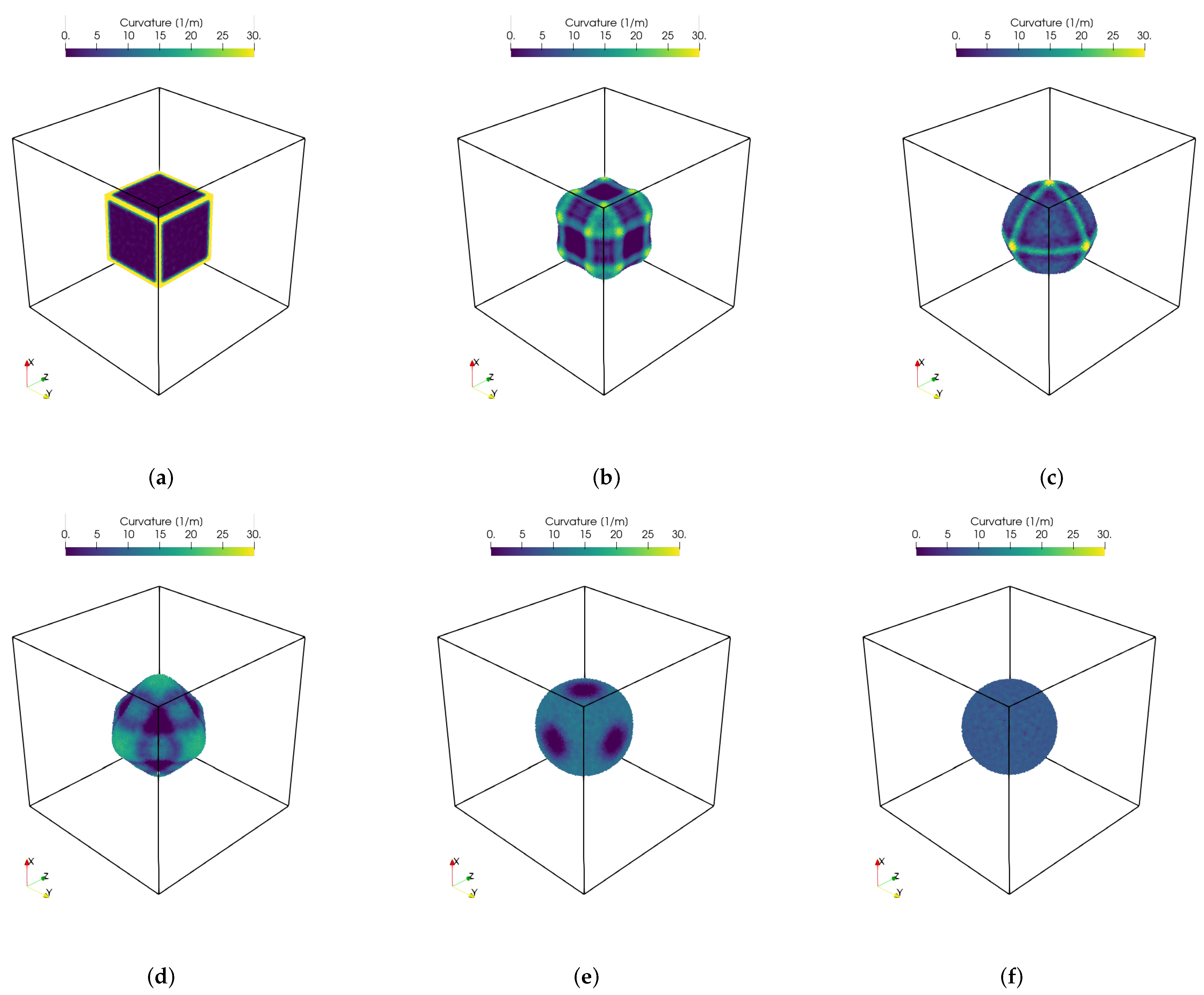
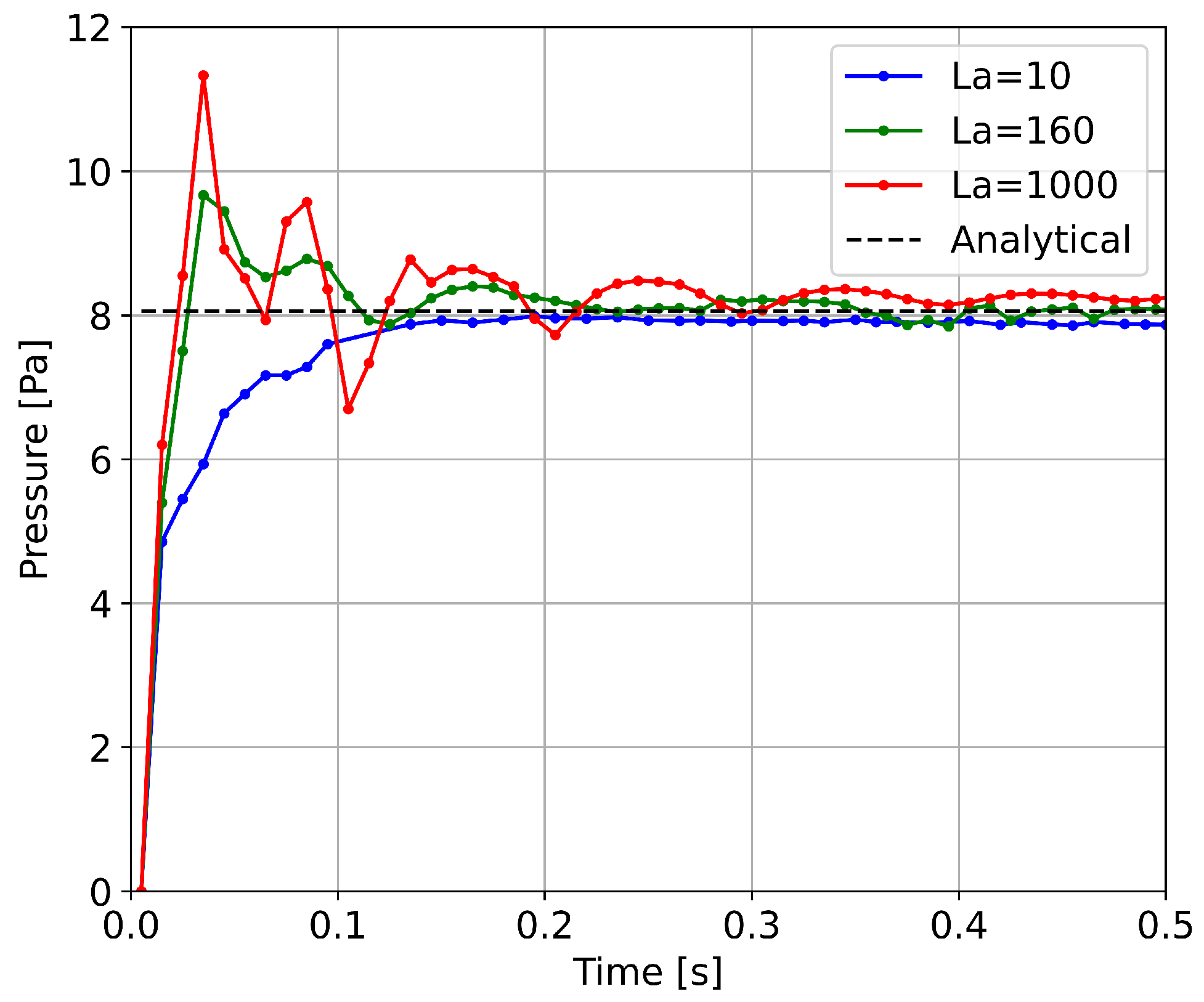
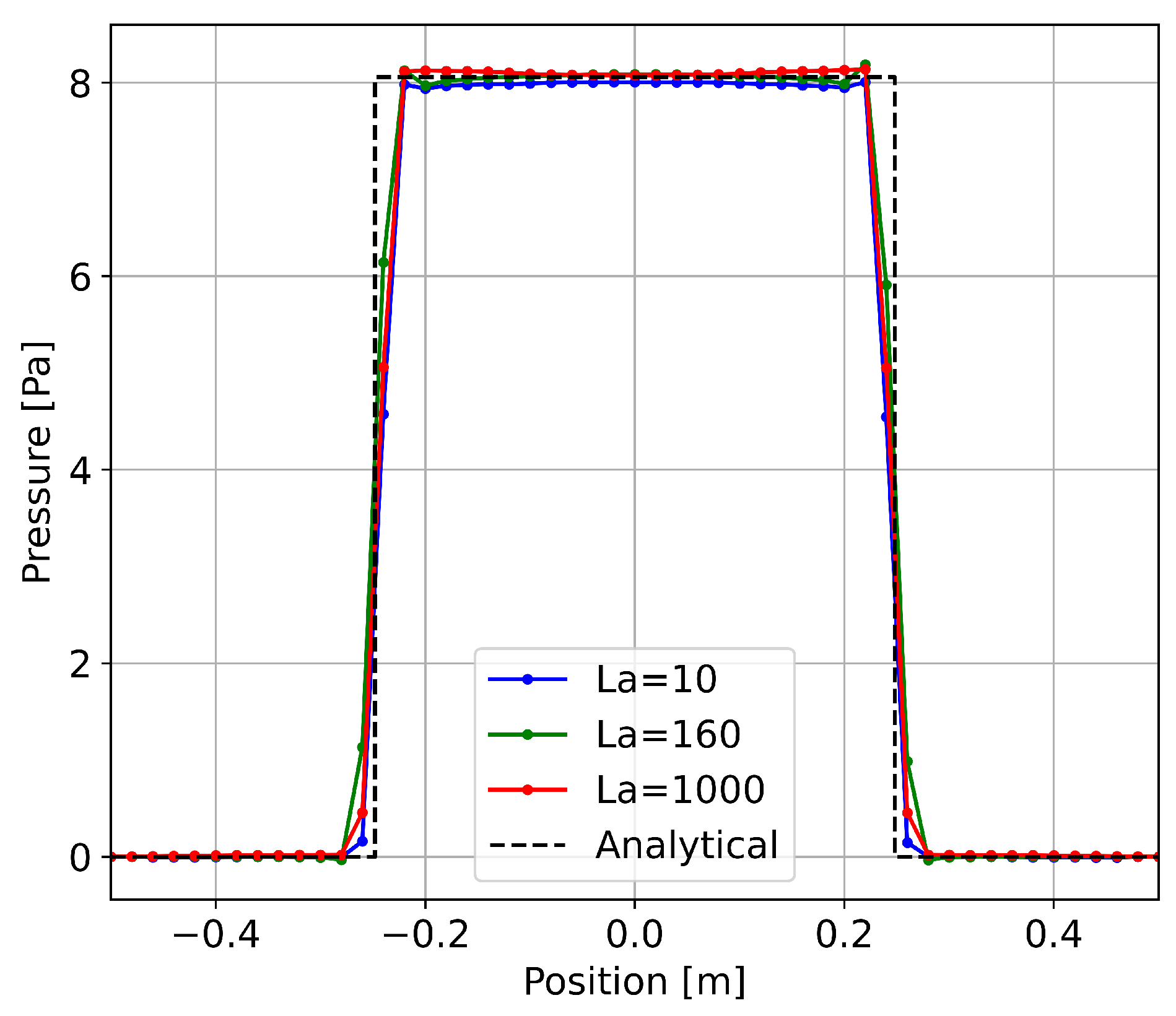
3.1. Square Droplet Relaxation
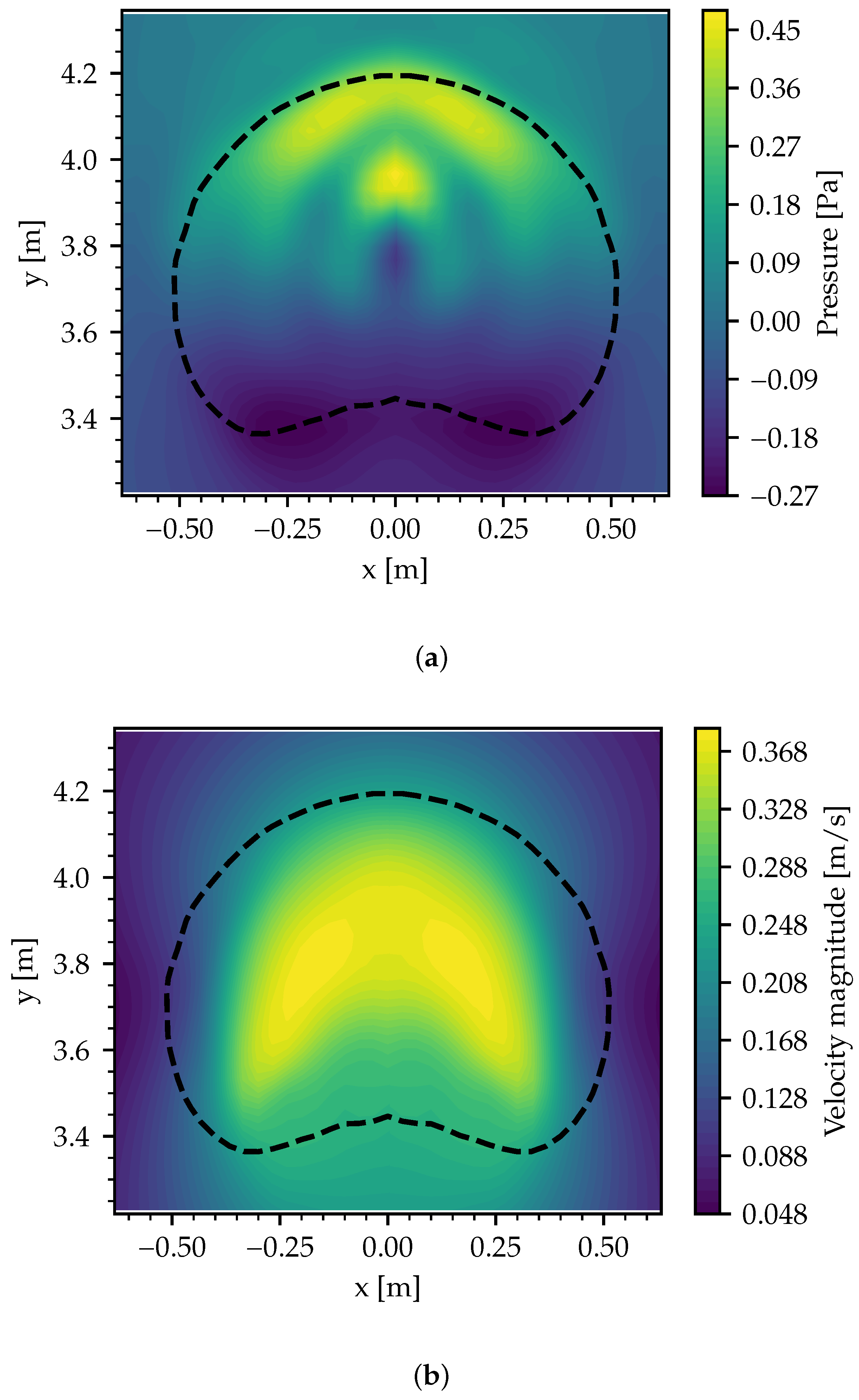
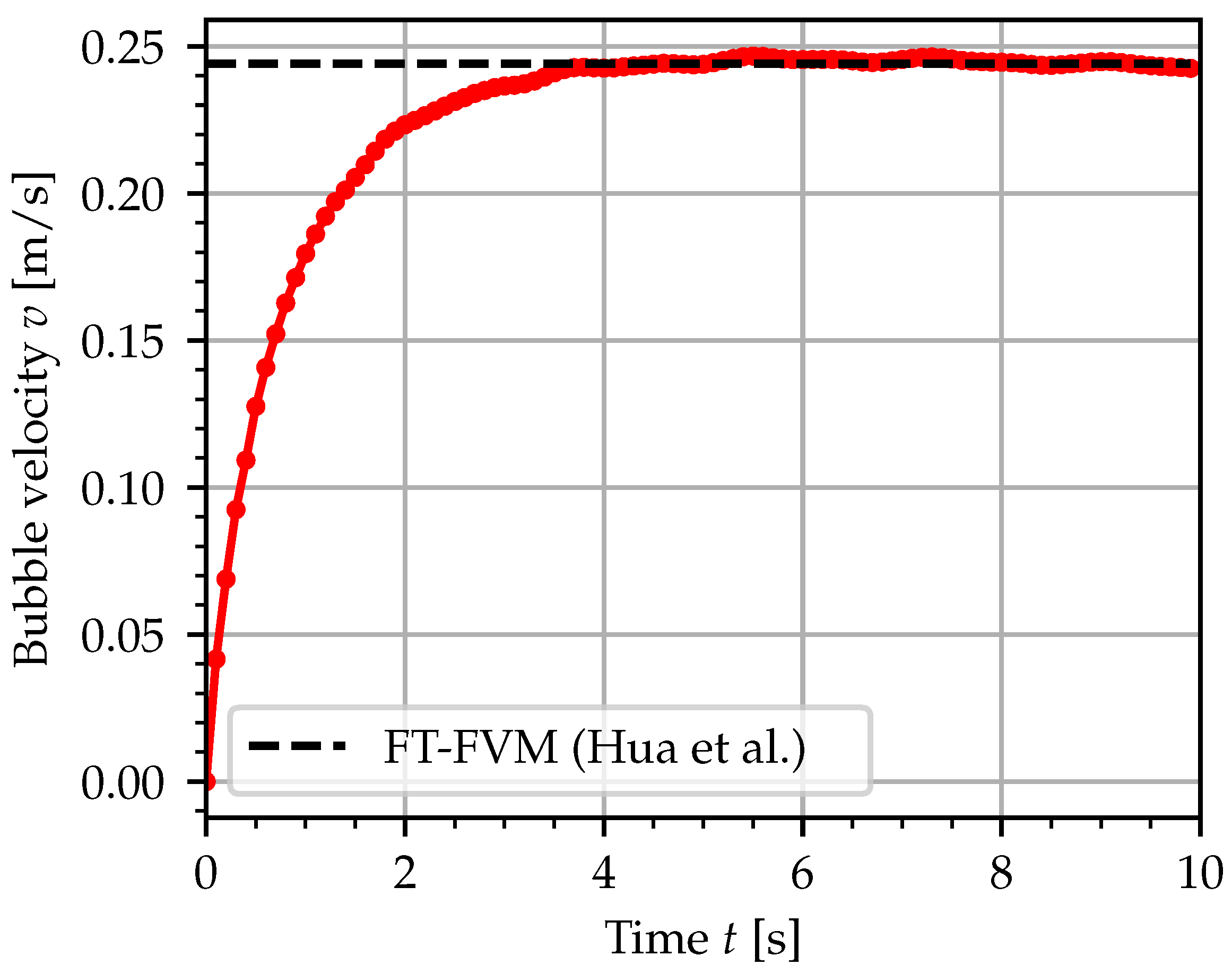
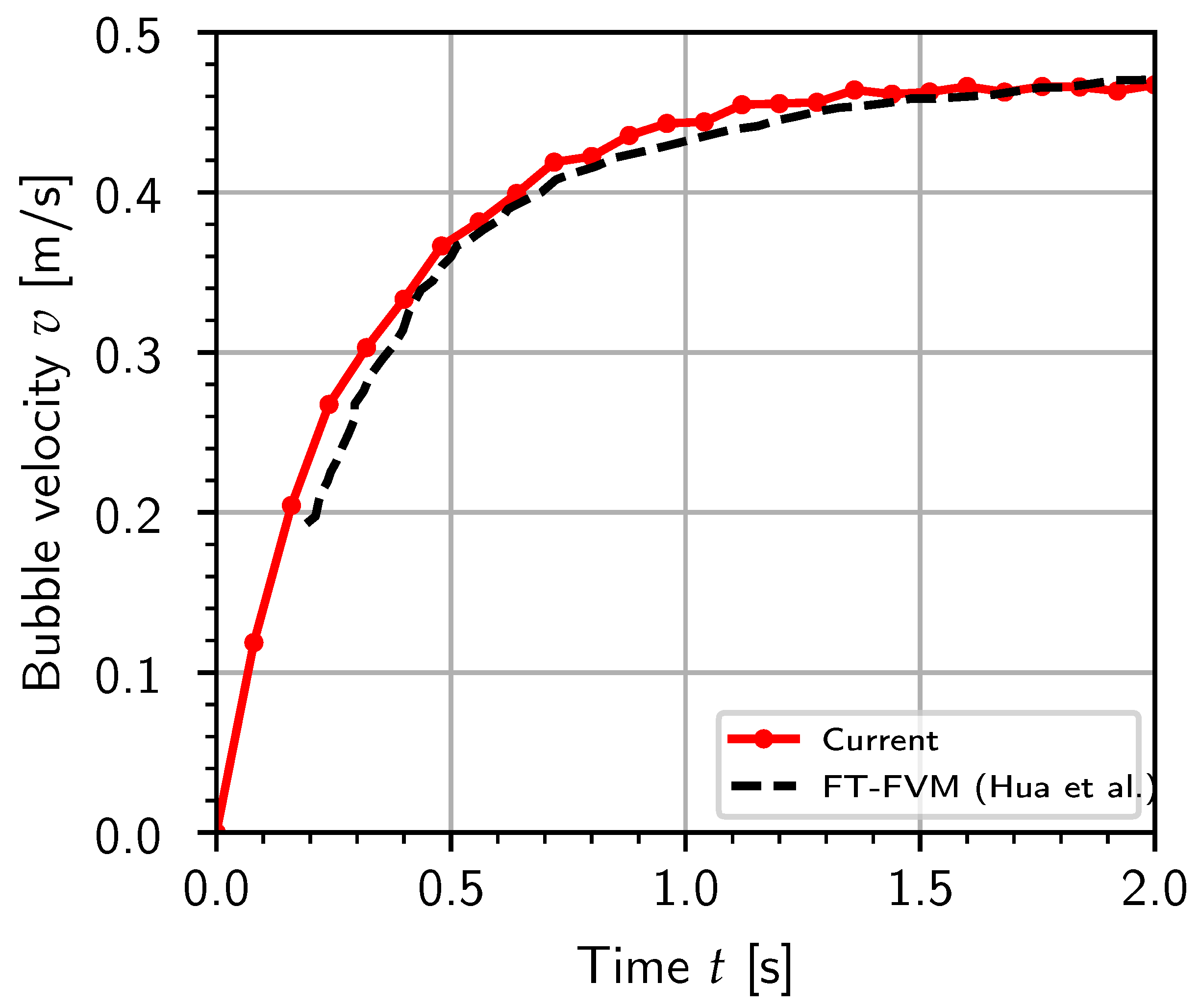
3.2. Rising Bubble
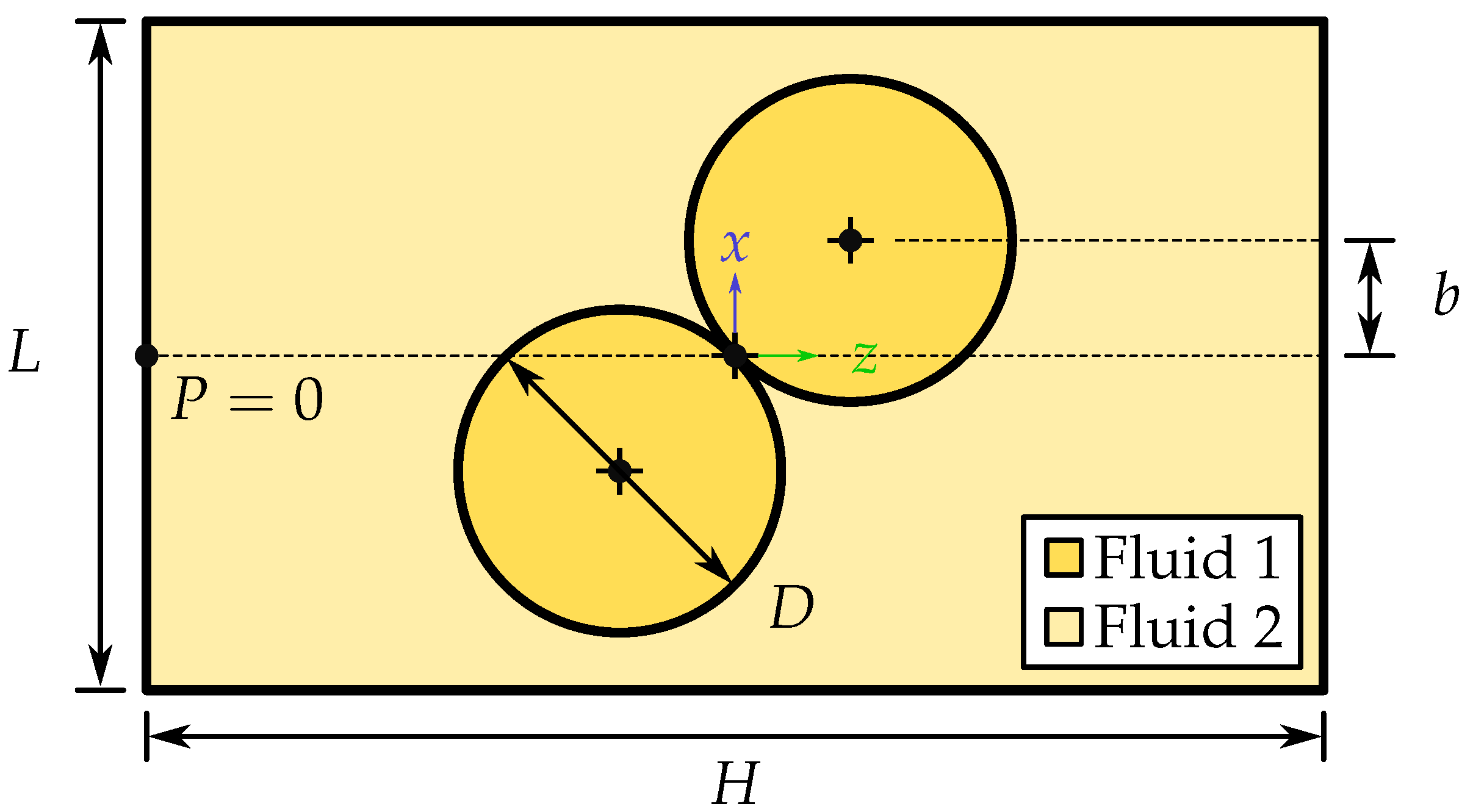
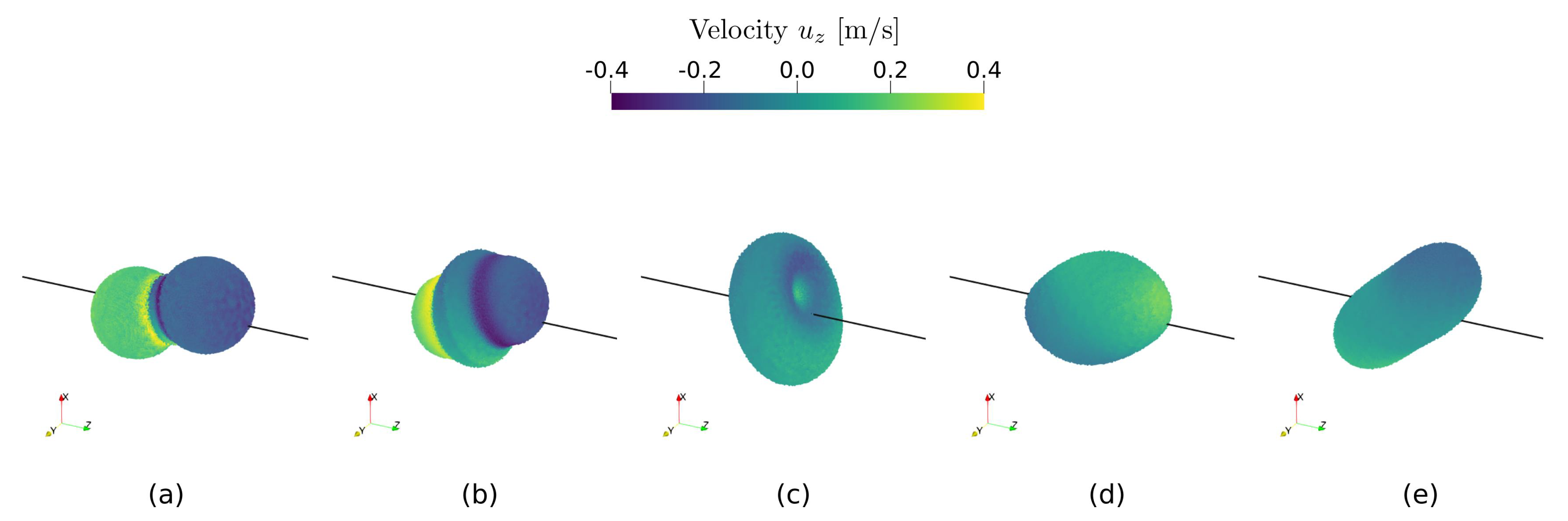
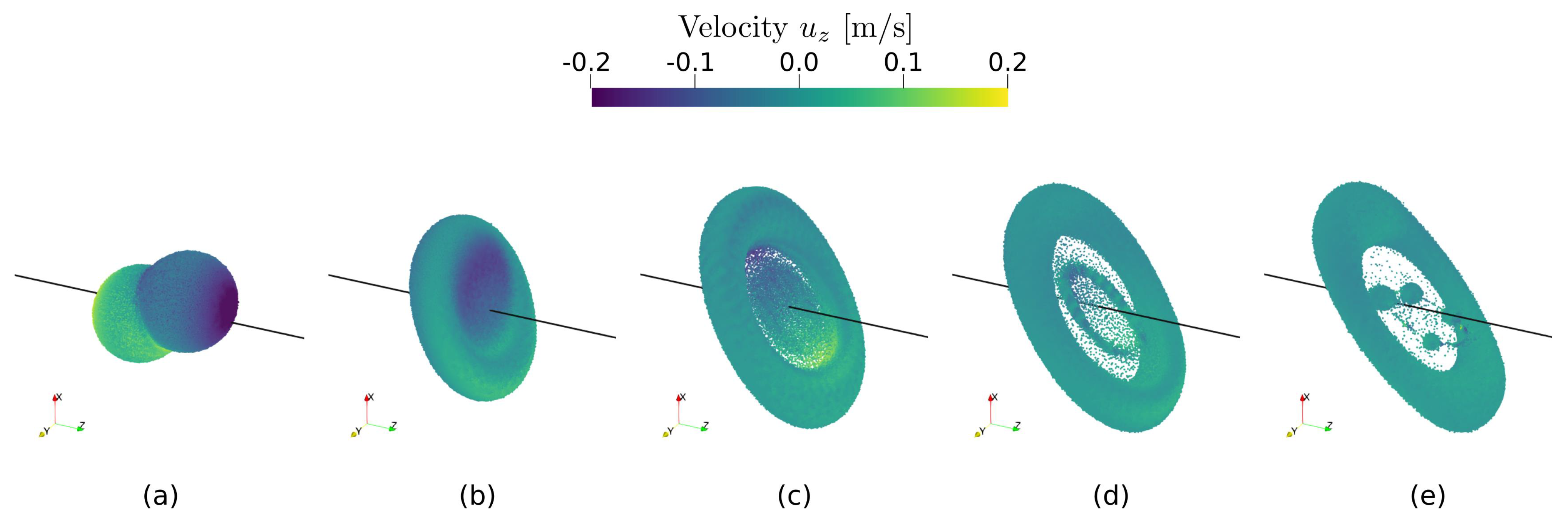
3.3. Colliding Droplets
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Brackbill, J.; Kothe, D.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Lafaurie, B.; Nardone, C.; Scardovelli, R.; Zaleski, S.; Zanetti, G. Modelling Merging and Fragmentation in Multiphase Flows with SURFER. J. Comput. Phys. 1994, 113, 134–147. [Google Scholar] [CrossRef]
- Hua, J.; Lou, J. Numerical simulation of bubble rising in viscous liquid. J. Comput. Phys. 2007, 222, 769–795. [Google Scholar] [CrossRef]
- Hu, X.; Adams, N. A multi-phase SPH method for macroscopic and mesoscopic flows. J. Comput. Phys. 2006, 213, 844–861. [Google Scholar] [CrossRef]
- Douillet-Grellier, T.; Leclaire, S.; Vidal, D.; Bertrand, F.; De Vuyst, F. Comparison of multiphase SPH and LBM approaches for the simulation of intermittent flows. Comput. Part. Mech. 2019, 6, 695–720. [Google Scholar] [CrossRef]
- Adami, S.; Hu, X.Y.; Adams, N.A. A new surface-tension formulation for multi-phase SPH using a reproducing divergence approximation. J. Comput. Phys. 2010, 229, 5011–5021. [Google Scholar] [CrossRef]
- Zhang, A.; Sun, P.; Ming, F. An SPH modeling of bubble rising and coalescing in three dimensions. Comput. Methods Appl. Mech. Eng. 2015, 294, 189–209. [Google Scholar] [CrossRef]
- Ming, F.R.; Sun, P.N.; Zhang, A.M. Numerical investigation of rising bubbles bursting at a free surface through a multiphase SPH model. Meccanica 2017, 52, 2665–2684. [Google Scholar] [CrossRef]
- Yan, J.; Li, S.; Zhang, A.M.; Kan, X.; Sun, P.N. Updated Lagrangian Particle Hydrodynamics (ULPH) modeling and simulation of multiphase flows. J. Comput. Phys. 2019, 393, 406–437. [Google Scholar] [CrossRef]
- Zainali, A.; Tofighi, N.; Shadloo, M.S.; Yildiz, M. Numerical investigation of Newtonian and non-Newtonian multiphase flows using ISPH method. Comput. Methods Appl. Mech. Eng. 2013, 254, 99–113. [Google Scholar] [CrossRef]
- Szewc, K.; Pozorski, J.; Minier, J.P. Spurious interface fragmentation in multiphase SPH. Int. J. Numer. Methods Eng. 2015, 103, 625–649. [Google Scholar] [CrossRef]
- Yeganehdoust, F.; Yaghoubi, M.; Emdad, H.; Ordoubadi, M. Numerical study of multiphase droplet dynamics and contact angles by smoothed particle hydrodynamics. Appl. Math. Model. 2016, 40, 8493–8512. [Google Scholar] [CrossRef]
- Yang, L.; Rakhsha, M.; Hu, W.; Negrut, D. A consistent multiphase flow model with a generalized particle shifting scheme resolved via incompressible SPH. J. Comput. Phys. 2022, 458, 111079. [Google Scholar] [CrossRef]
- Muradoglu, M.; Tryggvason, G. Simulations of soluble surfactants in 3D multiphase flow. J. Comput. Phys. 2014, 274, 737–757. [Google Scholar] [CrossRef]
- Colagrossi, A.; Landrini, M. Numerical simulation of interfacial flows by smoothed particle hydrodynamics. J. Comput. Phys. 2003, 191, 448–475. [Google Scholar] [CrossRef]
- Meng, Z.F.; Wang, P.P.; Zhang, A.M.; Ming, F.R.; Sun, P.N. A multiphase SPH model based on Roe’s approximate Riemann solver for hydraulic flows with complex interface. Comput. Methods Appl. Mech. Eng. 2020, 365, 112999. [Google Scholar] [CrossRef]
- Yang, Q.; Xu, F.; Yang, Y.; Wang, L. A multi-phase SPH model based on Riemann solvers for simulation of jet breakup. Eng. Anal. Bound. Elem. 2020, 111, 134–147. [Google Scholar] [CrossRef]
- Cheng, H.; Liu, Y.; Ming, F.; Sun, P. Investigation on the bouncing and coalescence behaviors of bubble pairs based on an improved APR-SPH method. Ocean. Eng. 2022, 255, 111401. [Google Scholar] [CrossRef]
- Chen, Z.; Zong, Z.; Liu, M.; Zou, L.; Li, H.; Shu, C. An SPH model for multiphase flows with complex interfaces and large density differences. J. Comput. Phys. 2015, 283, 169–188. [Google Scholar] [CrossRef]
- Zheng, B.; Chen, Z. A multiphase smoothed particle hydrodynamics model with lower numerical diffusion. J. Comput. Phys. 2019, 382, 177–201. [Google Scholar] [CrossRef]
- Rezavand, M.; Zhang, C.; Hu, X. A weakly compressible SPH method for violent multi-phase flows with high density ratio. J. Comput. Phys. 2020, 402, 109092. [Google Scholar] [CrossRef]
- Vahabi, M.; Kamkari, B. Simulating gas bubble shape during its rise in a confined polymeric solution by WC-SPH. Eur. J. Mech.-B/Fluids 2019, 75, 1–14. [Google Scholar] [CrossRef]
- He, F.; Zhang, H.; Huang, C.; Liu, M. A stable SPH model with large CFL numbers for multi-phase flows with large density ratios. J. Comput. Phys. 2022, 453, 110944. [Google Scholar] [CrossRef]
- Tong, M.; Browne, D.J. An incompressible multi-phase smoothed particle hydrodynamics (SPH) method for modelling thermocapillary flow. Int. J. Heat Mass Transf. 2014, 73, 284–292. [Google Scholar] [CrossRef]
- Cummins, S.J.; Rudman, M. An SPH Projection Method. J. Comput. Phys. 1999, 152, 584–607. [Google Scholar] [CrossRef]
- Xu, R.; Stansby, P.; Laurence, D. Accuracy and stability in incompressible SPH (ISPH) based on the projection method and a new approach. J. Comput. Phys. 2009, 228, 6703–6725. [Google Scholar] [CrossRef]
- Grenier, N.; Antuono, M.; Colagrossi, A.; Le Touzé, D.; Alessandrini, B. An Hamiltonian interface SPH formulation for multi-fluid and free surface flows. J. Comput. Phys. 2009, 228, 8380–8393. [Google Scholar] [CrossRef]
- Rezavand, M.; Taeibi-Rahni, M.; Rauch, W. An ISPH scheme for numerical simulation of multiphase flows with complex interfaces and high density ratios. Comput. Math. Appl. 2018, 75, 2658–2677. [Google Scholar] [CrossRef]
- Xu, Y.; Yang, G.; Zhu, Y.; Hu, D. A coupled SPH–FVM method for simulating incompressible interfacial flows with large density difference. Eng. Anal. Bound. Elem. 2021, 128, 227–243. [Google Scholar] [CrossRef]
- Zheng, B.; Sun, L.; Yu, P. A novel interface method for two-dimensional multiphase SPH: Interface detection and surface tension formulation. J. Comput. Phys. 2021, 431, 110119. [Google Scholar] [CrossRef]
- Geara, S.; Martin, S.; Adami, S.; Petry, W.; Allenou, J.; Stepnik, B.; Bonnefoy, O. A new SPH density formulation for 3D free-surface flows. Comput. Fluids 2022, 232, 105193. [Google Scholar] [CrossRef]
- Joubert, J.C.; Wilke, D.N.; Govender, N.; Pizette, P.; Basic, J.; Abriak, N.E. Boundary condition enforcement for renormalised weakly compressible meshless Lagrangian methods. Eng. Anal. Bound. Elem. 2021, 130, 332–351. [Google Scholar] [CrossRef]
- Basic, J.; Blagojevic, B.; Andrun, M.; Degiuli, N. A Lagrangian Finite Difference Method for Sloshing: Simulations and Comparison with Experiments. In Proceedings of the Twenty-Ninth International Ocean and Polar Engineering Conference, Honolulu, HI, USA, 11–16 October 2019; pp. 3412–3418. [Google Scholar]
- Joubert, J.C.; Wilke, D.N.; Pizette, P. On the momentum diffusion over multiphase surfaces with meshless methods. arXiv 2023, arXiv:2303.09978. [Google Scholar]
- Morris, J.P.; Fox, P.J.; Zhu, Y. Modeling low Reynolds number incompressible flows using SPH. J. Comput. Phys. 1997, 136, 214–226. [Google Scholar] [CrossRef]
- Lanson, N.; Vila, J.P. Renormalized Meshfree Schemes I: Consistency, Stability, and Hybrid Methods for Conservation Laws. SIAM J. Numer. Anal. 2008, 46, 1912–1934. [Google Scholar] [CrossRef]
- Lanson, N.; Vila, J.P. Renormalized Meshfree Schemes II: Convergence for Scalar Conservation Laws. SIAM J. Numer. Anal. 2008, 46, 1935–1964. [Google Scholar] [CrossRef]
- Basic, J.; Degiuli, N.; Ban, D. A class of renormalised meshless Laplacians for boundary value problems. J. Comput. Phys. 2018, 354, 269–287. [Google Scholar] [CrossRef]
- Inutsuka, S.-I. Reformulation of Smoothed Particle Hydrodynamics with Riemann Solver. J. Comput. Phys. 2002, 179, 238–267. [Google Scholar] [CrossRef]
- Puri, K.; Ramachandran, P. Approximate Riemann solvers for the Godunov SPH (GSPH). J. Comput. Phys. 2014, 270, 432–458. [Google Scholar] [CrossRef]
- Zhang, C.; Hu, X.; Adams, N. A weakly compressible SPH method based on a low-dissipation Riemann solver. J. Comput. Phys. 2017, 335, 605–620. [Google Scholar] [CrossRef]
- Mao, Z.; Liu, G.R. A Lagrangian gradient smoothing method for solid-flow problems using simplicial mesh. Int. J. Numer. Methods Eng. 2018, 113, 858–890. [Google Scholar] [CrossRef]
- Xia, X.; Liang, Q. A GPU-accelerated smoothed particle hydrodynamics (SPH) model for the shallow water equations. Environ. Model. Softw. 2016, 75, 28–43. [Google Scholar] [CrossRef]
- Zhan, L.; Peng, C.; Zhang, B.; Wu, W. A stabilized TL–WC SPH approach with GPU acceleration for three-dimensional fluid–structure interaction. J. Fluids Struct. 2019, 86, 329–353. [Google Scholar] [CrossRef]
- Afrasiabi, M.; Klippel, H.; Roethlin, M.; Wegener, K. An improved thermal model for SPH metal cutting simulations on GPU. Appl. Math. Model. 2021, 100, 728–750. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, Z.; He, F.; Liu, M. Numerical investigation on the water entry of a 3D circular cylinder based on a GPU-accelerated SPH method. Eur. J. Mech.-B/Fluids 2022, 94, 1–16. [Google Scholar] [CrossRef]
- Mao, Y.; Kong, Y.; Guan, M. GPU-accelerated SPH modeling of flow-driven sediment erosion with different rheological models and yield criteria. Powder Technol. 2022, 412, 118015. [Google Scholar] [CrossRef]
- Wen, X.; Zhao, W.; Wan, D. A multiphase MPS method for bubbly flows with complex interfaces. Ocean. Eng. 2021, 238, 109743. [Google Scholar] [CrossRef]
- Li, M.K.; Zhang, A.M.; Ming, F.R.; Sun, P.N.; Peng, Y.X. An axisymmetric multiphase SPH model for the simulation of rising bubble. Comput. Methods Appl. Mech. Eng. 2020, 366, 113039. [Google Scholar] [CrossRef]





| Differential Operator | Pairwise Term FLOPS | |
|---|---|---|
| Truncation tensor | ||
| Offset vector | ||
| Velocity gradient | ||
| Velocity Laplacian | ||
| Velocity divergence | ||
| Color gradient | ||
| Curvature | ||
| Dampening term | ||
| Pressure gradient | ||
| Pressure Laplacian |
| Parameter | Case 1 | Case 2 | Case 3 | ||
|---|---|---|---|---|---|
| Droplet density | 1 | 1 | 1 | ||
| Kinematic viscosity | , | ||||
| Surface tension coefficient | 1 | 1 | 1 | ||
| Density ratio | 1:1 | 10:1 | 100:1 | ||
| Laplace number | La | 10 | 160 | 1000 |
| Parameter | Case 1 | Case 2 | ||
|---|---|---|---|---|
| Bubble density | 1 | 0.001 | ||
| Bubble dynamic viscosity | ||||
| Surface tension coefficient | ||||
| Density ratio | ||||
| Viscosity ratio | ||||
| Reynolds number | Re | 8.75 | 13.95 | |
| Bond number | Bo | 116 | 116 |
| Parameter | Case 1 | Case 2 | Case 3 | ||
|---|---|---|---|---|---|
| Droplet density | 1000 | 1000 | 2 | ||
| Droplet viscosity | 2 | 10/11 | 2/1100 | ||
| Surface tension coefficient | 125/4 | 25/18 | 1/360 | ||
| Density ratio | |||||
| Viscosity ratio | |||||
| Reynolds number | Re | 250 | 550 | 550 | |
| Weber number | We | 8 | 180 | 180 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Joubert, J.C.; Wilke, D.N.; Pizette, P. A Generalized Finite Difference Scheme for Multiphase Flow. Math. Comput. Appl. 2023, 28, 51. https://doi.org/10.3390/mca28020051
Joubert JC, Wilke DN, Pizette P. A Generalized Finite Difference Scheme for Multiphase Flow. Mathematical and Computational Applications. 2023; 28(2):51. https://doi.org/10.3390/mca28020051
Chicago/Turabian StyleJoubert, Johannes C., Daniel N. Wilke, and Patrick Pizette. 2023. "A Generalized Finite Difference Scheme for Multiphase Flow" Mathematical and Computational Applications 28, no. 2: 51. https://doi.org/10.3390/mca28020051
APA StyleJoubert, J. C., Wilke, D. N., & Pizette, P. (2023). A Generalized Finite Difference Scheme for Multiphase Flow. Mathematical and Computational Applications, 28(2), 51. https://doi.org/10.3390/mca28020051









