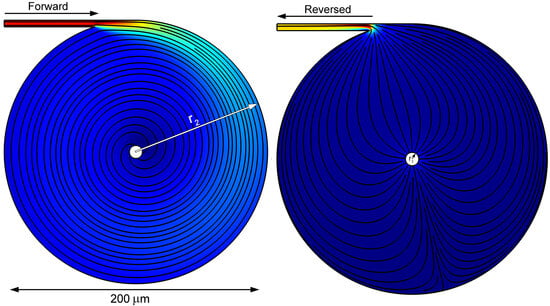
Design and Optimization of Microfluidic Vortex Diode
Abstract
1. Introduction
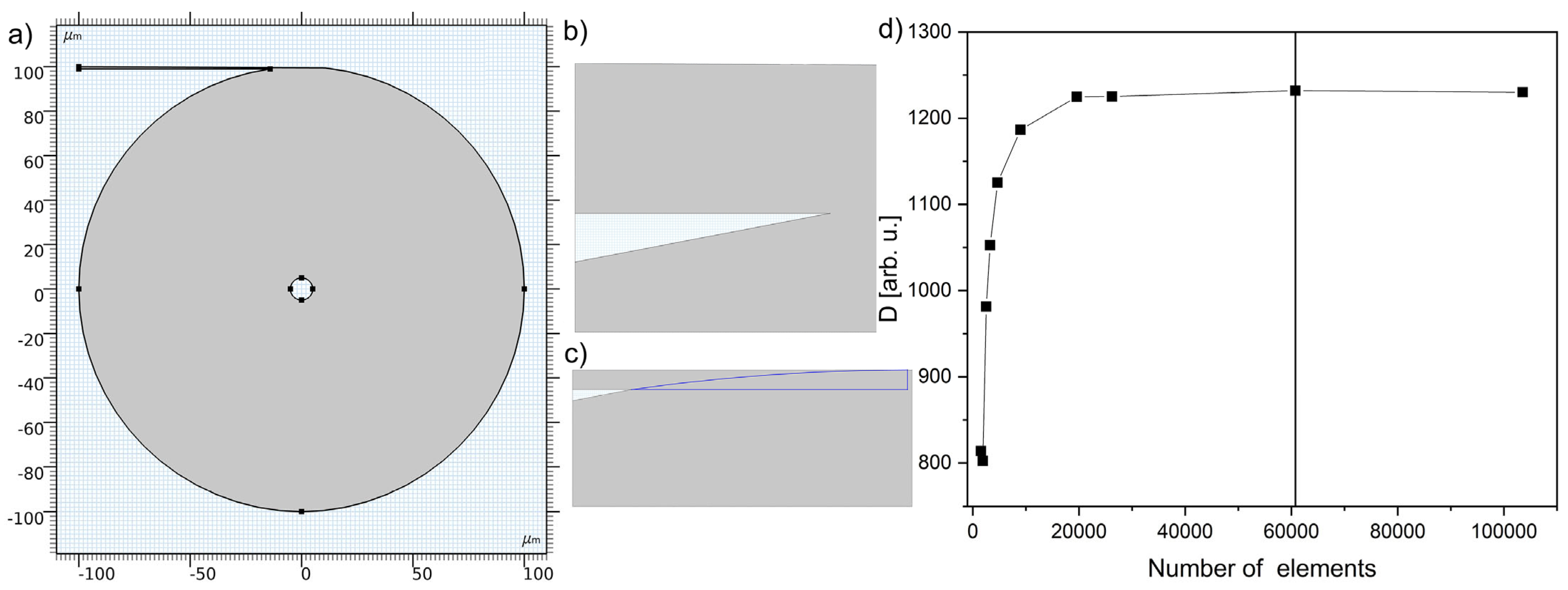
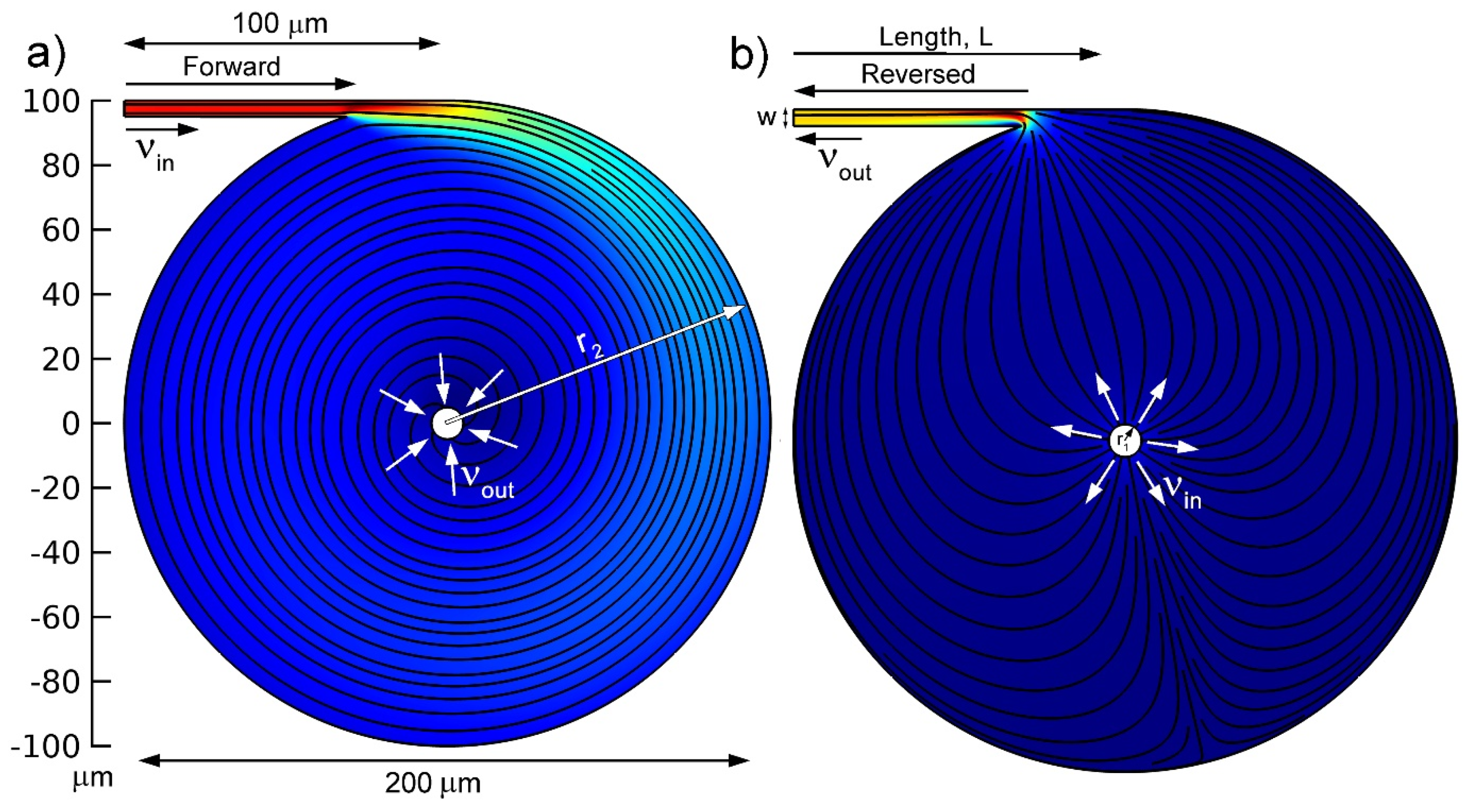
2. Model and Parameters
3. Results and Discussion
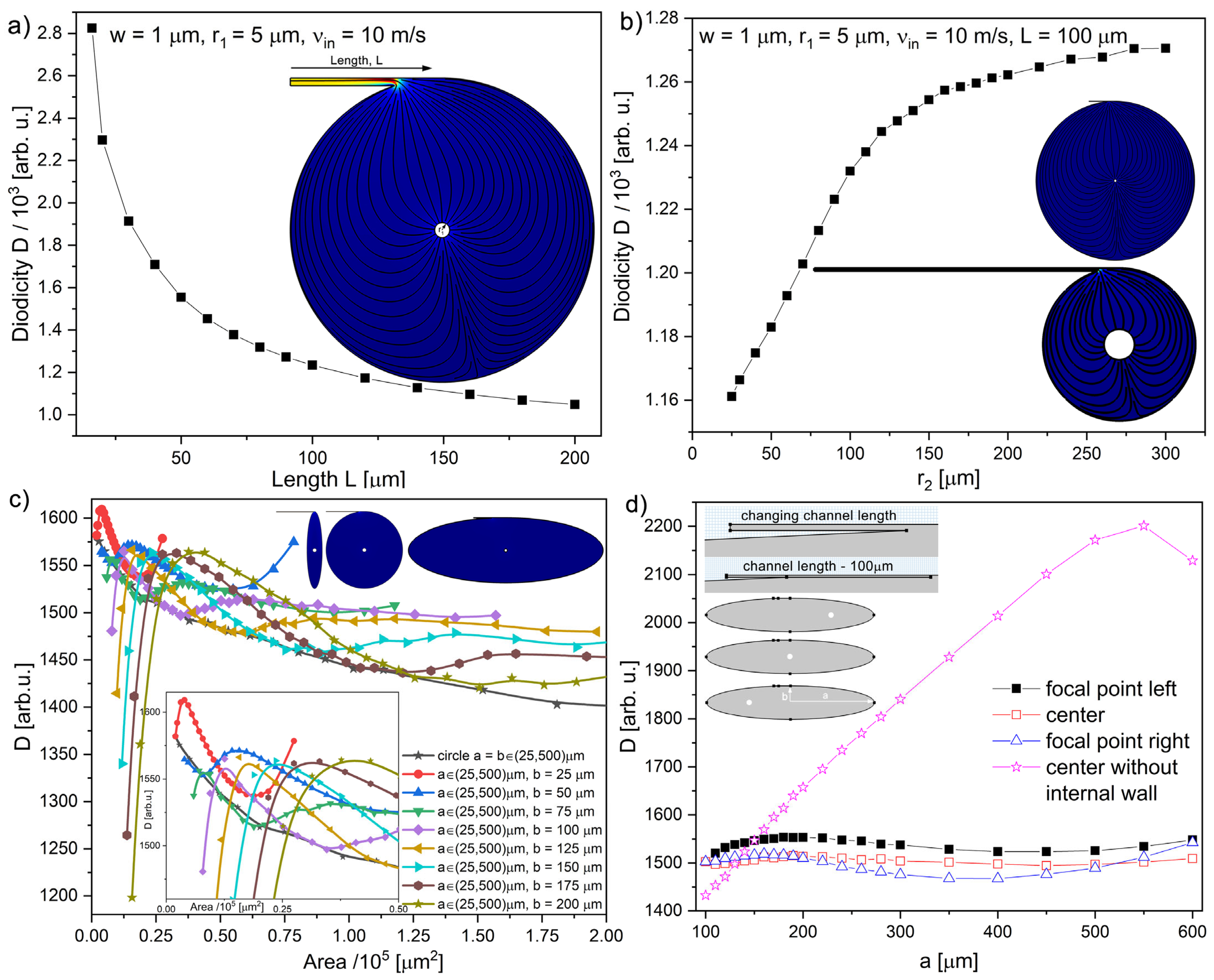
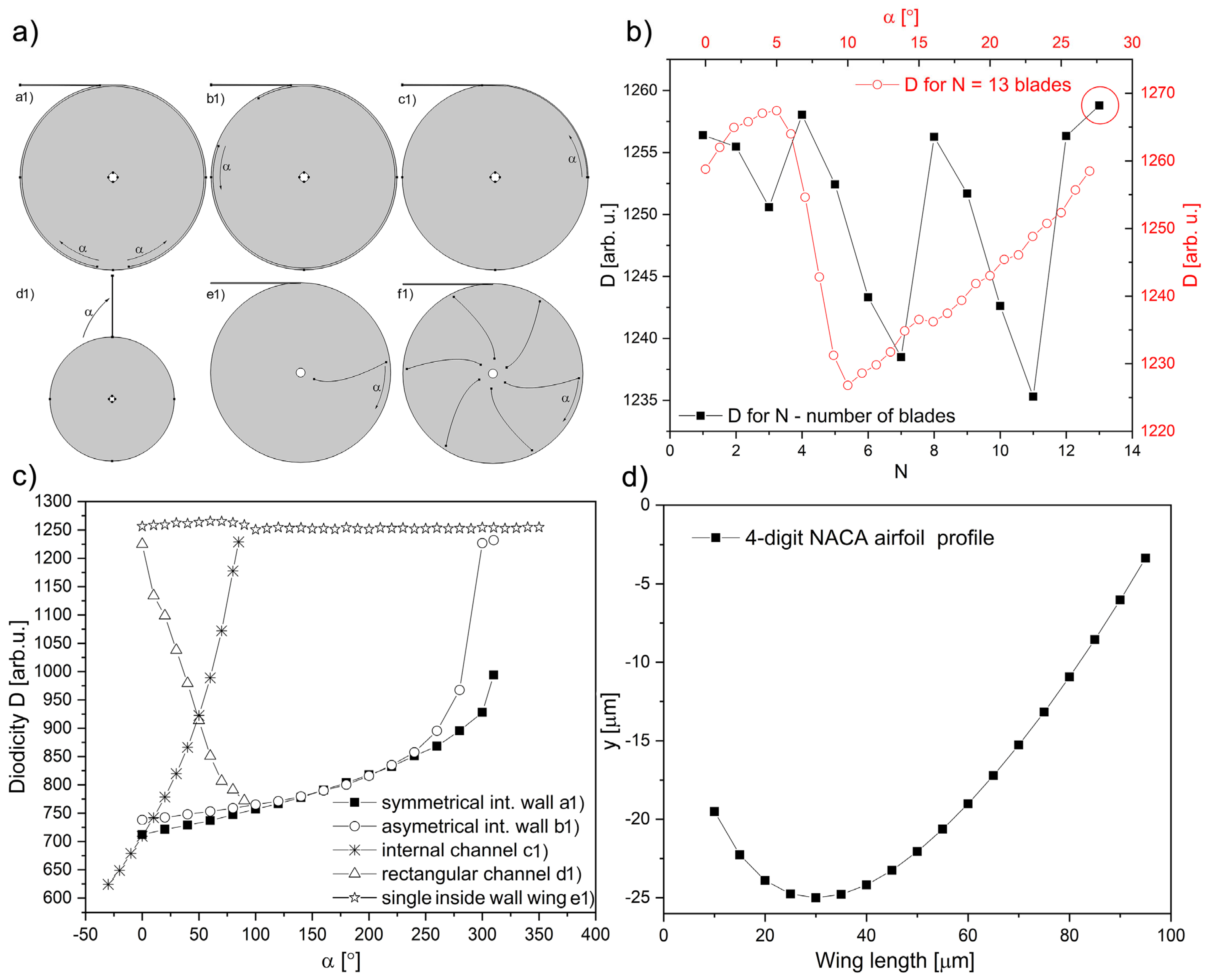
3.1. Wall Modifications
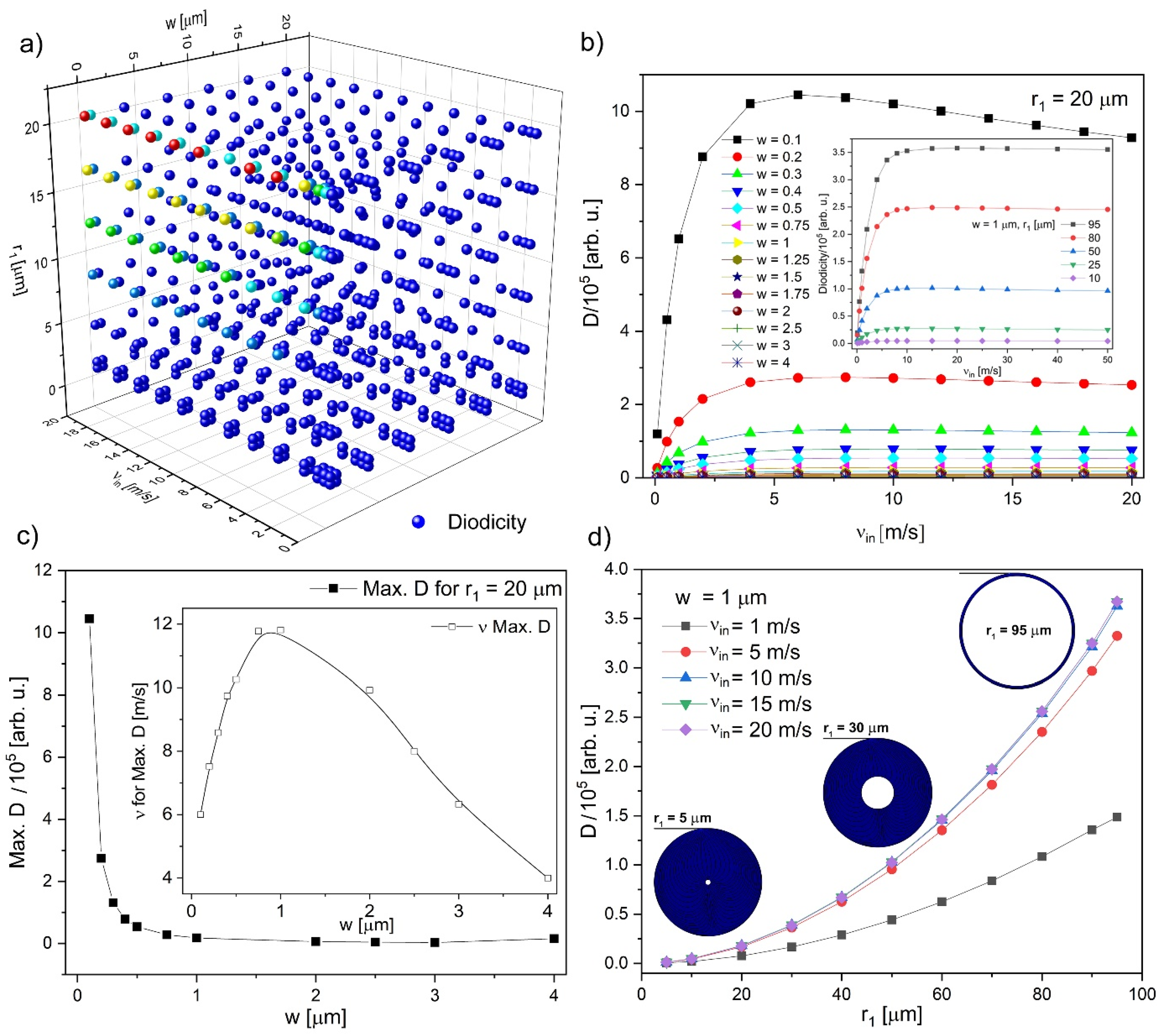
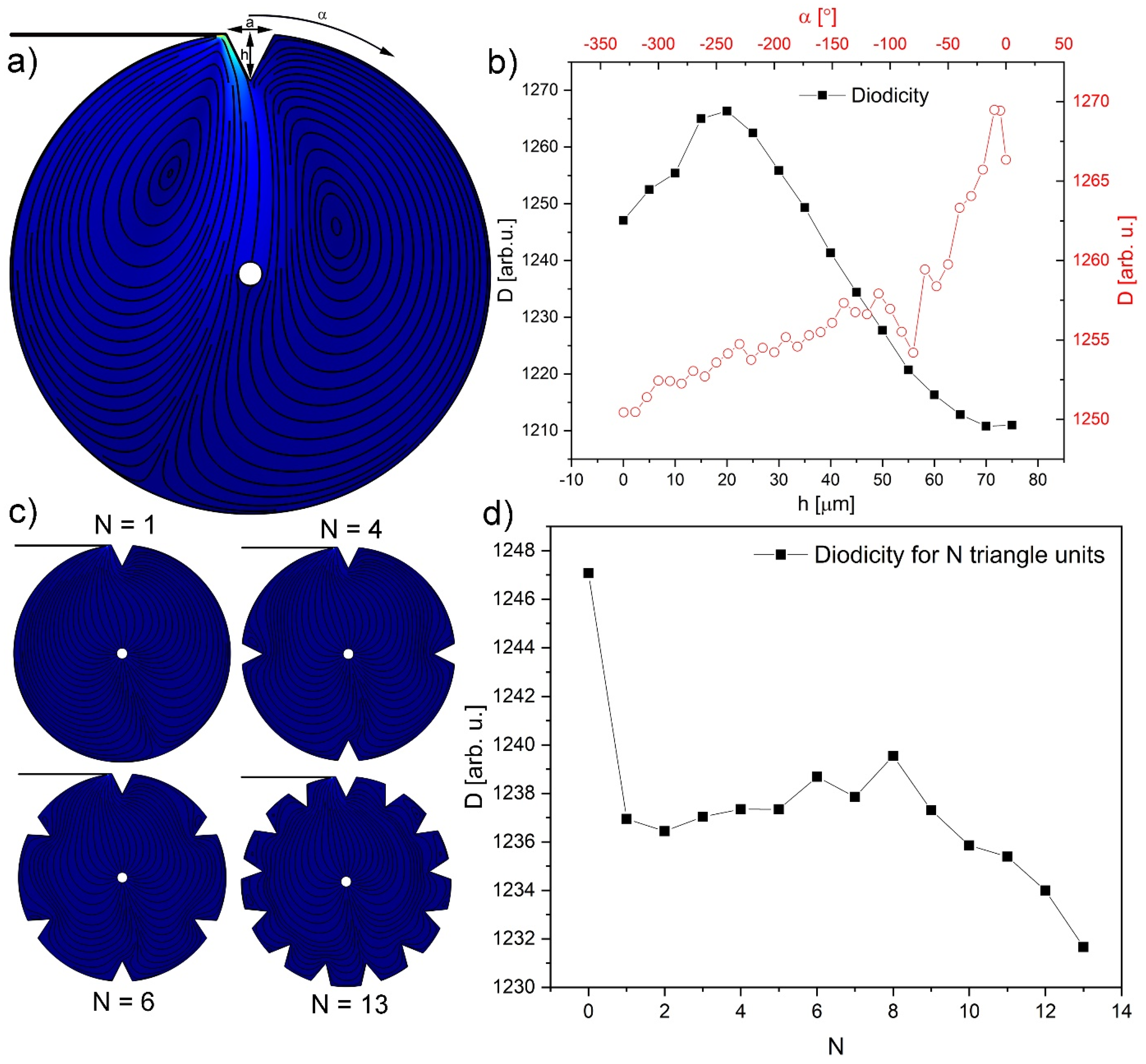
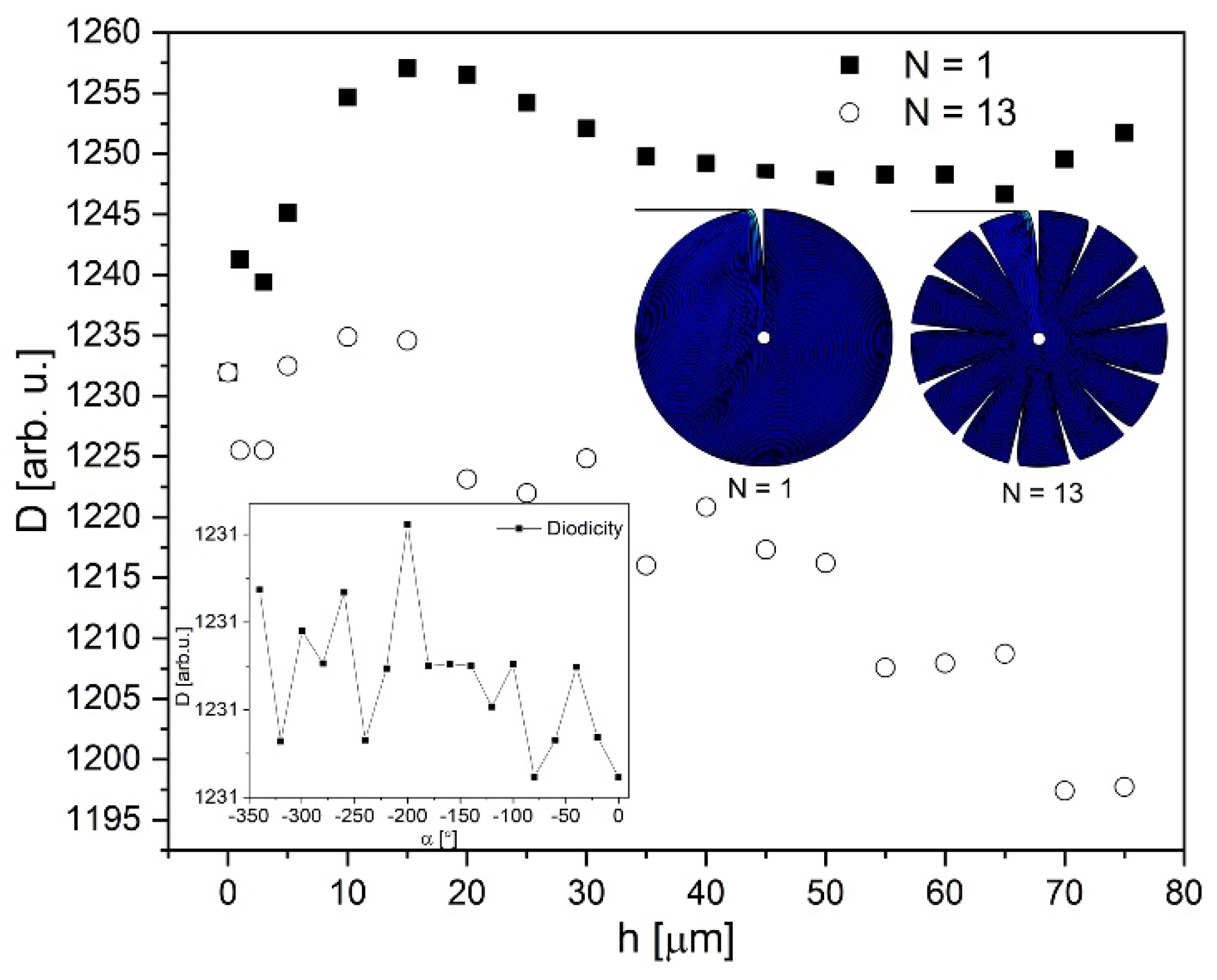
3.2. Internal Structure Modification
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dufour, I.; Français, O. Fluidic Microsystems. Microfluidics 2013, 349–388. [Google Scholar] [CrossRef]
- Barrot, C.; Delplanque, J.-P. Liquid Microflows: Particularities and Modeling. Microfluidics 2013, 89–120. [Google Scholar] [CrossRef]
- Anduze, M.; Colin, S.; Caen, R.; Camon, H.; Conedera, V.; Do Conto, T. Analysis and testing of a fluidic vortex microdiode. J. Micromech. Microeng. 2001, 11, 108–112. [Google Scholar] [CrossRef]
- Abgrall, P.; Gué, A.-M. Lab-on-chip technologies: Making a microfluidic network and coupling it into a complete microsystem-A review. J. Micromech. Microeng. 2007, 17, R15–R49. [Google Scholar] [CrossRef]
- Zhou, S.; Chen, B.; Fu, E.S.; Yan, H. Computer vision meets microfluidics: A label-free method for high-throughput cell analysis. Microsyst. Nanoeng. 2023, 9, 116. [Google Scholar] [CrossRef]
- Batista, C.C.S.; Jäger, A.; Albuquerque, B.L.; Pavlova, E.; Stepánek, P.; Giacomelli, F.C. Microfluidic-assisted synthesis of uniform polymer-stabilized silver colloids. Colloids Surfaces A Physicochem. Eng. Asp. 2021, 618, 126438. [Google Scholar] [CrossRef]
- Albuquerque, L.J.C.; Sincari, V.; Jager, A.; Konefal, R.; Panek, J.; Cernoch, P.; Pavlova, E.; Stepanek, P.; Giacomelli, F.C.; Jager, E. Microfluidic-Assisted Engineering of Quasi-Monodisperse pH-Responsive Polymersomes toward Advanced Platforms for the Intracellular Delivery of Hydrophilic Therapeutics. Langmuir 2019, 35, 8363–8372. [Google Scholar] [CrossRef]
- Sincari, V.; Jäger, E.; Loureiro, K.C.; Vragovic, M.; Hofmann, E.; Schlenk, M.; Filipová, M.; Rydvalová, E.; Štěpánek, P.; Hrubý, M.; et al. pH-Dependent disruption of giant polymer vesicles: A step towards biomimetic membranes. Polym. Chem. 2023, 14, 443–451. [Google Scholar] [CrossRef]
- De Oliveira, A.M.; Jäger, E.; Jäger, A.; Stepánek, P.; Giacomelli, F.C. Physicochemical aspects behind the size of biodegradable polymeric nanoparticles: A step forward. Colloids Surfaces A Physicochem. Eng. Asp. 2013, 436, 1092–1102. [Google Scholar] [CrossRef]
- Wang, M.; Fu, Q.; Liu, R.; Wang, C.; Li, X.; Sun, X.; Liu, G. A microfluidic manipulation platform based on droplet mixing technology. Chem. Eng. Sci. 2024, 298, 120422. [Google Scholar] [CrossRef]
- Czerwinska, J.; Jebauer, S. Secondary slip structures in heated micro-geometries. Int. J. Heat Mass Transf. 2011, 54, 1578–1586. [Google Scholar] [CrossRef]
- Chiarot, P.; Mrad, R.B.; Sullivan, P. A study of passive microfluidic mixers. In Proceedings of the 2004 International Conference on MEMS, NANO and Smart Systems, ICMENS 2004, Banff, AB, Canada, 25–27 August 2004; pp. 287–293. [Google Scholar]
- Cho, Y.-K.; Han, T.-H.; Ha, S.-J.; Lee, J.-W.; Kim, J.-S.; Kim, S.-M.; Cho, M.-W. Fabrication of passive micromixer using a digital micromirror device-based maskless lithography system. Int. J. Precis. Eng. Manuf. 2014, 15, 1417–1422. [Google Scholar] [CrossRef]
- Deshpande, M.; Gilbert, J.R.; Bardell, R.L.; Forster, F.R. Design analysis of no-moving-parts valves for micropumps. In Proceedings of the 1998 ASME International Mechanical Engineering Congress and Exposition, Anaheim, CA, USA, 15–20 November 1998; Volume 66, pp. 153–155. [Google Scholar]
- Zhou, P.; Zhang, T.; Simon, T.; Cui, T. A Fluidic Diode and Its Application to a Valveless Micropump. In Proceedings of the 2021 IEEE 34th International Conference on Micro Electro Mechanical Systems (MEMS), Virtual, 25–29 January 2021; pp. 1005–1008. [Google Scholar] [CrossRef]
- Okuhara, S.; Alam, M.M.A.; Takao, M.; Kinoue, Y. Performance of fluidic diode for a twin unidirectional impulse turbine. IOP Conf. Ser. Earth Environ. Sci. 2019, 240, 052011. [Google Scholar] [CrossRef]
- De Vries, S.F.; Florea, D.; Homburg, F.G.A.; Frijns, A.J.H. Design and operation of a Tesla-type valve for pulsating heat pipes. Int. J. Heat Mass Transf. 2017, 105, 1–11. [Google Scholar] [CrossRef]
- Thompson, S.M.; Ma, H.B.; Wilson, C. Investigation of a flat-plate oscillating heat pipe with Tesla-type check valves. Exp. Therm. Fluid Sci. 2011, 35, 1265–1273. [Google Scholar] [CrossRef]
- Lv, Q.; Chen, M.; Sun, X.; Christensen, R.; Blue, T.; Yoder, G.; Wilson, D.; Sabharwall, P. Design of fluidic diode for a high-temperature DRACS test facility. In Proceedings of the 2013 21st International Conference on Nuclear Engineering, ICONE 2013, Chengdu, China, 29 July–2 August 2013; Volume 4. [Google Scholar]
- Wang, B.; Su, H.; Zhang, B. Hydrodynamic cavitation as a promising route for wastewater treatment–A review. Chem. Eng. J. 2021, 412, 128685. [Google Scholar] [CrossRef]
- Bhandari, V.M.; Sorokhaibam, L.G.; Ranade, V.V. Industrial wastewater treatment for fertilizer industry—A case study. Desalin. Water Treat. 2016, 57, 27934–27944. [Google Scholar] [CrossRef]
- Patil, P.B.; Bhandari, V.M.; Ranade, V.V. Improving efficiency for removal of ammoniacal nitrogen from wastewaters using hydrodynamic cavitation. Ultrason. Sonochem. 2021, 70, 105306. [Google Scholar] [CrossRef]
- Kotowski, A.; Wójtowicz, P. Analysis of hydraulic parameters of cylindrical vortex regulators. Environ. Prot. Eng. 2008, 34, 43–56. [Google Scholar]
- Ochowiak, M.; Włodarczak, S.; Matuszak, M.; Krupińska, A.; Markowska, M. Flow Regulators-Design, Tests and Applications. In Practical Aspects of Chemical Engineering: Selected Contributions from PAIC 2019; Springer: Berlin/Heidelberg, Germany, 2020; pp. 261–270. [Google Scholar] [CrossRef]
- Jain, P.; Bhandari, V.M.; Balapure, K.; Jena, J.; Ranade, V.V.; Killedar, D.J. Hydrodynamic cavitation using vortex diode: An efficient approach for elimination of pathogenic bacteria from water. J. Environ. Manag. 2019, 242, 210–219. [Google Scholar] [CrossRef]
- Suryawanshi, N.B.; Bhandari, V.M.; Sorokhaibam, L.G.; Ranade, V.V. A Non-catalytic Deep Desulphurization Process using Hydrodynamic Cavitation. Sci. Rep. 2016, 6, 33021. [Google Scholar] [CrossRef] [PubMed]
- Suryawanshi, P.G.; Bhandari, V.M.; Sorokhaibam, L.G.; Ruparelia, J.P.; Ranade, V.V. Solvent degradation studies using hydrodynamic cavitation. Environ. Prog. Sustain. Energy 2018, 37, 295–304. [Google Scholar] [CrossRef]
- Suryawanshi, N.B.; Bhandari, V.M.; Sorokhaibam, L.G.; Ranade, V.V. Developing techno-economically sustainable methodologies for deep desulfurization using hydrodynamic cavitation. Fuel 2017, 210, 482–490. [Google Scholar] [CrossRef]
- Sarvothaman, V.P.; Kulkarni, S.R.; Subburaj, J.; Hariharan, S.L.; Velisoju, V.K.; Castaño, P.; Guida, P.; Prabhudharwadkar, D.M.; Roberts, W.L. Evaluating performance of vortex-diode based hydrodynamic cavitation device scale and pressure drop using coumarin dosimetry. Chem. Eng. J. 2024, 481, 148593. [Google Scholar] [CrossRef]
- Simpson, A.; Ranade, V.V. 110th Anniversary: Comparison of Cavitation Devices Based on Linear and Swirling Flows: Hydrodynamic Characteristics. Ind. Eng. Chem. Res. 2019, 58, 14488–14509. [Google Scholar] [CrossRef]
- Qu, S.-X.; Wu, Y.-H.; He, Z.-Z.; Chen, K. Surrogate Fluid Experimental Study and CFD Simulation on the Hydraulic Characteristics of Vortex Diode. Nucl. Sci. Eng. 2018, 189, 282–289. [Google Scholar] [CrossRef]
- Doddamani, H.; Abdus, S.; Manabu, T.; Shinya, O.; Ashraful Alam, M.M. Effect of Fluidic Diode on Performance of Unidirectional Impulse Turbine. J. Therm. Sci. 2024, 33, 807–814. [Google Scholar] [CrossRef]
- Dudhgaonkar, P.V.; Jayashankar, V.; Jalihal, P.; Kedarnath, S.; Setoguchi, T.; Takao, M.; Nagata, S.; Toyota, K. Fluidic Components for Oscillating Water Column Based Wave Energy Plants. In Proceedings of the Fluids Engineering Division Summer Meeting, Hamamatsu, Japan, 24–29 July 2011; pp. 1979–1983. [Google Scholar] [CrossRef]
- Hithaish, D.; Das, T.K.; Takao, M.; Samad, A. Design Optimization of a Fluidic Diode for a Wave Energy Converter via Artificial Intelligence-Based Technique. Arab. J. Sci. Eng. 2023, 48, 11407–11423. [Google Scholar] [CrossRef]
- Kerikous, E.; Hithaish, D.; Samad, A.; Hoerner, S.; Thévenin, D. Performance Enhancement of Fluidic Diode for a Wave Energy System through Genetic Algorithm. Proc. Eur. Wave Tidal Energy Conf. 2023, 15, 1–6. [Google Scholar] [CrossRef]
- Cao, Z.; Zhao, T.; Wang, Y.; Wang, H.; Zhai, C.; Lv, W. Novel fluid diode plate for use within ventilation system based on Tesla structure. Build. Environ. 2020, 185, 107257. [Google Scholar] [CrossRef]
- Adams, M.L.; Johnston, M.L.; Scherer, A.; Quake, S.R. Polydimethylsiloxane based microfluidic diode. J. Micromechanics Microengineering 2005, 15, 1517. [Google Scholar] [CrossRef]
- Kulkarni, A.A.; Ranade, V.V.; Rajeev, R.; Koganti, S.B. Pressure drop across vortex diodes: Experiments and design guidelines. Chem. Eng. Sci. 2009, 64, 1285–1292. [Google Scholar] [CrossRef]
- Kulkarni, A.A.; Ranade, V.V.; Rajeev, R.; Koganti, S.B. CFD simulation of flow in vortex diodes. AIChE J. 2008, 54, 1139–1152. [Google Scholar] [CrossRef]
- Saito, M.; Arai, F.; Yamanishi, Y.; Sakuma, S. Spatiotemporally controlled microvortices provide advanced microfluidic components. Proc. Natl. Acad. Sci. USA 2024, 121, e2306182121. [Google Scholar] [CrossRef]
- Chen, C.-N.; Zhou, L.-J.; Jiao, L.; Liu, J.-T.; Wang, L.-Q. Numerical simulation of axial port structure on vortex diode performance. J. Eng. Thermophys. 2010, 31, 185–188. [Google Scholar]
- Jiao, L.; Chen, C.-N.; Wu, C.-J.; Liu, J.-T.; Wang, L.-Q. Numerical simulation of tangential port on vortex diode performance. J. Eng. Thermophys. 2011, 32, 415–418. [Google Scholar]
- Jiao, L.; Chen, C.-N.; Liu, S.-G.; Yin, J.-L.; Sun, Q.-J.; Wang, L.-Q. Numerical simulation of three-dimensional strong rotational flow in vortex diode. J. Eng. Thermophys. 2011, 32, 1855–1858. [Google Scholar]
- Cao, Y.; Wu, Y.; Lin, C.; He, Z.; Chen, K. Numerical simulation of the performance of vortex diodes with chamfered vortex chambers. Nuclear Tech. 2015, 38, 010602. [Google Scholar] [CrossRef]
- Jiao, L.; Wu, C.-J.; Chen, C.-N.; Yin, J.-L.; Liu, J.-T.; Wang, L.-Q. Numerical simulation of cavitation performance for vortex diode. J. Eng. Thermophys. 2012, 33, 1519–1522. [Google Scholar]
- Jiao, L.; Zhang, P.P.; Chen, C.N.; Yin, J.L.; Wang, L.Q. Experimental study on the cavitation of vortex diode based on CFD. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Beijing, China, 19–23 August 2012; Volume 15. [Google Scholar]
- Wang, J.; Wei, Z.; Gou, J.; Xiao, Q.; Li, S.; Li, Y. CFD numerical simulation of water hammer in a vortex diode. In Proceedings of the 2018 26th International Conference on Nuclear Engineering, ICONE 2018, London, UK, 22–26 July 2018; Volume 8. [Google Scholar]
- Liu, X.; Zhang, H.; Han, X.; Zhao, L. Simulation of backward facing step flow at the outlet of micro-channel and optimal design of amperometric detection chip. In Proceedings of the 8th Annual IEEE International Conference on Nano/Micro Engineered and Molecular Systems, Suzhou, China, 7–10 April 2013; pp. 578–581. [Google Scholar] [CrossRef]
- Fouladi, K.; Czupryna, J. CFD-based optimization of micro vortex diodes. J. Appl. Fluid Mech. 2018, 11, 1231–1237. [Google Scholar] [CrossRef]
- Wilcox, D.C. Turbulence Modeling for CFD, 3rd ed.; DCW Industries: La Cañada, CA, USA, 2006; ISBN 1928729088, 978-1928729082. [Google Scholar]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method, 5th ed.; Longman Group Ltd.: Harlow, UK, 1995; ISBN 0-582-21884-5. [Google Scholar]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000; ISBN 9780521598866. [Google Scholar] [CrossRef]
| Pressure at flow entry and exit | |
| D | Diodicity |
| , , | Reynolds number, characteristic length, fluid dynamic viscosity |
| The radius of the circular, central channel | |
| Circumference of the circular channel | |
| Flow velocity vector, inflow velocity, outflow velocity | |
| Length and width of rectangular channel | |
| Diode radius | |
| The general rotation angle of specific detail | |
| A | The base length of the triangle, tooth element |
| h | The height of the triangle, tooth element |
| / | Difference in pressures—applied and at the end of the diode in the reversed/forward flow direction |
| Turbulent viscosity | |
| , , | Model constants, production term |
| Fluid density | |
| k, ε | Turbulent kinetic energy, turbulent dissipation rate |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tadyszak, K.; Jäger, A.; Pánek, J.; Hrubý, M. Design and Optimization of Microfluidic Vortex Diode. Math. Comput. Appl. 2024, 29, 97. https://doi.org/10.3390/mca29060097
Tadyszak K, Jäger A, Pánek J, Hrubý M. Design and Optimization of Microfluidic Vortex Diode. Mathematical and Computational Applications. 2024; 29(6):97. https://doi.org/10.3390/mca29060097
Chicago/Turabian StyleTadyszak, Krzysztof, Alessandro Jäger, Jiří Pánek, and Martin Hrubý. 2024. "Design and Optimization of Microfluidic Vortex Diode" Mathematical and Computational Applications 29, no. 6: 97. https://doi.org/10.3390/mca29060097
APA StyleTadyszak, K., Jäger, A., Pánek, J., & Hrubý, M. (2024). Design and Optimization of Microfluidic Vortex Diode. Mathematical and Computational Applications, 29(6), 97. https://doi.org/10.3390/mca29060097