Analysis and Optical System Design of the Lenslet-Array Integral Field Spectrometer

Abstract

To address the problem of slit limitation in traditional slit imaging spectrometers, which hampers fast the identification, efficient tracking, and precise avoidance of faint targets in lunar orbit, this article proposes a lenslet-array integral field spectrometer structure that is free of slits, static, and that is fast and efficient for the visible-to-near-infrared wavelength band. Firstly, the field of view segmentation model is analyzed, and the requirement of the telecentric degree of the pre-imaging system is obtained. Secondly, the influence of aberrations, such as spherical aberration and coma distortion on the micro-pupil dispersion model is analyzed. Based on this, the pre-imaging system is designed to meet the requirements of aberration correction and the telecentricity of the system. Finally, the structure of the spectral system is designed, and the integrated system is optimized. The smile of the lenslet-array integral field spectrometer is ±1 nm, and the MTF is greater than 0.7 at 60 lp/mm and close to the diffraction limit.

1. Introduction

The Moon is the only natural satellite of Earth. Due to its significant scientific and resource value, it has become the preferred target for deep space exploration by countries around the world and also the ideal outpost for human exploration in deep space in the future. However, exploring targets in the Earth–Moon space has challenges, such as low intensity, fast motion, etc. To achieve the detection of these targets, the detection equipment needs to be able to detect quickly, efficiently, and have the ability to detect weak targets while simultaneously achieving the three-dimensional information detection of spatial information intensity and spectral information to achieve the precise identification of Earth–Moon space targets.

Detection of the intensity information of Earth–Moon space targets can be achieved through large-aperture optical imaging lenses, while spectral dimension detection requires a high-spectral resolution imaging spectrometer [1,2,3]. However, current high-spectral resolution imaging spectrometers require a specific scanning method to obtain the required complete data cube, which wastes a lot of observation time. Furthermore, Earth–Moon space targets move quickly, and collisions may occur if they are not avoided quickly enough, resulting in devastating losses. For stationary targets on the same orbit with a distance of 100 km and relative motion, there is only 6 s available for avoidance. In addition, traditional high-spectral resolution imaging spectrometers require longer exposure times for the detection of weak targets. Within 6 s, it is impossible to scan, analyze and avoid the moving targets in question. Moreover, the images obtained from fast-moving targets are not obtained at the same time, resulting in significant errors and reduced recognition accuracy for Earth–Moon space targets [4,5,6].

A lenslet array integral field spectrometer can overcome the shortcomings of existing high-spectral resolution imaging spectrometers by enabling the acquisition of complete dynamic target three-dimensional data cubes in a single scan, avoiding the introduction of motion artifacts during the scanning process. The data obtained is simultaneous, improving the accuracy and consistency of observational data, and it has a faster detection speed without any limitation on energy input for the incident light. Also, this system has higher spectral energy and observation efficiency, which can achieve the precise identification of weak moving targets in Earth–Moon space and provide important technical means for exploring and developing the space [7,8,9,10].

In order to realize the application of the lenslet-array integral field spectrometer in detecting space targets in lunar orbit, this article analyzes the influence of anterior imaging system’s telecentricity on the system based on geometrical optics theory of micro-pupil. It proposes the requirements for the telecentricity of the anterior imaging system and develops initial structural calculation programs to obtain the optimal optical system parameters for micro-pupil distribution. Based on this, the optical system structure of the lenslet-array integral field spectrometer is designed to lay the theoretical foundation for promoting the practical application of the system in lunar orbit detection.

2. Basic Theory of Lenslet-Array Integral Field Spectrometer

Principle of Lenslet-Array Integral Field Spectrometer

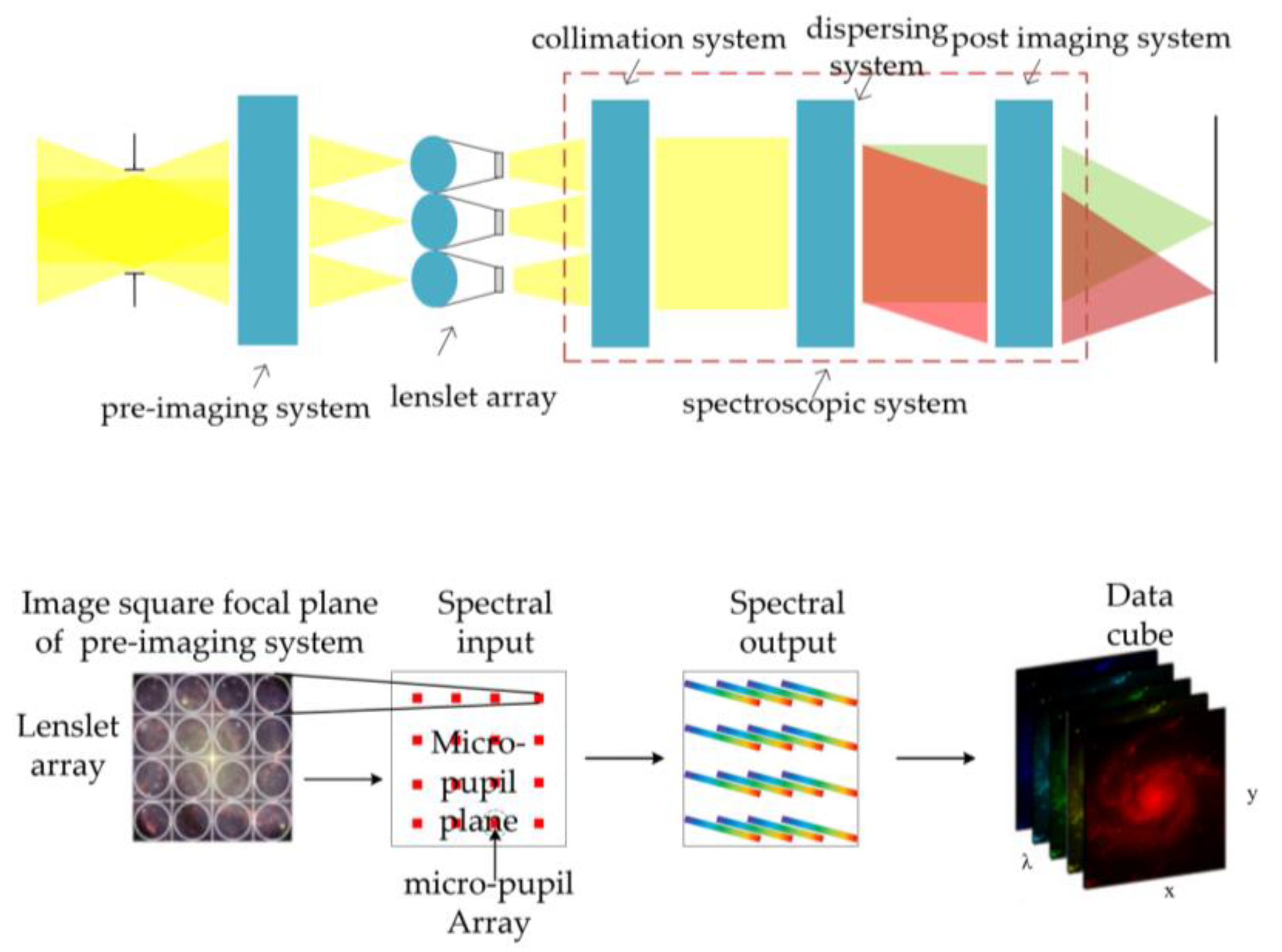
This paper presents the basic structure of a lenslet-array integral field spectrometer, as shown in Figure 1. The system consists of a pre-imaging system, a lenslet array, a collimation system, a dispersing system, and a post-imaging system. What needs to clarify is that the collimation system, dispersion system and post-imaging system are collectively referred to as spectroscopic system. The lenslet array is located at the focal plane of the pre-imaging system, with each lenslet corresponding to a specific field of view position. The pre-imaging system projects the collected image of the target onto the lenslet array, and the light passes through the lenslet array to form a corresponding array of micro-pupils on the focal plane of the lenslet array. Each micro-pupil serves as an entrance aperture for the spectrometer and contains all the light from the field of view where the lenslet is located. The collimation system after the lenslet array collimates the light, followed by dispersion for spectral separation. Subsequently, the post-imaging system images the different wavelengths of light onto the detector. The role of the lenslet array is to divide the images on the focal plane of the pre-imaging system into different fields of view and create micro-pupils on the focal plane. Different micro-pupils correspond to different field positions, allowing for the integration of field information through these micro-pupils. As a result, there is no need for scanning, and all the information from the entire field is obtained in a single scan, ensuring the accuracy of simultaneously acquired information [11,12,13].

In order to achieve uniform micro-pupil and improve the utilization of energy, square array lenses are selected. The formation of micro-pupil is shown in Figure 2. “a/2” is half the size of lenslet, “f” is the focal length of the pre-imaging system, “R” is the curvature radius of the lenslet, and “p” is the aperture of the lenslet.

The range of the field of view corresponding to each lens array is then determined.

$${\omega }_n=2\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}\left(\frac{a/2}{f}\right)$$

(1)

The size of the micro-pupil is $\varphi$, as shown in the figure. The expression for $\frac{\varphi }{2}$ is as follows:

$$\frac{\varphi }{2}=f\tan \left(i\right)-f\tan \left[\alpha \left(n-1\right)\right]+t\left\{\tan \left[\alpha \left(\frac{n-1}{n}\right)\right]-\tan \left(\frac{i}{n}\right)\right\}$$

(2)

$$i=\alpha -\frac{{\omega }_n}{2}$$

(3)

$$\alpha =\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{s}\mathrm{i}\mathrm{n}\left(\frac{p}{2R}\right)$$

(4)

Based on the above analysis, it can be seen that the size of the micro-pupil $\varphi$ is related to the focal length of the preceding telescope system and the size of the array lens. In order to obtain the optimal size of the micro-pupil $\varphi$ and ensure the rationality of the structure of the preceding imaging system and the lenslet array system, an initial structure calculation program was developed, as shown in Figure 3. When inputting p and f, the program outputs $\omega$, $\alpha$, $i$, and $\varphi$. The obtained value of $\varphi$ is then analyzed to determine whether it meets the system resolution requirements, and the validity of p,$f$, and R is confirmed. If all requirements are met, the design of the preceding imaging system is carried out based on the obtained data. If not, the program returns to the beginning and re-selects p, f, and R until the obtained data meets the system requirements.

3. Analysis and Design of Pre-Imaging Optics System

As the incident ‘‘slit’’ of the imaging spectrometer, the micro-pupil determines the imaging performance of the spectrometer system. In order to obtain a micro-pupil with good performance, no crosstalk, and an equal-phase wavefront, it is required that the main light rays of different field angles of the pre-imaging system are all perpendicular to the surface of the lenslet array [14]. Therefore, it is required that the pre-imaging system is an object-side telecentric optical path structure.

When the main light ray of a certain field of view of the pre-imaging system is not perpendicular to the surface of the lenslet array, that is, when the incident angle of the main light ray on the lenslet array at some field-of-view of the nth lens array is $\alpha$, and when $\alpha$ is greater than half of the field of view angle $\omega$ corresponding to each array lens, the originally supposed image point that should have been formed on the nth array lens will be imaged on its adjacent (n − 1)th array lens, causing crosstalk between adjacent lenses and making it difficult for the final image information to be processed properly, as shown in Figure 4. Therefore, the incident angle $\alpha$ of the main light ray of each field of view on the lenslet array must satisfy the following requirements.

$$\alpha \le \frac{{\omega }_n}{2}$$

(5)

After passing through the pre-imaging system, the image of the target object is imaged on a lenslet array. In order to ensure that each lens in the array can obtain a clear image of the target object, restrictions need to be placed on the field of view of the pre-imaging system. Taking the diagonal length $h$ of the lenslet array as the reference, the field of view angle 2$\omega$ of the pre-imaging system is

$$2\omega =2\arctan \left(\frac{h}{2f’}\right)$$

(6)

The lenslet-array integral field spectrometer system requires the correction of the secondary spectrum. If a refractive system is used, complex optical structures are required for correction. However, the reflective system does not produce aberrations and is more conducive to lightweight design.

Before the optical design of the pre-imaging system, it is necessary to establish a micro-pupil dispersion model and analyze the influence of spherical aberration, coma, and distortion on the micro-pupil array.

When there is no aberration in the pre-imaging system, the distribution of the micro-pupil array is shown in Figure 5a. It can be seen that the energy arrangement of the micro-pupil array is uniform, and the coordinate position arrangement is uniform grid structure.

Figure 5b shows that when a 5 lambda spherical aberration exists in the pre-imaging system, the distribution of the micro-pupil array, and the energy distribution of the micro-pupil array is no longer uniform; the middle part of the micro-pupil array has strong light, but the edge is weak. The arrangement of coordinate positions is no longer a uniform grid structure [15,16,17].

Figure 5c shows the distribution of the micro-pupil array when there is a 5 lambda coma in the pre-imaging system. The energy distribution of the micro-pupil array is no longer uniform; the lower part is strong, and the upper part is weak.

Figure 5d shows the distribution of the micro-pupil array when there is a 5 lambda distortion in the pre-imaging system. The arrangement of the micro-pupil array is no longer uniform, and the arrangement of coordinate positions is no longer uniform grid structure, but there is serious deformation.

It should be noted here that the F-number of the lenslet array used in the analysis of the entire article is 5.

We continued to search for the acceptable range of various aberrations. We assigned different values to each type of aberration and analyzed their respective impacts on the distribution of micro-pupils. In the end, when various aberrations individually act on the lenslet array, such as a spherical aberration with a magnitude of 2 lamda, a coma with a magnitude of 2 lamda, and a distortion with a magnitude of 2 lamda, there is no significant positional interference in the distribution of the micro-pupils, and the micro-pupil array remains uniform. The results are shown in Figure 6.

However, the system’s aberrations do not act solely on the lenslet array; they simultaneously affect the image plane of the lenslet array. Therefore, we analyzed the simultaneous impact of spherical aberration, coma, distortion, and other aberrations, each with a magnitude of 2 lamda, on the distribution of micro-pupils. The results are shown in Figure 7a.

From Figure 7a, it can be observed that although each aberration individually has a relatively small impact when its magnitude is 2 lamda on the lenslet array, their cumulative effect is significant when they act simultaneously. In order to determine the acceptable range of aberration values when they act simultaneously, we continued to analyze the simultaneous impact of various aberrations. In the end, we found that when the magnitudes of all aberrations are within the range of less than 1 lamda, the distribution of micro-pupils remains uniform. The results are shown in Figure 7b.

Therefore, when various aberrations are within the range of less than 1 lamda, the distribution of the micro-pupil array is uniform. Consequently, when designing the pre-imaging system, it is necessary to analyze the magnitudes of various aberrations, ensuring that they are all less than 1 lamda.

Spherical aberrations, coma, and distortion will affect spectral resolution and need to be carefully corrected. The degrees of freedom for correcting aberrations in a two-reflection system are limited. A co-axial three-reflection system has a central obstruction that affects the energy entering the system, reducing the optical system’s resolution. Depending on the off-axis method, there are two types of off-axis three-reflection systems: aperture off-axis and field off-axis. In an aperture off-axis three-reflection system, the aperture stop is placed on the main mirror, and the optical system is not symmetrical, so it cannot obtain a large field of view angle. In contrast, the aperture stop of a field off-axis three-reflection system is placed on the main mirror, and the optical system is more symmetrical, allowing for a larger field of view angle and better imaging quality [18,19,20,21,22,23,24].

Based on the above analysis, an off-axis three-reflection system with an image-side telecentric structure is used as the pre-imaging system. The incident angle of the main light ray at the image plane for each field of view must be less than half of the field of view angle corresponding to each array lens. Taking the diagonal length of the lenslet array as the benchmark for the field of view angle, the structural parameters of the designed pre-imaging system in this paper are shown in

Table 1. Structural parameters of the pre-imaging system.

Surface	Radius	Thickness	Conic Constant	4th Order Coefficient	6th Order Coefficient
Object surface	Infinity	310
Primary surface	−1159.2563	−300	−6.8237	−3.894345451185 × 10−10	7.889629261309 × 10−16
Second mirror	−390.4114	300	−0.9525	−1.164772530717 × 10−9	0
Third mirror	−585.4333	−270	−1.4897	−1.027301352431 × 10−9	−9.725869491468 × 10−16
Image	Infinity

. The wavelength range is 400~900 nm, the half-field angle $\omega$ is 2°, the focal length f’ is 600 mm, and the entrance pupil diameter is 120 mm. The incident angle of the main light ray at each field of view is less than 0.011°. The entrance pupil of the pre-imaging system is located in front of the first mirror, forming an image-side telecentric optical path. The primary, secondary, and tertiary mirrors all use second-order aspherical shapes to eliminate higher-order aberrations and reduce the number of mirrors in the system. A reflecting mirror is added after the tertiary mirror to fold the optical path and reduce the system’s size. The structure of the pre-imaging system is shown in Figure 8, and its modulation transfer function is shown in Figure 9. As shown in Figure 9, at a Nyquist spatial frequency of 60 lp/mm, the modulation transfer function is greater than 0.75, and the imaging quality is close to the diffraction limit. The point array diagram of the system is shown in Figure 10, and the Airy disk of each field of view is the outermost circular ring. The spot size of each field of view is smaller than the Airy disk, reaching the diffraction limit.

The main light-tracing of different fields of view is performed on the pre-imaging system by using real light-tracing, and the telecentric degree of different field of view is obtained, as shown in

Table 2. Analysis of the telecentricity of pre-imaging system.

Field	0°	1.23°	2.87°	4.1°
Telecentricity	0°	0.0001°	0.0002°	0.011°

.

4. Spectrometer System Design and Full System Integration

Collimating objective and imaging objective are crucial components of the prism-grating-type lenslet-array integral field spectrometer. The collimating objective serves the purpose of collimation. It transforms the beam of light coming from the incident slit into a parallel beam, which then enters the prism-grating combination dispersion element for spectral dispersion. Therefore, any aberrations affecting the collimation characteristics of the beam must be corrected, with spherical aberration being the primary concern. On the other hand, the imaging objective converges the dispersed light beam and forms an image on the image plane. Hence, corrections must be applied to address aberrations that affect imaging quality, including spherical aberration, astigmatism, coma, field curvature, distortion, chromatic aberration, and magnification aberration. In summary, the design requirements for the imaging objective are more stringent than those for the collimating objective. To reduce design and processing costs, it is possible to design the collimating objective and imaging objective with the same structure, while the collimating objective adopts the inverted structure of the imaging objective. This integrated imaging spectrometer exhibits optical symmetry, which aids in the correction and elimination of vertical aberrations in the system.

To ensure that the prism-grating-type lenslet-array integral field spectrometer matches the field of view and entrance pupil (position and size) of the pre-imaging lens and achieves uniform relative illuminance on the image plane, it is necessary to design the spectrometer system of the prism-grating-type lenslet-array integral field spectrometer as an object-side and image-side telecentric optical path. Therefore, the imaging objective should be designed as an image-side telecentric optical path, where the aperture stop is located at the object-side focal plane position, and the front focal length equals the preset distance from the grating to the first refractive surface of the imaging objective during system integration. In this way, the aperture stop becomes the entrance pupil, and all the main rays of the light entering the imaging objective pass through the object-side focus of the objective where the aperture stop is located. These main rays, after passing through the imaging objective, become parallel to the optical axis, achieve image-side telecentricity, and a uniform energy distribution can be obtained on the image plane.

The initial structure chosen for the imaging objective is the double-Gaussian lens to ensure the integration of the prism-grating-type hyperspectral imaging spectrometer. The aperture stop is placed 15 mm in front of the first refractive surface of the imaging objective (at least greater than the axial thickness of the prism-grating combination dispersion element). Using parameters such as focal length, back focal length, aperture position, image-side telecentricity, as primary constraints, and the surface curvature radius and center thickness of the lens, material refractive index and Abbe number, lens spacing as variables, the imaging objective is optimized using an interactive step-by-step approach.

With the primary aberrations of the imaging objective meeting the requirements, based on the characteristics of advanced aberrations, the approach for aberration correction or the direction of structural complexity is determined. According to the principle of axial aberration symmetrical cancellation and axial aberration symmetrical superposition, axial aberrations, such as spherical aberrations, comas, and field curvatures, are corrected through symmetrical changes in the lens. Astigmatism and distortion are axial aberrations that cancel symmetrically, and they are corrected through asymmetrical changes in the lens. In the design process of the double-Gaussian lens, the use of high refractive index glass has a positive effect. The increase in refractive index leads to an increase in the lens surface curvature radius, which is beneficial for reducing advanced aberrations. The increase in radius leads to a reduction in lens thickness, the shortening of the structure length, and a decrease in the height of the off-axis beam, achieving miniaturization. In the optimization process, increasing optimization variables by separating lens elements improves the imaging quality of the imaging objective.

The dispersion component of a transmission imaging spectrometer is usually a transmission splitting prism or a transmission grating. A prism or grating dispersion element used alone in an imaging spectrometer can introduce the bending of spectral lines (smile). The smile effect disrupts the alignment between the slit monochromatic image and the detector’s orbiting pixels, resulting in inconsistent central wavelengths and half-wave widths of different pixels in the same wavelength band, resulting in spectral aliasing of the image. The grating and prism compensate the smile because they have the dispersion of opposite signs; the dispersion formula of prism is $n\left(\lambda \right)=a+\frac{b}{{\lambda }^2}+\frac{c}{{\lambda }^4}$; and n is the refractive index at the wavelength; and A, B, and C are constants related to the dispersion properties of the prism material. The dispersion formula of the grating is $m\lambda =d(\sin i+\sin \theta )$; and m represents the order of the grating; $\lambda$ represents the wavelength of incident light; d represents the groove spacing of the grating, also known as the grating constant; $i$ represents the angle of incidence, which is the angle between the incident light ray and the normal to the grating surface; and $\theta$ represents the diffraction angle, which is the angle between the diffracted light ray and the normal to the grating surface. Therefore, the combination of the prism and grating can eliminate the smile. This design uses a combination of prism grating dispersion elements and an optical system to design and correct the smile. The final smile is less than half a pixel.

The final structural configuration of the spectral system is shown in Figure 11.

The MTFs of the spectrometer system are shown in Figure 12. We can see that the MTFs at the Nyquist frequency are all greater than 0.7 and are all close to the diffraction limit.

After the independent design of the pre-imaging and spectrometer systems is completed, a further combined optimization is required. However, because the pre-imaging and spectrometer systems have distinct characteristics, it is essential not to compromise their individual performances during the process of combined optimization. Instead, the goal is to balance the combined aberrations while ensuring that both systems can maintain their excellent performance when working independently. This process is referred to as the integrated optimization of the optical system of the imaging spectrometer.

The imaging and spectrometer systems share the same F-number and ensure aperture matching to ensure their seamless integration. An analysis of the aberration distribution for each system is performed. By combining the two systems, some positive and negative aberrations are canceled out, but some aberrations of the same sign accumulate. The focus is on the aberrations that accumulate when the two subsystems are combined, and system parameters are adjusted to ensure that the magnitude of the combined aberrations can be controlled within the design tolerance. The optical system, after integrated optimization, is shown in Figure 13.

The MTFs of the complete lenslet-array integral field spectrometer are shown in Figure 14. We can see that the MTFs at the Nyquist frequency are all greater than 0.7 and are all close to the diffraction limit.

After the prism-grating spectral imaging system corrects the spectral line bending and spectral bending by compensating the collimating objective and the imaging objective, the correction results are shown in the following table. As can be seen from

Table 3. Smile in different fields of view (The units of the smile in the table are μm).

	4.2°	2.94°	1.26°	0°	1.26°	2.94°	4.2°
400 nm	0	0	0	0	0	0	0
500 nm	−1	−1	0	0	0	−1	−1
600 nm	0	0	0	0	0	0	0
650 nm	0	0	0	0	0	0	0
700 nm	1	0	0	0	0	0	1
800 nm	1	0	0	0	0	0	0
900 nm	0	0	0	0	0	0	0

, the maximum amount of spectral line bending in the entire operating wavelength of the system is ±1 μm, which is less than 1/2 pixel size (the pixel size is 3.45 μm), and no subsequent processing is required. As can be seen from

Table 4. Keystone at different wavelengths and different fields of view (The units of the keystone in the table are μm).

Wavelength\Field	0°	1.26°	2.94°	4.2°
400 nm	0	−2	−4	−6
500 nm	0	−1	−1	−3
600 nm	0	0	0	−1
650 nm	0	0	0	0
700 nm	0	−1	−1	0
800 nm	0	−1	−1	0
900 nm	0	−2	−4	1

, the maximum correction band bend is −6 μm, which can be corrected by image fusion processing.

5. Conclusions

This article first analyzes the principle of how the micro-pupil is formed. Then, based on this principle, it examines the requirements for image-side telecentricity in the pre-imaging system. Next, it analyzes the impact of various aberrations on the system’s micro-pupils, deriving the aberration correction requirements for the pre-imaging system. Based on the aforementioned analysis, an optical system for the pre-imaging system is designed. This pre-imaging system adopts an off-axis three-reflection system structure with an image-side telecentric configuration. Subsequently, the design of a spectral imaging system is carried out. The spectrometer system is integrated and optimized in conjunction with the pre-imaging system. The design process also takes into consideration the correction of smile aberration. In the end, a lenslet-array integral field spectrometer is obtained, where the smile is within ±1 μm.

6. Discussion

Compared with other lenslet-array integral field spectrometers, this paper added the analysis of the formation principle of micro-pupil array, and on this basis, added the analysis of the system’s telecentric degree and determined the acceptable range of the telecentric degree. In addition, we also analyzed the simulation of the influence of spherical aberration, coma, and distortion of the pre-imaging system on the micro-pupil array. The influence of spherical aberration, coma aberration and distortion on the distribution of micro-pupil is obtained, which provides the optimization direction of specific aberration correction for the optical design of the system, defines the design objective, and greatly improves the accuracy and design efficiency of the optical design of the system. Moreover, the program for calculating the initial structure parameters is written to make the design more in line with the actual optical application scenario. Moreover, the design of this system adopts prism-grating combined dispersion element to correct the smile, combines with the back-end imaging system to correct the smile, and finally obtains the smile value of ±1 μm. The work in this paper will provide an important theoretical basis and technical means for the future application of the lenslet-array integral field spectrometer in the field of Earth–Moon space target detection.