Generating High-Power, Frequency Tunable Coherent THz Pulse in an X-ray Free-Electron Laser for THz Pump and X-ray Probe Experiments
Abstract
1. Introduction
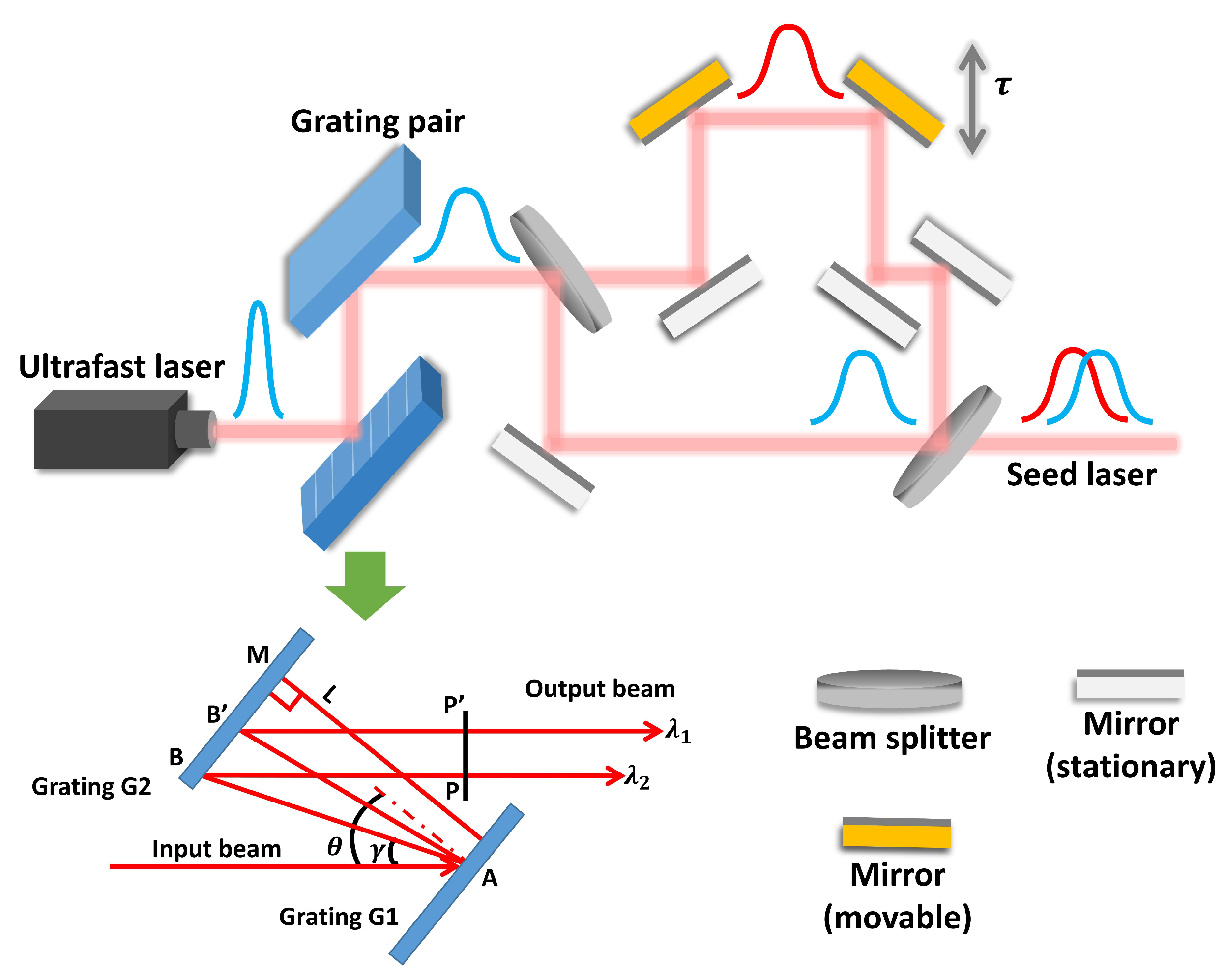
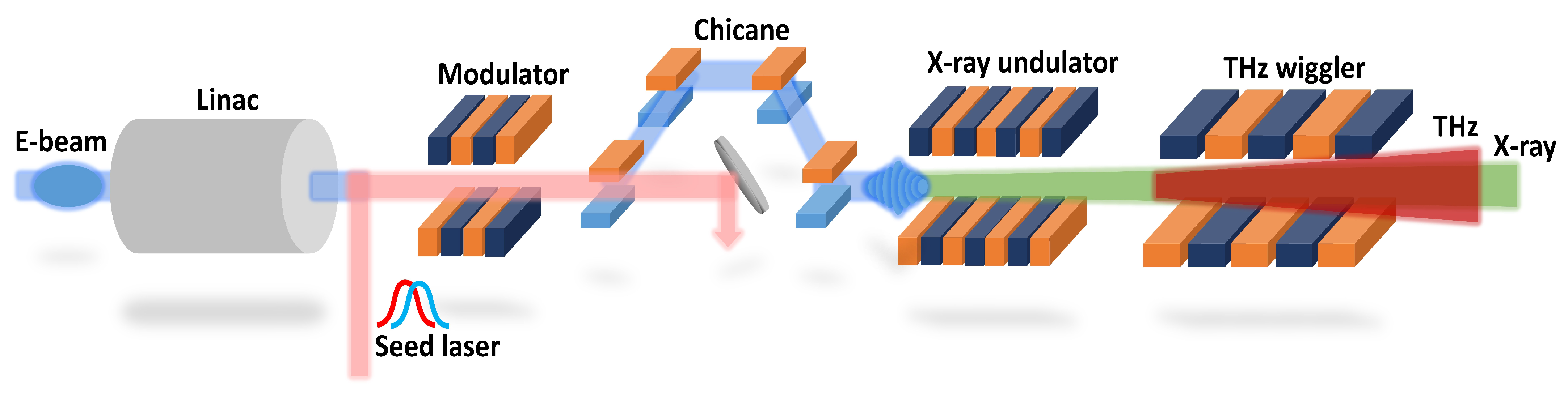
2. Working Principle
3. Results
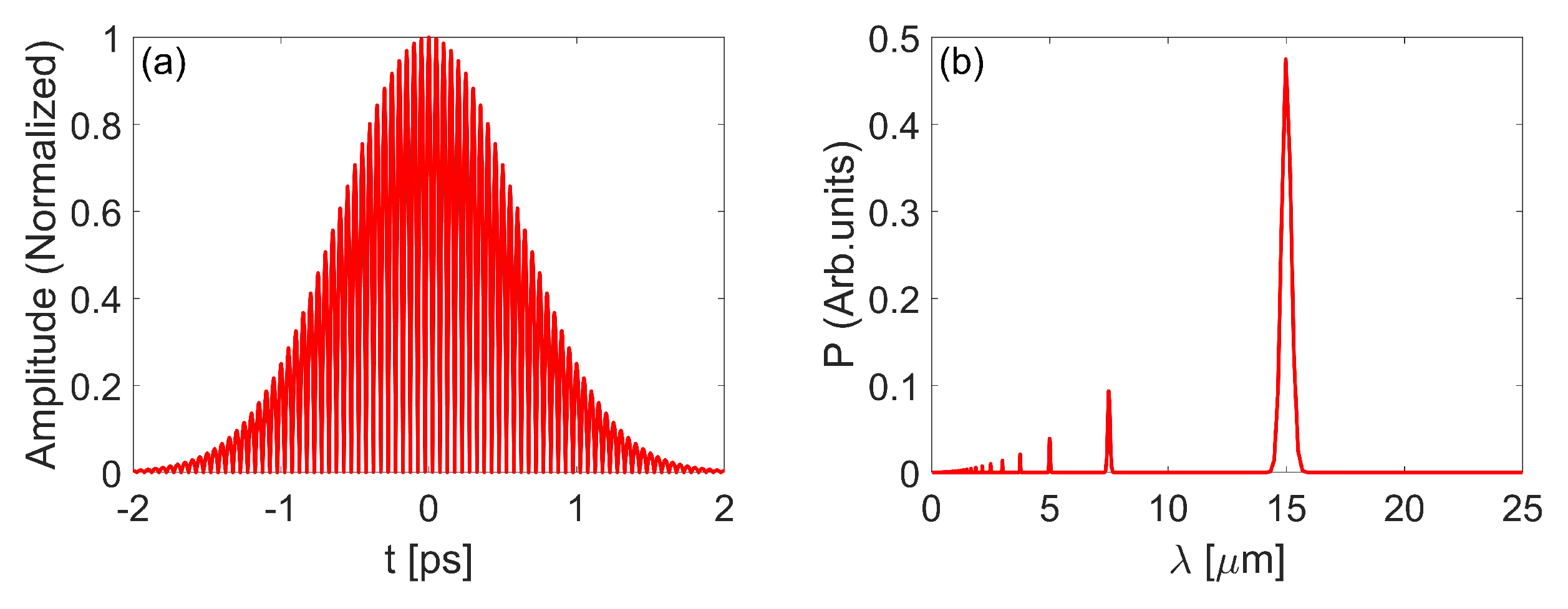
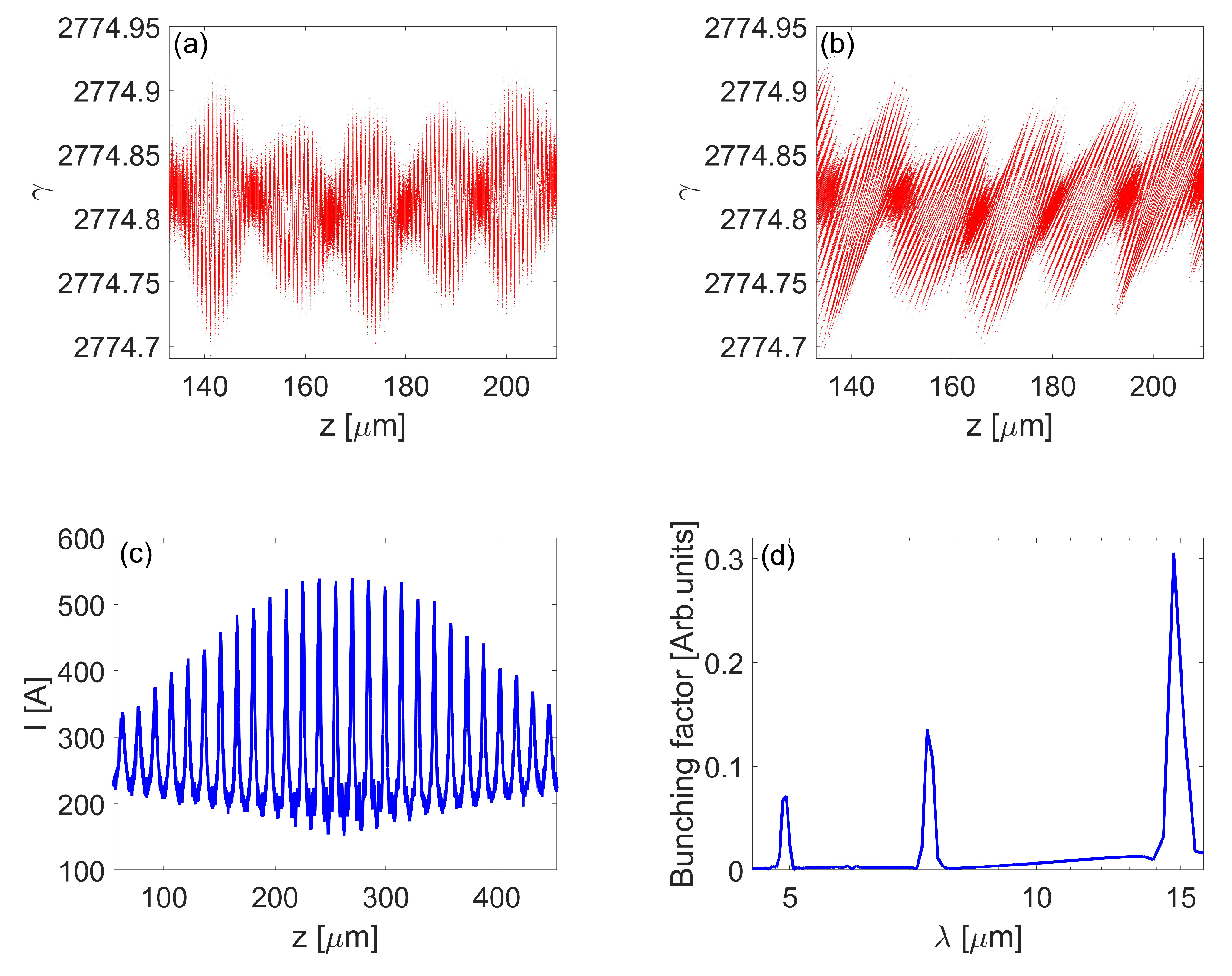
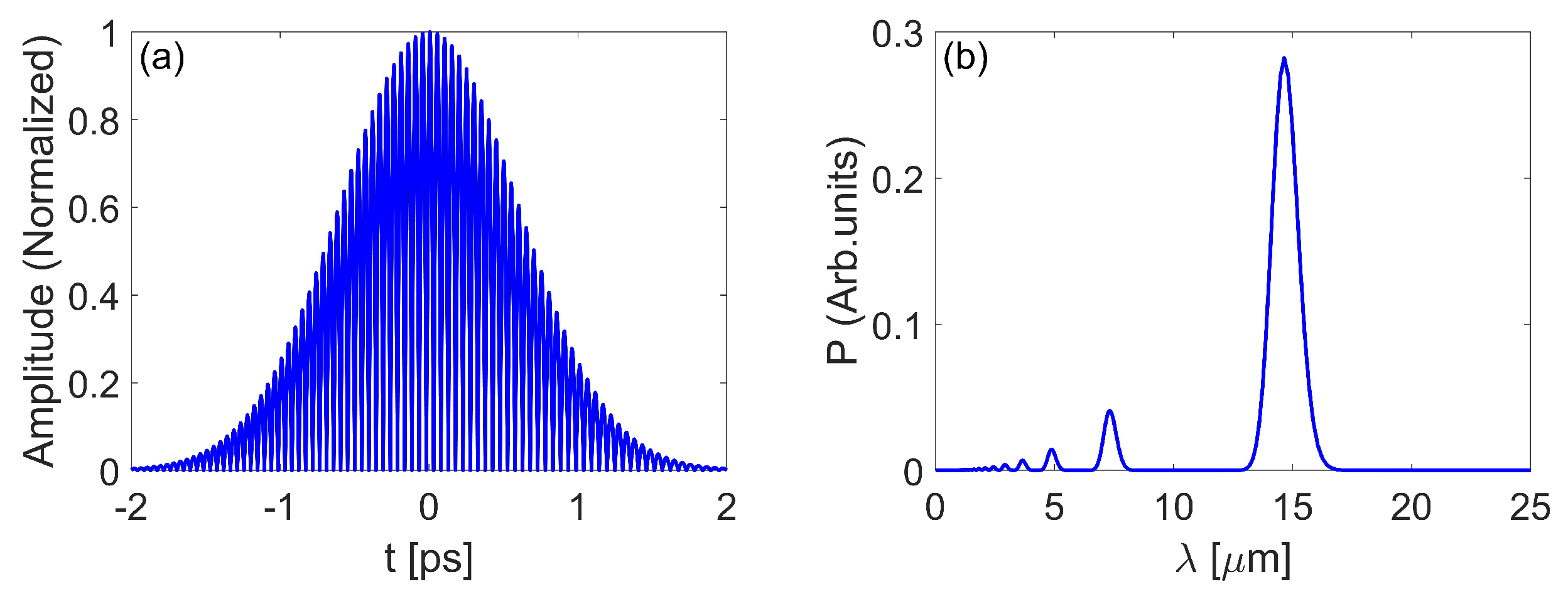
3.1. Generation of Frequency Beating Laser and Laser-Beam Modulation
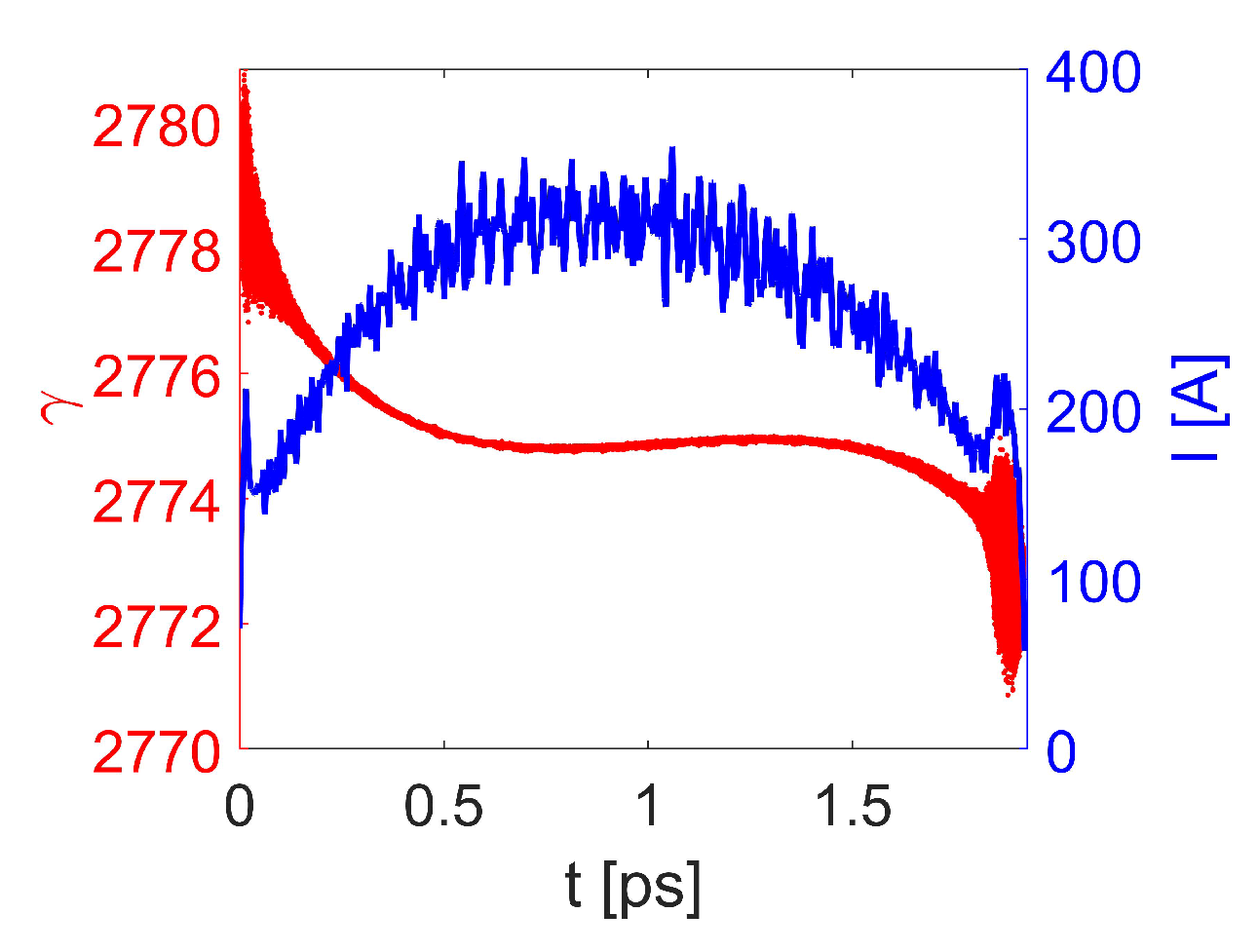
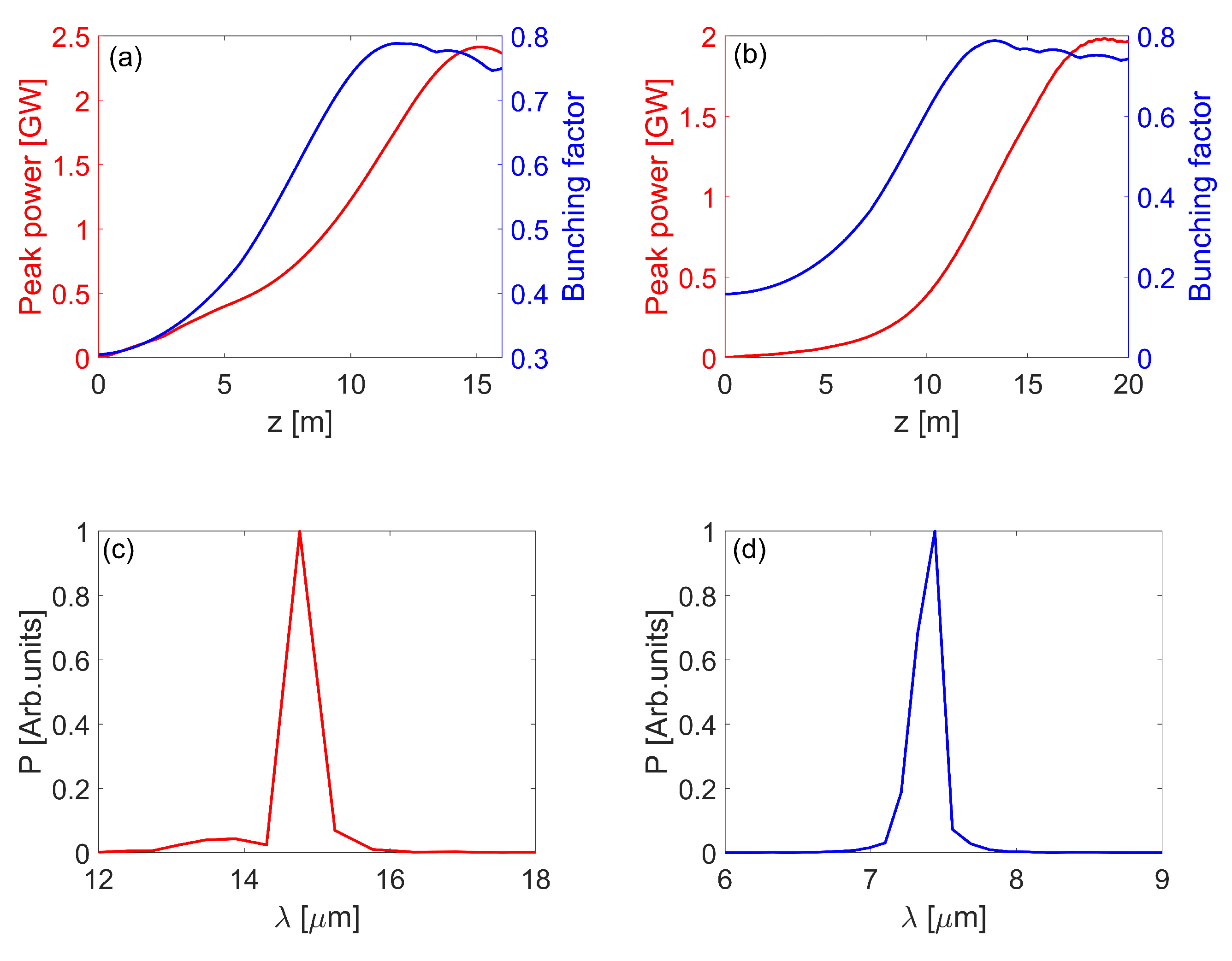
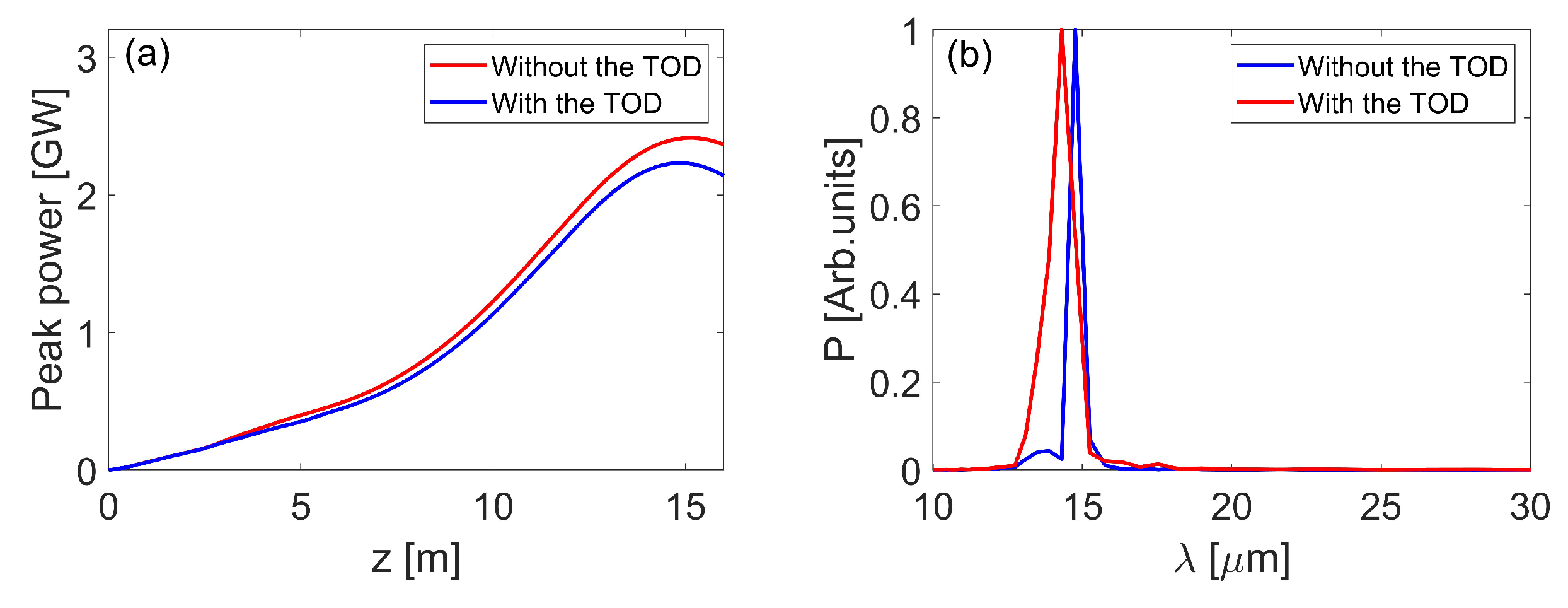
3.2. Generation of X-ray and THz Radiation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chaccour, C.; Soorki, M.N.; Saad, W.; Bennis, M.; Popovski, P.; Debbah, M. Seven Defining Features of Terahertz (THz) Wireless Systems: A Fellowship of Communication and Sensing. IEEE Commun. Surv. Tutor. 2022, 24, 967–993. [Google Scholar] [CrossRef]
- Serghiou, D.; Khalily, M.; Brown, T.W.C.; Tafazolli, R. Terahertz Channel Propagation Phenomena, Measurement Techniques and Modeling for 6G Wireless Communication Applications: A Survey, Open Challenges and Future Research Directions. IEEE Commun. Surv. Tutor. 2022, 24, 1957–1996. [Google Scholar] [CrossRef]
- Beiranvand, B.; Sobolev, A.S.; Kudryashov, A.V. Composite right/left-handed transmission line with array of thermocouples for generating terahertz radiation. Eur. Phys. J. Appl. Phys. 2020, 92, 20502. [Google Scholar] [CrossRef]
- Beiranvand, B.; Sobolev, A.S.; Larionov, M.Y.; Kuzmin, L.S. A Distributed Terahertz Metasurface with Cold-Electron Bolometers for Cosmology Missions. Appl. Sci. 2021, 11, 4459. [Google Scholar] [CrossRef]
- Zhong, Y.F.; Ren, J.J.; Li, L.J.; Zhang, J.Y.; Zhang, D.D.; Gu, J.; Xue, J.W.; Chen, Q. Measurement of Stress Optical Coefficient for Silicone Adhesive Based on Terahertz Time Domain Spectroscopy. Photonics 2022, 9, 929. [Google Scholar] [CrossRef]
- Tonouchi, M. Cutting-edge terahertz technology. Nat. Photonics 2007, 1, 97–105. [Google Scholar] [CrossRef]
- Mittleman, D.M. Perspective: Terahertz science and technology. J. Appl. Phys. 2017, 122, 230901. [Google Scholar] [CrossRef]
- Salen, P.; Basini, M.; Bonetti, S.; Hebling, J.; Krasilnikov, M.; Nikitin, A.Y.; Shamuilov, G.; Tibai, Z.; Zhaunerchyk, V.; Goryashko, V. Matter manipulation with extreme terahertz light: Progress in the enabling THz technology. Phys. Rep.-Rev. Sect. Phys. Lett. 2019, 836, 1–74. [Google Scholar] [CrossRef]
- Kovacs, K.; Balogh, E.; Hebling, J.; Tosa, V.; Varju, K. Quasi-Phase-Matching High-Harmonic Radiation Using Chirped THz Pulses. Phys. Rev. Lett. 2012, 108, 193903. [Google Scholar] [CrossRef]
- Nicoletti, D.; Cavalleri, A. Nonlinear light-matter interaction at terahertz frequencies. Adv. Opt. Photonics 2016, 8, 401–464. [Google Scholar] [CrossRef]
- Zhang, X.C.; Shkurinov, A.; Zhang, Y. Extreme terahertz science. Nat. Photonics 2017, 11, 16–18. [Google Scholar] [CrossRef]
- Zapolnova, E.; Pan, R.; Golz, T.; Sindik, M.; Nikolic, M.; Temme, M.; Rabasovic, M.; Grujic, D.; Chen, Z.; Toleikis, S.; et al. XUV-driven plasma switch for THz: New spatio-temporal overlap tool for XUV-THz pump-probe experiments at FELs. J. Synchrotron Rad. 2020, 27, 11–16. [Google Scholar] [CrossRef]
- Schmid, G.; Schnorr, K.; Augustin, S.; Meister, S.; Lindenblatt, H.; Trost, F.; Liu, Y.; Stojanovic, N.; Al-Shemmary, A.; Golz, T.; et al. Terahertz-Field-Induced Time Shifts in Atomic Photoemission. Phys. Rev. Lett. 2019, 122, 073001. [Google Scholar] [CrossRef]
- Fruehling, U.; Wieland, M.; Gensch, M.; Gebert, T.; Schuette, B.; Krikunova, M.; Kalms, R.; Budzyn, F.; Grimm, O.; Rossbach, J.; et al. Single-shot terahertz-field-driven X-ray streak camera. Nat. Photonics 2009, 3, 523–528. [Google Scholar] [CrossRef]
- Kampfrath, T.; Tanaka, K.; Nelson, K.A. Resonant and nonresonant control over matter and light by intense terahertz transients. Nat. Photonics 2013, 7, 680–690. [Google Scholar] [CrossRef]
- Vicario, C.; Monoszlai, B.; Hauri, C.P. GV/m Single-Cycle Terahertz Fields from a Laser-Driven Large-Size Partitioned Organic Crystal. Phys. Rev. Lett. 2014, 112, 213901. [Google Scholar] [CrossRef]
- Vicario, C.; Ovchinnikov, A.V.; Ashitkov, S.I.; Agranat, M.B.; Fortov, V.E.; Hauri, C.P. Generation of 0.9-mJ THz pulses in DSTMS pumped by a Cr:Mg2SiO4 laser. Opt. Lett. 2014, 39, 6632–6635. [Google Scholar] [CrossRef]
- Kim, K.Y.; Taylor, A.J.; Glownia, J.H.; Rodriguez, G. Coherent control of terahertz supercontinuum generation in ultrafast laser-gas interactions. Nat. Photonics 2008, 2, 605–609. [Google Scholar] [CrossRef]
- Liao, G.Q.; Li, Y.T.; Zhang, Y.H.; Liu, H.; Ge, X.L.; Yang, S.; Wei, W.Q.; Yuan, X.H.; Deng, Y.Q.; Zhu, B.J.; et al. Demonstration of Coherent Terahertz Transition Radiation from Relativistic Laser-Solid Interactions. Phys. Rev. Lett. 2016, 116, 205003. [Google Scholar] [CrossRef]
- Clerici, M.; Peccianti, M.; Schmidt, B.E.; Caspani, L.; Shalaby, M.; Giguere, M.; Lotti, A.; Couairon, A.; Legare, F.; Ozaki, T.; et al. Wavelength Scaling of Terahertz Generation by Gas Ionization. Phys. Rev. Lett. 2013, 110, 253901. [Google Scholar] [CrossRef]
- Gopal, A.; Herzer, S.; Schmidt, A.; Singh, P.; Reinhard, A.; Ziegler, W.; Broemmel, D.; Karmakar, A.; Gibbon, P.; Dillner, U.; et al. Observation of Gigawatt-Class THz Pulses from a Compact Laser-Driven Particle Accelerator. Phys. Rev. Lett. 2013, 111, 074802. [Google Scholar] [CrossRef]
- Stojanovic, N.; Drescher, M. Accelerator- and laser-based sources of high-field terahertz pulses. J. Phys. B At. Mol. Opt. Phys. 2013, 46, 192001. [Google Scholar] [CrossRef]
- Shalaby, M.; Hauri, C.P. Demonstration of a low-frequency three-dimensional terahertz bullet with extreme brightness. Nat. Commun. 2015, 6, 5976. [Google Scholar] [CrossRef] [PubMed]
- Fülöp, J.A.; Ollmann, Z.; Lombosi, C.; Skrobol, C.; Klingebiel, S.; Pálfalvi, L.; Krausz, F.; Karsch, S.; Hebling, J. Efficient generation of THz pulses with 0.4 mJ energy. Opt. Express 2014, 22, 20155–20163. [Google Scholar] [CrossRef] [PubMed]
- Leemans, W.; Geddes, C.; Faure, J.; Toth, C.; van Tilborg, J.; Schroeder, C.; Esarey, E.; Fubiani, G.; Auerbach, D.; Marcelis, B.; et al. Observation of terahertz emission from a laser-plasma accelerated electron bunch crossing a plasma-vacuum boundary. Phys. Rev. Lett. 2003, 91, 074802. [Google Scholar] [CrossRef]
- Byrd, J.; Leemans, W.; Loftsdottir, A.; Marcelis, B.; Martin, M.; McKinney, W.; Sannibale, F.; Scarvie, T.; Steier, C. Observation of broadband self-amplified spontaneous coherent terahertz synchrotron radiation in a storage ring. Phys. Rev. Lett. 2002, 89, 224801. [Google Scholar] [CrossRef]
- Abo-Bakr, M.; Feikes, J.; Holldack, K.; Wustefeld, G.; Hubers, H. Steady-state far-infrared coherent synchrotron radiation detected at BESSY II. Phys. Rev. Lett. 2002, 88, 254801. [Google Scholar] [CrossRef]
- Bielawski, S.; Evain, C.; Hara, T.; Hosaka, M.; Katoh, M.; Kimura, S.; Mochihashi, A.; Shimada, M.; Szwaj, C.; Takahashi, T.; et al. Tunable narrowband terahertz emission from mastered laser-electron beam interaction. Nat. Phys. 2008, 4, 390–393. [Google Scholar] [CrossRef]
- Daranciang, D.; Goodfellow, J.; Fuchs, M.; Wen, H.; Ghimire, S.; Reis, D.A.; Loos, H.; Fisher, A.S.; Lindenberg, A.M. Single-cycle terahertz pulses with > 0.2 V/angstrom field amplitudes via coherent transition radiation. Appl. Phys. Lett. 2011, 99, 141117. [Google Scholar] [CrossRef]
- Wu, Z.; Fisher, A.S.; Goodfellow, J.; Fuchs, M.; Daranciang, D.; Hogan, M.; Loos, H.; Lindenberg, A. Intense terahertz pulses from SLAC electron beams using coherent transition radiation. Rev. Sci. Instrum. 2013, 84, 022701. [Google Scholar] [CrossRef]
- Liao, G.; Li, Y.; Liu, H.; Scott, G.G.; Neely, D.; Zhang, Y.; Zhu, B.; Zhang, Z.; Armstrong, C.; Zemaityte, E.; et al. Multimillijoule coherent terahertz bursts from picosecond laser-irradiated metal foils. Proc. Natl. Acad. Sci. USA 2019, 116, 3994–3999. [Google Scholar] [CrossRef] [PubMed]
- Green, B.; Kovalev, S.; Asgekar, V.; Geloni, G.; Lehnert, U.; Golz, T.; Kuntzsch, M.; Bauer, C.; Hauser, J.; Voigtlaender, J.; et al. High-Field High-Repetition-Rate Sources for the Coherent THz Control of Matter. Sci. Rep. 2016, 6, 22256. [Google Scholar] [CrossRef] [PubMed]
- Tanikawa, T.; Karabekyan, S.; Kovalev, S.; Casalbuoni, S.; Asgekar, V.; Serkez, S.; Geloni, G.; Gensch, M. A superradiant THz undulator source for XFELs. J. Instrum. 2019, 14, P05024. [Google Scholar] [CrossRef]
- Tanaka, T. Difference frequency generation in free electron lasers. Opt. Lett. 2018, 43, 4485–4488. [Google Scholar] [CrossRef]
- Bonifacio, R.; Pellegrini, C.; Narducci, L. Collective Instabilities and High Gain Regime in a Free Electron Laser. Opt. Commun. 1985, 50, 373–378. [Google Scholar] [CrossRef]
- Andruszkow, J.; Aune, B.; Ayvazyan, V.; Baboi, N.; Bakker, R.; Balakin, V.; Barni, D.; Bazhan, A.; Bernard, M.; Bosotti, A.; et al. First observation of self-amplified spontaneous emission in a free-electron laser at 109 nm wavelength. Phys. Rev. Lett. 2000, 85, 3825–3829. [Google Scholar] [CrossRef]
- Huang, Z.; Kim, K.J. Review of X-ray free-electron laser theory. Phys. Rev. Spec. Top.-Accel. Beams 2007, 10, 034801. [Google Scholar] [CrossRef]
- Feng, C.; Deng, H.X. Review of fully coherent free-electron lasers. Nucl. Sci. Tech. 2018, 29, 160. [Google Scholar] [CrossRef]
- Zhang, Z.; Fisher, A.S.; Hoffmann, M.C.; Jacobson, B.; Kirchmann, P.S.; Lee, W.S.; Lindenberg, A.; Marinelli, A.; Nanni, E.; Schoenlein, R.; et al. A high-power, high-repetition-rate THz source for pump-probe experiments at Linac Coherent Light Source II. J. Synchrotron Rad. 2020, 27, 890–901. [Google Scholar] [CrossRef]
- Decker, F.J.; Gilevich, S.; Huang, Z.; Loos, H.; Marinelli, A.; Stan, C.; Turner, J.; Van Hoover, Z.; Vetter, S. Two Bunches with ns-Separation with LCLS. In Proceedings of the 37th International Free Electron Laser Conference, Daejeon, Republic of Korea, 23–28 August 2015; p. WEP023. [Google Scholar]
- Zapolnova, E.; Golz, T.; Pan, R.; Klose, K.; Schreiber, S.; Stojanovic, N. THz pulse doubler at FLASH: Double pulses for pump-probe experiments at X-ray FELs. J. Synchrotron Rad. 2018, 25, 39–43. [Google Scholar] [CrossRef]
- Pan, R.; Zapolnova, E.; Golz, T.; Krmpot, A.J.; Rabasovic, M.D.; Petrovic, J.; Asgekar, V.; Faatz, B.; Tavella, F.; Perucchi, A.; et al. Photon diagnostics at the FLASH THz beamline. J. Synchrotron Rad. 2019, 26, 700–707. [Google Scholar] [CrossRef]
- Tiedtke, K.; Azima, A.; von Bargen, N.; Bittner, L.; Bonfigt, S.; Duesterer, S.; Faatz, B.; Fruehling, U.; Gensch, M.; Gerth, C.; et al. The soft X-ray free-electron laser FLASH at DESY: Beamlines, diagnostics and end-stations. New J. Phys. 2009, 11, 023029. [Google Scholar] [CrossRef]
- Schneidmiller, E.A.; Yurkov, M.V.; Krasilnikov, M.; Stephan, F. Tunable IR/THz source for pump probe experiments at the European XFEL. In Advances in X-ray Free-Electron Lasers II: Instrumentation; Tschentscher, T., Tiedtke, K., Eds.; International Society for Optics and Photonics, SPIE: Prague, Czech Republic, 2013; Volume 8778. [Google Scholar]
- Decking, W.; Abeghyan, S.; Abramian, P.; Abramsky, A.; Aguirre, A.; Albrecht, C.; Alou, P.; Altarelli, M.; Altmann, P.; Amyan, K.; et al. A MHz-repetition-rate hard X-ray free-electron laser driven by a superconducting linear accelerator (vol 14, pg 6311, 2020). Nat. Photonics 2020, 14, 650. [Google Scholar] [CrossRef]
- Patterson, B.D.; Abela, R.; Braun, H.H.; Flechsig, U.; Ganter, R.; Kim, Y.; Kirk, E.; Oppelt, A.; Pedrozzi, M.; Reiche, S.; et al. Coherent science at the SwissFEL X-ray laser. New J. Phys. 2010, 12, 035012. [Google Scholar] [CrossRef]
- Milne, C.J.; Schietinger, T.; Aiba, M.; Alarcon, A.; Alex, J.; Anghel, A.; Arsov, V.; Beard, C.; Beaud, P.; Bettoni, S.; et al. SwissFEL: The Swiss X-ray Free Electron Laser. Appl. Sci. 2017, 7, 720. [Google Scholar] [CrossRef]
- Prat, E.; Abela, R.; Aiba, M.; Alarcon, A.; Alex, J.; Arbelo, Y.; Arrell, C.; Arsov, V.; Bacellar, C.; Beard, C.; et al. A compact and cost-effective hard X-ray free-electron laser driven by a high-brightness and low-energy electron beam. Nat. Photonics 2020, 14, 748–754. [Google Scholar] [CrossRef]
- Zhang, K.; Kang, Y.; Liu, T.; Wang, Z.; Feng, C.; Fang, W.; Zhao, Z. A Compact Accelerator-Based Light Source for High-Power, Full-Bandwidth Tunable Coherent THz Generation. Appl. Sci. 2021, 11, 11850. [Google Scholar] [CrossRef]
- Weling, A.; Auston, D. Novel sources and detectors for coherent tunable narrow-band terahertz radiation in free space. J. Opt. Soc. Am. Opt. Phys. 1996, 13, 2783–2791. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, W.; Jiang, S.; Li, C.; He, Z.; Zhang, S.; Jia, Q.; Wang, L.; He, D. Tuning electron bunch with a longitudinally shaped laser to generate half-cycle terahertz radiation pulse. J. Instrum. 2021, 16, P08019. [Google Scholar] [CrossRef]
- Treacy, E. Optical pulse compression with diffraction gratings. IEEE J. Quantum Electron. 1969, 5, 454–458. [Google Scholar] [CrossRef]
- Yu, L. Generation of intense uv radiation by subharmonically seeded single-pass free-electron lasers. Phys. Rev. A 1991, 44, 5178–5193. [Google Scholar] [CrossRef] [PubMed]
- Available online: http://tesla.desy.de/~{}meykopff/ (accessed on 19 December 2022).
- Zeng, L.; Feng, C.; Wang, X.; Zhang, K.; Qi, Z.; Zhao, Z. A Super-Fast Free-Electron Laser Simulation Code for Online Optimization. Photonics 2020, 7, 117. [Google Scholar] [CrossRef]
- Borland, M. ELEGANT: A Flexible SDDS-Compliant Code for Accelerator Simulation; US Department of Energy (US): Washington, DC, USA, 2000. [Google Scholar]
- Reiche, S. GENESIS 1.3: A fully 3D time-dependent FEL simulation code. Nuclear Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 1999, 429, 243–248. [Google Scholar] [CrossRef]
- Kang, Y.; Zhang, K.; Feng, C. Analysis of high order dispersion effects on a beat frequency-based THz free-electron laser. Proc. SPIE 2022. accepted. [Google Scholar]
- Ratner, D.; Fry, A.; Stupakov, G.; White, W. Laser phase errors in seeded free electron lasers. Phys. Rev. Spec. Top.-Accel. Beams 2012, 15, 030702. [Google Scholar] [CrossRef]
- Gensch, M.; Bittner, L.; Chesnov, A.; Delsim-Hashemi, H.; Drescher, M.; Faatz, B.; Feldhaus, J.; Fruehling, U.; Geloni, G.; Gerth, C.; et al. New infrared undulator beamline at FLASH. Infrared Phys. Technol. 2008, 51, 423–425. [Google Scholar] [CrossRef]
- Bajt, S.; Chapman, H.N.; Spiller, E.; Hau-Riege, S.; Alameda, J.; Nelson, A.J.; Walton, C.C.; Kjornrattanawanich, B.; Aquila, A.; Dollar, F.; et al. Multilayers for next generation X-ray sources. In Proceedings of the SPIE Conference on Damage to VUV, EUV and X-ray Optics, Prague, Czech Republic, 18–19 April 2007; Volume 6586. [Google Scholar]

| Parameters | Value |
|---|---|
| Laser wavelength | 800 nm |
| Laser pulse width | 15 fs |
| Peak power | 9 MW |
| Grating line | 250 |
| Incident angle | |
| Grating pair distance | 9 cm |
| Electron beam energy | 1.4 GeV |
| Energy spread (slice) | 0.001% |
| Bunch length | 570 m |
| Bunch charge | 500 pC |
| Undulator period | 1.6 cm |
| Wiggler period | 20 cm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, Y.; Wang, Z.; Zhang, K.; Feng, C. Generating High-Power, Frequency Tunable Coherent THz Pulse in an X-ray Free-Electron Laser for THz Pump and X-ray Probe Experiments. Photonics 2023, 10, 133. https://doi.org/10.3390/photonics10020133
Kang Y, Wang Z, Zhang K, Feng C. Generating High-Power, Frequency Tunable Coherent THz Pulse in an X-ray Free-Electron Laser for THz Pump and X-ray Probe Experiments. Photonics. 2023; 10(2):133. https://doi.org/10.3390/photonics10020133
Chicago/Turabian StyleKang, Yin, Zhen Wang, Kaiqing Zhang, and Chao Feng. 2023. "Generating High-Power, Frequency Tunable Coherent THz Pulse in an X-ray Free-Electron Laser for THz Pump and X-ray Probe Experiments" Photonics 10, no. 2: 133. https://doi.org/10.3390/photonics10020133
APA StyleKang, Y., Wang, Z., Zhang, K., & Feng, C. (2023). Generating High-Power, Frequency Tunable Coherent THz Pulse in an X-ray Free-Electron Laser for THz Pump and X-ray Probe Experiments. Photonics, 10(2), 133. https://doi.org/10.3390/photonics10020133





