Quantum State Tomography in Nonequilibrium Environments
Abstract
1. Introduction
2. Theoretical Framework
QST in Terms of Dynamic Generation of IC-POVMs
3. QST of Qubit Systems Coupled to Nonequilibrium Environments
3.1. QST of a Single Qubit System in Nonequilibrium Environments
3.2. QST of a Two-Qubit System in Nonequilibrium Environments
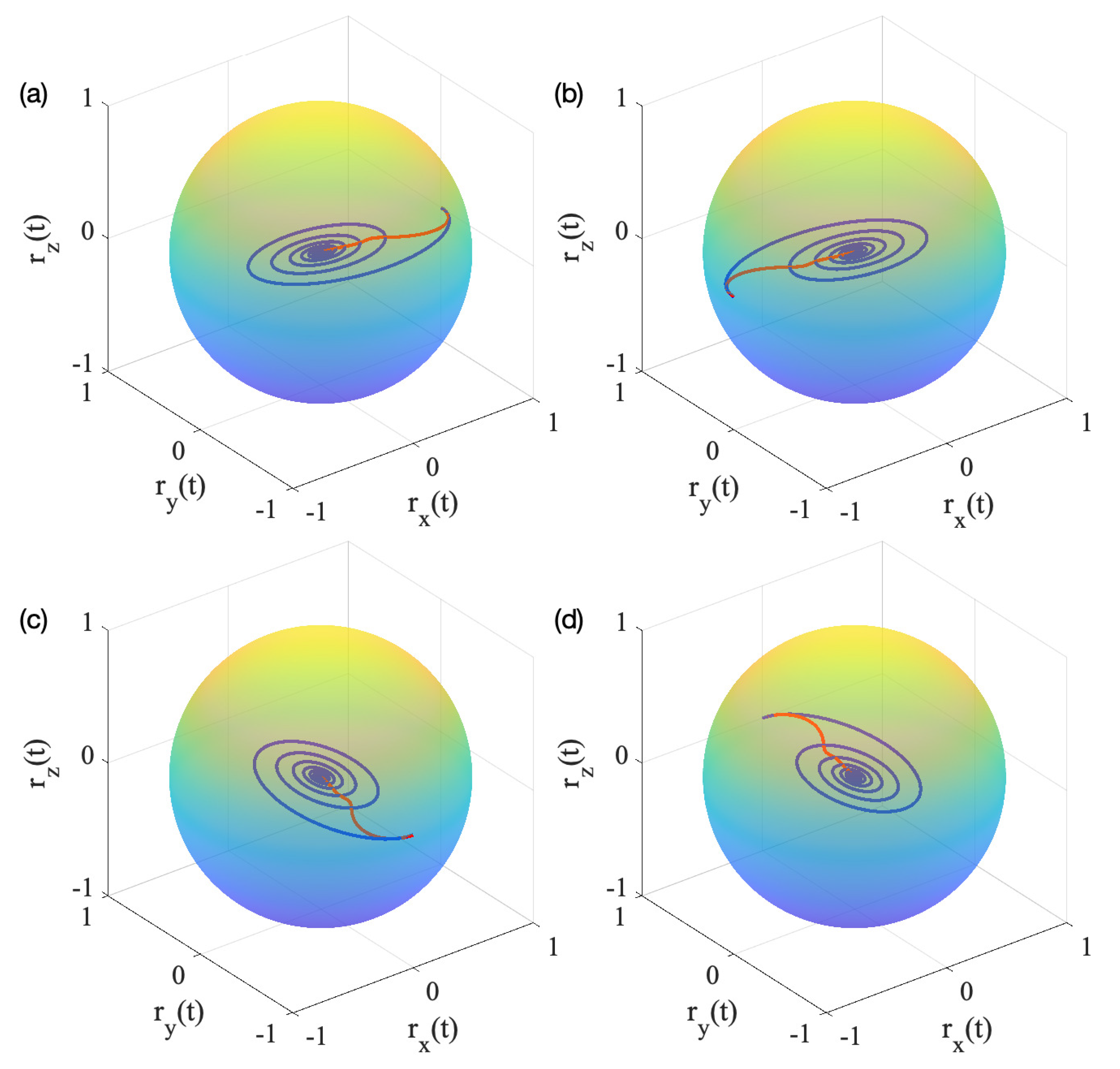
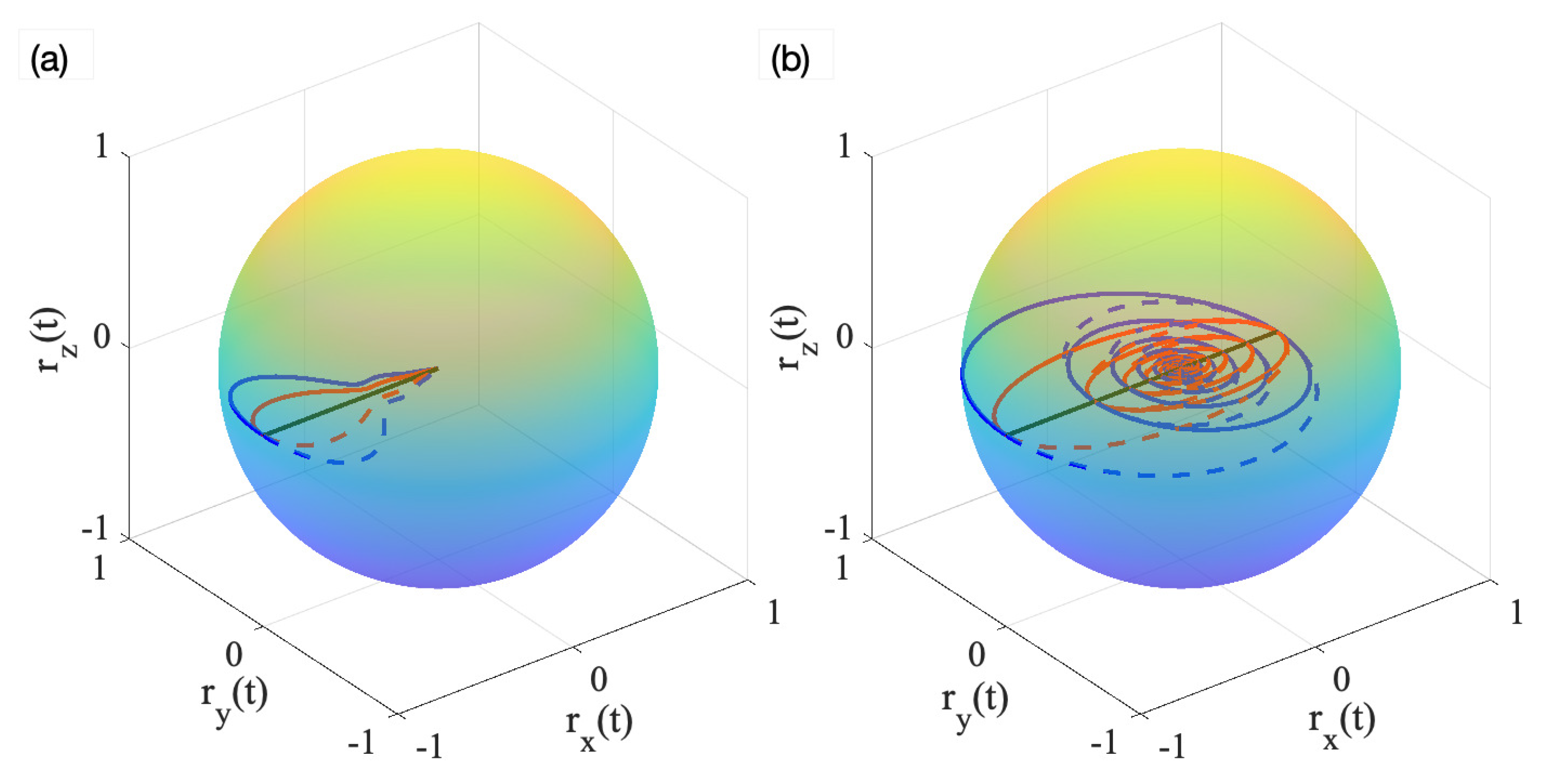
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| QST | quantum state tomography |
| MLE | maximum likelihood estimation |
| POVM | positive operator-valued measure |
| RTN | random telegraph noise |
Appendix A. State Representations of a d-Dimensional Quantum System
References
- Sedziak-Kacprowicz, K.; Czerwinski, A.; Kolenderski, P. Tomography of time-bin quantum states using time-resolved detection. Phys. Rev. A 2020, 102, 052420. [Google Scholar] [CrossRef]
- Czerwinski, A.; Sedziak-Kacprowicz, K.; Kolenderski, P. Phase estimation of time-bin qudits by time-resolved single-photon counting. Phys. Rev. A 2021, 103, 042402. [Google Scholar] [CrossRef]
- Czerwinski, A. Hamiltonian tomography by the quantum quench protocol with random noise. Phys. Rev. A 2021, 104, 052431. [Google Scholar] [CrossRef]
- Altepeter, J.B.; Branning, D.; Jeffrey, E.; Wei, T.C.; Kwiat, P.G.; Thew, R.T.; O’Brien, J.L.; Nielsen, M.A.; White, A.G. Ancilla-Assisted Quantum Process Tomography. Phys. Rev. Lett. 2003, 90, 193601. [Google Scholar] [CrossRef]
- O’Brien, J.L.; Pryde, G.J.; Gilchrist, A.; James, D.F.V.; Langford, N.K.; Ralph, T.C.; White, A.G. Quantum Process Tomography of a Controlled-NOT Gate. Phys. Rev. Lett. 2004, 93, 080502. [Google Scholar] [CrossRef]
- Mohseni, M.; Rezakhani, A.T.; Lidar, D.A. Quantum-process tomography: Resource analysis of different strategies. Phys. Rev. A 2008, 77, 032322. [Google Scholar] [CrossRef]
- White, G.; Pollock, F.; Hollenberg, L.; Modi, K.; Hill, C. Non-Markovian Quantum Process Tomography. PRX Quantum 2022, 3, 020344. [Google Scholar] [CrossRef]
- Luis, A.; Sánchez-Soto, L.L. Complete Characterization of Arbitrary Quantum Measurement Processes. Phys. Rev. Lett. 1999, 83, 3573–3576. [Google Scholar] [CrossRef]
- Lundeen, J.S.; Feito, A.; Coldenstrodt-Ronge, H.; Pregnell, K.L.; Silberhorn, C.; Ralph, T.C.; Eisert, J.; Plenio, M.B.; Walmsley, I.A. Tomography of quantum detectors. Nat. Phys. 2009, 5, 27. [Google Scholar] [CrossRef]
- Cónsul, R.; Luis, A. Detector self-tomography. Opt. Lett. 2020, 45, 6799. [Google Scholar] [CrossRef]
- James, D.F.V.; Kwiat, P.G.; Munro, W.J.; White, A.G. Measurement of qubits. Phys. Rev. A 2001, 64, 052312. [Google Scholar] [CrossRef]
- Thew, R.T.; Nemoto, K.; White, A.G.; Munro, W.J. Qudit quantum-state tomography. Phys. Rev. A 2002, 66, 012303. [Google Scholar] [CrossRef]
- Czerwinski, A. Quantum tomography of entangled qubits by time-resolved single-photon counting with time-continuous measurements. Quantum Inf. Process. 2021, 21, 332. [Google Scholar] [CrossRef]
- Christandl, M.; Renner, R. Reliable Quantum State Tomography. Phys. Rev. Lett. 2012, 109, 120403. [Google Scholar] [CrossRef]
- Xin, T.; Lu, D.; Klassen, J.; Yu, N.; Ji, Z.; Chen, J.; Ma, X.; Long, G.; Zeng, B.; Laflamme, R. Quantum State Tomography via Reduced Density Matrices. Phys. Rev. Lett. 2017, 118, 020401. [Google Scholar] [CrossRef]
- Bent, N.; Qassim, H.; Tahir, A.A.; Sych, D.; Leuchs, G.; Sánchez-Soto, L.L.; Karimi, E.; Boyd, R.W. Experimental Realization of Quantum Tomography of Photonic Qudits via Symmetric Informationally Complete Positive Operator-Valued Measures. Phys. Rev. X 2015, 5, 041006. [Google Scholar] [CrossRef]
- Gupta, R.; Xia, R.; Levine, R.D.; Kais, S. Maximal Entropy Approach for Quantum State Tomography. PRX Quantum 2021, 2, 010318. [Google Scholar] [CrossRef]
- Stricker, R.; Meth, M.; Postler, L.; Edmunds, C.; Ferrie, C.; Blatt, R.; Schindler, P.; Monz, T.; Kueng, R.; Ringbauer, M. Experimental Single-Setting Quantum State Tomography. PRX Quantum 2022, 3, 040310. [Google Scholar] [CrossRef]
- Czerwinski, A. Optimal evolution models for quantum tomography. J. Phys. A 2016, 49, 075301. [Google Scholar] [CrossRef]
- Czerwinski, A.; Szlachetka, J. Efficiency of photonic state tomography affected by fiber attenuation. Phys. Rev. A 2022, 105, 062437. [Google Scholar] [CrossRef]
- Czerwinski, A.; Czerwinska, K. Statistical Analysis of the Photon Loss in Fiber-Optic Communication. Photonics 2022, 9, 568. [Google Scholar] [CrossRef]
- Hradil, Z. Quantum-state estimation. Phys. Rev. A 1997, 55, R1561. [Google Scholar] [CrossRef]
- Opatrný, T.; Welsch, D.G.; Vogel, W. Least-squares inversion for density-matrix reconstruction. Phys. Rev. A 1997, 56, 1788. [Google Scholar] [CrossRef]
- Banaszek, K.; D’Ariano, G.M.; Paris, M.G.A.; Sacchi, M.F. Maximum-likelihood estimation of the density matrix. Phys. Rev. A 1999, 61, 010304. [Google Scholar] [CrossRef]
- Smolin, J.A.; Gambetta, J.M.; Smith, G. Efficient Method for Computing the Maximum-Likelihood Quantum State from Measurements with Additive Gaussian Noise. Phys. Rev. Lett. 2012, 108, 070502. [Google Scholar] [CrossRef]
- Shang, J.; Zhang, Z.; Ng, H.K. Superfast maximum-likelihood reconstruction for quantum tomography. Phys. Rev. A 2017, 95, 062336. [Google Scholar] [CrossRef]
- Breuer, H.P.; Petruccione, F. The Theory of Open Quantum Systems; Oxford University Press: New York, NY, USA, 2002. [Google Scholar]
- Schlosshauer, M. Decoherence and the Quantum-to-Classical Transition; Springer: Berlin/Heidelberg, Germnay, 2007. [Google Scholar]
- Schlosshauer, M. Quantum decoherence. Phys. Rep. 2019, 831, 1. [Google Scholar] [CrossRef]
- Carollo, A.; Valenti, D.; Spagnolo, B. Geometry of quantum phase transitions. Phys. Rep. 2020, 838, 1. [Google Scholar] [CrossRef]
- Piilo, J.; Maniscalco, S.; Härkönen, K.; Suominen, K.A. Non-Markovian Quantum Jumps. Phys. Rev. Lett. 2008, 100, 180402. [Google Scholar] [CrossRef]
- Breuer, H.; Laine, E.; Piilo, J. Measure for the Degree of Non-Markovian Behavior of Quantum Processes in Open Systems. Phys. Rev. Lett. 2009, 103, 210401. [Google Scholar] [CrossRef]
- Rivas, A.; Huelga, S.F.; Plenio, M.B. Entanglement and Non-Markovianity of Quantum Evolutions. Phys. Rev. Lett. 2010, 105, 050403. [Google Scholar] [CrossRef]
- Zhang, W.M.; Lo, P.Y.; Xiong, H.N.; Tu, M.W.Y.; Nori, F. General Non-Markovian Dynamics of Open Quantum Systems. Phys. Rev. Lett. 2012, 109, 170402. [Google Scholar] [CrossRef]
- Chruściński, D.; Maniscalco, S. Degree of Non-Markovianity of Quantum Evolution. Phys. Rev. Lett. 2014, 112, 120404. [Google Scholar] [CrossRef]
- Rivas, A.; Huelga, S.F.; Plenio, M.B. Quantum non-Markovianity: Characterization, quantification and detection. Rep. Prog. Phys. 2014, 77, 094001. [Google Scholar] [CrossRef]
- Fanchini, F.F.; Karpat, G.; Çakmak, B.; Castelano, L.K.; Aguilar, G.H.; Farías, O.J.; Walborn, S.P.; Ribeiro, P.H.S.; de Oliveira, M.C. Non-Markovianity through Accessible Information. Phys. Rev. Lett. 2014, 112, 210402. [Google Scholar] [CrossRef]
- Breuer, H.; Laine, E.; Piilo, J.; Vacchini, B. Colloquium: Non-Markovian dynamics in open quantum systems. Rev. Mod. Phys. 2016, 88, 021002. [Google Scholar] [CrossRef]
- de Vega, I.; Alonso, D. Dynamics of non-Markovian open quantum systems. Rev. Mod. Phys. 2017, 89, 015001. [Google Scholar] [CrossRef]
- Sun, S.; Zheng, Y. Distinct Bound of the Quantum Speed Limit via the Gauge Invariant Distance. Phys. Rev. Lett. 2019, 123, 180403. [Google Scholar] [CrossRef]
- Sun, S.; Peng, Y.; Hu, X.; Zheng, Y. Quantum Speed Limit Quantified by the Changing Rate of Phase. Phys. Rev. Lett. 2021, 127, 100404. [Google Scholar] [CrossRef]
- Hu, X.; Sun, S.; Zheng, Y. Quantum speed limit via the trajectory ensemble. Phys. Rev. A 2020, 101, 042107. [Google Scholar] [CrossRef]
- Czerwinski, A. Open quantum systems integrable by partial commutativity. Phys. Rev. A 2020, 102, 062423. [Google Scholar] [CrossRef]
- Zheng, L.; Peng, Y. Quantum decoherence of a two-level system in colored environments. Phys. Rev. A 2022, 105, 052443. [Google Scholar] [CrossRef]
- Lan, K.; Xie, S.; Cai, X. Geometric quantum speed limits for Markovian dynamics in open quantum systems. New J. Phys. 2022, 24, 055003. [Google Scholar] [CrossRef]
- Czerwinski, A. Dynamics of Open Quantum Systems-Markovian Semigroups and Beyond. Symmetry 2022, 14, 1752. [Google Scholar] [CrossRef]
- Hadipour, M.; Haseli, S.; Dolatkhah, H.; Haddadi, S.; Czerwinski, A. Quantum Speed Limit for a Moving Qubit inside a Leaky Cavity. Photonics 2022, 9, 875. [Google Scholar] [CrossRef]
- Schlosshauer, M. Decoherence, the measurement problem, and interpretations of quantum mechanics. Rev. Mod. Phys. 2005, 76, 1267. [Google Scholar] [CrossRef]
- Clerk, A.A.; Devoret, M.H.; Girvin, S.M.; Marquardt, F.; Schoelkopf, R.J. Introduction to quantum noise, measurement, and amplification. Rev. Mod. Phys. 2010, 82, 1155. [Google Scholar] [CrossRef]
- Gurvitz, S.A.; Fedichkin, L.; Mozyrsky, D.; Berman, G.P. Relaxation and the Zeno Effect in Qubit Measurements. Phys. Rev. Lett. 2003, 91, 066801. [Google Scholar] [CrossRef]
- Kang, L.; Zhang, Y.; Xu, X.; Tang, X. Quantum measurement of a double quantum dot coupled to two kinds of environment. Phys. Rev. B 2017, 96, 235417. [Google Scholar] [CrossRef]
- Lan, K.; Du, Q.; Kang, L.; Tang, X.; Jiang, L.; Zhang, Y.; Cai, X. Dynamics of an open double quantum dot system via quantum measurement. Phys. Rev. B 2020, 101, 174302. [Google Scholar] [CrossRef]
- Silberfarb, A.; Jessen, P.S.; Deutsch, I.H. Quantum State Reconstruction via Continuous Measurement. Phys. Rev. Lett. 2005, 95, 030402. [Google Scholar] [CrossRef]
- Smith, A.; Riofrío, C.A.; Anderson, B.E.; Sosa-Martinez, H.; Deutsch, I.H.; Jessen, P.S. Quantum state tomography by continuous measurement and compressed sensing. Phys. Rev. A 2013, 87, 030102. [Google Scholar] [CrossRef]
- Merkel, S.T.; Riofrío, C.A.; Flammia, S.T.; Deutsch, I.H. Random unitary maps for quantum state reconstruction. Phys. Rev. A 2010, 81, 032126. [Google Scholar] [CrossRef]
- Czerwinski, A. Quantum state tomography with informationally complete POVMs generated in the time domain. Quantum Inf. Process. 2021, 20, 105. [Google Scholar] [CrossRef]
- Czerwinski, A. Selected Concepts of Quantum State Tomography. Optics 2022, 3, 268. [Google Scholar] [CrossRef]
- Heinosaari, T.; Ziman, M. The Mathematical Language of Quantum Theory; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Martens, C.C. Communication: Decoherence in a nonequilibrium environment: An analytically solvable model. J. Chem. Phys. 2010, 133, 241101. [Google Scholar] [CrossRef]
- Martens, C.C. Quantum dephasing of a two-state system by a nonequilibrium harmonic oscillator. J. Chem. Phys. 2013, 139, 024109. [Google Scholar] [CrossRef]
- Lombardo, F.C.; Villar, P.I. Nonunitary geometric phases: A qubit coupled to an environment with random noise. Phys. Rev. A 2013, 87, 032338. [Google Scholar] [CrossRef]
- Lombardo, F.C.; Villar, P.I. Correction to the geometric phase by structured environments: The onset of non-Markovian effects. Phys. Rev. A 2015, 91, 042111. [Google Scholar] [CrossRef]
- Cai, X.; Zheng, Y. Decoherence induced by non-Markovian noise in a nonequilibrium environment. Phys. Rev. A 2016, 94, 042110. [Google Scholar] [CrossRef]
- Cai, X.; Zheng, Y. Non-Markovian decoherence dynamics in nonequilibrium environments. J. Chem. Phys. 2018, 149, 094107. [Google Scholar] [CrossRef] [PubMed]
- Cai, X.; Zheng, Y. Quantum dynamical speedup in a nonequilibrium environment. Phys. Rev. A 2017, 95, 052104. [Google Scholar] [CrossRef]
- Lin, D.; Zou, H.M.; Yang, J. Based-nonequilibrium-environment non-Markovianity, quantum Fisher information and quantum coherence. Phys. Scr. 2019, 95, 015103. [Google Scholar] [CrossRef]
- Cai, X.; Meng, R.; Zhang, Y.; Wang, L. Geometry of quantum evolution in a nonequilibrium environment. Europhys. Lett. 2019, 125, 30007. [Google Scholar] [CrossRef]
- Basit, A.; Ali, H.; Badshah, F.; Yang, X.F.; Ge, G.Q. Controlling sudden transition from classical to quantum decoherence via non-equilibrium environments. New J. Phys. 2020, 22, 033039. [Google Scholar] [CrossRef]
- Basit, A.; Ali, H.; Badshah, F.; Yang, X.F.; Ge, G. Nonequilibrium effects on one-norm geometric correlations and the emergence of a pointer-state basis in the weak- and strong-coupling regimes. Phys. Rev. A 2021, 104, 042417. [Google Scholar] [CrossRef]
- Chen, M.; Chen, H.; Han, T.; Cai, X. Disentanglement Dynamics in Nonequilibrium Environments. Entropy 2022, 24, 1330. [Google Scholar] [CrossRef]
- Tang, J.S.; Li, C.F.; Li, Y.L.; Zou, X.B.; Guo, G.C.; Breuer, H.P.; Laine, E.M.; Piilo, J. Measuring non-Markovianity of processes with controllable system-environment interaction. Europhys. Lett. 2012, 97, 10002. [Google Scholar] [CrossRef]
- Cai, X. Quantum Dynamics in a Fluctuating Environment. Entropy 2019, 21, 1040. [Google Scholar] [CrossRef]
- Fuliński, A. Non-Markovian noise. Phys. Rev. E 1994, 50, 2668. [Google Scholar] [CrossRef]
- Cai, X. Quantum dephasing induced by non-Markovian random telegraph noise. Sci. Rep. 2020, 10, 88. [Google Scholar] [CrossRef]
- Wootters, W.K.; Fields, B.D. Optimal state-determination by mutually unbiased measurements. Ann. Phys. 1989, 191, 363. [Google Scholar] [CrossRef]
- Yu, T.; Eberly, J.H. Finite-time Disentanglement via Spontaneous Emission. Phys. Rev. Lett. 2004, 93, 140404. [Google Scholar] [CrossRef]
- Bellomo, B.; Lo Franco, R.; Compagno, G. Non-Markovian Effects on the Dynamics of Entanglement. Phys. Rev. Lett. 2007, 99, 160502. [Google Scholar] [CrossRef]
- Nemoto, K. Generalized coherent states for SU(n) systems. J. Phys. A 2000, 33, 3493. [Google Scholar] [CrossRef]
- Bertlmann1, R.A.; Krammer, P. Bloch vectors for qudits. J. Phys. A 2008, 41, 235303. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; Han, T.; Chen, M.; Ren, J.; Cai, X.; Meng, X.; Peng, Y. Quantum State Tomography in Nonequilibrium Environments. Photonics 2023, 10, 134. https://doi.org/10.3390/photonics10020134
Chen H, Han T, Chen M, Ren J, Cai X, Meng X, Peng Y. Quantum State Tomography in Nonequilibrium Environments. Photonics. 2023; 10(2):134. https://doi.org/10.3390/photonics10020134
Chicago/Turabian StyleChen, Haonan, Tao Han, Mingli Chen, Jing Ren, Xiangji Cai, Xiangjia Meng, and Yonggang Peng. 2023. "Quantum State Tomography in Nonequilibrium Environments" Photonics 10, no. 2: 134. https://doi.org/10.3390/photonics10020134
APA StyleChen, H., Han, T., Chen, M., Ren, J., Cai, X., Meng, X., & Peng, Y. (2023). Quantum State Tomography in Nonequilibrium Environments. Photonics, 10(2), 134. https://doi.org/10.3390/photonics10020134





