Robust Pulse-Pumped Quadratic Soliton Assisted by Third-Order Nonlinearity
Abstract
:1. Introduction
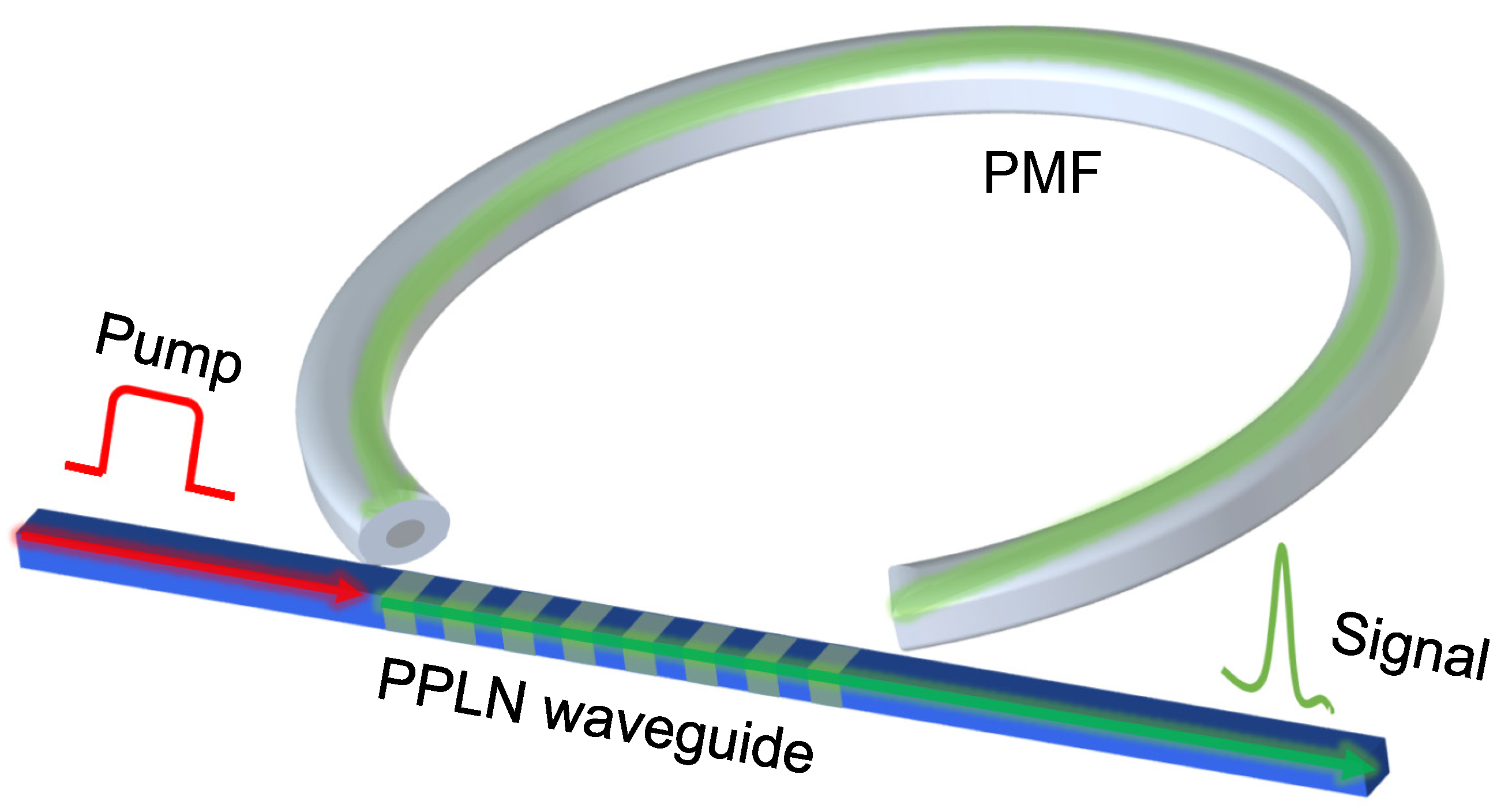
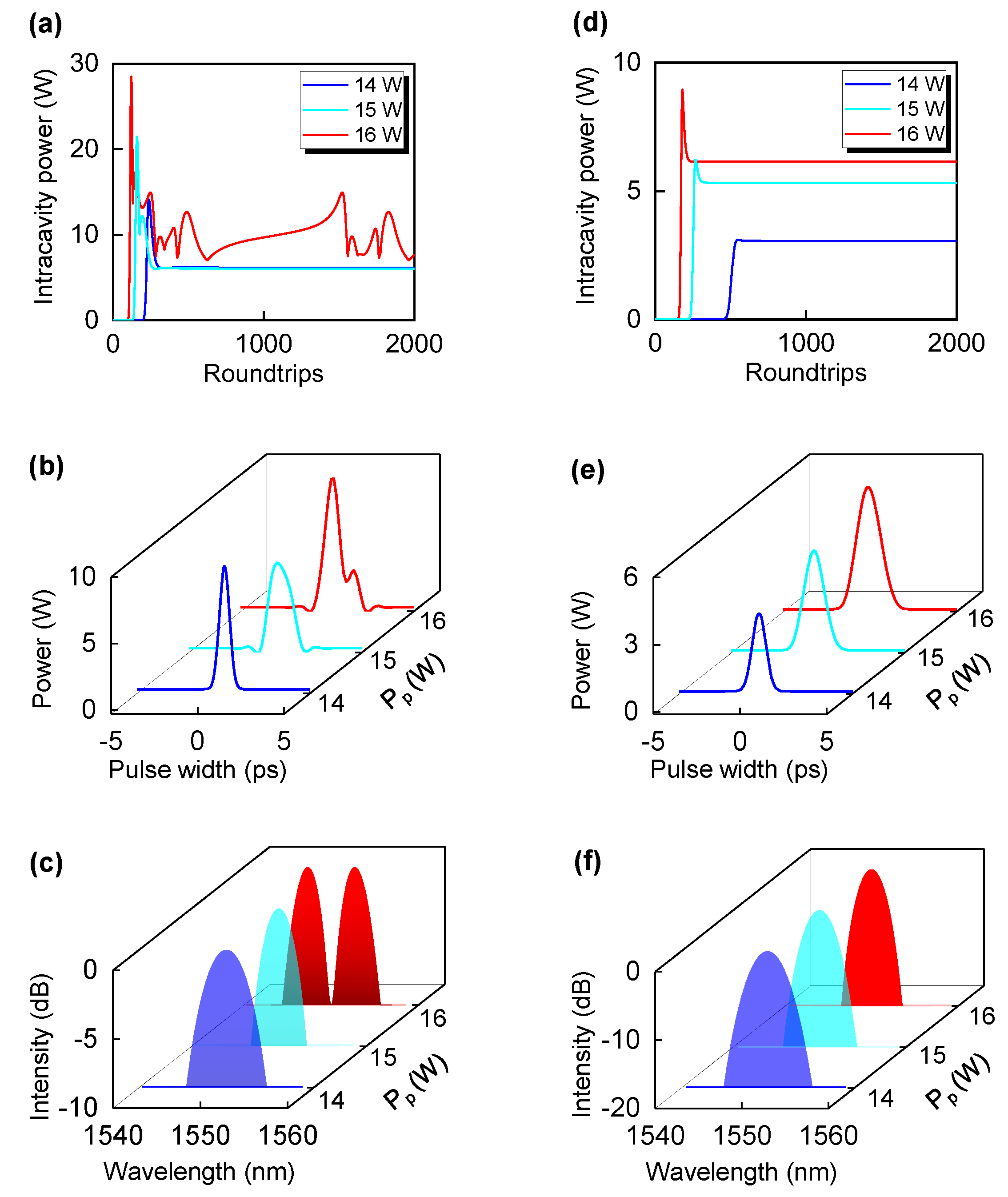
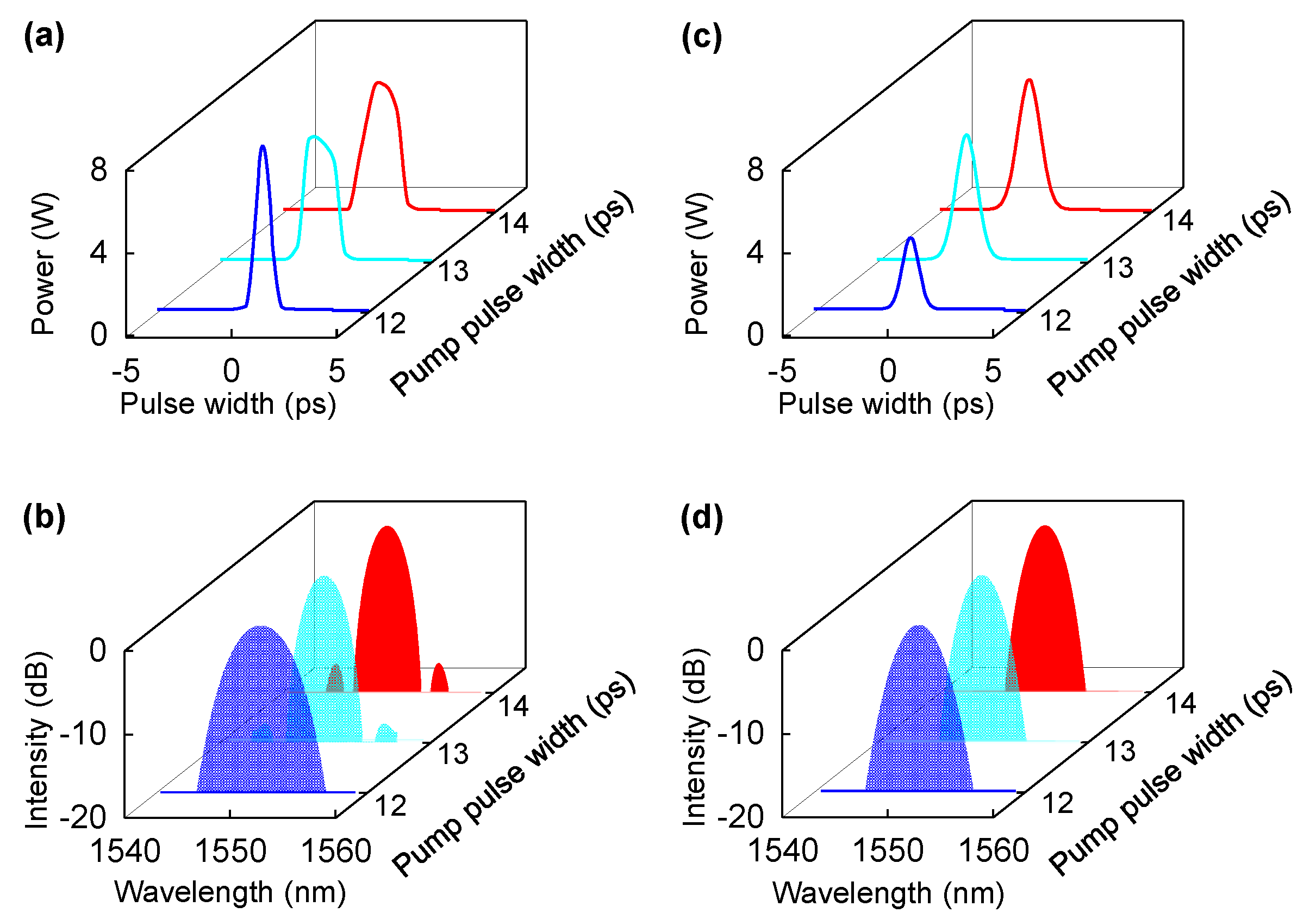
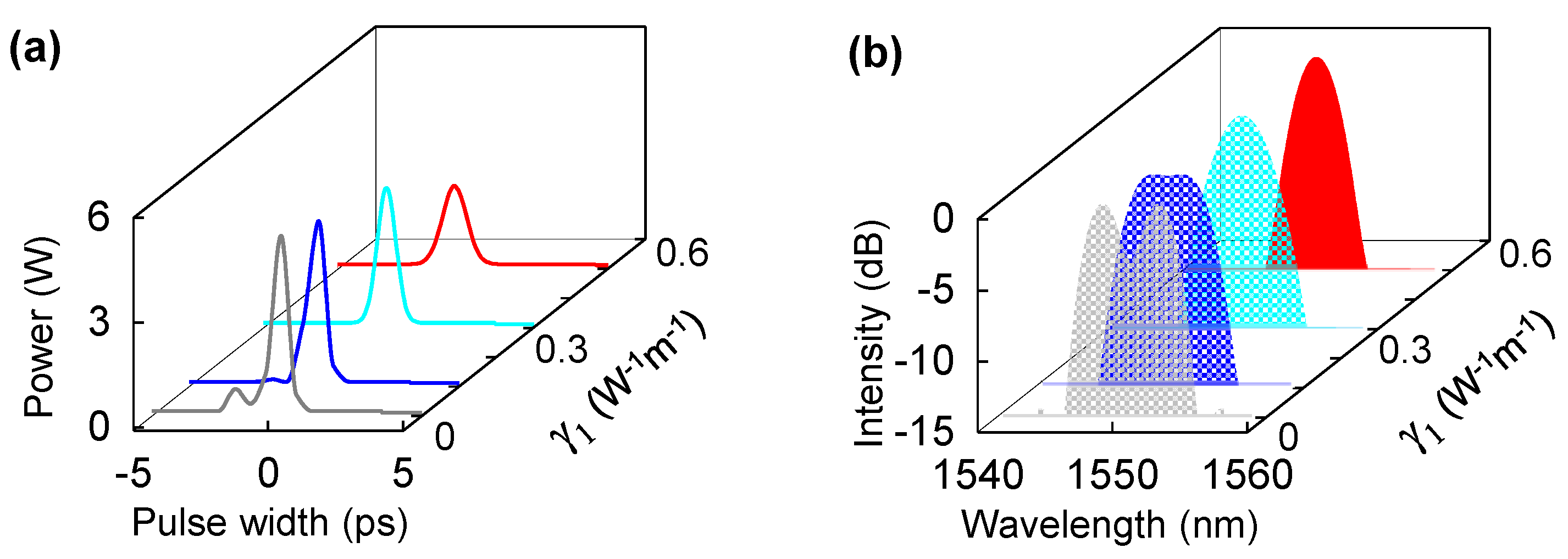
2. Theory and Simulation Results
3. Discussion and Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chang, L.; Liu, S.; Bowers, J.E. Integrated optical frequency comb technologies. Nat. Photonics 2022, 16, 95–108. [Google Scholar] [CrossRef]
- Gaeta, A.L.; Lipson, M.; Kippenberg, T.J. Photonic-chip-based frequency combs. Nat. Photonics 2019, 13, 158–169. [Google Scholar] [CrossRef]
- Kippenberg, T.J.; Gaeta, A.L.; Lipson, M.; Gorodetsky, M.L. Dissipative Kerr solitons in optical microresonators. Science 2018, 361, eaan8083. [Google Scholar] [CrossRef]
- Marin-Palomo, P.; Kemal, J.N.; Karpov, M.; Kordts, A.; Pfeifle, J.; Pfeiffer, M.H.; Trocha, P.; Wolf, S.; Brasch, V.; Anderson, M.H.; et al. Microresonator-based solitons for massively parallel coherent optical communications. Nature 2017, 546, 274–279. [Google Scholar] [CrossRef]
- Pfeifle, J.; Brasch, V.; Lauermann, M.; Yu, Y.; Wegner, D.; Herr, T.; Hartinger, K.; Schindler, P.; Li, J.; Hillerkuss, D.; et al. Coherent terabit communications with microresonator Kerr frequency combs. Nat. Photonics 2014, 8, 375–380. [Google Scholar] [CrossRef] [PubMed]
- Ye, J.; Schnatz, H.; Hollberg, L.W. Optical frequency combs: From frequency metrology to optical phase control. IEEE J. Sel. Top. Quantum Electron. 2003, 9, 1041–1058. [Google Scholar] [CrossRef]
- Collaboration, B.A.C.O.N.B. Frequency ratio measurements at 18-digit accuracy using an optical clock network. Nature 2021, 591, 564–569. [Google Scholar] [CrossRef]
- Papp, S.B.; Beha, K.; Del’Haye, P.; Quinlan, F.; Lee, H.; Vahala, K.J.; Diddams, S.A. Microresonator frequency comb optical clock. Optica 2014, 1, 10–14. [Google Scholar] [CrossRef]
- Suh, M.G.; Yi, X.; Lai, Y.H.; Leifer, S.; Grudinin, I.S.; Vasisht, G.; Martin, E.C.; Fitzgerald, M.P.; Doppmann, G.; Wang, J.; et al. Searching for exoplanets using a microresonator astrocomb. Nat. Photonics 2019, 13, 25–30. [Google Scholar] [CrossRef]
- Obrzud, E.; Rainer, M.; Harutyunyan, A.; Anderson, M.H.; Liu, J.; Geiselmann, M.; Chazelas, B.; Kundermann, S.; Lecomte, S.; Cecconi, M.; et al. A microphotonic astrocomb. Nat. Photonics 2019, 13, 31–35. [Google Scholar] [CrossRef] [Green Version]
- Suh, M.G.; Yang, Q.F.; Yang, K.Y.; Yi, X.; Vahala, K.J. Microresonator soliton dual-comb spectroscopy. Science 2016, 354, 600–603. [Google Scholar] [CrossRef] [PubMed]
- Coddington, I.; Newbury, N.; Swann, W. Dual-comb spectroscopy. Optica 2016, 3, 414–426. [Google Scholar] [CrossRef] [PubMed]
- Yu, M.; Okawachi, Y.; Griffith, A.G.; Picqué, N.; Lipson, M.; Gaeta, A.L. Silicon-chip-based mid-infrared dual-comb spectroscopy. Nat. Commun. 2018, 9, 1869. [Google Scholar] [CrossRef] [PubMed]
- Herr, T.; Hartinger, K.; Riemensberger, J.; Wang, C.; Gavartin, E.; Holzwarth, R.; Gorodetsky, M.; Kippenberg, T. Universal formation dynamics and noise of Kerr-frequency combs in microresonators. Nat. Photonics 2012, 6, 480–487. [Google Scholar] [CrossRef]
- Herr, T.; Brasch, V.; Jost, J.D.; Wang, C.Y.; Kondratiev, N.M.; Gorodetsky, M.L.; Kippenberg, T.J. Temporal solitons in optical microresonators. Nat. Photonics 2014, 8, 145–152. [Google Scholar] [CrossRef]
- Szabados, J.; Sturman, B.; Breunig, I. Frequency comb generation threshold via second-harmonic excitation in χ (2) optical microresonators. APL Photonics 2020, 5, 116102. [Google Scholar] [CrossRef]
- Herr, S.J.; Brasch, V.; Szabados, J.; Obrzud, E.; Jia, Y.; Lecomte, S.; Buse, K.; Breunig, I.; Herr, T. Frequency comb up- and down-conversion in synchronously driven χ(2) optical microresonators. Opt. Lett. 2018, 43, 5745–5748. [Google Scholar] [CrossRef]
- Nie, M.; Huang, S.W. Quadratic Solitons in Singly Resonant Degenerate Optical Parametric Oscillators. Phys. Rev. Appl. 2020, 13, 044046. [Google Scholar] [CrossRef]
- Li, J.; Bao, C.; Ji, Q.X.; Wang, H.; Wu, L.; Leifer, S.; Beichman, C.; Vahala, K. Efficiency of pulse pumped soliton microcombs. Optica 2022, 9, 231–239. [Google Scholar] [CrossRef]
- Obrzud, E.; Lecomte, S.; Herr, T. Temporal solitons in microresonators driven by optical pulses. Nat. Photonics 2017, 11, 600–607. [Google Scholar] [CrossRef] [Green Version]
- Anderson, M.H.; Bouchand, R.; Liu, J.; Weng, W.; Obrzud, E.; Herr, T.; Kippenberg, T.J. Photonic chip-based resonant supercontinuum via pulse-driven Kerr microresonator solitons. Optica 2021, 8, 771–779. [Google Scholar] [CrossRef]
- Brasch, V.; Obrzud, E.; Lecomte, S.; Herr, T. Nonlinear filtering of an optical pulse train using dissipative Kerr solitons. Optica 2019, 6, 1386–1393. [Google Scholar] [CrossRef]
- Weng, W.; Kaszubowska-Anandarajah, A.; He, J.; Lakshmijayasimha, P.D.; Lucas, E.; Liu, J.; Anandarajah, P.M.; Kippenberg, T.J. Gain-switched semiconductor laser driven soliton microcombs. Nat. Commun. 2021, 12, 1–9. [Google Scholar] [CrossRef]
- Xu, Y.; Lin, Y.; Nielsen, A.; Hendry, I.; Coen, S.; Erkintalo, M.; Ma, H.; Murdoch, S.G. Harmonic and rational harmonic driving of microresonator soliton frequency combs. Optica 2020, 7, 940–946. [Google Scholar] [CrossRef]
- Diddams, S.A.; Vahala, K.; Udem, T. Optical frequency combs: Coherently uniting the electromagnetic spectrum. Science 2020, 369, eaay3676. [Google Scholar] [CrossRef] [PubMed]
- Roy, A.; Nehra, R.; Jahani, S.; Ledezma, L.; Langrock, C.; Fejer, M.; Marandi, A. Temporal walk-off induced dissipative quadratic solitons. Nat. Photonics 2022, 16, 162–168. [Google Scholar] [CrossRef]
- Li, X.; Huang, X.; Chen, E.; Zhou, Y.; Han, Y. Dissipative-soliton-resonance and evolution in an all-normal dispersion Er-doped fiber laser. Opt. Laser Technol. 2022, 156, 108592. [Google Scholar] [CrossRef]
- Li, X.; Wang, Y.; Zhao, W.; Zhang, W.; Hu, X.; Gao, C.; Zhang, H.; Yang, Z.; Wang, H.; Wang, X.; et al. Numerical investigation of soliton molecules with variable separation in passively mode-locked fiber lasers. Opt. Commun. 2012, 285, 1356–1361. [Google Scholar] [CrossRef]
- Hansson, T.; Leo, F.; Erkintalo, M.; Coen, S.; Ricciardi, I.; De Rosa, M.; Wabnitz, S. Singly resonant second-harmonic-generation frequency combs. Phys. Rev. A 2017, 95, 013805. [Google Scholar] [CrossRef]
- Leo, F.; Hansson, T.; Ricciardi, I.; De Rosa, M.; Coen, S.; Wabnitz, S.; Erkintalo, M. Walk-Off-Induced Modulation Instability, Temporal Pattern Formation, and Frequency Comb Generation in Cavity-Enhanced Second-Harmonic Generation. Phys. Rev. Lett. 2016, 116, 033901. [Google Scholar] [CrossRef] [Green Version]
- Mosca, S.; Parisi, M.; Ricciardi, I.; Leo, F.; Hansson, T.; Erkintalo, M.; Maddaloni, P.; De Natale, P.; Wabnitz, S.; De Rosa, M. Modulation Instability Induced Frequency Comb Generation in a Continuously Pumped Optical Parametric Oscillator. Phys. Rev. Lett. 2018, 121, 093903. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.; Li, J.; Dai, F.; Wang, M.; Wang, C.; Wang, Q.; Tu, C.; Li, Y.; Wang, H.T. Kerr nonlinearity-assisted quadratic microcomb. Front. Phys. 2022, 10. [Google Scholar] [CrossRef]
- Li, Y.; Huang, S.W.; Li, B.; Liu, H.; Yang, J.; Vinod, A.K.; Wang, K.; Yu, M.; Kwong, D.L.; Wang, H.T.; et al. Real-time transition dynamics and stability of chip-scale dispersion-managed frequency microcombs. Light. Sci. Appl. 2020, 9, 52. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.; Al Sayem, A.; Gong, Z.; Surya, J.B.; Zou, C.L.; Tang, H.X. Ultralow-threshold thin-film lithium niobate optical parametric oscillator. Optica 2021, 8, 539–544. [Google Scholar] [CrossRef]
- Ledezma, L.; Sekine, R.; Guo, Q.; Nehra, R.; Jahani, S.; Marandi, A. Intense optical parametric amplification in dispersion-engineered nanophotonic lithium niobate waveguides. Optica 2022, 9, 303–308. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, K.; Li, J.; Dai, F.; Wang, M.; Wang, C.; Wang, Q.; Tu, C.; Li, Y.; Wang, H. Robust Pulse-Pumped Quadratic Soliton Assisted by Third-Order Nonlinearity. Photonics 2023, 10, 155. https://doi.org/10.3390/photonics10020155
Wang K, Li J, Dai F, Wang M, Wang C, Wang Q, Tu C, Li Y, Wang H. Robust Pulse-Pumped Quadratic Soliton Assisted by Third-Order Nonlinearity. Photonics. 2023; 10(2):155. https://doi.org/10.3390/photonics10020155
Chicago/Turabian StyleWang, Ke, Jing Li, Fan Dai, Mengshuai Wang, Chuanhang Wang, Qiang Wang, Chenghou Tu, Yongnan Li, and Huitian Wang. 2023. "Robust Pulse-Pumped Quadratic Soliton Assisted by Third-Order Nonlinearity" Photonics 10, no. 2: 155. https://doi.org/10.3390/photonics10020155
APA StyleWang, K., Li, J., Dai, F., Wang, M., Wang, C., Wang, Q., Tu, C., Li, Y., & Wang, H. (2023). Robust Pulse-Pumped Quadratic Soliton Assisted by Third-Order Nonlinearity. Photonics, 10(2), 155. https://doi.org/10.3390/photonics10020155





