Abstract
Indirect time-of-flight (ToF) imaging systems enable a broad array of applications owing to their high frame rate, strong durability, and low cost. However, the wiggling-related error caused by the harmonics in the emitted signal significantly affects the range accuracy of indirect ToF imaging systems. In this paper, we establish a mathematical model of the wiggling-related error and propose a wiggling-related error correction method for indirect ToF imaging systems. This method adds a delay measurement and utilizes raw intensity measurements to evaluate the system state based on an adaptive Kalman filter (AKF), which is easy to implement in most indirect ToF imaging systems. Simulation and experimental results show that the proposed method performed well in reducing the wiggling-related error and had good robustness in different integration times. Compared with the existing methods, the proposed method not only has better performance but also is easier to implement. We believe that this study provides effective guidance for researchers understanding the wiggling-related error and a potential direction for the accuracy improvement of indirect ToF imaging systems.
1. Introduction
Over the past years, traditional 2D images have been unable to meet the demand for information perception, and 3D images have been widely studied and applied. Depth imaging systems, including stereo vision [1], structured light [2], and time-of-flight (ToF) [3], can be used to obtain 3D images. ToF imaging possesses the advantages of high real-time performance, strong durability, small size, and low cost. Therefore, this imaging system is suitable for a wide array of applications, such as robot navigation [4], security system [5], 3D reconstruction [6], precision farming [7], human-computer interaction [8], etc.
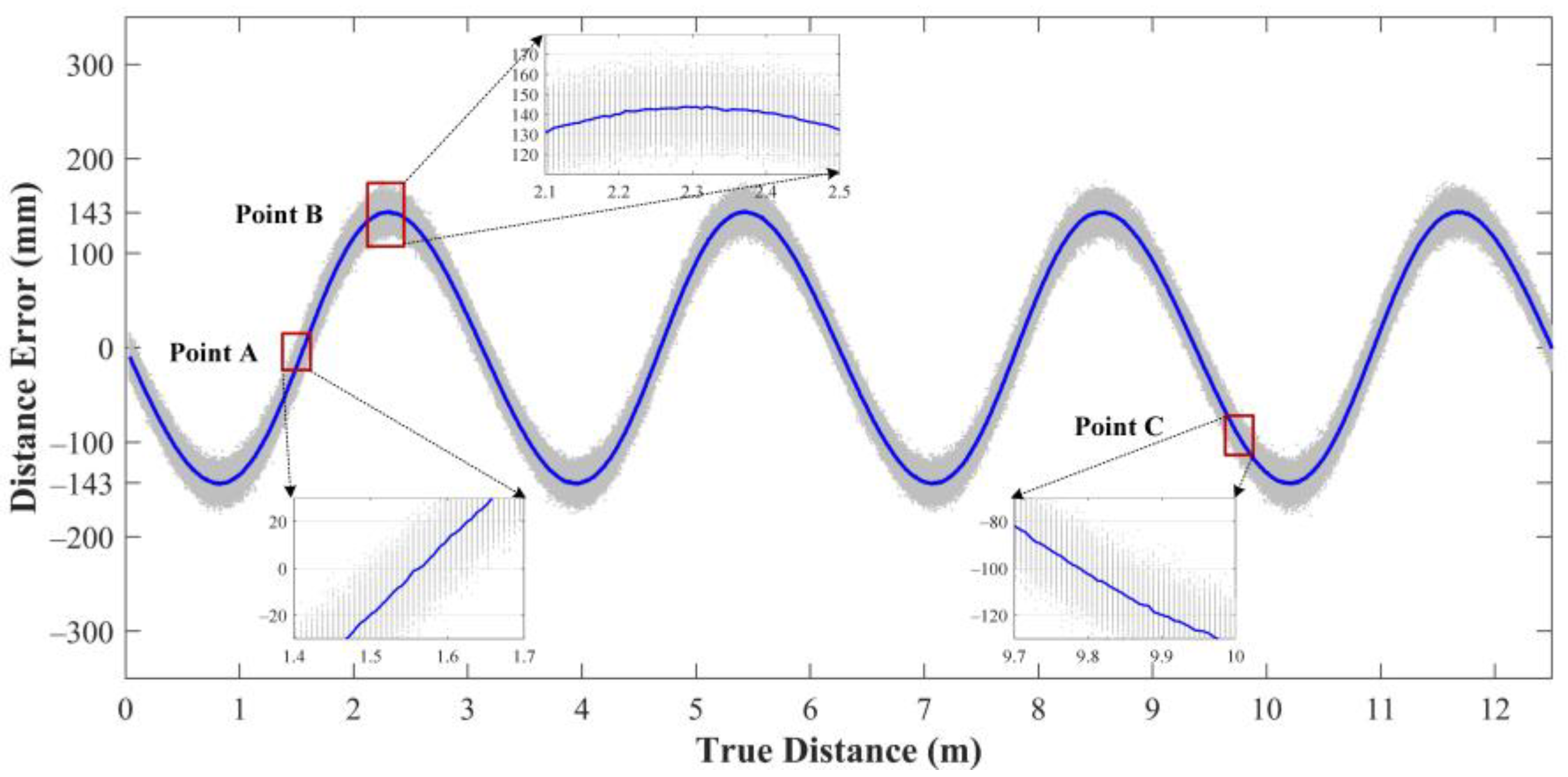
ToF imaging systems can be classified into direct ToF and indirect ToF imaging systems. Compared to direct ToF imaging systems, indirect ToF imaging systems have higher spatial resolution and are easier to implement [9,10]. Indirect ToF imaging systems provide range information by measuring the phase shift between the emitted and reflected sinusoidal amplitude modulated signals [11]. However, due to hardware limitations, non-sinusoidal amplitude modulated waveforms, such as square wave modulated signals, are typically used in indirect ToF imaging systems [12]. The unnecessary harmonics in the modulated signal will lead to a periodic systematic error known as the wiggling error [13]. On the other hand, the random error of range measurement caused by photon shot noise [14], called the wiggling random error in this paper, is also affected by the harmonics and presents a wiggling feature [15]. In this paper, the above two categories of errors are collectively referred to as the wiggling-related error. Figure 1 is a simulation of the wiggling-related error. As shown by the blue line in Figure 1, the wiggling error has four oscillations inside the unambiguous distance and reaches a value of up to ±143 mm. The maximum distance drift caused by the wiggling random error is more than 50 mm in the simulation (see Point B). In the actual measurement, the wiggling error and the wiggling random error are superimposed, which seriously impacts the range accuracy of ToF imaging systems. Thus, correcting the wiggling-related error for indirect ToF imaging systems is of great significance.
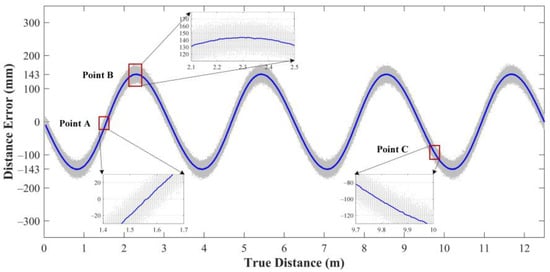
Figure 1.
Simulation of the wiggling-related error due to unnecessary harmonics from the square wave modulated signal. In the simulation, the modulation frequency is 12 MHz. At each true distance, the measurement is repeated 500 times. The gray dots are the range errors of single measurements, and the dispersion of the dots represents the magnitude of the wiggling random error. The blue line, which presents the wiggling error, connects the averages of range errors at different distances.
Much of the current research to correct or reduce the wiggling error is to use polynomial functions, look-up tables, B-spline functions, or damped sine functions to compensate for it [16]. Before the compensation, calibration experiments are required to evaluate the wiggling-related error, which is a time-consuming task. ToF imaging systems still need to be recalibrated if any system parameters change, e.g., the integration time, the modulation frequency, and the harmonic component. Beyond that, the amplitude-dependent error and the sensor-dependent error are coupled with the wiggling error in the experiments [17], and the effect of the wiggling random error is ignored during the compensation process. Therefore, the wrong compensation value often appears in the actual measurement, resulting in lower accuracy of ToF imaging systems.
It is more reasonable to directly avoid the wiggling-related error from its source, which means reducing its production instead of attempting to compensate for it. A number of studies have focused on reducing the wiggling-related error by optimizing the emitted signals of indirect ToF imaging systems. Hussmann et al. [18] developed an illumination module that emitted a sine-shape signal with no higher harmonics. Nevertheless, this method increased the random error of the system. Payne et al. [19] designed a harmonic rejection sampling methodology, which attenuated harmonics during the sampling. The experiments verified that this approach improved the measurement linearity in the raw measurements, but the random noise was also amplified. In [20,21], adjusting the duty cycle of the square wave signals proved to be effective in correcting the wiggling-related error. However, the ideal square wave is still challenging to produce, which limits this method.
The wiggling-related error can also be reduced by changing the calculation formula of the phase shift [22]. Drayton et al. [23] used the windowed discrete Fourier algorithm to calculate the phase shift. This algorithm had a good performance in reducing the error yet changed the sampling process of the ToF imaging system, which is difficult to implement in commercial indirect ToF imaging systems. The same problem also appeared in [15], where the third harmonic was eliminated with no significant increase in noise variance observed. In addition, Feigin et al. used the matrix pencil method to correct the wiggling error and the wiggling random error [24]. This method utilized the depth data of multiple frequencies and hence had low real-time performance.
All these methods suffer from technical disadvantages, such as an increase in the wiggling random error, difficulty to achieve, or low robustness. For this problem, we propose a wiggling-related error correction method for indirect ToF imaging systems. The main contributions include:
- To reduce the wiggling error, we propose a wiggling error cancelation method. This method adds a delay measurement without changing the hardware of ToF imaging systems, which is easy to implement in most indirect ToF imaging systems.
- To reduce the wiggling random error, we propose a wiggling random error reduction method based on an adaptive Kalman filter (AKF) for indirect ToF imaging systems. The method, which has good adaptive performance, utilizes the data of raw intensity measurements to evaluate the system state in real-time and calculates a more accurate phase.
- We establish a mathematical model of the wiggling-related error, which clearly shows the characteristics of the wiggling-related error. Combining (1) and (2), we propose a wiggling-related error correction method. The method is verified to have good performance and robustness in improving the range accuracy of indirect ToF imaging systems.
This article is organized as follows: Section 2 introduces the principle of ToF imaging systems and derives the mathematical model of the wiggling-related error. Section 3 describes the proposed wiggling-related error correction method in detail. Section 4 presents the simulation and experimental results and performs the discussions. Finally, the conclusions are presented in Section 5.
2. Principle
2.1. Principle of ToF Imaging Systems
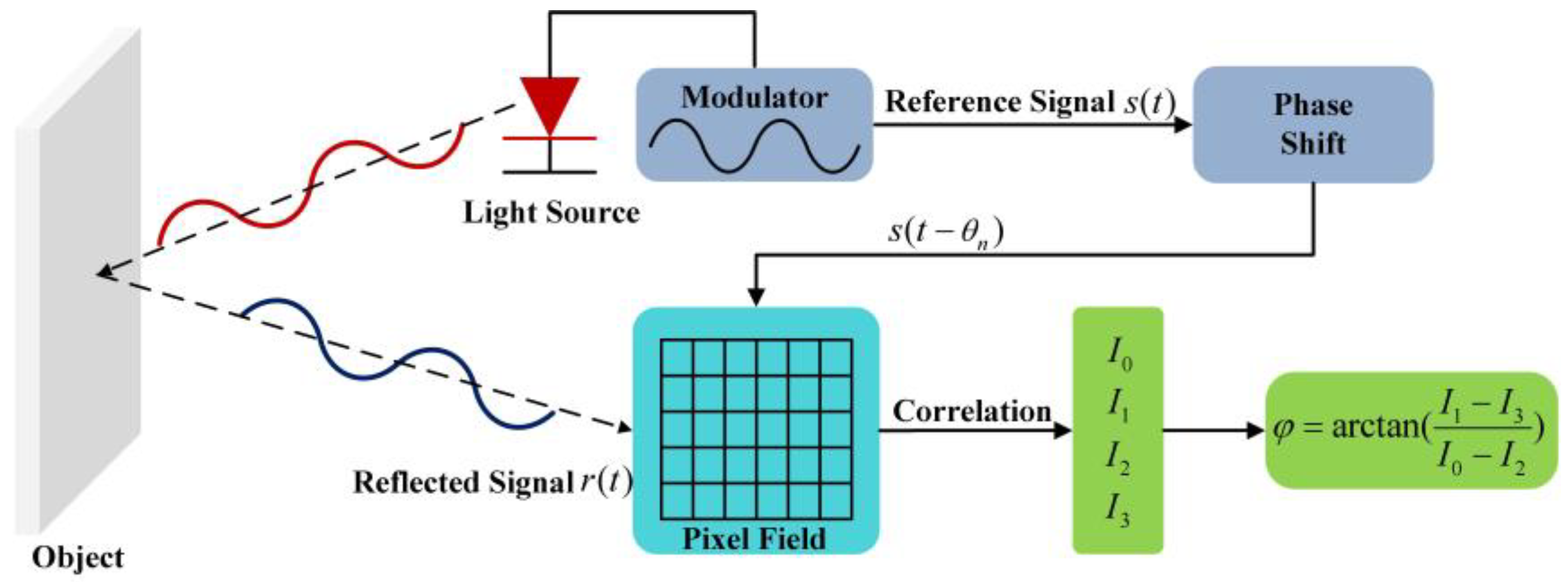
Indirect ToF imaging systems use cross-correlation to indirectly determine the phase shift of the reflected signal [25]. The working principle of the indirect ToF imaging system is illustrated in Figure 2. The light source, triggered by an internal reference signal , is used to emit the modulated near infrared (NIR) light. After being reflected by the object, the light will be detected by the pixel field of the ToF sensor. On each pixel, the reflected light is converted to an electronic signal and immediately correlates with the reference signal at four phase shifts with , producing four intensity measurements to [13,26]. The process can be expressed as a correlation function:
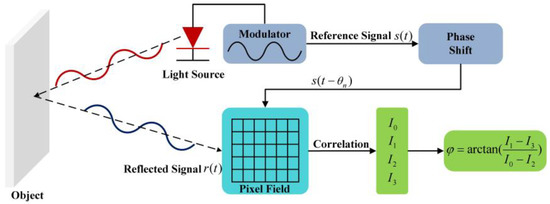
Figure 2.
The principle of an indirect ToF imaging system.
Both the reference and reflected signals are assumed to be sinusoidal functions:
where is the modulation frequency of ToF imaging systems, and is the phase shift relating to the round-trip time. and are the corresponding amplitudes of the reference and reflected signals. and are the corresponding offsets of the reference and reflected signals.
Substitute Equations (2) and (3) into Equation (1), the intensity measurements to are simplified to:
where represents the amplitude of the correlation function, which is related to the sensitivity of the ToF sensor, the amplitude of the reference signal, the reflectivity of the scene, and the attenuation of the light. represents the offset of the correlation function, which is determined by the intensity of the background light [23].
With the four-step phase shifting algorithm [27], the phase and amplitude can be estimated as:
From the measured phase and the speed of light c, the range is finally inferred by:
2.2. Analysis of the Wiggling-Related Error
Due to the harmonics in the modulated signal, indirect ToF imaging systems suffer from the wiggling-related error, which significantly impacts the range accuracy. The wiggling-related error consists of the wiggling error and the wiggling random error. In this section, a mathematical model is derived to predict the wiggling error and the wiggling random error.
2.2.1. Wiggling Error
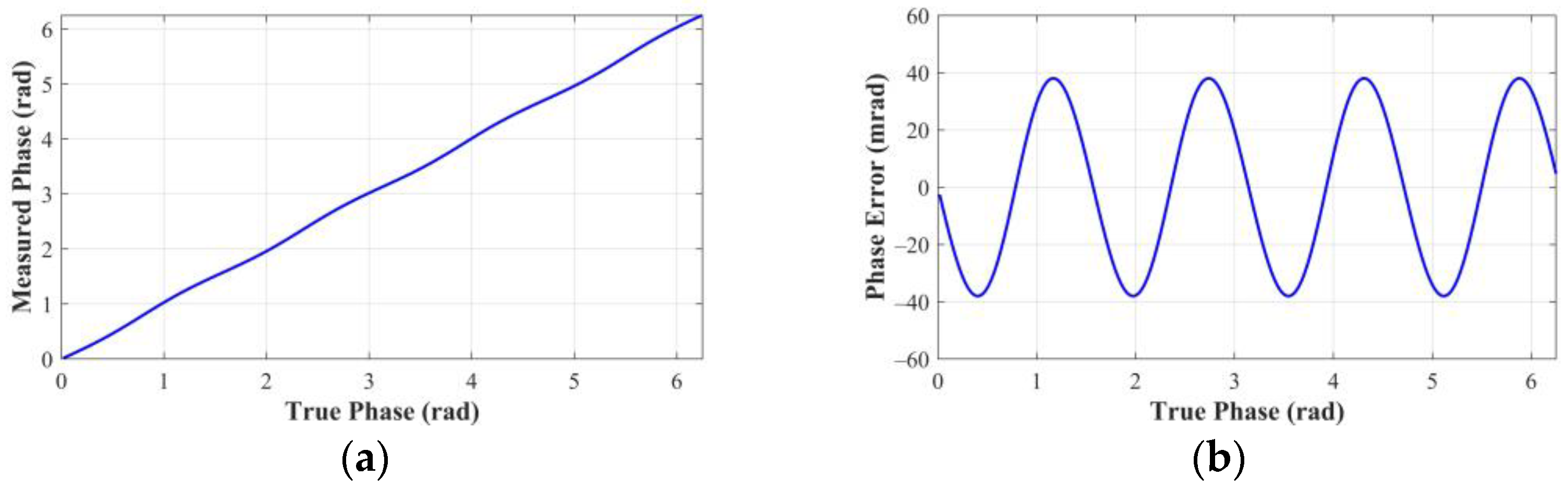
In the above, we assume that both the reference and reflected signals follow sinusoidal shapes. However, they are non-sinusoidal waveforms, causing higher-order harmonics in the correlation function. The higher-order odd harmonics cannot be filtered by the four-step phase shifting algorithm and thus will be aliased on the fundamental harmonic [28]. This leads to the wiggling error of the measured phase carried out with Equation (5). As illustrated in Figure 3a, there is a nonlinear relation between the measured phase and the true phase.
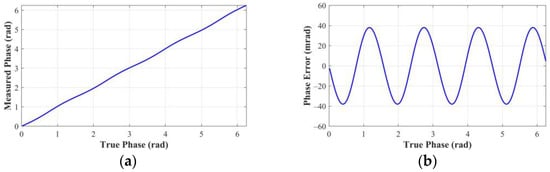
Figure 3.
Simulation of the wiggling error. In the simulation, LSB, LSB, LSB, and LSB. (a) Measured phase versus true phase. (b) Phase error versus true phase.
This paper considers odd harmonics up to the fifth-order, and the other higher harmonics can be ignored because of their insignificant amplitudes. According to [12], the intensity measurements of the correlation function with the third and fifth harmonics can be expressed as:
where , , and are the corresponding amplitudes of the fundamental, third-order, and fifth-order harmonics. Submitting Equation (8) into Equation (5), the measured phase can be written as:
The wiggling error can be derived as the following form [29]:
where and . Using the Taylor expansion, the above equation is simplified to:
Typically, we have , because is much larger than and is much larger than . Therefore, the part of in Equation (11) can be ignored. The wiggling error can be written in a more concise form:
where is a constant related to the harmonic component. Equation (12) indicates that the magnitude of the wiggling error depends on the true phase and the amplitudes of the harmonics. In the simulation, the wiggling error shows four sine periods as the true phase transverses from 0 to 2π (see Figure 3b). The maximum wiggling error reaches ±38.01 mrad, leading to a distance measurement error of ±75.62 mm under the modulation frequency of 12 MHz.
2.2.2. Wiggling Random Error
The main noise sources of indirect ToF imaging systems are photon shot noise, dark noise, and readout noise [30,31]. Among these noise sources, the shot noise is the dominant noise source in indirect ToF imaging systems [32]. This noise is introduced in the intensity measurement process, which can be regarded as counting photons by the charge and leads to a random error of phase measurement. In this paper, we focus on the random error caused by the photon shot noise. According to [12,33], we can approximate the intensity measurement as a random process with Gaussian distribution. Supposing the measured intensities to have the same variance , the variance of the measured phase can be estimated as [12]:
where is the measured amplitude calculated by Equation (6).
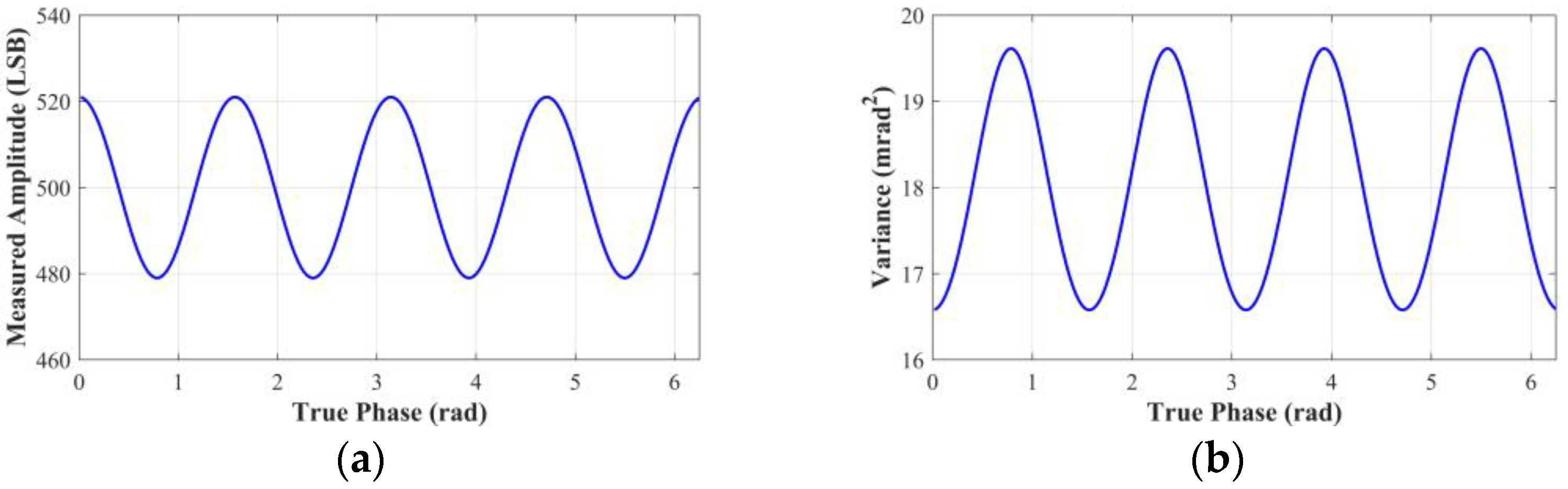
Normally, the variance in ToF imaging systems can be considered to be an invariant constant, which is a safe assumption for ideal scenes since intensities are generated through the same process with the same intensity of light by the charges in the ToF sensor. However, the measured amplitude is phase-dependent when harmonics are present, as shown in Figure 4a. It can be deduced from Equation (13) that the variance is therefore related to the true phase. As shown in Figure 4b, the magnitude of the variance also shows periodic oscillations, and the maximum variance of the measured phase is approximately 19.61 mrad2. Therefore, the presence of harmonics and shot noise causes the wiggling random error of the measured phase.
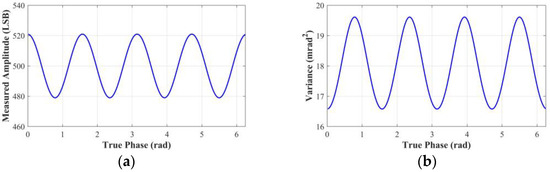
Figure 4.
Simulation of the wiggling random error. In the simulation, LSB, LSB, LSB, LSB, and LSB. (a) Measured amplitude versus true phase. (b) Variance of the measured phase versus true phase.
3. Methods
3.1. Wiggling Error Cancelation Method
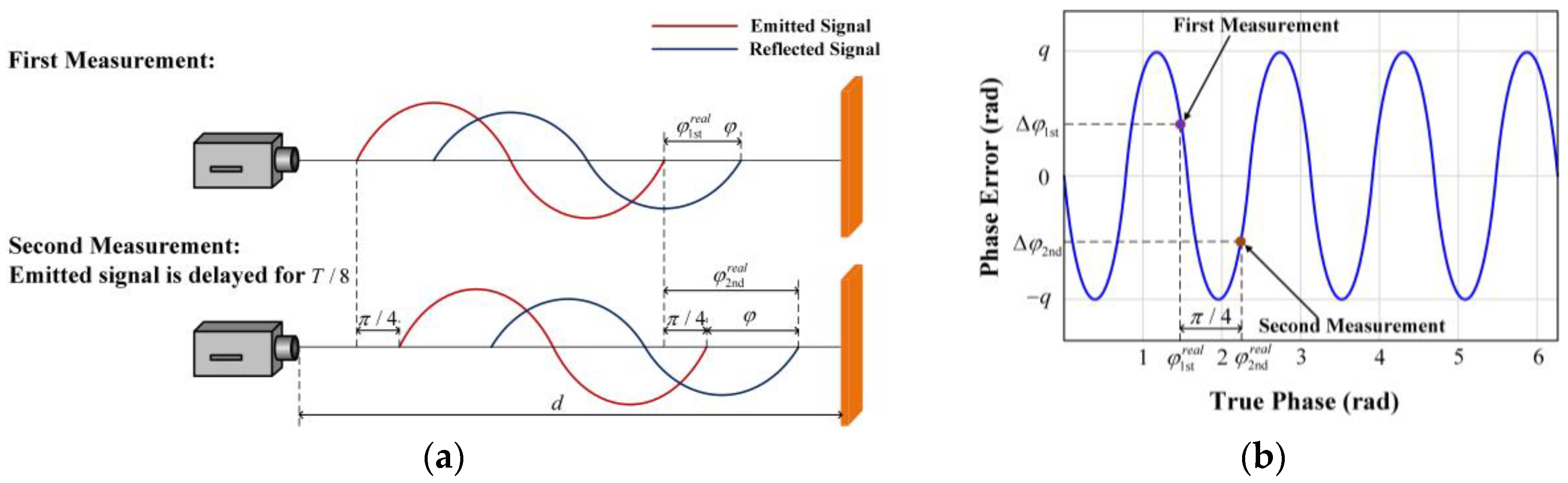
It can be seen from Figure 3b that the wiggling error of indirect ToF imaging systems is a sinusoidal periodic function. Taking advantage of the periodicity, we propose a wiggling error cancelation method (see Figure 5), which combines two phase measurements to eliminate the wiggling error.
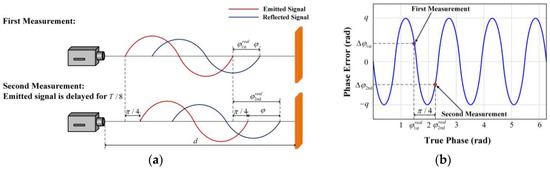
Figure 5.
The principle of the wiggling error cancelation method. (a) Scheme of the wiggling error cancelation method. (b) Wiggling error curve.
As illustrated in Figure 5a, the phase shift of the reflected signal is measured without other operations in the first measurement. Theoretically, the true phase, the wiggling error, and the measured phase are as follows:
where is the phase shift corresponding to the physical distance . In the second measurement, the emitted signal is delayed for T/8, which is equivalent to a phase delay of π/4. Therefore, the phase shift of the reflected signal will also increase by π/4. The true phase, the wiggling error, and the measured phase in the second measurement are as follows:
It can be inferred from Figure 5b, Equation (15), and Equation (18) that the wiggling errors of the two measurements are exactly opposite. Therefore, we add the measured phases of the two measurements to cancel the wiggling error and get the phase shift :
The operation process of the wiggling error cancelation method is as follows:
- In the first measurement, calculate the measured phase without other operations;
- In the second measurement, delay the emitted signal for T/8 and calculate the measured phase ;
- Combine and to calculate the measured phased after the wiggling error cancelation:
3.2. Wiggling Random Error Reduction Method
The magnitude of the measured phase’s variance (or noise level) may be different at different true distances, so traditional filtering algorithms are difficult to achieve a good effect in denoising. For this reason, this section depicts a wiggling random error reduction method based on an adaptive Kalman filter for indirect ToF imaging systems.
First, we establish the discrete linear system model of ToF imaging systems [34]. The Kalman filter assumes that the real state of the system at time is evolved from the state at time . The state-space equation and the observation equation are written as:
where is the system state vector, is the state transition matrix, and is the process noise with a Gaussian distribution, whose covariance matrix is . is the measurement vector, is the measurement matrix, is the measurement noise with a Gaussian distribution, whose covariance matrix is .
For ToF imaging systems, the measurement vector is formed by the intensity measurements to at time :
According to Equation (4), the intensity measurements at time can be written as:
Submitting Equation (25) into Equation (24), the measurement vector can be further derived as:
From the above description, we can obtain the system state vector and the measurement matrix :
In a static scene, we have . Thus, the state transition matrix can be expressed as:
Therefore, indirect ToF imaging systems are linearized. From the system state vector shown in Equation (27), the measured phase at time can be estimated as:
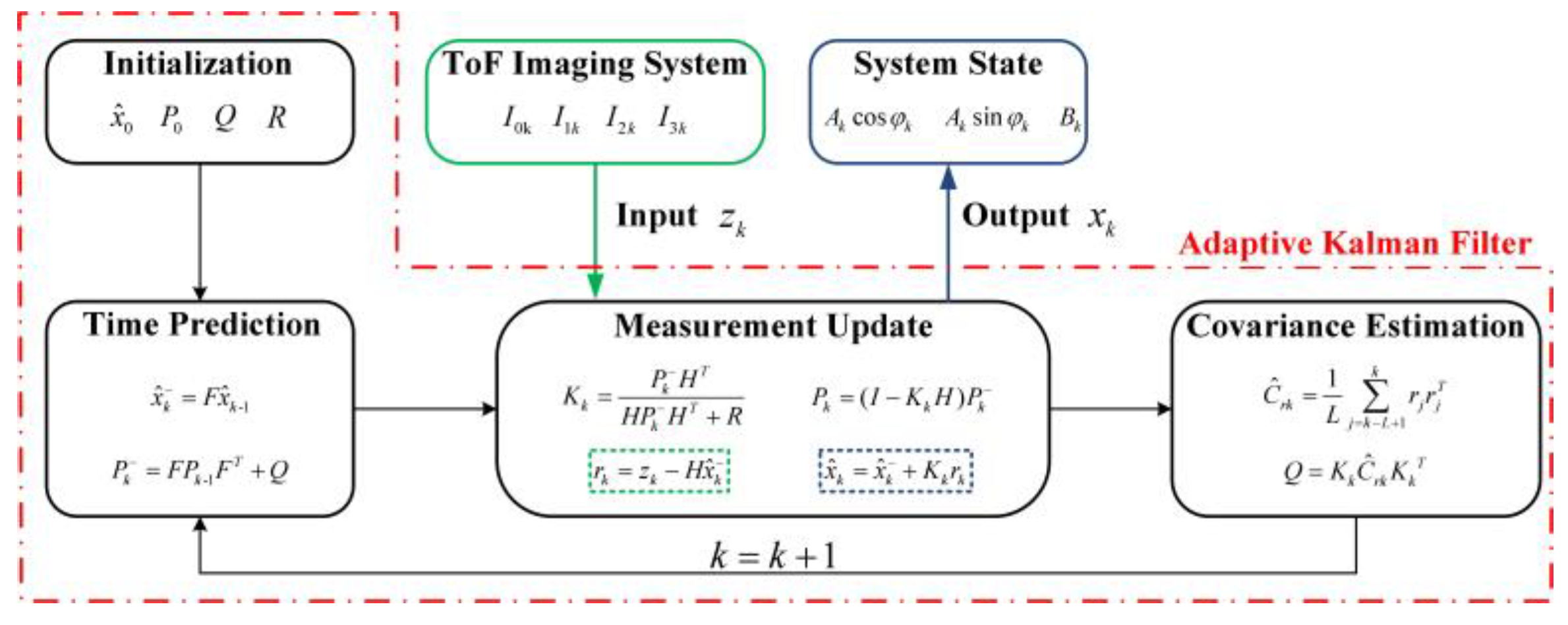
It can be noticed from Section 2.2 that the variance of the intensity measurement is constant, so the covariance matrix of the measurement noise can be regarded as a constant. However, due to the wiggling random error, the measured phase’s variance may differ at different true phases. It can be deduced that the level of process noise in Equation (22) varies with the phase. Therefore, the covariance matrix is not a constant and varies with the true phase. The standard Kalman filter (SKF) consists of prediction and update [35], where and are regarded as constants. Therefore, the SKF is hard to estimate the state of ToF imaging systems accurately. To address this issue, we introduce an evaluation stage based on the maximum likelihood criterion in the adaptive Kalman filter to adapt [36]. The AKF can adjust the filter gain factor according to the covariance matrix , effectively reducing the temporal Gaussian noise and hence the wiggling random error. The specific steps of the AKF are given as follows:
- Initialization: Initialize the state estimate , the error covariance matrix , the covariance matrix , and the covariance matrix ;
- Time Prediction: Calculate the predicted state estimate and the predicted error covariance matrix :
- Measurement Update: Calculate the Kalman gain , the updated error covariance matrix , the innovation sequence , and the updated state estimate :where is a 3 × 3 identity matrix;
- Covariance Estimation: Calculate the estimated covariance of the innovation sequence , and update the covariance matrix :where represents the length of the sliding window in the AKF.
The wiggling random error reduction method is illustrated in Figure 6. The method inputs the measurement vector (intensity measurements of a ToF imaging system) into the AKF, and outputs the system state vector . Combining Equation (30), we can calculate the measured phase after the wiggling random error reduction.
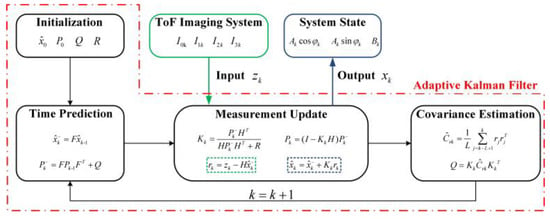
Figure 6.
The flowchart of the wiggling random error reduction method.
3.3. Wiggling-Related Error Correction Method
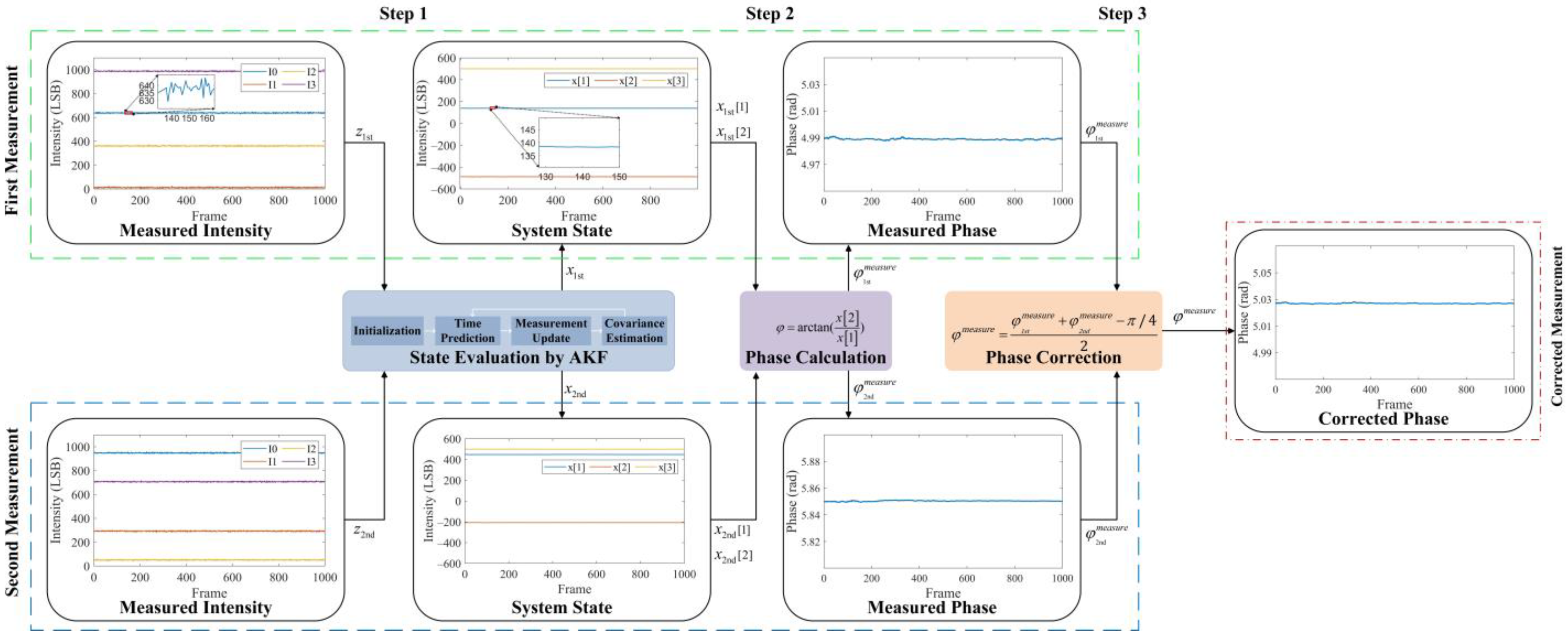
Combining the contents of Section 3.1 and Section 3.2, we propose a wiggling-related error correction method, shown in Figure 7. The ToF imaging system performs two measurements successively and obtain the measurement vectors and . Then, the corrected phase is obtained by the following three steps:
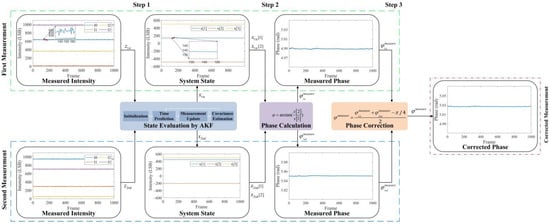
Figure 7.
The flowchart of the wiggling-related error correction method.
- State Evaluation: Input and into the AKF and obtain the system state vectors and ;
- Phase Calculation: Calculate the measured phases and for the two measurements. In this step, the wiggling random errors of two measurements are reduced;
- Phase Correction: Calculate the corrected phase . In this step, the wiggling error is reduced.
4. Results and Discussions
In this section, we first verify the performance of the wiggling-related error correction method by MATLAB simulation, where the intensity measurements are constructed according to the model in Section 2.2. Then, using the experimental platform built in Section 4.2, the derived mathematical model and effectiveness of the proposed method applied on real measurements are verified.
4.1. Simulation
In the simulation, two measurements were implemented at different true phases from 0 to 2π with steps of π/180. At each true phase, 2000 frames of data for the first and second measurements were simulated separately. The measured intensities of two measurements at the th true phase in the th frame were constructed with Equations (39) and (40), where is the true phase, and represents the Gaussian noise with a mean value of zero and a variance of . Table 1 lists the parameters used in the simulation.

Table 1.
The parameters used in the simulation.
For the measured phases, we applied the standard deviation (STD) to evaluate the wiggling random error. The Root-mean-square error (RMSE) was chosen to evaluate the wiggling-related error in general. Both the systematic error (wiggling error) and the random error affect the magnitude of the RMSE. The STD and the RMSE of the measured phase at the th true phase are expressed as:
where represents the number of measured frames at each phase, is the measured phase at the th true phase in the th frame, is the average of the measured phases at the th true phase.
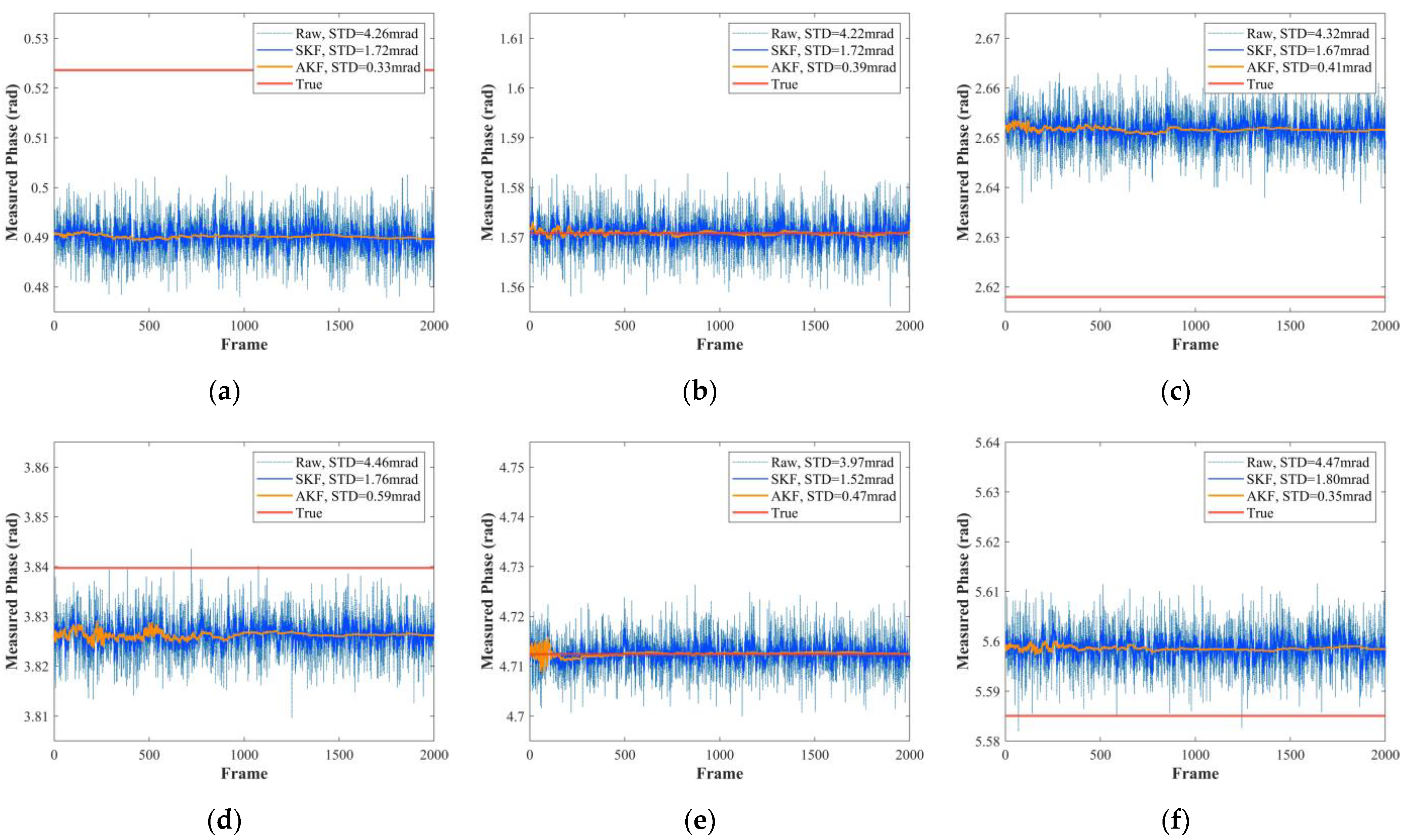
We first evaluated the denoising performance of the AKF. Figure 8a–c show the measured phase sequence at six of the true phases. In each figure, the true phase sequence was kept constant. We inputted the measurement vector sequences of the first measurement at different true phases into SKF or AKF and obtained the measured phase sequences. The raw measured phase sequences were obtained by Equation (5). It was obvious that AKF had better performance than SKF and effectively reduced the STD of the measured phase on the selected true phases, thereby reducing the wiggling random error. In addition, it can be found that there is a deviation between the measured phase and the true phase (see Figure 8a,c,d,f), which was caused by the wiggling error.
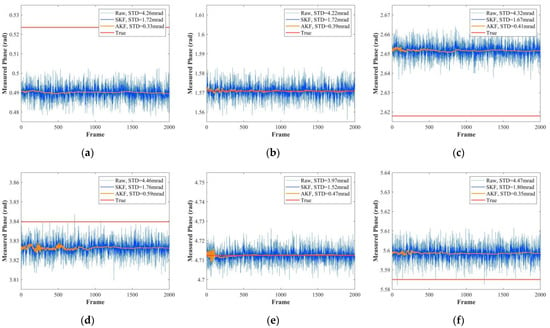
Figure 8.
Evaluation for the denoising performance of the AKF. Measured phase sequences at true phases of (a) π/6, (b) π/2, (c) 5π/6, (d) 11π/9, (e) 3π/2, and (f) 16π/9.
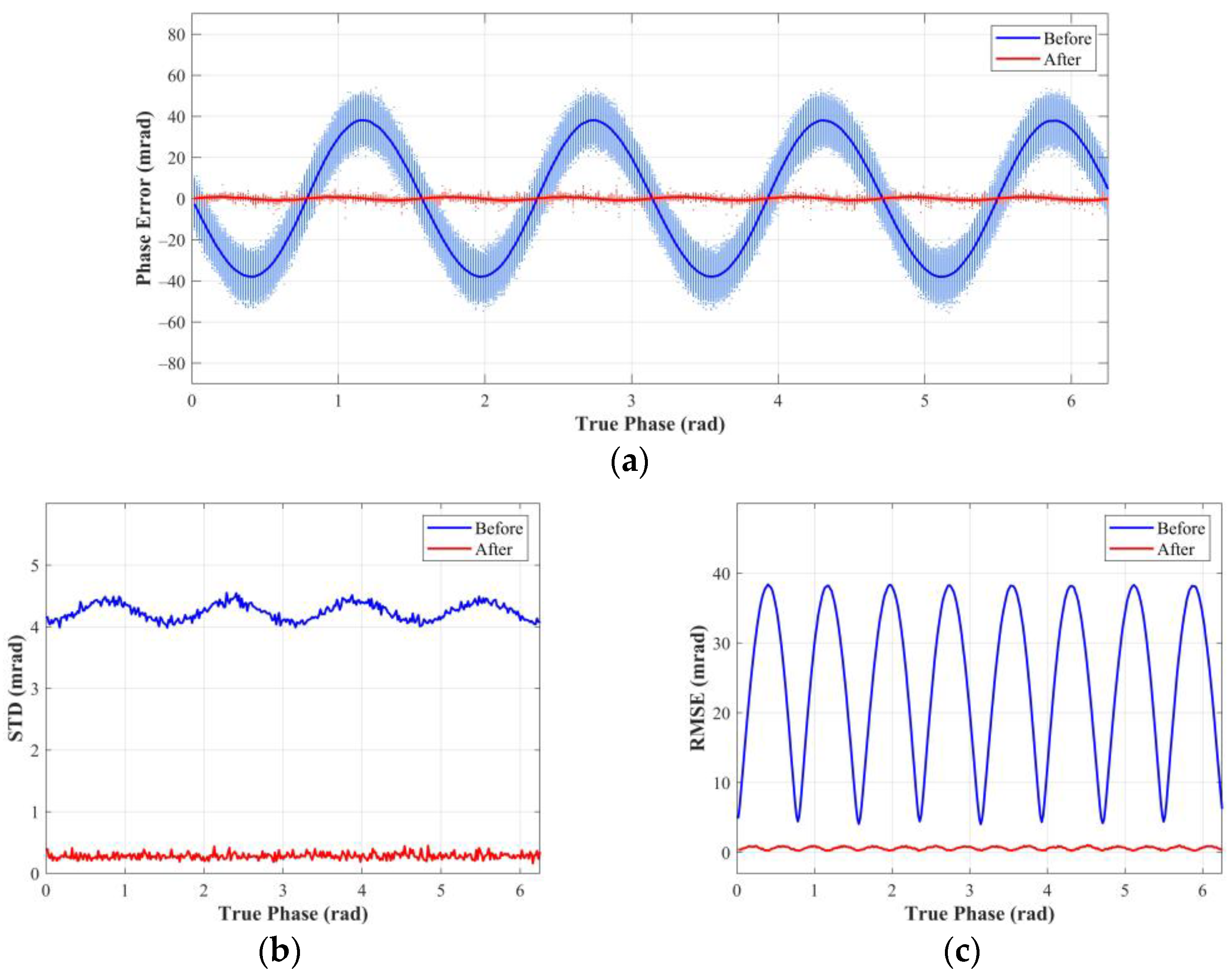
Furthermore, we evaluated the performance of the wiggling-related error correction method (see Figure 9). The measured phase before correction was calculated by Equation (5), using the first measurement. Using the two measurements shown in Equations (39) and (40), we obtained the corrected phase according to the method in Section 3.3. The phase error at each frame is plotted as the points in Figure 9a. The blue and red lines connect the average errors at different true phases before and after correction, representing the wiggling errors. Figure 9b,c show the STD and the RMSE of the measured phase, respectively, where the phase before correction, for fairness, uses double the first measurement data (4000 frames).
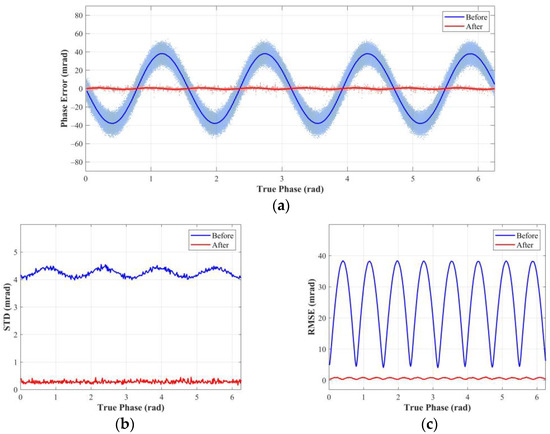
Figure 9.
Evaluation for the performance of the wiggling-related error correction method. (a) Phase error versus true phase. (b) STD of the measured phase versus true phase. (c) RMSE of the measured phase versus true phase.
The result, as shown in Figure 9a, shows a four-cycle wiggling error before correction. The peak-to-peak value (PPV) of the wiggling error was approximately 76.14 mrad. In contrast, the wiggling error significantly reduced after correction, and the PPV of the wiggling error reduced to about 1.83 mrad. The remaining wiggling error was caused by the part of in Equation (11). Moreover, there was a significant random error before correction. As we can see, the blue dots were distributed around the blue line. It can be noticed from the distribution of the red dots and Figure 9b that the random error greatly reduced. The arithmetic mean of STDs over all phases decreased from 4.24 to 0.28 mrad. In general, the proposed method performed well in the wiggling-related error correction. As illustrated in Figure 9c, the arithmetic mean of RMSEs over all phases reduced significantly from 24.81 to 0.60 mrad, which means that the wiggling-related error was only 2.4% of that before correction.
4.2. Experiment
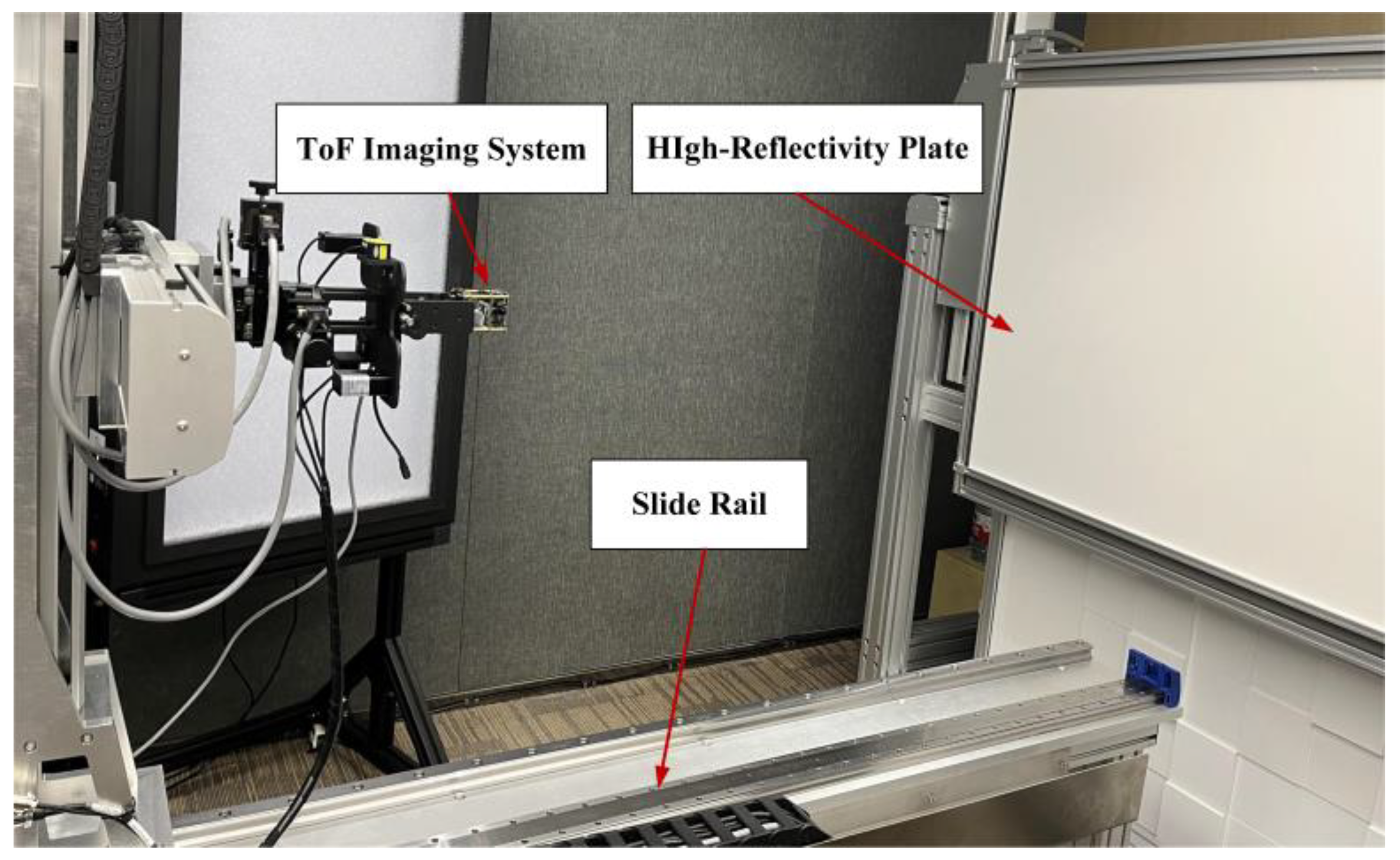
The experimental system is shown in Figure 10. We used a high-reflectivity plate as the measured object to avoid the amplitude-dependent error caused by non-linearities of the ToF sensor [17,37,38]. The ToF imaging system was attached to the slide rail. In the ToF imaging system, the delay generator of the ToF sensor could delay the emitted light signal by T/8 without changing the hardware, thereby realizing the wiggling error cancelation. The phase calculation and the phase correction were performed in the processing module of the ToF imaging system, where the parameters of AKF were the same as those set in the simulation.
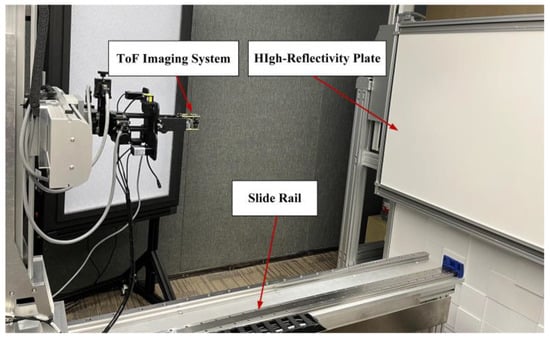
Figure 10.
The experimental system for the wiggling-related error correction.
To obtain the phase error for different true phases, we typically moved the plate to different distances. However, the wiggling-related error cannot be accurately presented by using this approach. On the one hand, the measured intensity is saturated at close distances, leading to a phase calculation bias. On the other hand, the amplitude of the reflected signal significantly decreases at long distances, which causes an amplitude-dependent error. A more sensible way is to add an electronic delay to the emitted signal. In this way, different distances are emulated by changing the delay. This approach minimizes the effect of the other errors on the experiment, such as the amplitude-dependent error, the multipath effect of the scene, and the non-uniformity error [39].
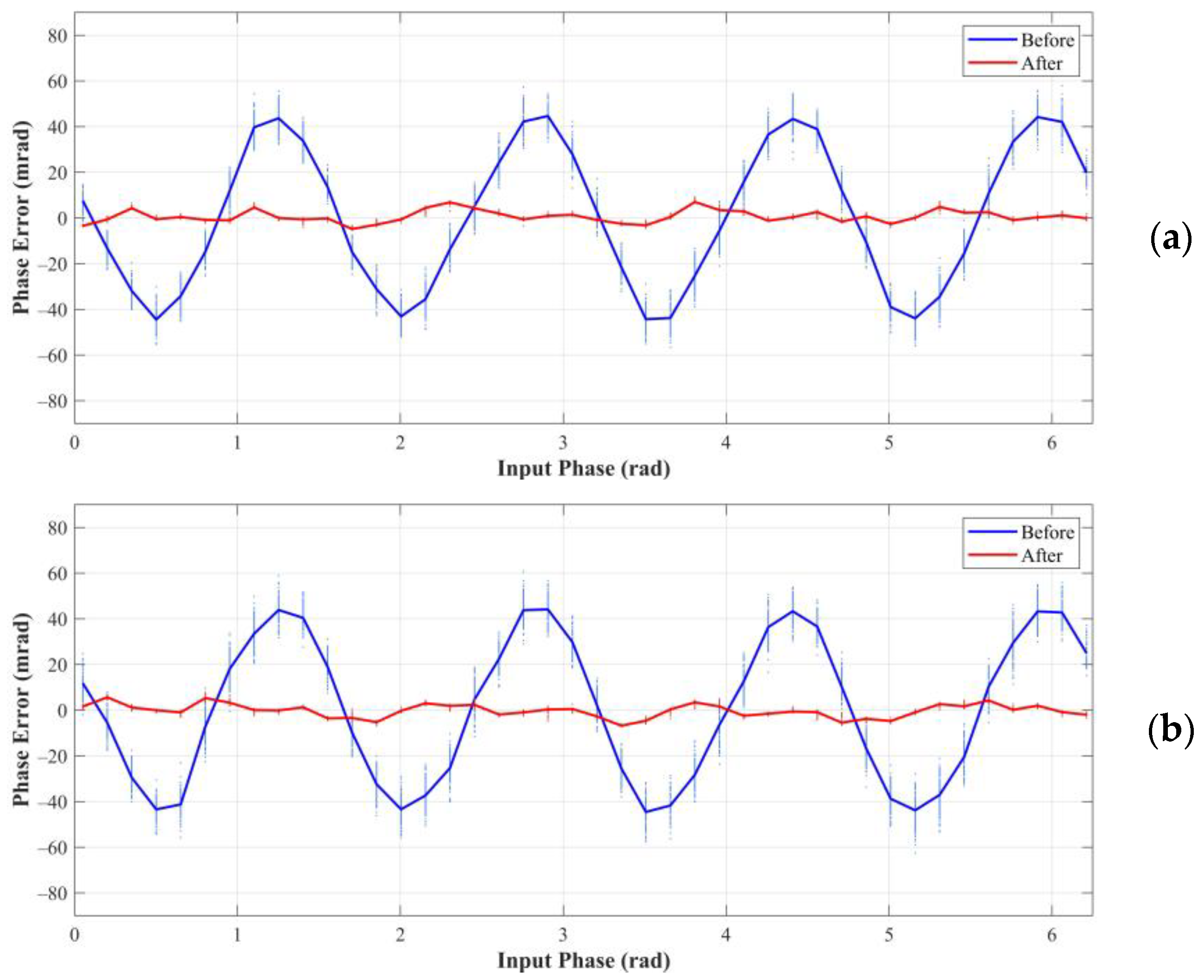
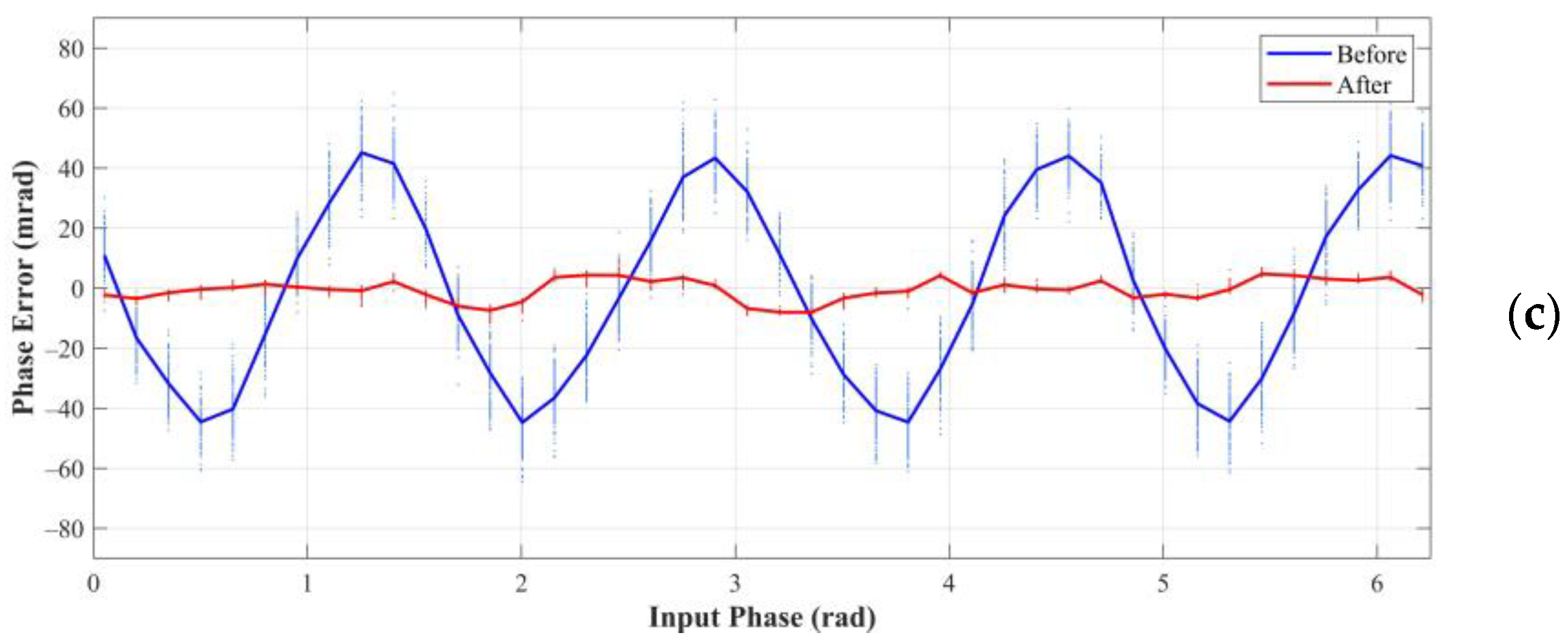
In the experiment, the modulation frequency of the ToF imaging system was set to 12 MHz. Therefore, the unambiguous distance was 12.5 m according to Equation (7). The physical distance between the plate and the ToF imaging system remained unchanged. Then, the electronic delay increased in steps of 2 ns, equivalent to an increase of 0.048π in the true phase, until the true phase spans 0 to 2π (0–12.5 m of the true distance). At each true phase, 200 frames of the data were captured. The experiment was carried out under the integration times of 600 μs, 400 μs, and 200 μs. The results are shown in Figure 11, Figure 12 and Figure 13. Table 2 gives the statistical parameters, including the PPV of wiggling error in Figure 11, the average of STDs in Figure 12 and the average of RMSEs in Figure 13.
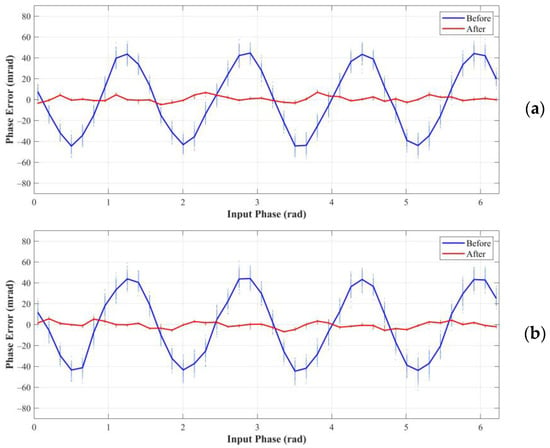
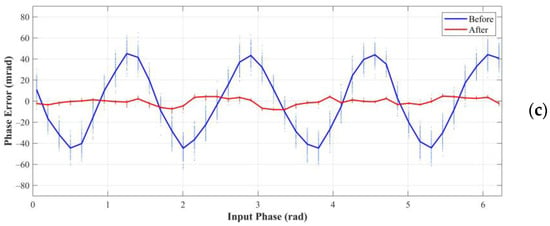
Figure 11.
Phase error of the measured phase for different true phases under integration times of (a) 600 μs, (b) 400 μs, and (c) 200 μs.
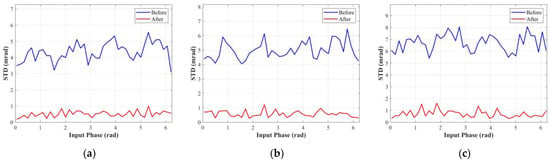
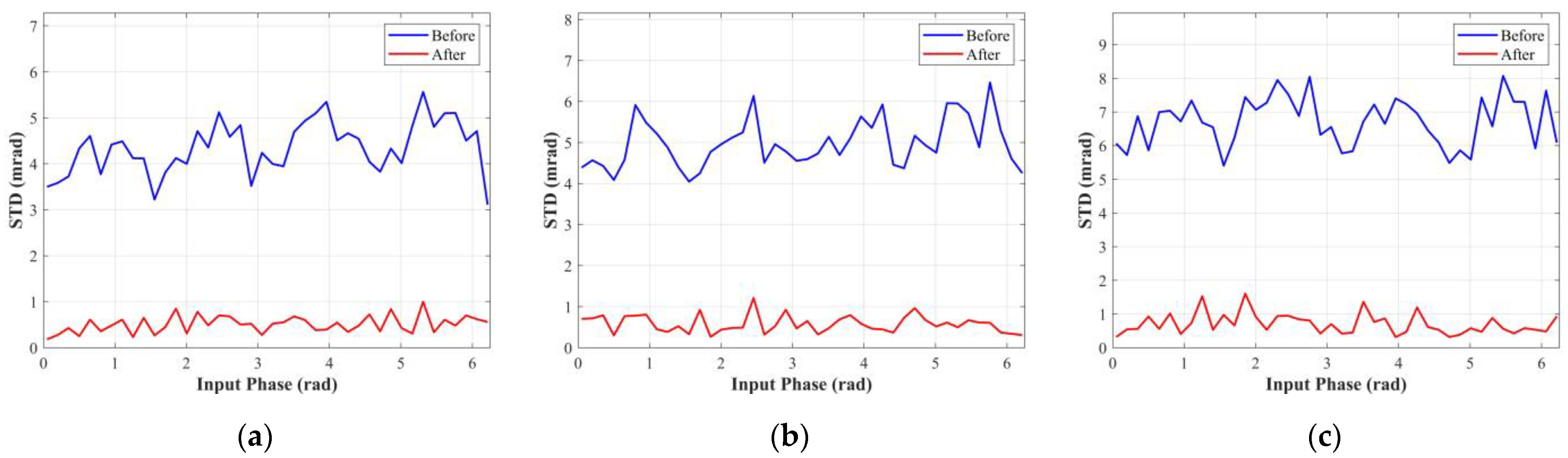
Figure 12.
STD of the measured phase for different true phases under integration times of (a) 600 μs, (b) 400 μs, and (c) 200 μs.
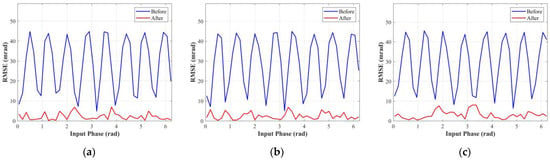
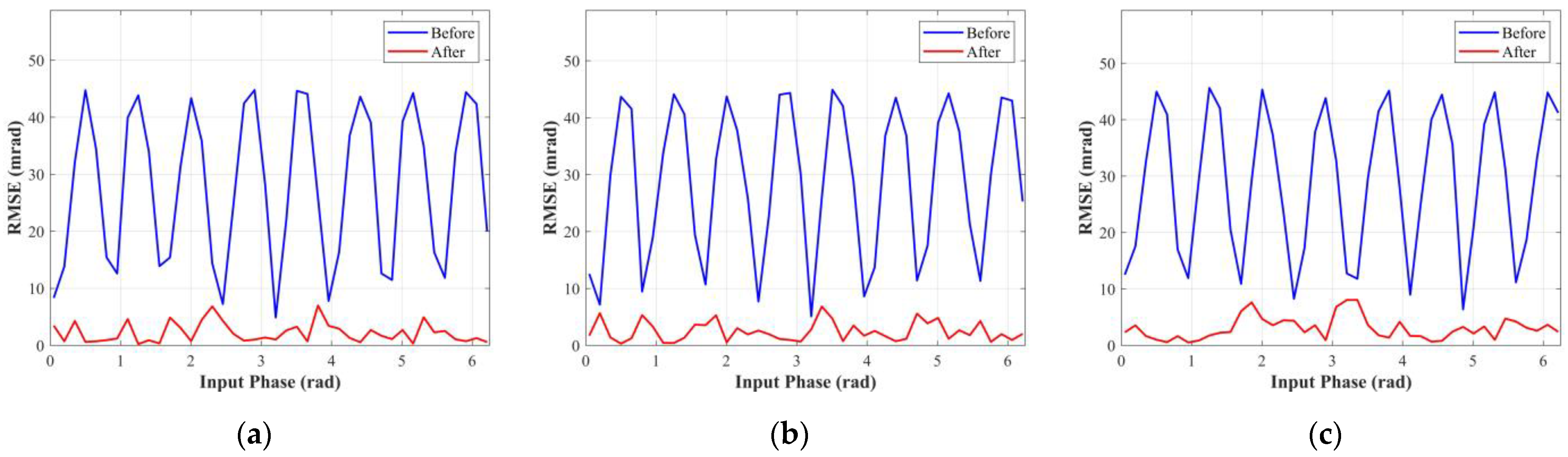
Figure 13.
RMSE of the measured phase for different true phases under integration times of (a) 600 μs, (b) 400 μs, and (c) 200 μs.
Figure 11 shows the phase error in the experiment. As expected, we can notice four oscillations with the true phase spanning 0 to 2π before correction. The PPVs of the wiggling errors at integration times of 600 μs,400 μs, and 200 μs were approximately 89.15, 88.70, and 89.90 mrad. This error was reduced to the PPVs of 11.85, 12.24, and 12.75 mrad after correction, which was a significant improvement.
As shown in Figure 12, the STD, which represents the magnitude of the wiggling random error, also demonstrated the predicted wiggling phenomenon. It can be noticed from Table 2 that the random error increased as the integration time decreased. At integration times of 600 μs, 400 μs, and 200 μs, values of are 4.35, 4.98, and 6.72 mrad, respectively. The proposed method had good adaptive performance and performed well in the wiggling random error reduction at various integration times. The values of were about 0.51, 0.58, and 0.71 mrad after correction.
Figure 13 shows the RMSE of the measured phase for different true phases. We compared the in Table 2, which represents the magnitude of the wiggling-related, and found that values of were reduced by about 92.2% (integration time of 600 μs), 91.5% (integration time of 400 μs), and 89.5% (integration time of 200 μs). Therefore, the proposed method can effectively improve the range accuracy of the indirect ToF imaging system and has certain robustness in different integration times.
It can be noticed from the experimental results that the wiggling-related error followed the shape of the simulation. However, the values of each parameter obtained in the experiment were larger than those in the simulation. This phenomenon was because the harmonic component of the emitted signal in the experiment was more complicated than the one in the simulation, and temperature also affected the results. Despite all this, experimental results can still verify the derived mathematical model. In addition, the performance of the proposed method degrades a little as the integration time decreases, which is caused by the PMD sensor’s nonlinearity.
To better illustrate the effectiveness of the proposed method, we compared the method with several existing methods in [15,18,20]. The PPV of the phase error, calculated as the difference between the maximum and minimum phase errors, was chosen to evaluate the wiggling-related error before and after correction. The result is shown in Table 3. Compared with the existing methods, the proposed method has the optimal performance in correcting the wiggling-related error. In addition, the existing methods require some hardware changes, while our method is easier to implement in most indirect ToF imaging systems.

Table 3.
Comparison of the proposed method with the existing methods. The phase error in [15] is obtained directly from the results of the paper, while the phase errors in [18,20] are calculated from the distance error and the modulation frequency in the corresponding documents. The data of the proposed method is calculated from the phase error under the integration time of 600 μs.
5. Conclusions
In this paper, we derive a mathematical model of the wiggling-related error and propose a wiggling-related error correction method for indirect ToF imaging systems. This method adds a delay measurement and utilizes raw intensity measurements to evaluate the system state based on the AKF, which is easy to implement in most indirect ToF imaging systems. Simulation and experimental results showed that the wiggling-related error is significant, and the proposed method has a good performance in reducing the wiggling-related error. The PPV of the wiggling error significantly reduced after correction (from 89.15 to 11.85 mrad at the integration time of 600 μs). Meanwhile, decreased by at least 88.3% (from 4.35 to 0.51 mrad at the integration time of 600 μs). Moreover, the proposed method had good robustness under different integration times. The values of reduced by about 92.2% (integration time of 600 μs), 91.5% (integration time of 400 μs), and 89.5% (integration time of 200 μs).
We believe that this study provides effective guidance for researchers understanding the wiggling-related error and a potential direction for the accuracy improvement of indirect ToF imaging systems. Our future works will further optimize the proposed method to develop ToF imaging systems with higher performance.
Author Contributions
Conceptualization, Z.Z. and P.S.; methodology, Z.Z. and P.S.; software, Z.Z. and W.Z.; validation, Z.Z., X.W. and W.Z.; formal analysis, Y.B.; investigation, X.W. and W.Z.; resources, P.S.; data curation, W.Z. and Y.B.; writing—original draft preparation, Z.Z., W.Z. and Y.B.; writing—review and editing, P.S. and X.W.; visualization, W.Z.; supervision, P.S.; project administration, P.S.; funding acquisition, P.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Defense Basic Scientific Research Program of China, grant number JCKY2019602B010.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to the secret for the institute.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Westheimer, G. Three-dimensional displays and stereo vision. Proc. R. Soc. B-Biol. Sci. 2011, 278, 2241–2248. [Google Scholar] [CrossRef] [PubMed]
- Gong, B.X.; Wang, G.Y. Underwater Image Recovery Using Structured Light. IEEE Access 2019, 7, 77183–77189. [Google Scholar] [CrossRef]
- Foix, S.; Alenya, G.; Torras, C. Lock-in Time-of-Flight (ToF) Cameras: A Survey. IEEE Sens. J. 2011, 11, 1917–1926. [Google Scholar] [CrossRef]
- Francis, S.L.; Anavatti, S.G.; Garratt, M.; Shim, H. A ToF-camera as a 3D Vision Sensor for Autonomous Mobile Robotics. Int. J. Adv. Robot. Syst. 2015, 12, 156. [Google Scholar] [CrossRef]
- Robla, S.; Llata, J.R.; Torre-Ferrero, C.; Sarabia, E.G.; Becerra, V.; Perez-Oria, J. Visual sensor fusion for active security in robotic industrial environments. EURASIP J. Adv. Signal Process. 2014, 1, 88. [Google Scholar] [CrossRef]
- Tong, J.; Zhou, J.; Liu, L.G.; Pan, Z.G.; Yan, H. Scanning 3D Full Human Bodies Using Kinects. IEEE Trans. Vis. Comput. Graph. 2012, 18, 643–650. [Google Scholar] [CrossRef] [PubMed]
- Vazquez-Arellano, M.; Reiser, D.; Paraforos, D.S.; Garrido-Izard, M.; Burce, M.E.; Griepentrog, H.W. 3-D reconstruction of maize plants using a time-of-flight camera. Comput. Electron. Agric. 2018, 145, 235–247. [Google Scholar] [CrossRef]
- Molina, J.; Pajuelo, J.A.; Martínez, J.M. Real-time Motion-based Hand Gestures Recognition from Time-of-Flight Video. J. Signal Process. Syst. Signal Image Video Technol. 2017, 86, 17–25. [Google Scholar] [CrossRef]
- Hu, C.Z.; Zhang, B.; Xin, Y.Z.; Li, D.; Guo, Z.Q.; Xue, Z.M.; Ke, Z.G.; Geng, L. Compact Numerical Modeling of Indirect Time-of-Flight CMOS Image Sensors. IEEE Trans. Electron. Devices 2022, 69, 6897–6903. [Google Scholar] [CrossRef]
- Keel, M.S.; Jin, Y.G.; Kim, Y.; Kim, D.; Kim, Y.; Bae, M.; Chung, B.; Son, S.; Kim, H.; An, T.; et al. A VGA Indirect Time-of-Flight CMOS Image Sensor With 4-Tap 7-μm Global-Shutter Pixel and Fixed-Pattern Phase Noise Self-Compensation. IEEE J. Solid-State Circuit 2020, 55, 889–897. [Google Scholar] [CrossRef]
- Chiabrando, F.; Chiabrando, R.; Piatti, D.; Rinaudo, F. Sensors for 3D Imaging: Metric Evaluation and Calibration of a CCD/CMOS Time-of-Flight Camera. Sensors 2009, 9, 10080–10096. [Google Scholar] [CrossRef]
- Rapp, H. Experimental and Theoretical Investigation of Correlating ToF-Camera Systems. Ph.D. Thesis, University of Heidelberg, Heidelberg, Germany, 2007. [Google Scholar]
- Lindner, M.; Schiller, I.; Schiller, I.; Koch, R. Time-of-Flight sensor calibration for accurate range sensing. Comput. Vis. Image Underst. 2010, 114, 1318–1328. [Google Scholar] [CrossRef]
- Illade-Quinteiro, J.; Brea, V.M.; Lopez, P.; Cabello, D.; Domenech-Asensi, G. Distance Measurement Error in Time-of-Flight Sensors Due to Shot Noise. Sensors 2015, 15, 4624–4642. [Google Scholar] [CrossRef]
- Streeter, L.; Dorrington, A.A. Simple harmonic error cancellation in time of flight range imaging. Opt. Lett. 2015, 40, 5391–5394. [Google Scholar] [CrossRef]
- He, Y.; Chen, S.Y. Recent Advances in 3D Data Acquisition and Processing by Time-of-Flight Camera. IEEE Access 2019, 7, 12495–12510. [Google Scholar] [CrossRef]
- Mersmann, S.; Seitel, A.; Erz, M.; Jaehne, B.; Nickel, F.; Mieth, M.; Mehrabi, A.; Maier-Hein, L. Calibration of time-of-flight cameras for accurate intraoperative surface reconstruction. Med. Phys. 2013, 40, 082701. [Google Scholar] [CrossRef] [PubMed]
- Hussmann, S.; Knoll, F.; Edeler, T. Modulation Method Including Noise Model for Minimizing the Wiggling Error of TOF Cameras. IEEE Trans. Instrum. Meas. 2014, 63, 1127–1136. [Google Scholar] [CrossRef]
- Payne, A.D.; Dorrington, A.A.; Cree, M.J.; Carnegie, D.A. Improved measurement linearity and precision for AMCW time-of-flight range imaging cameras. Appl. Optics 2010, 49, 4392–4403. [Google Scholar] [CrossRef]
- Payne, A.D.; Dorrington, A.A.; Cree, M.J. Illumination waveform optimization for time-of-flight range imaging cameras. In Proceedings of the SPIE, Videometrics, Range Imaging, and Applications XI, Munich, Germany, 25–26 May 2011. [Google Scholar]
- Xuan, V.N.; Weihs, W.; Loffeld, O. Illumination, phase step optimization and improvements in simultaneous multiple frequency measurement for Time-of-Flight sensors. In Proceedings of the 2015 International Conference on 3D Imaging (IC3D 2015), Liege, Belgium, 14–15 December 2015. [Google Scholar]
- Lindner, M.; Kolb, A.; Ringbeck, T. New insights into the calibration of ToF-sensors. In Proceedings of the 2008 IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops, Anchorage, AK, USA, 23–28 June 2008. [Google Scholar]
- Drayton, B.M.; Carnegie, D.A.; Dorrington, A.A. Phase Algorithms for Reducing Axial Motion and Linearity Error in Indirect Time of Flight Cameras. IEEE Sens. J. 2013, 13, 3386–3396. [Google Scholar] [CrossRef]
- Feigin, M.; Whyte, R.; Bhandari, A.; Dorington, A.; Raskar, R. Modeling “wiggling” as a multi-path interference problem in AMCW ToF imaging. Opt. Express 2015, 23, 19213–19225. [Google Scholar] [CrossRef]
- Lange, R. 3D Time-of-Flight Distance Measurement with Custom Solid-State Image Sensors in CMOS/CCD-Technology. Ph.D. Thesis, University of Siegen, Siegen, Germany, 2000. [Google Scholar]
- Frank, M.; Plaue, M.; Rapp, H.; Koethe, U.; Jaehne, B.; Hamprecht, F. Theoretical and experimental error analysis of continuous-wave time-of-flight range cameras. Opt. Eng. 2009, 48, 013602. [Google Scholar] [CrossRef]
- Zuo, C.; Feng, S.J.; Huang, L.; Tao, T.Y.; Yin, W.; Chen, Q.; Luan, X. Phase shifting algorithms for fringe projection profilometry: A review. Opt. Lasers Eng. 2018, 109, 23–59. [Google Scholar] [CrossRef]
- Surrel, Y. Design of algorithms for phase measurements by the use of phase stepping. Appl. Opt. 1996, 35, 51–60. [Google Scholar] [CrossRef]
- Pan, B.; Qian, K.M.; Huang, L.; Asundi, A. Phase error analysis and compensation for nonsinusoidal waveforms in phase-shifting digital fringe projection profilometry. Opt. Lett. 2009, 34, 416–418. [Google Scholar] [CrossRef]
- Schonlieb, A.; Almer, M.; Lugitsch, D.; Steger, C.; Holweg, G.; Druml, N. Coded Modulation Simulation Framework for Time-of-Flight Cameras. In Proceedings of the 2019 22nd Euromicro Conference on Digital System Design (DSD), Kallithea, Greece, 28–30 August 2019. [Google Scholar]
- Ortiz, S.; Sathiaseelan, M.A.; Cha, A. Time-of-flight camera characterization with functional modeling for synthetic scene generation. Opt. Express 2021, 29, 37661–37682. [Google Scholar] [CrossRef] [PubMed]
- Luan, X. Experimental Investigation of Photonic Mixer Device and Development of TOF 3D Ranging Systems Based on PMD Technology. Ph.D. Thesis, University of Siegen, Siegen, Germany, 2001. [Google Scholar]
- Belhedi, A.; Bartoli, A.; Bourgeois, S.; Gay-Bellile, V.; Hamrouni, K.; Sayd, P. Noise modelling in time-of-flight sensors with application to depth noise removal and uncertainty estimation in three-dimensional measurement. IET Comput. Vis. 2015, 9, 967–977. [Google Scholar] [CrossRef]
- Streeter, L. Time-of-Flight Range Image Measurement in the Presence of Transverse Motion Using the Kalman Filter. IEEE Trans. Instrum. Meas. 2018, 67, 1573–1578. [Google Scholar] [CrossRef]
- Li, M.H.; Kang, R.J.; Branson, D.T.; Dai, J.S. Model-Free Control for Continuum Robots Based on an Adaptive Kalman Filter. IEEE-ASME Trans. Mechatron. 2018, 23, 286–297. [Google Scholar] [CrossRef]
- Mohamed, A.H.; Schwarz, K.P. Adaptive Kalman Filtering for INS/GPS. J. Geodesy 1999, 73, 193–203. [Google Scholar] [CrossRef]
- Fursattel, P.; Placht, S.; Balda, M.; Schaller, C.; Hofmann, H.; Maier, A.; Riess, C. A Comparative Error Analysis of Current Time-of-Flight Sensors. IEEE Trans. Comput. Imaging 2016, 2, 27–41. [Google Scholar] [CrossRef]
- Schmidt, M. Analysis, Modeling and Dynamic Optimization of 3D Time-of-Flight Imaging Systems. Ph.D. Thesis, University of Heidelberg, Heidelberg, Germany, 2011. [Google Scholar]
- Wang, X.Q.; Song, P.; Zhang, W.Y.; Bai, Y.J.; Zheng, Z.L. A systematic non-uniformity correction method for correlation-based ToF imaging. Opt. Express 2022, 30, 1907–1924. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).