A DIDE-FPP Composite Algorithm for Accurate Tunnel Fire Location
Abstract
1. Introduction
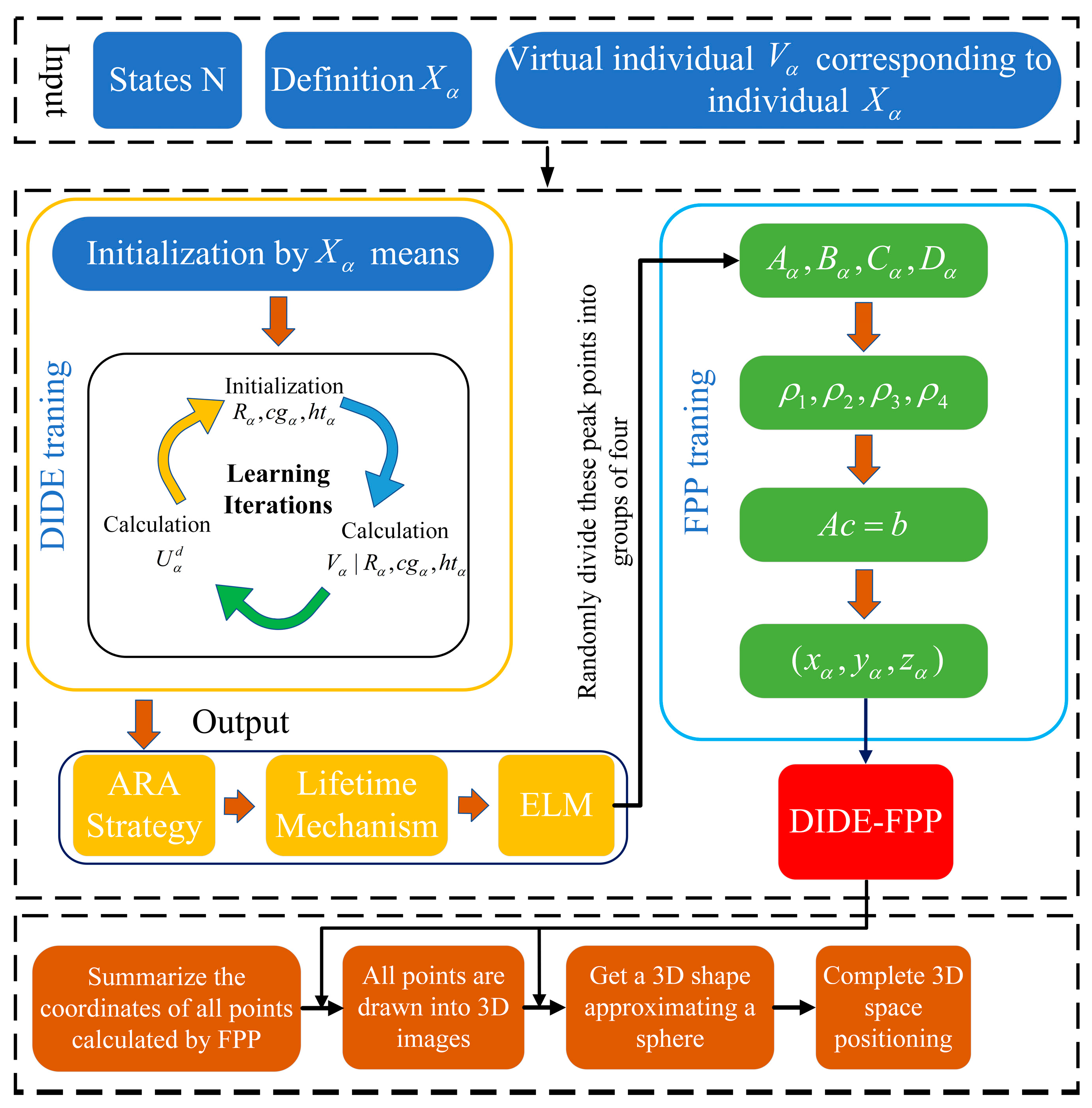
2. Algorithm and Principle
2.1. DIDE Algorithm
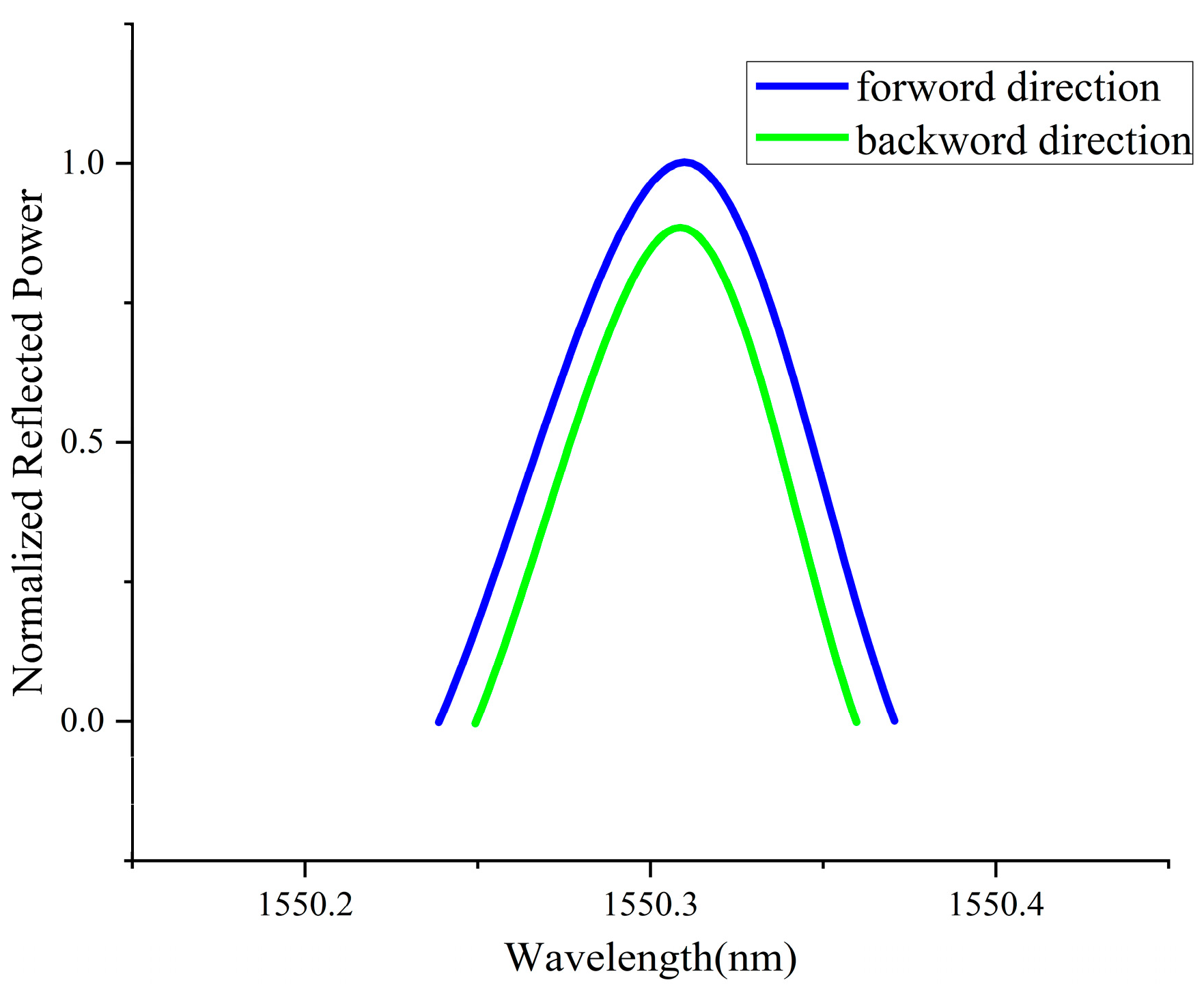
2.2. FPP Algorithm
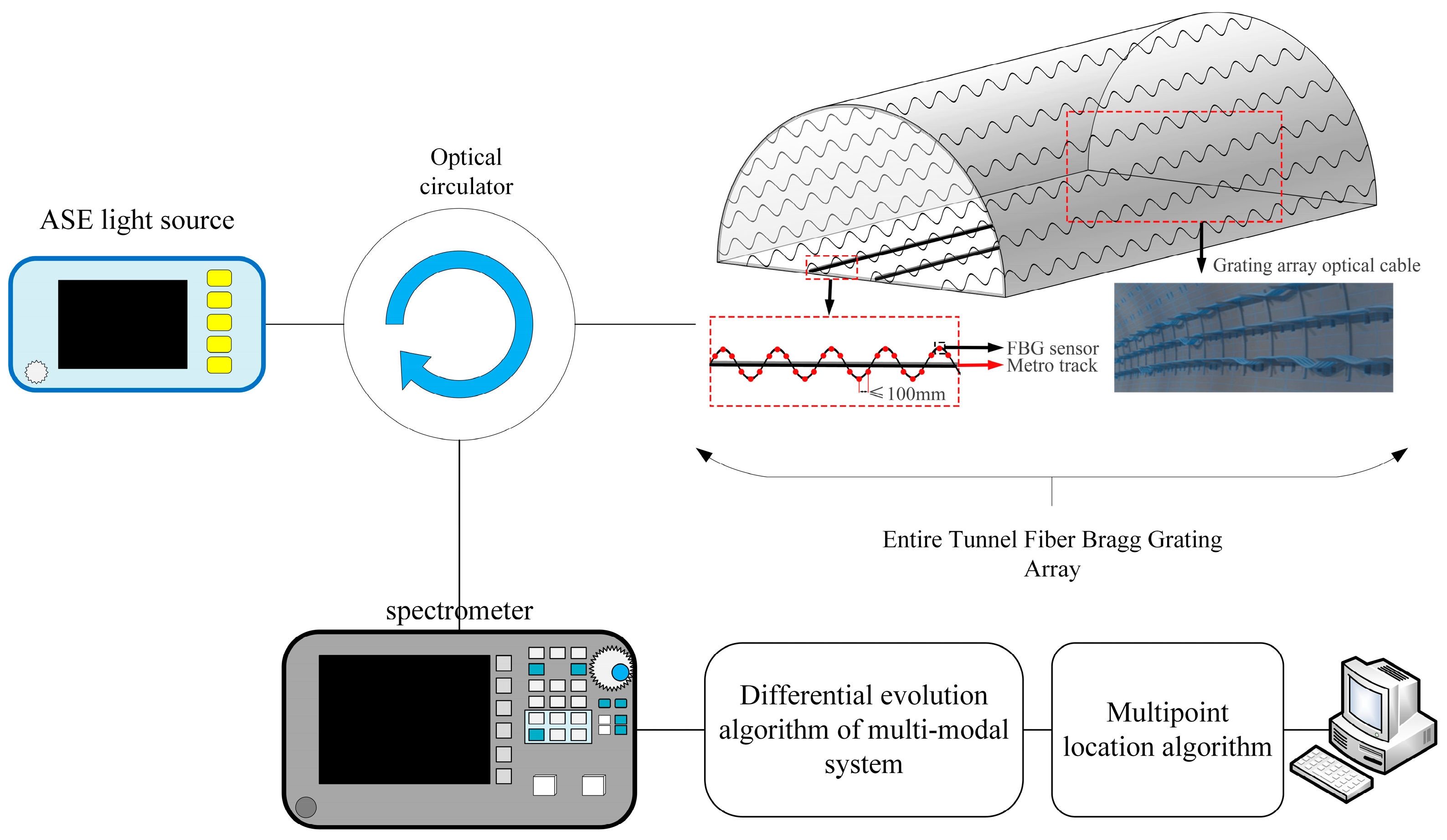
3. Experimental Comparison
4. Simulation and Discussion
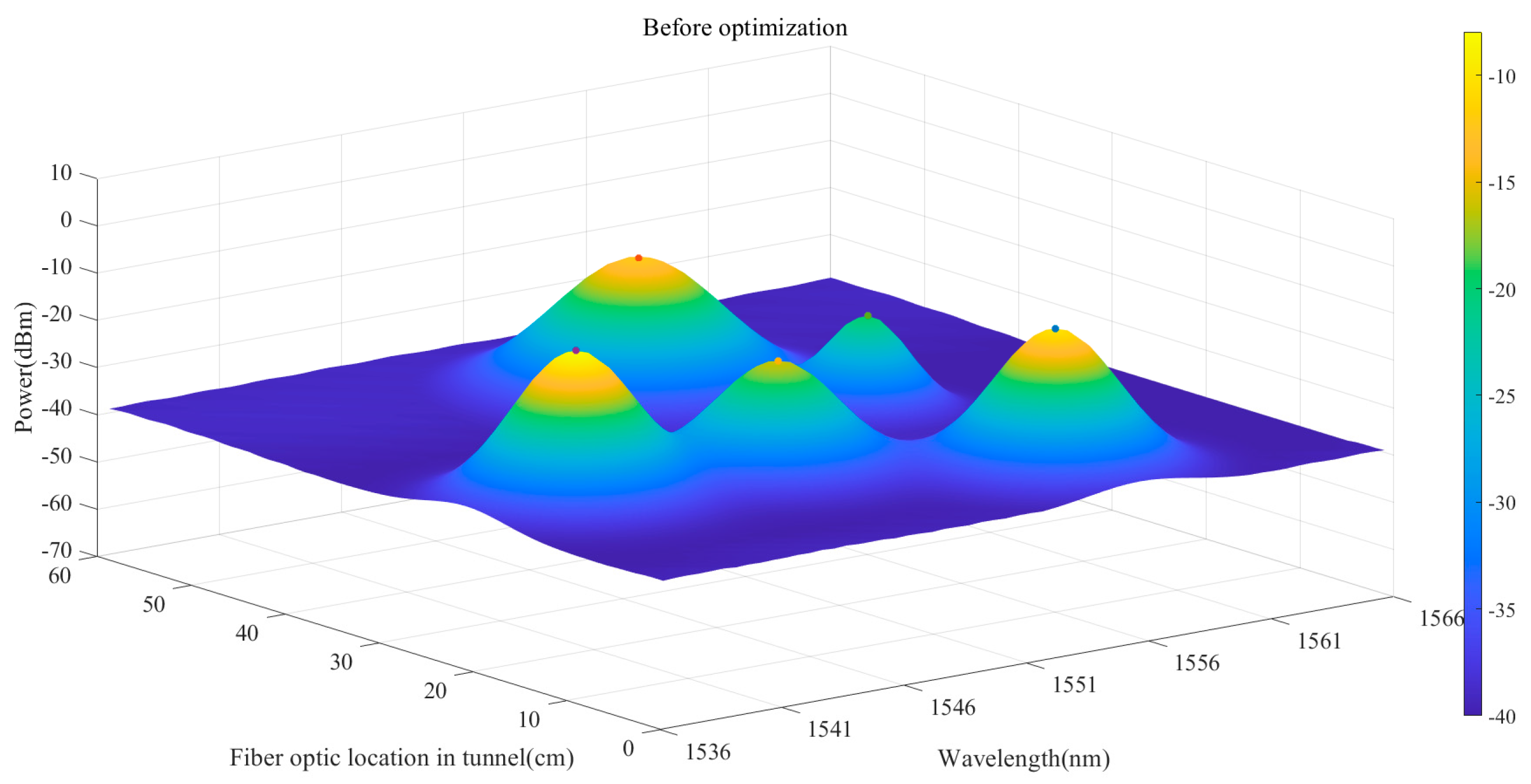
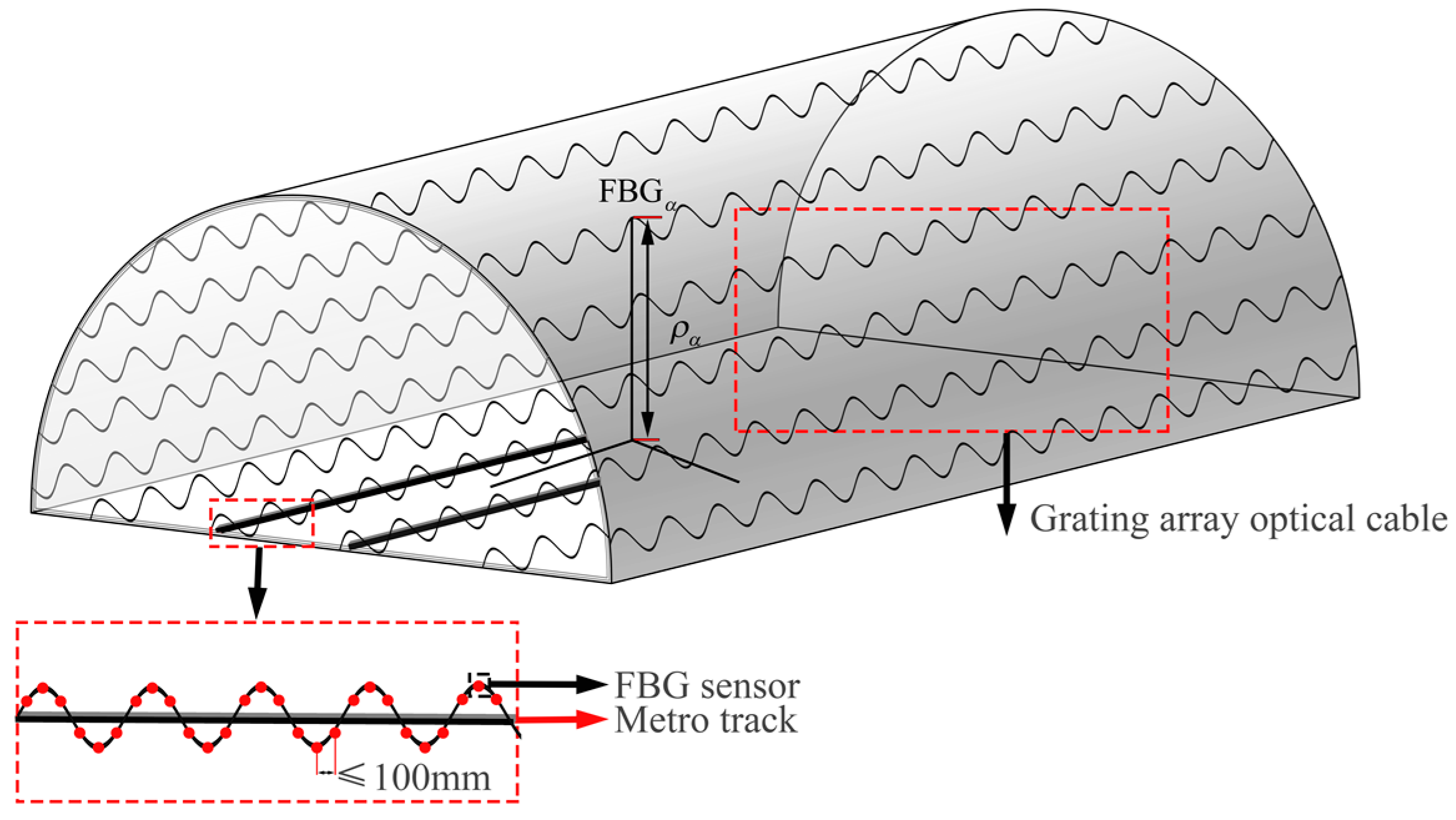
4.1. Experimental Scenario
4.2. Simulation System
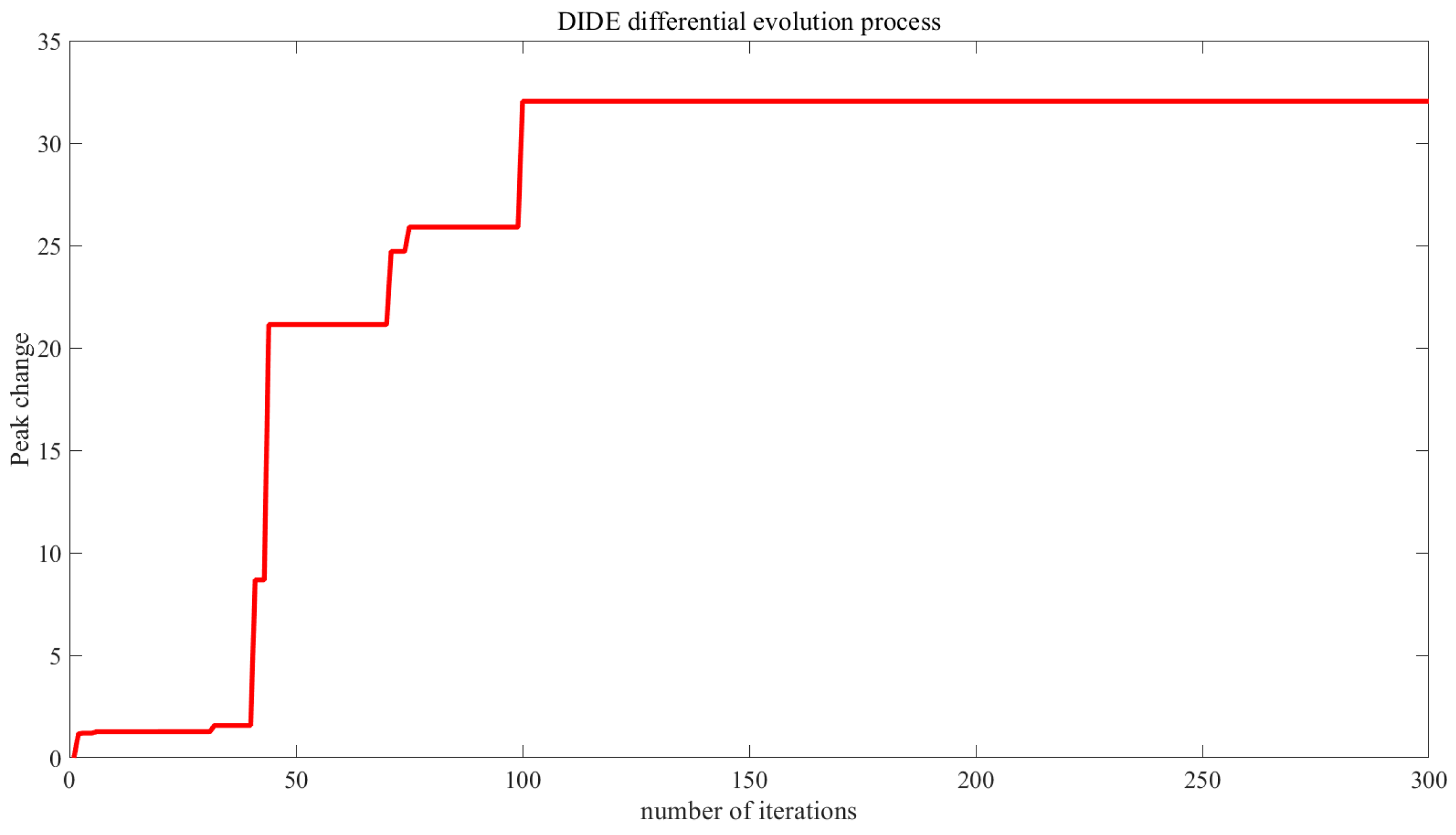
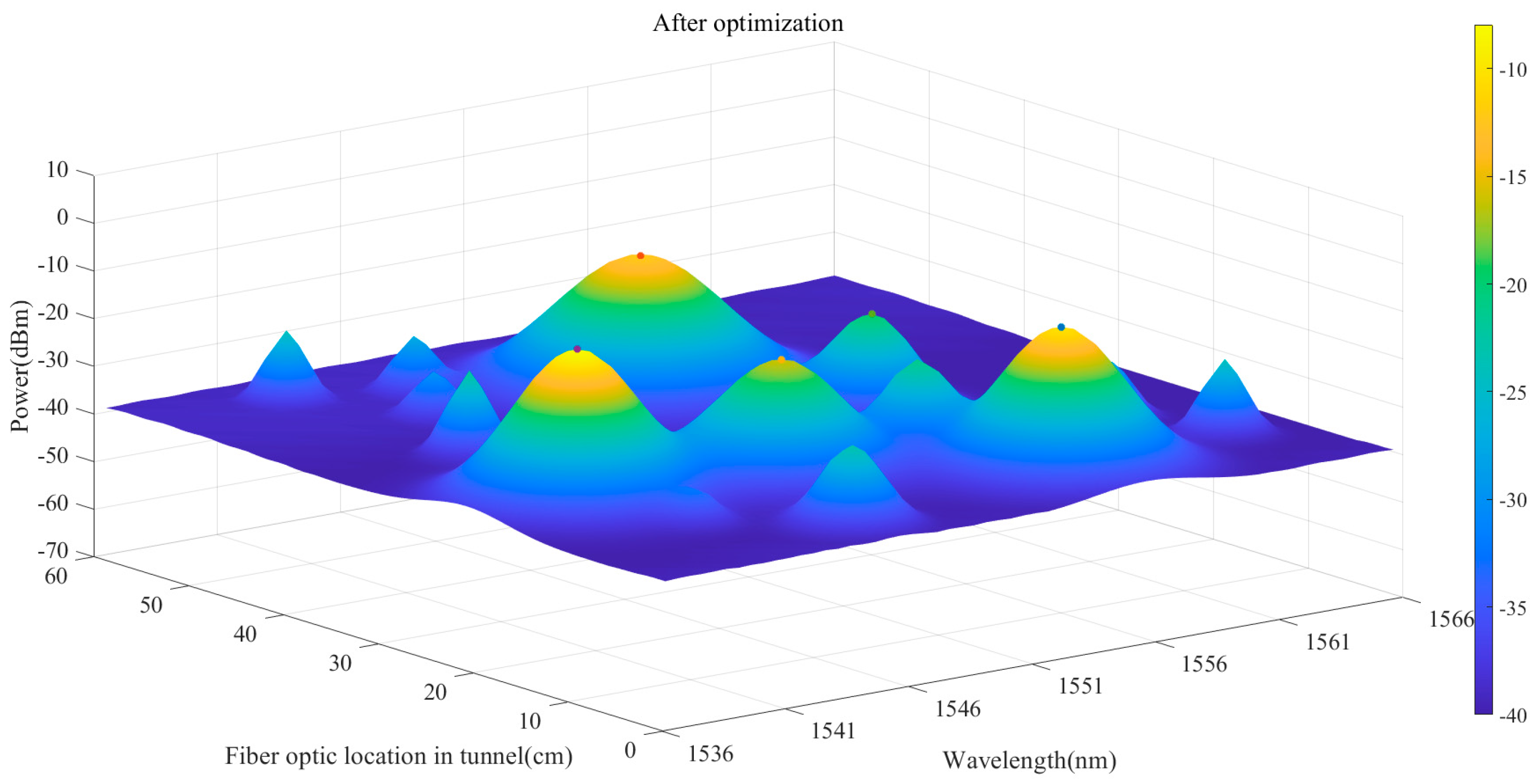
4.3. Discussion
4.3.1. Algorithm Performance Analysis
4.3.2. Analysis of Tunnel Fire Monitoring Technology
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yin, Q. Research on Temperature Distribution Characteristics of Tunnel Fire Based on Distributed Optical Fiber Monitoring. Ph.D. Thesis, Department of Electrical Engineering, Hubei University of Technology, Wuhan, China, 2021. [Google Scholar]
- Yan, B. High-Precision Visual Distributed Optical Fiber Raman Temperature Sensing Technology for Tunnel Fire Monitoring. Ph.D. Thesis, Department of Electrical Engineering, Taiyuan University of Technology, Taiyuan, China, 2020. [Google Scholar]
- Kersey, A.D. A review of recent developments in fiber optic sensor technology. Opt. Fiber Technol. 1996, 2, 291–317. [Google Scholar] [CrossRef]
- Kirkland, C.J. The fire in the channel tunnel. Tunn. Undergr. Space Technol. 2002, 17, 129–132. [Google Scholar] [CrossRef]
- Kelsey, A.; Ivings, M.J.; Hemingway, M.A.; Walsh, P.T.; Connolly, S. Sensitivity studies of offshore gas detector networks based on experimental simulations of high pressure gas releases. Process Saf. Environ. Prot. 2005, 83, 262–269. [Google Scholar] [CrossRef]
- Li, Y.; Hua, Z.; Yan, F.; Gang, P. Metal coating of fiber Bragg grating and the temperature sensing character after metallization. Opt. Fiber Technol. 2009, 15, 391–397. [Google Scholar] [CrossRef]
- Zhang, H.J.; Zhang, N.; Xiao, N.F. Fire detection and identification method based on visual attention mechanism. Optik 2015, 126, 5011–5018. [Google Scholar] [CrossRef]
- Muhammad, K.; Ahmad, J.; Lv, Z.; Bellavista, P.; Yang, P.; Baik, S.W. Efficient Deep CNN-Based Fire Detection and Localization in Video Surveillance Applications. IEEE Trans. Syst. Man Cybern. Syst. 2018, 49, 1419–1434. [Google Scholar] [CrossRef]
- Yan, B.; Li, J.; Zhang, M.; Zhang, J.; Qiao, L.; Wang, T. Raman Distributed Temperature Sensor with Optical Dynamic Difference Compensation and Visual Localization Technology for Tunnel Fire Detection. Sensors 2019, 19, 2320. [Google Scholar] [CrossRef] [PubMed]
- Lv, J.; Fang, N.; Wang, C.; Wang, L. Location method of Sagnac distributed optical fiber sensing system based on CNNs ensemble learning. Opt. Laser Technol. 2021, 138, 106841. [Google Scholar] [CrossRef]
- Yang, M.; Zhao, M.; Huang, D.; Su, X. A composite framework for photovoltaic day-ahead power prediction based on dual clustering of dynamic time warping distance and deep autoencoder. Renew. Energy 2022, 194, 659–673. [Google Scholar] [CrossRef]
- Chen, Z.-G.; Zhan, Z.-H.; Wang, H.; Zhang, J. Distributed Individuals for Multiple Peaks: A Novel Differential Evolution for Multimodal Optimization Problems. IEEE Trans. Evol. 2019, 24, 708–719. [Google Scholar] [CrossRef]
- Li, X.; Engelbrecht, A.; Epitropa, M.G. Benchmark Functions for CEC’2013 Special Session and Competition on Niching Methods for Multimodal Function Optimization; Technical Report; RMIT University, The Evolutionary Computing and Machine Learning Group: Melbourne, Australia, 2013. [Google Scholar]
- Thomsen, R. Multimodal Optimization Using Crowding-Based Differential Evolution. In Proceedings of the 2004 Congress on Evolutionary Computation (IEEE Cat. No.04TH8753), Portland, OR, USA, 19–23 June 2004; Volume 2, pp. 1382–1389. [Google Scholar]
- Li, X. Efficient Differential Evolution Using Speciation for Multimodal Function Optimization. In Proceedings of the 7th Annual Conference on Genetic and Evolutionary Computation, Washington, DC, USA, 25–29 June 2005; pp. 873–880. [Google Scholar]
- Qu, B.Y.; Suganthan, P.N.; Liang, J.J. Differential Evolution With Neighborhood Mutation for Multimodal Optimization. IEEE Trans. Evol. Comput. 2012, 16, 601–614. [Google Scholar] [CrossRef]
- Wang, Y.; Li, H.-X.; Yen, G.G.; Song, W. MOMMOP: Multiobjective Optimization for Locating Multiple Optimal Solutions of Multimodal Optimization Problems. IEEE Trans. Cybern. 2014, 45, 830–843. [Google Scholar] [CrossRef] [PubMed]
- Qu, B.Y.; Suganthan, P.N.; Das, S. A Distance-Based Locally Informed Particle Swarm Model for Multimodal Optimization. IEEE Trans. Evol. Comput. 2012, 17, 387–402. [Google Scholar] [CrossRef]
- Fieldsend, J.E. Running Up Those Hills: Multi-Modal Search with the Niching Migratory Multi-Swarm Optimizer. In Proceedings of the 2014 IEEE CEC, Beijing, China, 6–11 July 2014; pp. 2593–2600. [Google Scholar]
- Biswas, S.; Kundu, S.; Das, S. Inducing Niching Behavior in Differential Evolution Through Local Information Sharing. IEEE Trans. Evol. Comput. 2014, 19, 246–263. [Google Scholar] [CrossRef]
- Biswas, S.; Kundu, S.; Das, S. An Improved Parent-Centric Mutation With Normalized Neighborhoods for Inducing Niching Behavior in Differential Evolution. IEEE Trans. Cybern. 2014, 44, 1726–1737. [Google Scholar] [CrossRef] [PubMed]
- Cheng, R.; Li, M.; Li, K.; Yao, X. Evolutionary Multiobjective Optimization-Based Multimodal Optimization: Fitness Landscape Approximation and Peak Detection. IEEE Trans. Evol. Comput. 2017, 22, 692–706. [Google Scholar] [CrossRef]
- Gao, W.; Yen, G.G.; Liu, S. A Cluster-Based Differential Evolution With Self-Adaptive Strategy for Multimodal Optimization. IEEE Trans. Cybern. 2013, 44, 1314–1327. [Google Scholar] [CrossRef]
- Hu, C. Research on High-Speed Demodulation Method and Key Technology of Large-Capacity Fiber Grating Sensor Network. Ph.D. Thesis, Department of Electrical Engineering, Hubei University of Technology, Wuhan, China, 2015. [Google Scholar]
- GB50116-2013; Code for Design of Automatic Fire Alarm System. AQSIQ: Beijing, China, 2013.







| Function | Name | Local Optimum | Global Optimum | Dimesion Size |
|---|---|---|---|---|
| 0 | 3 | 2 | 1 | |
| Equal Maxima | 0 | 5 | 1 | |
| Uneven Decreasing Maxima | 4 | 1 | 1 | |
| Himmelblau | 0 | 4 | 2 | |
| Six-Hump Camel Back | 2 | 2 | 2 | |
| Shubert with 2D | many | 18 | 2 | |
| Vincent with 2D | 0 | 36 | 2 | |
| Shubert with 3D | many | 81 | 3 | |
| Vincent with 3D | 0 | 216 | 3 | |
| Modified Rastrigin | 0 | 12 | 2 | |
| Composition Function 1 with 2D | many | 6 | 2 | |
| Composition Function 2 with 2D | many | 8 | 2 | |
| Composition Function 3 with 2D | many | 6 | 2 | |
| Composition Function 3 with 3D | many | 6 | 3 | |
| Composition Function 4 with 3D | many | 8 | 3 | |
| Composition Function 3 with 5D | many | 6 | 5 | |
| Composition Function 4 with 5D | many | 8 | 5 | |
| Composition Function 3 with 10D | many | 6 | 10 | |
| Composition Function 4 with 10D | many | 8 | 10 | |
| Composition Function 4 with 20D | many | 8 | 20 |
| Function | MaxFEs |
|---|---|
| – | |
| – | |
| – | |
| – | |
| – |
| Method | PR | SR | PM | Reference |
|---|---|---|---|---|
| MOMMOP | 0.667 | 0.000 | 84.11% | [17] |
| NMMSO | 0.700 | 0.000 | 88.27% | [19] |
| PNPCDE | 0.317 | 0.000 | 39.97% | [21] |
| Self-CCDE | 0.640 | 0.000 | 80.71% | [23] |
| DIDE-FPP | 0.773 | 0.020 | 1 | This work |
| Method Name | Accuracy | Power Demand | Response Time | Reference |
|---|---|---|---|---|
| Based on Visual Attention Mechanism | Limited by the accuracy of camera | Power supply required | Slow | [7] |
| Efficient deep CNN-based | Limited by the accuracy of camera | Power supply required | Fast | [8] |
| Based on CNNs ensemble learning | Meter-level | Passive | Fast | [10] |
| Based on DIDE-FPP | Centimeter-level | Passive | Fast | This work |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, H.; Zhao, Y.; Wang, C.; Cui, L. A DIDE-FPP Composite Algorithm for Accurate Tunnel Fire Location. Photonics 2023, 10, 272. https://doi.org/10.3390/photonics10030272
Jiang H, Zhao Y, Wang C, Cui L. A DIDE-FPP Composite Algorithm for Accurate Tunnel Fire Location. Photonics. 2023; 10(3):272. https://doi.org/10.3390/photonics10030272
Chicago/Turabian StyleJiang, Hong, Yihan Zhao, Chenyang Wang, and Lina Cui. 2023. "A DIDE-FPP Composite Algorithm for Accurate Tunnel Fire Location" Photonics 10, no. 3: 272. https://doi.org/10.3390/photonics10030272
APA StyleJiang, H., Zhao, Y., Wang, C., & Cui, L. (2023). A DIDE-FPP Composite Algorithm for Accurate Tunnel Fire Location. Photonics, 10(3), 272. https://doi.org/10.3390/photonics10030272





