Next Article in Journal
Experimental Study on Measuring Petzval Image Plane of Streak Tube with Single Image
Next Article in Special Issue
Development of a Mode-Locked Fiber Laser Utilizing a Niobium Diselenide Saturable Absorber
Previous Article in Journal
Simulated Studies of Polarization-Selectivity Multi-Band Perfect Absorber Based on Elliptical Metamaterial with Filtering and Sensing Effect
Previous Article in Special Issue
Study on the Technology and Mechanism of Cleaning Architectural Aluminum Formwork for Concrete Pouring by High Energy and High Repetition Frequency Pulsed Laser
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Photonics
Volume 10
Issue 3
10.3390/photonics10030296
photonics-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Frequency Comb Generation Based on Brillouin Random Lasing Oscillation and Four-Wave Mixing Assisted with Nonlinear Optical Loop Mirror

by
Yuxi Pang
1,2,
Shaonian Ma
1,2,
Qiang Ji
1,2,
Xian Zhao
1,2,
Yongfu Li
1,2,
Zengguang Qin
2,3,
Zhaojun Liu
2,3 and
Yanping Xu
1,2,*
1
Center for Optics Research and Engineering, Shandong University, Qingdao 266237, China
2
Key Laboratory of Laser and Infrared System of Ministry of Education, Shandong University, Qingdao 266237, China
3
School of Information Science and Engineering, Shandong University, Qingdao 266237, China
*
Author to whom correspondence should be addressed.
Photonics 2023, 10(3), 296; https://doi.org/10.3390/photonics10030296
Submission received: 29 January 2023 / Revised: 28 February 2023 / Accepted: 7 March 2023 / Published: 11 March 2023
(This article belongs to the Special Issue Fiber Laser and Their Applications)
Browse Figures
Review Reports Versions Notes

Abstract

:
A frequency comb generator (FCG) based on dual-cavity Brillouin random fiber lasing oscillation in the 1.5 μm telecon spectral window is established and experimentally demonstrated. In the half-open main cavity of the dual cavity, the stimulated Brillouin scattering in highly nonlinear fiber (HNLF) and Rayleigh scattering in single-mode fiber are employed to provide sufficient Brillouin gain and the randomly distributed feedback, respectively, for random mode resonance. The sub-cavity includes an Er-doped fiber amplifier to couple back and boost lower-order Stokes and anti-Stokes light for the cascade of stimulated Brillouin scattering to generate multiple higher-order Stokes and anti-Stokes light. Meanwhile, efficient four-wave mixing is stimulated in the HNLF-based main cavity, further enhancing the number and intensity of the resonant Stokes and anti-Stokes light. By taking advantages of the unique transmission characteristics of nonlinear optical loop mirrors, the power deviation between Stokes and anti-Stokes lines is further optimized with 17 orders of stable Stokes lines and 15 orders of stable anti-Stokes lines achieved within the 10 dB power deviation, with maximum optical signal-to-noise ratio (OSNR) of ~22 dB and ~17 dB and minimum OSNR of ~10 dB and ~7.5 dB for Stokes and anti-Stokes lines, respectively. In addition, the dynamic characteristics of the proposed FCG have been experimentally investigated. Such an FCG with fixed frequency spacing will find promising applications in fields of optical communication, microwave, optical sensing, etc.

1. Introduction

Frequency comb generators (FCGs) based on fiber-optic lasing oscillation have received intense attention and active research due to their promising applications in fiber-optic communication (e.g., fiber-optic wavelength division multiplexing systems) [1], fiber-optic sensing [2], microwave photonics [3], optical component characterization [4], optical instrumentation testing [5], and so on. Up to now, a number of FCGs realized by fiber-optic lasing oscillation based on different principles and structures have been proposed, mainly including the introduction of actively modulated frequency-shifting devices in the resonant cavity of fiber lasers [6,7,8] and the incorporation of the passively modulated narrow-bandwidth multi-channel filter [9,10,11] or intensity-dependent loss structures [12,13] in the resonant cavity of fiber lasers with broadband gain. However, the active modulation method requires electrical devices, which will undoubtedly introduce large insertion loss and break the all-fiber structure of FCGs. The frequency comb obtained by passive modulation methods is heavily dependent on the fabrication accuracy of the modulating device, making the FCG hard to generate frequency combs with narrow linewidth and fixed frequency spacing, limiting the widespread application of FCG.
In recent years, random fiber lasers (RFLs) with randomly distributed feedback provided by Rayleigh scattering in optical fibers has received a lot of attention due to their unique properties. It is a dramatic step up from 3D random lasers whereby the one-dimensional waveguide constraints are provided by the optical fibers. Recently, works on RFLs based on a variety of gain mechanisms have been gradually reported, mainly including rare-earth-ion doped fiber amplifiers [14,15,16,17], non-linear stimulated scattering processes in optical fibers (e.g., Brillouin and Raman gain) [18,19,20,21] and semiconductor optical amplifiers [22,23,24]. In addition, the performances of RFL have been continuously improved, such as lower threshold [25,26,27], higher output power [28,29,30], wavelength tunability [31,32,33], higher coherence [18,22,34], narrower linewidth [18,22,34,35], lower noise [36,37,38] and more stable output power [26,39,40], which enables a wide range of applications for RFLs in optical measurement [41,42], microwave photonics [43,44], optical fiber communication [45,46,47], optical fiber sensing [48,49,50,51,52,53], laser imaging [54,55] and other fields [56,57]. More importantly, the fiber laser gained by the stimulated Brillouin scattering (SBS) mechanism can achieve multi-wavelength laser output with a fixed wavelength spacing thanks to the cascade of SBS and the Doppler shift provided by the acoustic-induced dynamic grating in the optical fiber [58]. In particular, the Brillouin random fiber lasers (BRFLs) can also achieve the narrow-linewidth multi-wavelength laser output thanks to the narrow gain bandwidth of stimulated Brillouin scattering, which significantly enhances the potential value of this light source for application [59]. As a result, this multi-wavelength Brillouin random fiber laser (MW-BRFL) has attracted a great deal of attention in the generation of frequency combs and has been heavily investigated. In 2018, Liang Zhang et al. first proposed a dual-cavity MW-BRFL, which combines a half-open resonant cavity and a feedback cavity, and achieved a high-quality multi-wavelength laser output. Its optical signal-to-noise ratio (OSNR), polarization state, and the number of Stokes lines were optimized in subsequent works by using non-uniform fiber [59], polarization-maintaining fiber [60,61] and random fiber grating [62], respectively. However, only 14 maximum Stokes lines were eventually achieved due to the limitation of the relatively high laser threshold, and the anti-Stokes lines have not been fully boosted to be studied and exploited for FCG due to the absence of an efficient excitation mechanism. Fei Wang et al. achieved a half-open linear-cavity MW-BRFL with multiple Stokes and anti-Stokes lines through four-wave mixing (FWM) by means of a highly nonlinear fiber (HNLF). However, the associated laser performance has not been optimized and some of the key lasing properties have not been explored, which are essential to characterizing the application prospects of the generated lasing combs [5,63].
In this work, we present and experimentally investigate a dual-cavity FCG based on Brillouin random lasing oscillation. The Brillouin gain in the resonant cavity is provided by the HNLF with a high nonlinear coefficient (≥10 W−1∙km−1 @1550 nm). Furthermore, the FWM effect in the HNLF is effectively excited under phase-matching conditions, which not only increases the number of Stokes lines but also boosts the power of the anti-Stokes lines to make them resonate in the main cavity. In addition, the nonlinear optical loop mirror (NOLM) with unique transmission spectrum is used to balance the resonant powers among Stokes and anti-Stokes lines of different orders to achieve a smaller power deviation. In the experiment, key lasing properties of the proposed FCG are investigated in detail, including the optical spectrum, linewidth, relative intensity noise (RIN), frequency noise (FN) and temporal characteristics.

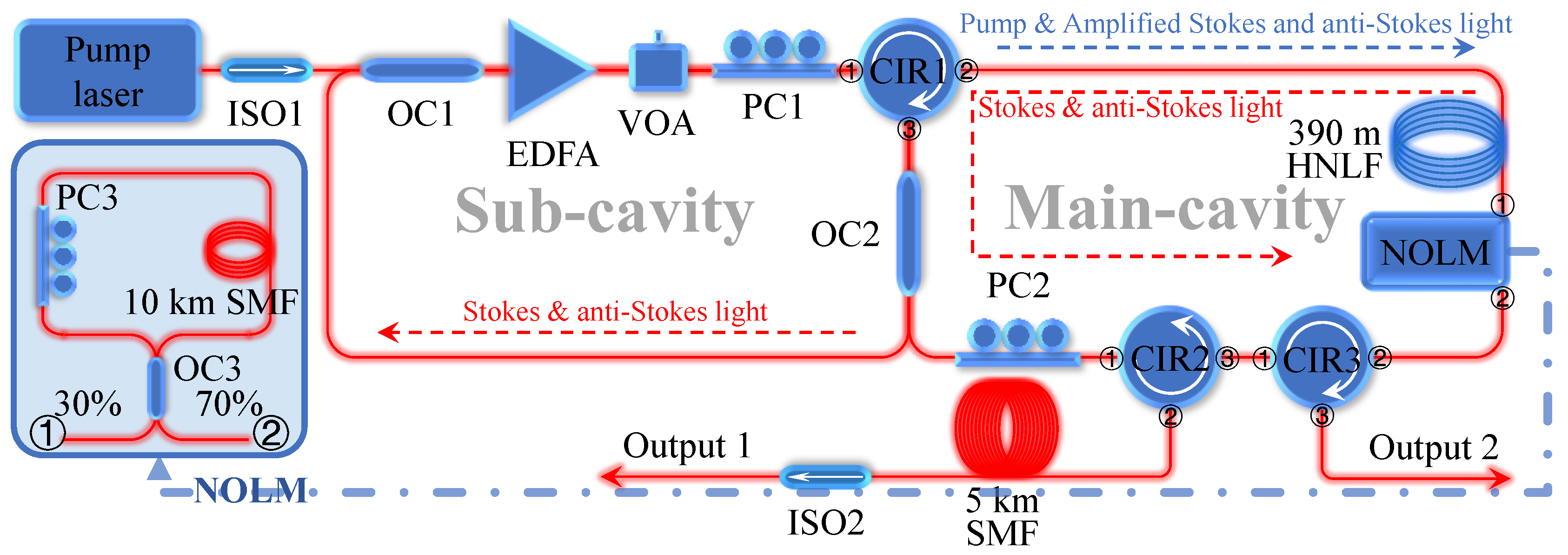
2. Experimental Setup and Operation Principle

The experimental configuration of the proposed FCG based on Brillouin random fiber lasing oscillation is shown in Figure 1, in which the dual-cavity structure consists of a main cavity on the right and a sub-cavity on the left. The pump light is provided by a semiconductor laser at the wavelength of 1550 nm with a maximum output power of 10 dBm and a linewidth of ~15 kHz (LIGHTPROMOTECH, NLLD 0175-3-34-2). After passing through an optical isolator (ISO), the first optical coupler (OC1), an erbium-doped fiber amplifier (EDFA), a variable optical attenuator (VOA) and the first polarization controller (PC1), the finely tuned pump light is launched into a 390 m long HNLF through the first circulator (CIR1) from port 1 to port 2 in the main cavity. The ISO is used to prevent any reflected light from returning to the pump laser to avoid possible damage. The EDFA enables power amplification for the pump laser, and the VOA is used to finely tune the power of the amplified pump light to investigate the pump-power-dependent characteristics of the FCG. PC1 is used to adjust the polarization state of the pump light to achieve maximum Brillouin gain in the 390 m long HNLF.
With the high non-linear coefficient (≥10 W−1∙km−1 @1550 nm), the HNLF as a Brillouin gain medium provides sufficient gain for the random mode resonance in the main cavity. When pump light is launched into the HNLF, the spontaneous Brillouin scattering (SpBS) is first triggered by thermal noise and produces Stokes light propagating in the opposite direction to the pump light. Due to the Doppler shift effect, this Stokes light exhibits a frequency downshift of ~10 GHz compared to the pump light. The power of the Stokes light generated by SpBS increases as the pump power increases. When the pump power reaches the threshold of the SBS in the Brillouin gain medium, the Stokes light initiated by SpBS will be significantly amplified by the SBS process. The amplified backward-propagating Stokes light in the Brillouin gain medium passes sequentially through ports 2 and 3 of CIR1 and is divided equally by OC2 into two beams. One beam enters the sub-cavity for further amplification and feedback, and the other beam continues propagating in the main cavity. In the main cavity, this part of the Stokes light then enters the 5 km single-mode fiber (SMF) through the second CIR (CIR2) from port 1 to port 2. Due to the non-uniform distribution of the refractive index along the fiber axis in the core of SMF, a small portion of the Stokes light is scattered back into the main cavity by the numerous scattering centers accumulated along the SMF as randomly distributed feedback for the random mode resonance. The constructive interference between multiply scattered Stokes light from the scattering centers results in coherent random spikes. The random feedback provided by the SMF for the Stokes light is eventually emitted from port 3 of CIR2 and re-enters the Brillouin gain medium after passing through the NOLM and the port1 and port2 of CIR3 to be further amplified as the seed for the SBS process. As the Stokes light is amplified during its cyclic reciprocation in the main cavity, its power increases rapidly. When the effective gain provided by the SBS process in the main cavity can overcome the total loss, the amplified Brillouin Stokes light will resonate in the main cavity and emit at the end of the 5 km SMF as the laser output of the BRFL. Meanwhile, the other beam split by OC2, identical to the resonant Stokes light in the main cavity, is injected into the sub-cavity, where it is recombined with the output of the semiconductor pump laser via OC1 and input into the EDFA at the same time. After being amplified by the EDFA, the resonant Stokes light is re-injected into the main-cavity via CIR1 as the pump light to generate the higher-order Stokes lights.
In the 390 m HNLF, multi-order Stokes resonant lights that satisfy the phase-matching condition is prone to induce FWM, which can boost Stokes and anti-Stokes light power and produce more higher-order Stokes and anti-Stokes lines. To satisfy the phase-matching condition for FWM in HNLF, the phase mismatch factor κ (κ = Δβ + 2γP) should be made as close to zero as possible. Here, γP is the nonlinear phase shift caused by self-phase modulation and cross-phase modulation, γ represents the nonlinear coefficient of fiber, and P denotes the pump power. Therefore, γP is always greater than zero. Δβ is the linear phase shift caused by different propagation constants, and it is greater than zero in the normal dispersion region, so κ will be positively beyond the zero point in this dispersion region. At the zero-dispersion wavelength, Δβ equals zero, and κ still remains greater than zero with the positive value of γP. Only in the anomalous dispersion region, where Δβ is negative, can it offset part of the positive value of γP and make κ closer to zero, meeting the phase-matching condition for FWM. The zero-dispersion wavelength of the HNLF used in this experiment is located within a narrow wavelength range near 1521 nm. Pumping with a 1550 nm laser can satisfy the phase-matching condition for FWM. In the formula for the phase mismatch factor, κ = Δβ + 2γP, Δβ = −2πc/λ02 [D (λP − λS)2]. After substituting the parameters in the expression of κ using the values in Table 1 for calculation, we can get κ = 0.00039143 m−1, which is very close to zero. It is worth noting that the forward-propagating multi-order Stokes light amplified by the EDFA is theoretically more susceptible to induce FWM due to its higher power than the backward-propagating Stokes light that has just been amplified or generated by the SBS process. Consequently, the frequency comb with multiple comb spikes and fixed frequency spacing can be efficiently generated at both output port 1 and output port 2.
The configuration of the NOLM is shown in the inset of Figure 1, which is constructed by a 70:30 OC3, a PC3 and a 10 km long SMF. PC3 was used for polarization biasing of the passing light in this loop to introduce a different phase difference. The 10 km SMF is utilized to provide the accumulation of nonlinear phase shift for the passing light. The transmission function of the NOLM can be written as
T = 1 − 2α(1 − α){1 + cos[θ + (1 − 2α)ϕ]}
where α is the coupling ratio of the OC3, θ is the additional phase difference induced by the PC3, ϕ = 2πn2PiL/λAeff is the nonlinear phase shift, n2 is the nonlinear refractive index coefficient of SMF, L is the length of loop, λ is the operating wavelength, Aeff is the effective fiber core area, and Pi is the input power for NOLM. Using Equation (1), the transmission characteristics of the NOLM with 75 km and 10 km long SMF were simulated for different θ (θ = 0.5π, 0.667π, π, 1.333π, 1.5π, i.e., different settings of PC3) as a function of input power, and the results are shown in Figure 2. The specific values used in the simulation are n2 = 3.2 × 10−20 m2/W, Aeff = 50 μm2, α = 0.3 and λ = 1550 nm. It can be seen in Figure 2, under specific PC3 setting, that the transmissivity of the NOLM can increase or decrease with increasing input power. When PC3 is set at a position where the transmissivity of the NOLM decreases as the input power, the NOLM can function as a power balancer, in which the higher power beam will experience greater loss than the lower power beam. According to the simulation results, the NOLM with 75 km-long delay fiber has a good power balance performance at this power level, and this performance will deteriorate if the delayed fiber is cut short. However, it is worth noting that the NOLM with long delay fiber is bound to cause large losses. So, to ensure efficient laser resonance, the delay fiber length of the NOLM in this case is set to 10 km and the corresponding simulation results of transmission characteristics are shown in Figure 2b. In addition, the coupling coefficient of the OC3 constituting the NOLM make an impact on the transmissivity of NOLM. As shown in Figure 3, the dependence of transmissivity on the input power of NOLMs with OCs of different coupling rates is analyzed. It can be seen from the figure that when the coupling coefficient of OC is 0.3 (i.e., coupling ratio of 70:30), the rate of change of the transmissivity of NOLM with the incident optical power is relatively large, regardless of the phase difference introduced by PC3. It is also observed from Figure 3 that the transmissivity of NOLM is completely insensitive to the incident optical power when the coupling rate of OC3 is set to 0.5. This is because the NOLM has to be established by using an OC with unequal split ratio so that the optical powers of the two light components propagating in the opposite directions within the loop are unequal, allowing the two lights to generate and accumulate a nonlinear phase shift difference in the delayed fiber, thus making the transmissivity of the NOLM dependent on the incident optical power.

3. Experimental Results and Analysis

3.1. Optical Spectrum

Firstly, the first-order Stokes light is resonated in the main cavity with the Brillouin gain and the effective randomly distributed feedback when the EDFA-amplified pump light was launched into the 390 m HNLF with above-threshold power. At the same time, a portion of the amplified Stokes light is guided into the sub-cavity by passing through OC2, where it is amplified by the EDFA and then sent into the main cavity as the pump light for the generation of Stokes lines of subsequent order. The Stokes light can resonate when the Brillouin gain in the main cavity overcomes the total roundtrip loss. As the output power of the EDFA increases, the number of Stokes lines generated in the main cavity gradually increases. Owing to the nature of cascaded SBS, the generated multi-order Stokes and anti-Stokes light is bound to have a power drop as the order increases, limited by the gain saturation of the EDFA. The cascaded SBS process will cease to generate higher-order Stokes light when the power of newly generated highest-order Stokes light does not reach the threshold for the SBS process to generate the next-order Stokes light.
In the experiment, the spectra of the random lasing emitted from output port 1 and output port 2 of the FCG are monitored by an optical spectrum analyzer (OSA) (YOKOGAWA, AQ6370D). With the pump laser output power of 8.65 mW and EDFA output power of 500 mW, the frequency comb with a fixed wavelength spacing of 0.076 nm were emitted at output port 1 and output port 2, and their optical spectra are shown in Figure 4. Figure 4a shows the spectrum of the forward-propagating frequency comb generated at the output port 2 within a wavelength range of 12 nm, and Figure 4b shows an enlarged view of this spectrum in a wavelength range of 2.2 nm. Up to 17 stable Stokes lines and 15 stable anti-Stokes lines with maximum OSNR of ~22 dB and ~17 dB and minimum OSNR of ~10 dB and ~7.5 dB were obtained within a 10 dB power deviation, respectively. Similarly, Figure 4c shows the spectrum of the backward-propagating frequency comb generated at the output port 1 within a wavelength range of 12 nm, and Figure 4d shows an enlarged view of this spectrum in a wavelength range of 2.2 nm. Comparing the spectra of the frequency comb generated at the two output ports, it can be seen that for both Stokes and anti-Stokes lines, the number of forward-propagating frequency comb lines measured at output port 2 is higher than that at output port 1 within a certain power deviation. Since the measurement of the spectrum is performed by the OSA scanning from short to long wavelength range over a period of time, the fluctuations within the spectrum reflect the wavelength instability of the light source to be measured. It is clear from the power fluctuations at the bottom of the scanned spectra that the stability of the forward-propagating frequency comb shows a higher level than that of the back-propagating frequency comb. The reason for this is that the forward-propagating Stokes light is justly amplified by the EDFA, propagates in the same direction as the amplified pump light and exhibits higher FWM efficiency, producing multiple idle lights with up-frequency-shift and down-frequency-shift and thus achieving a greater number of Stokes and anti-Stokes lines with higher stability. It is worth noting that the power difference (<5 dB) between first-order Stokes line and first-order anti-Stokes lines at output port 2 is significantly reduced compared to the power difference (~20 dB) at output port 1, which presents a better power flatness of the overall frequency comb. In addition, the minimum OSNRs of the forward-propagating and backward-propagating frequency comb within the power deviation are ~10 dB and ~28 dB, respectively, both of which exhibit relatively high capability of noise suppression, which is mainly due to the suppression effect of the random resonance in the main cavity on the spontaneous radiation generated by the EDFA. However, due to the fact that the forward-propagating Stokes and anti-Stokes light do not undergo random resonance processes to compress the generated noise after being amplified by the EDFA and before radiating at port 2, it thus exhibits a deterioration in OSNR.
To investigate the influence of the EDFA output power on the generated frequency combs, the pump laser output power was set to 8.65 mW and the EDFA output power was gradually adjusted from 150 mW to 850 mW, while the frequency combs generated at the output port 2 and output port 1 were monitored by an OSA within a wavelength range of 2.6 nm; the measurement results are shown in Figure 5a,b, respectively. When the EDFA output power is 150 mW, the spectrum of frequency combs generated at output port 2 exhibits 18 Stokes lines and 16 anti-Stokes lines, and the spectrum of frequency combs generated at output port 1 shows 17 Stokes lines and 13 anti-Stokes lines. It is worth noting that the power flatness and stability of the frequency combs generated at output port 2 are significantly higher than that generated at output port 1. With increasing EDFA output power, the number and the respective intensity of Stokes and anti-Stokes lines of the frequency combs emitted at both output ports gradually increase, and meanwhile the power flatness of the frequency combs gradually improves with the assistance of NOLM.
In the main cavity, both the FWM of Stokes light propagating in the forward and backward directions in the 390 m HNLF and the power balance provided by the NOLM are utilized to enhance the performance of the frequency combs based on Brillouin random fiber laser oscillation. Here, the performance enhancement effects of both mechanisms are further investigated. As shown in Figure 6a, the spectra of the frequency combs emitted at output port 2 and output port 1 with the EDFA output power of 850 mW and the pump laser output power of 8.65 mW are compared, and there is no NOLM addition at this time. It is obvious from the result that a larger number of Stokes and anti-Stokes lines in the forward-propagating frequency combs are effectively excited and their power flatness is significantly enhanced. This is because the backward-propagating Stokes light lacks the amplification provided by the EDFA, resulting in the more severe power decrease with the Stokes order due to the pump depletion effect. Consequently, the efficiency of FWM for higher orders of Brillouin Stokes and anti-Stokes light is significantly limited due to the low power of the high-order Stokes and anti-Stokes light, thus making it difficult for the anti-Stokes light to overcome the loss in the cavity and become resonant. In addition, in the backward direction which is opposite to the propagation direction of the pump light, only weak Rayleigh-scattered pump light joins the FWM process in that direction, which also limits the amplification for the backward-propagating anti-Stokes light through FWM. In contrast, the Stokes light in the forward-propagating frequency comb is amplified by the high-gain EDFA in the sub-cavity before it is launched into the HNLF. More importantly, the forward-propagating Stokes light propagates in the same direction with the high-power pump light, resulting in a much higher efficiency of the FWM than in the backward direction and facilitating the excitation and amplification of the forward-propagating anti-Stokes light. As shown in Figure 6b, after the NOLM was introduced into the main cavity, the flatness of the forward-propagating frequency combs was further improved by virtue of the unique input-power-dependent transmission characteristics of NOLM.

3.2. Linewidth

Linewidth is an important parameter to demonstrate the coherence of the laser beam. To characterize the linewidth of each Stokes and anti-Stokes random radiation of the proposed FCG, a delayed self-heterodyne (DSH) measurement device was built. First, each order of Stokes and anti-Stokes random radiation in the generated frequency combs is filtered by a tunable bandpass filter (Alnair, BVF-300CL-SM-FA) with a set bandwidth of 3.7 GHz. The selected Stokes/anti-Stokes light is then split into two parts by a 50:50 OC; one part is sent through an acousto-optic modulator (AOM) with an 80 MHz frequency downshift, and the other part is sent into a 100 km delayed line fiber. The two parts of the selected Stokes/anti-Stokes light with an 80 MHz frequency difference are then recombined at another 50:50 OC and form a beat light with a central frequency of 80 MHz. The generated beat light is detected by a photodetector (PD) (Thorlabs, PDB450) with a bandwidth of 350 MHz, the electrical spectrum of the beat light is analyzed by an electrical spectrum analyzer (ESA) and finally the spectral properties of selected Stokes/anti-Stokes light in the frequency domain is characterized.
The measured electrical spectrum of the beat signal of the Stokes lines from first-order to seventh-order is shown in Figure 7. Figure 7a shows an electrical spectrum comparison between the beat signal of the pump light and the Stokes light, from which it can be seen that the linewidth of the Stokes light is significantly narrowed compared to the pump light thanks to the SBS process. The 20 dB linewidths of the pump light and the first-order to seventh-order Stokes light were measured as 342.68, 8.687, 9.462, 8.823, 8.983, 13.475, 12.494 and 14.022 kHz, respectively. Correspondingly, the 3 dB linewidths of the pump light and Stokes lines were obtained by dividing the 20 dB linewidth by 2 × (99)1/2, which are 17.22, 0.4365, 0.4755, 0.4434, 0.4514, 0.6771, 0.628 and 0.7046 kHz, respectively. All the measured Stokes lines in the generated frequency combs exhibit sub-kHz linewidths, indicating that the coherence of Stokes light is substantially enhanced as it is being resonated in the half-open cavity.
In addition, the electrical spectra of the anti-Stokes lines from first-order to fourth-order in the generated frequency combs have also been experimentally investigated for the first time, and the measurement results are shown in Figure 8. The 20 dB linewidths of the first-order to fourth-order anti-Stokes light were measured as 54.948, 72.731, 124.943 and 171.911 kHz, respectively. Correspondingly, the 3 dB linewidths of the pump light and the first-order to fourth-order anti-Stokes lines were obtained by dividing the 20 dB linewidth by 2 × (99)1/2, which are 2.76, 3.65, 6.28 and 8.64 kHz, respectively. From the electrical spectrum comparison of the four orders of anti-Stokes and pump light as shown in Figure 8a, it is clear that the linewidth of the anti-Stokes line is much smaller than that of the pump light, mainly due to the linewidth-narrowing effect during the SBS process. As can be seen in Figure 8f, the linewidth of the first-order anti-Stokes line is wider than that of the first-order Stokes line, and this phenomenon is also present for Stokes and anti-Stokes lines of other orders, which is due to the stronger dependence of the generation of anti-Stokes light on the FWM process than that of Stokes light, making the coherence of anti-Stokes lines slightly worse than that of Stokes lines. However, although anti-Stokes lines exhibit slight linewidth broadening, the linewidth of kHz-level still proves that the anti-Stokes lines generated by the proposed FCG are highly coherent, which can provide the frequency combs required for a variety of application areas.

3.3. Relative Intensity Noise

The relative intensity noise (RIN) of the Stokes and anti-Stokes light of the generated frequency combs was measured, which was achieved by first recording the random laser emission and then calculating the power fluctuation normalized to the average power level. Similar to the linewidth measurement, the Stokes/anti-Stokes lines of the generated frequency combs were firstly selected using a filter with a 3.7 GHz bandwidth. In the experiments, the RINs of the Stokes light from first order to seventh order and anti-Stokes light from first order to fourth order were measured and compared with commercial semiconductor lasers. Firstly, the power of the light to be measured was adjusted to the same magnitude of 1 mW by a VOA and the output power of the commercial laser was also set to 1 mW in order to have a fair comparison. The time domain power traces of the light to be measured were then obtained by using a PD (Thorlabs, PDB435) with a bandwidth of 150 MHz and recorded by an oscilloscope (TELEDY LECROY, HDO6104). After data processing, the RIN of Stokes light for the first seven orders and anti-Stokes light for the first four orders as well as that of the semiconductor laser were obtained, as shown in Figure 9.
It can be seen from Figure 9 that the RIN of each selected Stokes line and the anti-Stokes line is higher than that of the commercial semiconductor laser, especially in the low-frequency region of <1 kHz due to the effects of transient temperature variation and mechanical vibrations in the environment to the resonant cavity. Furthermore, the RIN of both the Stokes and anti-Stokes lines increases with their order due to the intensity fluctuations of the pump light as well as low-order Stokes and anti-Stokes light that are undoubtedly transferred to the generated higher-order Stokes and anti-Stokes light during the cascaded SBS process, resulting in higher RIN of subsequent order Stokes and anti- Stokes lines. It is worth noting that, as shown in Figure 9b, the RIN deterioration of anti-Stokes light with increasing order is more severe than that of Stokes light, due to the fact that most of the anti-Stokes lines originate from unstable FWM with lower coupling efficiency, leading to the introduction of more noise.

3.4. Frequency Noise

The frequency noise of selected Stokes and anti-Stokes lines is also investigated and compared with the commercial semiconductor laser. The measurement setup is a 3 × 3 unbalanced Michelson fiber interferometer. In this measurement system, a 2 km SMF was inserted into one arm as the delay line, and two Faraday rotation mirrors (FRM) at one side are used to reflect the light and eliminate the additional optical path difference due to the birefringence in the fiber. The output interference signal is detected at another side by two PDs and read by an oscilloscope. The frequency noise was then demodulated by implementing the differential cross-multiplication algorithm on the data collected by the two PDs at a 10 kHz measuring bandwidth [37]. Finally, the measured frequency noise spectra are plotted as shown in Figure 10.
From Figure 10, it is clear that the frequency noise of both Stokes and anti-Stokes light is lower than that of commercial semiconductor lasers over the entire frequency range, which is mainly attributed to the suppression of the frequency noise in the half-open main cavity. Frequency noise suppression is mainly thanks to the suppression of the nominal 1/f noise from the thermal fluctuation that intrinsically exists in conventional cavity lasers because of the long cavity length and randomly distributed feedback from the Rayleigh scattering centers in the half-open main cavity. Furthermore, in agreement with the RIN measurement results, the frequency noise of both Stokes and anti-Stokes lines increases with the order number, which is caused by the transfer of noise from the pump light to the subsequently generated Stokes and anti-Stokes light during the cascade SBS process.

3.5. Temporal Characteristics

The temporal characteristics of Stokes lines in the generated frequency combs and its corresponding influence factors were experimentally investigated. Firstly, the pump power input to the EDFA was fixed at 3 mW and the EDFA output power was set at 350 mW. The temporal trace of the 1st-order Stokes lines selected by a filter with 3.7 GHz bandwidth was recorded by a PD and digitized by an oscilloscope. Then, the output power of the EDFA is gradually increased and the corresponding temporal trace of the 1st-order Stokes emission is shown in Figure 11. For fairness, the power of the first-order Stokes line to be measured generated with any EDFA output power is kept strictly at 1 mW by the VOA. From Figure 11, it can be seen that the first-order Stokes line exhibits a quasi-continuous laser emission when the EDFA output power is set at 350 mW. Subsequently, as the EDFA output power is increased, the temporal trace of the first-order Stokes line progressively exhibits more stochastic fluctuations and even sharp intensity fluctuation spikes, which are caused by the decrease in the proportion of the pump light at the input port of the EDFA as the proportion of Stokes and anti-Stokes light in the sub-cavity continues growing, absorbing most of the amplification provided by the EDFA and leading to a distinct reduction in the pump power amplification and a deteriorated SBS efficiency. When the output power of the EDFA reaches 450 mW, the first-order Stokes light exhibits severe stochastic intensity fluctuations, which indicates that the emission is only weakly resonated at this time.
In addition, in order to further demonstrate that the above-mentioned deterioration in the quality of the first-order Stokes light due to the decrease in the proportion of pump light in the EDFA input light, the relationship between the pump power and the state of the temporal trace of the first-order Stokes light has also been investigated and the results are shown in Figure 12. Firstly, the output power of the EDFA is set at 450 mW and the pump power is set at 3 mW, in which case the temporal trace of the first-order Stokes line exhibits severe stochastic intensity fluctuations as shown in Figure 12a. Subsequently, by gradually increasing the pump power from 3 mW to 5 mW, the time-domain intensity trace of the first-order Stokes line progressively stabilizes and the spikes of stochastic intensity fluctuation gradually decrease until they disappear, as shown in Figure 12a–e.
The above experiment shows that the generation of frequency combs in the dual-cavity Brillouin random oscillation device requires attention to the adjustment of the ratio of the power of the pump light to the power of the feedback light in the sub-cavity, in order to achieve more Stokes lines for the generated frequency combs and better stability and coherence of each order of Stokes light.
The noise of different-order Stokes and anti-Stokes lines of the generated frequency combs has been investigated above, revealing the noise transfer characteristics present in this Brillouin-scattering-based FCG. Therefore, in order to further investigate the dynamic properties of the Stokes and anti-Stokes lines of different orders, the temporal traces of different-order Stokes and anti-Stokes lines were studied in detail. Figure 13 and Figure 14 show the temporal traces of Stokes light of order one to seven and anti-Stokes light of order one to four filtered out by using a filter with 3.7 GHz bandwidth at the pump power of 8.65 mW and EDFA output power of 500 mW, respectively.
As can be seen in Figure 13, the temporal trace of the first-order Stokes line in the FCG is very stable, and there are hardly any intensity fluctuations in the time domain. However, the intensity fluctuations of the Stokes light appear and are gradually exacerbated as the order increases, which is consistent with the experimental results of the noise measurements. At the same time, the initial symmetric Gaussian distribution of the Stokes light temporal intensity trace becomes gradually asymmetric and eventually evolves to an approximate gamma distribution as the order increases. In fact, the main reason for the deterioration of the laser quality of higher-order Stokes light is none other than the transfer and accumulation of noise in the SBS process among different orders of Stokes and anti-Stokes lines and the extra noise introduction in the sub-cavity. In addition, with the introduction and accumulation of noise, the stability as well as the coherence of the higher-order Stokes light are reduced, making the Stokes light generated by the SBS process at this order more difficult to be resonated in the main cavity, which further deteriorates the coherence of the Stokes light at the next higher order. Thus, the time-domain intensity distribution of these Stokes lines has low stability, and coherence is similar to that of the Stokes light produced in the non-resonant SBS process. Moreover, a similar phenomenon is observed for the anti-Stokes lights of order one to four as illustrated in Figure 14, and the overdependence of the anti-Stokes lines on the parametric gain of the FWM leads to a faster stability deterioration of its temporal trace with order increase than that of the Stokes lines.
In summary, the data analysis shows that the laser quality of each order of Stokes and anti-Stokes light is different in the frequency combs generated by the proposed FCG based on SBS and FWM processes, and the laser quality will deteriorate with the order of SBS process, which is an issue worth being noted and resolved in future work.

4. Discussion

For laser-based frequency comb generators, the number, OSNR, power derivation of tooth and the stability and coherence of each tooth are critical. MW-BRFL with narrow bandwidth, inhomogeneity, high gain coefficient and efficient linewidth suppression characteristics of Brillouin gain and noise suppression capability of random distributed feedback provided by Rayleigh scattering can achieve narrow linewidth, low noise and relatively stable multi-wavelength laser output. In the recently published work, several typical MW-BRFLs have been implemented and characterized. In reference [59], the first MW-BRFL with a dual-cavity structure was proposed, where a 25 km SMF and a 5 km non-uniform fiber were used to provide Brillouin gain and random distributed feedback, respectively. Due to the low gain coefficient of the SMF and the limitation of the EDFA output power, multi-wavelength laser output with only six orders of Stokes lines was finally achieved. Subsequently, to enhance the stability of multi-wavelength laser output, a dual-cavity MW-BRFL based on a polarization-maintaining fiber was proposed to suppress noise and stabilize laser output by eliminating random changes in the polarization state of light in the resonant cavity [60,61]. In addition, another MW-BRFL based on random fiber grating is proposed. With the strong Rayleigh scattering effect in the centimeter-long random fiber grating, the number of generated Stokes lines in the laser output is raised to 14, while ensuring low noise and stability of the laser output [62]. However, the multi-wavelength laser output achieved by these efforts is bound to be bottlenecked by gain and pump power limitations, regardless of the method used to boost the number of Stokes lines. In this work, the introduction of the FWM effect in the fiber allows the anti-Stokes light, which has always been buried in the bottom noise, to be enabled and amplified, which undoubtedly increases the number of lasing lines in the laser output exponentially, without the need for excessive pump power. This allows this experiment to achieve a stable laser output with 17 orders of Stokes lines and 15 orders of anti-Stokes lines. Although the FWM effect in optical fibers is common, the present work provides an unprecedented and significant study on the properties of resonant anti-Stokes lines in MW-BRFL based on this effect.
It is worth noting that this experiment has proposed a novel MW-BRFL while there are still some points to be optimized. These include the enhancement of the Stokes line flatness, the laser output power, the number of Stokes/anti-Stokes lines, and the stability and linewidth of each order of Stokes/anti-Stokes lines. The improvement for line flatness can be achieved by optimizing the power-averaging capability of the NOLM by better balancing the relationship between its rate of transmissivity variation with incident optical power and the additional losses it introduces. The output power of the laser and the number of generated resonant lines can be achieved by the use of high-gain EDFA and higher-nonlinearity HNLF, in addition to optimizing the system structure and reducing intracavity losses. The optimization of the linewidth and stability of each order of Stokes/anti-Stokes lines needs to filter out the redundant random resonant modes within the Brillouin gain bandwidth by using a narrow-bandwidth optical fiber filter to compress the mode competition and multi-mode resonance.

5. Conclusions

In conclusion, a frequency comb generator was experimentally demonstrated based on the dual-cavity Brillouin random oscillator including a main cavity and a sub-cavity. The half-open main cavity incorporates a section of HNLF with a high nonlinearity coefficient (≥10 W−1∙km−1 @1550 nm) as Brillouin gain fiber, Rayleigh scattering fiber to provide random distributed feedback and the NOLM as a power balancer to obtain the Brillouin random resonance. The sub-cavity includes an EDFA to boost and couple back the low-order Stokes light for the cascade SBS process. Furthermore, the FWM effect in the HNLF is effectively excited under phase-matching conditions, which not only increases the number of frequency combs but also boosts the power of the multi-order Stokes and anti-Stokes light. The NOLM with its unique transmission spectrum is used to balance the power between the different orders of Stokes and anti-Stokes light to achieve a smaller power difference. Eventually, 17 orders of stable Stokes lines and 15 orders of stable anti-Stokes lines within a 10 dB power deviation were obtained with the minimum OSNR of ~10 dB and ~7.5 dB, respectively. In addition, the characteristics of FCG have been experimentally investigated. Both Stokes and anti-Stokes light exhibit the linewidths on the order of kHz or even sub-kHz and an inter-peak spacing of 0.076 nm. As the order of Stokes and anti-Stokes light increases, both RIN and frequency noise gradually accumulate, showing a tendency to become progressively more severe. Importantly, the properties of the anti-Stokes line in the generated frequency comb were studied for the first time. Experiments have demonstrated that the regulation of the power ratio of the pump light to the sub-cavity feedback light during the generation of the frequency combs deserves attention. Such an FCG with fixed frequency spacing will find promising applications in fields of optical communications, microwaves, optical sensing, etc.

Author Contributions

Conceptualization, Y.P. and Y.X.; methodology, Y.P. and Y.X.; software, Y.P.; validation, Y.P.; formal analysis, Y.P.; investigation, Y.P., S.M., Q.J. and Y.X.; resources, Y.X.; data curation, Y.P., S.M. and Q.J.; writing—original draft preparation, Y.P.; writing—review and editing, Y.P. and Y.X.; visualization, Y.P.; supervision, Y.X., X.Z., Y.L., Z.Q. and Z.L.; project administration, Y.X.; funding acquisition, Y.X. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by National Natural Science Foundation of China (62105180), Natural Science Foundation of Shandong Province (ZR2020MF110, ZR2020MF118), Taishan Scholar Foundation of Shandong Province (tsqn202211027) and Qilu Young Scholar Program of Shandong University.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Veselka, J.J.; Korotky, S.K. A Multiwavelength Source Having Precise Channel Spacing for WDM Systems. IEEE Photonics Technol. Lett. 1998, 10, 958–960. [Google Scholar] [CrossRef]
  2. Peng, P.-C.; Tseng, H.-Y.; Chi, S. Long-Distance FBG Sensor System Using a Linear-Cavity Fiber Raman Laser Scheme. IEEE Photonics Technol. Lett. 2004, 16, 575–577. [Google Scholar] [CrossRef]
  3. Yao, J. Microwave Photonics. J. Light. Technol. 2009, 27, 314–335. [Google Scholar] [CrossRef]
  4. Shahi, S.; Harun, S.W.; Ahmad, H. Multi-Wavelength Brillouin Fiber Laser Using Brillouin-Rayleigh Scatterings in Distributed Raman Amplifier. Laser Phys. Lett. 2009, 6, 737. [Google Scholar] [CrossRef]
  5. Wang, F.; Gong, Y. Tunable and Switchable Multi-Wavelength Erbium-Brillouin Random Fiber Laser Incorporating a Highly Nonlinear Fiber. J. Light. Technol. 2020, 38, 4093–4099. [Google Scholar] [CrossRef]
  6. Bellemare, A.; Karasek, M.; Rochette, M.; LRochelle, S.; Tetu, M. Room Temperature Multifrequency Erbium-Doped Fiber Lasers Anchored on the ITU Frequency Grid. J. Light. Technol. 2000, 18, 825–831. [Google Scholar] [CrossRef]
  7. Kim, S.K.; Chu, M.J.; Lee, J.H. Wideband Multiwavelength Erbium-Doped Fiber Ring Laser with Frequency Shifted Feedback. Opt. Commun. 2001, 190, 291–302. [Google Scholar] [CrossRef]
  8. Zhou, K.; Zhou, D.; Dong, F.; Ngo, N.Q. Room-Temperature Multiwavelength Erbium-Doped Fiber Ring Laser Employing Sinusoidal Phase-Modulation Feedback. Opt. Lett. 2003, 28, 893–895. [Google Scholar] [CrossRef] [PubMed]
  9. Vasseur, J.; Hanna, M.; Dudley, J.M.; Barry, J.R. Numerical and Theoretical Analysis of an Alternate Multiwavelength Mode-Locked Fiber Laser. IEEE Photonics Technol. Lett. 2005, 17, 2295–2297. [Google Scholar] [CrossRef] [Green Version]
  10. He, W.; Zhu, L.; Dong, M.; Lou, X.; Luo, F. Wavelength-Switchable and Stable-Ring-Cavity, Erbium-Doped Fiber Laser Based on Mach–Zehnder Interferometer and Tunable Filter. Laser Phys. 2018, 28, 045104. [Google Scholar] [CrossRef]
  11. Luo, A.-P.; Luo, Z.-C.; Xu, W.-C. Tunable and Switchable Multiwavelength Erbium-Doped Fiber Ring Laser Based on a Modified Dual-Pass Mach-Zehnder Interferometer. Opt. Lett. 2009, 34, 2135–2137. [Google Scholar] [CrossRef] [Green Version]
  12. Ma, L.; Kang, Z.; Qi, Y.; Jian, S. Tunable Dual-Wavelength Fiber Laser Based on an MMI Filter in a Cascaded Sagnac Loop Interferometer. Laser Phys. 2014, 24, 045102. [Google Scholar] [CrossRef]
  13. Xu, Z.W.; Zhang, Z.X. All-Normal-Dispersion Multi-Wavelength Dissipative Soliton Yb-Doped Fiber Laser. Laser Phys. Lett. 2013, 10, 085105. [Google Scholar] [CrossRef]
  14. Jin, X.; Lou, Z.; Zhang, H.; Xu, J.; Zhou, P.; Liu, Z. Random Distributed Feedback Fiber Laser at 2.1 μm. Opt. Lett. 2016, 41, 4923–4926. [Google Scholar] [CrossRef]
  15. Wang, L.; Dong, X.; Shum, P.P.; Su, H. Tunable Erbium-Doped Fiber Laser Based on Random Distributed Feedback. IEEE Photonics J. 2014, 6, 1–5. [Google Scholar] [CrossRef]
  16. Ma, R.; Quan, X.; Wu, H.; Gao, W.; Huang, D.; Wang, X.; Xu, S.; Fan, D.; Liu, J. 20 Watt-Level Single Transverse Mode Narrow Linewidth and Tunable Random Fiber Laser at 1.5 Μm Band. Opt. Express 2022, 30, 28795–28804. [Google Scholar] [CrossRef] [PubMed]
  17. Xu, Y.; Zhang, L.; Lu, P.; Mihailov, S.; Chen, L.; Bao, X. Time-Delay Signature Concealed Broadband Gain-Coupled Chaotic Laser with Fiber Random Grating Induced Distributed Feedback. Opt. Laser Technol. 2019, 109, 654–658. [Google Scholar] [CrossRef] [Green Version]
  18. Pang, M.; Bao, X.; Chen, L. Observation of Narrow Linewidth Spikes in the Coherent Brillouin Random Fiber Laser. Opt. Lett. 2013, 38, 1866–1868. [Google Scholar] [CrossRef]
  19. Zhang, L.; Xu, Y.; Gao, S.; Saxena, B.; Chen, L.; Bao, X. Linearly Polarized Low-Noise Brillouin Random Fiber Laser. Opt. Lett. 2017, 42, 739–742. [Google Scholar] [CrossRef]
  20. Wu, H.; Han, B.; Liu, Y. Tunable Narrowband Cascaded Random Raman Fiber Laser. Opt. Express 2021, 29, 21539–21550. [Google Scholar] [CrossRef]
  21. Xu, Y.; Lu, P.; Bao, X. Compact Single-End Pumped Brillouin Random Fiber Laser with Enhanced Distributed Feedback. Opt. Lett. 2020, 45, 4236–4239. [Google Scholar] [CrossRef]
  22. Xu, Y.; Zhang, L.; Chen, L.; Bao, X. Single-Mode SOA-Based 1kHz-Linewidth Dual-Wavelength Random Fiber Laser. Opt. Express 2017, 25, 15828–15837. [Google Scholar] [CrossRef] [PubMed]
  23. Tovar, P.; Temporão, G.; Weid, J.P. von der Longitudinal Mode Dynamics in SOA-Based Random Feedback Fiber Lasers. Opt. Express 2019, 27, 31001–31012. [Google Scholar] [CrossRef] [PubMed]
  24. Shawki, H.; Kotb, H.; Khalil, D. Modeling and Characterization of a Dual-Wavelength SOA-Based Single Longitudinal Mode Random Fiber Laser with Tunable Separation. OSA Contin. 2019, 2, 358–369. [Google Scholar] [CrossRef]
  25. Fan, M.; Wang, Z.; Wu, H.; Sun, W.; Zhang, L. Low-Threshold, High-Efficiency Random Fiber Laser with Linear Output. IEEE Photonics Technol. Lett. 2015, 27, 319–322. [Google Scholar] [CrossRef]
  26. Deng, J.; Han, M.; Xu, Z.; Du, Y.; Shu, X. Stable and Low-Threshold Random Fiber Laser via Anderson Localization. Opt. Express 2019, 27, 12987–12997. [Google Scholar] [CrossRef]
  27. Wu, H.; Wang, Z.; Sun, W.; He, Q.; Wei, Z.; Rao, Y.-J. 1.5 μm Low Threshold, High Efficiency Random Fiber Laser with Hybrid Erbium–Raman Gain. J. Light. Technol. 2018, 36, 844–849. [Google Scholar] [CrossRef]
  28. Wang, Z.; Wu, H.; Fan, M.; Zhang, L.; Rao, Y.; Zhang, W.; Jia, X. High Power Random Fiber Laser with Short Cavity Length: Theoretical and Experimental Investigations. IEEE J. Sel. Top. Quantum Electron. 2015, 21, 10–15. [Google Scholar] [CrossRef]
  29. Zhang, H.; Huang, L.; Song, J.; Wu, H.; Zhou, P.; Wang, X.; Wu, J.; Xu, J.; Wang, Z.; Xu, X.; et al. Quasi-Kilowatt Random Fiber Laser. Opt. Lett. 2019, 44, 2613–2616. [Google Scholar] [CrossRef]
  30. Ma, R.; Li, J.Q.; Guo, J.Y.; Wu, H.; Zhang, H.H.; Hu, B.; Rao, Y.J.; Zhang, W.L. High-Power Low Spatial Coherence Random Fiber Laser. Opt. Express 2019, 27, 8738–8744. [Google Scholar] [CrossRef] [Green Version]
  31. Babin, S.A.; El-Taher, A.E.; Harper, P.; Podivilov, E.V.; Turitsyn, S.K. Tunable Random Fiber Laser. Phys. Rev. A 2011, 84, 021805. [Google Scholar] [CrossRef] [Green Version]
  32. Zhang, Y.; Song, J.; Ye, J.; Xu, J.; Yao, T.; Zhou, P. Tunable Random Raman Fiber Laser at 1.7 μm Region with High Spectral Purity. Opt. Express 2019, 27, 28800–28807. [Google Scholar] [CrossRef] [PubMed]
  33. Du, X.; Zhang, H.; Wang, X.; Zhou, P. Tunable Random Distributed Feedback Fiber Laser Operating at 1 μm. Appl. Opt. 2015, 54, 908–911. [Google Scholar] [CrossRef] [PubMed]
  34. Ye, J.; Xu, J.; Zhang, H.; Zhou, P. Powerful Narrow Linewidth Random Fiber Laser. Photonic Sens. 2017, 7, 82–87. [Google Scholar] [CrossRef] [Green Version]
  35. Pang, Y.; Ma, S.; Zhao, X.; Qin, Z.; Liu, Z.; Xu, Y. Single-Longitudinal-Mode Short-Cavity Brillouin Random Fiber Laser via Frequency Auto-Tracking with Unpumped-EDF Sagnac Loop. Infrared Phys. Technol. 2022, 127, 104461. [Google Scholar] [CrossRef]
  36. Xu, Y.; Gao, S.; Lu, P.; Mihailov, S.; Chen, L.; Bao, X. Low-Noise Brillouin Random Fiber Laser with a Random Grating-Based Resonator. Opt. Lett. 2016, 41, 3197–3200. [Google Scholar] [CrossRef] [PubMed]
  37. Pang, Y.; Xu, Y.; Zhao, X.; Qin, Z.; Liu, Z. Low-Noise Brillouin Random Fiber Laser with Auto-Tracking Dynamic Fiber Grating Based on a Saturable Absorption Ring. Infrared Phys. Technol. 2022, 122, 104088. [Google Scholar] [CrossRef]
  38. Pang, Y.; Xu, Y.; Zhao, X.; Qin, Z.; Liu, Z. Low-Noise Narrow-Linewidth Brillouin Random Fiber Laser with Dynamic Fiber Grating. In Proceedings of the Conference on Lasers and Electro-Optics (2022), Paper JW3B.34, San Jose, CA, USA, 15 May 2022; Optica Publishing Group: Washington, DC, USA, 2022; p. JW3B.34. [Google Scholar]
  39. Du, X.; Zhang, H.; Xiao, H.; Zhou, P.; Liu, Z. Temporally Stable Random Fiber Laser Operates at 1070 Nm. IEEE Photonics J. 2015, 7, 1–7. [Google Scholar] [CrossRef]
  40. Pang, Y.; Xu, Y.; Zhao, X.; Qin, Z.; Liu, Z. Stabilized Narrow-Linewidth Brillouin Random Fiber Laser with a Double-Coupler Fiber Ring Resonator. J. Light. Technol. 2022, 40, 2988–2995. [Google Scholar] [CrossRef]
  41. Xu, Y.; Xiang, D.; Ou, Z.; Lu, P.; Bao, X. Random Fabry–Perot Resonator-Based Sub-KHz Brillouin Fiber Laser to Improve Spectral Resolution in Linewidth Measurement. Opt. Lett. 2015, 40, 1920. [Google Scholar] [CrossRef]
  42. Gao, S.; Zhang, L.; Xu, Y.; Lu, P.; Chen, L.; Bao, X. Tapered Fiber Based Brillouin Random Fiber Laser and Its Application for Linewidth Measurement. Opt. Express 2016, 24, 28353. [Google Scholar] [CrossRef] [PubMed]
  43. Feng, X.; Lu, C.; Tam, H.Y.; Wai, P.K.A. Reconfigurable Microwave Photonic Filter Using Multiwavelength Erbium-Doped Fiber Laser. IEEE Photon. Technol. Lett. 2007, 19, 1334–1336. [Google Scholar] [CrossRef]
  44. Shen, Y.; Wang, R.; Pu, T. A Novel Technique to Generate High-Frequency Microwave Signal Based on High-Order Stimulated Brillouin Scattering. Acta Opt. Sin. 2010, 30, 1571–1575. [Google Scholar] [CrossRef]
  45. Oehler, A.E.H.; Zeller, S.C.; Weingarten, K.J.; Keller, U. Broad Multiwavelength Source with 50 GHz Channel Spacing for Wavelength Division Multiplexing Applications in the Telecom C Band. Opt. Lett. 2008, 33, 2158. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  46. Oh, S.H.; Shin, J.-U.; Park, Y.-J.; Kim, S.-B.; Park, S.; Sung, H.-K.; Baek, Y.-S.; Oh, K.-R. Multiwavelength Lasers for WDM-PON Optical Line Terminal Source by Silica Planar Lightwave Circuit Hybrid Integration. IEEE Photon. Technol. Lett. 2007, 19, 1622–1624. [Google Scholar] [CrossRef]
  47. Xu, Y.; Lu, P.; Mihailov, S.; Bao, X. Real-Time Physical Random Bit Generation at Gbps Based on Random Fiber Lasers. Opt. Lett. 2017, 42, 4796–4799. [Google Scholar] [CrossRef]
  48. Zhu, T.; Ke, T.; Rao, Y.; Chiang, K.S. Fabry–Perot Optical Fiber Tip Sensor for High Temperature Measurement. Opt. Commun. 2010, 283, 3683–3685. [Google Scholar] [CrossRef]
  49. Han, Y.-G.; Tran, T.V.A.; Kim, S.-H.; Lee, S.B. Multiwavelength Raman-Fiber-Laser-Based Long-Distance Remote Sensor for Simultaneous Measurement of Strain and Temperature. Opt. Lett. 2005, 30, 1282. [Google Scholar] [CrossRef]
  50. Xu, Y.; Zhang, M.; Lu, P.; Mihailov, S.; Bao, X. Multi-Parameter Sensor Based on Random Fiber Lasers. AIP Adv. 2016, 6, 095009. [Google Scholar] [CrossRef] [Green Version]
  51. Xu, Y.; Zhang, M.; Lu, P.; Mihailov, S.; Bao, X. Multi-Parameter Fiber-Optic Sensors Based on Fiber Random Grating. In Proceedings of the 2017 25th Optical Fiber Sensors Conference (OFS), Jeju, Republic of Korea, 24–28 April 2017; pp. 1–4. [Google Scholar]
  52. Xu, Y.; Zhang, L.; Gao, S.; Lu, P.; Mihailov, S.; Bao, X. Highly Sensitive Fiber Random-Grating-Based Random Laser Sensor for Ultrasound Detection. Opt. Lett. 2017, 42, 1353–1356. [Google Scholar] [CrossRef] [PubMed]
  53. Xu, Y.; Lu, P.; Gao, S.; Xiang, D.; Lu, P.; Mihailov, S.; Bao, X. Optical Fiber Random Grating-Based Multiparameter Sensor. Opt. Lett. 2015, 40, 5514–5517. [Google Scholar] [CrossRef]
  54. Wu, H.; Han, B.; Wang, Z.; Genty, G.; Feng, G.; Liang, H. Temporal Ghost Imaging with Random Fiber Lasers. Opt. Express 2020, 28, 9957–9964. [Google Scholar] [CrossRef] [PubMed]
  55. Liu, Y.W.; Wang, Z.; Wang, S.S.; Ma, R.; Zhang, Y.; Zhang, W.L. Novel Illumination for Imaging Using Self-Modulated Coherent Random Fiber Laser. In Proceedings of the Conference on Lasers and Electro-Optics (2022), Paper JW3B.192, San Jose, CA, USA, 15 May 2022; Optica Publishing Group: Washington, DC, USA, 2022; p. JW3B.192. [Google Scholar]
  56. Gao, S.; Zhang, L.; Xu, Y.; Chen, L.; Bao, X. High-Speed Random Bit Generation via Brillouin Random Fiber Laser with Non-Uniform Fibers. IEEE Photon. Technol. Lett. 2017, 29, 1352–1355. [Google Scholar] [CrossRef]
  57. Xiang, D.; Lu, P.; Xu, Y.; Gao, S.; Chen, L.; Bao, X. Truly Random Bit Generation Based on a Novel Random Brillouin Fiber Laser. Opt. Lett. 2015, 40, 5415. [Google Scholar] [CrossRef]
  58. Harun, S.W.; Shirazi, M.R.; Ahmad, H. A New Configuration of Multi-Wavelength Brillouin Fiber Laser. Laser Phys. Lett. 2008, 5, 48–50. [Google Scholar] [CrossRef]
  59. Zhang, L.; Xu, Y.; Gao, S.; Saxena, B.; Chen, L.; Bao, X. Multiwavelength Coherent Brillouin Random Fiber Laser with Ultrahigh Optical Signal-to-Noise Ratio. IEEE J. Sel. Top. Quantum Electron. 2018, 24, 1–8. [Google Scholar] [CrossRef]
  60. Zhang, L.; Wang, Y.; Xu, Y.; Chen, L.; Bao, X. Linearly Polarized Multi-Wavelength Comb via Rayleigh Scattering Induced Brillouin Random Lasing Resonance. In Proceedings of the 2018 Optical Fiber Communications Conference and Exposition (OFC), San Diego, CA, USA, 11–15 March 2018; pp. 1–3. [Google Scholar]
  61. Zhang, L.; Wang, Y.; Xu, Y.; Zhou, D.; Chen, L.; Bao, X. Linearly Polarized Multi-Wavelength Fiber Laser Comb via Brillouin Random Lasing Oscillation. IEEE Photonics Technol. Lett. 2018, 30, 1005–1008. [Google Scholar] [CrossRef]
  62. Zhang, L.; Xu, Y.; Lu, P.; Mihailov, S.; Chen, L.; Bao, X. Multi-Wavelength Brillouin Random Fiber Laser via Distributed Feedback From a Random Fiber Grating. J. Light. Technol. 2018, 36, 2122–2128. [Google Scholar] [CrossRef]
  63. Wang, F.; Gong, Y. Switchable Wide-Band Multi-Wavelength Brillouin-Erbium Fiber Laser Based on Random Distributed Feedback. IEEE Access 2020, 8, 218614–218620. [Google Scholar] [CrossRef]
Photonics 10 00296 g001 550
Figure 1. Experimental setup of the proposed FCG. (ISO: isolator, OC: optical coupler (OC1 and OC2: 2 × 2 50:50, OC3: 2 × 2 70:30), EDFA: erbium-doped fiber amplifier, VOA: variable optical attenuator, PC: polarization controller, CIR: circulator, HNLF: highly nonlinear fiber, SMF: single-mode fiber, NOLM: nonlinear optical loop mirror).
Figure 1. Experimental setup of the proposed FCG. (ISO: isolator, OC: optical coupler (OC1 and OC2: 2 × 2 50:50, OC3: 2 × 2 70:30), EDFA: erbium-doped fiber amplifier, VOA: variable optical attenuator, PC: polarization controller, CIR: circulator, HNLF: highly nonlinear fiber, SMF: single-mode fiber, NOLM: nonlinear optical loop mirror).
Photonics 10 00296 g001
Photonics 10 00296 g002 550
Figure 2. Simulation of the transmission characteristic of NOLM as a function of input power for different θ with (a) 75 km long and (b) 10 km long delay fiber, respectively.
Figure 2. Simulation of the transmission characteristic of NOLM as a function of input power for different θ with (a) 75 km long and (b) 10 km long delay fiber, respectively.
Photonics 10 00296 g002
Photonics 10 00296 g003 550
Figure 3. Simulation of the transmission characteristic of NOLM with different coupling ratios of OC3 as a function of input power for different θ of (a) 0.5π, (b) 0.667π, (c) π, (d) 1.333π and (e) 1.5π with 10 km long delay fiber.
Figure 3. Simulation of the transmission characteristic of NOLM with different coupling ratios of OC3 as a function of input power for different θ of (a) 0.5π, (b) 0.667π, (c) π, (d) 1.333π and (e) 1.5π with 10 km long delay fiber.
Photonics 10 00296 g003
Photonics 10 00296 g004a 550Photonics 10 00296 g004b 550
Figure 4. Optical spectrum of (a) forward-propagating frequency comb in 12 nm wavelength span, (b) forward-propagating frequency comb in 2.2 nm wavelength span, (c) backward-propagating frequency comb in 12 nm wavelength span and (d) backward-propagating frequency comb in 2.2 nm wavelength span.
Figure 4. Optical spectrum of (a) forward-propagating frequency comb in 12 nm wavelength span, (b) forward-propagating frequency comb in 2.2 nm wavelength span, (c) backward-propagating frequency comb in 12 nm wavelength span and (d) backward-propagating frequency comb in 2.2 nm wavelength span.
Photonics 10 00296 g004aPhotonics 10 00296 g004b
Photonics 10 00296 g005 550
Figure 5. Optical spectrum evolution of (a) forward-propagating and (b) backward-propagating frequency combs in 2.6 nm wavelength span with the increase of EDFA output power from 150 mW to 850 mW.
Figure 5. Optical spectrum evolution of (a) forward-propagating and (b) backward-propagating frequency combs in 2.6 nm wavelength span with the increase of EDFA output power from 150 mW to 850 mW.
Photonics 10 00296 g005
Photonics 10 00296 g006 550
Figure 6. Optical spectrum comparison between (a) forward-propagating and backward-propagating frequency combs with EDFA output power of 900 mW; (b) forward-propagating frequency combs with or without NOLM.
Figure 6. Optical spectrum comparison between (a) forward-propagating and backward-propagating frequency combs with EDFA output power of 900 mW; (b) forward-propagating frequency combs with or without NOLM.
Photonics 10 00296 g006
Photonics 10 00296 g007a 550Photonics 10 00296 g007b 550
Figure 7. (a) DSH beating RF spectra of the pump laser and the 1st~7th order Stokes lines of the proposed FCG for comparison; (b–h) DSH beating RF spectra of the 1st~7th order Stokes lines of the proposed FCG, respectively.
Figure 7. (a) DSH beating RF spectra of the pump laser and the 1st~7th order Stokes lines of the proposed FCG for comparison; (b–h) DSH beating RF spectra of the 1st~7th order Stokes lines of the proposed FCG, respectively.
Photonics 10 00296 g007aPhotonics 10 00296 g007b
Photonics 10 00296 g008 550
Figure 8. DSH beating RF spectra of (a) the pump laser and the 1st~4th order anti-Stokes lines of the proposed FCG for comparation; (b–e) DSH beating RF spectra of the 1st~4th order anti-Stokes lines of the proposed FCG; (f) comparison of the 1st-order-Stokes line and the 1st-order-anti-Stokes line.
Figure 8. DSH beating RF spectra of (a) the pump laser and the 1st~4th order anti-Stokes lines of the proposed FCG for comparation; (b–e) DSH beating RF spectra of the 1st~4th order anti-Stokes lines of the proposed FCG; (f) comparison of the 1st-order-Stokes line and the 1st-order-anti-Stokes line.
Photonics 10 00296 g008
Photonics 10 00296 g009 550
Figure 9. Relative intensity noise of (a) the Stokes random emissions of the first seven orders and the pump laser and (b) the anti-Stokes random emissions of the first four orders and the pump laser.
Figure 9. Relative intensity noise of (a) the Stokes random emissions of the first seven orders and the pump laser and (b) the anti-Stokes random emissions of the first four orders and the pump laser.
Photonics 10 00296 g009
Photonics 10 00296 g010 550
Figure 10. Frequency noise of (a) Stokes light of the first five orders and the pump laser and (b) the anti-Stokes light of the first three orders and the pump laser.
Figure 10. Frequency noise of (a) Stokes light of the first five orders and the pump laser and (b) the anti-Stokes light of the first three orders and the pump laser.
Photonics 10 00296 g010
Photonics 10 00296 g011 550
Figure 11. Temporal traces of 1st-order Stokes light in generated frequency combs at the EDFA output power of (a) 350 mW, (b) 375 mW, (c) 400 mW, (d) 425 mW and (e) 450 mW, and at the pump power of 3 mW.
Figure 11. Temporal traces of 1st-order Stokes light in generated frequency combs at the EDFA output power of (a) 350 mW, (b) 375 mW, (c) 400 mW, (d) 425 mW and (e) 450 mW, and at the pump power of 3 mW.
Photonics 10 00296 g011
Photonics 10 00296 g012 550
Figure 12. Temporal trace of first-order Stokes light in generated FCG at the pump power of (a) 3 mW, (b) 3.5 mW, (c) 4 mW, (d) 4.5 mW and (e) 5 mW, and at the EDFA output power of 450 mW.
Figure 12. Temporal trace of first-order Stokes light in generated FCG at the pump power of (a) 3 mW, (b) 3.5 mW, (c) 4 mW, (d) 4.5 mW and (e) 5 mW, and at the EDFA output power of 450 mW.
Photonics 10 00296 g012
Photonics 10 00296 g013 550
Figure 13. (a-1–g-1) Temporal trace and (a-2–g-2) intensity distribution of 1st-order~7th-order Stokes light in generated FCG.
Figure 13. (a-1–g-1) Temporal trace and (a-2–g-2) intensity distribution of 1st-order~7th-order Stokes light in generated FCG.
Photonics 10 00296 g013
Photonics 10 00296 g014 550
Figure 14. (a-1–d-1) Temporal trace and (a-2–d-2) intensity distribution of 1st-order~4th-order anti-Stokes lines in the proposed FCG.
Figure 14. (a-1–d-1) Temporal trace and (a-2–d-2) intensity distribution of 1st-order~4th-order anti-Stokes lines in the proposed FCG.
Photonics 10 00296 g014
Table
Table 1. Experimental parameters for the calculation of κ.
Table 1. Experimental parameters for the calculation of κ.
Parameter NameValue
Dispersion (D) @1550 nm0.5753183 ps/nm‧km
Pump wavelength (λp)1550 nm
Signal wavelength (λs) @15th-Stokes1551.14 nm
Zero-dispersion wavelength (λ0)1521.78962 nm
Nonlinear coefficient (γ)10 W−1‧km−1
Pump power (P)50 mW
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Pang, Y.; Ma, S.; Ji, Q.; Zhao, X.; Li, Y.; Qin, Z.; Liu, Z.; Xu, Y. Frequency Comb Generation Based on Brillouin Random Lasing Oscillation and Four-Wave Mixing Assisted with Nonlinear Optical Loop Mirror. Photonics 2023, 10, 296. https://doi.org/10.3390/photonics10030296

AMA Style

Pang Y, Ma S, Ji Q, Zhao X, Li Y, Qin Z, Liu Z, Xu Y. Frequency Comb Generation Based on Brillouin Random Lasing Oscillation and Four-Wave Mixing Assisted with Nonlinear Optical Loop Mirror. Photonics. 2023; 10(3):296. https://doi.org/10.3390/photonics10030296

Chicago/Turabian Style

Pang, Yuxi, Shaonian Ma, Qiang Ji, Xian Zhao, Yongfu Li, Zengguang Qin, Zhaojun Liu, and Yanping Xu. 2023. "Frequency Comb Generation Based on Brillouin Random Lasing Oscillation and Four-Wave Mixing Assisted with Nonlinear Optical Loop Mirror" Photonics 10, no. 3: 296. https://doi.org/10.3390/photonics10030296

APA Style

Pang, Y., Ma, S., Ji, Q., Zhao, X., Li, Y., Qin, Z., Liu, Z., & Xu, Y. (2023). Frequency Comb Generation Based on Brillouin Random Lasing Oscillation and Four-Wave Mixing Assisted with Nonlinear Optical Loop Mirror. Photonics, 10(3), 296. https://doi.org/10.3390/photonics10030296

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop