Non-Collinear Attosecond Streaking without the Time Delay Scan
Abstract
:1. Introduction
2. Scheme and Methods
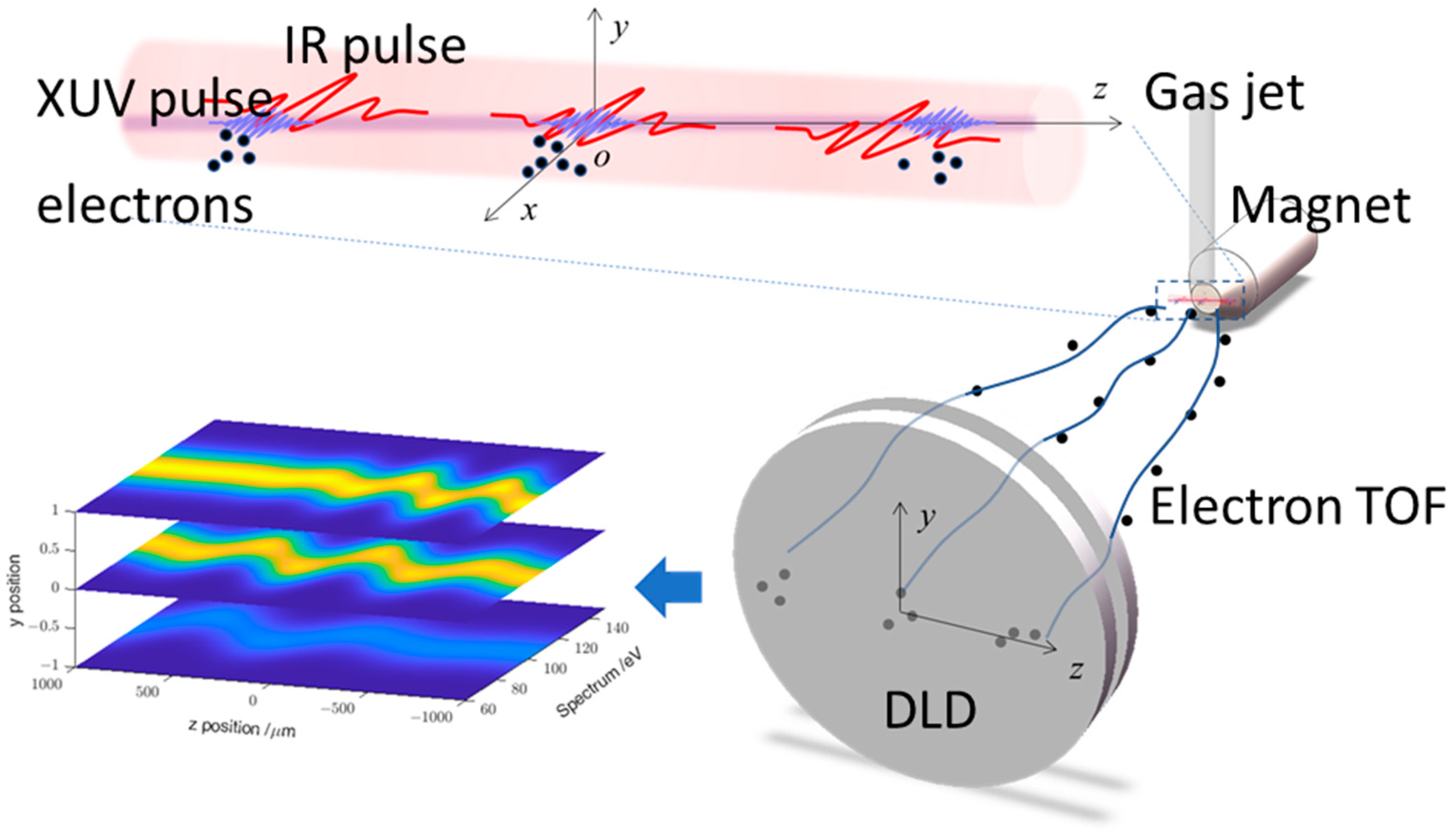
2.1. General Scheme
2.2. Mapping Time-Delay to Space
2.3. Time-Delay Resolution
2.4. XUV Pulse Retrieval
3. Results
3.1. Temporal Domain Characterization
3.2. Spatial Domain Characterization
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Paul, P.M.; Toma, E.S.; Breger, P.; Mullot, G.; Augé, F.; Balcou, P.; Muller, H.G.; Agostini, P. Observation of a Train of Attosecond Pulses from High Harmonic Generation. Science 2001, 292, 1689. [Google Scholar] [CrossRef] [PubMed]
- Hentschel, M.; Kienberger, R.; Spielmann, C.; Reider, G.A.; Milosevic, N.; Brabec, T.; Corkum, P.; Heinzmann, U.; Drescher, M.; Krausz, F. Attosecond metrology. Nature 2001, 414, 509–513. [Google Scholar] [CrossRef] [PubMed]
- Kienberger, R.; Goulielmakis, E.; Uiberacker, M.; Baltuska, A.; Yakovlev, V.; Bammer, F.; Scrinzi, A.; Westerwalbesloh, T.; Kleineberg, U.; Heinzmann, U.; et al. Atomic transient recorder. Nature 2004, 427, 817–821. [Google Scholar] [CrossRef] [PubMed]
- Drescher, M.; Hentschel, M.; Kienberger, R.; Uiberacker, M.; Yakovlev, V.; Scrinzi, A.; Westerwalbesloh, T.; Kleineberg, U.; Heinzmann, U.; Krausz, F. Time-resolved atomic inner-shell spectroscopy. Nature 2002, 419, 803–807. [Google Scholar] [CrossRef]
- Cavalieri, A.L.; Muller, N.; Uphues, T.; Yakovlev, V.S.; Baltuska, A.; Horvath, B.; Schmidt, B.; Blumel, L.; Holzwarth, R.; Hendel, S.; et al. Attosecond spectroscopy in condensed matter. Nature 2007, 449, 1029–1032. [Google Scholar] [CrossRef]
- Krausz, F.; Stockman, M.I. Attosecond metrology: From electron capture to future signal processing. Nat. Photonics 2014, 8, 205–213. [Google Scholar] [CrossRef]
- Schlaepfer, F.; Lucchini, M.; Sato, S.A.; Volkov, M.; Kasmi, L.; Hartmann, N.; Rubio, A.; Gallmann, L.; Keller, U. Attosecond optical-field-enhanced carrier injection into the GaAs conduction band. Nat. Phys. 2018, 14, 560–564. [Google Scholar] [CrossRef] [Green Version]
- Fu, Y.; Nishimura, K.; Shao, R.; Suda, A.; Midorikawa, K.; Lan, P.; Takahashi, E.J. High efficiency ultrafast water-window harmonic generation for single-shot soft X-ray spectroscopy. Commun. Phys. 2020, 3, 92. [Google Scholar] [CrossRef]
- Liang, J.; Zhou, Y.; Liao, Y.; Jiang, W.-C.; Li, M.; Lu, P. Direct Visualization of Deforming Atomic Wavefunction in Ultraintense High-Frequency Laser Pulses. Ultra. Sci. 2022, 2022, 9842716. [Google Scholar] [CrossRef]
- Li, J.; Ren, X.; Yin, Y.; Zhao, K.; Chew, A.; Cheng, Y.; Cunningham, E.; Wang, Y.; Hu, S.; Wu, Y.; et al. 53-Attosecond X-ray pulses reach the carbon K-edge. Nat. Commun. 2017, 8, 186. [Google Scholar] [CrossRef] [Green Version]
- Gaumnitz, T.; Jain, A.; Pertot, Y.; Huppert, M.; Jordan, I.; Ardana-lamas, F.; Worner, H.J. Streaking of 43-attosecond soft-X-ray pulses generated by a passively CEP-stable mid-infrared driver. Opt. Express 2017, 25, 27506. [Google Scholar] [CrossRef] [PubMed]
- Drescher, M.; Hentschel, M.; Kienberger, R.; Tempea, G.; Spielmann, C.; Reider, G.A.; Corkum, P.B.; Krausz, F. X-ray Pulses Approaching the Attosecond Frontier. Science 2001, 291, 1923. [Google Scholar] [CrossRef] [PubMed]
- Muller, H.G. Reconstruction of attosecond harmonic beating by interference of two-photon transitions. Appl. Phys. B 2002, 74, S17–S21. [Google Scholar] [CrossRef]
- Itatani, J.; Quéré, F.; Yudin, G.L.; Ivanov, M.Y.; Krausz, F.; Corkum, P.B. Attosecond Streak Camera. Phys. Rev. Lett. 2002, 88, 173903. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mairesse, Y.; Quéré, F. Frequency-resolved optical gating for complete reconstruction of attosecond bursts. Phys. Rev. A 2005, 71, 011401. [Google Scholar] [CrossRef]
- Gagnon, J.; Goulielmakis, E.; Yakovlev, V.S. The accurate FROG characterization of attosecond pulses from streaking measurements. Appl. Phys. B 2008, 92, 25–32. [Google Scholar] [CrossRef] [Green Version]
- Chini, M.; Gilbertson, S.; Khan, S.D.; Chang, Z. Characterizing ultrabroadband attosecond lasers. Opt. Express 2010, 18, 13006. [Google Scholar] [CrossRef] [Green Version]
- Lucchini, M.; Brugmann, M.H.; Ludwig, A.; Gallmann, L.; Keller, U.; Feurer, T. Ptychographic reconstruction of attosecond pulses. Opt. Express 2015, 23, 29502. [Google Scholar] [CrossRef] [Green Version]
- Keathley, P.D.; Bhardwaj, S.; Moses, J.; Laurent, G.; Kärtner, F.X. Volkov transform generalized projection algorithm for attosecond pulse characterization. New J. Phys. 2016, 18, 073009. [Google Scholar] [CrossRef]
- Zhao, X.; Wei, H.; Wu, Y.; Lin, C.D. Phase-retrieval algorithm for the characterization of broadband single attosecond pulses. Phys. Rev. A 2017, 95, 043407. [Google Scholar] [CrossRef] [Green Version]
- Zhao, X.; Wang, S.-J.; Yu, W.-W.; Wei, H.; Wei, C.; Wang, B.; Chen, J.; Lin, C.D. Metrology of Time-Domain Soft X-ray Attosecond Pulses and Reevaluation of Pulse Durations of Three Recent Experiments. Phys. Rev. Appl. 2020, 13, 034043. [Google Scholar] [CrossRef] [Green Version]
- Laurent, G.; Cao, W.; Ben-Itzhak, I.; Cocke, C.L. Attosecond pulse characterization. Opt. Express 2013, 21, 16914. [Google Scholar] [CrossRef] [Green Version]
- White, J.; Chang, Z. Attosecond streaking phase retrieval with neural network. Opt. Express 2019, 27, 4799–4807. [Google Scholar] [CrossRef]
- Dudovich, N.; Smirnova, O.; Levesque, J.; Mairesse, Y.; Ivanov, M.Y.; Villeneuve, D.M.; Corkum, P.B. Measuring and controlling the birth of attosecond XUV pulses. Nat. Phys. 2006, 2, 781–786. [Google Scholar] [CrossRef]
- Kim, K.T.; Zhang, C.; Shiner, A.D.; Kirkwood, S.E.; Frumker, E.; Gariepy, G.; Naumov, A.; Villeneuve, D.M.; Corkum, P.B. Manipulation of quantum paths for space-time characterization of attosecond pulses. Nat. Phys. 2013, 9, 159–163. [Google Scholar] [CrossRef] [Green Version]
- He, L.; Hu, J.; Sun, S.; He, Y.; Deng, Y.; Lan, P.; Lu, P. All-optical spatio-temporal metrology for isolated attosecond pulses. J. Phys. B At. Mol. Opt. Phys. 2022, 55, 205601. [Google Scholar] [CrossRef]
- Yang, Z.; Cao, W.; Chen, X.; Zhang, J.; Mo, Y.; Xu, H.; Mi, K.; Zhang, Q.; Lan, P.; Lu, P. All-optical frequency-resolved optical gating for isolated attosecond pulse reconstruction. Opt. Lett. 2020, 45, 567–570. [Google Scholar] [CrossRef] [Green Version]
- Xue, B.; Tamaru, Y.; Fu, Y.; Yuan, H.; Lan, P.; Mucke, O.D.; Suda, A.; Midorikawa, K.; Takahashi, E.J. A Custom-Tailored Multi-TW Optical Electric Field for Gigawatt Soft-X-ray Isolated Attosecond Pulses. Ultra. Sci. 2021, 2021, 9828026. [Google Scholar] [CrossRef]
- Xue, B.; Midorikawa, K.; Takahashi, E.J. Gigawatt-class, tabletop, isolated-attosecond-pulse light source. Optica 2022, 9, 360. [Google Scholar] [CrossRef]
- Kane, D.J.; Trebino, R. Single-Shot Measurement of the Intensity and Phase of an Arbitrary Ultrashort Pulse By Using Frequency-Resolved Optical Gating. Opt. Lett. 1993, 18, 823–825. [Google Scholar] [CrossRef]
- Liu, Y.; Beetar, J.E.; Nesper, J.; Gholam-Mirzaei, S.; Chini, M. Single-shot measurement of few-cycle optical waveforms on a chip. Nat. Photonics 2022, 16, 109–112. [Google Scholar] [CrossRef]
- Gagnon, J. Attosecond Electron Spectroscopy Theory and its Application. Ph.D. Thesis, LMU Munchen, Munchen, Germany, 2010. [Google Scholar]
- The Center for X-ray Optics of Lawrence Berkeley National Laboratory. Available online: https://henke.lbl.gov/optical_constants/ (accessed on 9 December 2022).
- Chang, Z. Fundamentals of Attosecond Optics; CRC: Boca Raton, FL, USA, 2011; pp. 17–18. [Google Scholar]
- Börzsönyi, A.; Heiner, Z.; Kalashnikov, M.P.; Kovács, A.P.; Osvay, K. Dispersion measurement of inert gases and gas mixtures at 800 nm. Appl. Opt. 2008, 47, 4856–4863. [Google Scholar] [CrossRef] [PubMed]
- Zhong, S.; He, X.; Ye, P.; Zhan, M.; Teng, H.; Wei, Z. Effects of driving laser jitter on the attosecond streaking measurement. Opt. Express 2013, 21, 17498. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Chini, M.; Khan, S.D.; Chen, S.; Gilbertson, S.; Feng, X.; Mashiko, H.; Chang, Z. Practical issues of retrieving isolated attosecond pulses. J. Phys. B At. Mol. Opt. Phys. 2009, 42, 134007. [Google Scholar] [CrossRef]
- Kruit, P.; Read, F.H. Magnetic field paralleliser for 2π electron-spectrometer and electron-image magnifier. J. Phys. E Sci. Instrum. 1983, 16, 313. [Google Scholar] [CrossRef]
- Dubbers, D. Magnetic guidance of charged particles. Phys. Lett. B 2015, 748, 306–310. [Google Scholar] [CrossRef] [Green Version]
- Sjue, S.K.L.; Broussard, L.J.; Makela, M.; McGaughey, P.L.; Young, A.R.; Zeck, B.A. Radial distribution of charged particles in a magnetic field. Rev. Sci. Instrum. 2015, 86, 023102. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Q.; Zhao, K.; Chang, Z. High resolution electron spectrometers for characterizing the contrast of isolated 25 as pulses. J. Elect. Spectr. Rel. Phen. 2014, 195, 48–54. [Google Scholar] [CrossRef]
- Kurahashi, N.; Thurmer, S.; Liu, S.Y.; Yamamoto, Y.-I.; Karashima, S.; Bhattacharya, A.; Ogi, Y.; Horio, T.; Suzuki, T. Design and characterization of a magnetic bottle electron spectrometer for time-resolved extreme UV and X-ray photoemission spectroscopy of liquid microjets. Struct. Dyn. 2021, 8, 034303. [Google Scholar] [CrossRef]
- Hirvonen, L.M.; Becker, W.; Milnes, J.; Conneely, T.; Smietana, S.; Marois, A.L.; Jagutzki, O.; Suhling, K. Picosecond wide-field time-correlated single photon counting fluorescence microscopy with a delay line anode detector. Appl. Phys. Lett. 2016, 109, 071101. [Google Scholar] [CrossRef] [Green Version]
- Bromberger, H.; Passow, C.; Pennicard, D.; Boll, R.; Correa, J.; He, L.; Johny, M.; Papadopoulou, C.; Tul-Noor, A.; Wiese, J.; et al. Shot-by-shot 250 kHz 3D ion and MHz photoelectron imaging using Timepix3. J. Phys. B At. Mol. Opt. Phys. 2022, 55, 144001. [Google Scholar] [CrossRef]
- Pi, L.-W.; Hu, S.X.; Starace, A.F. Favorable target positions for intense laser acceleration of electrons in hydrogen-like, highly-charged ions. Phys. Plasmas 2015, 22, 093111. [Google Scholar] [CrossRef] [Green Version]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, P.; Wang, X.; Cao, H.; Yuan, H.; Pi, L.-W.; Wang, Y.; Fu, Y.; Bai, Y.; Zhao, W. Non-Collinear Attosecond Streaking without the Time Delay Scan. Photonics 2023, 10, 331. https://doi.org/10.3390/photonics10030331
Xu P, Wang X, Cao H, Yuan H, Pi L-W, Wang Y, Fu Y, Bai Y, Zhao W. Non-Collinear Attosecond Streaking without the Time Delay Scan. Photonics. 2023; 10(3):331. https://doi.org/10.3390/photonics10030331
Chicago/Turabian StyleXu, Peng, Xianglin Wang, Huabao Cao, Hao Yuan, Liang-Wen Pi, Yishan Wang, Yuxi Fu, Yonglin Bai, and Wei Zhao. 2023. "Non-Collinear Attosecond Streaking without the Time Delay Scan" Photonics 10, no. 3: 331. https://doi.org/10.3390/photonics10030331
APA StyleXu, P., Wang, X., Cao, H., Yuan, H., Pi, L. -W., Wang, Y., Fu, Y., Bai, Y., & Zhao, W. (2023). Non-Collinear Attosecond Streaking without the Time Delay Scan. Photonics, 10(3), 331. https://doi.org/10.3390/photonics10030331




