2 × 2 Compact Silicon Waveguide-Based Optical Logic Functions at 1.55 μm
Abstract
:1. Introduction
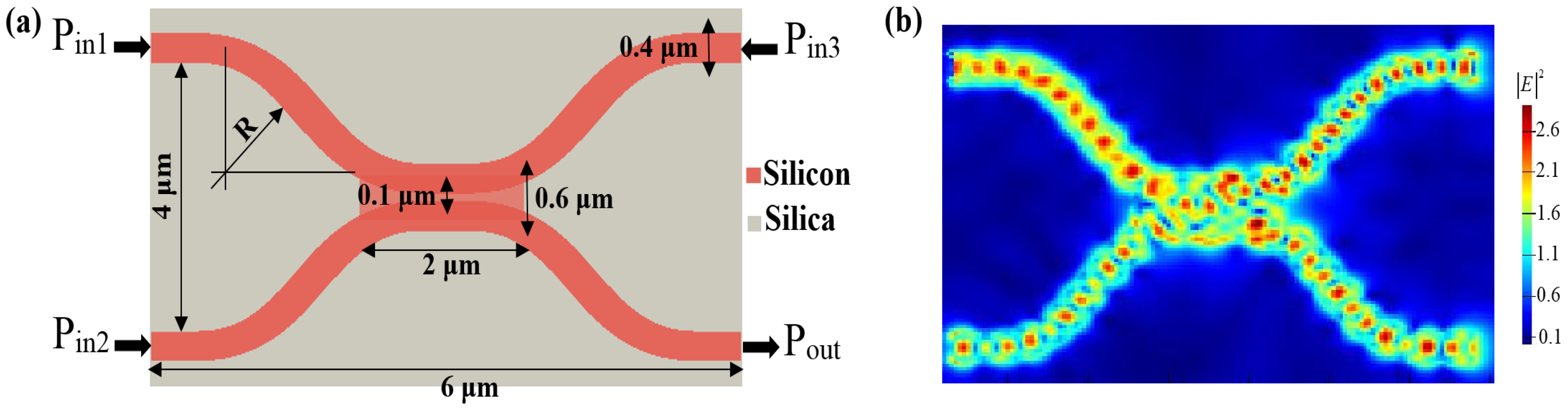
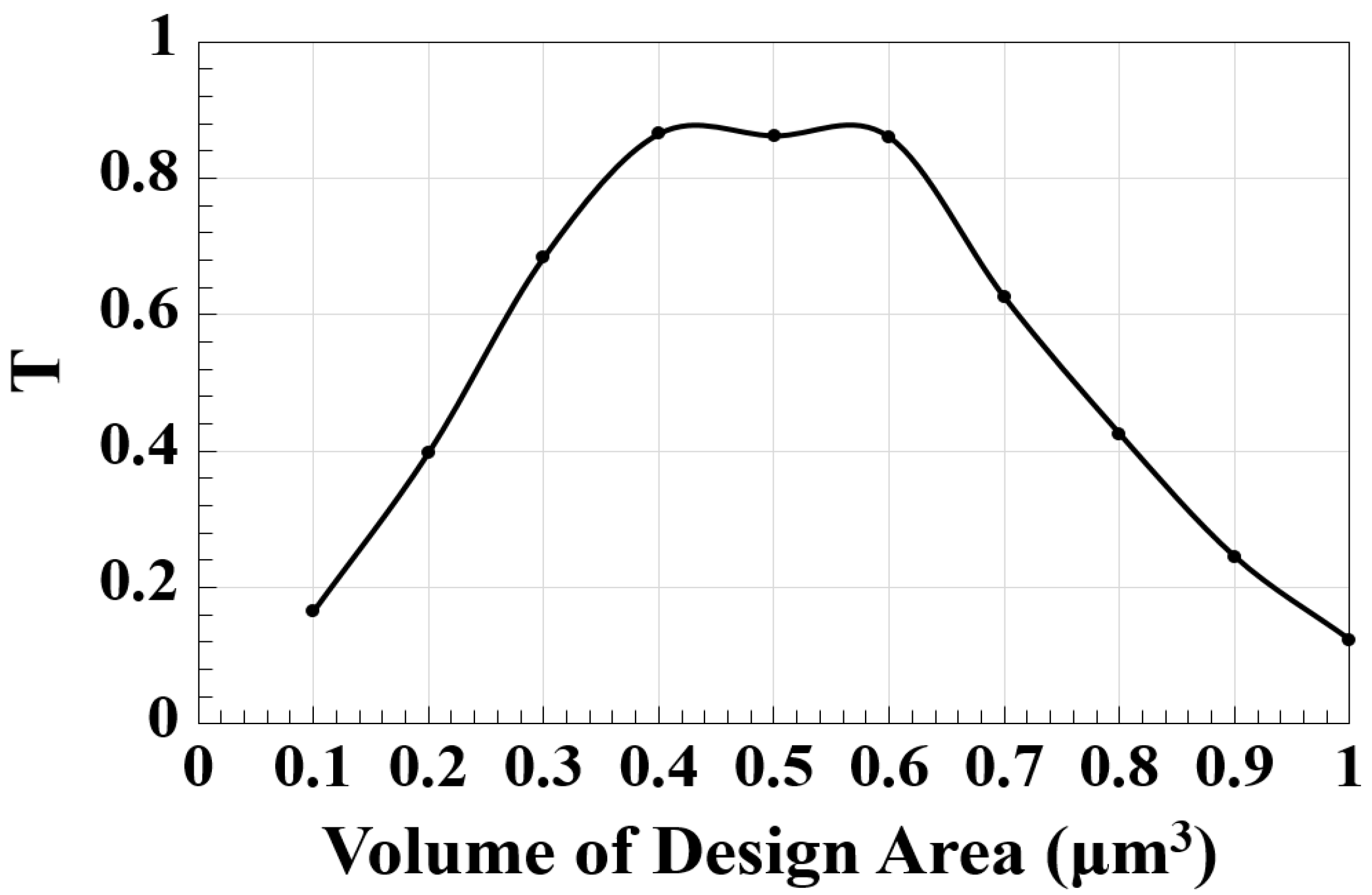
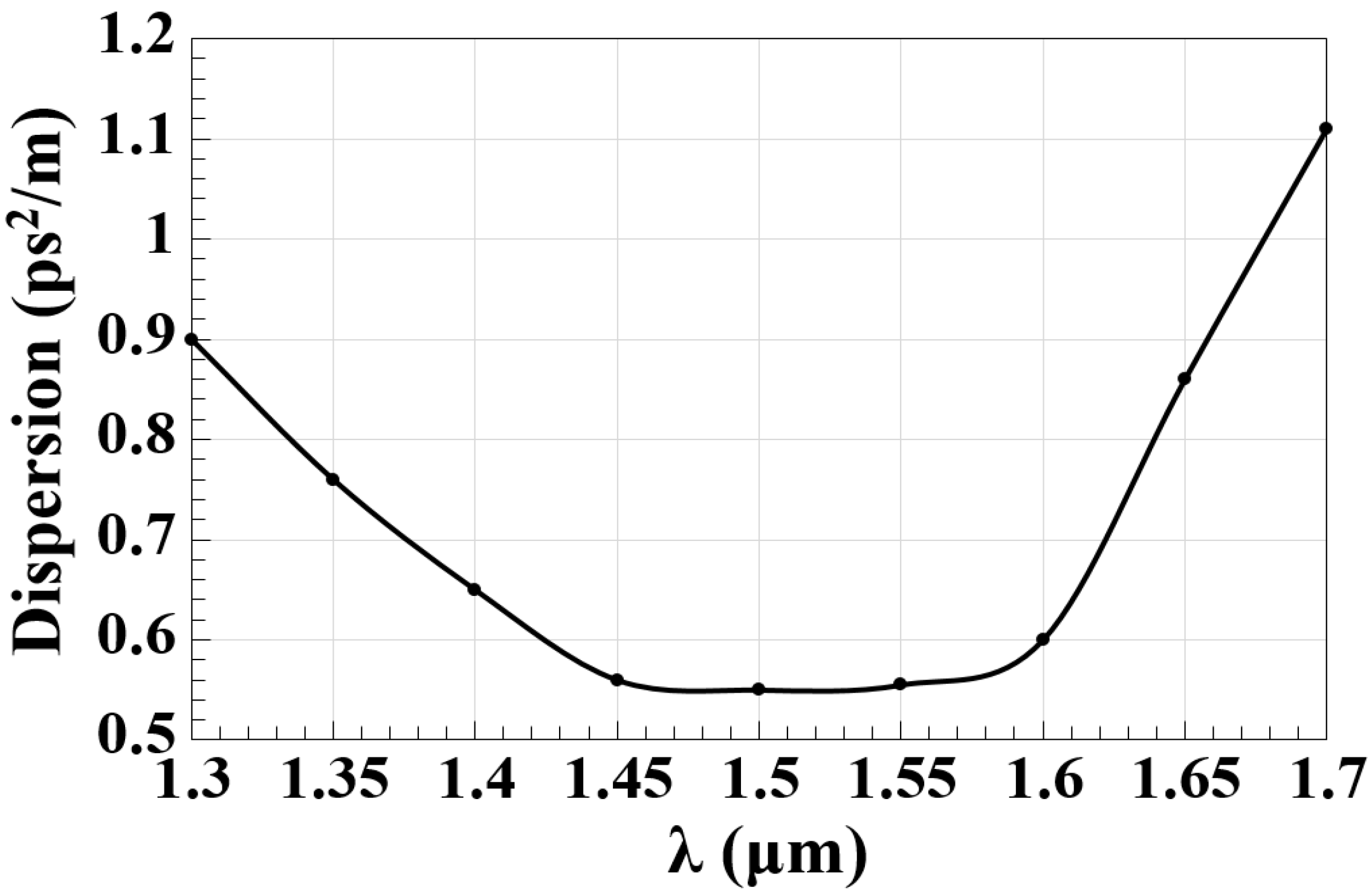
2. 2 × 2 Silicon Waveguide
3. Logic Functions
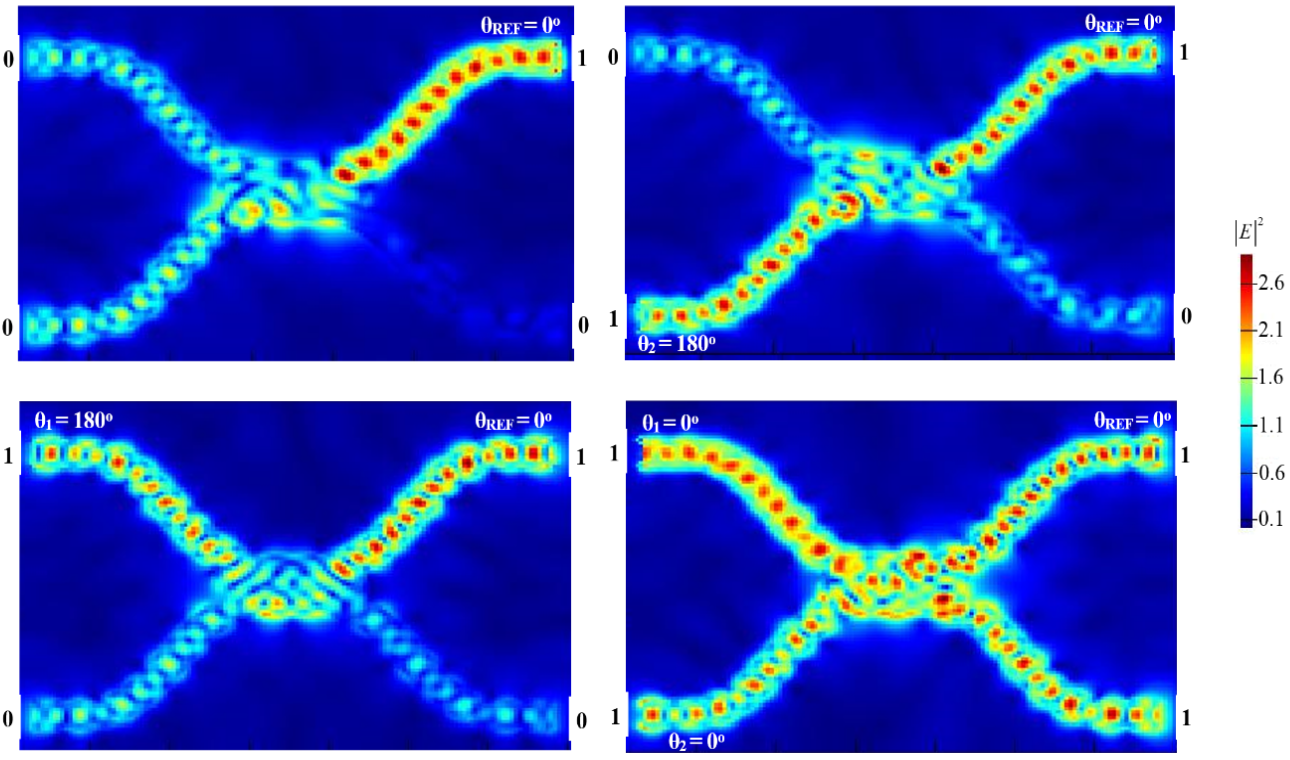
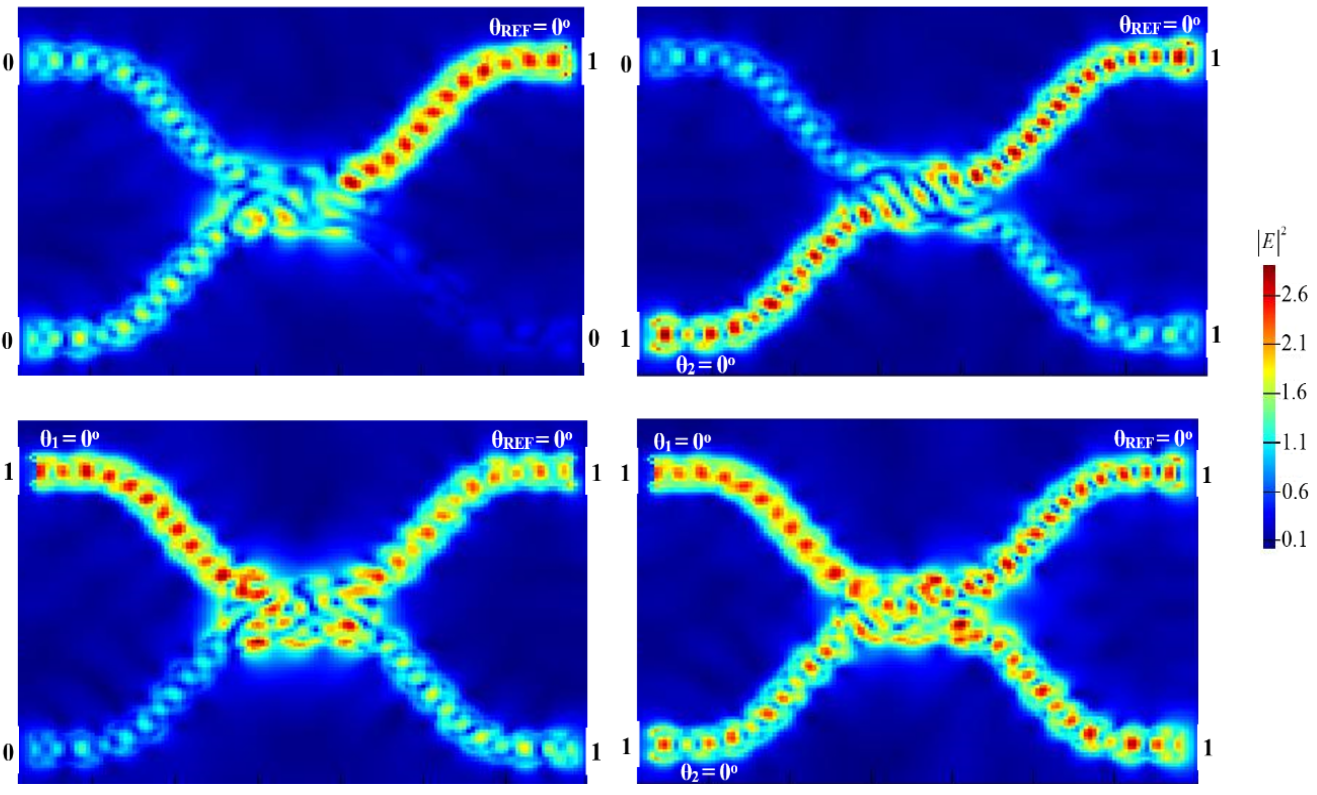
3.1. XOR
3.2. AND
3.3. OR
3.4. NOT
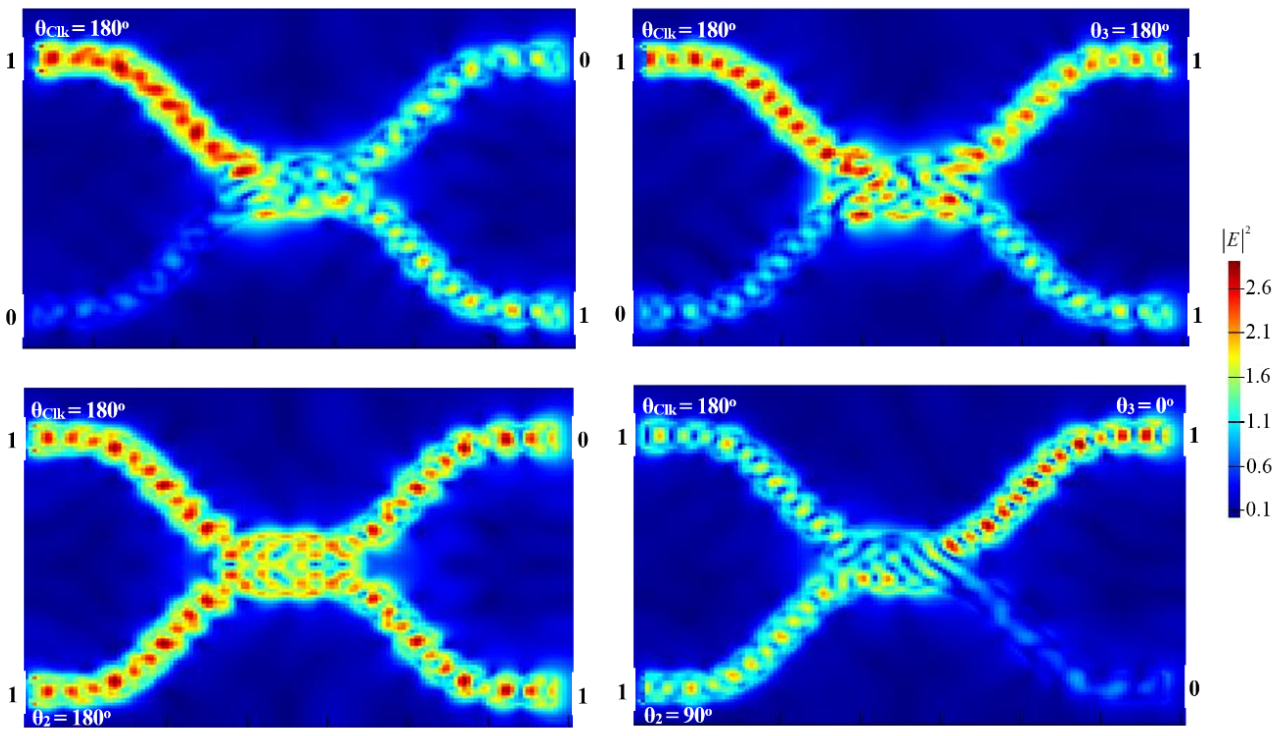
3.5. NOR
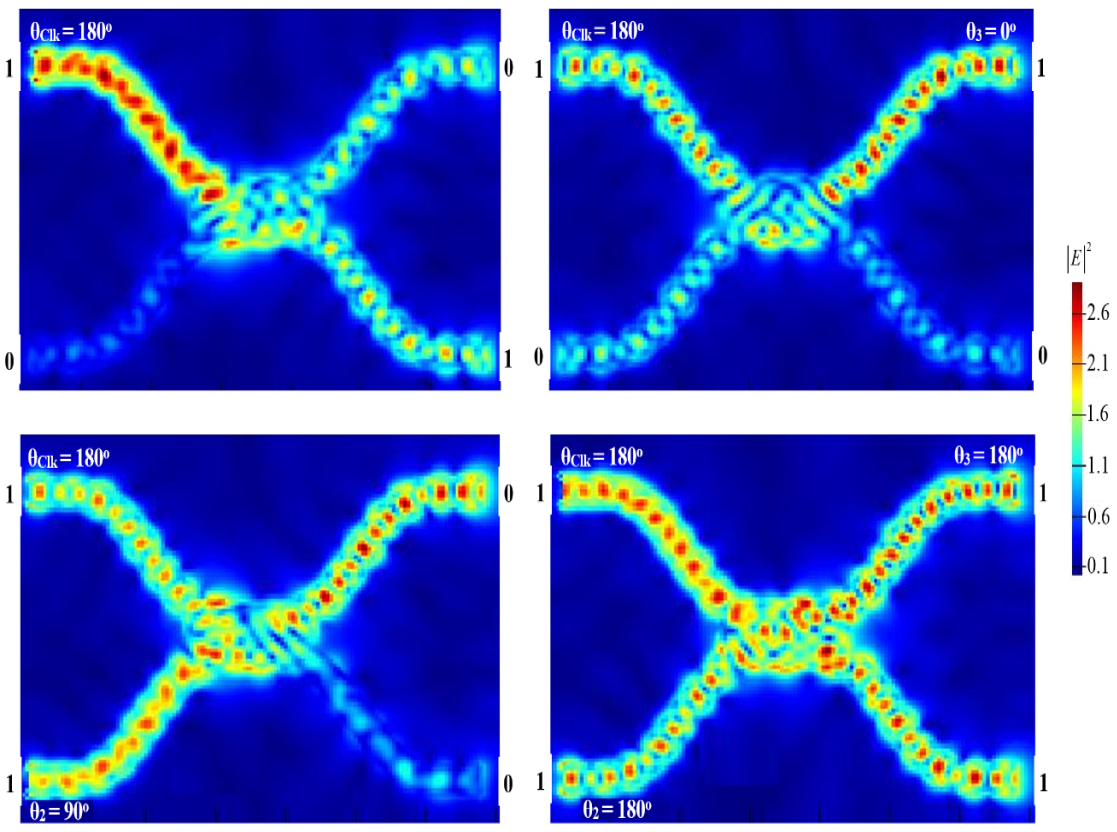
3.6. NAND
3.7. XNOR
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tong, X.C. Silicon-on-Insulator Waveguides. In Advanced Materials for Integrated Optical Waveguides; Springer Series in Advanced Microelectronics; Springer: Berlin/Heidelberg, Germany, 2014; Volume 46, pp. 253–287. [Google Scholar]
- Peng, Z.; Feng, J.; Du, T.; Cheng, W.; Wang, Y.; Zang, S.; Cheng, H.; Ren, X.; Shuai, Y.; Liu, H.; et al. Series of ultra-low loss and ultra-compact multichannel silicon waveguide crossing. Opt. Express 2022, 30, 27366–27380. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Zhang, Y.; Yang, S.; Novack, A.; Ding, R.; Lim, A.E.; Lo, G.; Baehr-Jones, T.; Hochberg, M. Ultralow loss single layer submicron silicon waveguide crossing for SOI optical interconnect. Opt. Express 2013, 21, 29374–29382. [Google Scholar] [CrossRef] [PubMed]
- Sanchis, P.; Villalba, P.; Cuesta, F.; Håkansson, A.; Griol, A.; Galán, J.V.; Brimont, A.; Martí, J. Highly efficient crossing structure for silicon-on-insulator waveguides. Opt. Lett. 2009, 34, 2760–2762. [Google Scholar] [CrossRef] [PubMed]
- Bogaerts, W.; Dumon, P.; Thourhout, D.V.; Baets, R. Low-loss, low-cross-talk crossings for silicon-on-insulator nanophotonic waveguides. Opt. Lett. 2007, 32, 2801–2803. [Google Scholar] [CrossRef] [Green Version]
- Brunetti, G.; Marocco, G.; Benedetto, A.D.; Agostino Giorgio, A.; Mario Nicola Armenise, M.N.; Ciminelli, C. Design of a large bandwidth 2 × 2 interferometric switching cell based on a sub-wavelength grating. J. Opt. 2021, 23, 085801. [Google Scholar] [CrossRef]
- Chang, W.; Lu, L.; Ren, X.; Lu, L.; Cheng, M.; Liu, D.; Zhang, M. An ultracompact multimode waveguide crossing based on subwavelength asymmetric Y-junction. IEEE Photonics J. 2018, 10, 1–8. [Google Scholar] [CrossRef]
- Chen, C.H.; Chiu, C.H. Taper-integrated multimode-interference based waveguide crossing design. IEEE J. Quantum Electron. 2010, 46, 1656–1661. [Google Scholar] [CrossRef]
- Gilarlue, M.; Badri, S.H. Photonic crystal waveguide crossing based on transformation optics. Opt. Commun. 2019, 450, 308–315. [Google Scholar] [CrossRef] [Green Version]
- Lu, L.; Zhang, M.; Zhou, F.; Chang, W.; Tang, J.; Li, D.; Ren, X.; Pan, Z.; Cheng, M.; Liu, D. Inverse-designed ultra-compact star-crossings based on PhC-like subwavelength structures for optical intercross connect. Opt. Express 2017, 25, 18355–18364. [Google Scholar] [CrossRef]
- Priya, N.H.; Swarnakar, S.; Krishna, S.V.; Kumar, S. Design and analysis of an optical three-input AND gate using a photonic crystal fiber. Appl. Opt. 2022, 61, 77–83. [Google Scholar]
- Priya, N.H.; Swarnakar, S.; Krishna, S.V.; Kumar, S. Design and analysis of a photonic crystal-based all-optical 3-input OR gate for high-speed optical processing. Opt. Quantum Electron. 2021, 53, 720. [Google Scholar] [CrossRef]
- Rao, D.G.S.; Swarnakar, S.; Palacharla, V.; Raju, K.S.R.; Kumar, S. Design of all-optical AND, OR, and XOR logic gates using photonic crystals for switching applications. Photonic Netw. Commun. 2021, 41, 109–118. [Google Scholar] [CrossRef]
- Rani, P.; Kalra, Y.; Sinha, R.K. Design of all optical logic gates in photonic crystal waveguides. Optik 2015, 126, 950–955. [Google Scholar] [CrossRef]
- Yao, C.; Kotb, A.; Wang, B.; Singh, S.; Guo, C. All-optical logic gates using dielectric-loaded waveguides with quasi-rhombus metasurfaces. Opt. Lett. 2020, 45, 3769–3772. [Google Scholar] [CrossRef]
- Pan, D.; Wei, H.; Xu, H. Optical interferometric logic gates based on metal slot waveguide network realizing whole fundamental logic operations. Opt. Express 2013, 21, 9556. [Google Scholar] [CrossRef] [Green Version]
- Bian, Y.; Gong, Q. Compact all-optical interferometric logic gates based on one-dimensional metal-insulator-metal structures. Opt. Commun. 2014, 313, 27–35. [Google Scholar] [CrossRef]
- Al-Musawi, H.K.; Al-Janabi, A.K.; Al-Abassi, S.A.W.; Abusiba, N.A.A.; Al-Fatlawi, N.A.Q. Plasmonic logic gates based on dielectric-metal-dielectric design with two optical communication bands. Optik 2020, 223, 165416. [Google Scholar] [CrossRef]
- Kotb, A.; Zoiros, K.E.; Li, W. Silicon-on-silica waveguides-based all-optical logic gates at 1.55 μm. Phys. Scr. 2023, 98, 035517. [Google Scholar] [CrossRef]
- Kotb, A.; Zoiros, K.E. K-shaped silicon waveguides for logic operations at 1.55 μm. Electronics 2022, 11, 3748. [Google Scholar] [CrossRef]
- Neseli1, B.; Yilmaz, Y.A.; Kurt, H.; Turduev, M. Inverse design of ultra-compact photonic gates for all-optical logic operations. J. Phys. D Appl. Phys. 2022, 55, 215107. [Google Scholar] [CrossRef]
- Kita, S.; Nozaki, K.; Takata, K.; Shinya, A.; Notomi, M. Ultrashort low-loss Ψ gates for linear optical logic on Si photonics platform. Commun. Phys. 2020, 3, 33. [Google Scholar] [CrossRef] [Green Version]
- Zoiros, K.E.; Papadopoulos, G.; Houbavlis, T.; Kanellos, G.T. Theoretical analysis and performance investigation of ultrafast all-optical Boolean XOR gate with semiconductor optical amplifier-assisted Sagnac interferometer. Opt. Commun. 2006, 258, 114–134. [Google Scholar] [CrossRef]
- Han, Q.; Robin, D.; Gervais, A.; Ménard, M.; Shi, W. Phase errors and statistical analysis of silicon-nitride arrayed waveguide gratings. Opt. Express 2022, 30, 42784–42800. [Google Scholar] [CrossRef] [PubMed]
- Khan, U.; Fiers, M.; Xing, Y.; Bogaerts, W. Experimental phase error extraction and modelling in silicon photonic arrayed waveguide gratings. Proc. SPIE 2020, 11285, 1128510. [Google Scholar]
- Goh, T.; Suzuki, S.; Sugita, A. Estimation of waveguide phase error in silica-based waveguides. J. Light. Technol. 1997, 15, 2107–2113. [Google Scholar] [CrossRef]
- Vlasov, Y.A.; McNab, S.J. Losses in single-mode silicon-on-insulator strip waveguides and bends. Opt. Express 2004, 12, 1622–1631. [Google Scholar] [CrossRef]
- Bienstman, P.; Six, E.; Roelens, M.; Vanwolleghem, M.; Baets, R. Calculation of bending losses in dielectric waveguides using eigenmode expansion and perfectly matched layers. IEEE Photonics Technol. Lett. 2002, 14, 164–166. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Yue, Y.; Beausoleil, R.C.; Willner, A.E. Flattened dispersion in silicon slot waveguides. Opt. Express 2010, 18, 20529–20534. [Google Scholar] [CrossRef]
- Yin, L.; Lin, Q.; Agrawal, G.P. Dispersion tailoring and soliton propagation in silicon waveguides. Opt. Lett. 2006, 31, 1295–1297. [Google Scholar] [CrossRef]
- Dadap, J.I.; Panoiu, N.C.; Chen, X.; Hsieh, I.W.; Liu, X.; Chou, C.Y.; Dulkeith, E.; McNab, S.J.; Xia, F.; Green, W.M.J.; et al. Nonlinear-optical phase modification in dispersion engineered Si photonic wires. Opt. Express 2008, 16, 1280–1299. [Google Scholar] [CrossRef] [Green Version]
- Hu, Y.; Yang, Z.; Chen, N.; Hu, H.; Zhang, B.; Yang, H.; Lu, X.; Zhang, X.; Xu, J. 3 X 40 Gbit/s all-optical logic operation based on low-loss triple-mode silicon waveguide. Micromachines 2022, 13, 90. [Google Scholar] [CrossRef]
- Crisp, J.; Elliott, B. Introduction to Fiber Optics, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Vercruysse, D.; Sapra, N.V.; Su, L.; Trivedi, R.; Vučković, J. Analytical level set fabrication constraints for inverse design. Sci. Rep. 2019, 9, 8999. [Google Scholar] [CrossRef] [Green Version]
- Sean Molesky, S.; Zin Lin, Z.; Alexander, Y.; Piggott, A.Y.; Weiliang Jin, W.; Vucković, J.; Rodriguez, A.W. Outlook for inverse design in nanophotonics. Nat. Photonics 2018, 12, 659–670. [Google Scholar] [CrossRef] [Green Version]
- Lu, J.; Vuckovic, J. Nanophotonic Computational Design. Opt. Express 2013, 21, 7748–7759. [Google Scholar] [CrossRef]
- Jensen, J.S.; Sigmund, O. Topology optimization for nano-photonics. Laser Photonics Rev. 2011, 5, 308–321. [Google Scholar] [CrossRef]
- Shen, B.; Wang, P.; Polson, R.; Menon, R. Integrated metamaterials for efficient and compact free-space-to-waveguide coupling. Opt. Express 2014, 22, 27175–27182. [Google Scholar] [CrossRef]
- Piggott, A.Y.; Lu, J.; Lagoudakis, K.G.; Petykiewicz, J.; Babinec, T.M.; Vučković, J. Inverse design and demonstration of a compact and broadband on-chip wavelength demultiplexer. Nat. Photonics 2015, 9, 374–377. [Google Scholar] [CrossRef] [Green Version]
- Shen, B.; Wang, P.; Polson, R.; Menon, R. An integrated-nanophotonics polarization beam splitter with 2.4 × 2.4 μm2 footprint. Nat. Photonics 2015, 9, 378–382. [Google Scholar] [CrossRef]
- Sell, D.; Yang, J.; Doshay, S.; Yang, R.; Fan, J.A. Large-Angle, Multifunctional Metagratings Based on Freeform Multimode Geometries. Nano Lett. 2017, 17, 3752–3757. [Google Scholar] [CrossRef]
- Yu, Z.; Cui, H.; Sun, X. Genetically optimized on-chip wideband ultracompact refectors and Fabry–Perot cavities. Photonics Res. 2017, 5, B15–B19. [Google Scholar] [CrossRef]
- Su, L.; Piggott, A.Y.; Sapra, N.V.; Petykiewicz, J.; Vučković, J. Inverse Design and Demonstration of a Compact on-Chip Narrowband Tree-Channel Wavelength Demultiplexer. ACS Photonics 2018, 5, 301–305. [Google Scholar] [CrossRef] [Green Version]
- Sitawarin, C.; Jin, W.; Lin, Z.; Rodriguez, A.W. Inverse-designed photonic fbers and metasurfaces for nonlinear frequency conversion. Photonics Res. 2018, 6, 82–89. [Google Scholar] [CrossRef]
- Pestourie, R.; Pérez-Arancibia, C.; Lin, Z.; Shin, W.; Capasso, F.; Johnson, S.G. Inverse design of large-area metasurfaces. Opt. Express 2018, 26, 33732–33747. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Shi, Y.; Hughes, T.; Zhao, Z.; Fan, S. Adjoint-based optimization of active nanophotonic devices. Opt. Express 2018, 26, 3236–3248. [Google Scholar] [CrossRef]
- Gao, L.; Chen, L.; Wei, H.; Xu, H. Lithographically fabricated gold nanowire waveguides for plasmonic routers and logic gates. Nanoscale 2018, 10, 14771. [Google Scholar] [CrossRef] [Green Version]
- Donzella, V.; Sherwali, A.; Flueckiger, J.; Grist, S.M.; Fard, S.T.; Chrostowski, L. Design and fabrication of SOI micro-ring resonators based on sub-wavelength grating waveguides. Opt. Express 2015, 23, 4791–4803. [Google Scholar] [CrossRef]
- Fu, Y.; Hu, X.; Lu, C.; Yue, S.; Yang, H.; Gong, Q. All-optical logic gates based on nanoscale plasmonic slot waveguides. Nano Lett. 2012, 12, 5784–5790. [Google Scholar] [CrossRef]







| Pin1 | Pin2 | Pin3 (REF) | T | Pout | CR (dB) |
|---|---|---|---|---|---|
| 0 | 0 | 1 | 0.009 | 0 | 39.64 |
| 0 | 1 | 1 | 0.524 | 1 | |
| 1 | 0 | 1 | 0.552 | 1 | |
| 1 | 1 | 1 | 0.012 | 0 |
| Pin1 | Pin2 | Pin3 (REF) | T | Pout | CR (dB) |
|---|---|---|---|---|---|
| 0 | 0 | 1 | 0.009 | 0 | 31 |
| 0 | 1 | 1 | 0.055 | 0 | |
| 1 | 0 | 1 | 0.053 | 0 | |
| 1 | 1 | 1 | 0.865 | 1 |
| Pin1 | Pin2 | Pin3 (REF) | T | Pout | CR (dB) |
|---|---|---|---|---|---|
| 0 | 0 | 1 | 0.009 | 0 | 42.75 |
| 0 | 1 | 1 | 0.524 | 1 | |
| 1 | 0 | 1 | 0.552 | 1 | |
| 1 | 1 | 1 | 0.865 | 1 |
| Operation | CR (dB) Without REF | CR (dB) With REF |
|---|---|---|
| XOR | 6.5 | 39.64 |
| AND | 5.2 | 31 |
| OR | 6.8 | 42.75 |
| Pin1 (Clk) | Pin2 | T | Pout | CR (dB) |
|---|---|---|---|---|
| 1 | 0 | 0.552 | 1 | 24.63 |
| 1 | 1 | 0.047 | 0 |
| Pin1 (Clk) | Pin2 | Pin3 | T | Pout | CR (dB) |
|---|---|---|---|---|---|
| 1 | 0 | 0 | 0.552 | 1 | 25.53 |
| 1 | 0 | 1 | 0.054 | 0 | |
| 1 | 1 | 0 | 0.052 | 0 | |
| 1 | 1 | 1 | 0.023 | 0 |
| Pin1 (Clk) | Pin2 | Pin3 | T | Pout | CR (dB) |
|---|---|---|---|---|---|
| 1 | 0 | 0 | 0.552 | 1 | 33.38 |
| 1 | 0 | 1 | 0.525 | 1 | |
| 1 | 1 | 0 | 0.865 | 1 | |
| 1 | 1 | 1 | 0.023 | 0 |
| Pin1 (Clk) | Pin2 | Pin3 | T | Pout | CR (dB) |
|---|---|---|---|---|---|
| 1 | 0 | 0 | 0.552 | 1 | 26 |
| 1 | 0 | 1 | 0.054 | 0 | |
| 1 | 1 | 0 | 0.052 | 0 | |
| 1 | 1 | 1 | 0.865 | 1 |
| Operations | Design | Wavelength (nm) | CR (dB) | Ref. |
|---|---|---|---|---|
| AND, XOR, OR | T-shaped photonic crystal waveguides | 1550 | 8.29–33.05 | [11,12,13] |
| AND, XOR, OR, NOT, NAND, NOR, XNOR | Photonic crystal waveguides | 1550 | 5.42–9.59 | [14] |
| XOR, AND, OR, NOR, NAND, XNOR | Dielectric-loaded waveguides | 471 | 24.41–33.39 | [15] |
| NOT, XOR, AND, OR, NOR, NAND, XNOR | Metal slot waveguide | 632.8 | 6–16 | [16] |
| NOT, XOR, AND, OR, NOR, NAND, XNOR | Metal–insulator–metal structures | 632.8 | 15 | [17] |
| NOT, XOR, AND, OR, NOR, NAND, XNOR | Dielectric–metal–dielectric design | 900 and 1330 | 5.37–22 | [18] |
| AND, XOR, OR, NOT, NAND, NOR, XNOR | Silicon-on-silica waveguides | 1550 | 20.51–30.33 | [19] |
| AND, XOR, OR, NOT, NAND, NOR, XNOR | K-shaped silicon waveguides | 1550 | 30.5–34 | [20] |
| AND, OR, NOT, NAND | Inverse design on silicon platforms | 1300 | 0.5–5.79 | [21] |
| AND, NOR, XNOR | Silicon photonics platform | 1550 | >10 dB | [22] |
| XOR, AND, OR, NOT, NOR, NAND, XNOR | 2 × 2 silicon-on-silica waveguides | 1550 | 24.63–42.75 | This work |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kotb, A.; Zoiros, K.E. 2 × 2 Compact Silicon Waveguide-Based Optical Logic Functions at 1.55 μm. Photonics 2023, 10, 403. https://doi.org/10.3390/photonics10040403
Kotb A, Zoiros KE. 2 × 2 Compact Silicon Waveguide-Based Optical Logic Functions at 1.55 μm. Photonics. 2023; 10(4):403. https://doi.org/10.3390/photonics10040403
Chicago/Turabian StyleKotb, Amer, and Kyriakos E. Zoiros. 2023. "2 × 2 Compact Silicon Waveguide-Based Optical Logic Functions at 1.55 μm" Photonics 10, no. 4: 403. https://doi.org/10.3390/photonics10040403
APA StyleKotb, A., & Zoiros, K. E. (2023). 2 × 2 Compact Silicon Waveguide-Based Optical Logic Functions at 1.55 μm. Photonics, 10(4), 403. https://doi.org/10.3390/photonics10040403






