Statistical Properties of Partially Coherent Higher-Order Laguerre-Gaussian Power-Exponent Phase Vortex Beams

Abstract

In this paper, partially coherent radially polarized (RP) Laguerre-Gaussian (LG) rotationally symmetrical power-exponent phase vortex (RSPEPV) beams with the LG-correlated Schell-model (LGSM) were introduced. The statistical properties of the tightly focused beams, including intensity distribution, degrees of polarization and coherence, and Stokes vector, were studied based on vectorial Richards-Wolf diffraction integral theory. Moreover, when the distance between focal plane and the observation plane z = 0, the relationships between the tight-focusing properties of RP-LG-RSPEPV beams with LGSM and the order of LGSM p’, topological charges l, power exponent n, spatial correlation δ, and radial index p were investigated. The results show that by changing the order of LGSM, topological charge, power exponent, spatial correlation length, and radial index, the focal spot distribution of various shapes can be obtained. This work provides ideas for the application of partially coherent beams in particle capture and optical tweezers.

1. Introduction

Power-exponent phase vortex (PEPV) beams are special optical vortexes with different phase velocities within the transverse dimension [1,2,3,4,5,6]. According to the intensity distribution, PEPV beams can be categorized as asymmetric and rotationally symmetric. In the phase distribution of an asymmetric power-exponential phase vortex (APEPV) beam, the angle of each sector is different, so that the phase velocity of each sector is different, which leads to its optical intensity distribution resembling a “C” shape [1,6]. These unique properties give it some advantages in optical manipulation, and a study has shown that particles can be moved along specified curved paths by tuning the topological charge and power exponent of the APEPV beams [7]. Further, for rotationally symmetric power-exponent phase vortex (RSPEPV) beams, the angle of each sector in its phase distribution is the same. However, the phase velocity within the same sector is different, thus forming a rotationally symmetric and blade-like intensity distribution [8,9]. The number of the “blade” is equal to the topological charges of the RSPEPV beams, which makes it possible to manipulate multiple particles of the same type simultaneously [10]. At present, the research on RSPEPV beams is mainly in the field of fully coherent beams, such as self-focusing Airy [11], radially polarized or scalar RSPEPV beams [6,9], as mentioned in our previous works. However, there is little research into partially coherent higher-order LG-RSPEPV beams in this field.

In addition, apart from controlling the light intensity and phase to achieve specific practical requirements, polarization and coherence are also two important controllable parameters [12,13,14]. For example, a very strong longitudinal component can be generated by using radially polarized (RP) beams to pass through a high-numerical aperture (NA) focusing system [15,16], which has potential applications in particle trapping [17]. Further, the size of the tightly focused beam is generally in the subwavelength size, which also promotes the development of an optical needle [18], optical field manipulation [19], and quantum optics [20]. Therefore, the tight-focusing characteristics of radially polarized beams have always been the focus of research [15,16]. Partially coherent vector beams have advantages over fully coherent beams in the fields of light trapping [21,22], free-space optical (FSO) communication [23] and high-resolution imaging [24]. Specifically, by tuning the spatial coherence of radially polarization beams, it is possible to trap types of particles with different sizes and refractive indices [21,22]. In previous works, we have investigated the propagation properties of partially coherent [3] Laguerre-Gaussian (LG) APEPV beams [1], tightly focused properties of RSPEPV beams [2], and 0-order LG-RSPEPV [25] beams, and pointed out some of their application advantages in optical trapping [10]. However, they may not provide the opportunity to manipulate different types of quantitative particles simultaneously. The high-order LG-RSPEPV beam has a controllable number of outer rings and complex structures. By adjusting the topological charge, the radial index of LG beams, the order of the LGSM and coherence length, the radiation force of the beams can be modulated, which provides a way to solve this problem.

In this paper, partially coherent radially polarized RP-LG RSPEPV beams with an LG-correlated Schell-model (LGSM) were introduced. Based on vectorial Richards-Wolf diffraction integral theory, the intensity distribution, degree of polarization and coherence, and Stokes vector of the tightly focused beams are investigated. Moreover, by adjusting the parameters including power exponent n, radial index p, topological charges l, spatial correlation δ, radial index p, and the order of LGSM p’, the statistical characteristics of the beams in the focal plane were investigated. Combing the characteristics of RP-LG-RSPEPV and LGSM, the beam shape can be controlled from multiple parameters. This work presents the opportunity to manipulate different types of quantitative particles simultaneously.

2. Theory

2.1. Theory for RP-LG-RSPEPV Beams with LGSM

Firstly, in the polar coordinates’ system, the RSPEPV beams at the source plane can be characterized as follows [2]:

$$E(r,\phi )=A_{0}E(r)\exp \left[2\pi {\left(\frac{\mathit{rem}\left(l\phi ,2\pi \right)}{2\pi }\right)}^n\right],$$

(1)

where r and φ are polar coordinates; l denotes topological charges; n is the power exponent; A₀ is the amplitude of the incident beam, which is equal to 1 for convenience; rem(x,y) represent remainder function; E(r) is the expression of different beam modes, and E(r) could be equal to the Airy function [11], the Lorentz-Gaussian function [26], or the Bessel-Gaussian [27] function to obtain different forms of RSPEPV beams. However, the Laguerre-Gaussian function is introduced in this paper,

$$E_{\mathrm{LG}}\left(r\right)=\frac{\sqrt{2p!/\pi (\left|l\right|+p)!}}{w}{\left(\frac{\sqrt{2}r}{w}\right)}^{\left|l\right|}{L}_p^{\left|l\right|}\left(\frac{2r^2}{w^2}\right)\exp \left(\frac{-r^2}{w^2}\right),$$

(2)

where $L_p^{\left|l\right|}=(\cdot )$ is the Laguerre polynomials, and w is the beam width.

$$L_p^{\left|l\right|}\left(x\right)={\displaystyle \sum _{m=0}^p{\left(-1\right)}^m}\frac{\left(\left|l\right|+p\right)!}{(p-m)!(\left|l\right|+m)!m!}{x}^m,$$

(3)

Then, substituting Equation (2) into Equation (1), the LG-PEPV beams at the source plane can be written as

$$E_{\mathrm{LG}-\mathrm{PEPV}}\left(r,\phi \right)=\frac{\sqrt{2p!/\pi (\left|l\right|+p)!}}{w}{\left(\frac{\sqrt{2}r}{w}\right)}^{\left|l\right|}{L}_p^{\left|l\right|}\left(\frac{2r^2}{w^2}\right)\exp \left(\frac{-r^2}{w^2}\right)\exp \left[2\pi {\left(\frac{\mathit{rem}\left(l\phi ,2\pi \right)}{2\pi }\right)}^n\right],$$

(4)

Secondly, the coherent RP beams in the Cartesian coordinate system can be characterized [16]:

$$\mathbf{E}\left(r,\phi \right)=E_0\left(r,\phi \right)\left[r\left(\cos m\phi \cdot e_{\mathit{x}}+\sin m\phi \cdot e_{\mathit{y}}\right)\right],$$

(5)

where e_x and e_y are the unit vectors in the x and y directions, respectively; E₀(r, φ) is the electric field expression of the beams; m is the order of the cylindrical vector beams. In this paper, we only consider the RP beam, i.e., the case of m = 1. Substituting Equation (4) into Equation (5), we can obtain the mathematical model of the RP-LG-RSPEPV beams at the source plane.

Further, according to the unified theory of coherent and polarization, the second-order statistical properties of the vector partially coherent beams can be characterized by a 2 × 2 cross-spectral density (CSD) matrix, which can be expressed as follows [16]:

$$W\left(r_1,r_2\right)=\left[\begin{array}{cc}{W}_{xx}\left(r_1,r_2\right)& W_{xy}\left(r_1,r_2\right)\\ W_{yx}\left(r_1,r_2\right)& W_{yy}\left(r_1,r_2\right)\end{array}\right].$$

(6)

where r₁, r₂ are any two position vectors on the source plane, and the expression of CSD with LGSM is [28]

$$\begin{array}{cc}\hfill W_{\alpha \beta }\left(r_1,r_2\right)& =〈E_{\alpha }\left(r_1\right)E_{\beta }^{\ast }\left(r_2\right)〉,\left(\alpha =x,y;\beta =x,y\right),\hfill \\ & =A_{\alpha }{A}_{\beta }{B}_{\alpha \beta }\exp \left[-\frac{{\mathbf{r}}_1^2+{\mathbf{r}}_2^2}{w_0{}^2}-\frac{{({\mathbf{r}}_1-{\mathbf{r}}_2)}^2}{2{\delta }_{\alpha \beta }{}^2}\right]L_{p\prime }^0\left[\frac{{({\mathbf{r}}_1-{\mathbf{r}}_2)}^2}{2{\delta }_{\alpha \beta }{}^2}\right].\hfill \end{array}$$

(7)

In Equation (7), E_x(r) and E_y(r) denote two orthogonal random electric field components along the x and y directions, respectively. ‘*’ denotes a complex conjugate; ‘< >’ represents the ensemble average; A_x and A_y are the amplitudes in the x and y directions of electric field, respectively; and B_xy represents the correlation coefficient of the single point. It is worth mentioning that to achieve radial polarization, the conditions of $B_{xy(yx)}=B_{xx(yy)}=1$, ${\delta }_{xy(yx)}=B_{xx(yy)}=\delta$. δ is the spatial correlation length of the partially coherent beam [16].

Combining Equations (4) and (7), the theoretical model of RP-LG-RSPEPV beams on the source plane can be given as

$$\begin{array}{cc}\hfill W_{\alpha \beta }\left(r_1,r_2,0\right)& =\frac{2p!/\pi (\left|l\right|+p)!}{w^2}{\left(\frac{2r_1{r}_2}{w}\right)}^{\left|l\right|}{L}_p^{\left|l\right|}\left(\frac{2r_1{}^2}{w^2}\right)L_p^{\left|l\right|}\left(\frac{2r_2{}^2}{w^2}\right)\hfill \\ & \exp \left(-\frac{{\mathbf{r}}_1{}^2+{\mathbf{r}}_2{}^2}{w_0{}^2}-\frac{{({\mathbf{r}}_1-{\mathbf{r}}_2)}^2}{2\delta }\right)L_{p^{\prime }}^0\left(\frac{{\left({\mathbf{r}}_1-{\mathbf{r}}_2\right)}^2}{2{\delta }^2}\right)\hfill \\ & \exp \left[i2\pi {\left(\frac{\mathit{rem}\left(l{\phi }_1,2\pi \right)}{2\pi }\right)}^n-i2\pi {\left(\frac{\mathit{rem}\left(l{\phi }_2,2\pi \right)}{2\pi }\right)}^n\right],\hfill \end{array}$$

(8)

where the p and p’ are the radial index of the RP-LG-RSPEPV beams and the order of LGSM, respectively. When the p’ = 0, the LGSM reduces to the conventional Gaussian-correlated Schell-model (GSM).

2.2. Theory for the Tight-Focusing of RP-LG-RSPEPV Beams with LGSM

In this part, the theory for the tight-focusing of RP-RSPEPV beams with LGSM is introduced. Firstly, the schematic diagram of RP beams through a lens with high numerical aperture (NA) is shown in Figure 1.

According to the Richards-Wolf vectorial diffraction integral theory and the sine condition of the aplanatic lens, that is, ρ = f·sin θ, the vectorial electric field of the RP beam at the focal plane can be characterized [16]:

$$\begin{array}{c}{E}_f\left(\rho ,\varphi ,z\right)=\left[\begin{array}{c}{E}_{fx}\\ E_{fy}\\ E_{fz}\end{array}\right]=-\frac{{\mathit{ikn}}_{1}f}{2\pi }{\displaystyle {\int }_0^{{\theta }_{\max }}{\displaystyle {\int }_0^{2\pi }\left[\begin{array}{c}{A}_x\left(\theta ,\phi \right)\\ A_y\left(\theta ,\phi \right)\\ A_z\left(\theta ,\phi \right)\end{array}\right]\sqrt{\cos \theta }\sin \theta }}\\ \times \exp \left[{\mathit{ikn}}_1\left(z\cos \theta +\rho \sin \theta \cos \left(\phi -\varphi \right)\right)\right]d\phi d\theta ,\end{array}$$

(9)

With

$$\left[\begin{array}{c}{A}_x\left(\theta ,\phi \right)\\ A_y\left(\theta ,\phi \right)\\ A_z\left(\theta ,\phi \right)\end{array}\right]=\left[\begin{array}{c}{l}_x\left(\theta ,\phi \right)\left(\cos \theta +{\sin }^2\phi \left(1-\cos \theta \right)\right)+l_y\left(\theta ,\phi \right)\cos \phi \sin \phi \left(\cos \theta -1\right)\\ l_x\left(\theta ,\phi \right)\cos \phi \sin \phi \left(\cos \theta -1\right)+l_y\left(\theta ,\varphi \right)\left(\cos \theta +{\cos }^2\phi \left(1-\cos \theta \right)\right)\\ -l_x\left(\theta ,\varphi \right)\sin \theta \cos \phi -l_y\left(\theta ,\varphi \right)\sin \theta \sin \phi \end{array}\right]$$

(10)

where ρ, ϕ, z are the cylindrical coordinates of the focal plane; f is the focal length of the lens; k = 2π/λ is the wave number; n₁ is the refractive index of the surrounding medium; θ is the NA angle; the maximal NA angle is defined as θ_max = arcsin(NA/n); l_x(θ, and φ) and l_y(θ, φ) are the apodization functions of the aperture surface, which can be obtained by taking $x=\rho \cos \phi$ and $y=\rho \sin \phi$ into the $E_{\alpha }(x,y)$.

Further, when the RP-LG-RSPEPV beam with LGSM is focused by a high-NA objective, the statistical properties of the beam near the focused region can be given by a 3 × 3 CSD matrix:

$$W\left(r_1,r_2,{\varphi }_1,{\varphi }_2,z\right)=\left[\begin{array}{ccc}{W}_{xx}\left(r_1,r_2,{\varphi }_1,{\varphi }_2,z\right)& W_{xy}\left(r_1,r_2,{\varphi }_1,{\varphi }_2,z\right)& W_{xz}\left(r_1,r_2,{\varphi }_1,{\varphi }_2,z\right)\\ W_{yx}\left(r_1,r_2,{\varphi }_1,{\varphi }_2,z\right)& W_{yy}\left(r_1,r_2,{\varphi }_1,{\varphi }_2,z\right)& W_{yz}\left(r_1,r_2,{\varphi }_1,{\varphi }_2,z\right)\\ W_{zx}\left(r_1,r_2,{\varphi }_1,{\varphi }_2,z\right)& W_{zy}\left(r_1,r_2,{\varphi }_1,{\varphi }_2,z\right)& W_{zz}\left(r_1,r_2,{\varphi }_1,{\varphi }_2,z\right)\end{array}\right].$$

(11)

where

$$W_{f\alpha \beta }\left(r_1,{\varphi }_1,r_2,{\varphi }_2,z\right)=〈E_{f\alpha }\left(r_1,{\varphi }_1,z\right)E_{f\beta }{}^{*}\left(r_2,{\varphi }_2,z\right)〉.$$

(12)

In the focal plane, the expression for the diagonal elements of the CSD matrix can represent the average intensity distribution of the tightly focused RP-LG-RSPEPV beam with LGSM near the focal region. Specifically, it can be written as

$$\begin{array}{cc}\hfill W_{xx}\left(r_1,{\varphi }_1,r_2,{\varphi }_2,z\right)& =\frac{f^2}{{\lambda }^2}{\displaystyle \underset{0}{\overset{\alpha }{\int }}{\displaystyle \underset{0}{\overset{\alpha }{\int }}{\displaystyle \underset{0}{\overset{2\pi }{\int }}{\displaystyle \underset{0}{\overset{2\pi }{\int }}{W}_0\left({\theta }_1,{\theta }_2,{\phi }_1,{\phi }_2\right)}}}}\times {\left(\cos {\theta }_1\cos {\theta }_2\right)}^{3/2}{(\sin {\theta }_1\sin {\theta }_2)}^2\hfill \\ & \times \exp \left[-ikz\cos {\theta }_1-ik{r}_1\sin {\theta }_1\cos \left({\phi }_1-{\varphi }_1\right)\right]\hfill \\ & \times \exp \left[ikz\cos {\theta }_2+ik{r}_2\sin {\theta }_2\cos \left({\phi }_2-{\varphi }_2\right)\right]\hfill \\ & \times \cos {\phi }_1\cos {\phi }_{2}d{\theta }_{1}d{\theta }_{2}d{\phi }_{1}d{\phi }_2,\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill W_{yy}\left(r_1,{\varphi }_1,r_2,{\varphi }_2,z\right)& =\frac{f^2}{{\lambda }^2}{\displaystyle \underset{0}{\overset{\alpha }{\int }}{\displaystyle \underset{0}{\overset{\alpha }{\int }}{\displaystyle \underset{0}{\overset{2\pi }{\int }}{\displaystyle \underset{0}{\overset{2\pi }{\int }}{W}_0\left({\theta }_1,{\theta }_2,{\phi }_1,{\phi }_2\right)}}}}\times {\left(\cos {\theta }_1\cos {\theta }_2\right)}^{3/2}{(\sin {\theta }_1\sin {\theta }_2)}^2\hfill \\ & \times \exp \left[-ikz\cos {\theta }_1-ik{r}_1\sin {\theta }_1\cos \left({\phi }_1-{\varphi }_1\right)\right]\hfill \\ & \times \exp \left[ikz\cos {\theta }_2+ik{r}_2\sin {\theta }_2\cos \left({\phi }_2-{\varphi }_2\right)\right]\hfill \\ & \times \sin {\phi }_1\sin {\phi }_{2}d{\theta }_{1}d{\theta }_{2}d{\phi }_{1}d{\phi }_2,\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill W_{zz}\left(r_1,{\varphi }_1,r_2,{\varphi }_2,z\right)& =\frac{f^2}{{\lambda }^2}{\displaystyle \underset{0}{\overset{\alpha }{\int }}{\displaystyle \underset{0}{\overset{\alpha }{\int }}{\displaystyle \underset{0}{\overset{2\pi }{\int }}{\displaystyle \underset{0}{\overset{2\pi }{\int }}{W}_0\left({\theta }_1,{\theta }_2,{\phi }_1,{\phi }_2\right)}}}}\times {\left(\cos {\theta }_1\cos {\theta }_2\right)}^{1/2}\hfill \\ & \times \exp \left[-ikz\cos {\theta }_1-ik{r}_1\sin {\theta }_1\cos \left({\phi }_1-{\varphi }_1\right)\right]\hfill \\ & \times \exp \left[ikz\cos {\theta }_2+ik{r}_2\sin {\theta }_2\cos \left({\phi }_2-{\varphi }_2\right)\right]\hfill \\ & \times {(\sin {\theta }_1\sin {\theta }_2)}^{3}d{\theta }_{1}d{\theta }_{2}d{\phi }_{1}d{\phi }_2.\hfill \end{array}$$

(15)

where

$$\begin{array}{cc}\hfill W_0({\theta }_1,{\theta }_2,{\phi }_1,{\phi }_2)& =\frac{2p!/\pi (\left|l\right|+p)!}{w^2}{\left(\frac{2f^2\sin {\theta }_1\sin {\theta }_2\cos \left({\phi }_1-{\phi }_2\right)}{w^2}\right)}^l\hfill \\ & \times \exp \left[-\frac{f^2\left({\sin }^2{\theta }_1+{\sin }^2{\theta }_2\right)}{w^2}\right]L_p^{\left|l\right|}\left(\frac{2f{(\sin {\theta }_1)}^2}{w^2}\right)L_p^{\left|l\right|}\left(\frac{2f{(\sin {\theta }_2)}^2}{w^2}\right)\hfill \\ & \times \exp \left[i2\pi {\left(\frac{\mathit{rem}\left(l{\phi }_1,2\pi \right)}{2\pi }\right)}^n-i2\pi {\left(\frac{\mathit{rem}\left(l{\phi }_2,2\pi \right)}{2\pi }\right)}^n\right]\hfill \\ & \times \exp \left[-\frac{f^2\left({\sin }^2{\theta }_1+{\sin }^2{\theta }_2-\sin {\theta }_1\sin {\theta }_2\cos \left({\phi }_1-{\phi }_2\right)\right)}{2{\delta }^2}\right]\hfill \\ & \times L_{p\prime }^0\left(\frac{f^2\left({\sin }^2{\theta }_1+{\sin }^2{\theta }_2-\sin {\theta }_1\sin {\theta }_2\cos \left({\phi }_1-{\phi }_2\right)\right)}{2{\delta }^2}\right).\hfill \end{array}$$

(16)

Setting r₁ = r₂ = r, ϕ₁ = ϕ₂ = ϕ, the intensity of transverse, longitudinal and total component at the focal plane can be expressed as

$$I_{tra}\left(\rho ,\varphi ,z\right)=E_{fx}\left(\rho ,\varphi ,z\right)\cdot E_{fx}^{*}\left(\rho ,\varphi ,z\right)+E_{fy}\left(\rho ,\varphi ,z\right)\cdot E_{fy}^{*}\left(\rho ,\varphi ,z\right)$$

(17)

$$I_z\left(\rho ,\varphi ,z\right)=E_z\left(\rho ,\varphi ,z\right)\cdot E_z^{*}\left(\rho ,\varphi ,z\right)$$

(18)

$$I_{total}\left(\rho ,\varphi ,z\right)=I_{tra}\left(\rho ,\varphi ,z\right)+I_z\left(\rho ,\varphi ,z\right)$$

(19)

3. Results and Discussions

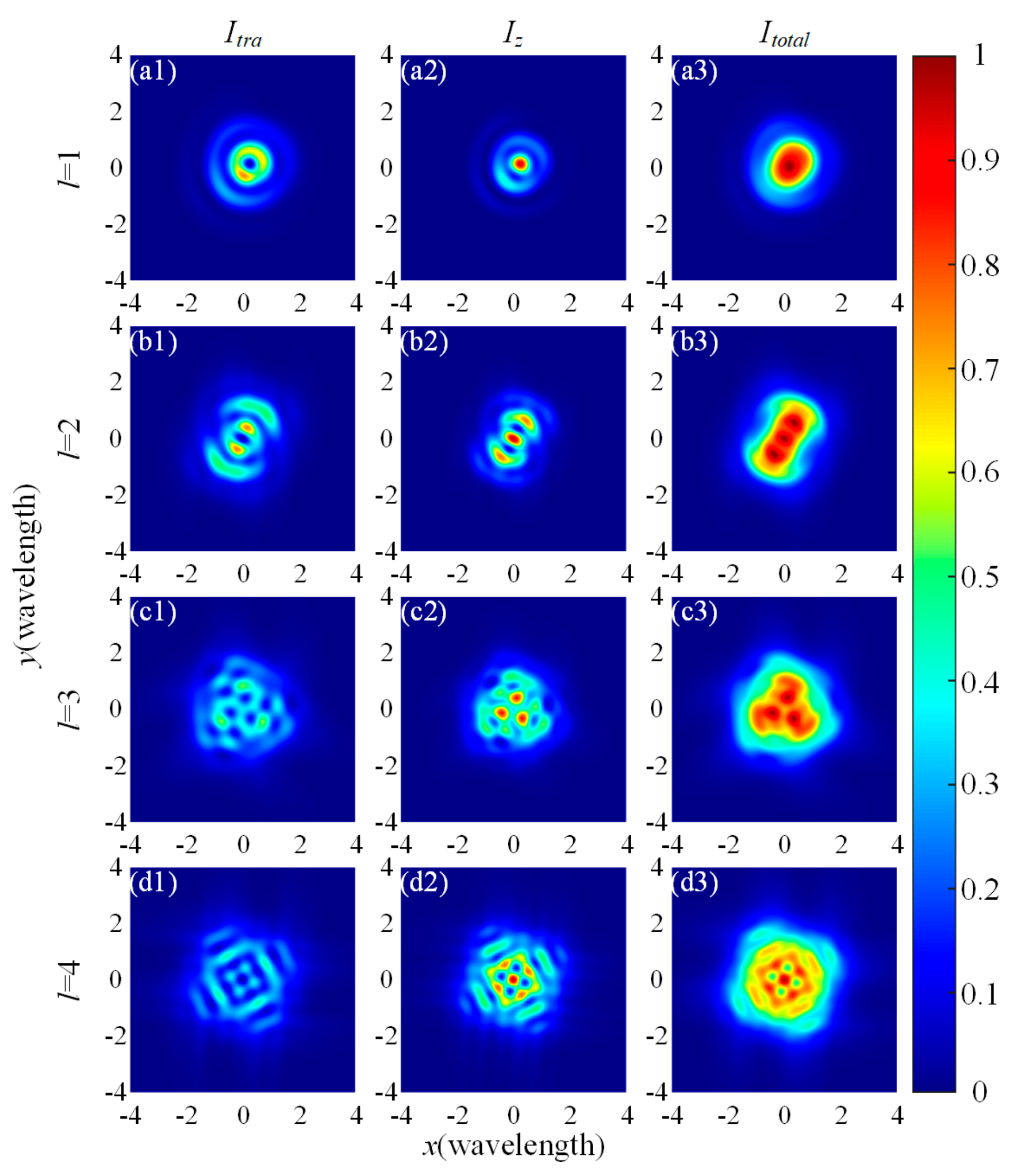
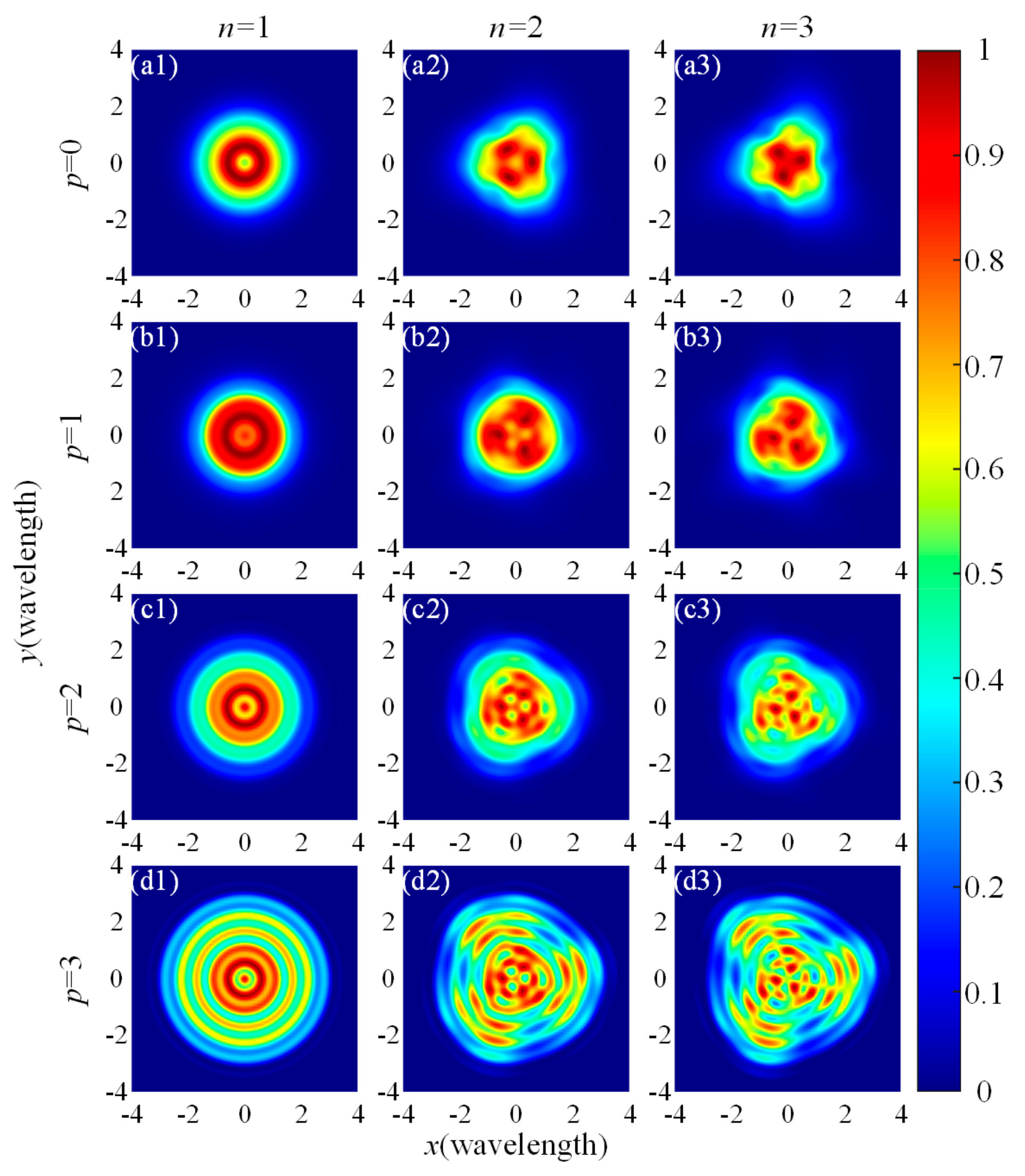
3.1. The Relationships between Tight-Focusing Properties and Topological Charges, the Power Exponent and Radial Index

In this section, we will investigate how the topological charge l, the power exponent n and the radial index p of the RP-LG-RSPEPV beams affect the intensity distribution of the beams passing through a high-NA lens by numerical simulation. In the following simulation calculation, the wavelength of the beams is set as 632.8 nm, the NA of the lens is set as 0.98, the beams’ width is w = 2 mm, the spatial correlation length of the beams is set as 5 mm, the refractive index of the surrounding medium n₁ = 1, and the focal length of the lens is f = 3 mm.

Figure 2 shows the normalized intensity distribution of each component of the different topological charges l of the tight focusing RP-LG-RSPEPV beams at the focal plane when the power exponent n = 4, the spatial correlation length δ = 0.005 m, the radial order p = 1, and the order of LGSM p’ = 1. It can be seen clearly that when the topological charge increases, the intensity of the transverse component decreases, while the intensity of the longitudinal component increases, which may mean that the beams with large waist width are more likely to generate longitudinal components with powerful intensity when passing through a high-NA lens. Additionally, the size of the beams becomes larger, and the outer ring of the total intensity distribution gradually becomes clear as the topological charges increases. This is because in the process of tight-focusing, when the beam size increases, the transverse component of light intensity weakens while the longitudinal component gradually increases. From Figure 2, the intensity of the outer ring is mainly concentrated in the longitudinal component of light intensity. In addition, Figure 2a1–a3 is an APEPV, because when the topological charge is 1, the expression of APEPV and RSPEPV is the same. In optical capture, particles can be quantitatively captured by adjusting the topological charge number [10].

To further reveal the influence of power exponent n and radial index p on the intensity distribution of RP-LG-RSPEPV beams at the focal plane, the intensity distribution of RP-LG-RSPEPV beams with a different power exponent n and radial index p, when the topological charges l = 3, the spatial correlation length δ = 0.005 m, and the order of LGSM p’ = 1, are shown in Figure 3. The results showed that the number of outer rings is equal to the radial index p. However, when the topological charge of the beam is small, it cannot be found in the total field distribution. As the topological charge increases, the outer ring becomes clearer. The extra outer ring is caused by the Bessel function in the tight-focusing mathematical model, and the larger the beam size, the more obvious the influence of the Bessel function. With the increase in the power index n, the light intensity is fan-like, and the larger the n, the clearer the contour of the fan-like light intensity. Observing Figure 3a2,b2, it can be found that the total field distribution of beam intensity was more concentrated with the increase in radial order p. It is worth noting that the hollow focal field of the rotationally symmetric focal spot may help to trap irregular particles or manipulate particles.

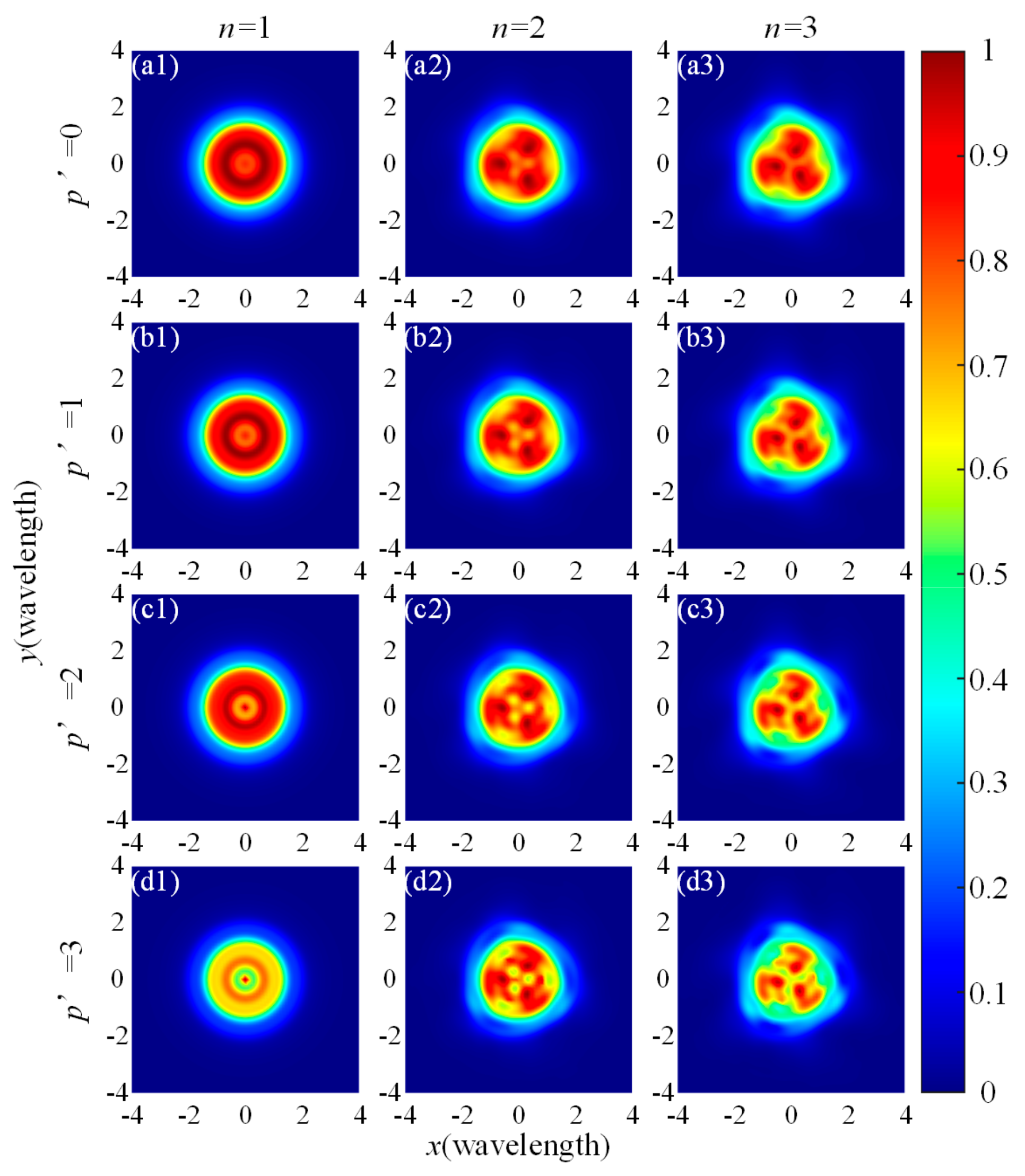
3.2. The Relationships between Tight-Focusing Properties and the Spatial Correlation Length, and the Order of LGSM

To learn more about the influence of the spatial correlation length δ and the order of LGSM p’ on the intensity distribution of RP-LG-RSPEPV after it is tightly focused, we calculated the normalized focal intensity distribution of topological charge l = 3, spatial correlation length δ = 0.005 m, and p = 1, with the change in the order of LGSM p’ and power exponent n in Figure 4. One can see from Figure 4 that the total intensity of the beam decreases when the order of LGSM p’ increases, which is more obvious when the power exponent n increases. In fact, the weakening of light intensity may reflect the weakening of coherence, because the lasers always have strong correlation and light intensity. However, this alone cannot explain why the RS-LG-RSPEPV beams have different degrees of coherence under different orders of LGSM. This can be described by the degree of coherence at the plane of z = 0, which itself can be given by

$${\mu }_{\alpha \beta }=\frac{W_{\alpha \beta }\left(r_1,r_2,0\right)}{\sqrt{W_{\alpha \alpha }\left(r_1,r_2,0\right)W_{\beta \beta }\left(r_1,r_2,0\right)}}(\alpha ,\beta =x,y,z).$$

(20)

Figure 5 shows the normalized focal intensity distribution of topological charge l = 3, power exponent n = 4, and p = 1, with the change in the order of LGSM p’ and the spatial correlation length. It is interesting to observe in Figure 5 that when the orders of LGSM p’ are 0 and 1, with the increase in the spatial coherence length δ, the total light intensity distribution profile at the focal plane gradually becomes clear, and the normalized light intensity is gradually reduced. On the contrary, the beam energy is more concentrated. When p’ is 2 and 3, the normalized light intensity gradually increases. Both the orders of LGSM and the spatial coherence length will affect the total intensity distribution of the focal spot in the RP-LG-RSPEPV with LGSM.

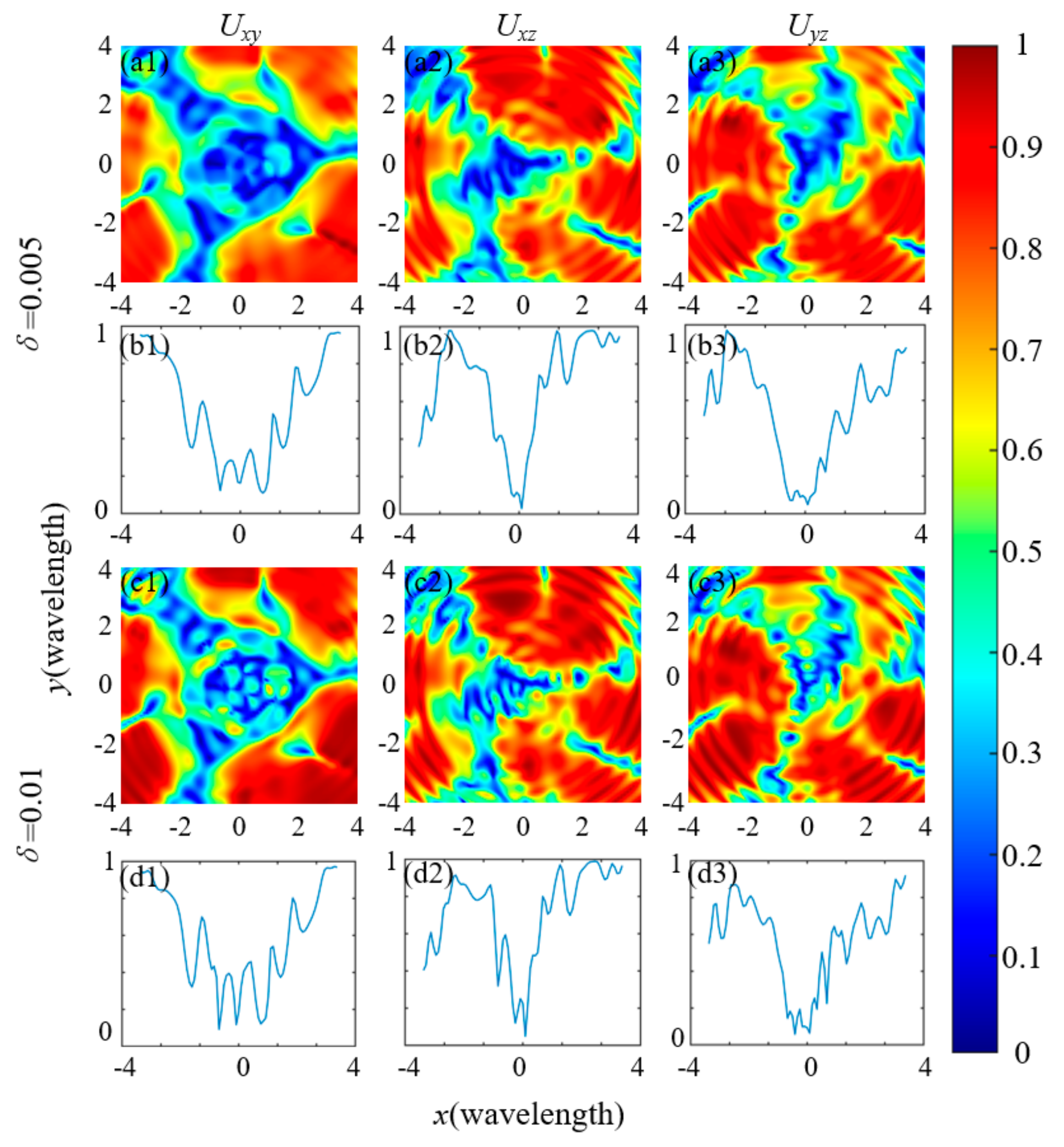
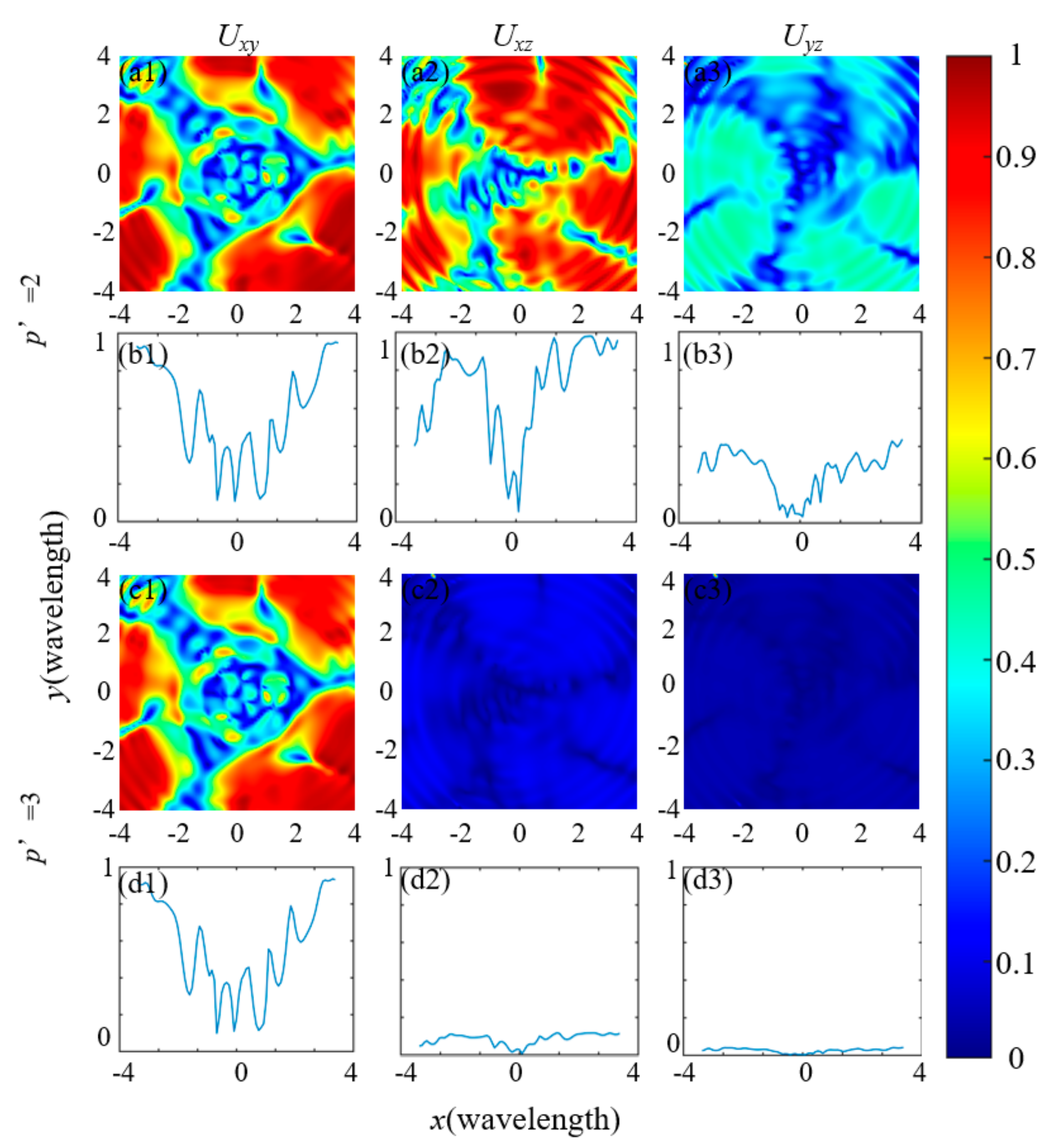
3.3. Degree of Polarization and Degree of Coherence of Tightly Focused RP-LG-RSPEPV Beams in the Transverse Direction

The degree of polarization and degree of coherence in the transverse mode of the beam in the focal plane will directly affect the total field distribution of the beam. Therefore, in this section, we discuss the Stokes parameters of the beam in the transverse section and the degree of coherence between the components. The Stokes parameters in the transverse plane of the RP-LG-RSPEPV are given as follows [29]:

$$\left\{\begin{array}{c}{S}_0\left(r_1,r_2,0\right)=W_{xx}\left(r_1,r_2,0\right)+W_{yy}\left(r_1,r_2,0\right)\\ S_1\left(r_1,r_2,0\right)=W_{xx}\left(r_1,r_2,0\right)-W_{yy}\left(r_1,r_2,0\right)\\ S_2\left(r_1,r_2,0\right)=W_{xy}\left(r_1,r_2,0\right)+W_{yx}\left(r_1,r_2,0\right)\\ S_3\left(r_1,r_2,0\right)=i\left(W_{yx}\left(r_1,r_2,0\right)+W_{xy}\left(r_1,r_2,0\right)\right)\end{array}\right.$$

(21)

Firstly, the Stokes parameters of different power exponents n in the transverse plane when the l = 3, p’ = 1, and δ = 0.005 m are given in Figure 6. It can be found that the increase in power exponent n makes the linear polarization component of the tightly focused RP-LG-RSPEPV beam irregular. However, there is still a spatially inhomogeneous polarization distribution, that is, it still has vector characteristics. In addition, subsequently, the tightly focused RP-LG-RSPEPV beam has a circularly polarized component, as shown in Figure 6d1–d3. This may be related to the conservation of total angular momentum, which produces spin angular momentum in the process of tight-focusing [30].

Further, we can learn more about the polarization of the RP-LG-RSPEPV beams with different spatial coherence lengths δ and l = 3, p’ = 1, and n = 4 after tight-focusing by looking to Figure 7. It can be found that the values of the S₁, S₂, S₃ in the majority of the tightly focused RP-LG-RSPEPV beams are less than 1, which indicates that the tight-focusing will depolarize the RP-LG-RSPEPV beams. This phenomenon is more obvious for the S₃ component of the RP-LG-RSPEPV beams in the transverse plane, when the spatial coherence is small. However, with the change in the spatial coherence length δ, depolarization has little effect on S₁ and S₂.

Then, the degree of coherence between each component is given in Figure 8, when the spatial coherence length δ changes with topological charge l = 3, radial index p = 1, the order of LGSM p’ = 1, and the power exponent n = 4. It can be found that the spatial coherence length will affect the coherence between the components of the LG beam. The larger the spatial coherence length, the higher the degree of the coherence in the RP-LG-RSPEPV beams. Besides, any two components of a tightly focused beam are partially coherent, which indicates that tight-focusing will reduce the correlation between any two components of the three orthogonal electric field components. The influence of the coherence width on the coherence degree may be affected by the special correlation function of the incident beam. Controlling the structure of the correlation function can determine the transverse field distribution and the longitudinal field distribution of the closely focused radially polarized partially coherent beam. In practical applications, we can adjust multiple parameters of the RP-LG-RSPEPV beam to adjust the light field distribution of the beam.

In addition, the degree of coherence between each component is shown in Figure 9, when the order of LGSM p’ changes with topological charge l = 3, radial index p = 1, the spatial coherence length δ = 0.015 m, and the power exponent n = 4. The results indicated that as the order of LGSM increases, the coherence of the beam decreases. The increase in the order of LGSM had a greater impact on the degree of coherence U_xz and U_yz, but had a smaller impact on the degree of coherence U_xy.

4. Conclusions

In this paper, RP-LG-RSPEPV beams with LGSM were introduced. The tight-focusing properties of the beams, including intensity distribution, the degree of polarization and coherence, and Stokes parameters, are studied based on Richards-Wolf diffraction vectorial integral theory. Moreover, the relationship between the tight-focusing properties of RP-LG-RSPEPV beams with LGSM and its power exponent n, radial index p, and topological charges l was explored. The results show that tight-focusing will cause the depolarization of the RP-LG beam, especially the component S₃ in the transverse plane. The decrease in spatial coherence length δ and the increase in the order of LGSM p’ will reduce the coherence of RP-LG-PSPEPV beams, especially the components U_xz and U_yz. The RP-LG-RSPEPV beams’ intensity can be adjusted by changing the parameters of the beam. This work may be of great significance for optical tweezers and particle manipulation.