A Highly Birefringent Photonic Crystal Fiber with Three Rows of Circular Air Holes
Abstract
:1. Introduction
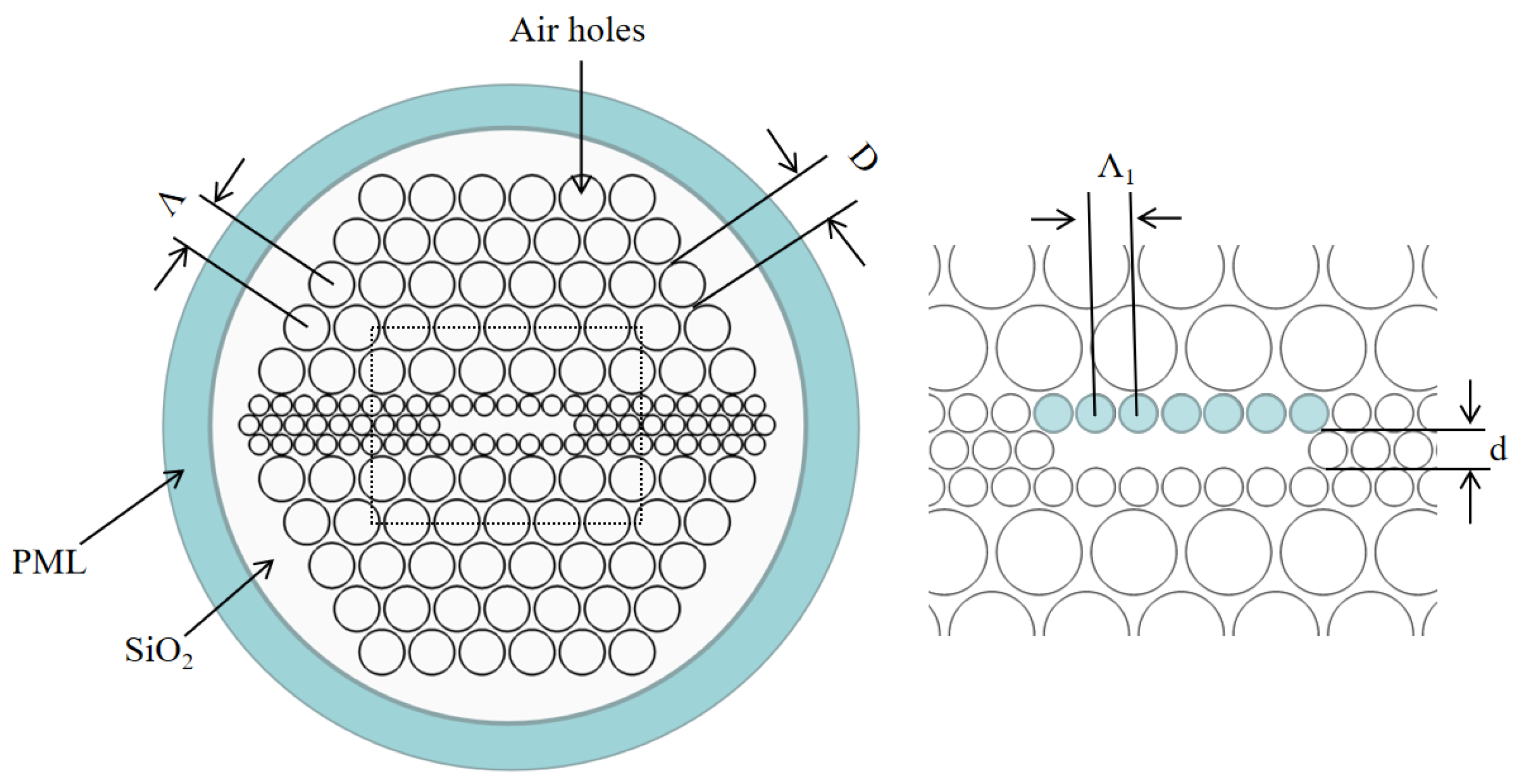
2. Basic Theory
3. Numerical Simulation and Result Analysis
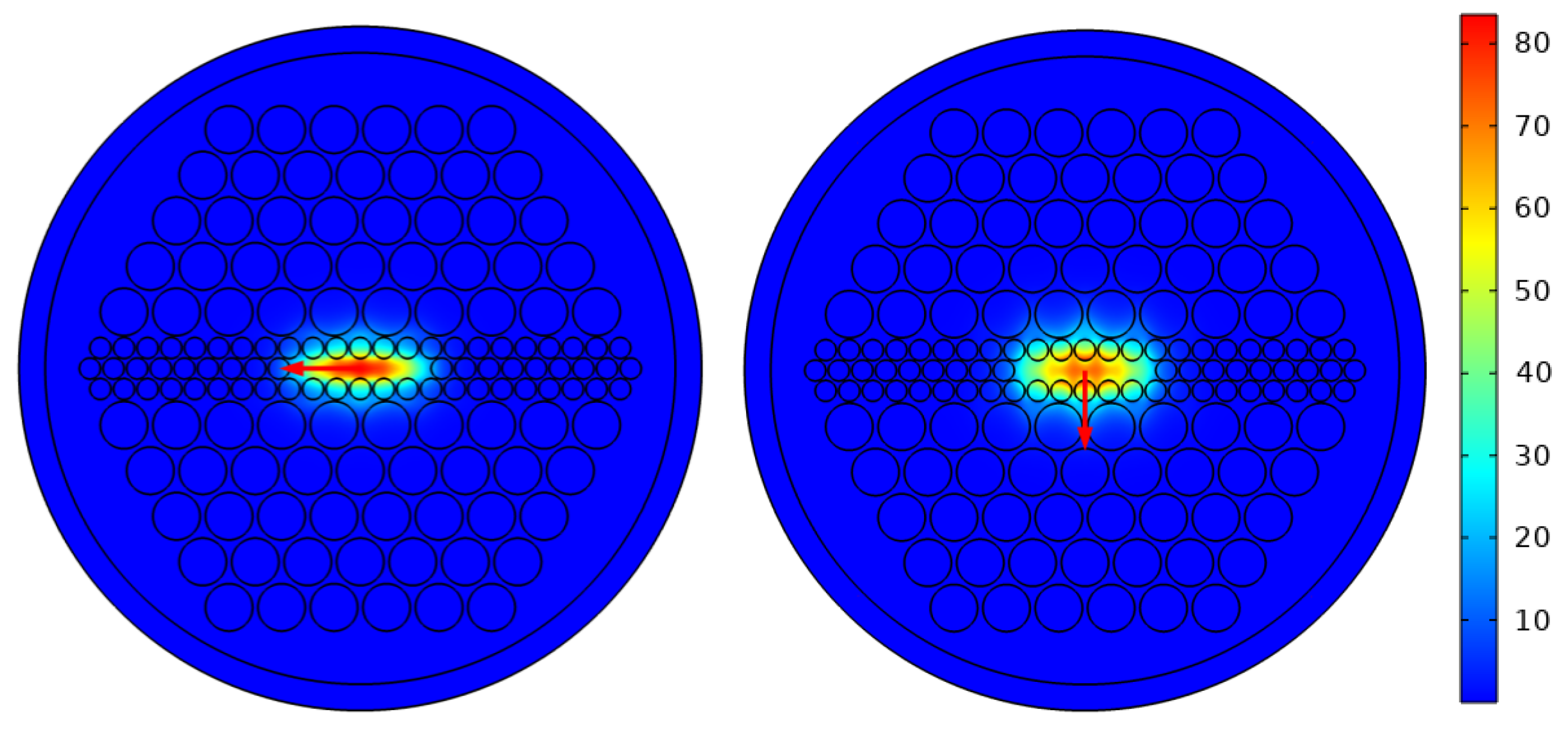
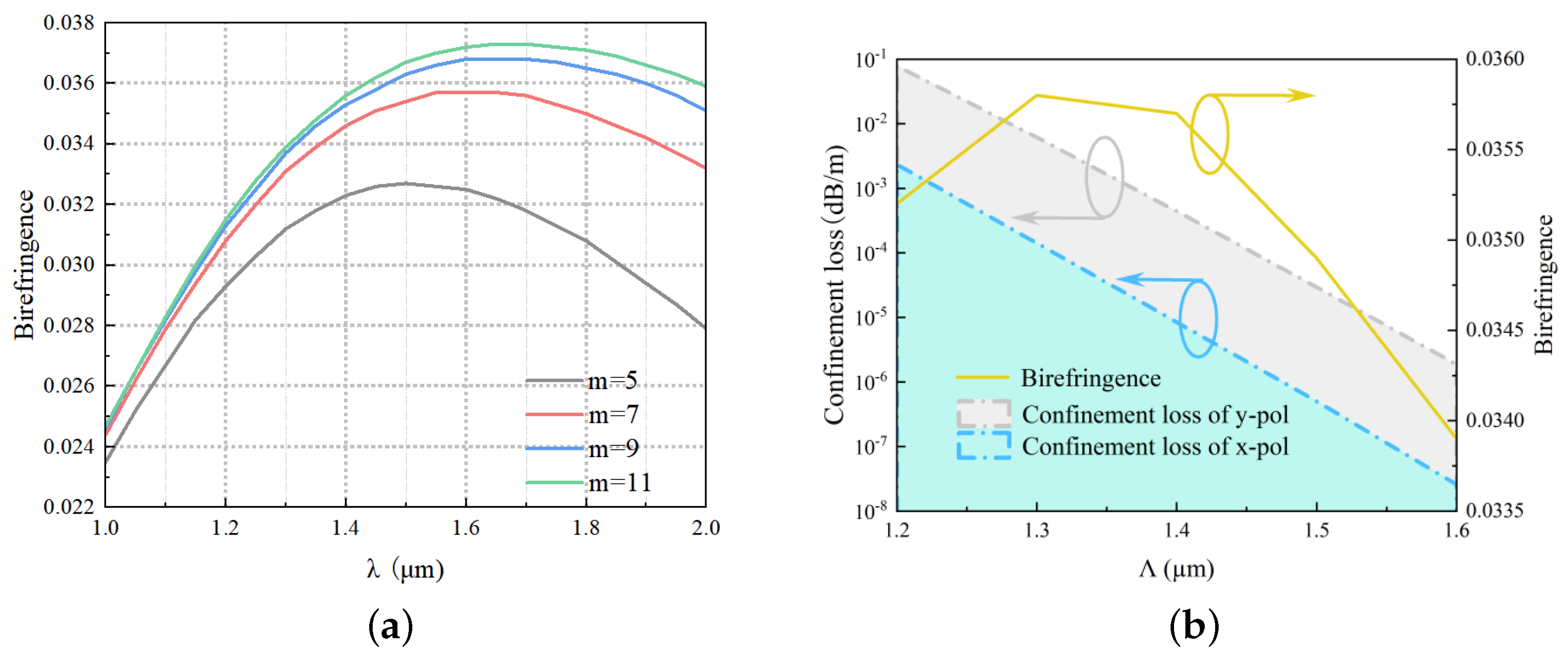
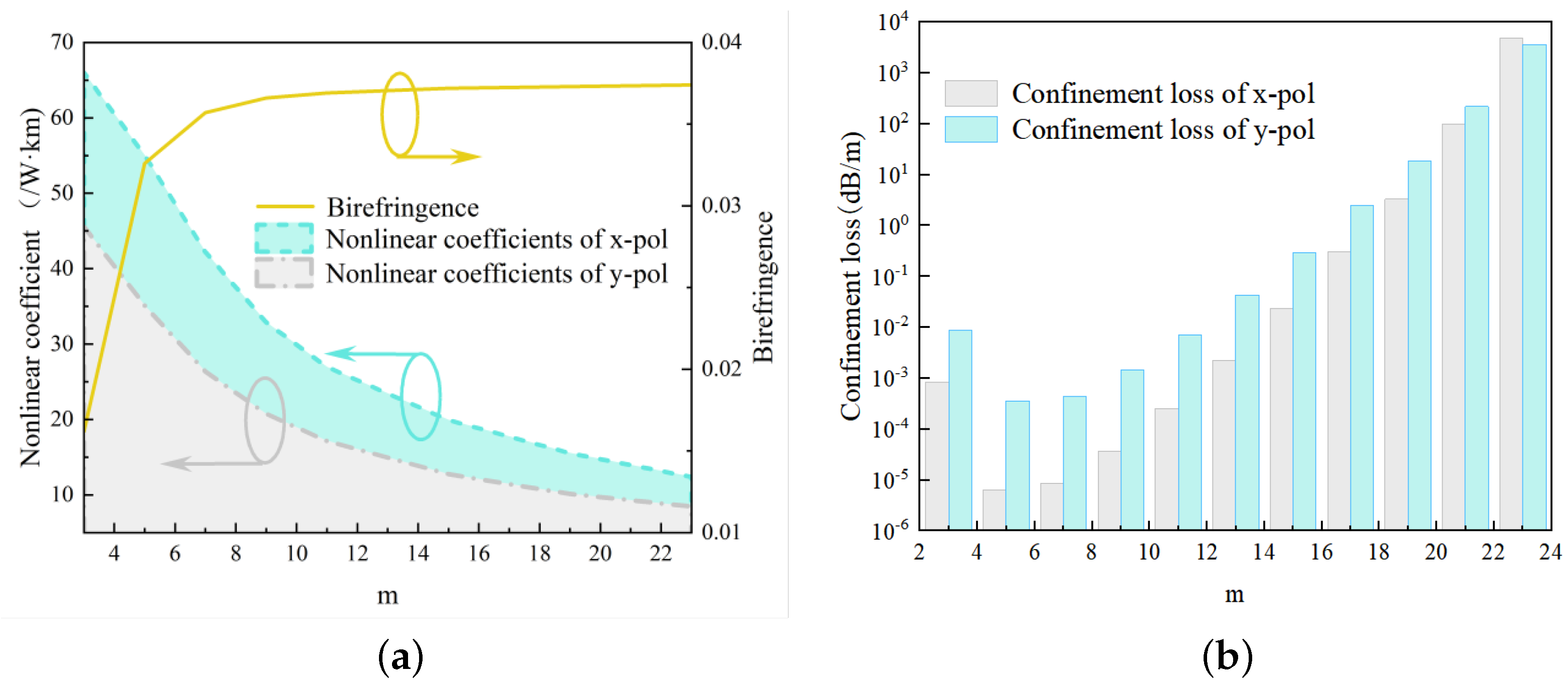
3.1. Birefringence
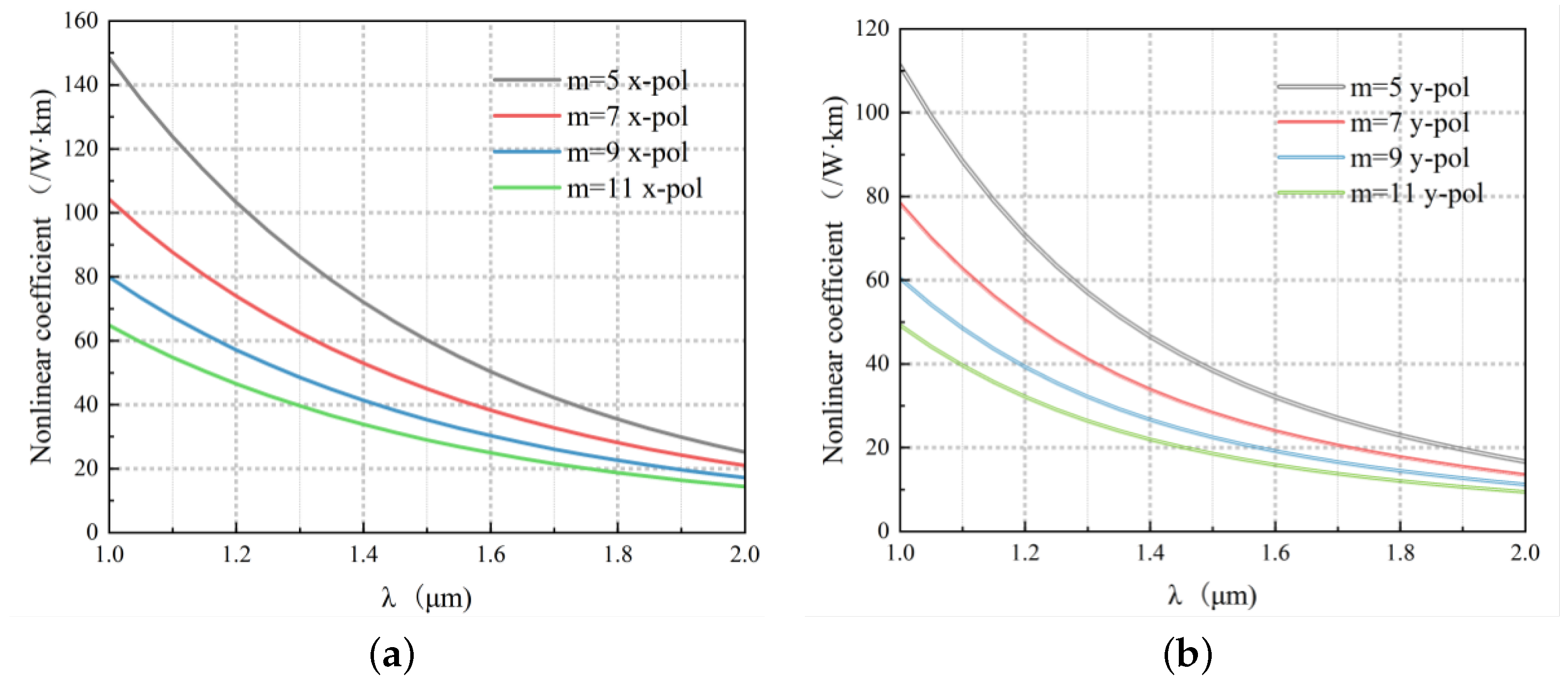
3.2. Nonlinear Coefficient
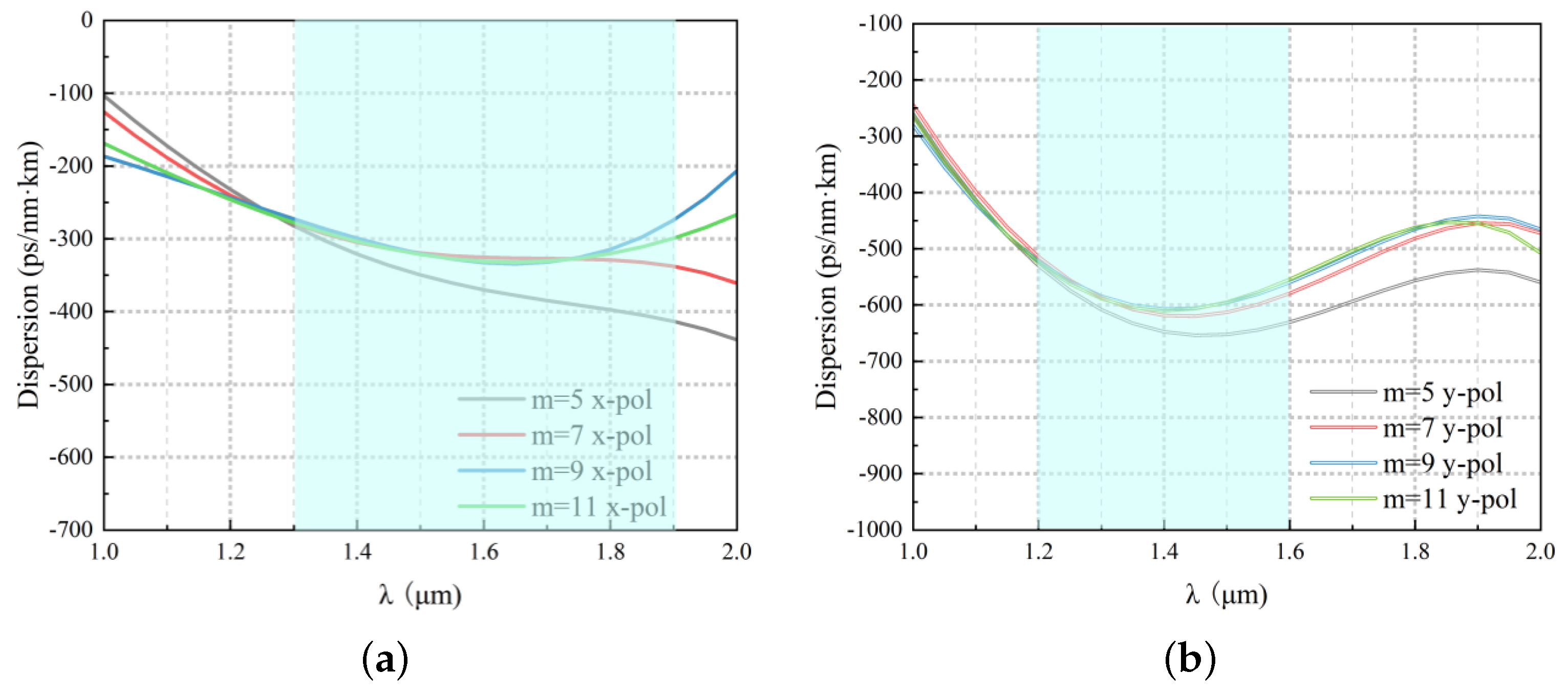
3.3. Dispersion
3.4. Confinement Loss
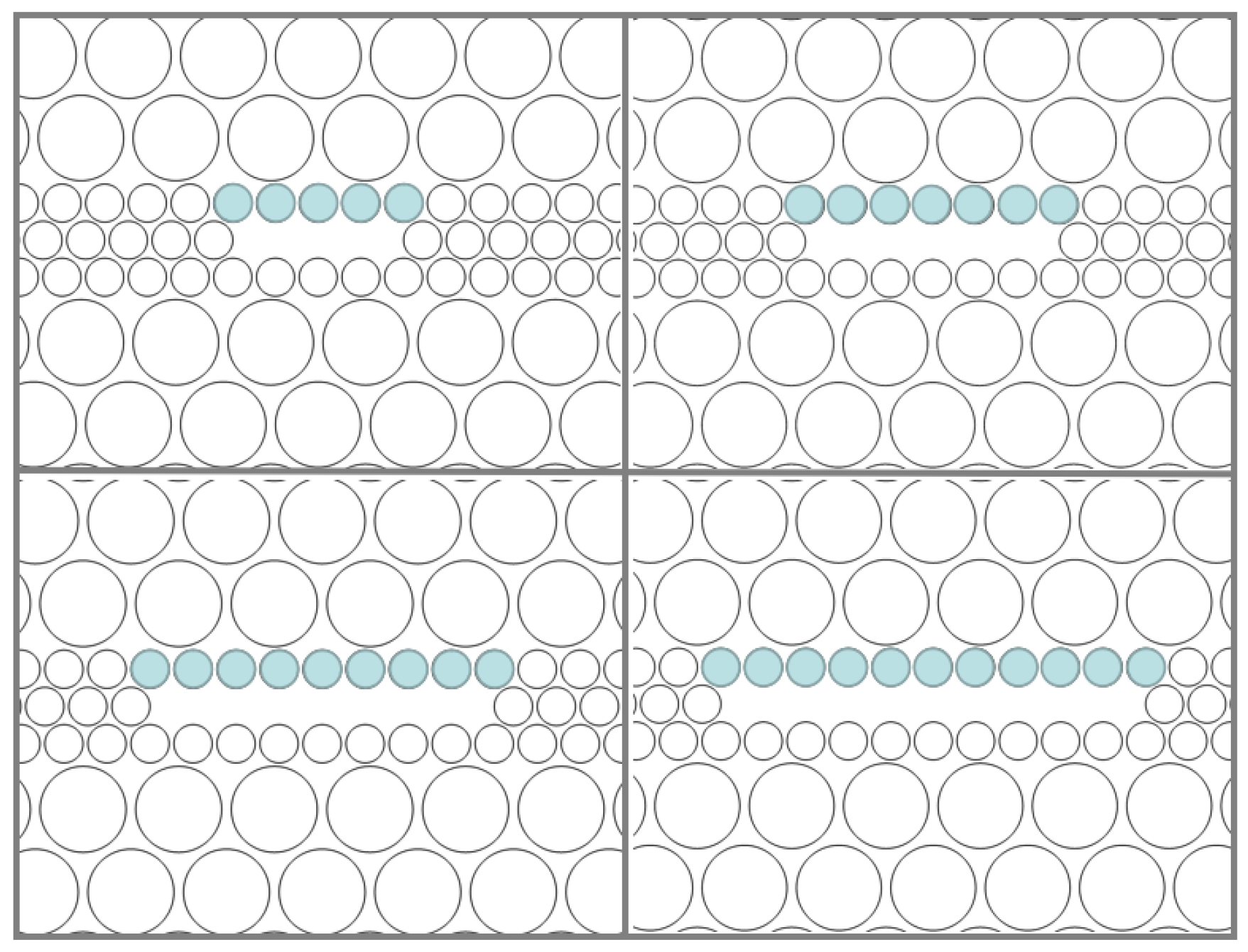
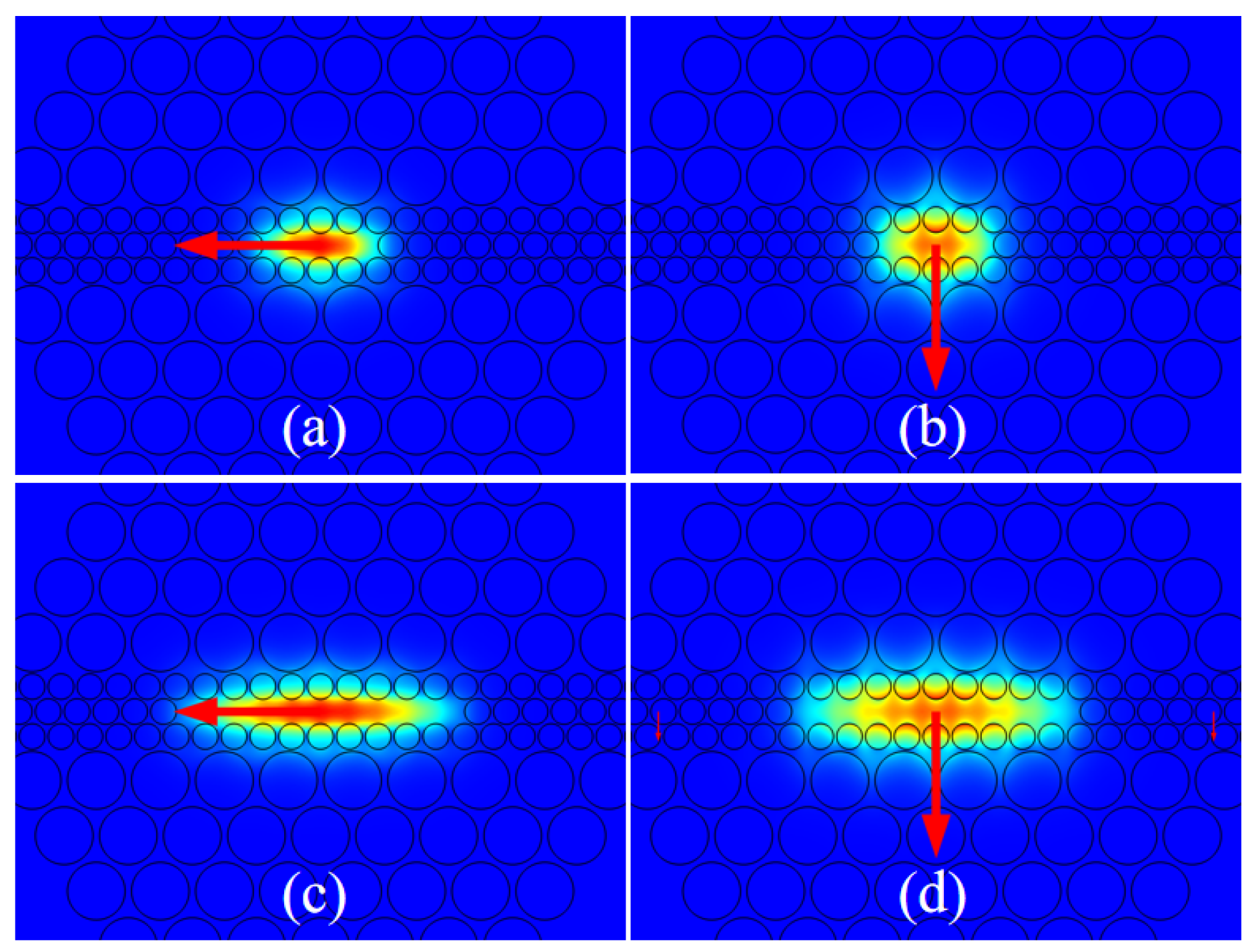
3.5. Exploring Model Limits
3.6. Manufacturing Feasibility
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Knight, J.; Birks, T.; Russell, P.S.J.; Atkin, D. All-silica single-mode optical fiber with photonic crystal cladding. Opt. Lett. 1996, 21, 1547–1549. [Google Scholar] [CrossRef] [PubMed]
- Paul, B.K.; Ahmed, K.; Asaduzzaman, S.; Islam, M.S. Folded cladding porous shaped photonic crystal fiber with high sensitivity in optical sensing applications: Design and analysis. Sens. Bio-Sens. Res. 2017, 12, 36–42. [Google Scholar] [CrossRef]
- Mortensen, N.A.; Nielsen, M.D.; Folkenberg, J.R.; Jakobsen, C.; Simonsen, H.R. Photonic crystal fiber with a hybrid honeycomb cladding. Opt. Express 2004, 12, 468–472. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, K.; Morshed, M. Design and numerical analysis of microstructured-core octagonal photonic crystal fiber for sensing applications. Sens. Bio-Sens. Res. 2016, 7, 1–6. [Google Scholar] [CrossRef]
- Agrawal, A.; Kejalakshmy, N.; Rahman, B.A.; Grattan, K.T. Soft glass equiangular spiral photonic crystal fiber for supercontinuum generation. IEEE Photonics Technol. Lett. 2009, 21, 1722–1724. [Google Scholar] [CrossRef]
- Bala, A.; Chowdhury, K.R.; Mia, M.B.; Faisal, M. Highly birefringent, highly negative dispersion compensating photonic crystal fiber. Appl. Opt. 2017, 56, 7256–7261. [Google Scholar] [CrossRef]
- Liang, S.; Yang, Y.; Kang, S.; Zhang, Y.; Sheng, X.; Lou, S.; Wang, X.; Zhang, W.; Zhao, T. Influences of asymmetrical geometric structures on the birefringence of index-guiding photonic crystal fiber. Optik 2019, 180, 973–983. [Google Scholar] [CrossRef]
- Sharma, M.; Dixit, V.; Konar, S.; Ahmed, K.; Dhasarathan, V. Endlessly single-mode photonic crystal fiber with high birefringence for sensing applications. Mod. Phys. Lett. B 2020, 34, 2050077. [Google Scholar] [CrossRef]
- Mondal, K. A comparative study of birefringence in photonic crystal fiber employing various lattice geometries with all-circular air holes. Optik 2020, 215, 164699. [Google Scholar] [CrossRef]
- Yang, T.; Zhang, L.; Shi, Y.; Liu, S.; Dong, Y. A highly birefringent photonic crystal fiber for terahertz spectroscopic chemical sensing. Sensors 2021, 21, 1799. [Google Scholar] [CrossRef] [PubMed]
- Saha, R.; Hossain, M.M.; Rahaman, M.E.; Mondal, H.S. Design and analysis of high birefringence and nonlinearity with small confinement loss photonic crystal fiber. Front. Optoelectron. 2019, 12, 165–173. [Google Scholar] [CrossRef]
- Faisal, M.; Bala, A.; Roy Chowdhury, K.; Mia, M.B. Highly birefringent large negative dispersion-flattened photonic crystal fibre for broadband residual dispersion compensation. J. Mod. Opt. 2018, 65, 1577–1583. [Google Scholar] [CrossRef]
- Mia, M.M.A.; Islam, M.A.; Miah, M.S.; Bhowmik, B.; Mahir, S.M.; Biswas, S.K. Highly Birefringent Dispersion Compensating Index Guiding Square Photonic Crystal Fiber with Large Nonlinearity for Fiber Optic Transmission System. In Proceedings of the 2020 International Conference on Computer, Electrical & Communication Engineering (ICCECE), Kolkata, India, 17–18 January 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–5. [Google Scholar]
- Hossain, S.; Shah, S.; Faisal, M. Ultra-high birefringent, highly nonlinear Ge20Sb15Se65 chalcogenide glass photonic crystal fiber with zero dispersion wavelength for mid-infrared applications. Optik 2021, 225, 165753. [Google Scholar] [CrossRef]
- Alishacelestin, X.; Raja, A.S.; Muthu, K.E.; Selvendran, S. A novel ultra-high birefringent photonic crystal fiber for nonlinear applications. Braz. J. Phys. 2021, 51, 605–617. [Google Scholar] [CrossRef]
- Choyon, A.S.J.; Chowdhury, R. Multifunctional chalcogenide (As2S3, As2Se3) dual-core photonic crystal fiber with elliptical air-hole for mid-IR optical communications: Design and analysis. Optik 2022, 258, 168857. [Google Scholar] [CrossRef]
- Yang, T.-Y.; Jiang, H.-M.; Wang, E.-L.; Xie, K. Photonic crystal fibers with large birefringence and high nonlinearity in near-infrared band. J. Infrared Millim. Waves 2015, 35, 350–354. [Google Scholar]
- Dadkhahfard, S.; Mirsalehi, M.M. Highly birefringent photonic crystal fiber with flattened negative dispersion over the S+ C+ L+ U wavelength bands. In Proceedings of the 2017 Iranian Conference on Electrical Engineering (ICEE), Tehran, Iran, 2–4 May 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1655–1659. [Google Scholar]
- Liu, Q.; Ren, Z.; Liu, W.; Sun, Y.; Lv, T.; Liu, C.; Lu, W.; Li, B.; Jiang, Y.; Sun, T.; et al. A photonic quasi-crystal fiber composed of circular air holes with high birefringence and low confinement loss. Optik 2021, 231, 166497. [Google Scholar] [CrossRef]
- Alishacelestin, X.; Raja, A.S.; Selvendran, S. A highly birefringent photonic crystal fiber with compact cladding layers suitable for fiber optic gyroscope application. Laser Phys. 2021, 31, 065101. [Google Scholar] [CrossRef]
- Naeem, K.; Chung, Y.; Kim, B.H. Sagnac interferometer based on a highly-birefringent two-core PCF: Theory, experiment, and sensing characteristics. J. Light. Technol. 2020, 38, 5177–5190. [Google Scholar] [CrossRef]
- Hu, D.J.J.; Ho, H.P. Recent advances in plasmonic photonic crystal fibers: Design, fabrication and applications. Adv. Opt. Photonics 2017, 9, 257–314. [Google Scholar] [CrossRef]
- Kim, B.; Kim, T.H.; Cui, L.; Chung, Y. Twin core photonic crystal fiber for in-line Mach-Zehnder interferometric sensing applications. Opt. Express 2009, 17, 15502–15507. [Google Scholar] [CrossRef]
- Chen, H.; Wei, H.; Liu, T.; Zhou, X.; Yan, P.; Chen, Z.; Chen, S.; Li, J.; Hou, J.; Lu, Q. All-fiber-integrated high-power supercontinuum sources based on multi-core photonic crystal fibers. IEEE J. Sel. Top. Quantum Electron. 2014, 20, 64–71. [Google Scholar] [CrossRef]
- Katsuyama, T.; Matsumura, H.; Suganuma, T. Propagation characteristics of single polarization fibers. Appl. Opt. 1983, 22, 1748–1753. [Google Scholar] [CrossRef]
- Noda, J.; Okamoto, K.; Sasaki, Y. Polarization-maintaining fibers and their applications. J. Light. Technol. 1986, 4, 1071–1089. [Google Scholar] [CrossRef]
- Varnham, M.; Payne, D.; Birch, R.; Tarbox, E. Single-polarisation operation of highly birefringent bow-tie optical fibres. Electron. Lett. 1989, 25, S42–S44. [Google Scholar] [CrossRef]
- Ghanbari, A.; Olyaee, S. Highly Nonlinear Composite-Photonic Crystal Fibers with Simplified Manufacturing Process and Efficient Mid-IR Applications. Crystals 2023, 13, 226. [Google Scholar] [CrossRef]
- Jones, D.J.; Diddams, S.A.; Ranka, J.K.; Stentz, A.; Windeler, R.S.; Hall, J.L.; Cundiff, S.T. Carrier-envelope phase control of femtosecond mode-locked lasers and direct optical frequency synthesis. Science 2000, 288, 635–639. [Google Scholar] [CrossRef] [PubMed]
- Holzwarth, R.; Udem, T.; Hänsch, T.W.; Knight, J.; Wadsworth, W.; Russell, P.S.J. Optical frequency synthesizer for precision spectroscopy. Phys. Rev. Lett. 2000, 85, 2264. [Google Scholar] [CrossRef] [PubMed]
- Udem, T.; Holzwarth, R.; Hänsch, T.W. Optical frequency metrology. Nature 2002, 416, 233–237. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Zhao, Y.; Nelson, J.; Chen, Z.; Windeler, R.S. Ultrahigh-resolution optical coherence tomography by broadband continuum generation from a photonic crystal fiber. Opt. Lett. 2003, 28, 182–184. [Google Scholar] [CrossRef]
- Humbert, G.; Wadsworth, W.; Leon-Saval, S.; Knight, J.; Birks, T.; Russell, P.S.J.; Lederer, M.; Kopf, D.; Wiesauer, K.; Breuer, E.; et al. Supercontinuum generation system for optical coherence tomography based on tapered photonic crystal fibre. Opt. Express 2006, 14, 1596–1603. [Google Scholar] [CrossRef] [PubMed]
- Hartl, I.; Li, X.; Chudoba, C.; Ghanta, R.; Ko, T.; Fujimoto, J.; Ranka, J.; Windeler, R. Ultrahigh-resolution optical coherence tomography using continuum generation in an air–silica microstructure optical fiber. Opt. Lett. 2001, 26, 608–610. [Google Scholar] [CrossRef] [PubMed]
- Loh, W.; Laming, R.I.; Robinson, N.; Cavaciuti, A.; Vaninetti, F.; Anderson, C.; Zervas, M.; Cole, M. Dispersion compensation over distances in excess of 500 km for 10-Gb/s systems using chirped fiber gratings. IEEE Photonics Technol. Lett. 1996, 8, 944–946. [Google Scholar] [CrossRef]
- Gruner-Nielsen, L.; Wandel, M.; Kristensen, P.; Jorgensen, C.; Jorgensen, L.V.; Edvold, B.; Pálsdóttir, B.; Jakobsen, D. Dispersion-compensating fibers. J. Light. Technol. 2005, 23, 3566–3579. [Google Scholar] [CrossRef]
- Russell, P. Photonic crystal fibers. Science 2003, 299, 358–362. [Google Scholar] [CrossRef] [PubMed]
- Buczynski, R. Photonic crystal fibers. Acta Phys. Pol. A 2004, 106, 141–167. [Google Scholar] [CrossRef]
- Mori, A. 1.5 μm band zero-dispersion shifted tellurite photonic crystal fibre with a nonlinear coefficient γ of 675 W−1·km−1. ECOC2004 Stockh. 2004, 10025088940. [Google Scholar]
- Selleri, S.; Vincetti, L.; Cucinotta, A.; Zoboli, M. Complex FEM modal solver of optical waveguides with PML boundary conditions. Opt. Quantum Electron. 2001, 33, 359–371. [Google Scholar] [CrossRef]
- Kristensen, J.T.; Houmann, A.; Liu, X.; Turchinovich, D. Low-loss polarization-maintaining fusion splicing of single-mode fibers and hollow-core photonic crystal fibers, relevant for monolithic fiber laser pulse compression. Opt. Express 2008, 16, 9986–9995. [Google Scholar] [CrossRef]
- Benabid, F. Hollow-core photonic bandgap fibre: New light guidance for new science and technology. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2006, 364, 3439–3462. [Google Scholar] [CrossRef]
- Wadsworth, W.; Witkowska, A.; Leon-Saval, S.; Birks, T. Hole inflation and tapering of stock photonic crystal fibres. Opt. Express 2005, 13, 6541–6549. [Google Scholar] [CrossRef] [PubMed]
- Chaudhuri, P.R.; Roy, S. Determining properties of fabricated index-guiding photonic crystal fibers using SEM micrograph and mode convergence algorithm. J. Light. Technol. 2008, 26, 379–386. [Google Scholar] [CrossRef]
- Xiao, L.; Demokan, M.; Jin, W.; Wang, Y.; Zhao, C.L. Fusion splicing photonic crystal fibers and conventional single-mode fibers: Microhole collapse effect. J. Light. Technol. 2007, 25, 3563–3574. [Google Scholar] [CrossRef]
- Holdynski, Z.; Napierala, M.; Jozwik, M.; Szostkiwicz, L.; Mergo, P.; Nasilowski, T. Three fold symmetric microstructured fibers for customized sub-nanosecond supercontinuum generation. Opt. Commun. 2017, 393, 45–48. [Google Scholar] [CrossRef]
- Cho, T.Y.; Kim, G.H.; Lee, K.I.; Lee, S.B.; Jeong, J.M. Study on the fabrication process of polarization maintaining photonic crystal fibers and their optical properties. J. Opt. Soc. Korea 2008, 12, 19–24. [Google Scholar] [CrossRef]
- Martynkien, T.; Statkiewicz-Barabach, G.; Olszewski, J.; Wojcik, J.; Mergo, P.; Geernaert, T.; Sonnenfeld, C.; Anuszkiewicz, A.; Szczurowski, M.K.; Tarnowski, K.; et al. Highly birefringent microstructured fibers with enhanced sensitivity to hydrostatic pressure. Opt. Express 2010, 18, 15113–15121. [Google Scholar] [CrossRef]
- Geernaert, T.; Kalli, K.; Koutsides, C.; Komodromos, M.; Nasilowski, T.; Urbanczyk, W.; Wojcik, J.; Berghmans, F.; Thienpont, H. Point-by-point fiber Bragg grating inscription in free-standing step-index and photonic crystal fibers using near-IR femtosecond laser. Opt. Lett. 2010, 35, 1647–1649. [Google Scholar] [CrossRef]
- Martynkien, T.; Szpulak, M.; Statkiewicz, G.; Golojuch, G.; Olszewski, J.; Urbanczyk, W.; Wojcik, J.; Mergo, P.; Makara, M.; Nasilowski, T.; et al. Measurements of sensitivity to hydrostatic pressure and temperature in highly birefringent photonic crystal fibers. Opt. Quantum Electron. 2007, 39, 481–489. [Google Scholar] [CrossRef]
- Prabu, K.; Malavika, R. Highly birefringent photonic crystal fiber with hybrid cladding. Opt. Fiber Technol. 2019, 47, 21–26. [Google Scholar] [CrossRef]
- Hasan, M.R.; Islam, M.A.; Rifat, A.A.; Hasan, M.I. A single-mode highly birefringent dispersion-compensating photonic crystal fiber using hybrid cladding. J. Mod. Opt. 2017, 64, 218–225. [Google Scholar] [CrossRef]
- Halder, A.; Anower, M.S. Relative dispersion slope matched highly birefringent and highly nonlinear dispersion compensating hybrid photonic crystal fiber. Photonics Nanostruct.-Fundam. Appl. 2019, 35, 100704. [Google Scholar] [CrossRef]
- Yu, B.; Rui, H. A simple design of highly birefringent and nonlinear photonic crystal fiber with ultra-flattened dispersion. Opt. Quantum Electron. 2019, 51, 1–13. [Google Scholar] [CrossRef]
- Wang, E.; Cheng, P.; Zhao, W.; Li, J.; Han, Q.; Zhou, X. Photonic crystal fibers with high birefringence and multiple zero dispersion wavelengths. Opt. Fiber Technol. 2020, 58, 102309. [Google Scholar] [CrossRef]
- Hossain, M.M.; Ahsan, M.S.; Sikder, N.; Rahaman, M.E.; Al-Mamun Bulbul, A.; Mondal, H.S. High birefringence and broadband dispersion compensation photonic crystal fiber. J. Opt. Commun. 2021, 000010151520200140. [Google Scholar] [CrossRef]


| The Variation of d | Birefringence | NC | CL |
|---|---|---|---|
| (W/km) | (dB/m) | ||
| −5% | 3.48 × 10 | 40.28(x), 25.59(y) | 4.37 × 10 |
| 0 | 3.57 × 10 | 41.47(x), 26.05(y) | 8.47 × 10 |
| +5% | 3.61 × 10 | 41.58(x), 26.27(y) | 2.86 × 10 |
| References | Birefringence | NC | CL | Type |
|---|---|---|---|---|
| (W/km) | (dB/m) | |||
| [51] | 1.46 × 10 | 76.41 | 6.1 × 10 | elliptical |
| [18] | 3.3 × 10 | - | 6 × 10 | elliptical |
| [52] | 2.64 × 10 | 53.1 | 8.13 × 10 | elliptical |
| [53] | 3.0 × 10 | 33.76 | - | elliptical |
| [7] | 3.28 × 10 | - | - | rectangular |
| [54] | 1.52 × 10 | 42.58 | - | elliptical |
| [12] | 4.4 × 10 | - | 1.61 × 10 | rectangular |
| [15] | 4.51 × 10 | 61.95 | - | elliptical |
| [55] | 2.28 × 10 | - | - | rectangular |
| [56] | 2.48 × 10 | - | 6 × 10 | rectangular |
| The designed PCF | 3.57 × 10 | 41.47 | 8.47 × 10 | rectangular |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Wen, J.; Zhou, Z.; Dong, Y.; Yang, T. A Highly Birefringent Photonic Crystal Fiber with Three Rows of Circular Air Holes. Photonics 2023, 10, 527. https://doi.org/10.3390/photonics10050527
Liu Z, Wen J, Zhou Z, Dong Y, Yang T. A Highly Birefringent Photonic Crystal Fiber with Three Rows of Circular Air Holes. Photonics. 2023; 10(5):527. https://doi.org/10.3390/photonics10050527
Chicago/Turabian StyleLiu, Zihan, Jialin Wen, Zhengyong Zhou, Yuming Dong, and Tianyu Yang. 2023. "A Highly Birefringent Photonic Crystal Fiber with Three Rows of Circular Air Holes" Photonics 10, no. 5: 527. https://doi.org/10.3390/photonics10050527
APA StyleLiu, Z., Wen, J., Zhou, Z., Dong, Y., & Yang, T. (2023). A Highly Birefringent Photonic Crystal Fiber with Three Rows of Circular Air Holes. Photonics, 10(5), 527. https://doi.org/10.3390/photonics10050527





