Supercontinuum Shaping via Hollow Core Anti-Resonant Fiber
Abstract
:1. Introduction
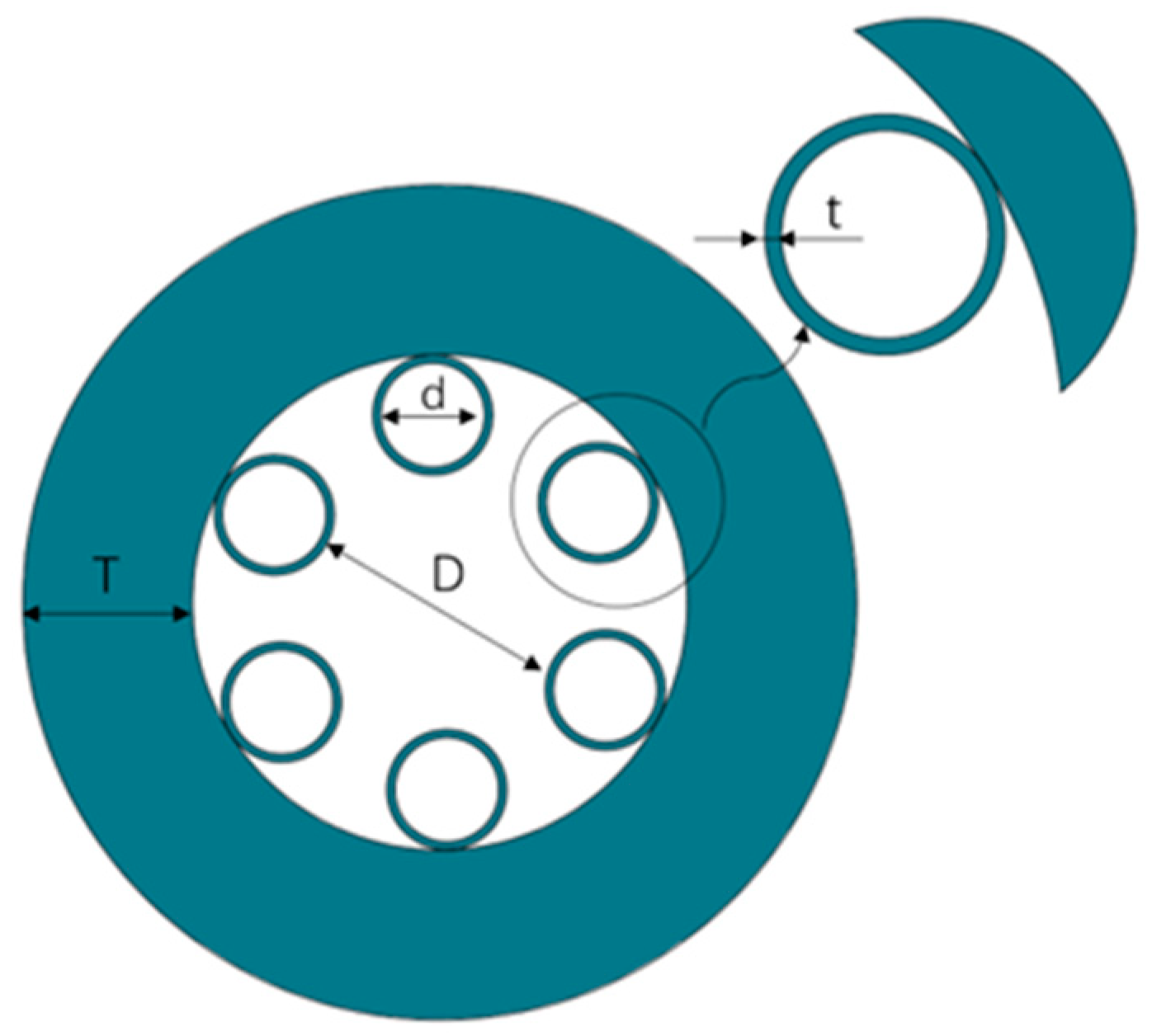
2. Methods
3. Materials
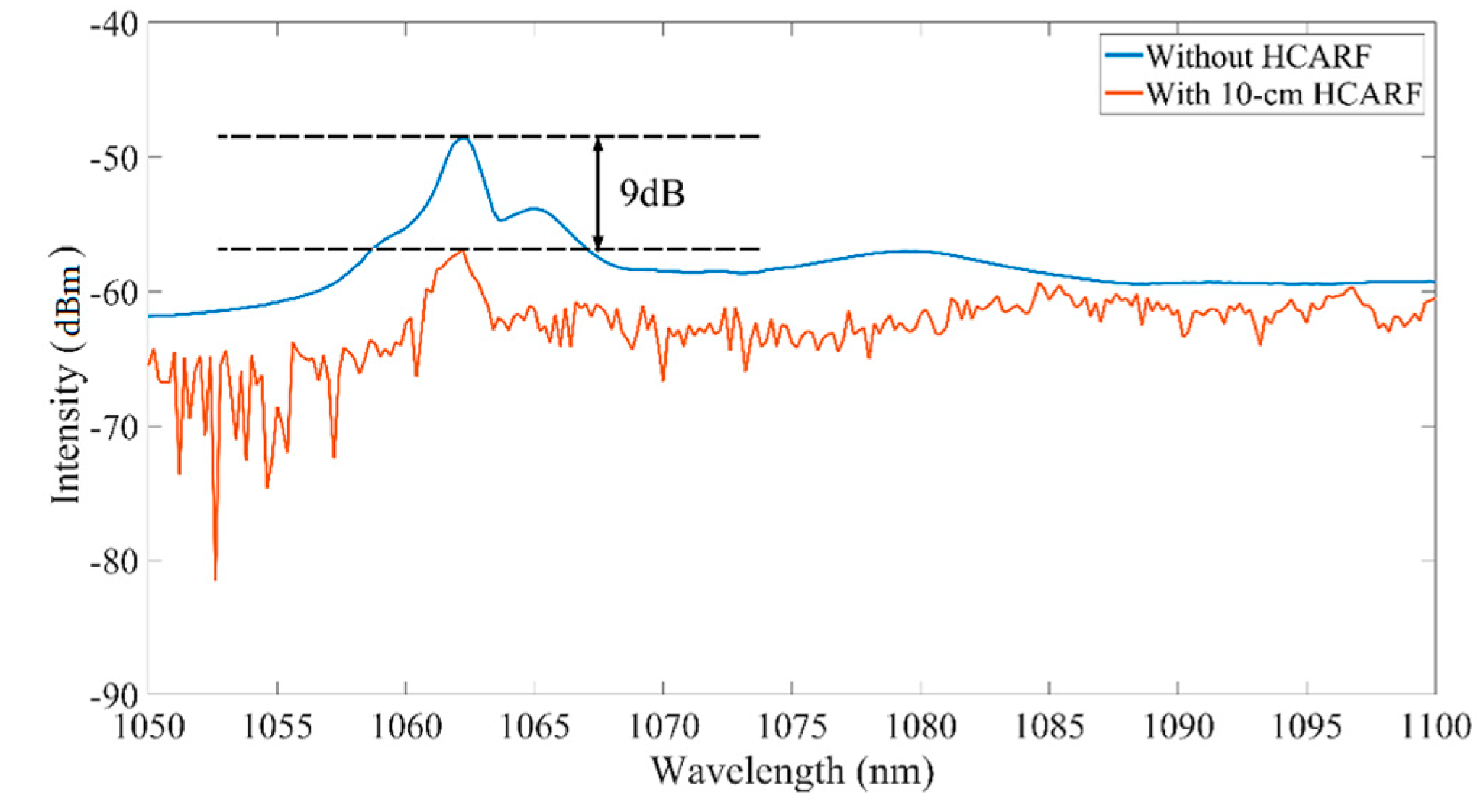
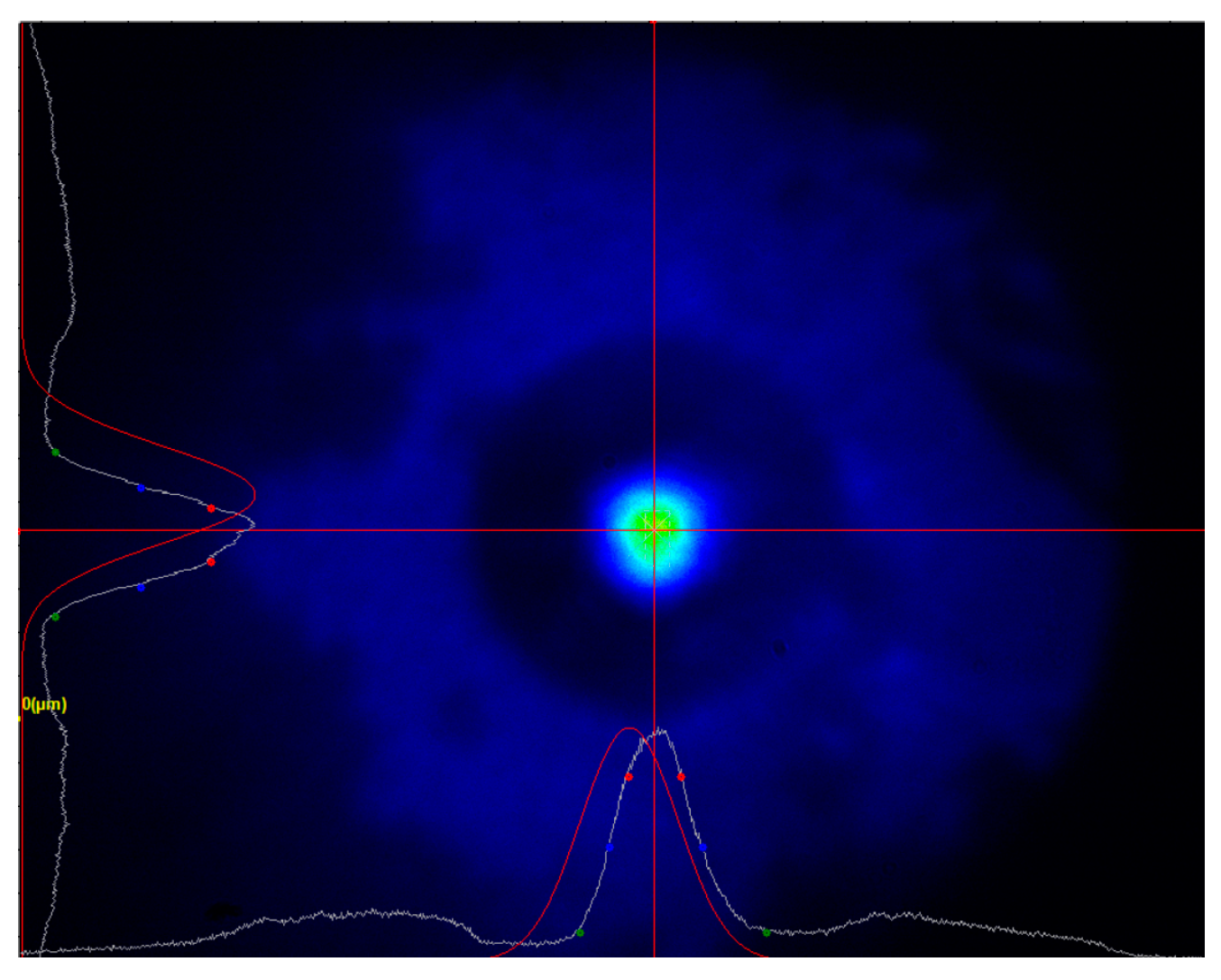
4. Results and Discussion
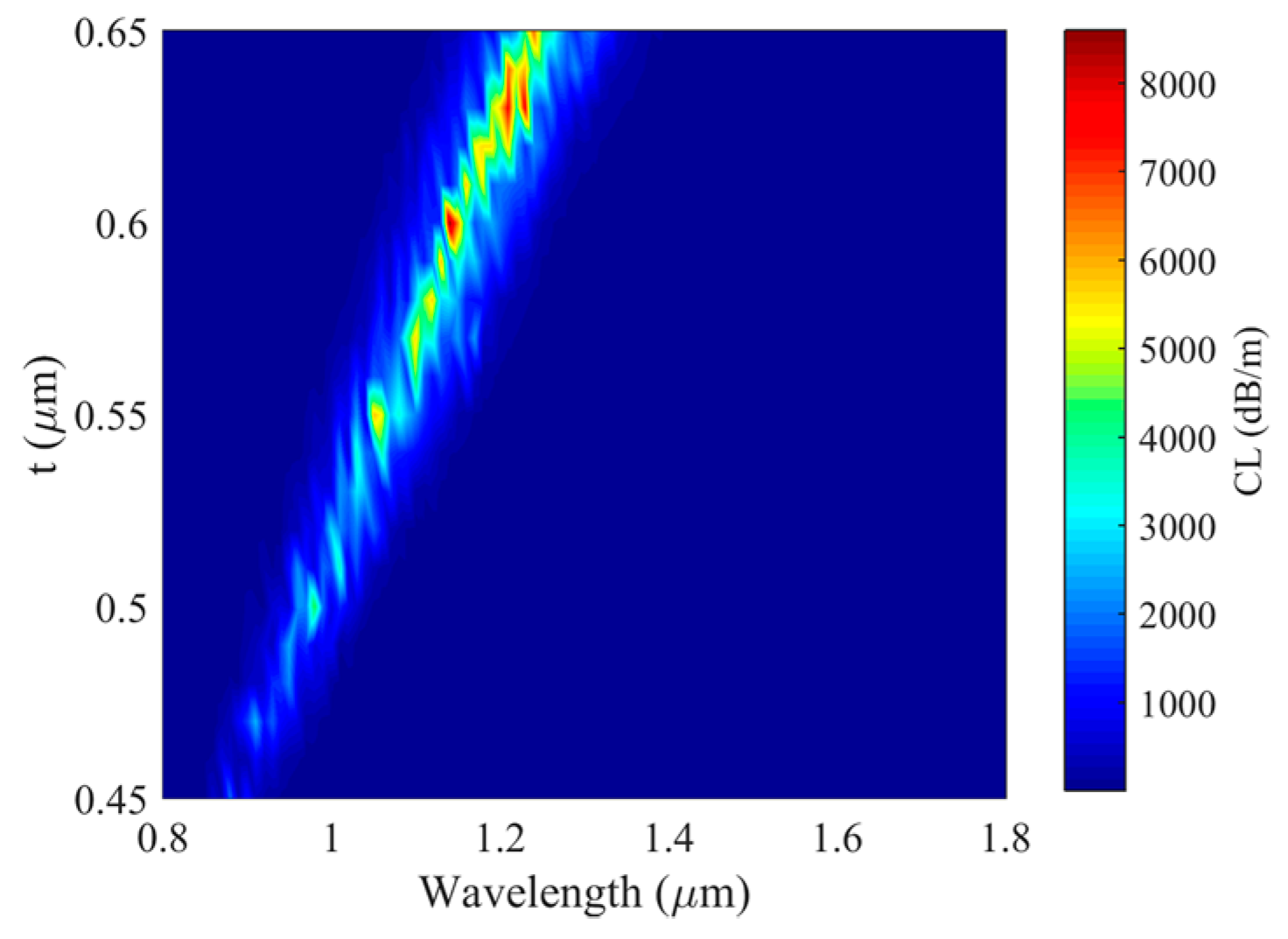
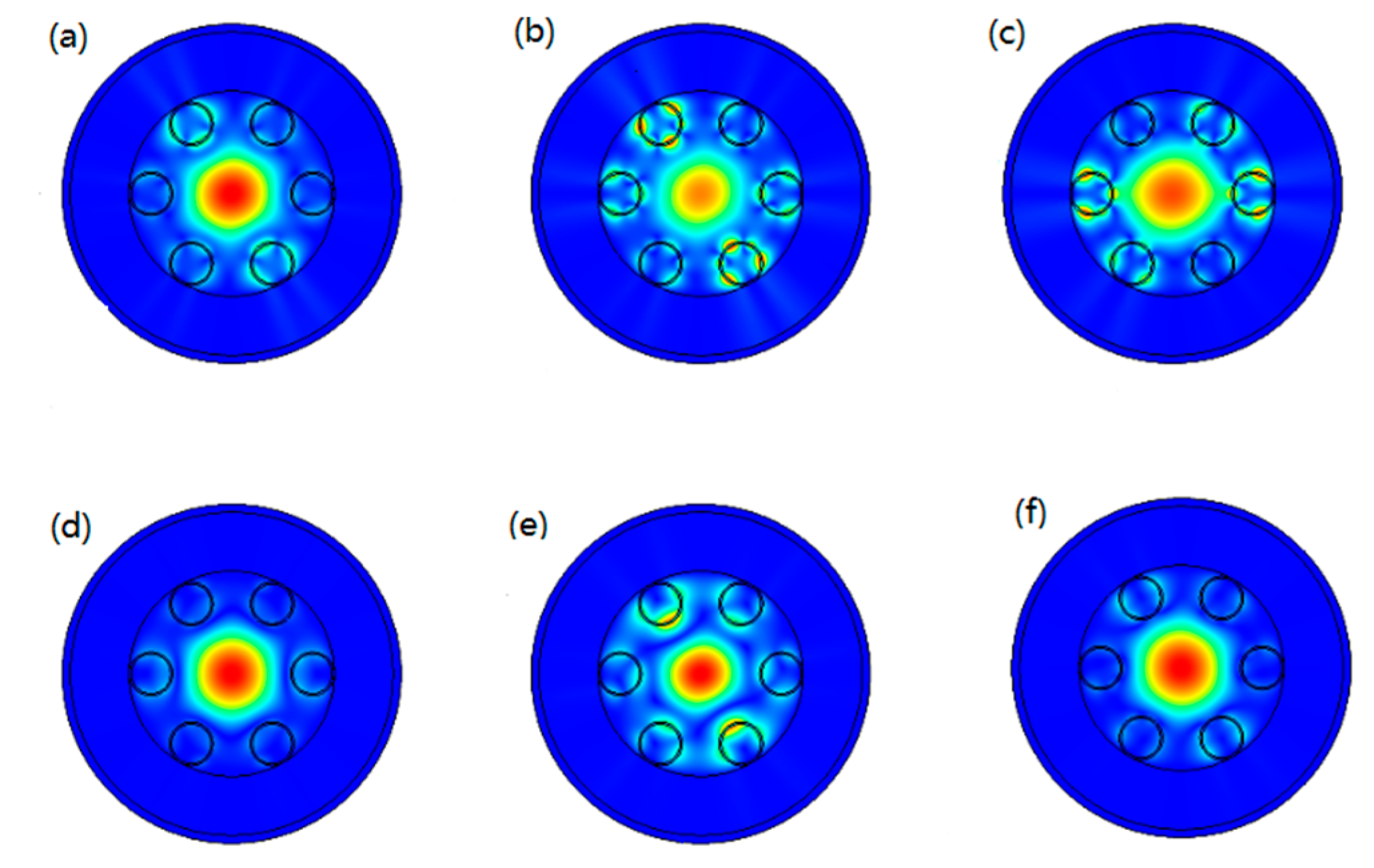
4.1. Simulation
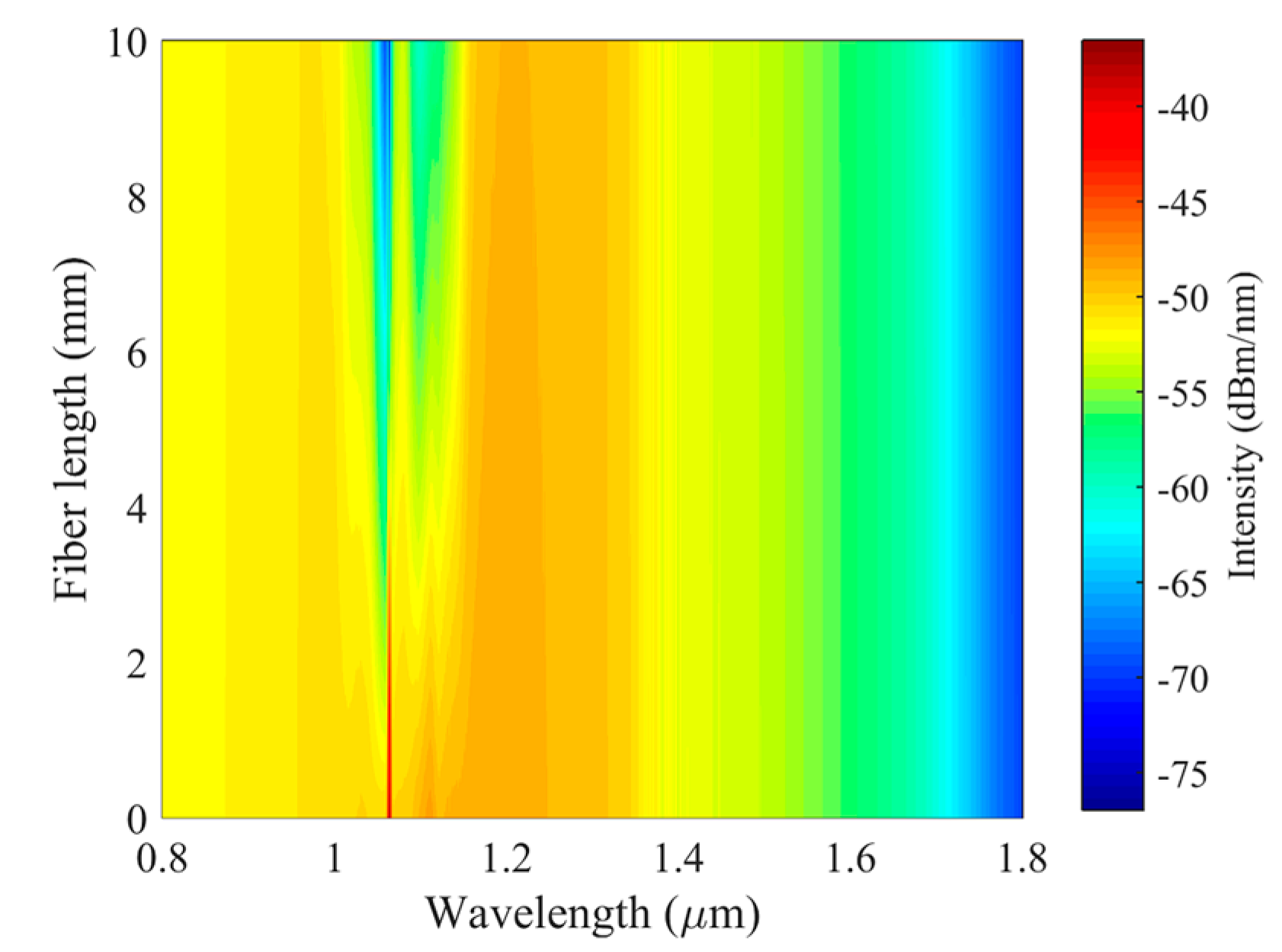
4.2. Experiment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Halder, A.; Jukna, V.; Koivurova, M.; Dubietis, A.; Turunen, J. Coherence of bulk-generated supercontinuum. Photonics Res. 2019, 7, 1345–1353. [Google Scholar] [CrossRef]
- Lafforgue, C.; Guerber, S.; Ramirez, J.M.; Marcaud, G.; Alonso-Ramos, C.; Le Roux, X.; Marris-Morini, D.; Cassan, E.; Baudot, C.; Boeuf, F.; et al. Broadband supercontinuum generation in nitrogen-rich silicon nitride waveguides using a 300 mm industrial platform. Photonics Res. 2020, 8, 352–358. [Google Scholar] [CrossRef]
- Tao, Y.; Chen, S.-P. All-fiber high-power linearly polarized supercontinuum generation from polarization-maintaining photonic crystal fibers. High Power Laser Sci. Eng. 2019, 7, e28. [Google Scholar] [CrossRef]
- Théberge, F.; Bérubé, N.; Poulain, S.; Cozic, S.; Robichaud, L.-R.; Bernier, M.; Vallée, R. Watt-level and spectrally flat mid-infrared supercontinuum in fluoroindate fibers. Photonics Res. 2018, 6, 609–613. [Google Scholar] [CrossRef]
- Apolonski, A.; Povazay, B.; Unterhuber, A.; Drexler, W.; Wadsworth, W.J.; Knight, J.C.; Russell, P.S.J. Spectral shaping of supercontinuum in a cobweb photonic-crystal fiber with sub-20-fs pulses. J. Opt. Soc. Am. B 2002, 19, 2165–2170. [Google Scholar] [CrossRef]
- Mejean, G.; Kasparian, J.; Salmon, E.; Yu, J.; Wolf, J.P.; Bourayou, R.; Sauerbrey, R.; Rodriguez, M.; Woste, L.; Lehmann, H.; et al. Towards a supercontinuum-based infrared lidar. Appl. Phys. B Lasers Opt. 2003, 77, 357–359. [Google Scholar] [CrossRef]
- Chiu, L.D.; Su, L.; Reichelt, S.; Amos, W.B. Use of a white light supercontinuum laser for confocal interference-reflection microscopy. J. Microsc. 2012, 246, 153–159. [Google Scholar] [CrossRef]
- Vengsarkar, A.M.; Lemaire, P.J.; Judkins, J.B.; Bhatia, V.; Erdogan, T.; Sipe, J.E. Long-period fiber gratings as band-rejection filters. J. Light. Technol. 1996, 14, 58–65. [Google Scholar] [CrossRef]
- Wysocki, P.F.; Judkins, J.B.; Espindola, R.P.; Andrejco, M.; Vengsarkar, A.M. Broad-band erbium-doped fiber amplifier flattened beyond 40 nm using long-period grating filter. IEEE Photonics Technol. Lett. 1997, 9, 1343–1345. [Google Scholar] [CrossRef]
- Feng, W.; Gu, Z. Ultra-Broadband Optical Filter Based on Chirped Long-Period Fiber Grating and PMTP. IEEE Photonics Technol. Lett. 2018, 30, 1361–1363. [Google Scholar] [CrossRef]
- Liu, X.; Wang, W.; Sahu, J.K.; Clarkson, W.A. Highly nonlinear H-shaped four-hole fiber in S + C+ L band pumped by picosecond pulses at 1064, 1200, and 1340 nm. Opt. Lett. 2009, 34, 3474–3476. [Google Scholar]
- Birks, T.A.; Roberts, P.J.; Russell, P.S.J.; Atkin, D.M.; Shepherd, T.J. Full 2-D photonic bandgaps in silica/air structures. Electron. Lett. 1995, 31, 1941–1943. [Google Scholar] [CrossRef]
- Poletti, F. Nested antiresonant nodeless hollow core fiber. Opt. Express 2014, 22, 23807–23828. [Google Scholar] [CrossRef]
- Markos, C.; Travers, J.C.; Abdolvand, A.; Eggleton, B.J.; Bang, O. Hybrid photonic-crystal fiber. Rev. Mod. Phys. 2017, 89, 045003. [Google Scholar] [CrossRef]
- Yu, F.; Knight, J.C. Negative Curvature Hollow-Core Optical Fiber. IEEE J. Sel. Top. Quantum Electron. 2016, 22, 146–155. [Google Scholar] [CrossRef]
- Wei, C.; Weiblen, R.J.; Menyuk, C.R.; Hu, J. Negative curvature fibers. Adv. Opt. Photonics 2017, 9, 504–561. [Google Scholar] [CrossRef]
- Huang, W.; Cui, Y.; Li, Z.; Zhou, Z.; Wang, Z. 1.56 μm and 2.86 μm Raman lasers based on gas-filled anti-resonance hollow-core fiber. Chin. Opt. Lett. 2019, 17, 071406. [Google Scholar] [CrossRef]
- Huang, W.; Cui, Y.; Zhou, Z.; Li, Z.; Chen, Y.; Wang, Z. Towards all-fiber structure pulsed mid-infrared laser by gas-filled hollow-core fibers. Chin. Opt. Lett. 2019, 17, 091402. [Google Scholar] [CrossRef]
- Belardi, W.; Knight, J.C. Hollow antiresonant fibers with reduced attenuation. Opt. Lett. 2014, 39, 1853–1856. [Google Scholar] [CrossRef]
- Bird, D. Attenuation of model hollow-core, anti-resonant fibres. Opt. Express 2017, 25, 23215–23237. [Google Scholar] [CrossRef]
- Debord, B.; Amsanpally, A.; Chafer, M.; Baz, A.; Maurel, M.; Blondy, J.M.; Hugonnot, E.; Scol, F.; Vincetti, L.; Gérôme, F.; et al. Ultralow transmission loss in inhibited-coupling guiding hollow fibers. Optica 2017, 4, 209–217. [Google Scholar] [CrossRef]
- Huang, Y.; Li, Q.; Han, J.; Jia, Z.; Yu, Y.; Yang, Y.; Xiao, J.; Wu, J.; Zhang, D.; Huang, Y.; et al. Temporal soliton and optical frequency comb generation in a Brillouin laser cavity. Optica 2019, 6, 1491–1497. [Google Scholar] [CrossRef]
- Wu, D.; Yu, F.; Liao, M. Understanding the material loss of anti-resonant hollow-core fibers. Opt. Express 2020, 28, 11840–11851. [Google Scholar] [CrossRef] [PubMed]
- Yan, S.; Lou, S.; Wang, X.; Zhang, W.; Zhao, T. Single-mode large-mode-area double-ring hollow-core anti-resonant fiber for high power delivery in mid-infrared region. Opt. Fiber Technol. 2018, 46, 118–124. [Google Scholar] [CrossRef]
- Yu, F.; Wadsworth, W.J.; Knight, J.C. Low loss silica hollow core fibers for 3–4 µm. Opt. Express 2012, 20, 11153–11158. [Google Scholar] [CrossRef]
- Sollapur, R.; Kartashov, D.; Zurch, M.; Hoffmann, A.; Grigorova, T.; Sauer, G.; Hartung, A.; Schwuchow, A.; Bierlich, J.; Kobelke, J.; et al. Resonance-enhanced multi-octave supercontinuum generation in antiresonant hollow-core fibers. Light Sci. Appl. 2017, 6, e17124. [Google Scholar] [CrossRef]
- Hong, Y.F.; Gao, S.F.; Ding, W.; Zhang, X.; Jia, A.Q.; Sheng, Y.L.; Wang, P.; Wang, Y.Y. Highly Birefringent Anti-Resonant Hollow-Core Fiber with a Bi-Thickness Fourfold Semi-Tube Structure. Laser Photonics Rev. 2022, 16, 2100365. [Google Scholar] [CrossRef]
- Zhao, X.; Wu, X.; Lan, X.; Luo, J.; Zhang, L.; Li, P.; Xiang, J.; Ma, W.; Wang, S. 5-tube hollow-core anti-resonant fiber with ultralow loss and single mod. Opt. Commun. 2021, 501, 127347. [Google Scholar] [CrossRef]
- Arman, H.; Olyaee, S. Realization of low confinement loss acetylene gas sensor by using hollow-core photonic bandgap fiber. Opt. Quantum Electron. 2021, 53, 328. [Google Scholar] [CrossRef]
- Hayes, J.R.; Sandoghchi, S.R.; Bradley, T.D.; Liu, Z.; Slav, R.; Gouveia, M.A.; Wheeler, N.V.; Jasion, G.; Chen, Y.; Fokoua, E.N.; et al. Antiresonant Hollow Core Fiber With an Octave Spanning Bandwidth for Short Haul Data Communications. J. Light. Technol. 2017, 35, 437–442. [Google Scholar] [CrossRef]
- Lægsgaard, J.; Bang, O. Hollow-core anti-resonant fibers: Guidance and loss reduction in the presence of micro-structured cladding. J. Opt. Soc. Am. B 2016, 33, 566–574. [Google Scholar]
- Knight, J.C.; Broeng, J.; Birks, T.A.; Russell, P.S.J. Photonic band gap guidance in optical fibers. Science 1998, 282, 1476–1478. [Google Scholar] [CrossRef]
- Habib, M.S.; Bang, O.; Bache, M. Highly Nonlinear and Low-Loss Hollow Core Anti-Resonant Fibers. In OSA Technical Digest (Online); paper OTh1E.3; Optical Society of America: Washington, DC, USA, 2013. [Google Scholar]
- Yin, D.; Schmidt, H. Integrated ARROW waveguides with hollow cores. Opt. Express 2004, 12, 2710–2715. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Yong, K.-T.; Yoo, S. A Method to Process Hollow-Core Anti-Resonant Fibers into Fiber Filters. Fibers 2018, 6, 89. [Google Scholar] [CrossRef]
- Xiao, L.; Demokan, M.S.; Jin, W. Fusion Splicing Photonic Crystal Fibers and Conventional Single-Mode Fibers: Microhole Collapse Effect. J. Light. Technol. 2007, 25, 3563–3574. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ge, M.; Chen, L.; Liao, M.; Yu, F.; Wu, D.; Wang, T.; Gao, W.; Hu, L. Supercontinuum Shaping via Hollow Core Anti-Resonant Fiber. Photonics 2023, 10, 528. https://doi.org/10.3390/photonics10050528
Ge M, Chen L, Liao M, Yu F, Wu D, Wang T, Gao W, Hu L. Supercontinuum Shaping via Hollow Core Anti-Resonant Fiber. Photonics. 2023; 10(5):528. https://doi.org/10.3390/photonics10050528
Chicago/Turabian StyleGe, Mengying, Liang Chen, Meisong Liao, Fei Yu, Dakun Wu, Tianxing Wang, Weiqing Gao, and Lili Hu. 2023. "Supercontinuum Shaping via Hollow Core Anti-Resonant Fiber" Photonics 10, no. 5: 528. https://doi.org/10.3390/photonics10050528
APA StyleGe, M., Chen, L., Liao, M., Yu, F., Wu, D., Wang, T., Gao, W., & Hu, L. (2023). Supercontinuum Shaping via Hollow Core Anti-Resonant Fiber. Photonics, 10(5), 528. https://doi.org/10.3390/photonics10050528





