Enhanced Spin Hall Shift by Multipoles of Different Orders in Spherical Particles
Abstract
1. Introduction
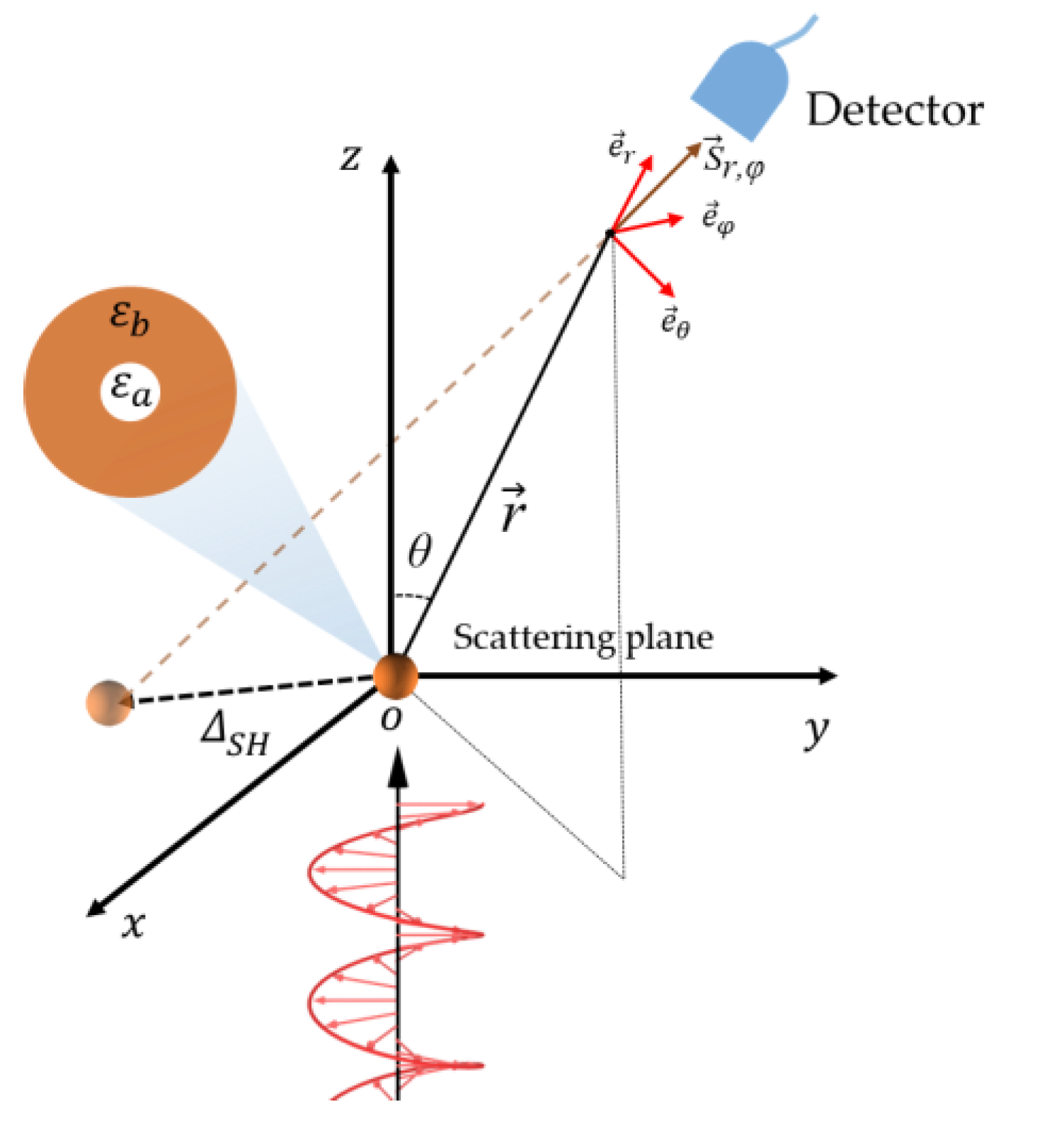
2. Structure and Theoretical Formula
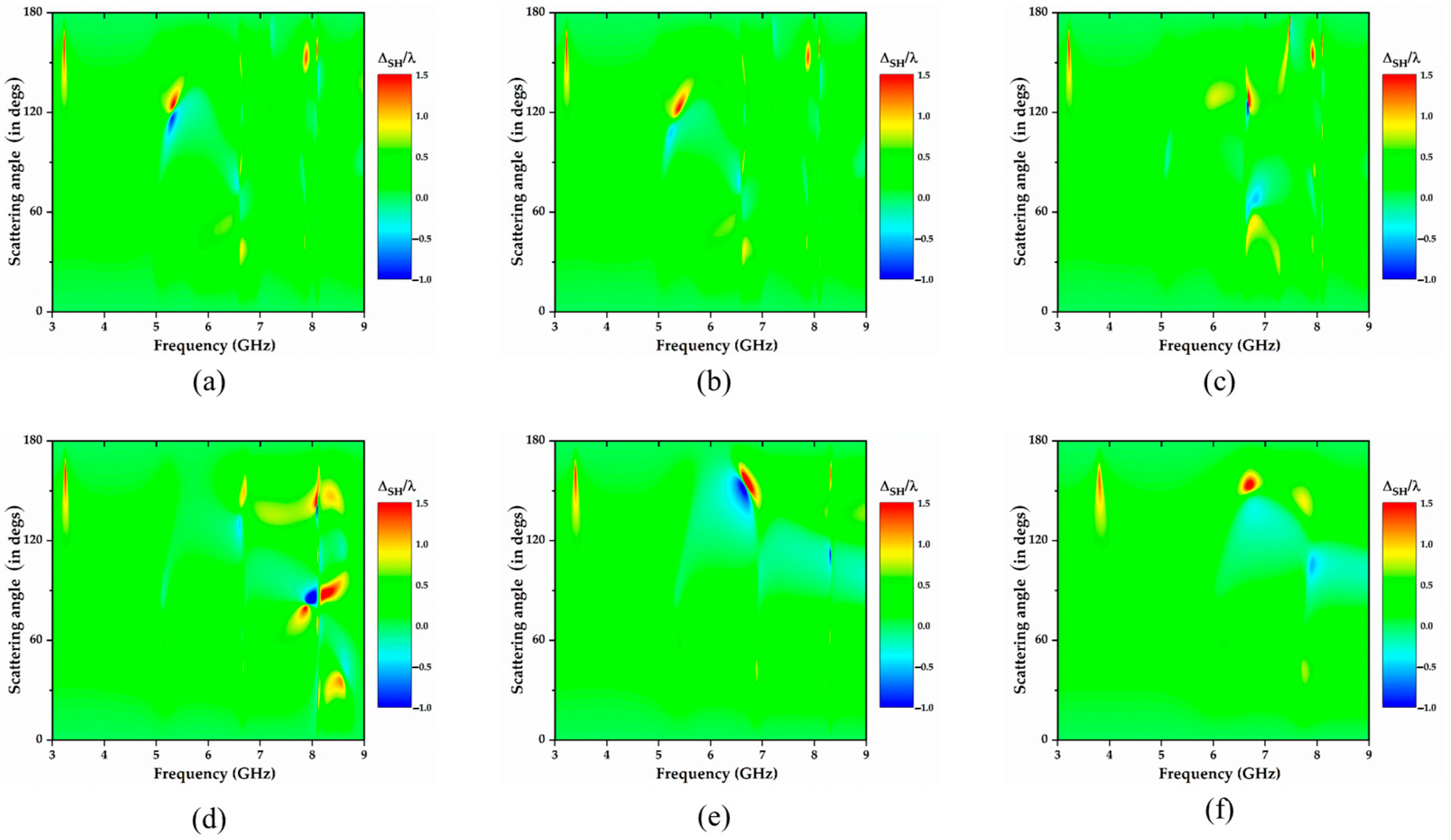
3. Simulation Result
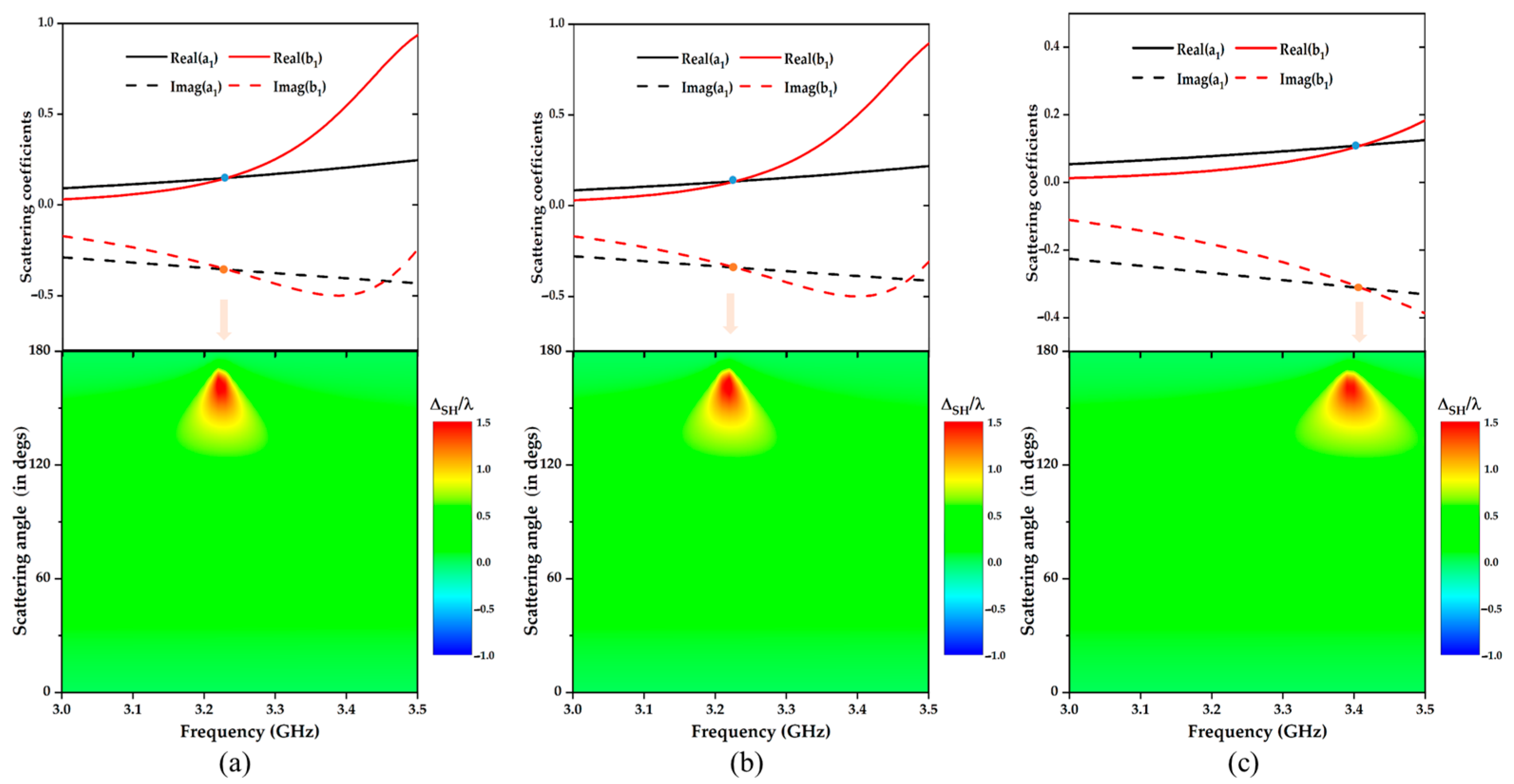
3.1. Overlap of Electric Dipole and Magnetic Dipole
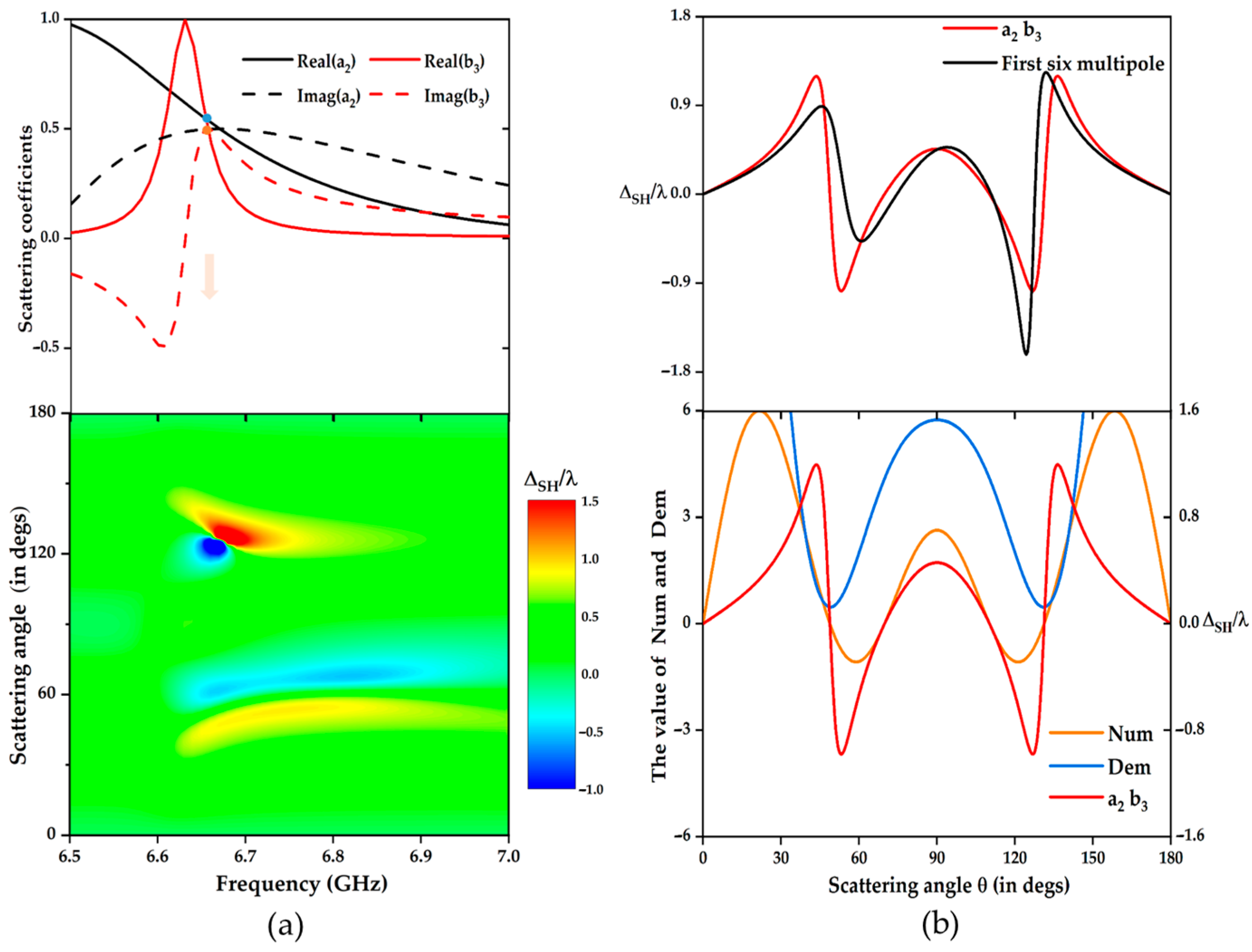
3.2. Overlap of Electric Quadrupole and Magnetic Octupole
3.3. Overlap of Electric Octupole and Magnetic Dipole
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Ling, X.; Zhou, X.; Huang, K.; Liu, Y.; Qiu, C.-W.; Luo, H.; Wen, S. Recent Advances in the Spin Hall Effect of Light. Rep. Prog. Phys. 2017, 80, 066401. [Google Scholar] [CrossRef]
- Bliokh, K.Y.; Rodríguez-Fortuño, F.J.; Nori, F.; Zayats, A.V. Spin–Orbit Interactions of Light. Nat. Photonics 2015, 9, 796–808. [Google Scholar] [CrossRef]
- Bliokh, K.Y.; Nori, F. Transverse and Longitudinal Angular Momenta of Light. Phys. Rep. 2015, 592, 1–38. [Google Scholar] [CrossRef]
- Onoda, M.; Murakami, S.; Nagaosa, N. Hall Effect of Light. Phys. Rev. Lett. 2004, 93, 083901. [Google Scholar] [CrossRef] [PubMed]
- Bliokh, K.Y.; Bliokh, Y.P. Conservation of Angular Momentum, Transverse Shift, and Spin Hall Effect in Reflection and Refraction of an Electromagnetic Wave Packet. Phys. Rev. Lett. 2006, 96, 073903. [Google Scholar] [CrossRef] [PubMed]
- Hosten, O.; Kwiat, P. Observation of the Spin Hall Effect of Light via Weak Measurements. Science 2008, 319, 787–790. [Google Scholar] [CrossRef]
- Xiang, Y.; Jiang, X.; You, Q.; Guo, J.; Dai, X. Enhanced Spin Hall Effect of Reflected Light with Guided-Wave Surface Plasmon Resonance. Photonics Res. 2017, 5, 467. [Google Scholar] [CrossRef]
- Tang, T.; Li, C.; Luo, L. Enhanced Spin Hall Effect of Tunneling Light in Hyperbolic Metamaterial Waveguide. Sci. Rep. 2016, 6, 30762. [Google Scholar] [CrossRef]
- Fu, Y.-Y.; Fei, Y.; Dong, D.-X.; Liu, Y.-W. Photonic Spin Hall Effect in PT Symmetric Metamaterials. Front. Phys. 2019, 14, 62601. [Google Scholar] [CrossRef]
- Yin, X.; Ye, Z.; Rho, J.; Wang, Y.; Zhang, X. Photonic Spin Hall Effect at Metasurfaces. Science 2013, 339, 1405–1407. [Google Scholar] [CrossRef]
- Kim, M.; Lee, D.; Yang, Y.; Kim, Y.; Rho, J. Reaching the Highest Efficiency of Spin Hall Effect of Light in the Near-Infrared Using All-Dielectric Metasurfaces. Nat. Commun. 2022, 13, 2036. [Google Scholar] [CrossRef] [PubMed]
- Slobozhanyuk, A.P.; Poddubny, A.N.; Sinev, I.S.; Samusev, A.K.; Yu, Y.F.; Kuznetsov, A.I.; Miroshnichenko, A.E.; Kivshar, Y.S. Enhanced Photonic Spin Hall Effect with Subwavelength Topological Edge States. Laser Photonics Rev. 2016, 10, 656–664. [Google Scholar] [CrossRef]
- Luo, H.; Zhou, X.; Shu, W.; Wen, S.; Fan, D. Enhanced and Switchable Spin Hall Effect of Light near the Brewster Angle on Reflection. Phys. Rev. A 2011, 84, 043806. [Google Scholar] [CrossRef]
- Zhou, X.; Ling, X.; Luo, H.; Wen, S. Identifying Graphene Layers via Spin Hall Effect of Light. Appl. Phys. Lett. 2012, 101, 251602. [Google Scholar] [CrossRef]
- Chen, S.; Zhou, X.; Ling, X.; Shu, W.; Luo, H.; Wen, S. Measurement of the Optical Constants of Monolayer MoS 2 via the Photonic Spin Hall Effect. Appl. Phys. Lett. 2021, 118, 111104. [Google Scholar] [CrossRef]
- Wang, R.; He, S.; Luo, H. Photonic Spin-Hall Differential Microscopy. Phys. Rev. Appl. 2022, 18, 044016. [Google Scholar] [CrossRef]
- Zhou, X.; Xiao, Z.; Luo, H.; Wen, S. Experimental Observation of the Spin Hall Effect of Light on a Nanometal Film via Weak Measurements. Phys. Rev. A 2012, 85, 043809. [Google Scholar] [CrossRef]
- Qiu, X.; Zhou, X.; Hu, D.; Du, J.; Gao, F.; Zhang, Z.; Luo, H. Determination of Magneto-Optical Constant of Fe Films with Weak Measurements. Appl. Phys. Lett. 2014, 105, 131111. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Stafeev, S.S.; Kozlova, E.S.; Nalimov, A.G. Spin-Orbital Conversion of a Strongly Focused Light Wave with High-Order Cylindrical–Circular Polarization. Sensors 2021, 21, 6424. [Google Scholar] [CrossRef]
- Zhu, W.; Zheng, H.; Zhong, Y.; Yu, J.; Chen, Z. Wave-Vector-Varying Pancharatnam-Berry Phase Photonic Spin Hall Effect. Phys. Rev. Lett. 2021, 126, 083901. [Google Scholar] [CrossRef]
- Zhou, X.; Lin, X.; Xiao, Z.; Low, T.; Alù, A.; Zhang, B.; Sun, H. Controlling Photonic Spin Hall Effect via Exceptional Points. Phys. Rev. B 2019, 100, 115429. [Google Scholar] [CrossRef]
- Mazanov, M.; Yermakov, O.; Bogdanov, A.; Lavrinenko, A. On Anomalous Optical Beam Shifts at Near-Normal Incidence. APL Photonics 2022, 7, 101301. [Google Scholar] [CrossRef]
- Haefner, D.; Sukhov, S.; Dogariu, A. Spin Hall Effect of Light in Spherical Geometry. Phys. Rev. Lett. 2009, 102, 123903. [Google Scholar] [CrossRef]
- Mansha, S.; Dutta Gupta, S.; Banerjee, A.; Ghosh, N. Giant Goos–Hänchen Shift in Scattering: The Role of Interfering Localized Plasmon Modes. Opt. Lett. 2014, 39, 4100. [Google Scholar] [CrossRef]
- Gao, D.; Shi, R.; Miroshnichenko, A.E.; Gao, L. Enhanced Spin Hall Effect of Light in Spheres with Dual Symmetry. Laser Photonics Rev. 2018, 12, 1800130. [Google Scholar] [CrossRef]
- Zhang, Q.; Gao, D.L.; Gao, L. Tunable Spin Hall Shift of Light from Graphene-Wrapped Spheres. Opt. Express 2021, 29, 9816. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Shu, J.; Arnoldus, H.F. Far-Field Detection of the Dipole Vortex. Opt. Lett. 2008, 33, 2269–2271. [Google Scholar] [CrossRef] [PubMed]
- Dogariu, A.; Schwartz, C. Conservation of Angular Momentum of Light in Single Scattering. Opt. Express 2006, 14, 8425. [Google Scholar] [CrossRef]
- Arnoldus, H.F.; Foley, J.T. The Dipole Vortex. Opt. Commun. 2004, 231, 115–128. [Google Scholar] [CrossRef]
- Arnoldus, H.F.; Li, X.; Shu, J. Subwavelength Displacement of the Far-Field Image of a Radiating Dipole. Opt. Lett. 2008, 33, 1446. [Google Scholar] [CrossRef]
- Olmos-Trigo, J.; Sanz-Fernández, C.; García-Etxarri, A.; Molina-Terriza, G.; Bergeret, F.S.; Sáenz, J.J. Enhanced Spin-Orbit Optical Mirages from Dual Nanospheres. Phys. Rev. A 2019, 99, 013852. [Google Scholar] [CrossRef]
- Shi, R.; Gao, D.L.; Hu, H.; Wang, Y.Q.; Gao, L. Enhanced Broadband Spin Hall Effects by Core-Shell Nanoparticles. Opt. Express 2019, 27, 4808. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Hu, H.; Zhang, Q.; Gao, D.L.; Gao, L. Topologically-Tuned Spin Hall Shift around Fano Resonance. Opt. Express 2020, 28, 21641. [Google Scholar] [CrossRef] [PubMed]
- Ali, R. Chirality-Assisted Spin Hall Effect of Light in the Vicinity of the Quasi-Antidual Symmetry Mode of a Chiral Sphere. Phys. Rev. A 2022, 106, 063508. [Google Scholar] [CrossRef]
- Li, W.; Liu, J.; Gao, Y.; Zhou, K.; Liu, S. Photonic Spin Hall Effect on an Ellipsoidal Rayleigh Particle in Scattering Far-Field. Opt. Express 2019, 27, 28194. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Xu, P.; Gao, L.; Miroshnichenko, A.E.; Gao, D. Wavelength-Scale Spin Hall Shift of Light with Morphology-Enhanced Scattering Efficiency from Nanoparticles. Laser Photonics Rev. 2022, 16, 2200289. [Google Scholar] [CrossRef]
- Ruffino, F. Light-Scattering Simulations from Spherical Bimetallic Core–Shell Nanoparticles. Micromachines 2021, 12, 359. [Google Scholar] [CrossRef]
- Liberal, I.; Ederra, I.; Gonzalo, R.; Ziolkowski, R.W. Superbackscattering from Single Dielectric Particles. J. Opt. 2015, 17, 072001. [Google Scholar] [CrossRef]
- Powell, A.W.; Hibbins, A.P.; Sambles, J.R. Multiband Superbackscattering via Mode Superposition in a Single Dielectric Particle. Appl. Phys. Lett. 2021, 118, 251107. [Google Scholar] [CrossRef]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; Wiley-VCH: Weinheim, Germany, 2004; ISBN 978-0-471-29340-8. [Google Scholar]
- Liu, W.; Miroshnichenko, A.E.; Neshev, D.N.; Kivshar, Y.S. Broadband Unidirectional Scattering by Magneto-Electric Core–Shell Nanoparticles. ACS Nano 2012, 6, 5489–5497. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, J.; Lei, B.; Ma, H.; Xie, W.; Hu, H. Ultra-Directional Forward Scattering by Individual Core-Shell Nanoparticles. Opt. Express 2014, 22, 16178. [Google Scholar] [CrossRef] [PubMed]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, R.; Gao, D.; Gao, L. Enhanced Spin Hall Shift by Multipoles of Different Orders in Spherical Particles. Photonics 2023, 10, 732. https://doi.org/10.3390/photonics10070732
Li R, Gao D, Gao L. Enhanced Spin Hall Shift by Multipoles of Different Orders in Spherical Particles. Photonics. 2023; 10(7):732. https://doi.org/10.3390/photonics10070732
Chicago/Turabian StyleLi, Rudao, Dongliang Gao, and Lei Gao. 2023. "Enhanced Spin Hall Shift by Multipoles of Different Orders in Spherical Particles" Photonics 10, no. 7: 732. https://doi.org/10.3390/photonics10070732
APA StyleLi, R., Gao, D., & Gao, L. (2023). Enhanced Spin Hall Shift by Multipoles of Different Orders in Spherical Particles. Photonics, 10(7), 732. https://doi.org/10.3390/photonics10070732




