High Efficient Random Laser with Cavity Based on the Erbium-Doped Germanophosphosilicate Artificial Rayleigh Fiber
Abstract
:1. Introduction
2. Materials and Methods
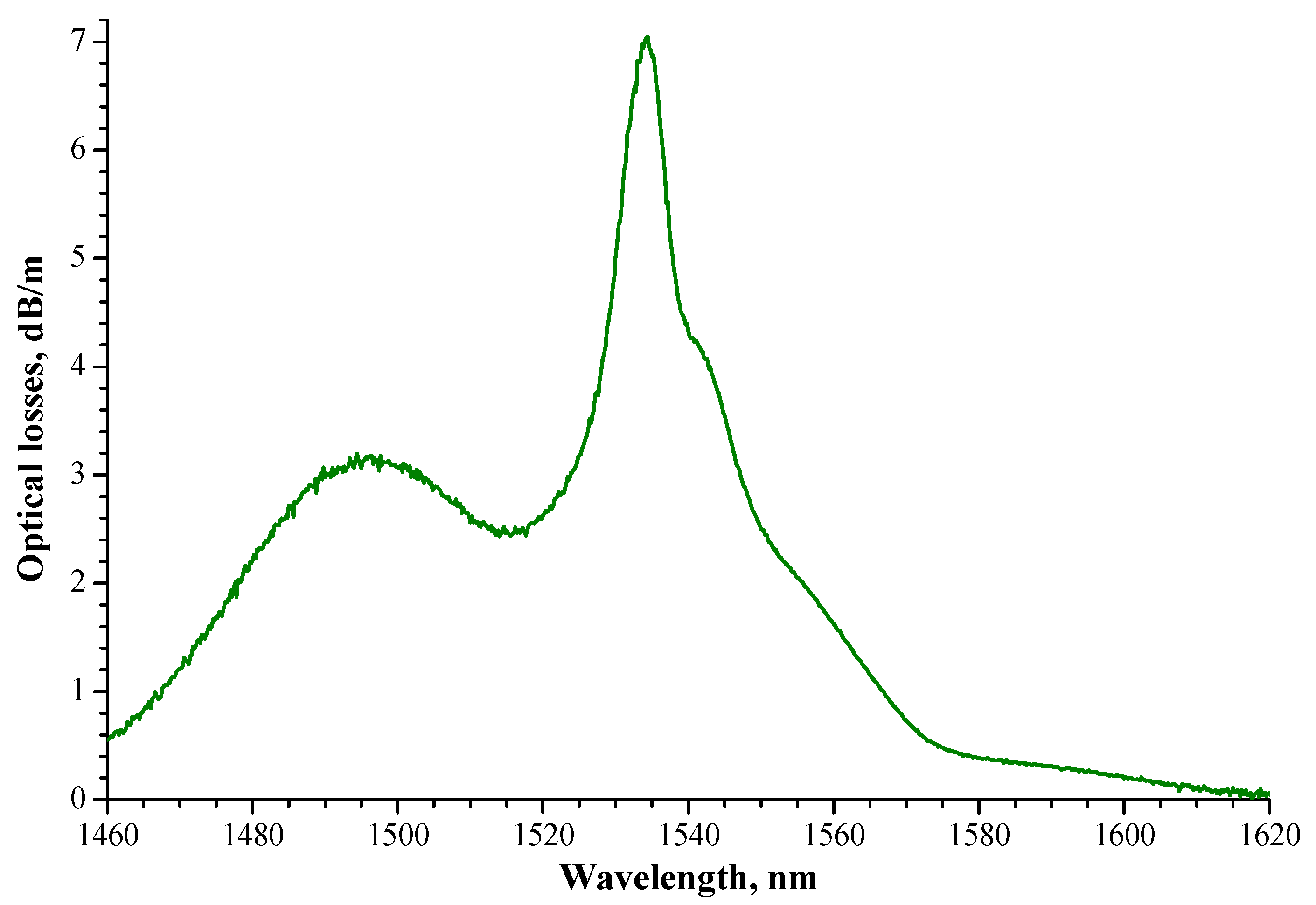
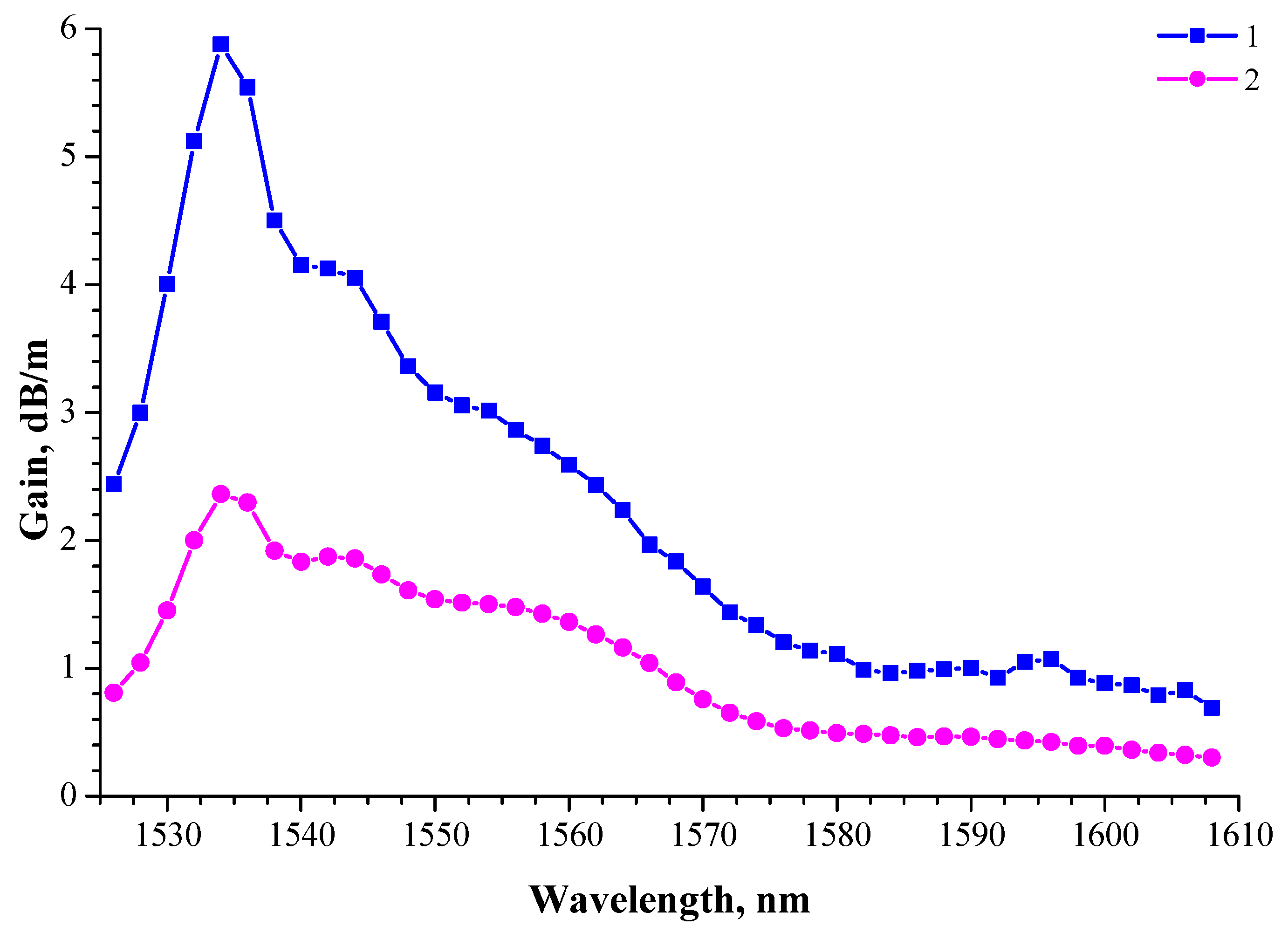
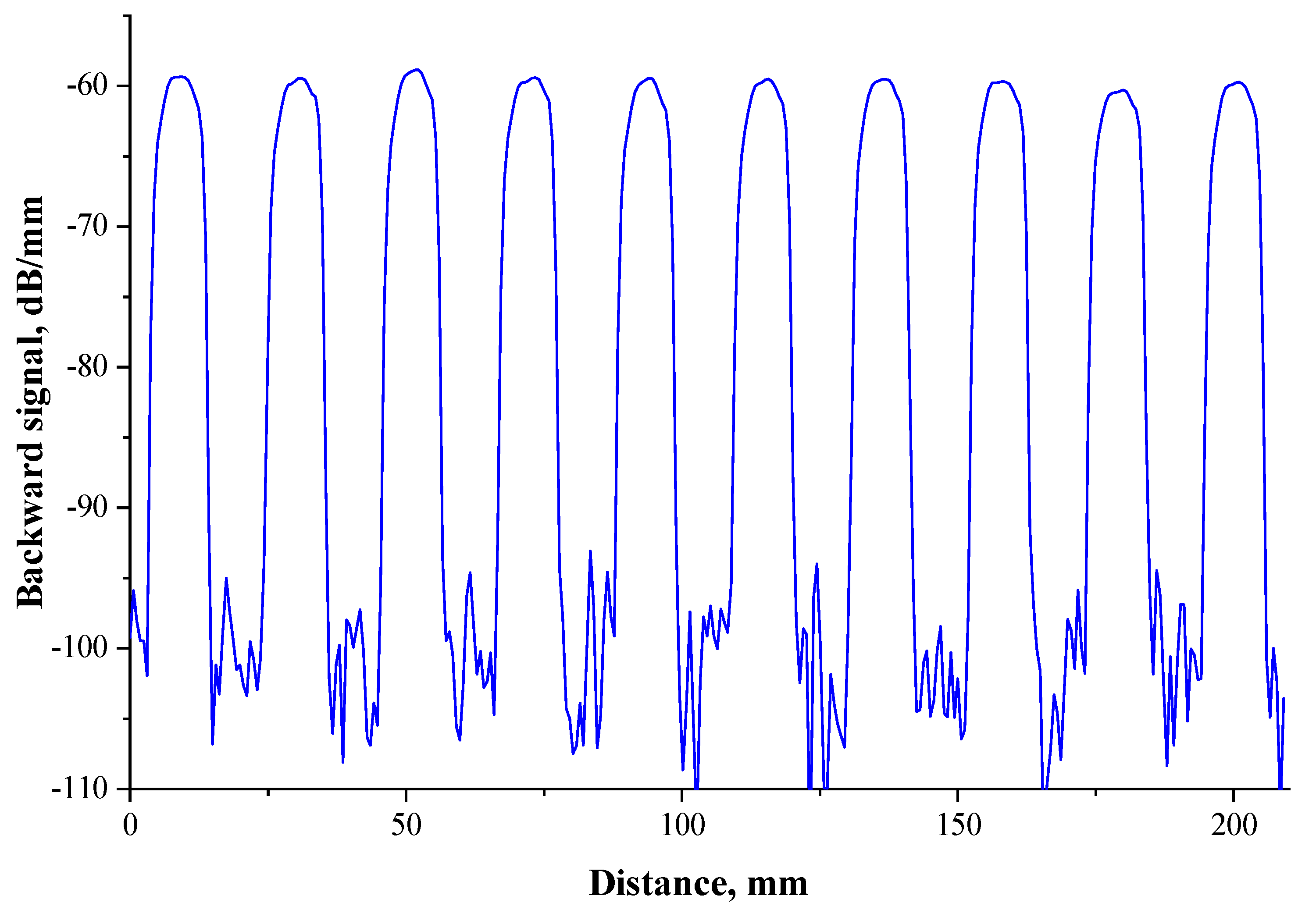
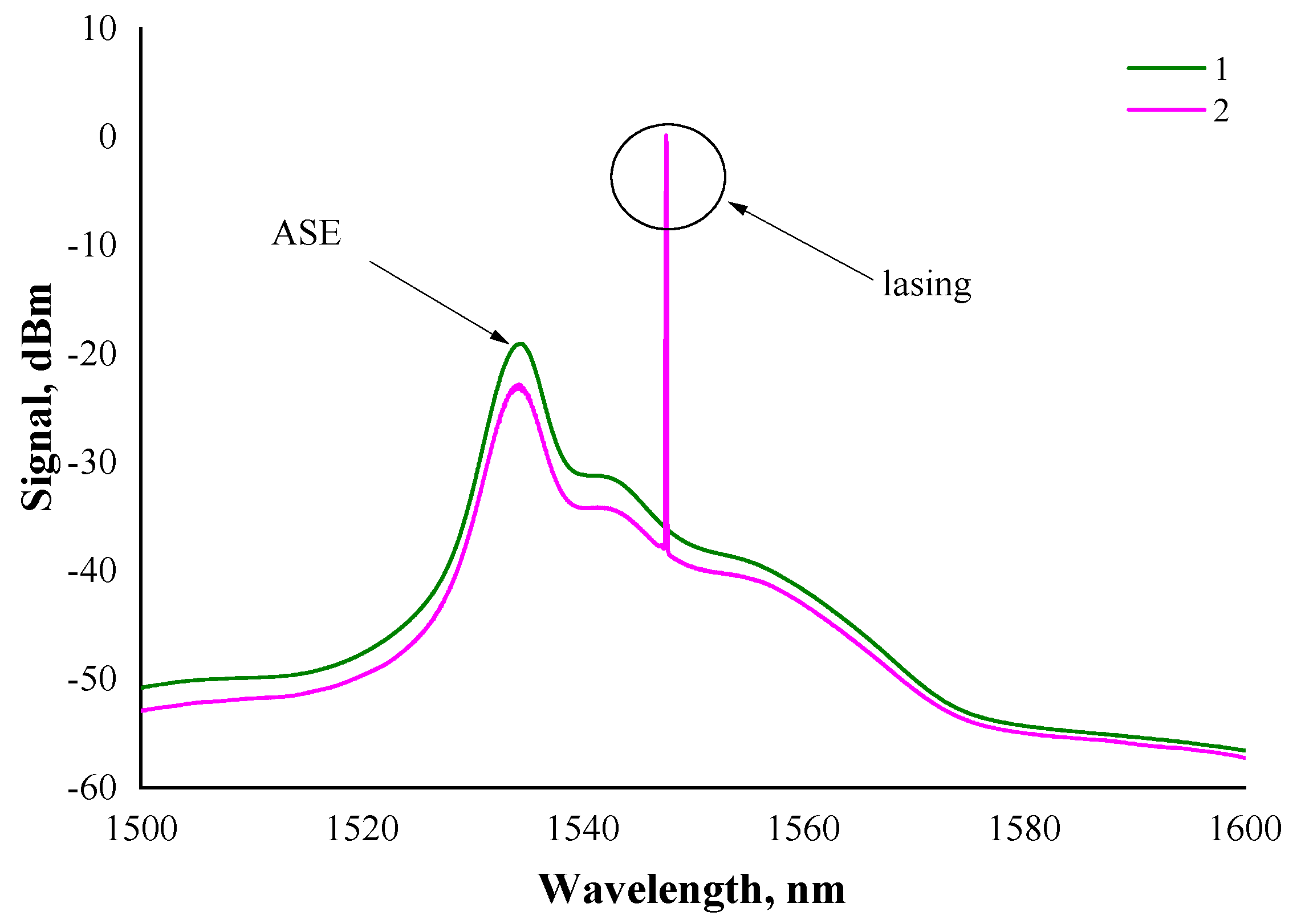
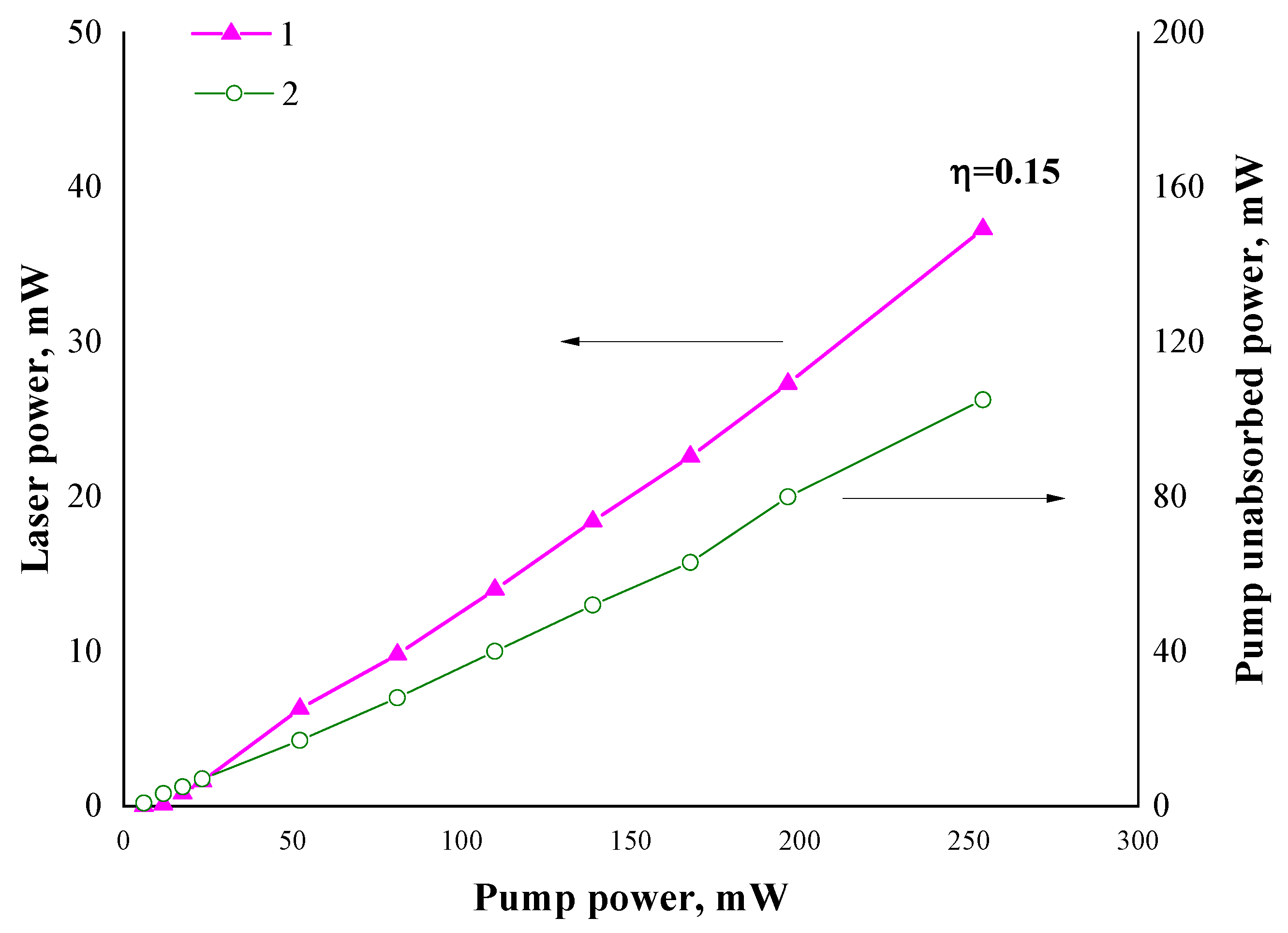
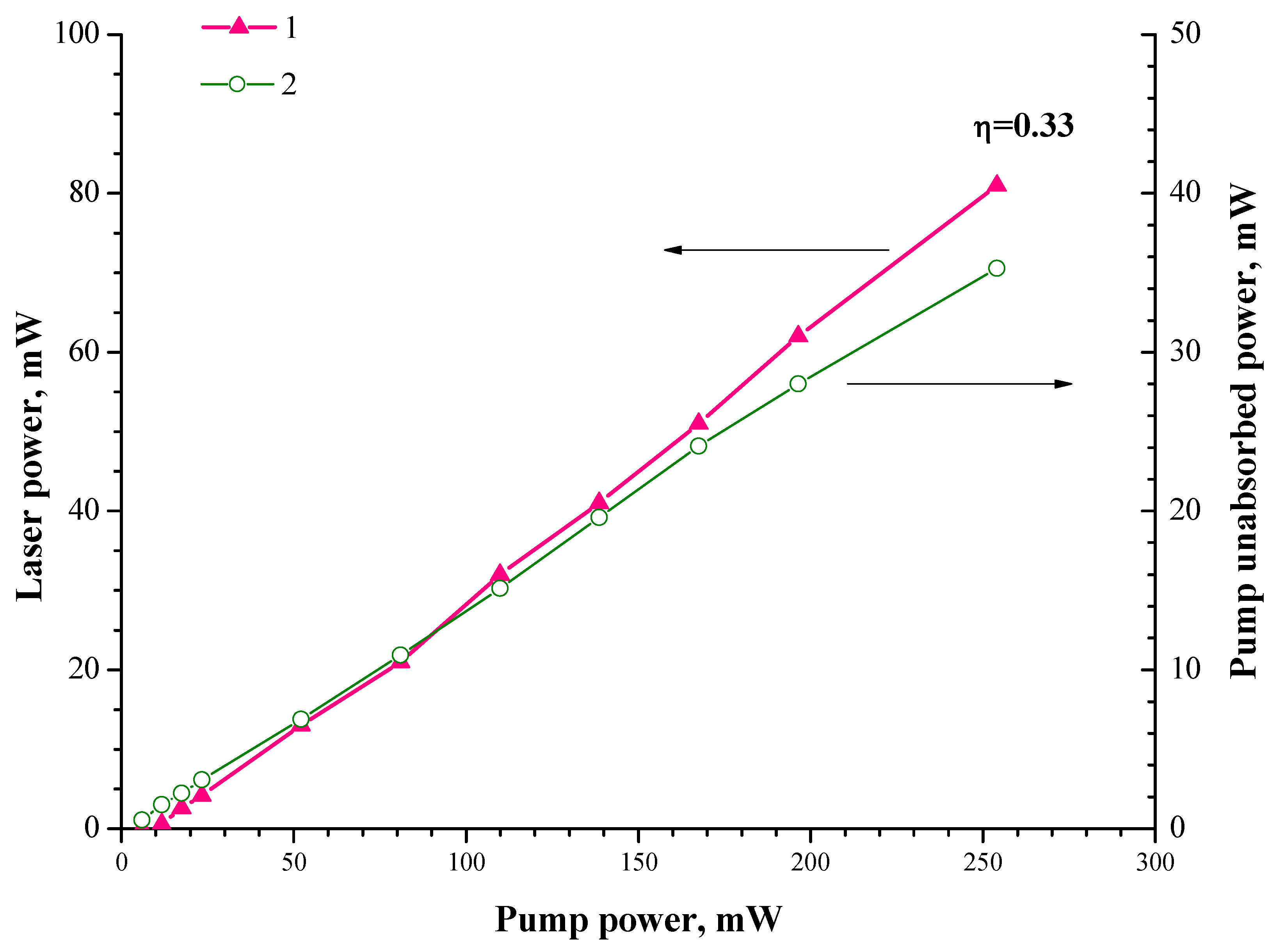
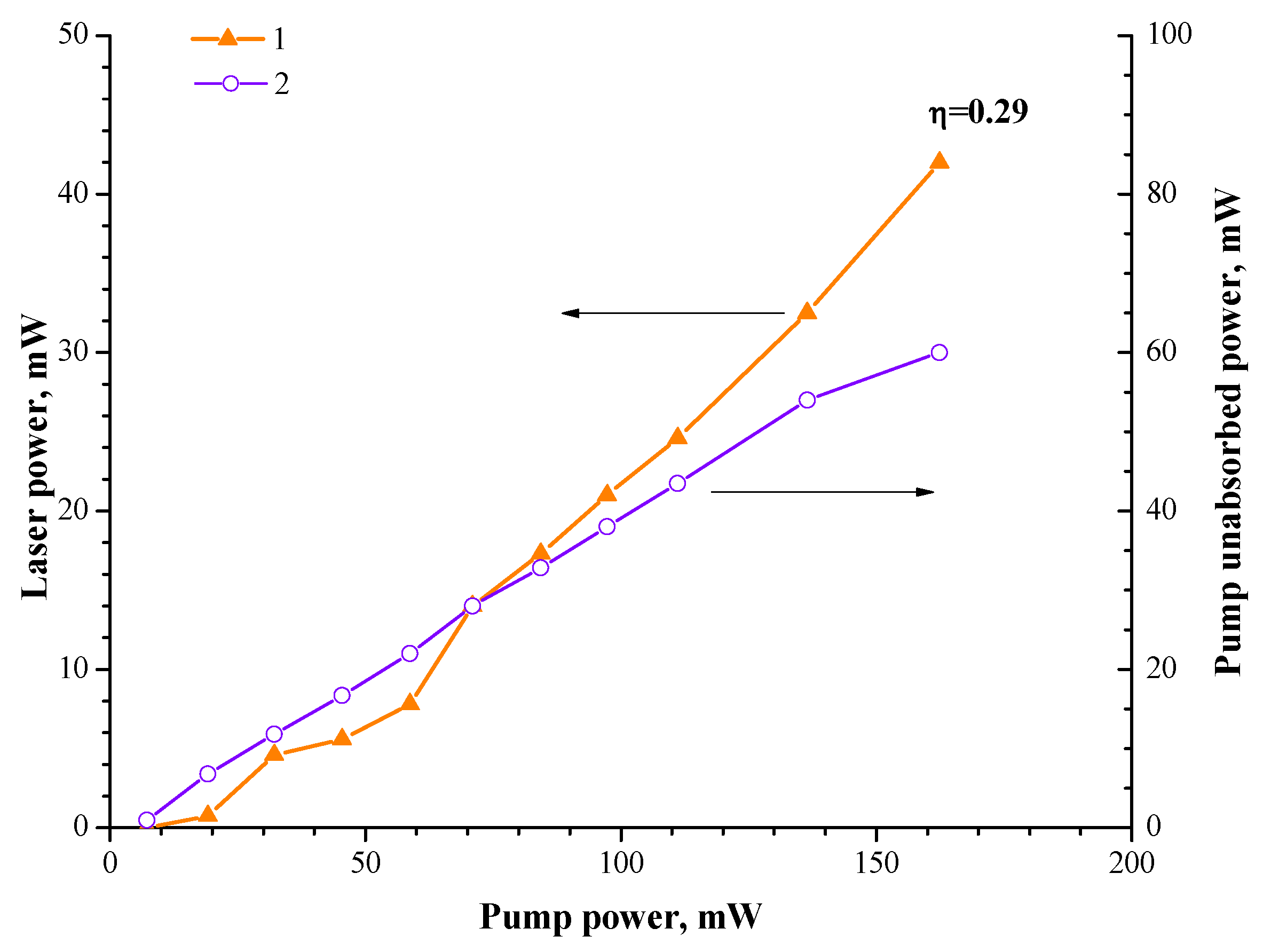
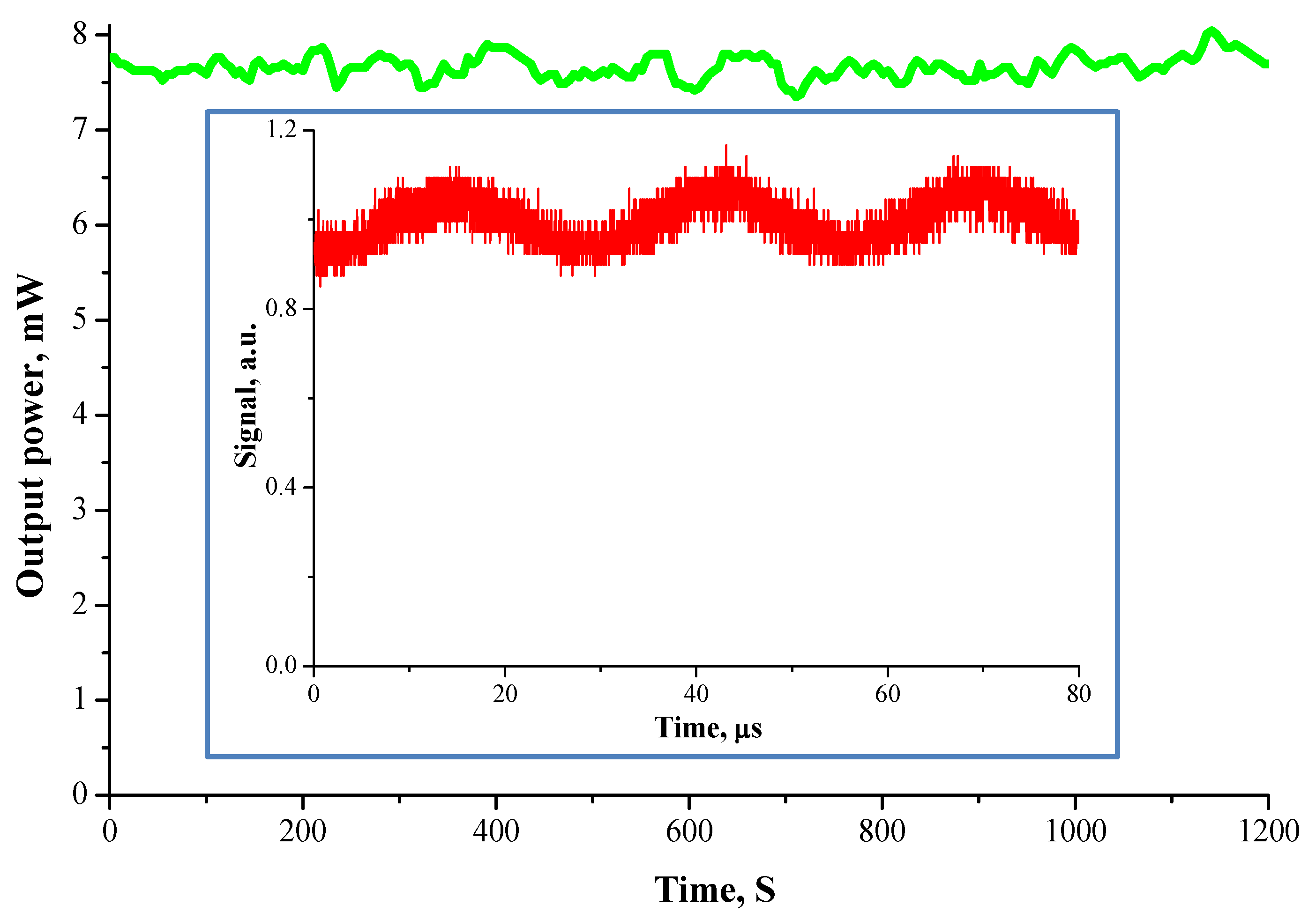
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fotiadi, A.A.; Kiyan, R.V. Cooperative stimulated Brillouin and Rayleigh backscattering process in optical fiber. Opt. Lett. 1998, 23, 1805–1807. [Google Scholar] [CrossRef]
- Turitsyn, S.; Babin, S.; El-Taher, A.; Harper, P.; Churkin, D.; Kablukov, S.; Ania-Castañón, J.; Karalekas, V.; Podivilov, E. Random distributed feedback fibre laser. Nat. Photonics 2010, 4, 231. [Google Scholar] [CrossRef]
- Fotiadi, A.A. Random lasers: An incoherent fibre laser. Nat. Photonics 2010, 4, 204–205. [Google Scholar] [CrossRef]
- Turitsyn, S.K.; Babin, S.A.; Churkin, D.V.; Vatnik, I.D.; Nikulin, M.; Podivilov, E.V. Random distributed feedback Fibre lasers. Phys. Rep. 2014, 542, 133–193. [Google Scholar] [CrossRef]
- Lizárraga, N.; Puente, N.P.; Chaikina, E.I.; Leskova, T.A.; Méndez, E.R. Single-mode Er-doped fiber random laser with distributed Bragg grating feedback. Opt. Express 2009, 17, 395–404. [Google Scholar] [CrossRef] [PubMed]
- Skvortsov, M.I.; Abdullina, S.R.; Vlasov, A.A.; Zlobina, E.A.; Lobach, I.A.; Terentyev, V.S.; Babin, S.A. FBG array-based random distributed feedback Raman fibre laser. Quantum Electron. 2017, 47, 696. [Google Scholar] [CrossRef]
- Bronnikov, K.; Wolf, A.; Yakushin, S.; Dostovalov, A.; Egorova, O.; Zhuravlev, S.; Semjonov, S.; Wabnitz, S.; Babin, S. Durable shape sensor based on FBG array inscribed in polyimide-coated multicore optical fiber. Opt. Express 2019, 27, 38421. [Google Scholar] [CrossRef] [Green Version]
- Przhiialkovskii, D.; Butov, O. High-precision point-by-point fiber Bragg grating inscription. Results Phys. 2021, 30, 104902. [Google Scholar] [CrossRef]
- Askins, C.G.; Putnam, M.A.; Williams, G.M.; Fiebele, E.J. Stepped-wavelength optical-fiber Bragg grating arrays fabricated in line on a draw tower. Opt. Lett. 1994, 19, 147–149. [Google Scholar] [CrossRef]
- Guo, H.; Tang, J.; Li, X.; Zheng, Y.; Yu, H.; Yu, H. On-line writing identical and weak fiber Bragg grating arrays. Chin. Opt. Lett. 2013, 11, 030602. [Google Scholar]
- Zaitsev, I.; Butov, O.; Voloshin, V.; Vorob’ev, I.; Vyatkin, M.; Kolosovskii, A.; Popov, S.; Chamorovskii, Y. Optical Fiber with Distributed BraggType Reflector. J. Comm. Technol. Elec. 2016, 61, 639. [Google Scholar] [CrossRef]
- Popov, S.; Butov, O.; Kolosovski, A.; Voloshin, V.; Vorob’ev, I.; Vyatkin, M.; Fotiadi, A.; Chamorovski, Y. Optical Fibres with Arrays of FBG: Properties and Application. In Proceedings of the PIERS, IEEE Xplore, 1568, St. Petersburg, Russia, 22–25 May 2017. [Google Scholar]
- Chamorovskiy, Y.; Butov, O.; Kolosovskiy, A.; Popov, S.; Voloshin, V.; Vorob’ev, I.; Vyatkin, M. Metal-coated Bragg grating reflecting fibre. Opt. Fiber Technol. 2017, 34, 30. [Google Scholar] [CrossRef]
- Chamorovskiy, Y.; Butov, O.; Kolosovskiy, A.; Popov, S.; Voloshin, V.; Vorob’ev, I.; Vyatkin, M.; Odnobludov, M. Long tapered fiber with array of FBG. Opt. Fiber Technol. 2019, 50, 95. [Google Scholar] [CrossRef]
- Popov, S.; Butov, O.; Kolosovskii, A.; Voloshin, V.; Vorob’ev, I.; Isaev, V.; Vyatkin, M.; Fotiadi, A.; Chamorovsky, Y. Optical fibres and fibre tapers with an array of Bragg gratings. Quantum Electron. 2019, 49, 1127. [Google Scholar] [CrossRef]
- Kharasov, D.; Bengalskii, D.; Vyatkin, M.; Nanii, O.; Fomiryakov, E.; Nikitin, S.; Popov, S.; Chamorovsky, Y.; Treshchikov, V. Extending the operation range of a phase-sensitive optical time-domain reflectometer by using fibre with chirped Bragg gratings. Quantum Electron. 2020, 50, 510. [Google Scholar] [CrossRef]
- Popov, S.; Chamorovsky, Y.; Mégret, P.; Zolotovskii, I.; Fotiadi, A. Brillouin Random Lasing in Artifice Rayleigh Fiber. In Proceedings of the ECOC, IEEE Xplore, 1, Valensia, Spain, 27 September–1 October 2015. [Google Scholar]
- Popov, S.; Butov, O.; Chamorovskiy, Y.; Isaev, V.; Kolosovskiy, A.; Voloshin, V.; Vorob’ev, I.; Vyatkin, M.; Mégret, P.; Odnoblyudov, M.; et al. Brillouin lasing in single-mode tapered optical fiber with inscribed Fiber Bragg Grating Array. Results Phys. 2018, 9, 625. [Google Scholar] [CrossRef]
- Popov, S.; Butov, O.; Chamorovski, Y.; Isaev, V.; Mégret, P.; Korobko, D.; Zolotovskii, I.; Fotiadi, A. Narrow linewidth short cavity Brillouin random laser based on Bragg grating array fiber and dynamical population inversion gratings. Results Phys. 2018, 9, 806–808. [Google Scholar] [CrossRef]
- Popov, S.; Butov, O.; Bazakutsa, A.; Vyatkin, M.; Chamorovskii, Y.; Fotiadi, A. Random lasing in a short Er-doped artificial Rayleigh fiber. Results Phys. 2020, 16, 102868. [Google Scholar] [CrossRef]
- Popov, S.M.; Butov, O.V.; Bazakutsa, A.P.; Vyatkin, M.Y.; Chamorovskiy, Y.K.; Panajotov, K.; Fotiadi, A.A. Narrow linewidth random laser based on short Er-doped artifice Rayleigh fiber. Proc. SPIE 2020, 11357, 318–327. [Google Scholar]
- Rybaltovsky, A.; Popov, S.; Lipatov, D.; Umnikov, A.; Abramov, A.; Morozov, O.; Ryakhovskiy, D.; Voloshin, V.; Kolosovskii, A.; Vorob’ev, I.; et al. Photosensitive Yb-doped germanophosphosilicate artificial Rayleigh fibers as a base of random lasers. Fibers 2021, 9, 53. [Google Scholar] [CrossRef]
- Skvortsov, M.I.; Wolf, A.A.; Dostovalov, A.V.; Egorova, O.N.; Semjonov, S.L.; Babin, S.A. Narrow-Linewidth Er-Doped Fiber Lasers With Random Distributed Feedback Provided By Artificial Rayleigh Scattering. J. Light. Technol. 2022, 6, 1829–1835. [Google Scholar] [CrossRef]
- Skvortsov, M.I.; Abdullina, S.R.; Wolf, A.A.; Dostovalov, A.V.; Churin, A.E.; Egorova, O.N.; Semjonov, S.L.; Proskurina, K.V.; Babin, S.A. Single-frequency erbium-doped fibre laser with random distributed feedback based on disordered structures produced by femtosecond laser radiation. Quantum Electron. 2021, 51, 1051–1055. [Google Scholar] [CrossRef]
- Rybaltovsky, A.; Popov, S.; Ryakhovskiy, D.; Abramov, A.; Umnikov, A.; Medvedkov, O.; Voloshin, V.; Kolosovskii, A.; Vorob’ev, I.; Chamorovskiy, Y.; et al. Random Laser Based on Ytterbium-Doped Fiber with a Bragg Grating Array as the Source of Continuous-Wave 976 nm Wavelength Radiation. Photonics 2022, 9, 840. [Google Scholar] [CrossRef]
- Popov, S.M.; Butov, O.V.; Kolosovskii, A.O.; Voloshin, V.V.; Vorob’ev, I.L.; Isaev, V.A.; Ryakhovskii, D.V.; Vyatkin, M.Y.; Rybaltovskii, A.A.; Fotiadi, A.A.; et al. Optical fibres with an inscribed fibre Bragg grating array for sensor systems and random lasers. Quantum Electron. 2021, 51, 1101–1106. [Google Scholar] [CrossRef]
- Spirin, V.; López-Mercado, C.; Kinet, D.; Mégret, P.; Zolotovskiy, I.; Fotiadi, A. Single longitudinal-mode brillouin fiberlaser passively stabilized at pump resonance frequency with dynamic population inversion grating. Laser Phys. Lett. 2013, 10, 015102. [Google Scholar] [CrossRef]
- Lobach, I.A.; Drobyshev, R.V.; Fotiadi, A.A.; Podivilov, E.V.; Kablukov, S.I.; Babin, S.A. Open-cavity fiber laser with distributed feedback based on externally or self-induced dynamic gratings. Opt. Lett. 2017, 42, 4207–4210. [Google Scholar] [CrossRef]
- Web-Site of Optosystems. Available online: https://optosystems.ru/en/product/cl-5000/ (accessed on 22 May 2023).
- Soller, B.; Gifford, D.; Wolfe, M.; Froggatt, M. High resolution optical frequency domain reflectometry for characterization of components and assemblies. Opt. Express 2005, 13, 666. [Google Scholar] [CrossRef] [Green Version]
- Smirnov, A.M.; Bazakutsa, A.P.; Chamorovskiy, Y.K.; Nechepurenko, I.A.; Dorofeenko, A.V.; Butov, O.V. Thermal Switching of Lasing Regimes in Heavily Doped Er3+ Fiber Lasers. ACS Photonics 2018, 5, 5038–5046. [Google Scholar] [CrossRef] [Green Version]
- Skvortsov, M.; Wolf, A.; Dostovalov, A.; Vlasov, A.; Akulov, V.; Babin, S. Distributed feedback fiber laser based on a fiber Bragg grating inscribed using the femtosecond point-by-point technique. Laser Phys. Lett. 2018, 15, 035103. [Google Scholar] [CrossRef]
- Richter, L.E.; Mandelberg, H.I.; Kruger, M.S.; Mcgrath, P.A. Linewidth determination from self-heterodyne measurements with subcoherence delay times. IEEE J. Quantum Electron. 1986, 22, 2070–2074. [Google Scholar] [CrossRef]
- Zhang, W.L.; Rao, Y.J.; Zhu, J.M.; Wang, Z.X.; Jia, X.H. Low threshold 2nd-order random lasing of a fiber laser with a half-opened cavity. Opt. Express 2012, 20, 14400–14405. [Google Scholar] [CrossRef] [PubMed]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Popov, S.; Rybaltovsky, A.; Bazakutsa, A.; Smirnov, A.; Ryakhovskiy, D.; Voloshin, V.; Kolosovskii, A.; Vorob’ev, I.; Isaev, V.; Chamorovskiy, Y.; et al. High Efficient Random Laser with Cavity Based on the Erbium-Doped Germanophosphosilicate Artificial Rayleigh Fiber. Photonics 2023, 10, 748. https://doi.org/10.3390/photonics10070748
Popov S, Rybaltovsky A, Bazakutsa A, Smirnov A, Ryakhovskiy D, Voloshin V, Kolosovskii A, Vorob’ev I, Isaev V, Chamorovskiy Y, et al. High Efficient Random Laser with Cavity Based on the Erbium-Doped Germanophosphosilicate Artificial Rayleigh Fiber. Photonics. 2023; 10(7):748. https://doi.org/10.3390/photonics10070748
Chicago/Turabian StylePopov, Sergei, Andrey Rybaltovsky, Alexei Bazakutsa, Alexander Smirnov, Dmitry Ryakhovskiy, Viktor Voloshin, Alexander Kolosovskii, Igor Vorob’ev, Viktor Isaev, Yuriy Chamorovskiy, and et al. 2023. "High Efficient Random Laser with Cavity Based on the Erbium-Doped Germanophosphosilicate Artificial Rayleigh Fiber" Photonics 10, no. 7: 748. https://doi.org/10.3390/photonics10070748
APA StylePopov, S., Rybaltovsky, A., Bazakutsa, A., Smirnov, A., Ryakhovskiy, D., Voloshin, V., Kolosovskii, A., Vorob’ev, I., Isaev, V., Chamorovskiy, Y., Lipatov, D., & Butov, O. (2023). High Efficient Random Laser with Cavity Based on the Erbium-Doped Germanophosphosilicate Artificial Rayleigh Fiber. Photonics, 10(7), 748. https://doi.org/10.3390/photonics10070748




