Fourier Ptychography-Based Measurement of Beam Divergence Angle for Vertical Cavity Surface-Emitting Laser
Abstract
:1. Introduction
2. Method
2.1. CCD Imaging Measurement Method for VCSEL Beam Divergence Angle
2.2. Fourier Ptychographic Capturing Method and Algorithm
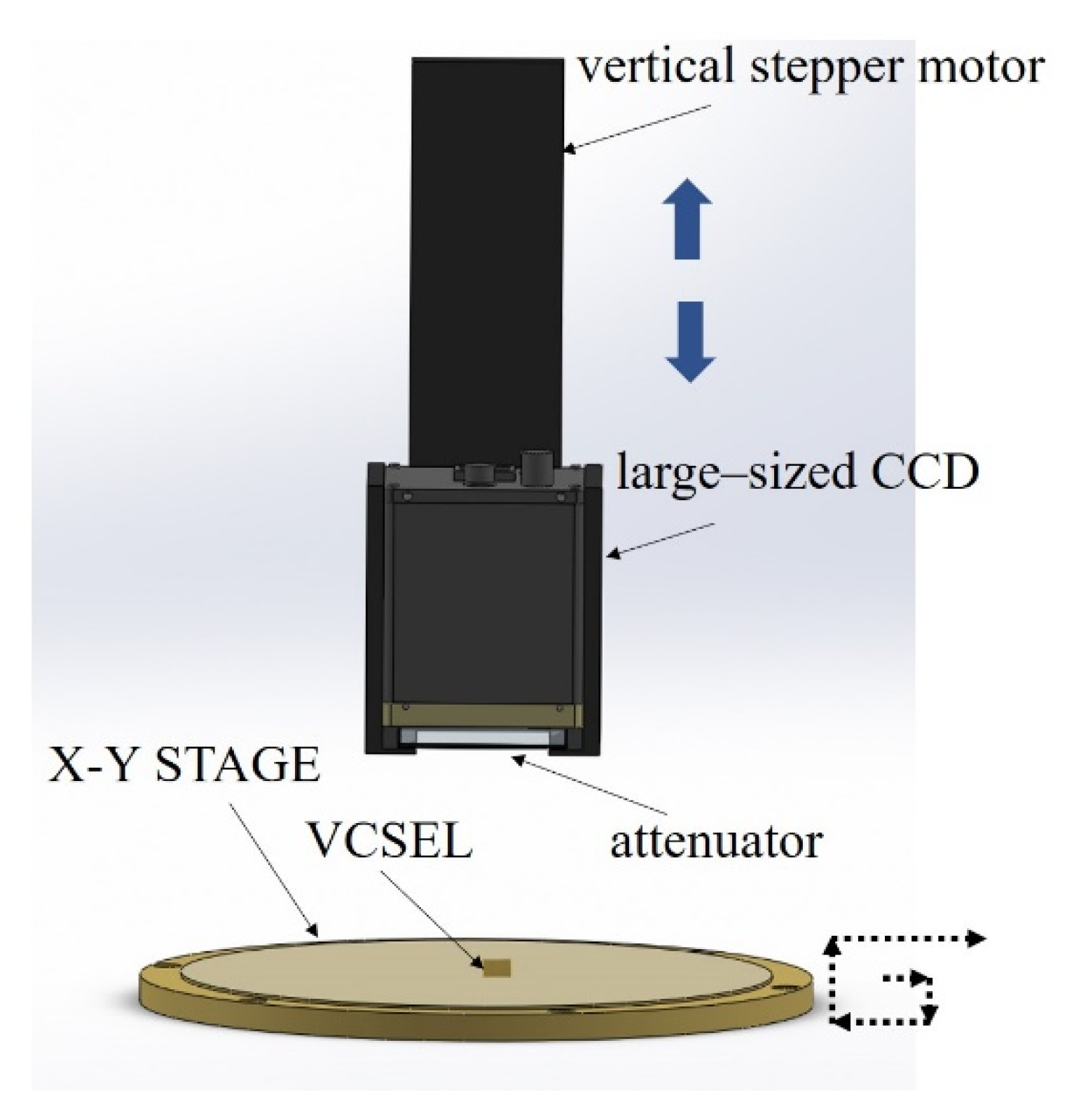
3. FP Beam Divergence Angle Measurement System
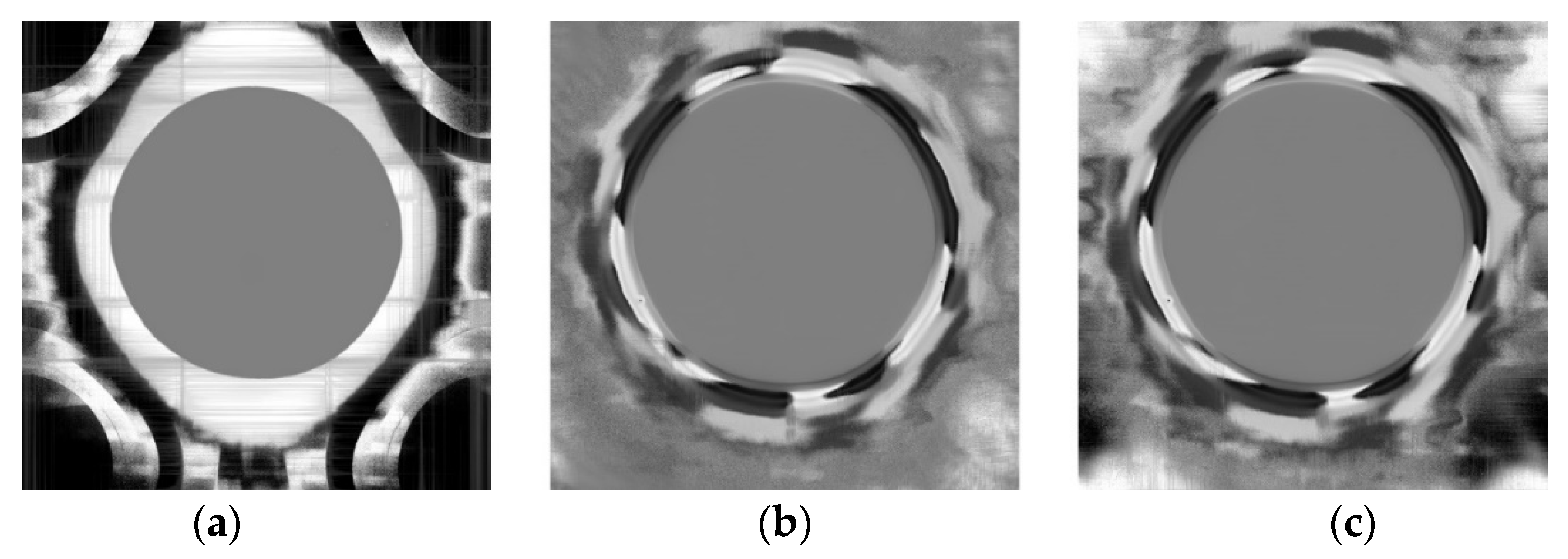
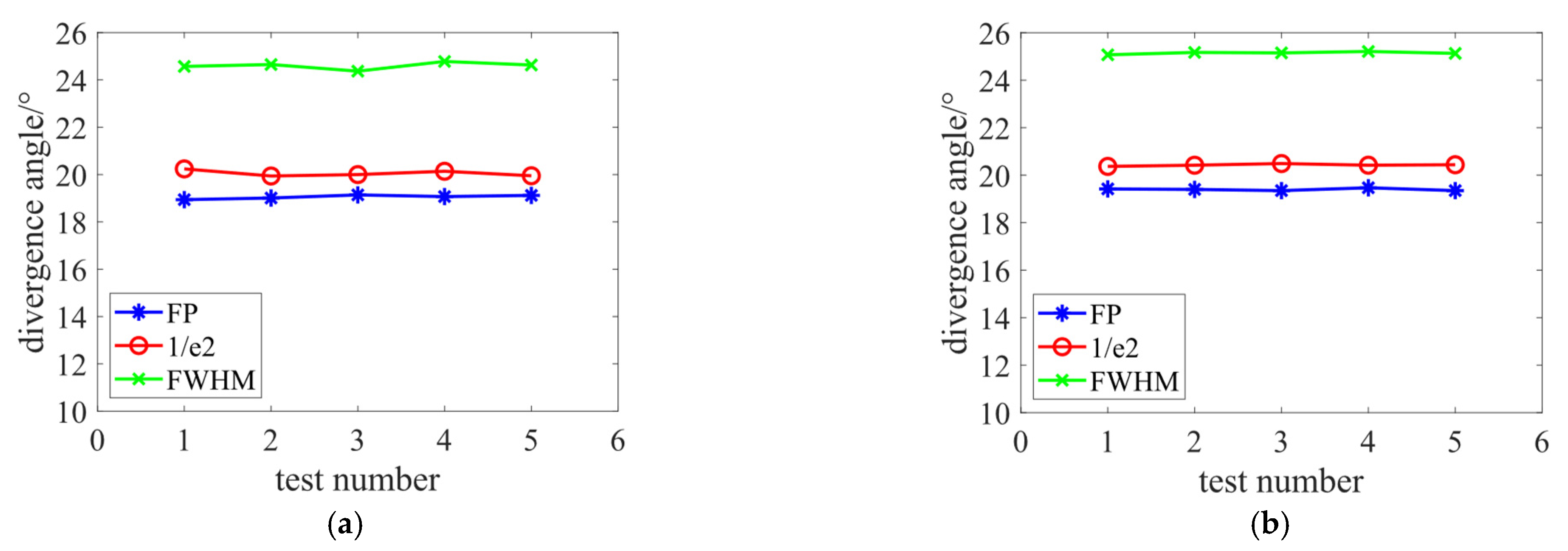
4. Experimental Results and Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Koyama, F. Recent advances of VCSEL photonics. J. Light. Technol. 2006, 24, 4502–4513. [Google Scholar] [CrossRef]
- Michalzik, R. VCSEL fundamentals. In VCSELs: Fundamentals, Technology and Applications of Vertical-Cavity Surface-Emitting Lasers; Springer: Berlin/Heidelberg, Germany, 2012; pp. 19–75. [Google Scholar]
- Dummer, M.; Johnson, K.; Rothwell, S.; Tatah, K.; Hibbs-Brenner, M. The role of VCSELs in 3D sensing and LiDAR. In Optical Interconnects XXI; SPIE: Bellingham, WA, USA, 2021; pp. 42–55. [Google Scholar]
- Giovane, L.M.; Wang, J.; Murty, M.R.; Harren, A.L.; Cheng, A.-N.; Dolfi, D.; Feng, Z.-W.; Leong, N.; Sridhara, A.; Taslim, S.-J. Development of next generation data communication VCSELs. In Proceedings of the 2020 Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 8–12 March 2020; pp. 1–3. [Google Scholar]
- Ledentsov, N.; Shchukin, V.; Kalosha, V.; Turkiewicz, J.; Ledentsov, N. Development of VCSELs and VCSEL-based Links for Data Communication beyond 50 Gb/s. In Optical Fiber Communication Conference; Optica Publishing Group: Washington, DC, USA, 2020; p. M2A-3. [Google Scholar]
- Tian, Y.; Liu, Q.; Zhang, Y.; Hou, X.; Zhang, Y. Obtaining colored patterns on polyamide fabric with laser pretreatment and pomegranate peel dyeing. Text. Res. J. 2022, 92, 2080–2089. [Google Scholar] [CrossRef]
- Nayak, R.; Padhye, R. The use of laser in garment manufacturing: An overview. Fash. Text. 2016, 3, 5. [Google Scholar] [CrossRef] [Green Version]
- Sarkar, J.; Al Faruque, M.A.; Khalil, E. Predicting the tearing strength of laser engraved denim garments using a fuzzy logic approach. Heliyon 2022, 8, e08740. [Google Scholar] [CrossRef]
- Bartol, K.; Bojanić, D.; Petković, T.; Pribanić, T. A review of body measurement using 3D scanning. IEEE Access 2021, 9, 67281–67301. [Google Scholar] [CrossRef]
- Xia, S.; Guo, S.; Li, J.; Istook, C. Comparison of different body measurement techniques: 3D stationary scanner, 3D handheld scanner, and tape measurement. J. Text. Inst. 2019, 110, 1103–1113. [Google Scholar] [CrossRef]
- Du, W.; Zuo, D.; Gan, H.; Yi, C. Comparative study on the effects of laser bleaching and conventional bleaching on the physical properties of indigo kapok/cotton denim fabrics. Appl. Sci. 2019, 9, 4662. [Google Scholar] [CrossRef] [Green Version]
- Nayak, R.; Gon, D.P.; Khandual, A. Application of LASER in Apparel Industry. Man-Made Text. India 2008, 51, 341–346. [Google Scholar]
- Mahdieh, M. Numerical approach to laser beam propagation through turbulent atmosphere and evaluation of beam quality factor. Opt. Commun. 2008, 281, 3395–3402. [Google Scholar] [CrossRef]
- Soskind, Y.; Anisimov, I. Laser cavity mode formation employing diffractive phase structures. In Laser Technology for Defense and Security XII; SPIE: Bellingham, WA, USA, 2016; pp. 85–92. [Google Scholar]
- Zhou, P.; Liu, Z.; Xu, X.; Chen, Z.; Wang, X. Beam quality factor for coherently combined fiber laser beams. Opt. Laser Technol. 2009, 41, 268–271. [Google Scholar] [CrossRef]
- Sasnett, M. Propagation of multimode laser beams–the M2 factor. In The Physics and Technology of Laser Resonators; CRC Press: Boca Raton, FL, USA, 2020; pp. 132–142. [Google Scholar]
- Siegman, A.E. Defining, measuring, and optimizing laser beam quality. Laser Reson. Coherent Opt. Model. Technol. Appl. 1993, 1868, 2–12. [Google Scholar]
- Kudryashov, A.V.; Sheldakova, J.V.; Paxton, A.H.; Kudryashov, A.V.; Zavalova, V.Y.; Ilchenko, V.S.; Cherezova, T.Y. Beam quality measurements with Shack-Hartmann wavefront sensor and M2-sensor: Comparison of two methods. In Laser Resonators and Beam Control IX; SPIE: Bellingham, WA, USA, 2007. [Google Scholar]
- de Araújo, M.A.; Silva, R.; de Lima, E.; Pereira, D.P.; de Oliveira, P.C. Measurement of Gaussian laser beam radius using the knife-edge technique: Improvement on data analysis. Appl. Opt. 2009, 48, 393–396. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, D.; Wang, Y.; Xiao, W.; Jiang, C. Measurement of laser energy distribution on the target surface of CCD detector by image fusion method. In Sixth International Symposium on Laser Interaction with Matter; SPIE: Bellingham, WA, USA, 2022; pp. 17–23. [Google Scholar]
- Schulze, C.; Flamm, D.; Duparré, M.; Forbes, A. Beam-quality measurements using a spatial light modulator. Opt. Lett. 2012, 37, 4687–4689. [Google Scholar] [CrossRef]
- Pan, S.; Ma, J.; Zhu, R.; Ba, T.; Zuo, C.; Chen, F.; Dou, J.; Wei, C.; Zhou, W. Real-time complex amplitude reconstruction method for beam quality M(2) factor measurement. Opt. Express 2017, 25, 20142–20155. [Google Scholar] [CrossRef] [Green Version]
- Du, M.; Loetgering, L.; Eikema, K.S.E.; Witte, S. Measuring laser beam quality, wavefronts, and lens aberrations using ptychography. Opt. Express 2020, 28, 5022–5034. [Google Scholar] [CrossRef]
- Kang, J.; Chen, S.; Yang, W. Measuring far-field beam divergence angle of supercontinuum fiber sources. J. Nonlinear Opt. Phys. Mater. 2022, 31, 2350003. [Google Scholar] [CrossRef]
- Zheng, G.; Horstmeyer, R.; Yang, C. Wide-field, high-resolution Fourier ptychographic microscopy. Nat. Photonics 2013, 7, 739–745. [Google Scholar] [CrossRef] [Green Version]
- Alda, J. Laser and Gaussian beam propagation and transformation. Encycl. Opt. Eng. 2003, 999, 1013. [Google Scholar]
- ISO 11146-1:2005; ISO 11146-1 Lasers and Laser-Related Equipment—Test Methods for Laser Beam Widths, Divergence Angles and Beam Propagation Ratios—Part 1: Stigmatic and Simple Astigmatic Beams. International Standardization for Standardization-ISO: Geneva, Switzerland, 2005.
- Healey, G.E.; Kondepudy, R. Radiometric CCD camera calibration and noise estimation. IEEE Trans. Pattern Anal. Mach. Intell. 1994, 16, 267–276. [Google Scholar] [CrossRef] [Green Version]
- Santos, C.N.; Chrétien, S.; Merella, L.; Vandewal, M. Visible and near-infrared laser dazzling of CCD and CMOS cameras. In Technologies for Optical Countermeasures XV; SPIE: Bellingham, WA, USA, 2018; pp. 179–187. [Google Scholar]
- Schwarz, B.; Ritt, G.; Eberle, B. Impact of threshold assessment methods in laser-induced damage measurements using the examples of CCD, CMOS, and DMD. Appl. Opt. 2021, 60, F39–F49. [Google Scholar] [CrossRef]
- Sharma, P.; Guler, Z.; Jackson, N. Development and characterization of confocal sputtered piezoelectric zinc oxide thin film. Vacuum 2021, 184, 109930. [Google Scholar] [CrossRef]
- Fienup, J.R. Phase retrieval algorithms: A comparison. Appl. Opt. 1982, 21, 2758–2769. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Holloway, J.; Wu, Y.; Sharma, M.K.; Cossairt, O.; Veeraraghavan, A. SAVI: Synthetic apertures for long-range, subdiffraction-limited visible imaging using Fourier ptychography. Sci. Adv. 2017, 3, e1602564. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ou, X.; Zheng, G.; Yang, C. Embedded pupil function recovery for Fourier ptychographic microscopy. Opt. Express 2014, 22, 4960–4972. [Google Scholar] [CrossRef] [Green Version]
- Dewey, C.W.; Brunke, M.W.; Sakovitch, K. Transcranial photobiomodulation (laser) therapy for cognitive impairment: A review of molecular mechanisms and potential application to canine cognitive dysfunction (CCD). Open Vet. J. 2022, 12, 256–263. [Google Scholar] [CrossRef]
- Faraji, H.; MacLean, W.J. CCD noise removal in digital images. IEEE Trans. Image Process. 2006, 15, 2676–2685. [Google Scholar] [CrossRef]






| Parameter | Value |
|---|---|
| Resolution | 6600 (H) × 4400 (V) |
| Pixel size | 5.5 μm |
| CCD size | 36.17 mm (H) × 24.11 mm (V) |
| Gain | 0–36 dB |
| Minimum S/N Ratio | 60 dB |
| Output Format | Mono8-14 bit, Color8-12 bit |
| Operating temperature | −40–85 °C |
| Method | Group | Mean | Variance | ||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |||
| 1/e2 | 20.24° | 19.94° | 20.00° | 20.14° | 19.95° | 20.05° | 0.0172 |
| FWHM | 24.57° | 24.65° | 24.37° | 24.78° | 24.63° | 24.60° | 0.2199 |
| FP | 18.94° | 19.01° | 19.14° | 19.07° | 19.12° | 19.09° | 0.0067 |
| Method | Group | Mean | Variance | ||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |||
| 1/e2 | 20.37° | 20.42° | 20.49° | 20.42° | 20.44° | 20.43° | 0.0019 |
| FWHM | 25.07° | 25.17° | 25.15° | 25.21° | 25.13° | 25.15° | 0.0025 |
| FP | 19.42° | 19.40° | 19.35° | 19.47° | 19.35° | 19.40° | 0.0029 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, L.; Qian, X.; Ai, L. Fourier Ptychography-Based Measurement of Beam Divergence Angle for Vertical Cavity Surface-Emitting Laser. Photonics 2023, 10, 777. https://doi.org/10.3390/photonics10070777
Jia L, Qian X, Ai L. Fourier Ptychography-Based Measurement of Beam Divergence Angle for Vertical Cavity Surface-Emitting Laser. Photonics. 2023; 10(7):777. https://doi.org/10.3390/photonics10070777
Chicago/Turabian StyleJia, Leilei, Xin Qian, and Lingyu Ai. 2023. "Fourier Ptychography-Based Measurement of Beam Divergence Angle for Vertical Cavity Surface-Emitting Laser" Photonics 10, no. 7: 777. https://doi.org/10.3390/photonics10070777
APA StyleJia, L., Qian, X., & Ai, L. (2023). Fourier Ptychography-Based Measurement of Beam Divergence Angle for Vertical Cavity Surface-Emitting Laser. Photonics, 10(7), 777. https://doi.org/10.3390/photonics10070777





