Laser Ultrasonic Automatic Detection Method for Surface Microcracks on Metallic Cylinders
Abstract
:1. Introduction
2. Materials and Methods
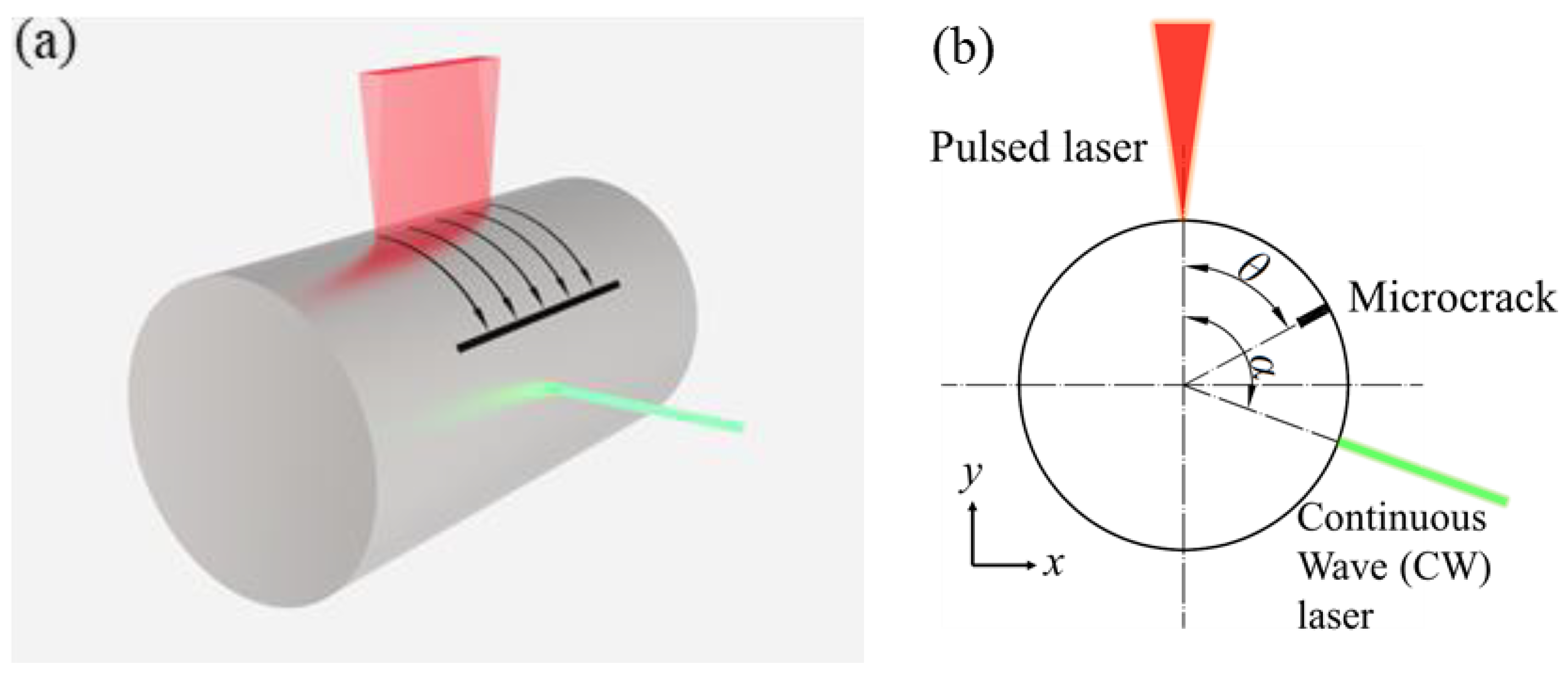
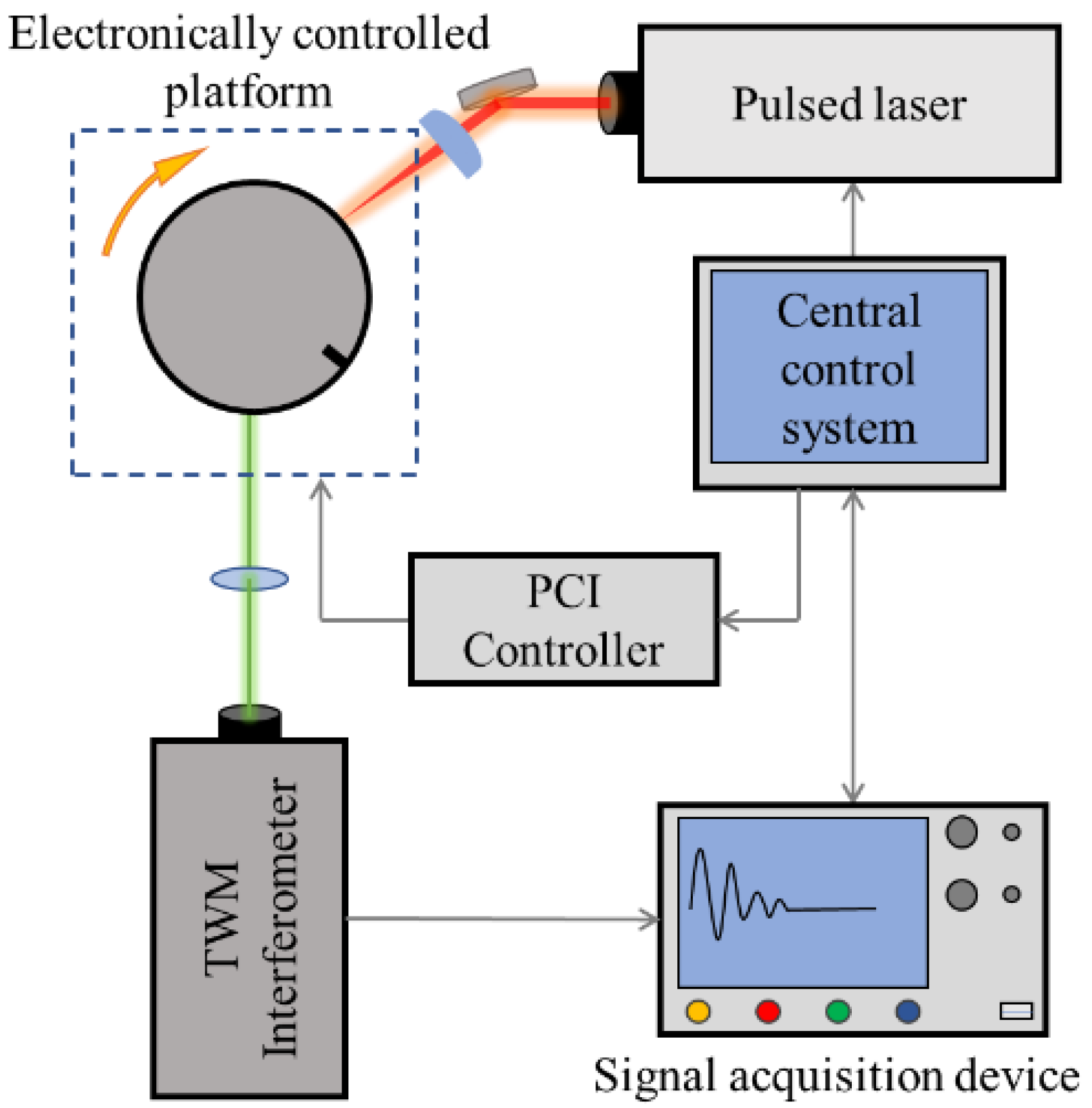
2.1. Methods
2.2. Materials
3. Results and Analysis
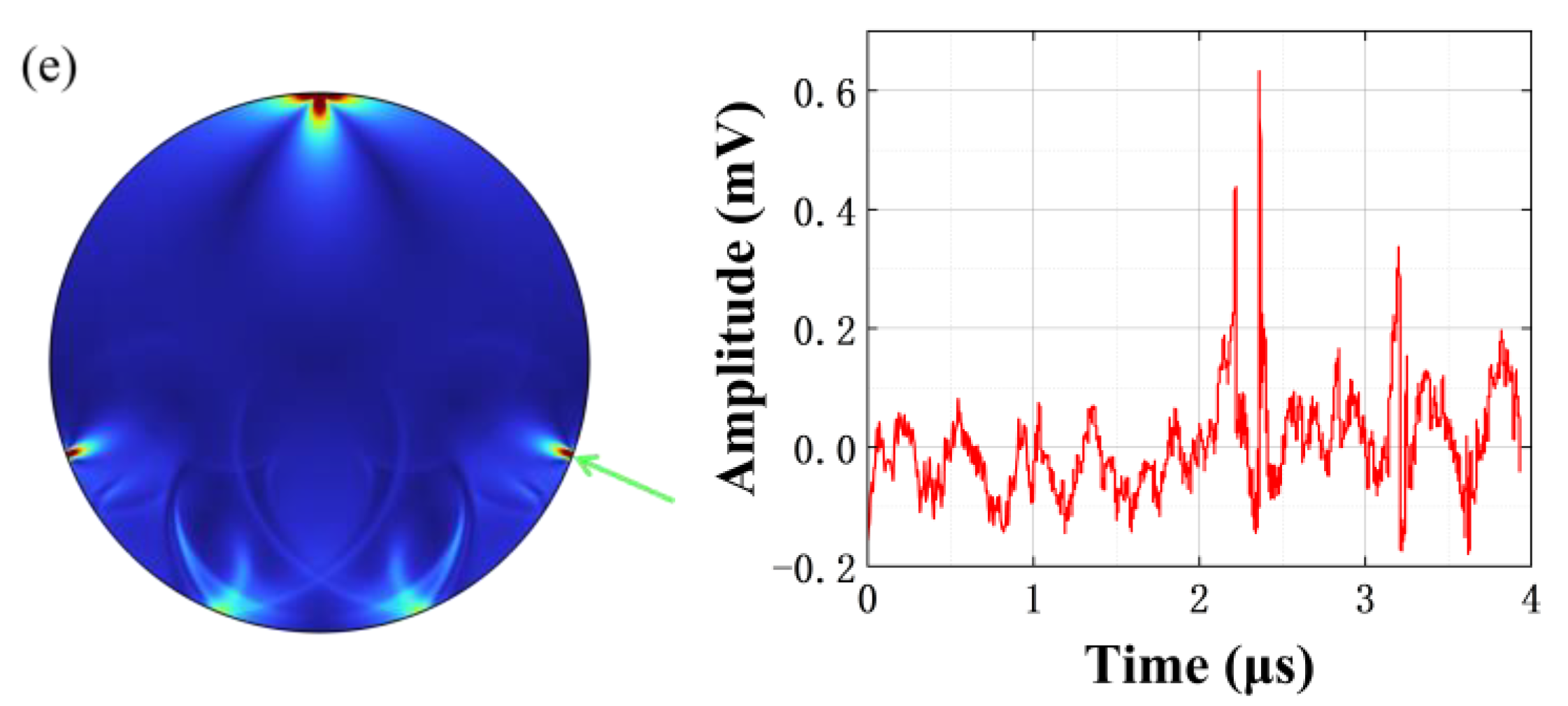
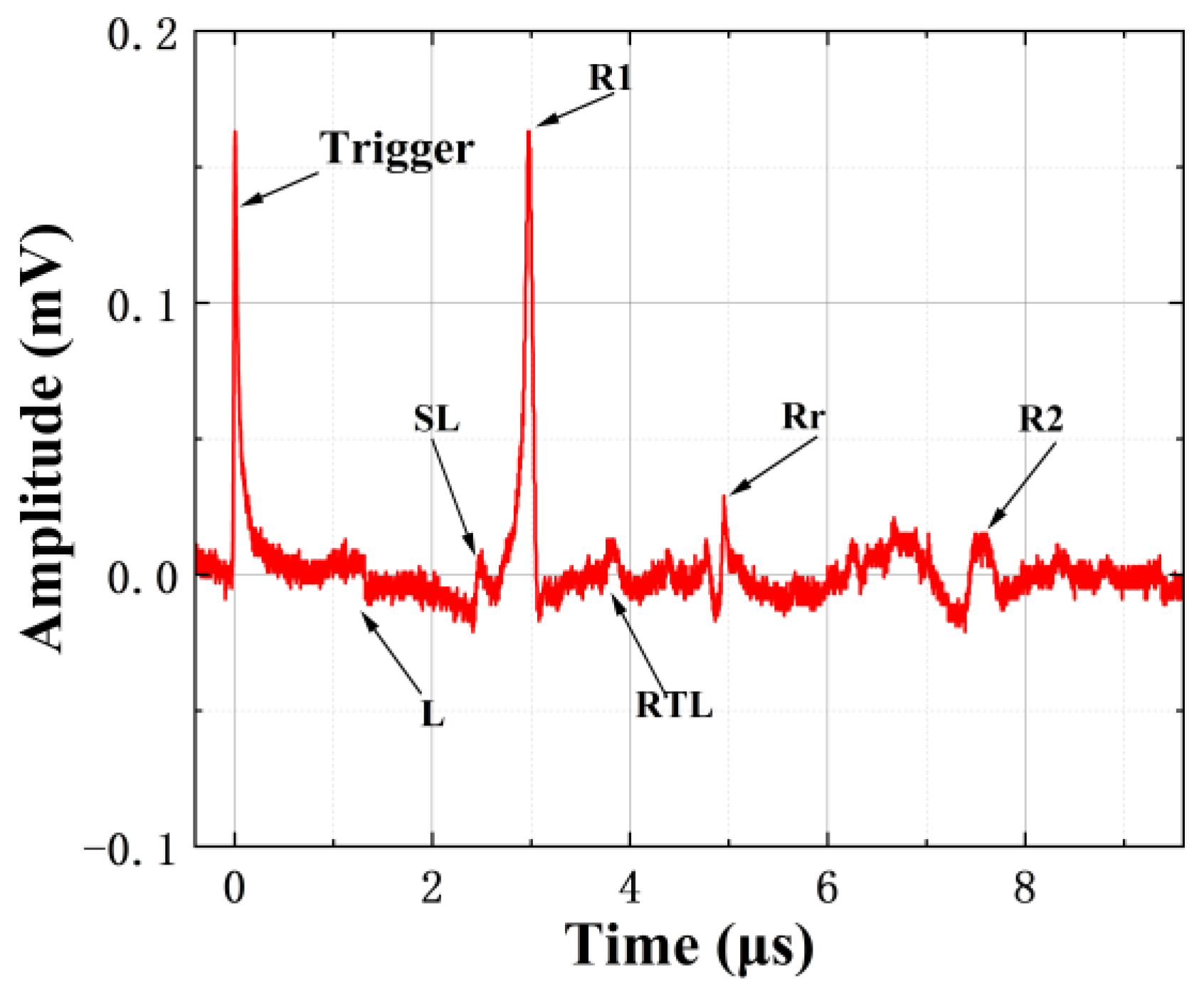
3.1. Surface Wave Analysis
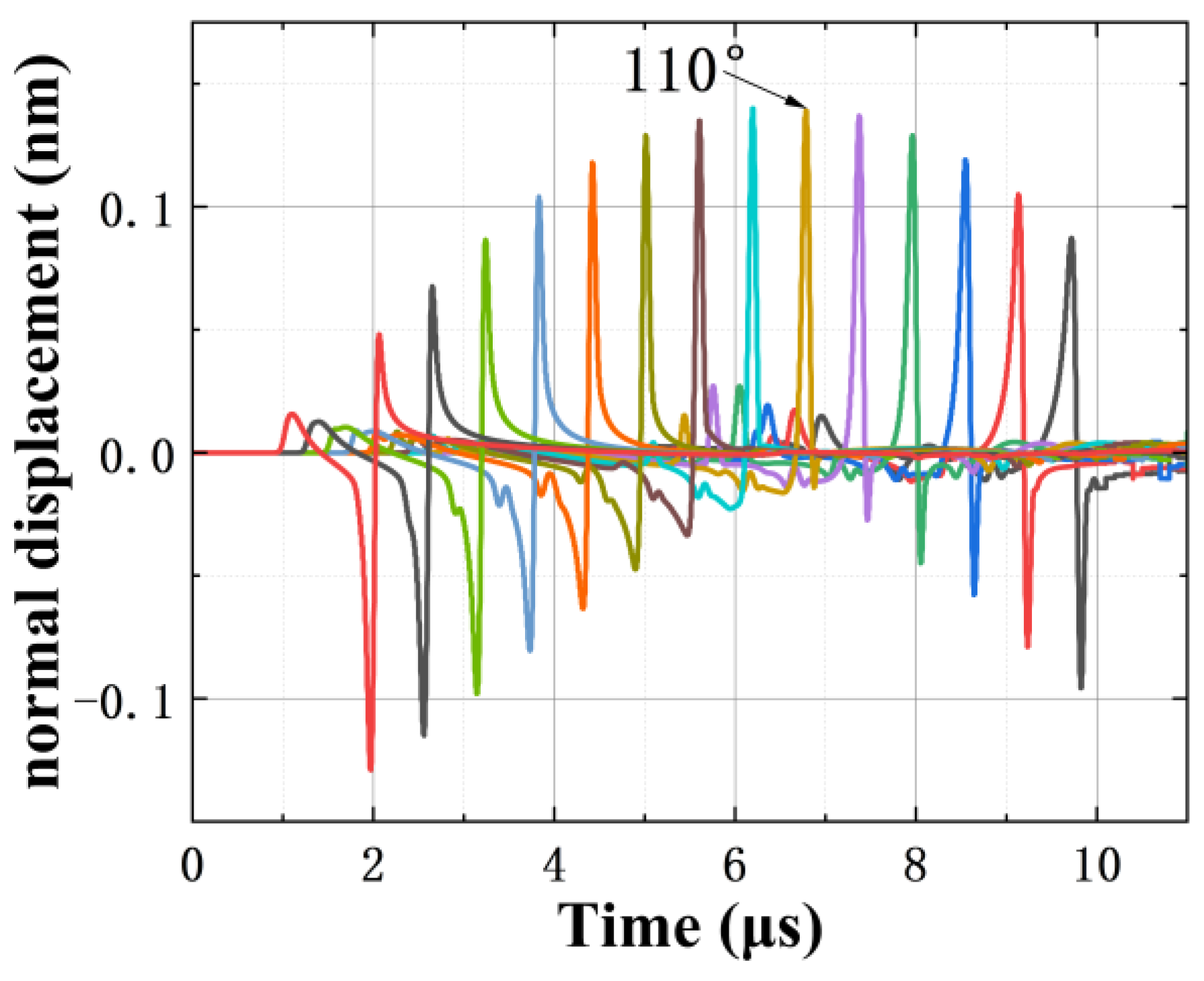
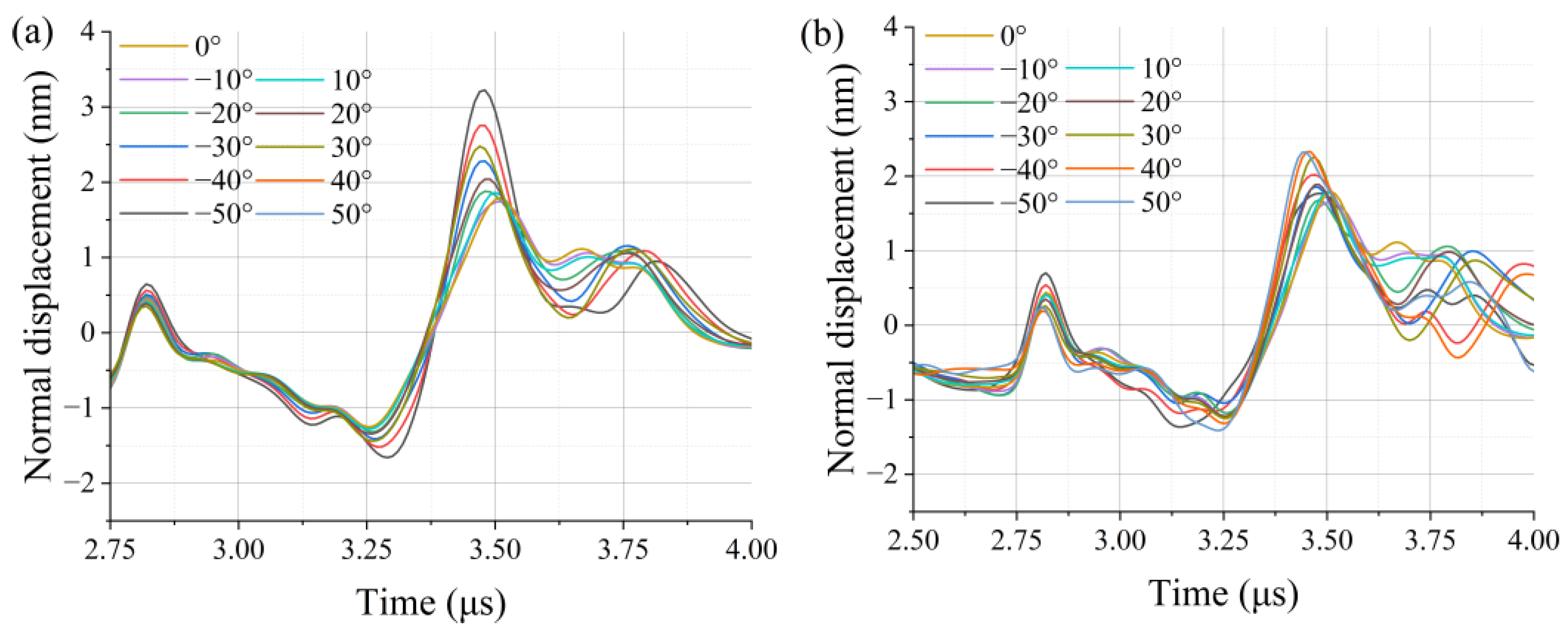
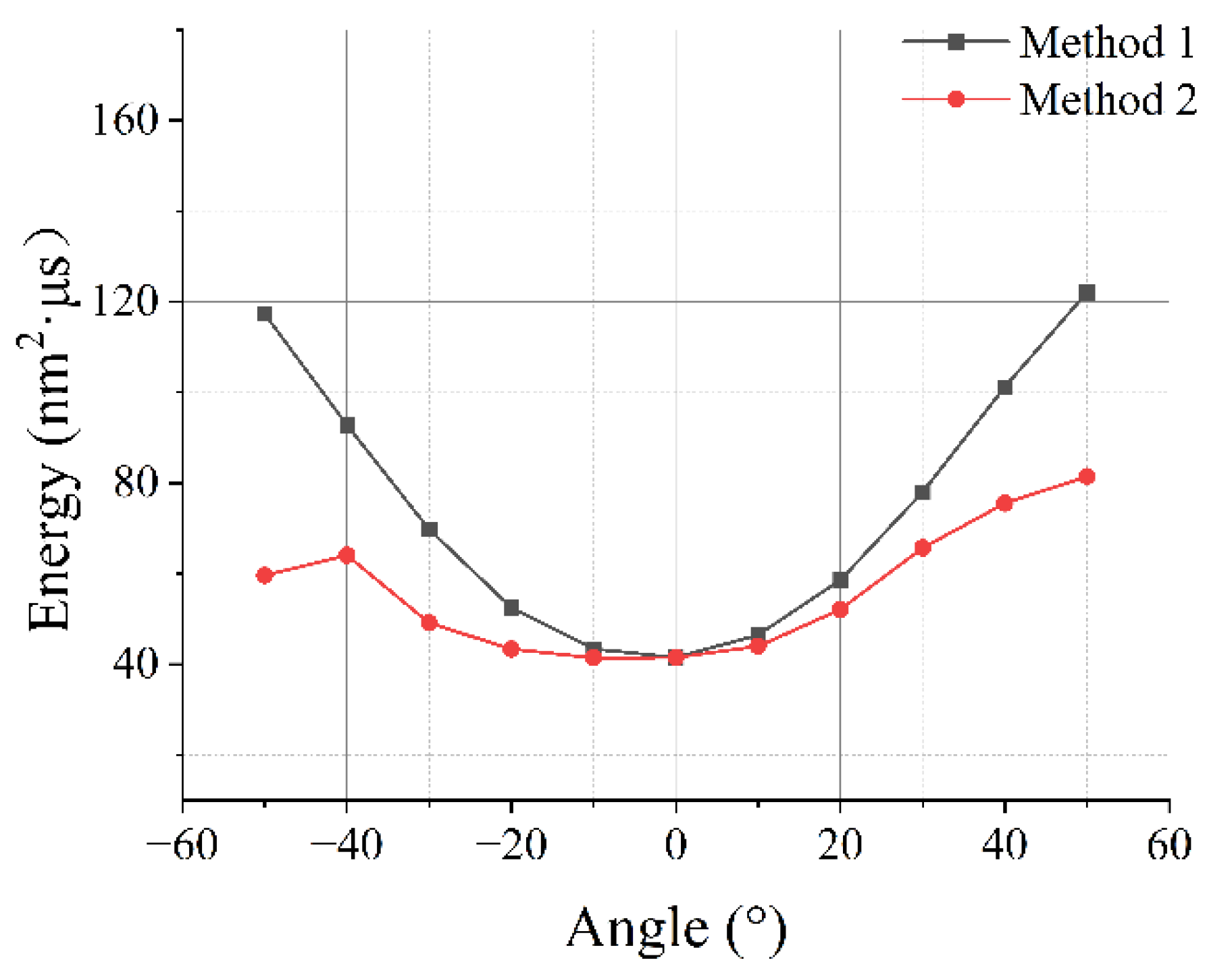
3.2. Identification of the Surface Microcrack’s Location
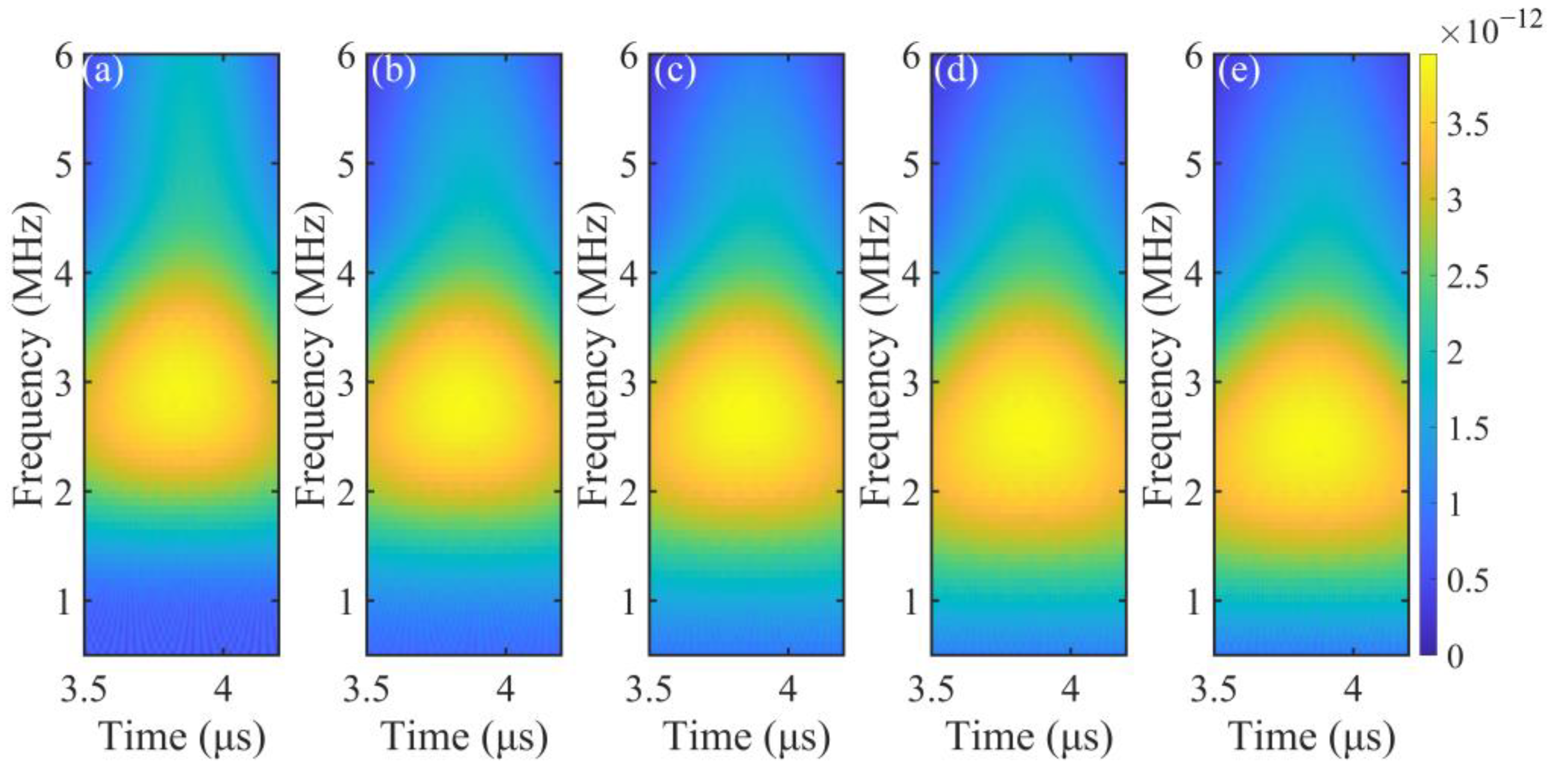
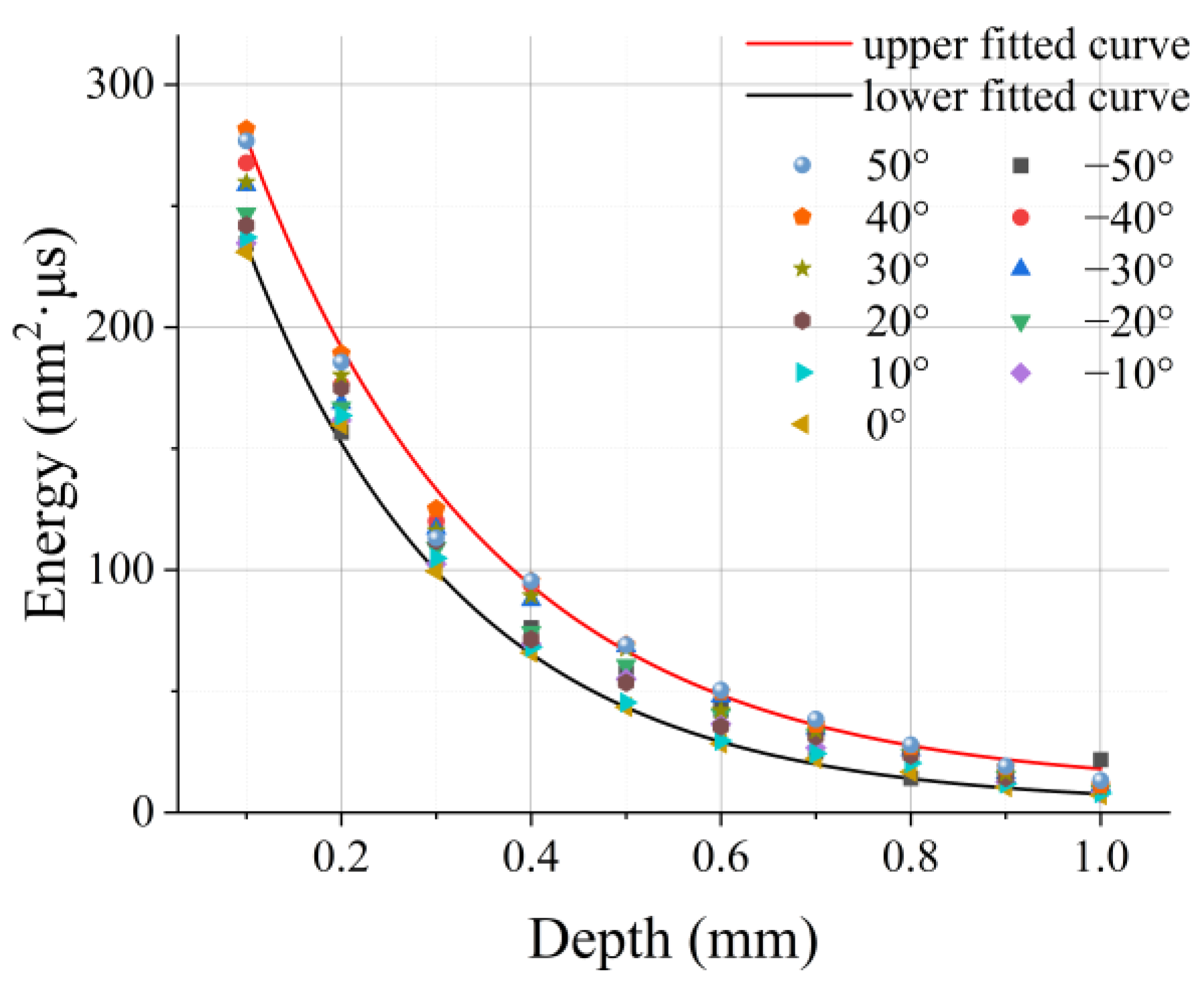
3.3. Identification of the Surface Microcrack’s Depth
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Laber, K.; Dyja, H. The Effect of the Normalizing Rolling of S355J2G3 Steel Round Bars on the Selected Mechanical Properties of Finished Product. In Proceedings of the 5th International Conference on Mechatronic Systems and Materials, Vilnius, Lithuania, 22–25 October 2010; pp. 294–299. [Google Scholar]
- Yun, J.P.; Shin, W.C.; Koo, G.; Kim, M.S.; Lee, C.; Lee, S.J. Automated defect inspection system for metal surfaces based on deep learning and data augmentation. J. Manuf. Syst. 2020, 55, 317–324. [Google Scholar] [CrossRef]
- Fan, E.; Li, Y.; You, Y.; Lu, X. Effect of crystallographic orientation on crack growth behaviour of HSLA steel. Int. J. Miner. Metall. Mater. 2022, 29, 1532–1542. [Google Scholar] [CrossRef]
- Shi, W.; Zhang, J.; Li, L.; Li, Z.; Zhang, Y.; Xiong, X.; Wang, T.; Huang, Q. Analysis of Efficient and Fast Prediction Method for the Kinematics Solution of the Steel Bar Grinding Robot. Appl. Sci. 2023, 13, 1212. [Google Scholar] [CrossRef]
- Kasai, N.; Takada, A.; Fukuoka, K.; Aiyama, H.; Hashimoto, M. Quantitative investigation of a standard test shim for magnetic particle testing. NDT E Int. 2011, 44, 421–426. [Google Scholar] [CrossRef]
- Kudinov, I.I.; Golovkov, A.N.; Shishkin, P.A.; Skorobogatko, D.S.; Andreev, A.I.; Generalov, A.S. Evaluating the Efficiency of Using Ultraviolet Radiation Sources in Carrying Out Fluorescent penetrant Testing. Russ. J. Nondestruct. Test. 2022, 58, 57–69. [Google Scholar] [CrossRef]
- Chen, Y.; Feng, B.; Kang, Y.; Liu, B.; Wang, S.; Duan, Z. A Novel Thermography-Based Dry Magnetic Particle Testing Method. IEEE Trans. Instrum. Meas. 2022, 71, 9505309. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, X. Research on laser ultrasonic surface defect identification based on a support vector machine. Sci. Prog. 2021, 104, 00368504211059038. [Google Scholar] [CrossRef]
- Lu, Z.; Zhang, Q.; Liu, X. New Magnetic Particle Cassette NDT Intelligent Detection Device. In Proceedings of the 2013 Fourth International Conference on Intelligent Systems Design and Engineering Applications, Zhangjiajie, China, 6–7 November 2013; pp. 403–406. [Google Scholar]
- Xu, G.; Guan, X.; Qiao, Y.; Gao, Y. Analysis and Innovation for Penetrant Testing for Airplane Parts. In Proceedings of the Asia-Pacific International Symposium on Aerospace Technology (APISAT), Shanghai, China, 24–26 September 2014; Chinese Society Aeronaut & Astronaut: Shanghai, China, 2014; pp. 1438–1442. [Google Scholar]
- Kiselev, E.K.; Gol’dshtein, A.E. Eddy-Current System for Testing Inner Diameter of Pipes. Russ. J. Nondestruct. Test. 2019, 55, 210–216. [Google Scholar] [CrossRef]
- Tian, Y.; Xu, G.; Wei, L.; Zhou, G.; Lin, Y.; Fan, Q.; Gu, X. Phased array ultrasonic S-scan testing of near-detection-surface defects based on a background subtraction algorithm. Mater. Res. Express 2022, 9, 036507. [Google Scholar] [CrossRef]
- Zeng, W.; Yao, Y. Numerical simulation of laser-generated ultrasonic waves for detection surface defect on a cylinder pipe. Optik 2020, 212, 164650. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, X.; Yang, Q.; Xue, R.; Zhang, J.; Sun, Y.; Xu, D.; Krishnaswamy, S. Research on epoxy resin curing monitoring using laser ultrasonic. Measurement 2020, 158, 107737. [Google Scholar] [CrossRef]
- Zhang, F.; Zhang, Y.; Wang, T.; Zhang, W.; Gong, P.; Yin, A. The effect of copper grain size on laser ultrasonic backscattered signal. Rev. Sci. Instrum. 2022, 93, 084901. [Google Scholar] [CrossRef] [PubMed]
- Qian, F.; Xing, G.; Yang, P.; Hu, P.; Zou, L.; Koukoulas, T. Laser-induced ultrasonic measurements for the detection and reconstruction of surface defects. Acta Acust. 2021, 5, 38. [Google Scholar] [CrossRef]
- Zeng, W.; Yao, F. Numerical simulation of laser-generated ultrasonic waves for identification of branched-breaking defects. Optik 2020, 208, 164435. [Google Scholar] [CrossRef]
- Kenderian, S. Phase and Dispersion of Cylindrical Surface Waves. Res. Nondestruct. Eval. 2010, 21, 224–240. [Google Scholar] [CrossRef]
- Hu, W.-X.; Qian, M.-L. Propagating Properties of Cylindrical Rayleigh Waves Generated by a Pulsed Laser Line Source. Chin. Phys. Lett. 2004, 21, 1294–1297. [Google Scholar] [CrossRef]
- Zhao, Y.; Sun, J.H.; Ma, J.; Liu, S.; Guo, R.; Song, J.F.; Jia, Z.Q. Application of the hybrid laser ultrasonic method in rail inspection. Insight 2014, 56, 360–366. [Google Scholar] [CrossRef]
- Li, H.Y.; Liu, Y.H.; Deng, J.; An, Z.W.; Pan, Q.H. Depth and Angle Evaluation of Oblique Surface Cracks Using a Support Vector Machine Based on Seven Parameters. Appl. Sci. 2022, 12, 8124. [Google Scholar] [CrossRef]
- Zeng, W.; Qi, S.K.; Liu, L.; Yao, Y.Y. Research on laser-generated Rayleigh waves with angled surface crack by finite element method. Optik 2019, 181, 57–62. [Google Scholar] [CrossRef]
- Li, H.; Pan, Q.; Zhang, X.; An, Z. An Approach to Size Sub-Wavelength Surface Crack Measurements Using Rayleigh Waves Based on Laser Ultrasounds. Sensors 2020, 20, 5077. [Google Scholar] [CrossRef]
- Yang, S.-J.; Kim, H.-S.; Jun, J.-H.; Chung, S.-C.; Park, J.-R. Changes in laser-induced thermoelastic effects depending on the position of an absorbing layer in indirect laser stimulation. J. Korean Phys. Soc. 2022, 80, 293–298. [Google Scholar] [CrossRef]
- Achenbach, J.D. Laser excitation of surface wave motion. J. Mech. Phys. Solids 2003, 51, 1885–1902. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, X.; Yang, Q.; Dong, F.; Du, X.; Yin, A. Characterization of mean grain size of interstitial-free steel based on laser ultrasonic. J. Mater. Sci. 2018, 53, 8510–8522. [Google Scholar] [CrossRef]
- Dong, F.; Wang, X.; Yang, Q.; Liu, H.; Xu, D.; Sun, Y.; Zhang, Y.; Xue, R.; Krishnaswamy, S. In-situ measurement of Ti-6Al-4V grain size distribution using laser-ultrasonic technique. Scr. Mater. 2018, 154, 40–44. [Google Scholar] [CrossRef]
- Stojkov, P.; Timotijevic, D.; Belic, M.R. Symmetries of two-wave mixing in photorefractive crystals. Opt. Lett. 1992, 17, 1406. [Google Scholar] [CrossRef]
- Clorennec, D.; Royer, D. Analysis of surface acoustic wave propagation on a cylinder using laser ultrasonics. Appl. Phys. Lett. 2003, 82, 4608–4610. [Google Scholar] [CrossRef]
- Liu, X.; Yang, S.; Liu, Y. Numerical Study for Surface-breaking Crack Detection on a Cylinder Using Laser-generated Ultrasound. In Proceedings of the 2018 15th International Conference on Ubiquitous Robots (UR), Honolulu, HI, USA, 26–30 June 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 797–802. [Google Scholar]
- Clorennec, D.; Royer, D.; Walaszek, H. Nondestructive evaluation of cylindrical parts using laser ultrasonics. Ultrasonics 2002, 40, 783–789. [Google Scholar] [CrossRef]
- Arias, I.; Achenbach, J.D. In A model for the ultrasonic detection of surface-breaking cracks by the Scanning Laser-Source technique. In Proceedings of the Conference on Nondestructive Evaluation and Health Monitoring of Aerospace Materials and Composites III, San Diego, CA, USA, 16–17 March 2004; pp. 123–131. [Google Scholar]
- Pan, Y.; Rossignol, C.; Audoin, B. Acoustic Waves Generated by a Laser Line Pulse in Cylinders; Application to the Elastic Constants Measurement. J. Acoust. Soc. Am. 2004, 115, 1537–1545. [Google Scholar] [CrossRef]
- Guo, S.; Feng, H.; Feng, W.; Lv, G.; Chen, D.; Liu, Y.; Wu, X. Automatic Quantification of Subsurface Defects by Analyzing Laser Ultrasonic Signals Using Convolutional Neural Networks and Wavelet Transform. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2021, 68, 3216–3225. [Google Scholar] [CrossRef]
- Li, H.; Zhi, B.; Pan, Q.; An, Z.; Yu, R. Photoacoustic Detection Method for Depth of Surface Narrow Defects. Acta Opt. Sinica 2021, 42, 0212001. [Google Scholar]
- Chen, D.; Lv, G.; Guo, S.; Zuo, R.; Liu, Y.; Zhang, K.; Su, Z.; Feng, W. Subsurface Defect Detection Using Phase Evolution of Line Laser-Generated Rayleigh Waves. Opt. Laser Technol. 2020, 131, 106410. [Google Scholar] [CrossRef]





| Parameters | Values |
|---|---|
| Wavelength (nm) | 1064 |
| Pulse width (ns) | 8 |
| Pulse energy (mJ) | 200 |
| Repetition frequency (Hz) | 1~10 |
| Divergency angle (mrad) | 1 |
| Beam diameter (mm) | 6 |
| Parameters | Values |
|---|---|
| Wavelength (nm) | 532 |
| Power (W) | 2 |
| Linewidth (nm) | <10−5 |
| Beam diameter (1/e2, mm) | ~1.5 |
| Divergency angle (mrad) | <1.5 |
| Power fluctuation range (%) | 2 |
| Spatial mode | TEM00 |
| C% | Mn% | Si% | S% | P% |
|---|---|---|---|---|
| 0.22 | 1.4 | 0.35 | 0.05 | 0.045 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Xu, Z.; Feng, S.; Zhang, H.; Wang, W.; Liu, Y.; Zhu, B.; Shi, W. Laser Ultrasonic Automatic Detection Method for Surface Microcracks on Metallic Cylinders. Photonics 2023, 10, 798. https://doi.org/10.3390/photonics10070798
Zhang Y, Xu Z, Feng S, Zhang H, Wang W, Liu Y, Zhu B, Shi W. Laser Ultrasonic Automatic Detection Method for Surface Microcracks on Metallic Cylinders. Photonics. 2023; 10(7):798. https://doi.org/10.3390/photonics10070798
Chicago/Turabian StyleZhang, Yanjie, Zhiqi Xu, Siyu Feng, Haowei Zhang, Wei Wang, Yaxing Liu, Bo Zhu, and Wei Shi. 2023. "Laser Ultrasonic Automatic Detection Method for Surface Microcracks on Metallic Cylinders" Photonics 10, no. 7: 798. https://doi.org/10.3390/photonics10070798
APA StyleZhang, Y., Xu, Z., Feng, S., Zhang, H., Wang, W., Liu, Y., Zhu, B., & Shi, W. (2023). Laser Ultrasonic Automatic Detection Method for Surface Microcracks on Metallic Cylinders. Photonics, 10(7), 798. https://doi.org/10.3390/photonics10070798





