Cap Layer Effect on Key Features of Persistent Photoconductivity Spectra in HgTe/CdHgTe Double Quantum Well Heterostructures
Abstract
:1. Introduction
2. Materials and Methods
2.1. Samples under Study
2.2. PPC Spectra Measurements
2.3. Resistance Kinetics Measurements and Magnetotransport Measurements
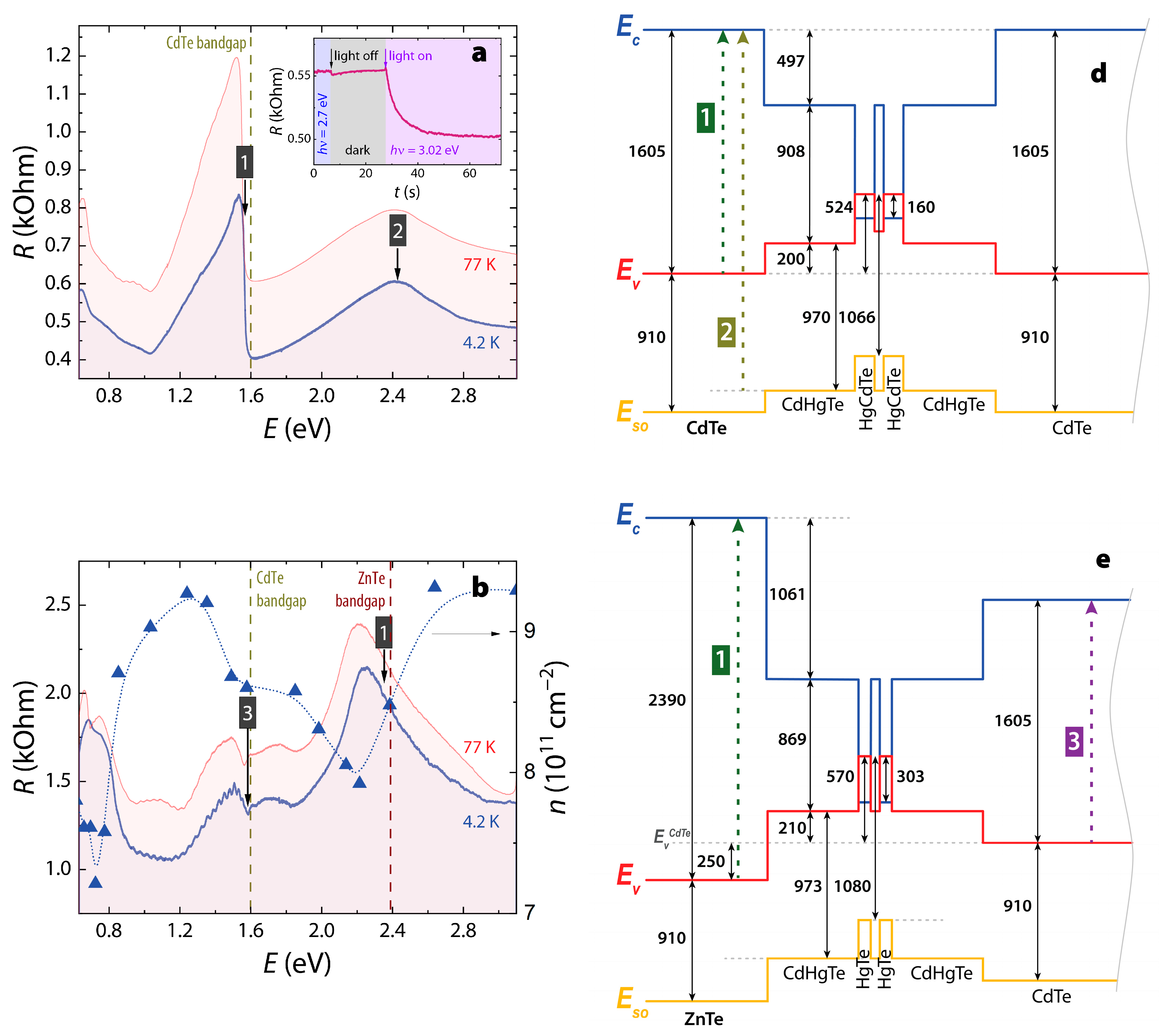
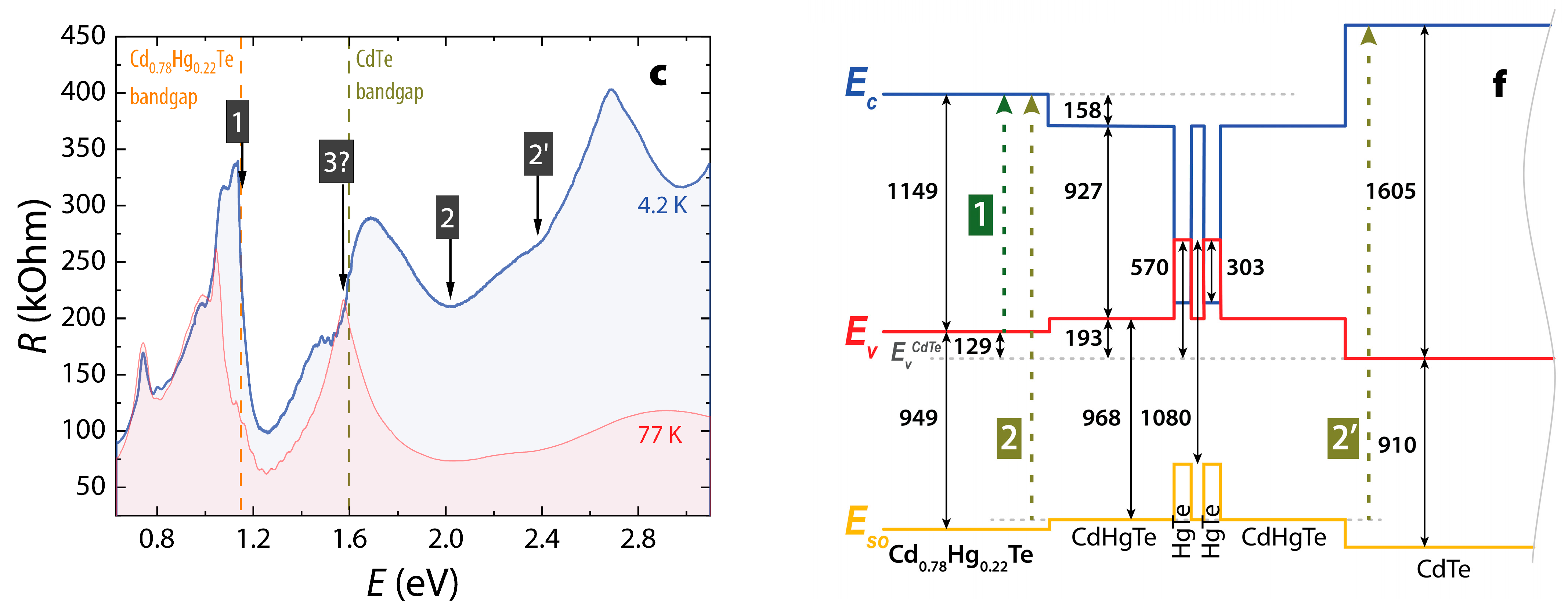
2.4. Energy Diagram Calculations
3. Results and Discussion
3.1. Key Features of the PPC Spectra
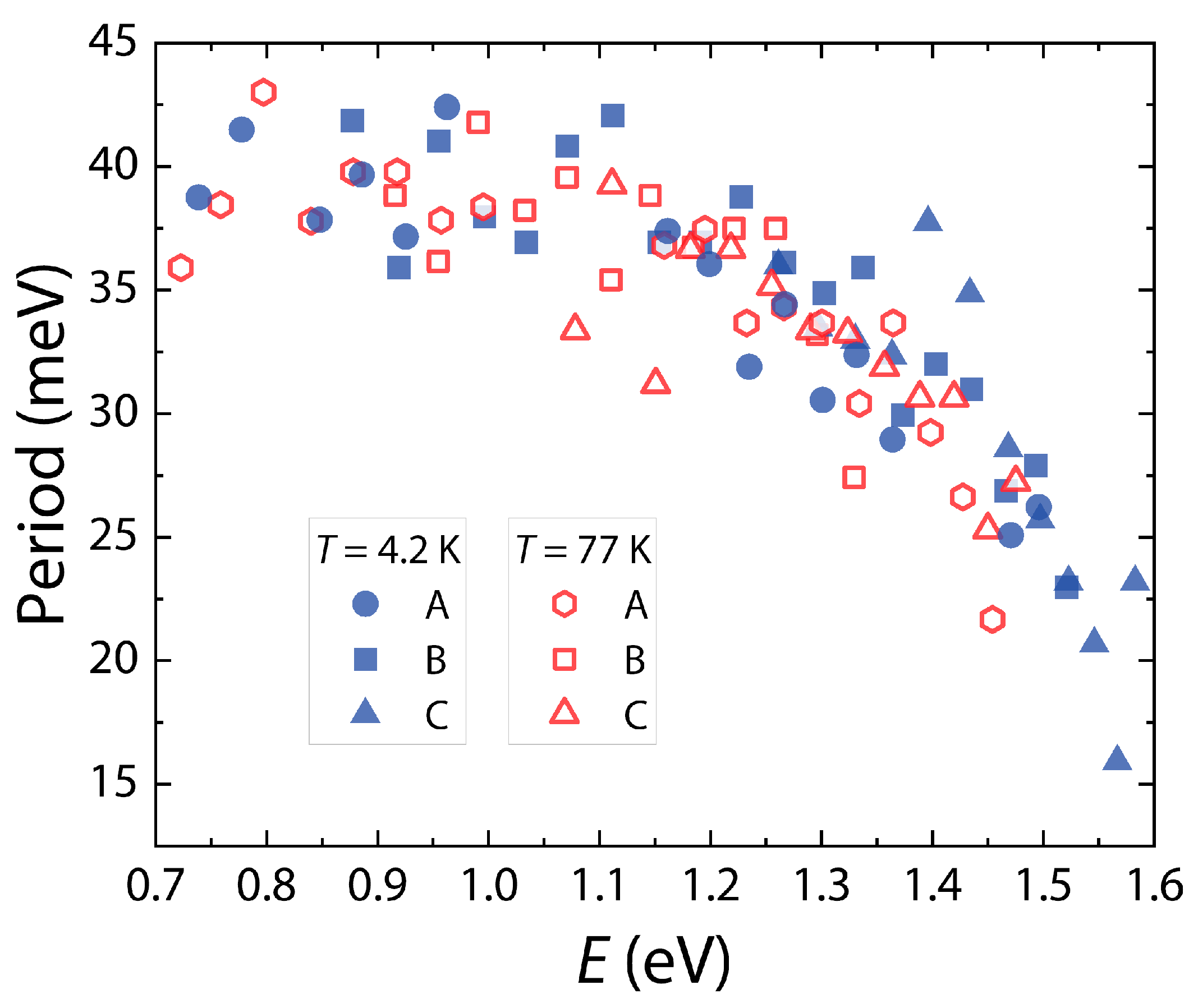
3.2. Oscillations in the PPC Spectra
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wright, H.C.; Downey, R.J.; Canning, J.R. Conductivity storage in CdS. J. Phys. D Appl. Phys. 1968, 1, 1593. [Google Scholar] [CrossRef]
- Lang, D.V.; Logan, R.A.; Jaros, M. Trapping characteristics and a donor-complex (DX) model for the persistent-photoconductivity trapping center in Te-doped AlxGa1−xAs. Phys. Rev. B 1979, 19, 1015. [Google Scholar] [CrossRef]
- Akimov, B.A.; Brandt, N.B.; Gas’kov, A.M.; Zlomanov, V.P.; Ryabova, L.I.; Khokhlov, D.R. Gallium impurity states and photoelectric phenomena in PbTe-Ga alloys. Sov. Phys. Semicond. 1983, 17, 53. [Google Scholar]
- Hirsch, M.T.; Wolk, J.A.; Walukiewicz, W.; Haller, E.E. Persistent photoconductivity in n-type GaN. Appl. Phys. Lett. 1997, 71, 1098. [Google Scholar] [CrossRef]
- Tsai, L.C.; Huang, C.F.; Fan, J.C.; Chang, Y.H.; Chen, Y.F.; Tsai, W.C.; Chang, C.Y. Persistent photoconductivity in SiGe/Si quantum wells. J. Appl. Phys. 1998, 84, 877. [Google Scholar] [CrossRef]
- Anderson, D.A.; Bass, S.J.; Kane, M.J.; Taylor, L.L. Transport and persistent photoconductivity in InGaAs/InP single quantum wells. Appl. Phys. Lett. 1986, 49, 1360. [Google Scholar] [CrossRef]
- Kastalsky, A.; Hwang, J.C.M. Study of persistent photoconductivity effect in n-type selectively doped AlGaAs/GaAs heterojunction. Solid State Commun. 1984, 51, 317. [Google Scholar] [CrossRef]
- Chen, J.; Yang, C.H.; Wilson, R.A.; Yang, M.J. Observation of negative persistent photoconductivity in an n-channel GaAs/AlxGa1−xAs single heterojunction. Appl. Phys. Lett. 1992, 60, 2113. [Google Scholar] [CrossRef]
- Lo, I.; Mitchel, W.C.; Manasreh, M.O.; Stutz, C.E.; Evans, K.R. Negative persistent photoconductivity in the Al0.6Ga0.4Sb/InAs quantum wells. Appl. Phys. Lett. 1992, 60, 751. [Google Scholar] [CrossRef]
- Chaves, A.S.; Chacham, H. Negative photoconductivity in semiconductor heterostructures. Appl. Phys. Lett. 1995, 66, 727. [Google Scholar] [CrossRef]
- Gauer, C.; Scriba, J.; Wixforth, A.A.; Kotthaus, J.P.; Nguyen, C.; Tuttle, G.; English, J.H.; Kroemer, H. Photoconductivity in AlSb/InAs quantum wells. Semicond. Sci. Technol. 1993, 8, S137. [Google Scholar] [CrossRef]
- Aleshkin, V.Y.; Gavrilenko, V.I.; Gaponova, D.M.; Ikonnikov, A.V.; Marem’yanin, K.V.; Morozov, S.V.; Sadofyev, Y.G.; Johnson, S.R.; Zhang, Y.H. Spectra of persistent photoconductivity in InAs/AlSb quantum-well heterostructures. Semiconductors 2005, 39, 22. [Google Scholar] [CrossRef]
- Gavrilenko, V.I.; Ikonnikov, A.V.; Krishtopenko, S.S.; Lastovkin, A.A.; Marem’yanin, K.V.; Sadofyev, Y.G.; Spirin, K.E. Persistent photoconductivity in InAs/AlSb heterostructures with double quantum wells. Semiconductors 2010, 44, 616. [Google Scholar] [CrossRef]
- Spirin, K.E.; Gaponova, D.M.; Gavrilenko, V.I.; Mikhailov, N.N.; Dvoretsky, S.A. Residual-photoconductivity spectra in HgTe/CdHgTe quantum-well heterostructures. Semiconductors 2019, 53, 1363. [Google Scholar] [CrossRef]
- Spirin, K.E.; Gaponova, D.M.; Marem’yanin, K.V.; Rumyantsev, V.V.; Gavrilenko, V.I.; Mikhailov, N.N.; Dvoretsky, S.A. Bipolar persistent photoconductivity in HgTe/CdHgTe (013) double quantum-well heterostructures. Semiconductors 2018, 52, 1586. [Google Scholar] [CrossRef]
- Nikolaev, I.D.; Kazakov, A.S.; Drozdov, K.A.; Bannikov, M.I.; Spirin, K.E.; Menshchikov, R.V.; Dvoretsky, S.A.; Mikhailov, N.N.; Khokhlov, D.R.; Ikonnikov, A.V. Bipolar persistent photoconductivity in HgTe/CdHgTe double quantum well heterostructures and its application for reversible change in the conductivity type. J. Appl. Phys. 2022, 132, 234301. [Google Scholar] [CrossRef]
- König, M.; Wiedmann, S.; Brüne, C.; Roth, A.; Buhmann, H.; Molenkamp, L.W.; Qi, X.-L.; Zhang, S.-C. Quantum spin Hall insulator state in HgTe quantum wells. Science 2007, 318, 766. [Google Scholar] [CrossRef] [Green Version]
- Krishtopenko, S.S.; Knap, W.; Teppe, F. Phase transitions in two tunnel-coupled HgTe quantum wells: Bilayer graphene analogy and beyond. Sci. Rep. 2016, 6, 30755. [Google Scholar] [CrossRef] [Green Version]
- Krishtopenko, S.S. Higher-order topological insulator in cubic semiconductor quantum wells. Sci. Rep. 2021, 11, 21060. [Google Scholar] [CrossRef]
- Schindler, F.; Cook, A.M.; Vergniory, M.G.; Wang, Z.; Parkin, S.S.; Bernevig, B.A.; Neupert, T. Higher-order topological insulators. Science advances. Sci. Adv. 2018, 4, eaat0346. [Google Scholar] [CrossRef] [Green Version]
- Kim, M.; Jacob, Z.; Rho, J. Recent advances in 2D, 3D and higher-order topological photonics. Light Sci. Appl. 2020, 9, 130. [Google Scholar] [CrossRef] [PubMed]
- Xie, B.; Wang, H.X.; Zhang, X.; Zhan, P.; Jiang, J.H.; Lu, M.; Chen, Y. Higher-order band topology. Nat. Rev. Phys. 2021, 3, 520. [Google Scholar] [CrossRef]
- Lunczer, L.; Leubner, P.; Endres, M.; Müller, V.L.; Brüne, C.; Buhmann, H.; Molenkamp, L.W. Approaching quantization in macroscopic quantum spin Hall devices through gate training. Phys. Rev. Lett. 2019, 123, 047701. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gusev, G.M.; Olshanetsky, E.B.; Hernandez, F.G.G.; Raichev, O.E.; Mikhailov, N.N.; Dvoretsky, S.A. Two-dimensional topological insulator state in double HgTe quantum well. Phys. Rev. B 2020, 101, 241302. [Google Scholar] [CrossRef]
- Mikhailov, N.N.; Smirnov, R.N.; Dvoretsky, S.A.; Sidorov, Y.G.; Shvets, V.A.; Spesivtsev, E.V.; Rykhlitski, S.V. Growth of Hg1–xCdxTe nanostructures by molecular beam epitaxy with ellipsometric control. Int. J. Nanotechnol. 2006, 3, 120. [Google Scholar] [CrossRef]
- Laurenti, J.P.; Camassel, J.; Bouhemadou, A.; Toulouse, B.; Legros, R.; Lusson, A. Temperature dependence of the fundamental absorption edge of mercury cadmium telluride. J. Appl. Phys. 1990, 67, 6454. [Google Scholar] [CrossRef]
- Rogalsky, A. Hg1-xZnxTe as a potential infrared detector material. Prog. Quant. Electr. 1989, 13, 299. [Google Scholar] [CrossRef]
- Novik, G.; Pfeuffer-Jeschke, A.; Jungwirth, T.; Latussek, V.; Becker, C.R.; Landwehr, G.; Buhmann, H.; Molenkamp, L.W. Band structure of semimagnetic Hg1–yMnyTe quantum well. Phys. Rev. B 2005, 72, 035321. [Google Scholar] [CrossRef] [Green Version]
- Grinyaev, S.N.; Kataev, S.G. Electronic structure of ZnxCdyHg1-x-yTe alloys and related heterojunctions. Phys. B Condens. Matter 1993, 191, 317. [Google Scholar] [CrossRef]
- Marple, D.T.F. Refractive index of ZnSe, ZnTe, and CdTe. J. Appl. Phys. 1964, 35, 539. [Google Scholar] [CrossRef]
| Sample | No. | d, nm | t, nm | x, % | y, % | Cap Layer | R4.2 K, kOhm | R77 K, kOhm |
|---|---|---|---|---|---|---|---|---|
| A | 170320 | 6.5 | 3 | 65 | ~8 | CdTe | 0.58 | 2.17 |
| B | 220912 | 4 | 3 | 63 | 0 | ZnTe | 121 | 23.6 |
| C | 220909 | 4 | 3 | 66 | 0 | Cd0.85Hg0.15Te | 107 | 140 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sotnichuk, M.K.; Kazakov, A.S.; Nikolaev, I.D.; Drozdov, K.A.; Menshchikov, R.V.; Dvoretsky, S.A.; Mikhailov, N.N.; Khokhlov, D.R.; Ikonnikov, A.V. Cap Layer Effect on Key Features of Persistent Photoconductivity Spectra in HgTe/CdHgTe Double Quantum Well Heterostructures. Photonics 2023, 10, 877. https://doi.org/10.3390/photonics10080877
Sotnichuk MK, Kazakov AS, Nikolaev ID, Drozdov KA, Menshchikov RV, Dvoretsky SA, Mikhailov NN, Khokhlov DR, Ikonnikov AV. Cap Layer Effect on Key Features of Persistent Photoconductivity Spectra in HgTe/CdHgTe Double Quantum Well Heterostructures. Photonics. 2023; 10(8):877. https://doi.org/10.3390/photonics10080877
Chicago/Turabian StyleSotnichuk, Mikhail K., Aleksei S. Kazakov, Ilya D. Nikolaev, Konstantin A. Drozdov, Roman V. Menshchikov, Sergey A. Dvoretsky, Nikolay N. Mikhailov, Dmitry R. Khokhlov, and Anton V. Ikonnikov. 2023. "Cap Layer Effect on Key Features of Persistent Photoconductivity Spectra in HgTe/CdHgTe Double Quantum Well Heterostructures" Photonics 10, no. 8: 877. https://doi.org/10.3390/photonics10080877
APA StyleSotnichuk, M. K., Kazakov, A. S., Nikolaev, I. D., Drozdov, K. A., Menshchikov, R. V., Dvoretsky, S. A., Mikhailov, N. N., Khokhlov, D. R., & Ikonnikov, A. V. (2023). Cap Layer Effect on Key Features of Persistent Photoconductivity Spectra in HgTe/CdHgTe Double Quantum Well Heterostructures. Photonics, 10(8), 877. https://doi.org/10.3390/photonics10080877






