Density-Functional Study of the Si/SiO2 Interfaces in Short-Period Superlattices: Vibrational States and Raman Spectra
Abstract
:1. Introduction
2. Computational Details
3. Results and Discussion
3.1. Bulk Crystals
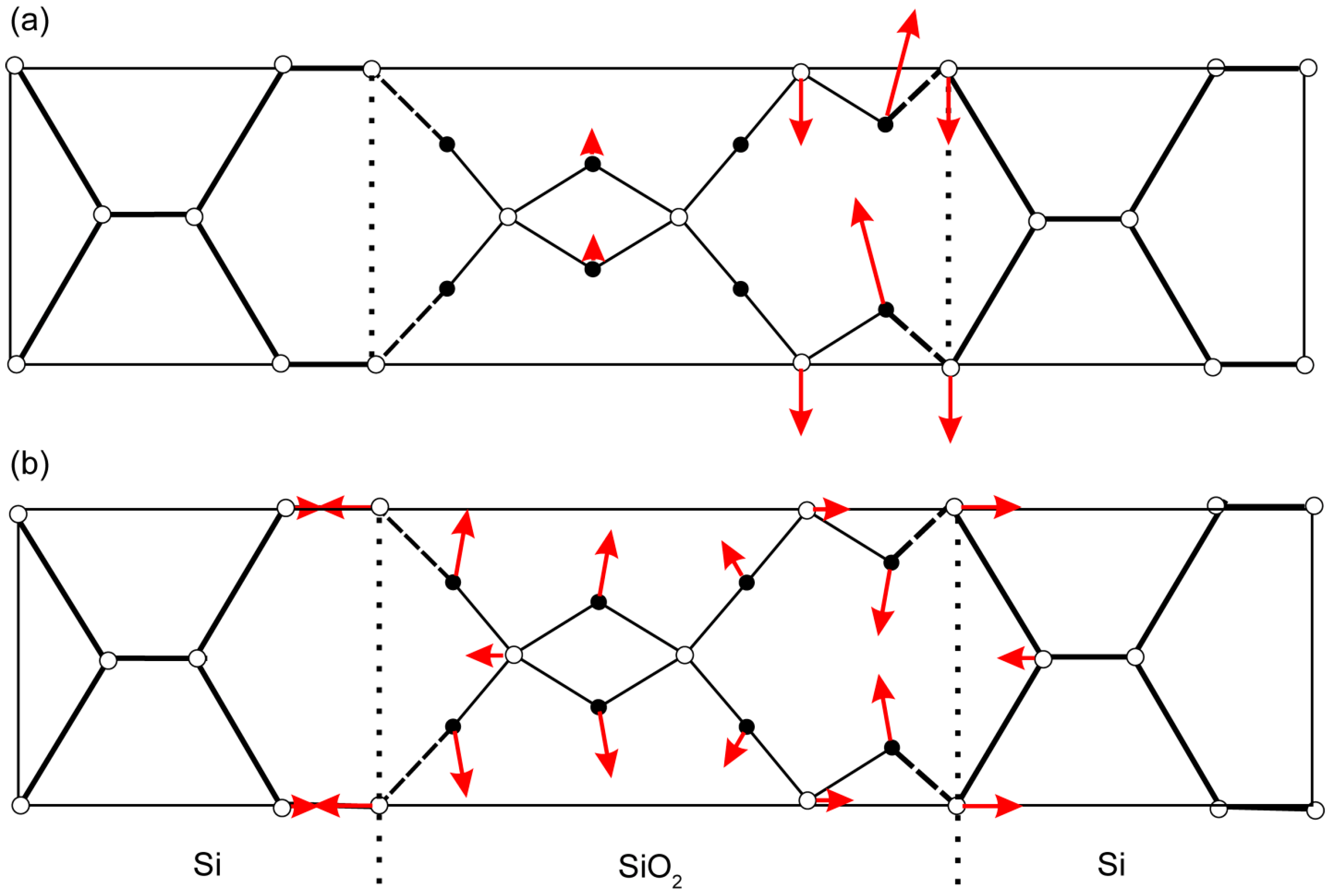
3.2. Phonons in 4 × 4 I1 SL
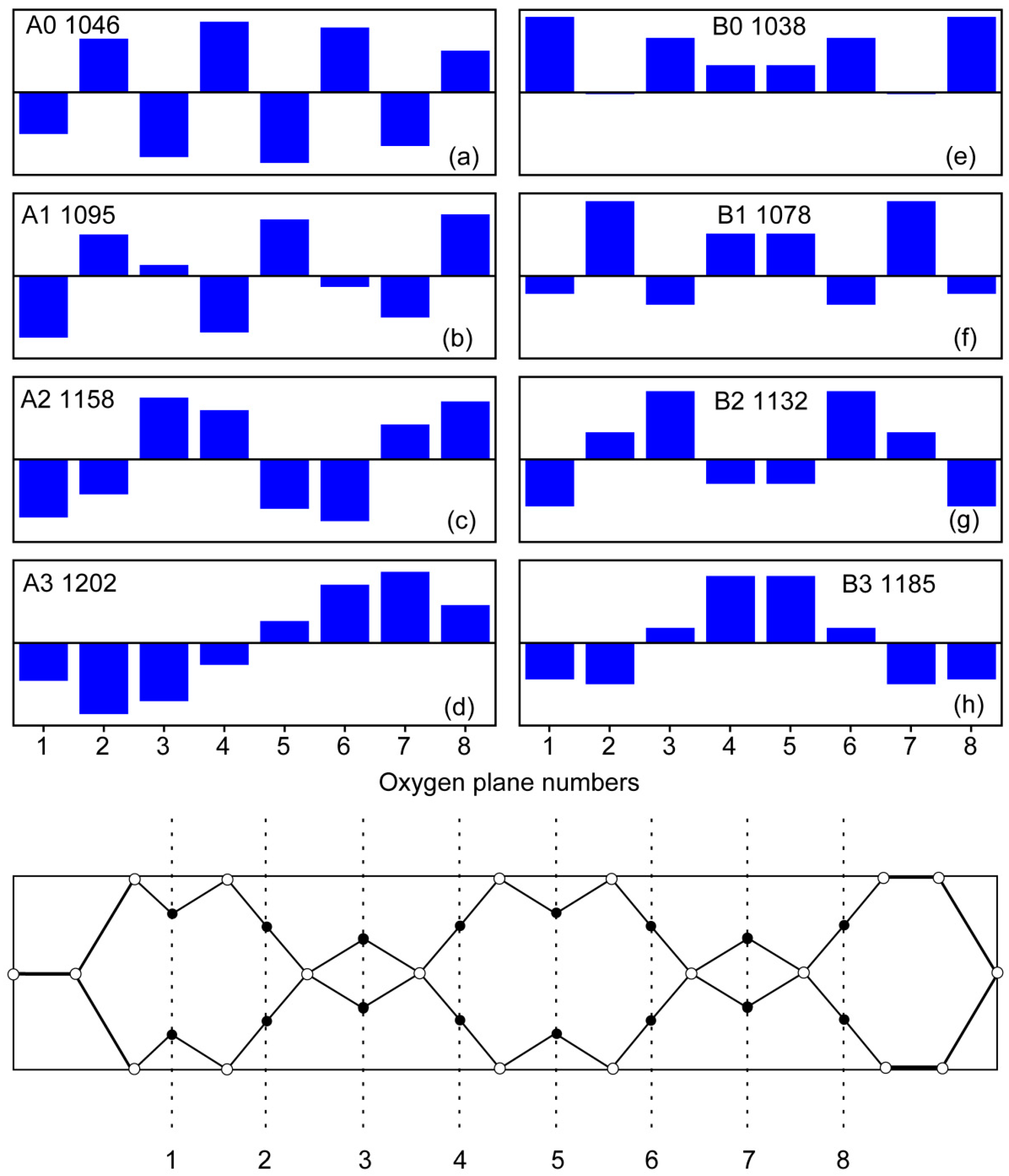
3.3. Phonons in I1 SLs of Different Sizes
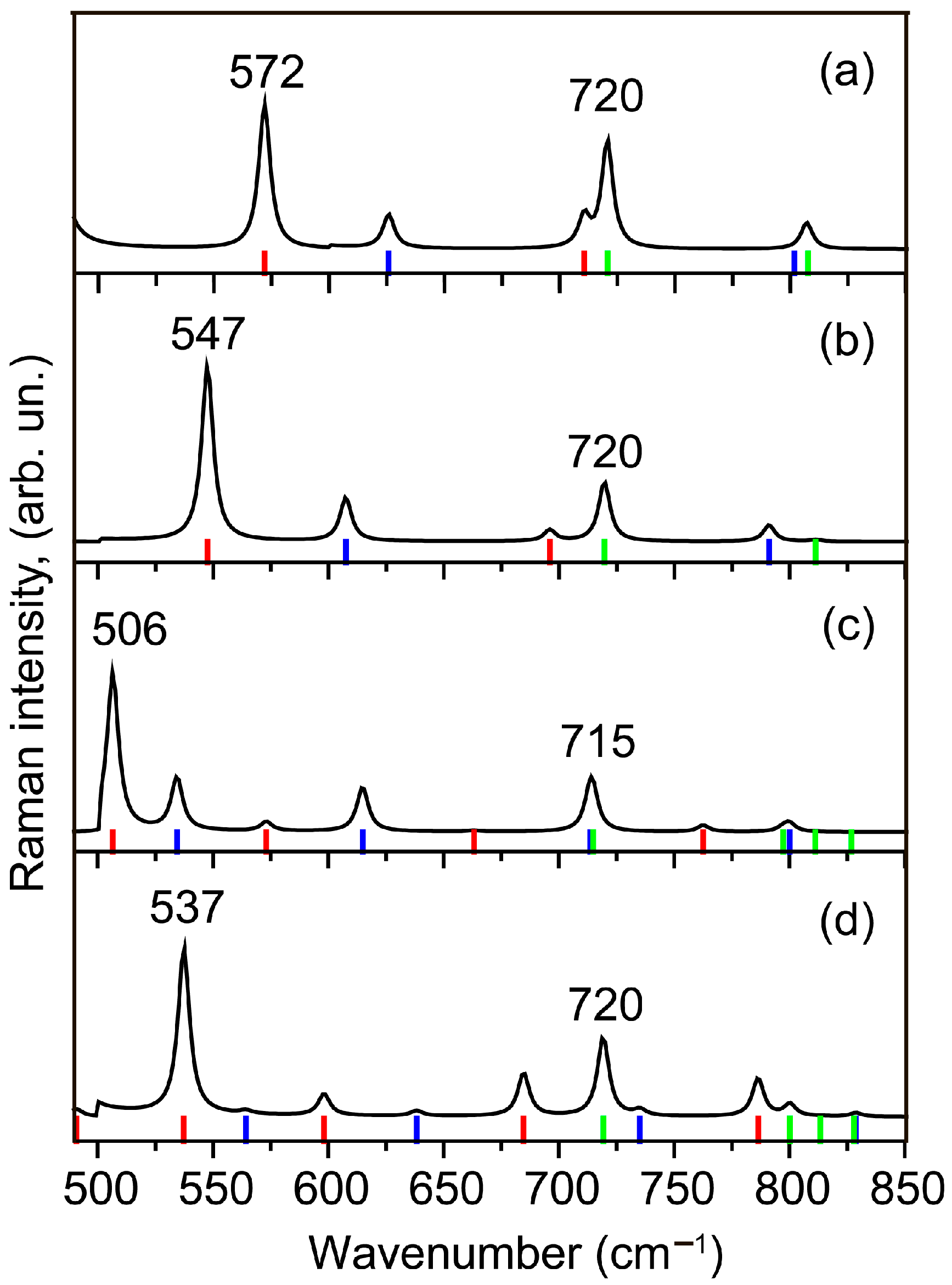
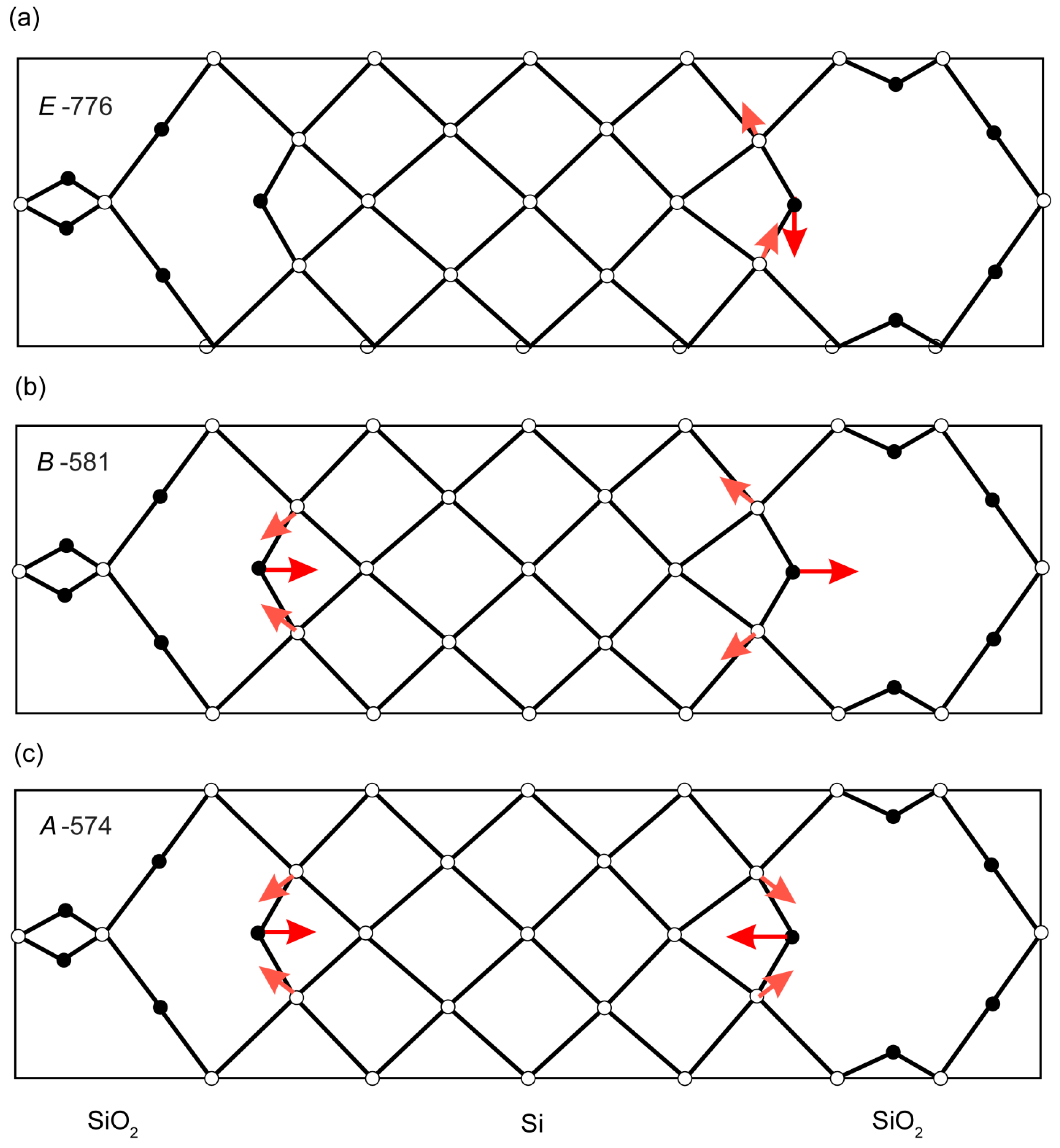
3.4. Phonons and Raman Spectra of the I2 Type SLs
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lockwood, D.J.; Lu, Z.H.; Baribeau, J.M. Quantum confined luminescence in Si/SiO2 superlattices. Phys. Rev. Lett. 1996, 76, 539–541. [Google Scholar] [CrossRef] [PubMed]
- Lockwood, D.J. Quantum confined luminescence in Si/SiO2 superlattices. Phase Trans. 1999, 68, 151–168. [Google Scholar] [CrossRef]
- Kato, Y.; Tanemura, T.; Hoshino, H.; Miura, K.; Hanaizumi, O. Fabrication of amorphous Si/SiO2 superlattices by using RF sputtering and their luminescence properties. IEICE Tech. Rep. 2006, 105, 35–39. [Google Scholar]
- Kamaev, G.N.; Cherkova, S.G.; Gismatulin, A.A.; Volodin, V.A.; Skuratov, V.A. Swift heavy ion stimulated formation of the Si quantum dots in Si/SiO2 multilayer heterostructures. Proc. SPIE 2019, 11022, 276–281. [Google Scholar] [CrossRef]
- Yazicioglu, D.; Gutsch, S.; Zacharias, M. Effects of field enhanced charge transfer on the luminescence properties of Si/SiO2 superlattices. Sci. Rep. 2022, 12, 2641. [Google Scholar] [CrossRef]
- Ye, K.; Li, K.; Lu, Y.; Guo, Z.; Ni, N.; Liu, H.; Huang, Y.; Ji, H.; Wang, P. An overview of advanced methods for the characterization of oxygen vacancies in materials. Trends Analyt. Chem. 2019, 116, 102–108. [Google Scholar] [CrossRef]
- Pantelides, S.T. Si/SiO2 and SiC/SiO2 Interfaces for MOSFETs—Challenges and Advances. Mater. Sci. Forum 2006, 527, 935–948. Available online: https://www.scientific.net/MSF.527-529.935 (accessed on 27 July 2023). [CrossRef]
- Li, P.; Song, Y.; Zuo, X. Computational Study on Interfaces and Interface Defects of Amorphous Silica and Silicon. Phys. Status Solidi RRL 2018, 13, 1800547. [Google Scholar] [CrossRef]
- Radamson, H.H.; Zhu, H.; Wu, Z.; He, X.; Lin, H.; Liu, J.; Xiang, J.; Kong, Z.; Xiong, W.; Li, J.; et al. State of the Art and Future Perspectives in Advanced CMOS Technology. Nanomaterials 2020, 10, 1555. [Google Scholar] [CrossRef] [PubMed]
- Zheng, T.; Li, Z. The present status of Si/SiO2 superlattice research into optoelectronic applications. Superlattice Microst. 2005, 37, 227–247. [Google Scholar] [CrossRef]
- Liu, N.; Sun, J.; Pan, S.; Chen, Z.; Shi, W.; Wang, R.; Wang, X. Third-order optical nonlinear properties of amorphous Si/SiO2 superlattices fabricated by magnetron sputtering. Opt. Commun. 2000, 176, 239–243. [Google Scholar] [CrossRef]
- Yamada, S.; Konagai, M.; Miyajima, S. Investigation of the optical absorption in Si/SiO2 superlattice for the application to solar cells. Jpn. J. Appl. Phys. 2016, 55, 04ES06. [Google Scholar] [CrossRef]
- Kageshima, H.; Shiraishi, K. Silicon-kicking-out mechanism in initial oxide formation on hydrogen-terminated silicon (100) surfaces. Appl. Surf. Sci. 1998, 130, 176–181. [Google Scholar] [CrossRef]
- Hane, M.; Miyamoto, Y.; Oshiyama, A. Atomic and electronic structures of an interface between silicon and β-cristobalite. Phys. Rev. B 1990, 41, 12637–12640. [Google Scholar] [CrossRef]
- Yamasaki, T.; Kaneta, C.; Uchiyama, T.; Uda, T.; Terakura, K. Geometric and electronic structures of SiO2/Si (001) interfaces. Phys. Rev. B 2001, 63, 115314. [Google Scholar] [CrossRef]
- Yamashita, Y.; Yamamoto, S.; Mukai, K.; Yoshinobu, J.; Harada, Y.; Tokushima, T.; Takeuchi, T.; Takata, Y.; Shin, S.; Akagi, K.; et al. Direct observation of site-specific valence electronic structure at the SiO2/Siinterface. Phys. Rev. B 2006, 73, 045336. [Google Scholar] [CrossRef] [Green Version]
- Markov, S.; Sushko, P.V.; Roy, S.; Fiegna, C.; Sangiorgi, E.; Shluger, A.L.; Asenov, A. Si-SiO2 interface band-gap transition—Effects on MOS inversion layer. Phys. Stat. Sol. 2008, 205, 1290–1295. [Google Scholar] [CrossRef]
- Ribeiro, M.; Fonseca, L.R.C. Accurate prediction of the Si/SiO2 interface band offset using the self-consistent ab initio DFT/LDA-1/2 method. Phys. Rev. B 2009, 79, 241312. [Google Scholar] [CrossRef]
- Pasquarello, A.; Hybertsen, M.S.; Car, R. Structurally relaxed models of the Si(001)–SiO2 interface. Appl. Phys. Lett. 1996, 68, 625–627. [Google Scholar] [CrossRef]
- Korkin, A.; Greer, J.C.; Bersuker, G.; Karasiev, V.V.; Bartlett, R.J. Computational design of Si∕SiO2 interfaces: Stress and strain on the atomic scale. Phys. Rev. B 2006, 73, 165312. [Google Scholar] [CrossRef]
- Herman, F.; Kasowski, R.V. Electronic structure of defects at Si/SiO2 Interfaces. J. Vac. Sci. Technol. 1981, 19, 395–401. [Google Scholar] [CrossRef]
- Tit, N.; Dharma-wardana, M.W.C. Quantum confinement and direct-bandgap character of Si/SiO2 superlattices. Solid State Commun. 1998, 106, 121. [Google Scholar] [CrossRef]
- Buczko, R.; Pennycook, S.J.; Pantelides, S.T. Bonding Arrangements at the Si-SiO2 and SiC-SiO2 Interfaces and a Possible Origin of their Contrasting Properties. Phys. Rev. Lett. 2000, 84, 943–946. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Degoli, E.; Ossicini, S. The electronic and optical properties of Si/SiO2 superlattices: Role of confined and defect states. Surface Sci. 2000, 470, 32–42. [Google Scholar] [CrossRef]
- Carrier, P.; Lewis, L.J.; Dharma-wardana, M.W.C. Optical properties of structurally relaxed Si/SiO2 superlattices: The role of bonding at interfaces. Phys. Rev. B 2002, 65, 165339. [Google Scholar] [CrossRef] [Green Version]
- Watarai, Q.M.; Nakamura, J.; Natori, A. Band discontinuity at ultrathin SiO2/Si(001)interfaces. Phys. Rev. B 2004, 69, 035312. [Google Scholar] [CrossRef]
- Giustino, F.; Bongiorno, A.; Pasquarello, A. Atomistic models of the Si(100)–SiO2 interface: Structural, electronic and dielectric properties. J. Phys. Condens. Matter 2005, 17, 2065. [Google Scholar] [CrossRef]
- Seino, K.; Wagner, J.-M.; Bechstedt, F. Quasiparticle effect on electron confinement in Si∕SiO2 quantum-well structures. Appl. Phys. Lett. 2007, 90, 253109. [Google Scholar] [CrossRef]
- Seino, K.; Bechstedt, F. Effective density of states and carrier masses for Si/SiO2 superlattices from first principles. Semicond. Sci. Technol. 2011, 26, 014024. [Google Scholar] [CrossRef]
- Davydov, V.; Roginskii, E.; Kitaev, Y.; Smirnov, A.; Eliseyev, I.; Nechaev, D.; Jmerik, V.; Smirnov, M. Phonons in Short-Period GaN/AlN Superlattices: Group-Theoretical Analysis, Ab initio Calculations, and Raman Spectra. Nanomaterials 2021, 11, 286. [Google Scholar] [CrossRef]
- Khriachtchev, L.; Räsänen, M.; Novikov, S.; Kilpelä, O.; Sinkkonen, J. Raman scattering from very thin Si layers of Si/SiO2 superlattices: Experimental evidence of structural modification in the 0.8–3.5 nm thickness region. J. Appl. Phys. 1999, 86, 5601–5608. [Google Scholar] [CrossRef]
- Benyoucef, M.; Kuball, M.; Sun, J.M.; Zhong, G.Z.; Fan, X.W. Raman scattering and photoluminescence studies on Si/SiO2 superlattices. J. Appl. Phys. 2001, 89, 7903–7907. [Google Scholar] [CrossRef]
- Jin, B.; Wang, X.; Chen, J.; Cheng, X.; Chen, Z. Fabrication of strained silicon on insulator by strain transfer process. Appl. Phys. Lett. 2005, 87, 051921. [Google Scholar] [CrossRef]
- Novikov, S.; Sinkkonen, J.; Khriachtchev, L.; Räsänen, M.; Sitnikova, A. Free-standing Si/SiO2 superlattices: Fabrication procedure and optical, structural, and light-emitting properties. Proc. SPIE Nanophotonics 2006, 6195, 619512. [Google Scholar] [CrossRef]
- Huang, S.; Xiao, H.; Shou, S. Annealing temperature dependence of Raman scattering in Si/SiO2 superlattice prepared by magnetron sputtering. Appl. Surf. Sci. 2009, 255, 4547–4550. [Google Scholar] [CrossRef]
- Borowicz, P.; Latek, M.; Rzodkiewicz, W.; Łaszcz, A.; Czerwinski, A.; Ratajczak, J. Deep-ultraviolet Raman investigation of silicon oxide: Thin film on silicon substrate versus bulk material. Adv. Nat. Sci. Nanosci. Nanotechnol. 2012, 3, 045003. [Google Scholar] [CrossRef]
- Borowicz, P.; Taube, A.; Rzodkiewicz, W.; Latek, M.; GieraBtowska, S. Raman Spectra of High-κ Dielectric Layers Investigated with Micro-Raman Spectroscopy Comparison with Silicon Dioxide. Sci. World J. 2013, 2013, 20881. [Google Scholar] [CrossRef] [Green Version]
- Smirnov, M.B.; Pankin, D.V.; Roginskii, E.M.; Savin, A.V. Quantum-chemical study of structure and vibrational spectra of Si/SiO2 superlattices. Phys. Solid State 2022, 64, 1675–1684. [Google Scholar]
- Smirnov, M.B.; Roginskii, E.M.; Savin, A.V.; Mazhenov, N.A.; Pankin, D.V. Density-functional study of the Si/SiO2 interfaces in short-period superlattices. I. Structures and energies. Coatings 2023, 13, 1231. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.; Burke, K. Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces. Phys. Rev. Lett. 2008, 100, 136406. [Google Scholar] [CrossRef] [Green Version]
- Gonze, X.; Beuken, J.M.; Caracas, R.; Detraux, F.; Fuchs, M.; Rignanese, G.M.; Sindic, L.; Verstraete, M.; Zerah, G.; Jollet, F.; et al. First-principles computation of material properties: The ABINIT software project. Comput. Mater. Sci. 2002, 25, 478–492. [Google Scholar] [CrossRef]
- Gonze, X.; Rignanese, G.M.; Verstraete, M.; Beuken, J.M.; Pouillon, Y.; Caracas, R.; Jollet, F.; Torrent, M.; Zerah, G.; Mikami, M.; et al. A brief introduction to the ABINIT software package. Z. Fur. Krist. 2005, 220, 558–562. [Google Scholar] [CrossRef]
- Gonze, X.; Amadon, B.; Anglade, P.-M.; Beuken, J.-M.; Bottin, F.; Boulanger, P.; Bruneval, F.; Caliste, D.; Caracas, R.; Côté, M.; et al. ABINIT: First-principles approach to material and nanosystem properties. Comput. Phys. Commun. 2009, 180, 2582–2615. [Google Scholar] [CrossRef]
- Hamann, D.R. Optimized norm-conserving Vanderbilt pseudopotentials. Phys. Rev. B 2013, 88, 085117. [Google Scholar] [CrossRef] [Green Version]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillonin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Gonze, X.; Lee, C. Dynamical matrices, Born effective charges, dielectric permittivity tensors, and interatomic force constants density-functional perturbation theory. Phys. Rev. B 1997, 55, 10355–10368. [Google Scholar] [CrossRef]
- Gonze, X.; Vigneron, J.-P. Density-functional approach to nonlinear-response coefficients of solids. Phys. Rev. B 1989, 39, 13120–13128. [Google Scholar] [CrossRef] [PubMed]
- Giannozzi, P.; de Gironcoli, S.; Pavone, P.; Baroni, S. Ab initiocalculation of phonon dispersions in semiconductors. Phys. Rev. B 1991, 43, 7231–7242. [Google Scholar] [CrossRef]
- Nilsson, G.; Nelin, G. Study of the Homology between Silicon and Germanium by Thermal-Neutron Spectrometry. Phys. Rev. B 1972, 6, 3777–3782. [Google Scholar] [CrossRef]
- Coh, S.; Vanderbilt, D. Structural stability and lattice dynamics of SiO2 cristobalite. Phys. Rev. B 2008, 78, 054117. [Google Scholar] [CrossRef] [Green Version]
- Swainson, I.P.; Dove, M.T.; Palmer, D.C. Infrared and Raman spectroscopy studies of the α-β phase transition in cristobalite. Phys. Chem. Miner. 2003, 30, 353–365. [Google Scholar] [CrossRef]
- Mizokami, K.; Togo, A.; Tanaka, I. Lattice thermal conductivities of two SiO2 polymorphs by first-principles calculations and the phonon Boltzmann transport equation. Phys. Rev. B 2018, 97, 224306. [Google Scholar] [CrossRef] [Green Version]
- Etchepare, J.; Merian, M.; Smetankine, L. Vibrational normal modes of SiO2. I. α and β quartz. J. Chem. Phys. 1974, 60, 1873–1876. [Google Scholar] [CrossRef]
- Etchepare, J.; Merian, M.; Kaplan, P. Vibrational normal modes of SiO2. II. Cristobalite and tridymite. J. Chem. Phys. 1978, 68, 1531–1537. [Google Scholar] [CrossRef]
- Nakashima, S.; Mitani, T.; Ninomiya, M.; Matsumoto, K. Raman investigation of strain in Si∕SiGe heterostructures: Precise determination of the strain-shift coefficient of Si bands. J. Appl. Phys. 2006, 99, 053512. [Google Scholar] [CrossRef]
- Peng, C.-Y.; Huang, C.-F.; Fu, Y.-C.; Yang, Y.-H.; Lai, C.-Y.; Chang, S.-T.; Liu, C.W. Comprehensive study of the Raman shifts of strained silicon and germanium. J. Appl. Phys. 2009, 105, 083537. [Google Scholar] [CrossRef]
- Wagner, J.-M.; Bechstedt, F. Phonon deformation potentials of α-GaN and -AlN: An ab initio calculation. Appl. Phys. Lett. 2000, 77, 346–348. [Google Scholar] [CrossRef]
- Callsen, G.; Reparaz, J.S.; Wagner, M.R.; Kirste, R.; Nenstiel, C.; Hoffmann, A.; Phillips, M.R. Phonon deformation potentials in wurtzite GaN and ZnO determined by uniaxial pressure dependent Raman measurements. Appl. Phys. Lett. 2011, 98, 061906-1–061906-4. [Google Scholar] [CrossRef] [Green Version]
- Badger, R.M. A Relation Between Internuclear Distances and Bond Force Constants. J. Chem. Phys. 1934, 2, 128–131. [Google Scholar] [CrossRef] [Green Version]
- Lin, S.-Y. Vibrational local modes of a-SiO2:H and variation of local modes in different local environments. J. Appl. Phys. 1997, 82, 5976–5982. [Google Scholar] [CrossRef]
- Yahagi, Y.; Yagi, T.; Yamawaki, H.; Aoki, K. Infrared absorption spectra of the high-pressure phases of cristobalite and their coordination numbers of silicon atoms. Solid State Commun. 1994, 89, 945–948. [Google Scholar] [CrossRef]
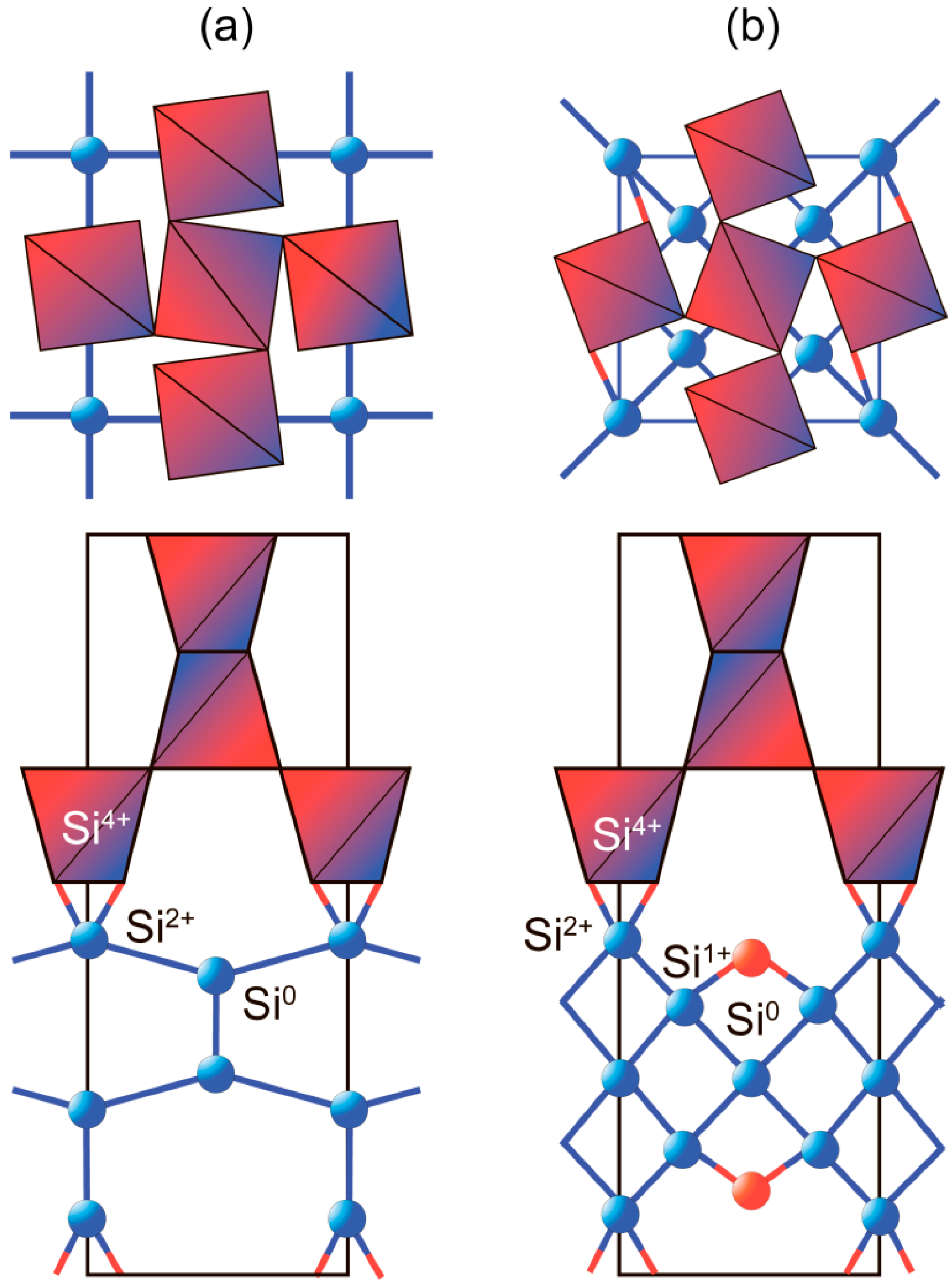
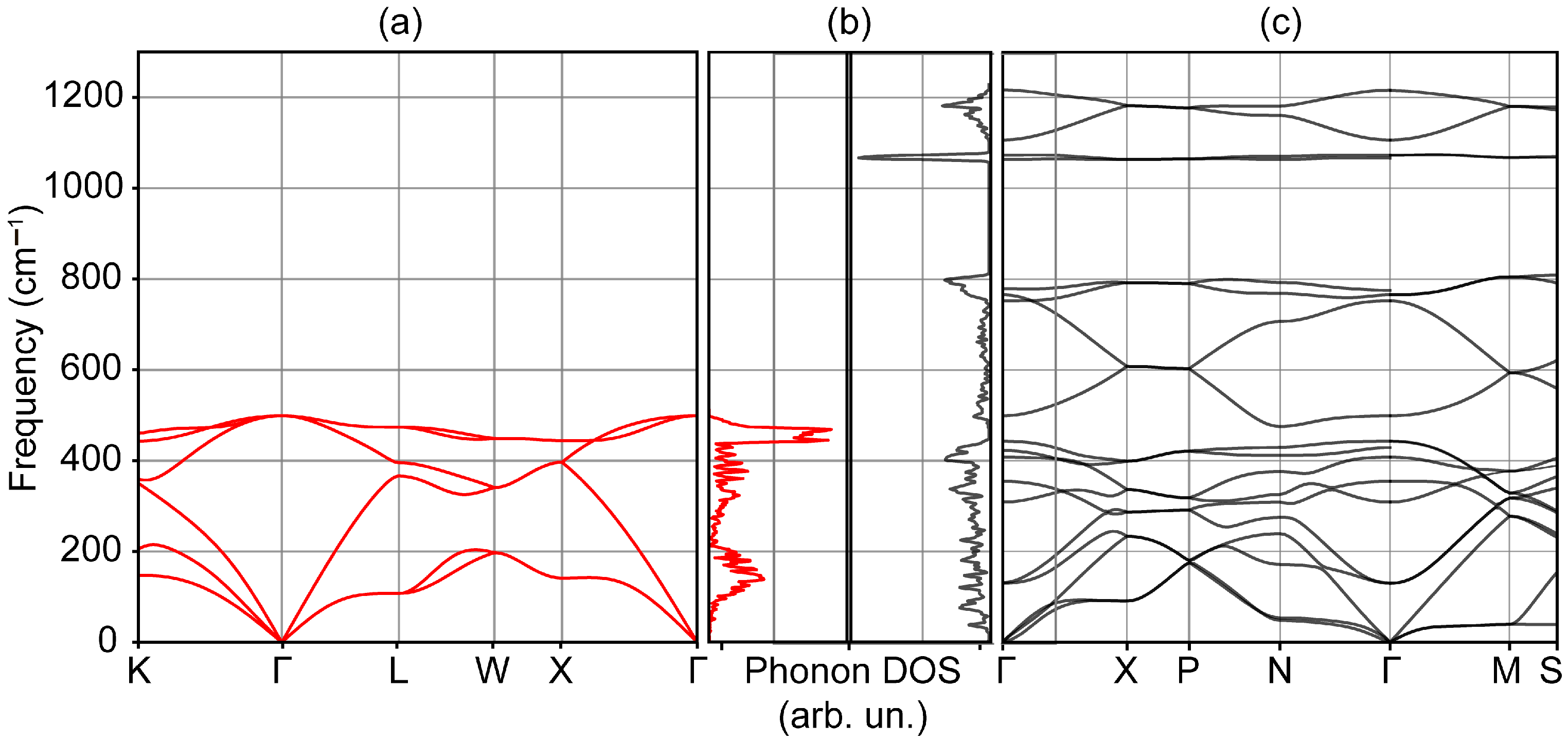
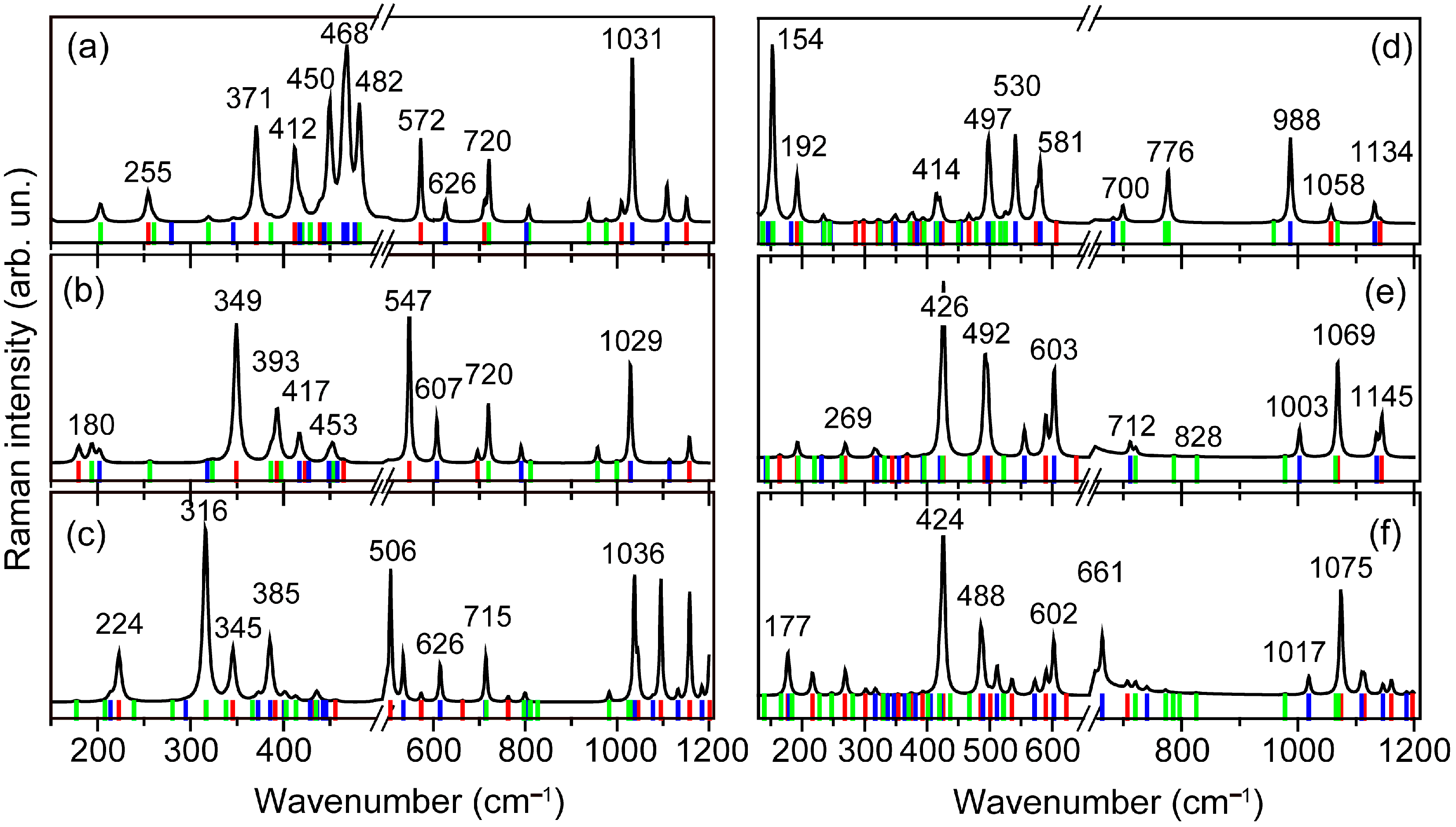
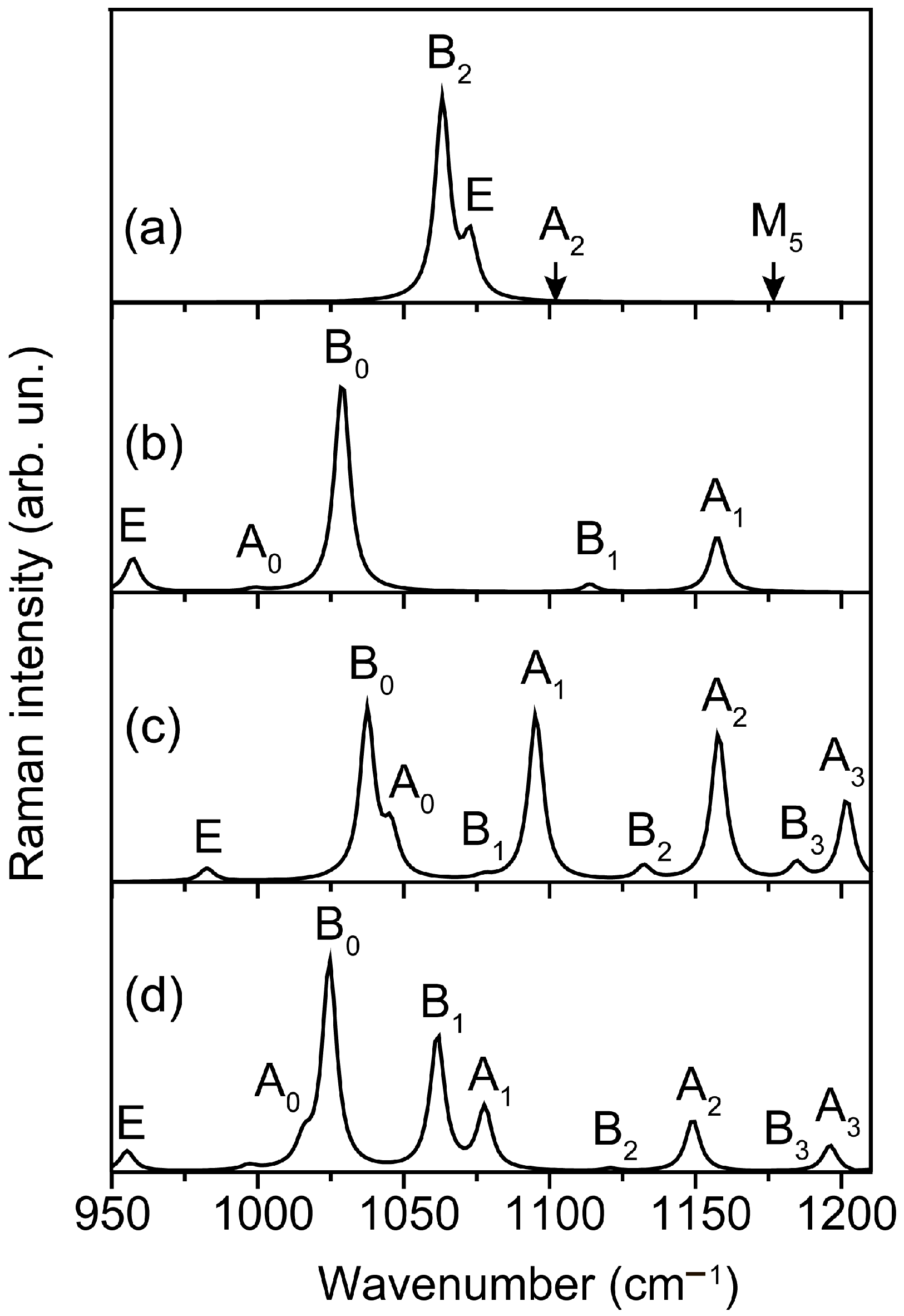
| Irreducible Representation Symmetry | Theory DFT Calculations (This Work) | Theory DFT Calculations [48] | Experiment [49] |
|---|---|---|---|
| Tg | 502 | 517 | 521 |
| X2 | 141 | 146 | 150 |
| X1 | 396 | 414 | 410 |
| X4 | 444 | 466 | 463 |
| Г-Point | M-Point | |||||
|---|---|---|---|---|---|---|
| IR* Symmetry | Theory DFT Calculations TO (LO) This Work | Theory DFT Calculations [50] | Experiment [51] | IR* Symmetry | Theory DFT Calculations This Work | Theory DFT Calculations [50] |
| A2 | 1106 | 1097 | 1144 | M5 | 1177 | 1162 |
| E | 1073 (1212) | 1047 | 1100 | M3M4 | 1071 | 1045 |
| B2 | 1063 (1216) | 1038 | 1076 | M1M2 | 798 | 780 |
| E | 765 (796) | 748 | 794 | M5 | 595 | 586 |
| B1 | 752 | 737 | 785 | M5 | 376 | 372 |
| E | 443 (482) | 444 | 480 | M3M4 | 335 | 336 |
| B2 | 422(497) | 425 | 426 | M1M2 | 317 | 316 |
| B1 | 408 | 406 | M5 | 279 | 281 | |
| A2 | 354 | 357 | 380 | M3M4 | 28 | 35 |
| A1 | 309 | 289 | 300 | |||
| E | 130 (133) | 126 | ||||
| SL (Space Group #81) | -SiO2 (Space Group #122) | Si (Space Group #227) |
|---|---|---|
| 9A | A1 + 2A2 + 4M5 (1) | X1(1) |
| 11B | 2B1 +3B2 + 4M5 (1) | X1 (1) + Tg (1) + Tu (1) |
| 14E (2) | 5E (2) + 2M12 (2) + 3M34 (2) | Tg (2) + Tu (2) +X3 (2) + X4 (2) |
| Assignment | Si4/(SiO2)4 | -SiO2 | Si | ||||
|---|---|---|---|---|---|---|---|
| Г(A) | Г(B) | Г(E) | Г | M | Г | X | |
| v(Si-O/O) | 1157 1028 | 1114 1029 | 999 957 | 1106 A2 1073 E 1063 B2 | 1177 M5 1071 M34 | ||
| v(Si-O/Si) | 696 | 791 608 | 811 720 | 765 E 752 B1 | 798 M12 595 M5 | ||
| δ(SiO2) + v(Si-Si) Lattice modes | 547 464 423 393 349 180 | 458 449 427 417 318 202 0 | 453 397 387 323 256 193 123 96 58 0 | 443 E 422 B2 408 B1 354 A2 309 A1 130 E 0 B2 | 376 M5 335 M34 317 M12 279 M5 28 M34 | 502 Tg 0 Tu | 444 X4 396 X1 141 X3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Smirnov, M.; Roginskii, E.; Savin, A.; Oreshonkov, A.; Pankin, D. Density-Functional Study of the Si/SiO2 Interfaces in Short-Period Superlattices: Vibrational States and Raman Spectra. Photonics 2023, 10, 902. https://doi.org/10.3390/photonics10080902
Smirnov M, Roginskii E, Savin A, Oreshonkov A, Pankin D. Density-Functional Study of the Si/SiO2 Interfaces in Short-Period Superlattices: Vibrational States and Raman Spectra. Photonics. 2023; 10(8):902. https://doi.org/10.3390/photonics10080902
Chicago/Turabian StyleSmirnov, Mikhail, Evgenii Roginskii, Aleksandr Savin, Aleksandr Oreshonkov, and Dmitrii Pankin. 2023. "Density-Functional Study of the Si/SiO2 Interfaces in Short-Period Superlattices: Vibrational States and Raman Spectra" Photonics 10, no. 8: 902. https://doi.org/10.3390/photonics10080902
APA StyleSmirnov, M., Roginskii, E., Savin, A., Oreshonkov, A., & Pankin, D. (2023). Density-Functional Study of the Si/SiO2 Interfaces in Short-Period Superlattices: Vibrational States and Raman Spectra. Photonics, 10(8), 902. https://doi.org/10.3390/photonics10080902






