A Novel Reconfigurable Nonlinear Cascaded MZM Mixer, Amplitude Shift Key Modulator (ASK), Frequency Hopping and Phase Shifter
Abstract
1. Introduction
2. Analytical Model
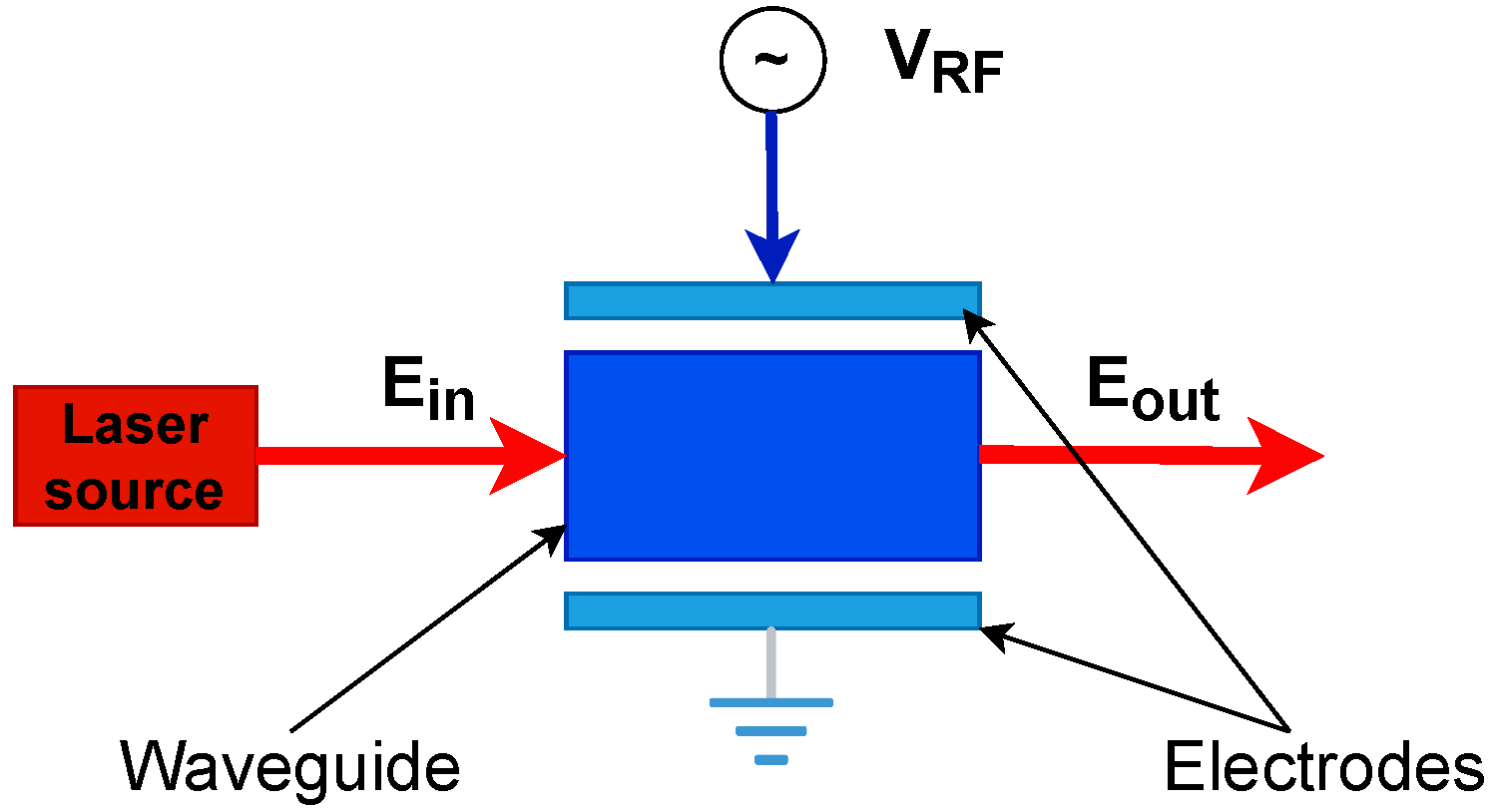
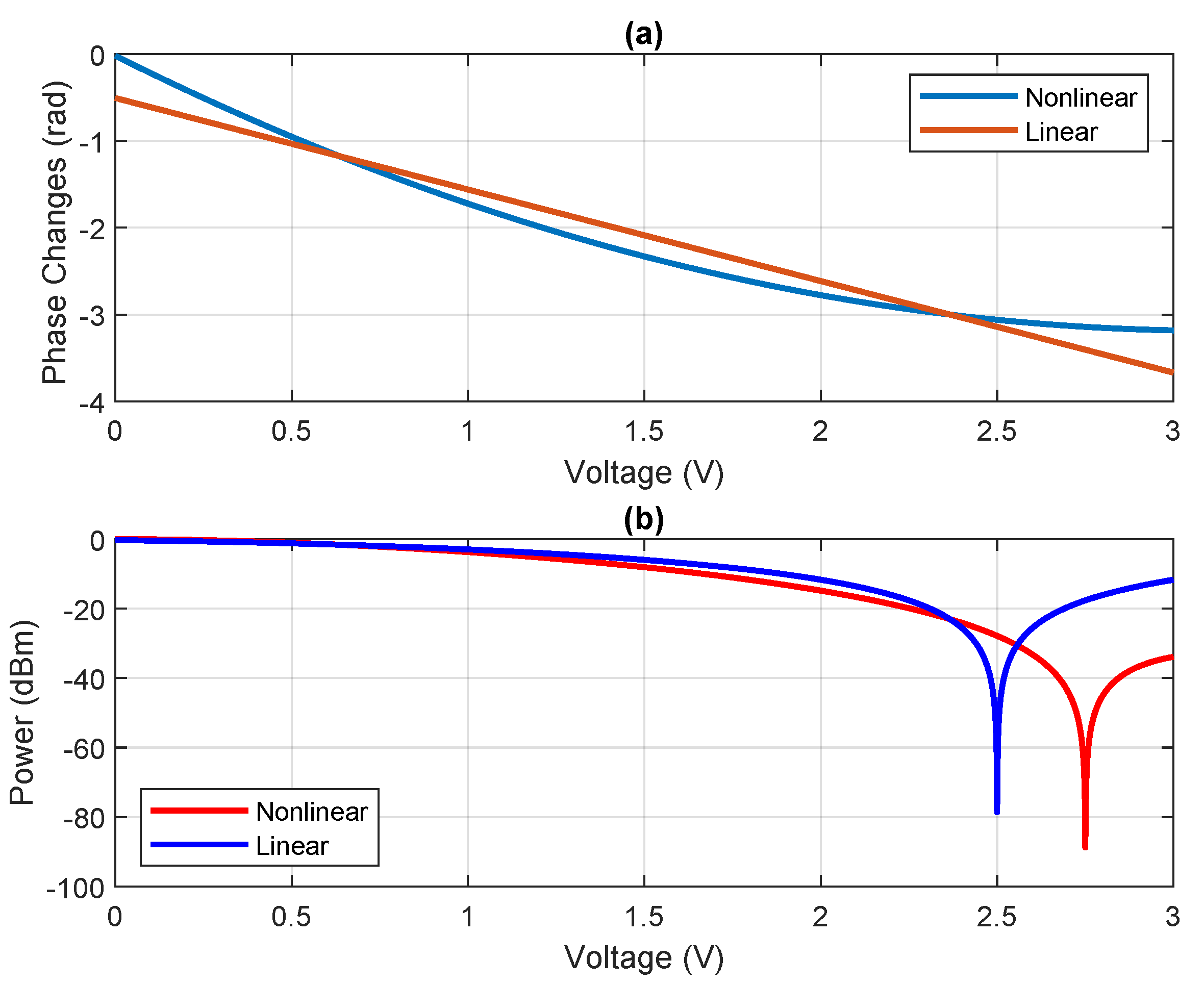
2.1. PM Analytical Model
2.2. MZM Analytical Model
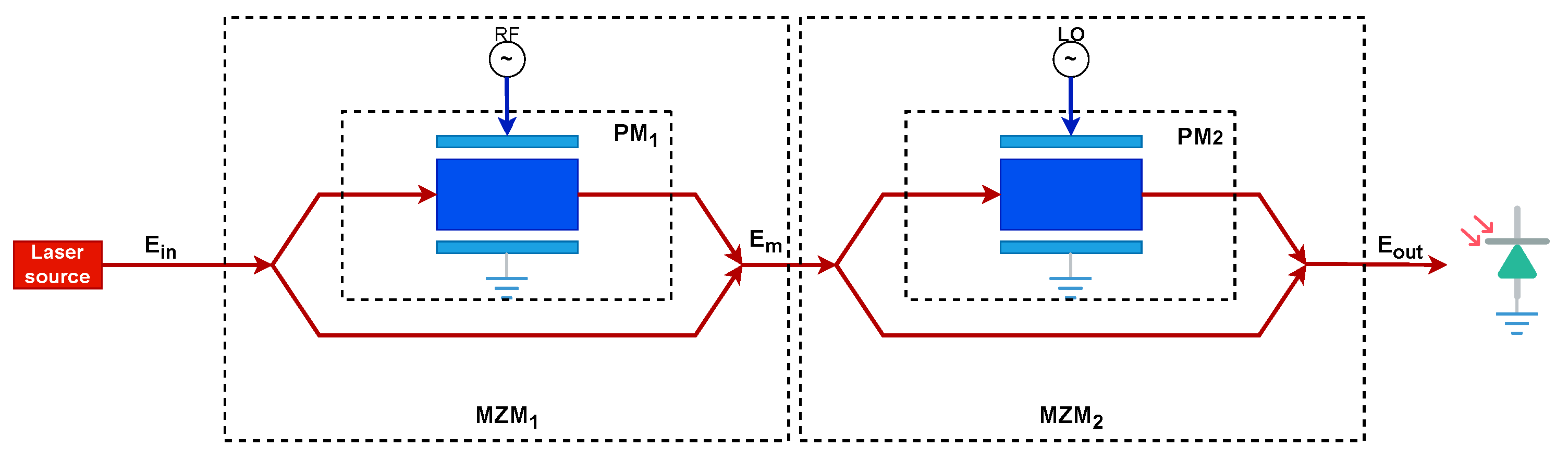
2.3. Cascaded MZM Mixer Model
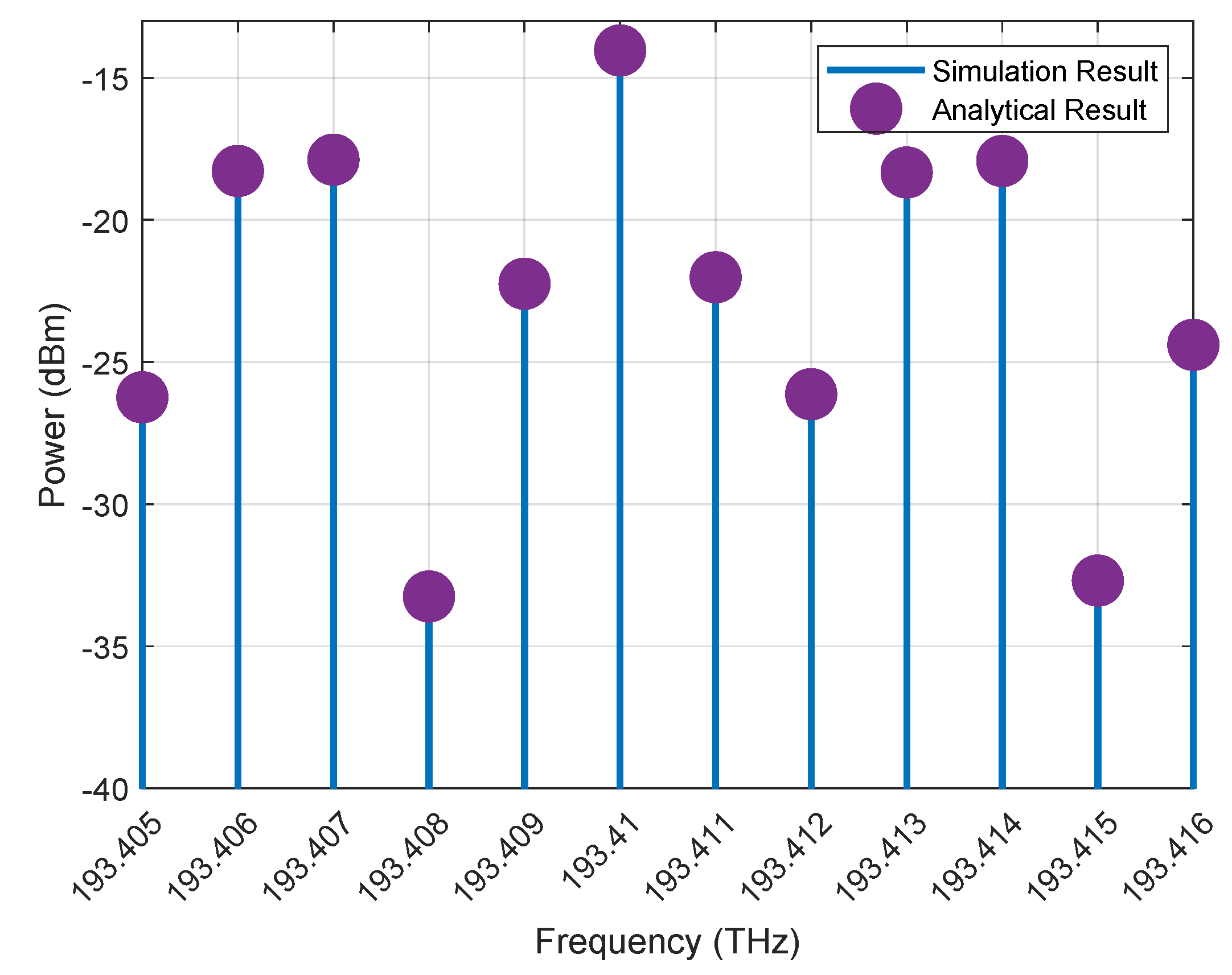
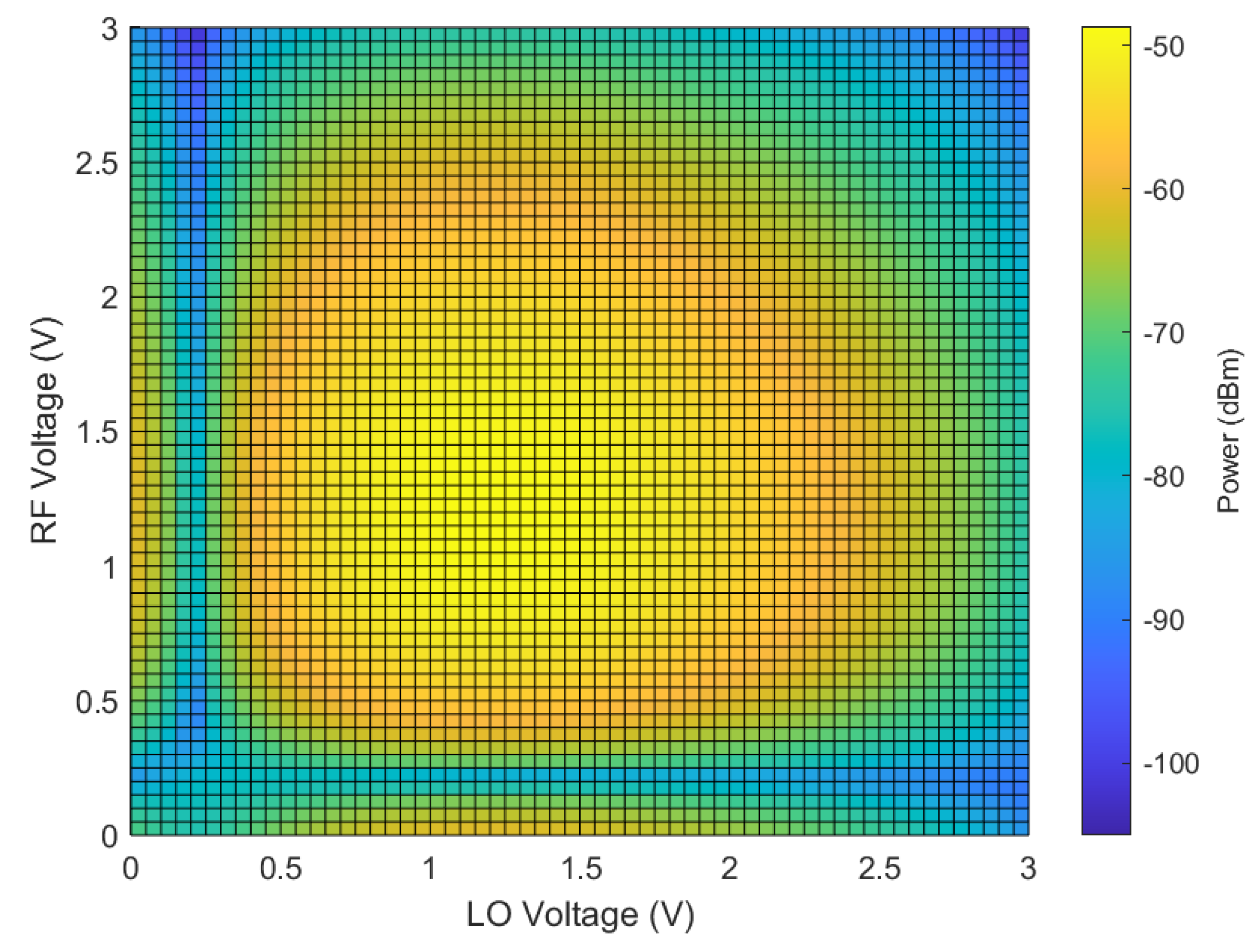
2.4. Photo Diode Current and Frequency Combination
2.5. Conversion Loss
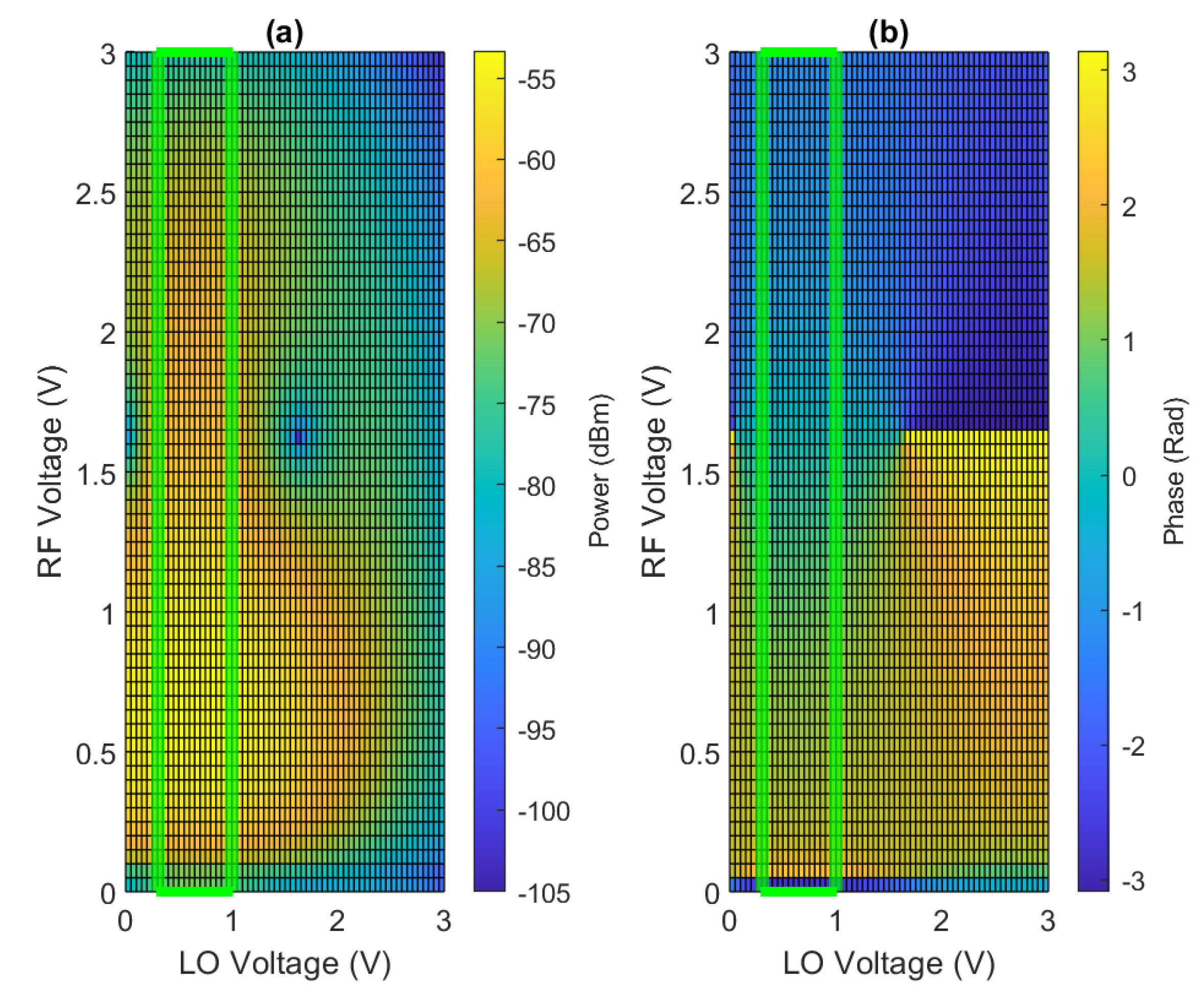
3. Various Configurations
3.1. Frequency Hopping
3.2. Amplitude Shift Key Modulation (ASK)
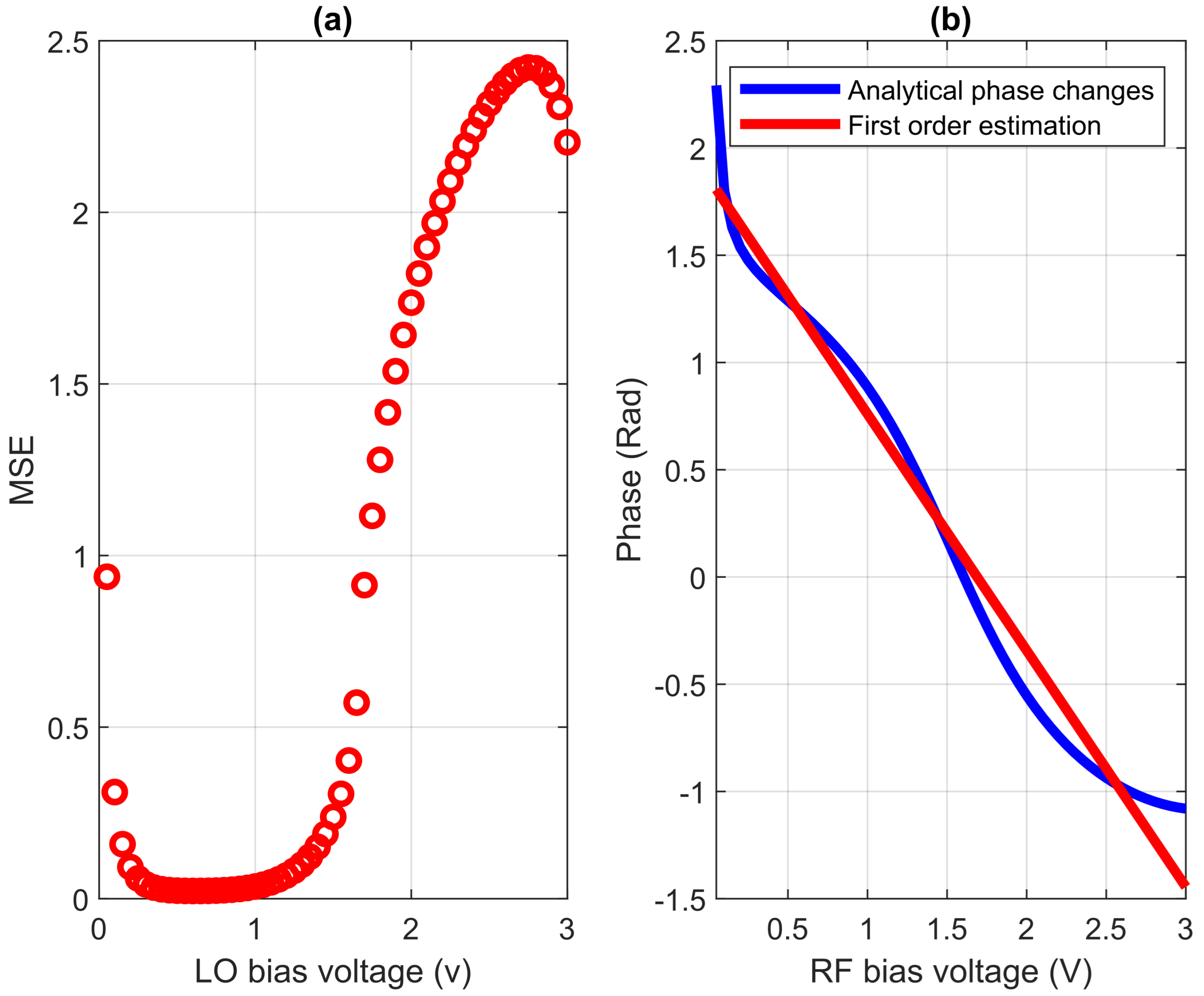
3.3. Phase Shifter
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Capmany, J.; Novak, D. Microwave photonics combines two worlds. Nat. Photonics 2007, 1, 319. [Google Scholar] [CrossRef]
- Juodawlkis, P.W.; Twichell, J.C.; Betts, G.E.; Hargreaves, J.J.; Younger, R.D.; Wasserman, J.L.; O’Donnell, F.J.; Ray, K.G.; Williamson, R.C. Optically sampled analog-to-digital converters. IEEE Trans. Microw. Theory Tech. 2001, 49, 1840–1853. [Google Scholar] [CrossRef]
- Capmany, J.; Ortega, B.; Pastor, D. A tutorial on microwave photonic filters. J. Light. Technol. 2006, 24, 21–29. [Google Scholar] [CrossRef]
- Supradeepa, V.R.; Long, C.M.; Wu, R.; Ferdous, F.; Hamidi, E.; Leaird, D.E.; Weiner, A.M. Comb-based radiofrequency photonic filters with rapid tunability and high selectivity. Nat. Photonics 2012, 6, 186–194. [Google Scholar] [CrossRef]
- Loo, R.Y.; Tangonan, G.L.; Yen, H.W.; Jones, V.L.; Ng, W.W.; Lewis, J.B.; Lee, J.J.; Livingston, S. Photonics for phased-array antennas. Photonics Radio Freq. 1996, 2844, 234–240. [Google Scholar]
- Tang, Z.; Li, Y.; Yao, J.; Pan, S. Photonics-based microwave frequency mixing: Methodology and applications. Laser Photonics Rev. 2020, 14, 1800350. [Google Scholar] [CrossRef]
- Winnall, S.T.; Lindsay, A.C.; Knight, G.A. A wide-band microwave photonic phase and frequency shifter. IEEE Trans. Microw. Theory Tech. 1997, 45, 1003–1006. [Google Scholar] [CrossRef]
- Khan, M.H.; Shen, H.; Xuan, Y.; Zhao, L.; Xiao, S.; Leaird, D.E.; Weiner, A.M.; Qi, M. Ultrabroad-bandwidth arbitrary radiofrequency waveform generation with a silicon photonic chip-based spectral shaper. Nat. Photonics 2010, 4, 117–122. [Google Scholar]
- Yao, J.; Zeng, F.; Wang, Q. Photonic generation of ultrawideband signals. J. Lightwave Technol. 2007, 25, 3219–3235. [Google Scholar]
- Liu, Y.Q.; Sun, J.; Shu, Y.; Wu, L.; Lu, L.; Qi, K.; Che, Y.; Li, L.; Yin, H. High numerical aperture and large focusing efficiency metalens based on multilayer transmitarray elements. Opt. Lasers Eng. 2021, 147, 106734. [Google Scholar] [CrossRef]
- Liu, Y.Q.; Ren, Z.; Shu, Y.; Wu, L.; Sun, J.; Cai, H.; Zhang, X.; Lu, L.; Qi, K.; Li, L.; et al. Broadband, large-numerical-aperture and high-efficiency microwave metalens by using a double-layer transmissive metasurface. Appl. Phys. Express 2022, 15, 014003. [Google Scholar]
- Maleki, L. The optoelectronic oscillator. Nat. Photonics 2011, 5, 728–730. [Google Scholar] [CrossRef]
- Yao, X.S.; Maleki, L. Optoelectronic microwave oscillator. JOSA B 1996, 13, 1725–1735. [Google Scholar] [CrossRef]
- Liu, M.; Yin, X.; Ulin-Avila, E.; Geng, B.; Zentgraf, T.; Ju, L.; Wang, F.; Zhang, X. A graphene-based broadband optical modulator. Nature 2011, 474, 64–67. [Google Scholar] [CrossRef] [PubMed]
- Gu, T.; Petrone, N.; McMillan, J.; van der Zande, A.; Yu, M.; Lo, G.Q.; Kwong, D.L.; Hone, J.; Wong, C.W. Regenerative oscillation and four-wave mixing in graphene optoelectronics. Nat. Photonics 2012, 6, 554–559. [Google Scholar] [CrossRef]
- Zhang, H.; Tang, D.; Zhao, L.; Bao, Q.; Loh, K.P. Vector dissipative solitons in graphene mode locked fiber lasers. Opt. Commun. 2010, 283, 3334–3338. [Google Scholar] [CrossRef]
- Paris, M.G.A.; Genoni, M.G.; Shammah, N.; Teklu, B. Quantifying the nonlinearity of a quantum oscillator. Phys. Rev. A Mol. Opt. Phys. 2014, 90, 012104. [Google Scholar] [CrossRef]
- Teklu, B.; Ferraro, A.; Paternostro, M.; Paris, M.G.A. Nonlinearity and nonclassicality in a nanomechanical resonator. EPJ Quantum Technol. 2015, 2, 1–10. [Google Scholar] [CrossRef]
- Olivares, S.; Cialdi, S.; Castelli, F.; Paris, M.G.A. Homodyne detection as a near-optimum receiver for phase-shift-keyed binary communication in the presence of phase diffusion. Phys. Rev. A Mol. Opt. Phys. 2013, 87, 050303. [Google Scholar]
- Chan, E.H.W.; Minasian, R.A. Microwave photonic downconverter with high conversion efficiency. J. Lightwave Technol. 2012, 30, 3580–3585. [Google Scholar] [CrossRef]
- Gopalakrishnan, G.K.; Moeller, R.P.; Howerton, M.M.; Burns, W.K.; Williams, K.J.; Esman, R.D. A low-loss downconverting analog fiber-optic link. IEEE Trans. Microw. Theory Tech. 1995, 43, 2318–2323. [Google Scholar] [CrossRef]
- Keshavarz, H.; Hosseini, S.E.; Jamshidi, K.; Plettemeier, D. Silicon Photonic-Based Integrated Microwave Photonic Reconfigurable Mixer, Phase Shifter, and Frequency Doubler. J. Light. Tech. 2021, 39, 7698–7705. [Google Scholar] [CrossRef]
- Zhang, W.; Wen, A.; Gao, Y.; Li, X.; Shang, S. Microwave photonic frequency conversion with high conversion efficiency and elimination of dispersion-induced power fading. IEEE Photonics J. 2016, 8, 5500909. [Google Scholar] [CrossRef]
- Jiang, T.; Wu, R.; Yu, S.; Wang, D.; Gu, W. Microwave photonic phase-tunable mixer. Opt. Express 2017, 25, 4519–4527. [Google Scholar] [CrossRef] [PubMed]
- Tang, Z.; Pan, S. Reconfigurable microwave photonic mixer with minimized path separation and large suppression of mixing spurs. Opt. Lett. 2017, 42, 33–36. [Google Scholar] [CrossRef]
- Li, H.; Zhao, S.; Lin, T.; Zhang, K.; Jiang, W.; Wang, G.; Li, X. A filterless reconfigurable frequency mixer based on a wideband photonic microwave phase shifter. Opt. Commun. 2020, 475, 126224. [Google Scholar] [CrossRef]
- Urick, V.J.; Williams, K.J.; McKinney, J.D. Fundamentals of Microwave Photonics; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; National Bureau of Standards Applied Mathematics Series 55. Tenth Printing; ERIC: Fort Collins, CO, USA, 1972.
- Keshavarz, H.; Hosseini, S.E.; Abiri, H.; Jamshidi, K.; Plettemeier, D. Bias-Free Silicon-Based Optical Single-Sideband Modulator without 2nd-Order Sideband. IEEE Photonics J. 2020, 12, 5501816. [Google Scholar] [CrossRef]
- Cox, C.H. Analog Optical Links: Theory and Practice; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Liu, Q.; Fok, M.P. Ultrafast and wideband microwave photonic frequency-hopping systems: A review. Appl. Sci. 2020, 10, 521. [Google Scholar] [CrossRef]
- Pan, S.; Zhang, Y. Tunable and wideband microwave photonic phase shifter based on a single-sideband polarization modulator and a polarizer. Opt. Lett. 2012, 37, 4483–4485. [Google Scholar] [CrossRef]
- Niu, T.; Wang, X.D.; Chan, E.H.; Feng, X.; Guan, B.O. Dual-polarization dual-parallel MZM and optical phase shifter based microwave photonic phase controller. IEEE Photonics J. 2016, 8, 5501114. [Google Scholar] [CrossRef]
- Pan, S.; Ye, X.; Zhang, Y.; Zhang, F. Microwave photonic array radars. IEEE J. Microw. 2021, 1, 176–190. [Google Scholar] [CrossRef]


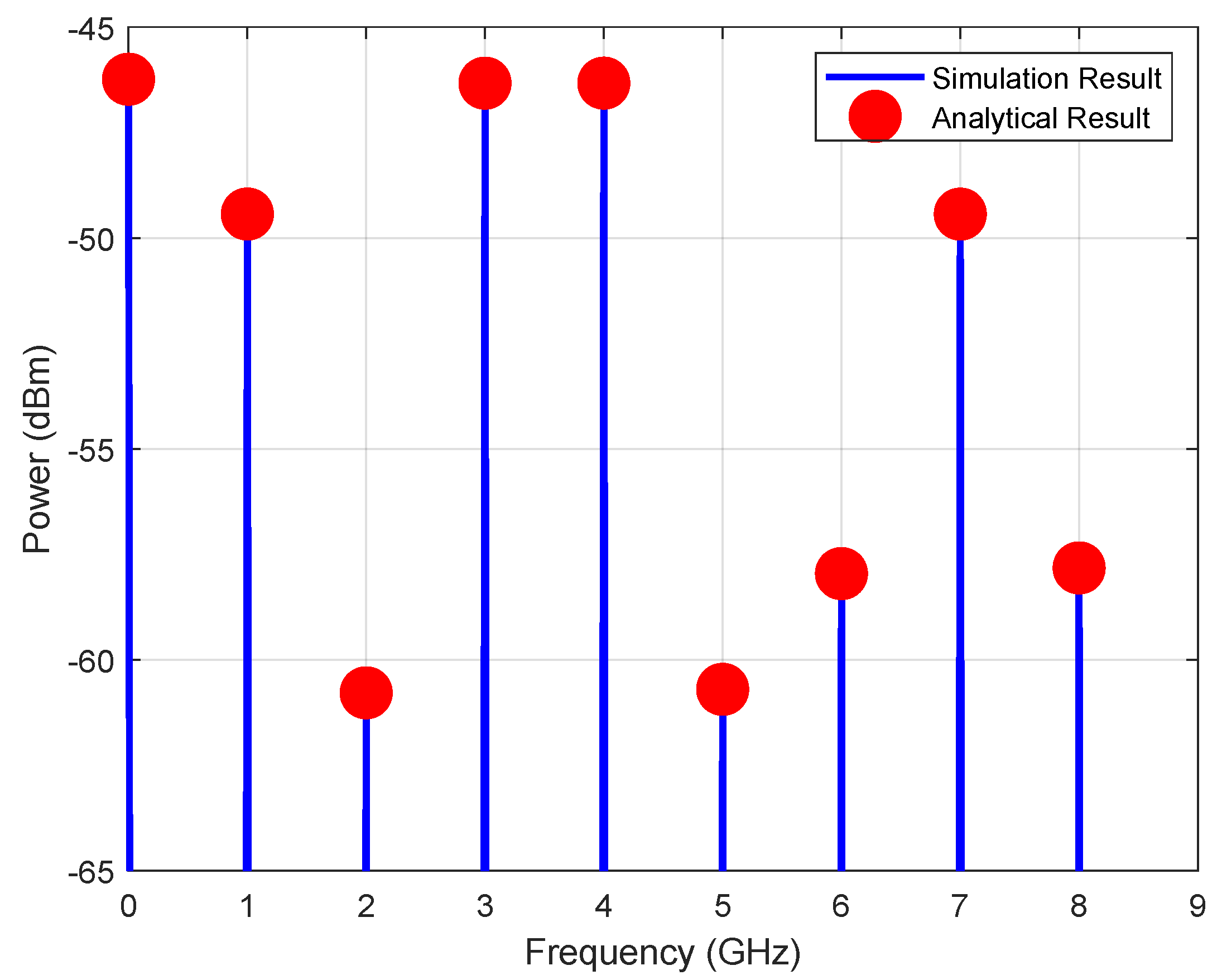
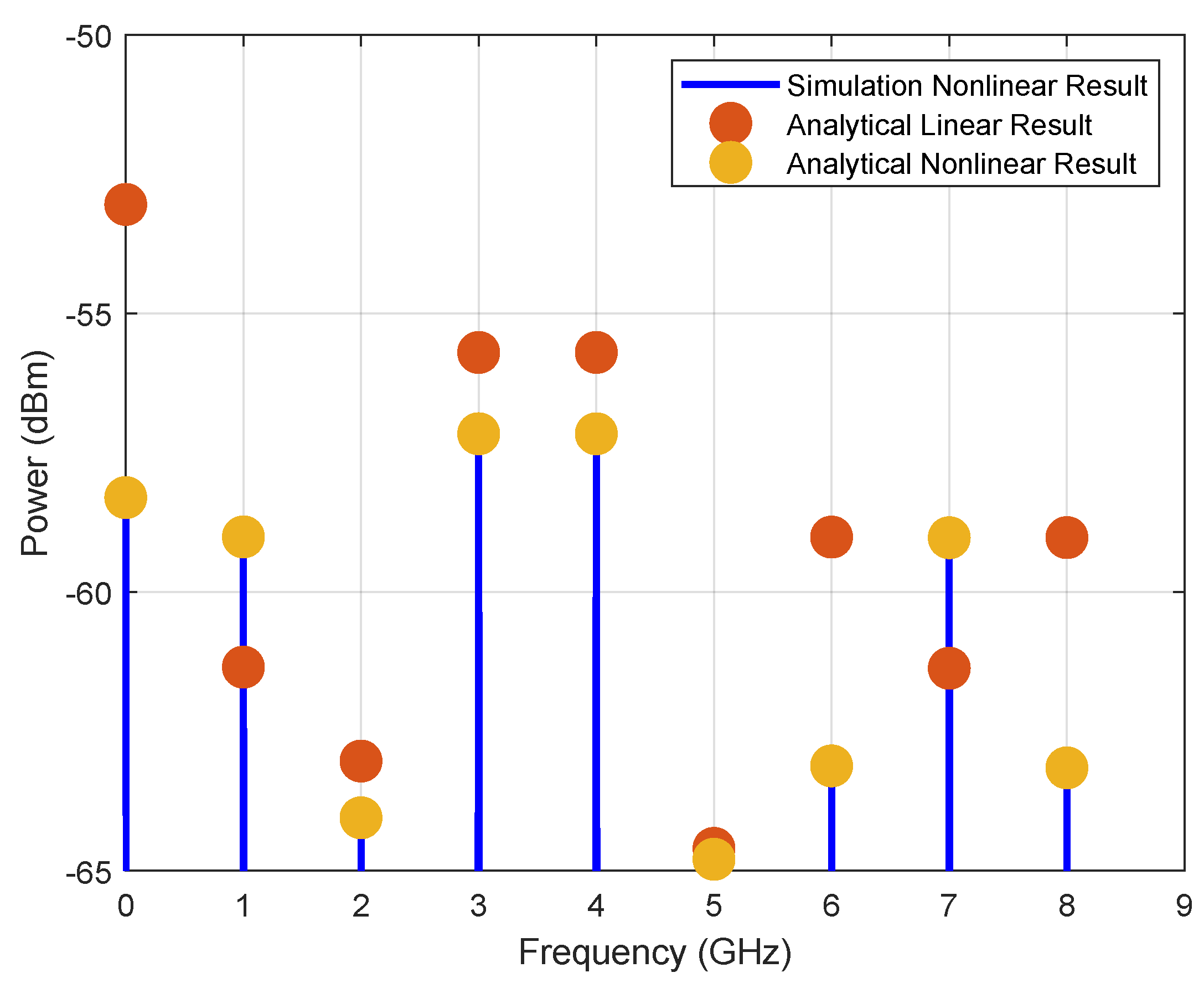

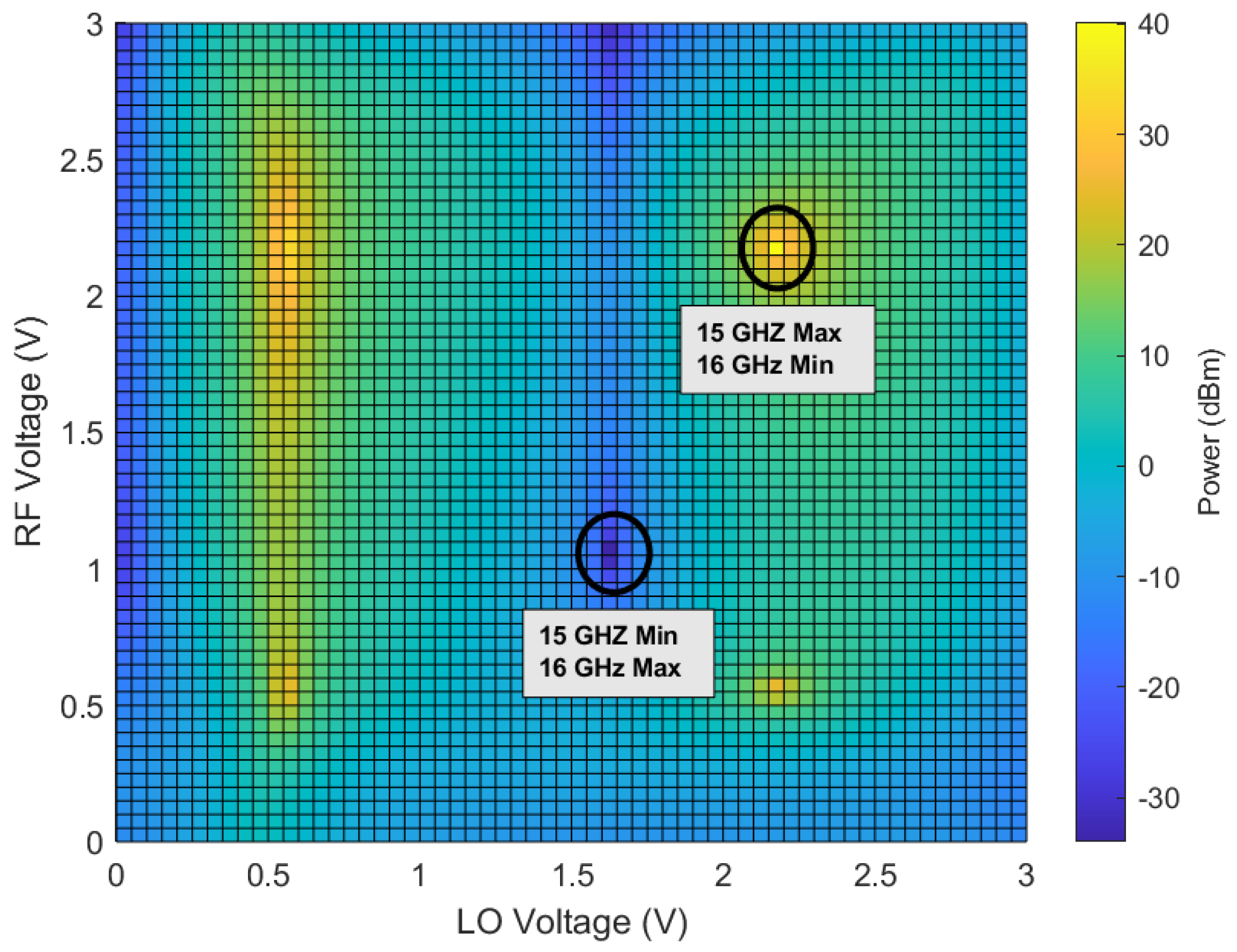
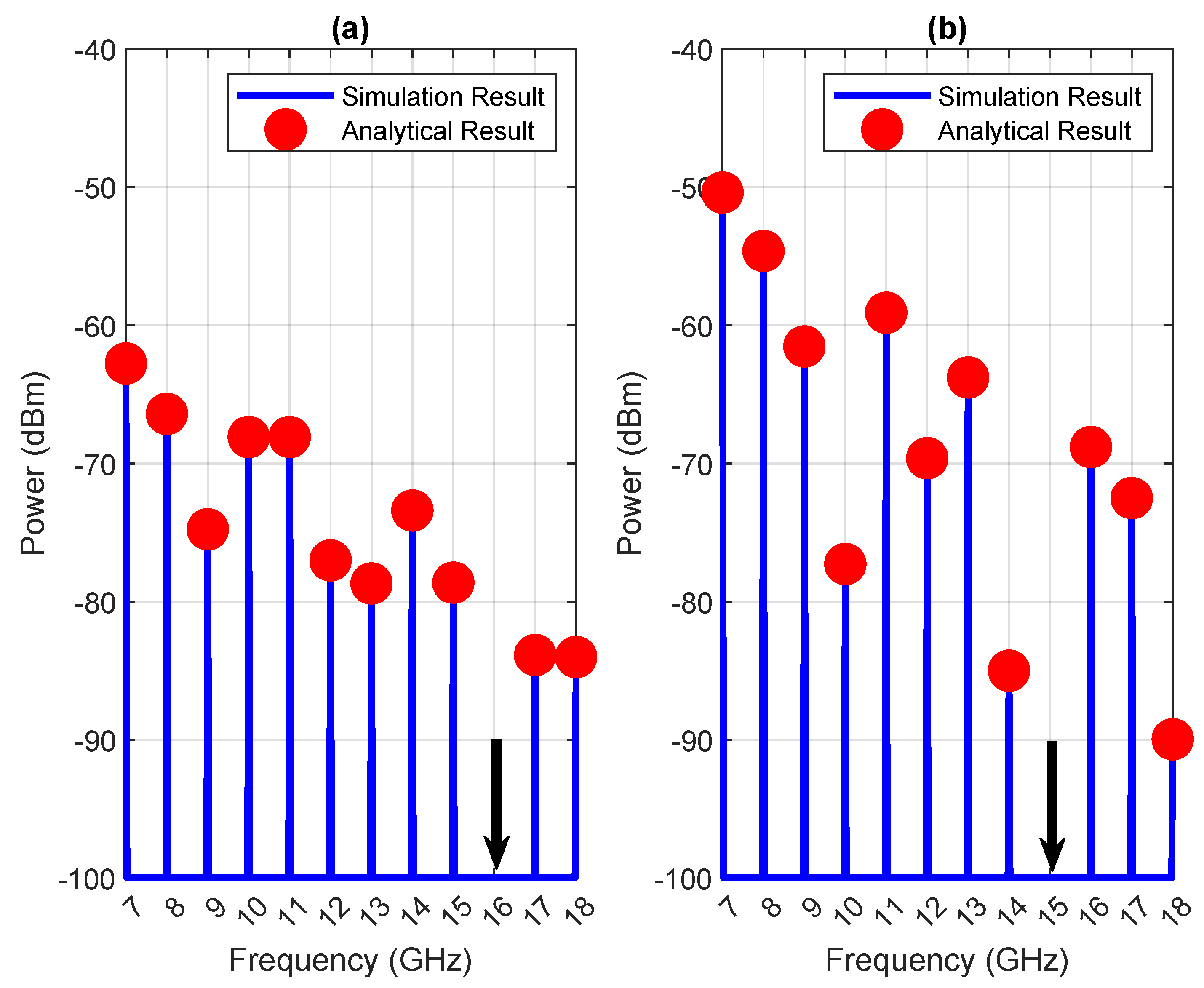


| Model | |||
|---|---|---|---|
| Nonlinear | |||
| Linear | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Darabi, E.; Keshavarz, H.; Monteiro, P. A Novel Reconfigurable Nonlinear Cascaded MZM Mixer, Amplitude Shift Key Modulator (ASK), Frequency Hopping and Phase Shifter. Photonics 2023, 10, 916. https://doi.org/10.3390/photonics10080916
Darabi E, Keshavarz H, Monteiro P. A Novel Reconfigurable Nonlinear Cascaded MZM Mixer, Amplitude Shift Key Modulator (ASK), Frequency Hopping and Phase Shifter. Photonics. 2023; 10(8):916. https://doi.org/10.3390/photonics10080916
Chicago/Turabian StyleDarabi, Ebrahim, Heidar Keshavarz, and Paulo Monteiro. 2023. "A Novel Reconfigurable Nonlinear Cascaded MZM Mixer, Amplitude Shift Key Modulator (ASK), Frequency Hopping and Phase Shifter" Photonics 10, no. 8: 916. https://doi.org/10.3390/photonics10080916
APA StyleDarabi, E., Keshavarz, H., & Monteiro, P. (2023). A Novel Reconfigurable Nonlinear Cascaded MZM Mixer, Amplitude Shift Key Modulator (ASK), Frequency Hopping and Phase Shifter. Photonics, 10(8), 916. https://doi.org/10.3390/photonics10080916






