Some Optical Properties of LiNbO3:Gd3+(0.003):Mg2+(0.65 wt %) Single Crystal: A Promising Material for Laser Radiation Conversion
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. Transmission Spectra of the LiNbO3:Gd:Mg Crystal
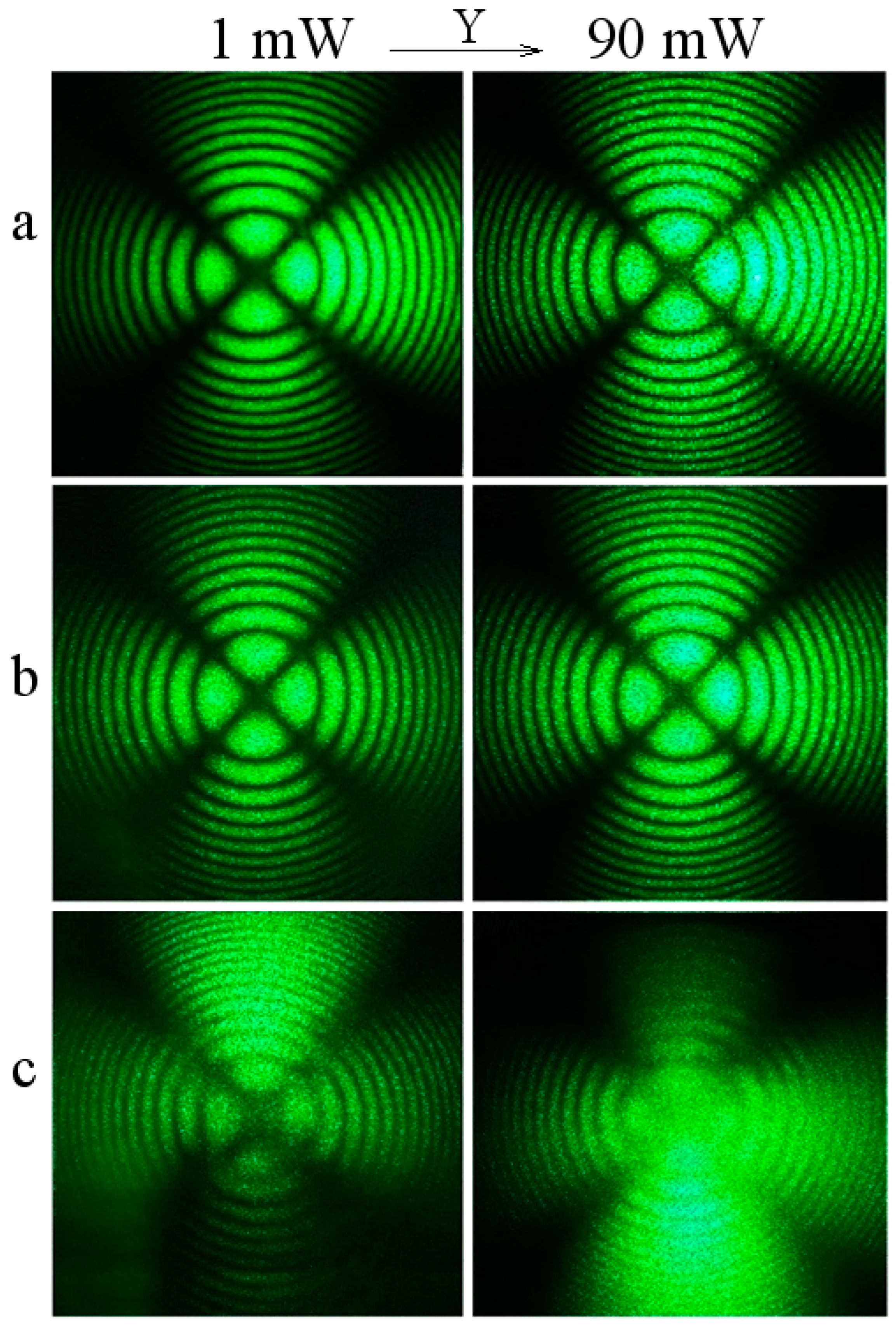
3.2. Laser Conoscopy of the LiNbO3:Gd:Mg Crystal
3.3. PILS of the LiNbO3:Gd:Mg Crystal
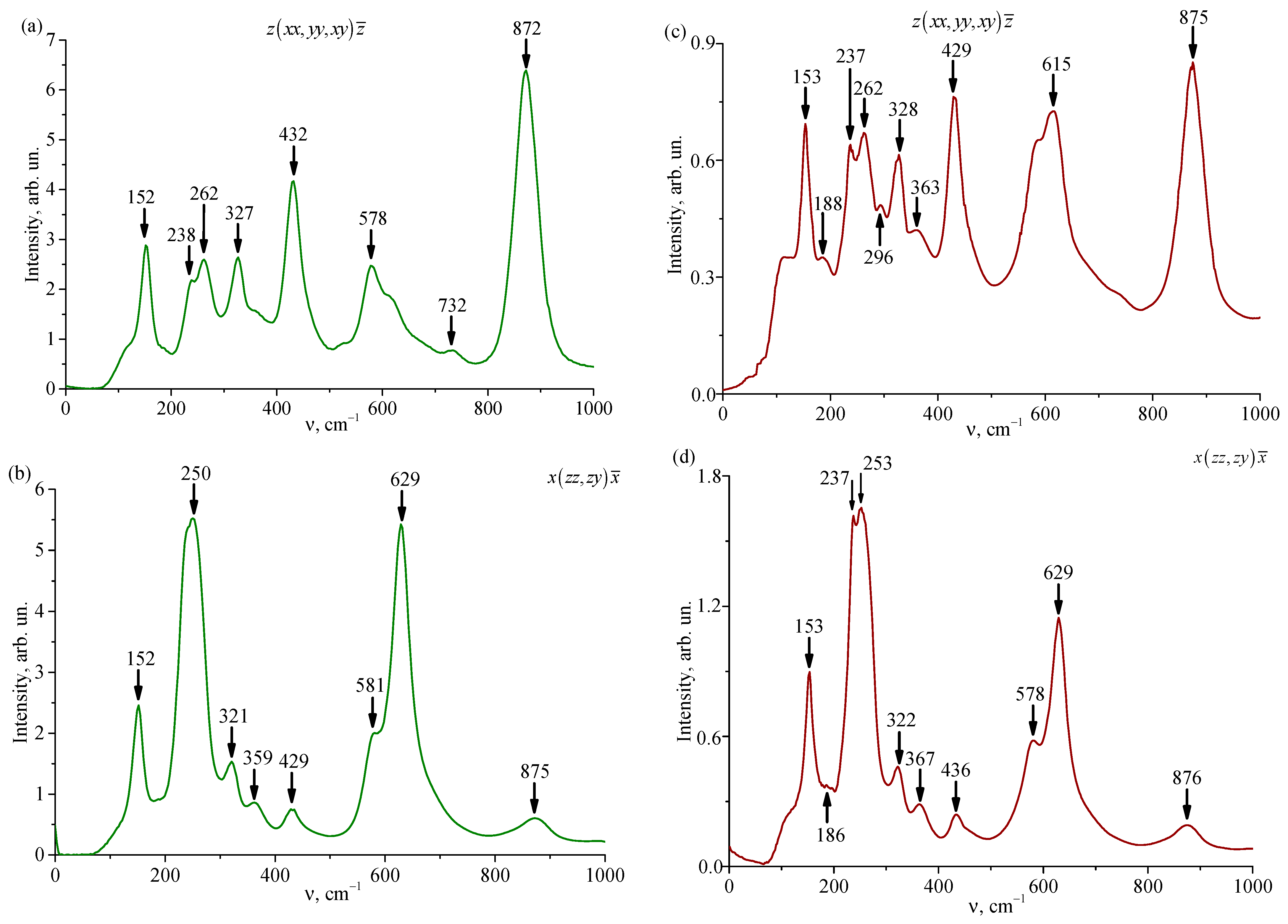
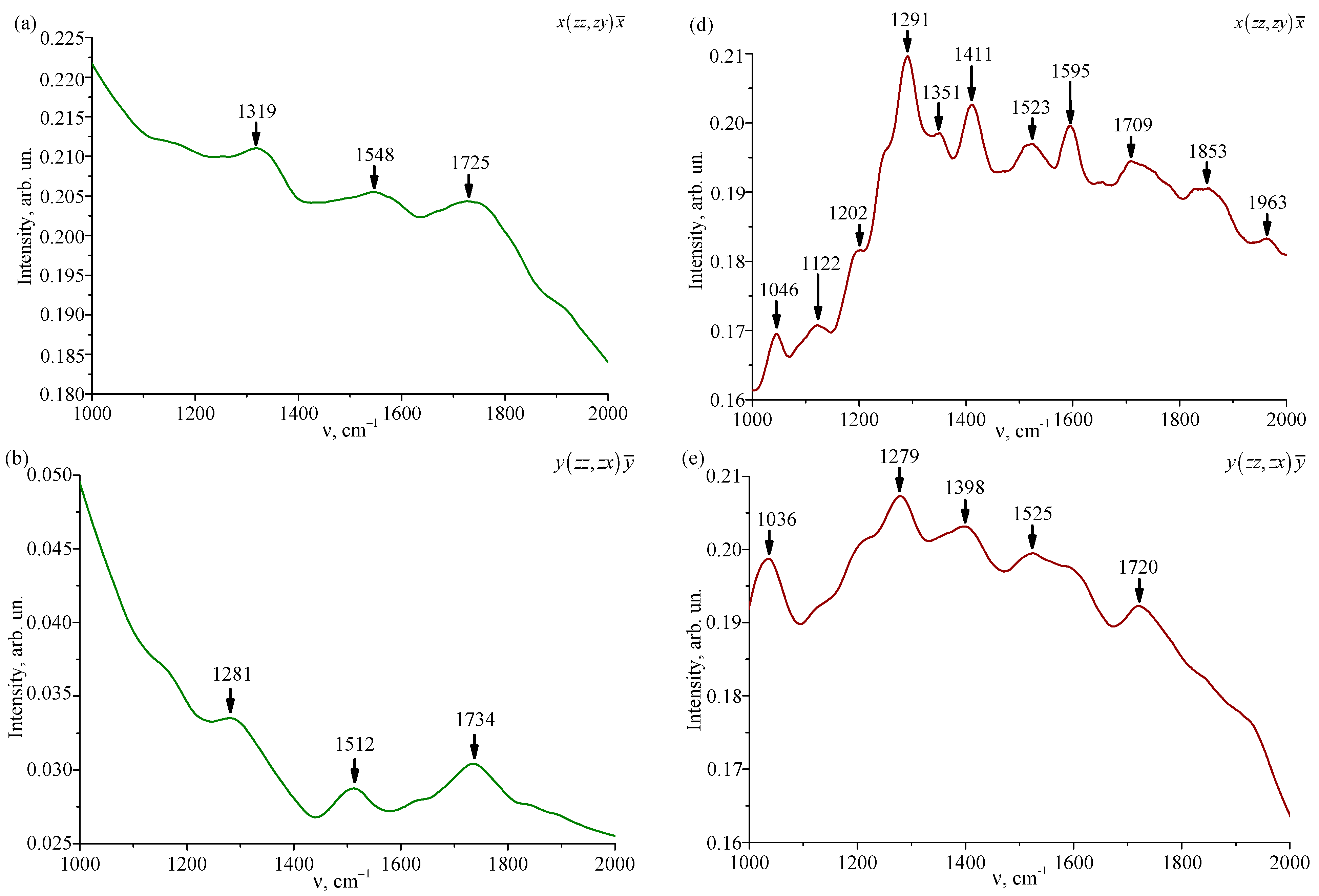
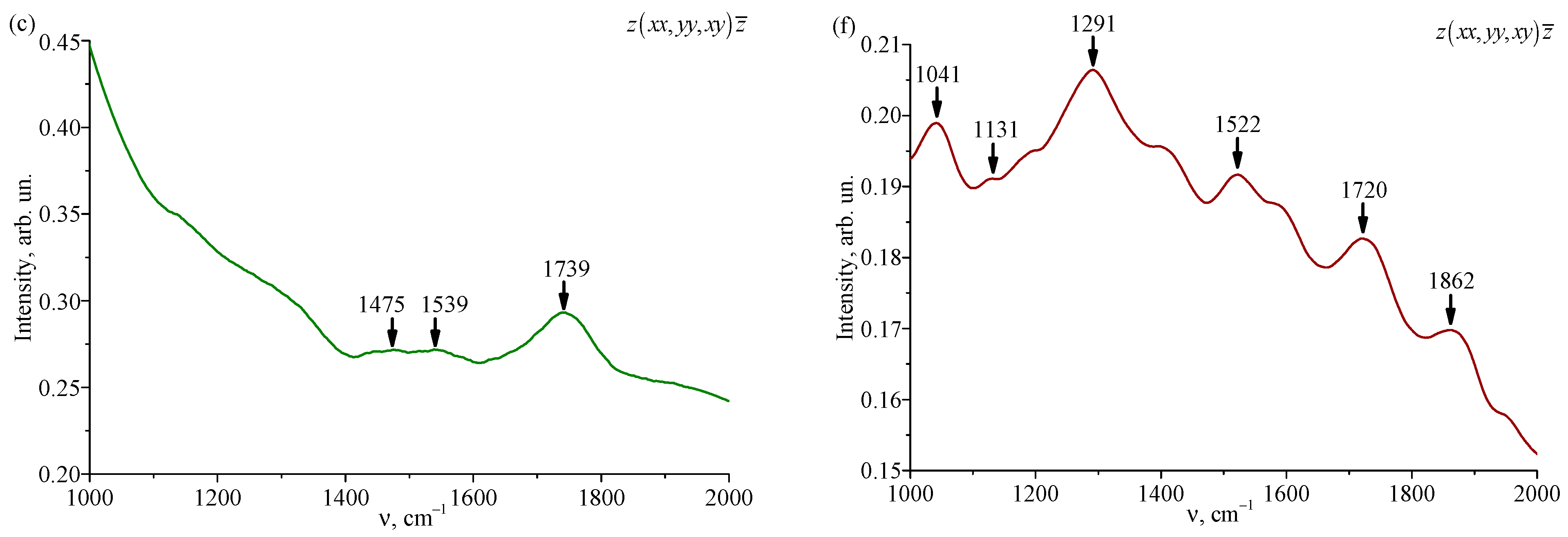
3.4. Raman Spectra of the LiNbO3:Gd:Mg Crystal
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Arizmendi, L. Photonic applications of lithium niobate crystals. Phys. Stat. Sol. 2004, 201, 253–283. [Google Scholar] [CrossRef]
- Günter, P.; Huighard, J.P. Photorefractive Materials and Their Applications. 1. Basis Effects; Springer: New York, NY, USA, 2006. [Google Scholar]
- Wang, Y.; Wang, R.; Yuan, J.; Wang, Y. Terahertz generation from Cu ion implantation into lithium niobate. J. Lumin. 2014, 147, 242–244. [Google Scholar] [CrossRef]
- Warrier, A.M.; Lin, J.; Pask, H.M.; Lee, A.J.; Spence, D.J. Multiwavelength ultrafast LiNbO3 Raman laser. Opt. Express 2015, 23, 25582–25587. [Google Scholar] [CrossRef]
- Yu, M.; Okawachi, Y.; Cheng, R.; Wang, C.; Zhang, M.; Gaeta, A.L.; Lončar, M. Raman lasing and soliton mode-locking in lithium niobate microresonators. Light Sci. Appl. 2020, 9, 9. [Google Scholar] [CrossRef] [Green Version]
- Lengyel, K.; Péter, Á.; Kovács, L.; Corradi, G.; Pálfalvi, L.; Hebling, J.; Unferdorben, M.; Dravecz, G.; Hajdara, I.; Szaller, Z.; et al. Growth, defect structure, and THz application of stoichiometric lithium niobate. Appl. Phys. Rev. 2015, 2, 040601. [Google Scholar] [CrossRef] [Green Version]
- Sidorov, N.V.; Palatnikov, M.N.; Teplyakova, N.A.; Birukova, I.V.; Titov, R.A.; Makarova, O.V.; Masloboeva, S.M. Single Crystals of Lithium Niobate and Tantalate of Different Composition and Genesis; RAS: Moscow, Russia, 2022. (In Russian) [Google Scholar]
- Fontana, M.D.; Bourson, P. Microstructure and defects probed by Raman spectroscopy in lithium niobate crystals and devices. Appl. Phys. Rev. 2015, 2, 040602. [Google Scholar] [CrossRef]
- Blistanov, A.A.; Lyubchenko, V.M.; Goryunov, A.N. Recombination processes in LiNbO3 crystals. Crystallogr. Rep. 1998, 43, 78–82. [Google Scholar]
- Xing, L.; Yang, W.; Lin, J. Impact of crystal defect on upconverted white-light emission in lanthanide-doped LiNbO3 single crystal. Opt. Mater. 2018, 84, 215–220. [Google Scholar] [CrossRef]
- Grachev, V.G.; Malovichko, G.I. Structures of impurity defects in lithium niobate and tantalate derived from electron paramagnetic and electron nuclear double resonance data. Crystals 2021, 11, 339. [Google Scholar] [CrossRef]
- Kemlin, V.; Jegouso, D.; Debray, J.; Boursier, E.; Segonds, P.; Boulanger, B.; Ishizuki, H.; Taira, T.; Mennerat, G.; Melkonian, J.-M.; et al. Dual-wavelength source from 5% MgO:PPLN cylinders for the characterization of nonlinear infrared crystals. Opt. Express 2013, 21, 28886–28891. [Google Scholar] [CrossRef]
- Murray, R.T.; Runcorn, T.H.; Guha, S.; Taylor, J.R. High average power parametric wavelength conversion at 3.31–3.48 μm in MgO:PPLN. Opt. Express 2017, 25, 6421–6430. [Google Scholar] [CrossRef]
- Shur, V.Y.; Akhmatkhanov, A.R.; Baturin, I.S. Micro- and nano-domain engineering in lithium niobate. Appl. Phys. Rev. 2015, 2, 040604. [Google Scholar] [CrossRef]
- Choge, D.K.; Chen, H.; Guo, L.; Li, G.; Liang, W. Simultaneous second-harmonic, sum-frequency generation and stimulated Raman scattering in MgO:PPLN. Materials 2018, 11, 2266. [Google Scholar] [CrossRef] [Green Version]
- Sidorov, N.V.; Bobreva, L.A.; Teplyakova, N.A.; Palatnikov, M.N.; Makarova, O.V. A comparative study of the structure and chemical homogeneity of LiNbO3:Mg (~5.3 mol%) crystals grown from charges of different origins. Inorg. Mater. 2019, 55, 1132–1137. [Google Scholar] [CrossRef]
- Kong, T.; Luo, Y.; Wang, W.; Kong, H.; Fan, Z.; Liu, H. Enhanced ultraviolet damage resistance in magnesium doped lithium niobate crystals through zirconium co-doping. Materials 2021, 14, 1017. [Google Scholar] [CrossRef]
- Liu, J.; Liu, A.; Chen, Y.; Tu, X.; Zheng, Y. Growth and optical properties of Pr-Mg co-doped LiNbO3 crystal using Bridgman method. Phys. B Condens. Matter 2022, 224, 413419. [Google Scholar] [CrossRef]
- Zhang, P.; Yin, J.; Zhang, L.; Liu, Y.; Hong, J.; Ning, K.; Chen, Z.; Wang, X.; Shi, C.; Hang, Y. Efficient enhanced 1. 54 μm emission in Er/Yb:LiNbO3 crystal codoped with Mg2+ ions, Opt. Mater. 2014, 36, 1986–1990. [Google Scholar] [CrossRef]
- Sidorov, N.V.; Volk, T.R.; Mavrin, B.N.; Kalinnikov, V.T. Lithium Niobate: Defects, Photorefraction, Vibrational Spectra, Polaritons; Nauka: Moscow, Russia, 2003. (In Russian) [Google Scholar]
- Irzhak, A.; Irzhak, D.; Pundikov, K.; Sergeev, A. Changing of LiNbO3 Raman spectra under external electric field applying. Opt. Mater. 2022, 133, 112988. [Google Scholar] [CrossRef]
- Irzhak, A.; Irzhak, D.; Khvostikov, V.; Pundikov, K.; Roshchupkin, D.; Fahrtdinov, R. Effect of local changes in the composition of the LiNb1−xTaxO3 single crystal on the Raman spectra. J. Raman Spectrosc. 2022, 53, 969–976. [Google Scholar] [CrossRef]
- Gorelik, V.S.; Abdurakhmonov, S.D. Overtone Raman scattering in lithium niobate single crystal doped with terbium. Crystallogr. Rep. 2022, 67, 252–255. [Google Scholar] [CrossRef]
- Anikiev, A.A.; Umarov, M.F.; Scott, J.F. Processing and characterization of improved congruent lithium niobate. AIP Adv. 2018, 8, 115016. [Google Scholar] [CrossRef] [Green Version]
- Anikiev, A.A.; Umarov, M.F. Quasi-elastic light scattering in congruent lithium niobate crystals. Opt. Spectrosc. 2018, 125, 22–27. [Google Scholar] [CrossRef]
- Rygula, A.; Majzner, K.; Marzec, K.M.; Kaczor, A.; Pilarczyk, M.; Baranska, M. Raman spectroscopy of proteins: A review. J. Raman Spectrosc. 2013, 44, 1061–1076. [Google Scholar] [CrossRef]
- Antunes, E.F.; Lobo, A.O.; Corat, E.J.; Trava-Airoldi, V.J.; Martin, A.A.; Veríssimo, C. Comparative study of first- and second-order Raman spectra of MWCNT at visible and infrared laser excitation. Carbon 2006, 44, 2202–2211. [Google Scholar] [CrossRef]
- Singh, E.; Pionteck, M.N.; Reitzig, S.; Lange, M.; Rusing, M.; Eng, L.M.; Sanna, S. Vibrational properties of LiNbO3 and LiTaO3 under uniaxial stress. Phys. Rev. Mater. 2023, 7, 024420. [Google Scholar] [CrossRef]
- Quispe-Siccha, R.; Mejía-Uriarte, E.V.; Villagrán-Muniz, M.; Jaque, D.; García Solé, J.; Jaque, F.; Sato-Berrú, R.Y.; Camarillo, E.; Hernández, J.; Murrieta, H. The effect of Nd and Mg doping on the micro-Raman spectra of LiNbO3 single-crystals. J. Phys. Condens. Matter 2009, 21, 145401. [Google Scholar] [CrossRef] [PubMed]
- Rahman, M.K.R.; Riscob, B.; Bhatt, R.; Bhaumik, I.; Ganesamoorthy, S.; Vijayan, N.; Bhagavannarayana, G.; Karnal, A.K.; Nair, L. Investigations on crystalline perfection, Raman spectra and optical characteristics of transition metal (Ru) co-doped Mg:LiNbO3 single crystals. ACS Omega 2021, 6, 10807–10815. [Google Scholar] [CrossRef] [PubMed]
- Tejerina, M.R.; Pereira da Silva, K.; Goñi, A.R.; Torchia, G.A. Hydrostatic-pressure dependence of Raman-active optical phonons in Nd:Mg:LiNbO3. Opt. Mater. 2013, 36, 581–583. [Google Scholar] [CrossRef]
- Sidorov, N.V.; Pikoul, O.Y.; Teplyakova, N.A.; Palatnikov, M.N. Laser Conoscopy and Photoinduced Light Scattering in Research of Properties of Optically Nonlinear Lithium Niobate Crystal; RAS: Moscow, Russia, 2019. (In Russian) [Google Scholar]
- Palatnikov, M.N.; Sidorov, N.V.; Kadetova, A.V.; Teplyakova, N.A.; Makarova, O.V.; Manukovskaya, D.V. Concentration threshold in optically nonlinear LiNbO3:Tb crystals. Opt. Laser Technol. 2021, 137, 106821. [Google Scholar] [CrossRef]
- Akhmadullin, I.S.; Golenishchev-Kutuzov, V.A.; Migachev, S.A.; Mironov, S.P. Low-temperature electrical conductivity of congruent lithium niobate. Phys. Solid State 1998, 40, 1190–1192. [Google Scholar] [CrossRef]
- Goulkov, M.; Imlau, M.; Woike, T. Photorefractive parameters of lithium niobate crystals from photoindused light scattering. Phys. Rev. B 2008, 77, 235110. [Google Scholar] [CrossRef]
- Ridah, A.; Bourson, P.; Fontana, M.D.; Malovichko, G. The composition dependence of the Raman spectrum and new assignment of the phonons in LiNbO3. J. Phys. Cond. Matter 1997, 9, 9687–9693. [Google Scholar] [CrossRef]
- Parlinsky, K.; Li, Z.Q.; Kawazoe, Y. Ab initio calculations of phonons in LiNbO3. Phys. Rev. B 2000, 61, 272–278. [Google Scholar] [CrossRef] [Green Version]
- Li, R. Vibrational spectra and electro-optic effect of ferroelectric LiNbO3 crystal. Phys. Stat. Sol. 2023, 260, 2300051. [Google Scholar] [CrossRef]
- Friedrich, M.; Riefer, A.; Sanna, S.; Schmidt, W.G.; Schindlmayr, A. Phonon dispersion and zero-point renormalization of LiNbO3 from density-functional perturbation theory. J. Phys. Cond. Matter 2015, 27, 385402. [Google Scholar] [CrossRef] [Green Version]
- Kong, Y.; Xu, J.; Chen, X.; Zhang, C.; Zhang, W.; Zhang, G. Ilmenite-like stacking defect in nonstoichiometric lithium niobate crystals investigated by Raman scattering spectra. J. Appl. Phys. 2000, 87, 4410–4414. [Google Scholar] [CrossRef]
- Yang, X.; Lan, G.; Li, B.; Wang, H. Raman spectra and directional dispersion in LiNbO3 and LiTaO3. Phys. Stat. Sol. 1987, 142, 287–300. [Google Scholar] [CrossRef]
- Veithen, M.; Ghosez, P. First-principles study of the dielectric and dynamical properties of lithium niobate. Phys. Rev. B 2002, 65, 214302. [Google Scholar] [CrossRef]
- Nogueira, B.A.; Milani, A.; Castiglioni, C.; Fausto, R. The correlation between experimental polarized Raman spectra and their density functional theory prediction in the LCAO framework: The R3c LiNbO3 crystal as a test case. J. Raman Spectrosc. 2021, 52, 995–1010. [Google Scholar] [CrossRef]
- Okamoto, Y.; Wang, P.-C.; Scott, J.F. Analysis of quasielastic light scattering in LiNbO3 near TC. Phys. Rev. B 1985, 32, 6787–6792. [Google Scholar] [CrossRef]
- Sidorov, N.; Palatnikov, M.; Pyatyshev, A. Raman scattering in double-doped single crystal LiTaO3:Cr(0.2):Nd(0.45wt.%). Photonics 2022, 9, 712. [Google Scholar] [CrossRef]
- Sidorov, N.; Palatnikov, M.; Pyatyshev, A.; Sverbil, P. Second-order Raman scattering in ferroelectric ceramic solid solutions LiNbxTa1−xO3. Crystals 2022, 12, 456. [Google Scholar] [CrossRef]
- Palatnikov, M.; Sidorov, N.; Pyatyshev, A.; Skrabatun, A. Comparison of Raman spectra of optically nonlinear LiTaO3:Cr3+ (0.005 wt%) crystal laser excited in visible (532 nm) and near-IR (785 nm) areas. Photonics 2023, 10, 439. [Google Scholar] [CrossRef]


| Impurity | Mn | Ni | Al | Fe | Cr, Cu, V | Pb, Sn | Bi | Mg | Si, Ti, Mo, Ca, Co | Sb | Zr | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C·10−3, wt % | Charge | <0.2 | <0.3 | <0.3 | <0.3 | 0.3 | <0.5 | 0.5 | 0.5 | 1 | 2.1 | <10 |
| Crystal cone | <0.2 | <0.3 | <0.3 | 0.32 | 0.3 | <0.5 | 0.5 | 0.53 | 1 | 1.7 | 10 | |
| Crystal bottom | <0.2 | <0.3 | 1 | 0.38 | 0.3 | <0.5 | 0.5 | 0.58 | 1 | 2 | 10 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sidorov, N.; Palatnikov, M.; Teplyakova, N.; Pyatyshev, A.; Skrabatun, A. Some Optical Properties of LiNbO3:Gd3+(0.003):Mg2+(0.65 wt %) Single Crystal: A Promising Material for Laser Radiation Conversion. Photonics 2023, 10, 921. https://doi.org/10.3390/photonics10080921
Sidorov N, Palatnikov M, Teplyakova N, Pyatyshev A, Skrabatun A. Some Optical Properties of LiNbO3:Gd3+(0.003):Mg2+(0.65 wt %) Single Crystal: A Promising Material for Laser Radiation Conversion. Photonics. 2023; 10(8):921. https://doi.org/10.3390/photonics10080921
Chicago/Turabian StyleSidorov, Nikolay, Mikhail Palatnikov, Natalya Teplyakova, Alexander Pyatyshev, and Alexander Skrabatun. 2023. "Some Optical Properties of LiNbO3:Gd3+(0.003):Mg2+(0.65 wt %) Single Crystal: A Promising Material for Laser Radiation Conversion" Photonics 10, no. 8: 921. https://doi.org/10.3390/photonics10080921
APA StyleSidorov, N., Palatnikov, M., Teplyakova, N., Pyatyshev, A., & Skrabatun, A. (2023). Some Optical Properties of LiNbO3:Gd3+(0.003):Mg2+(0.65 wt %) Single Crystal: A Promising Material for Laser Radiation Conversion. Photonics, 10(8), 921. https://doi.org/10.3390/photonics10080921







