Quantum Applications of an Atomic Ensemble Inside a Laser Cavity
Abstract
1. Introduction
2. Theoretical
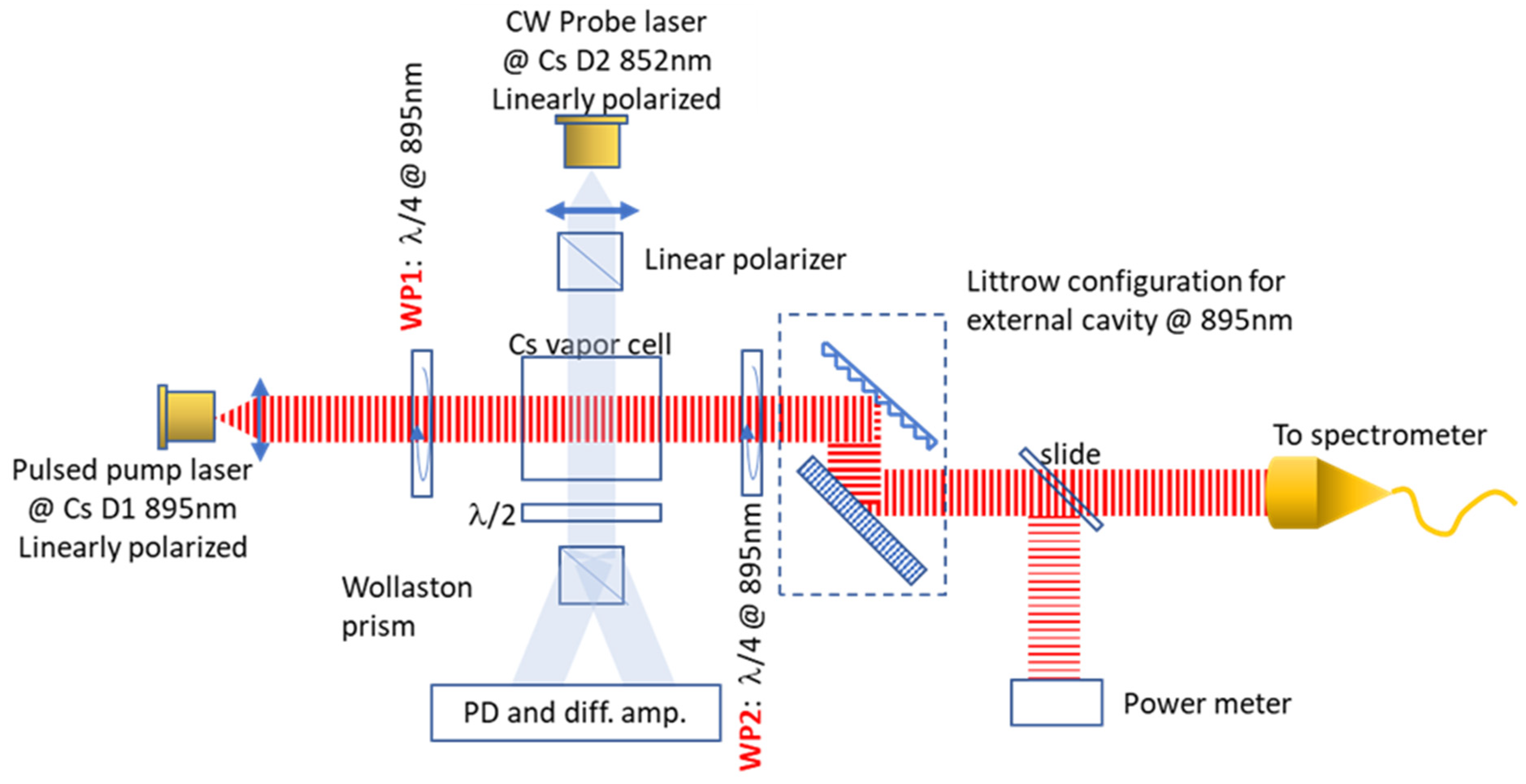
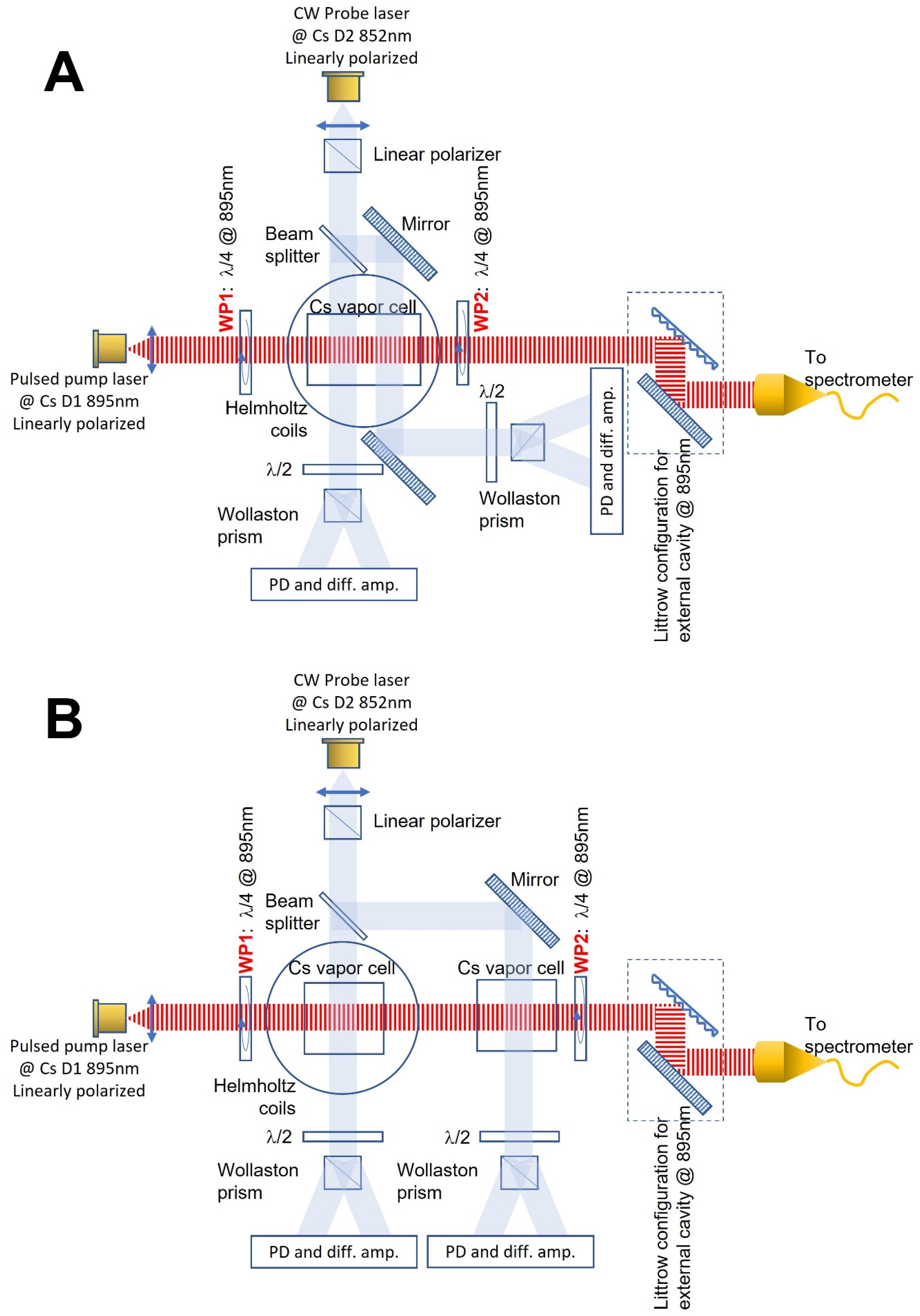
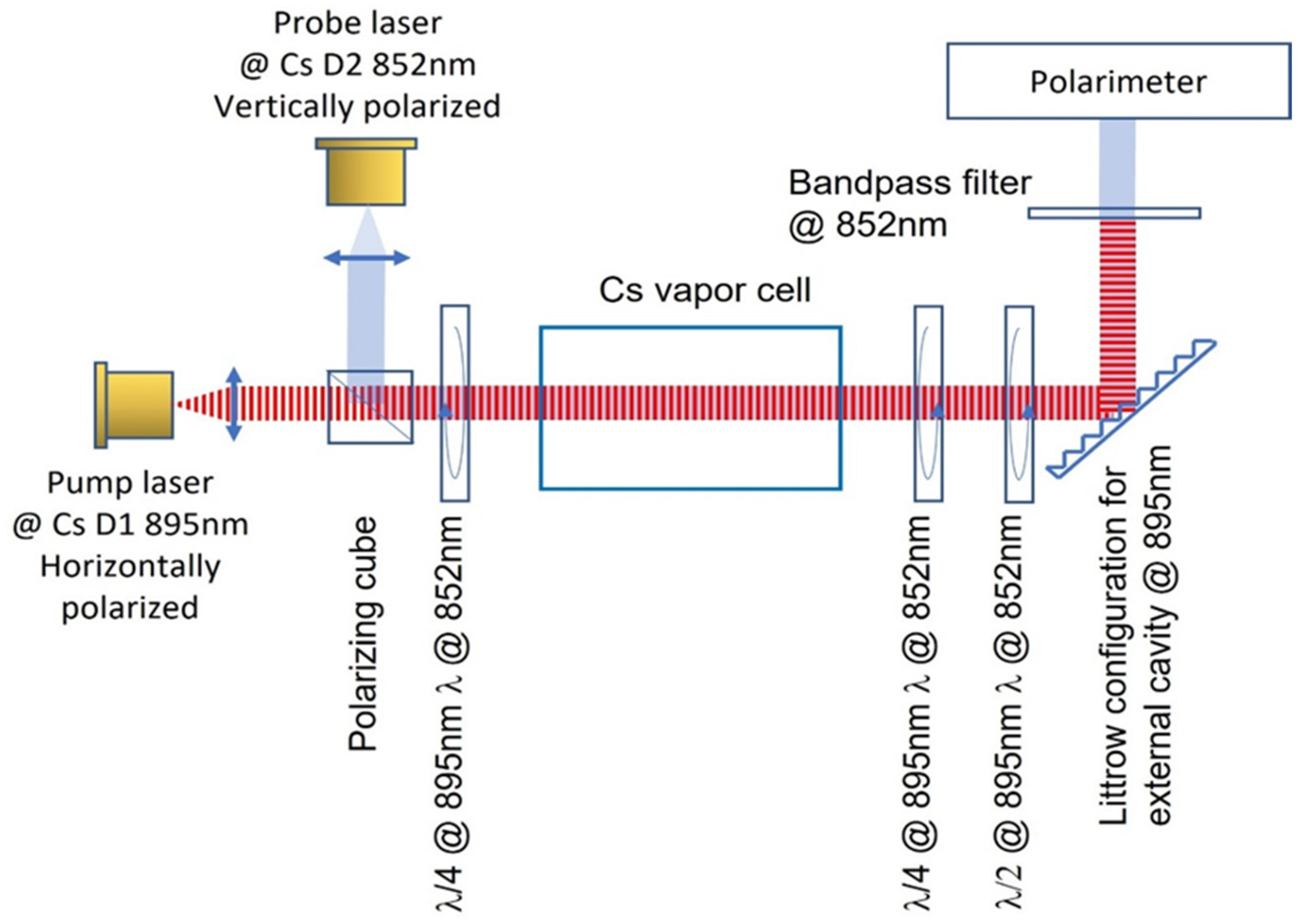
3. Experimental
4. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
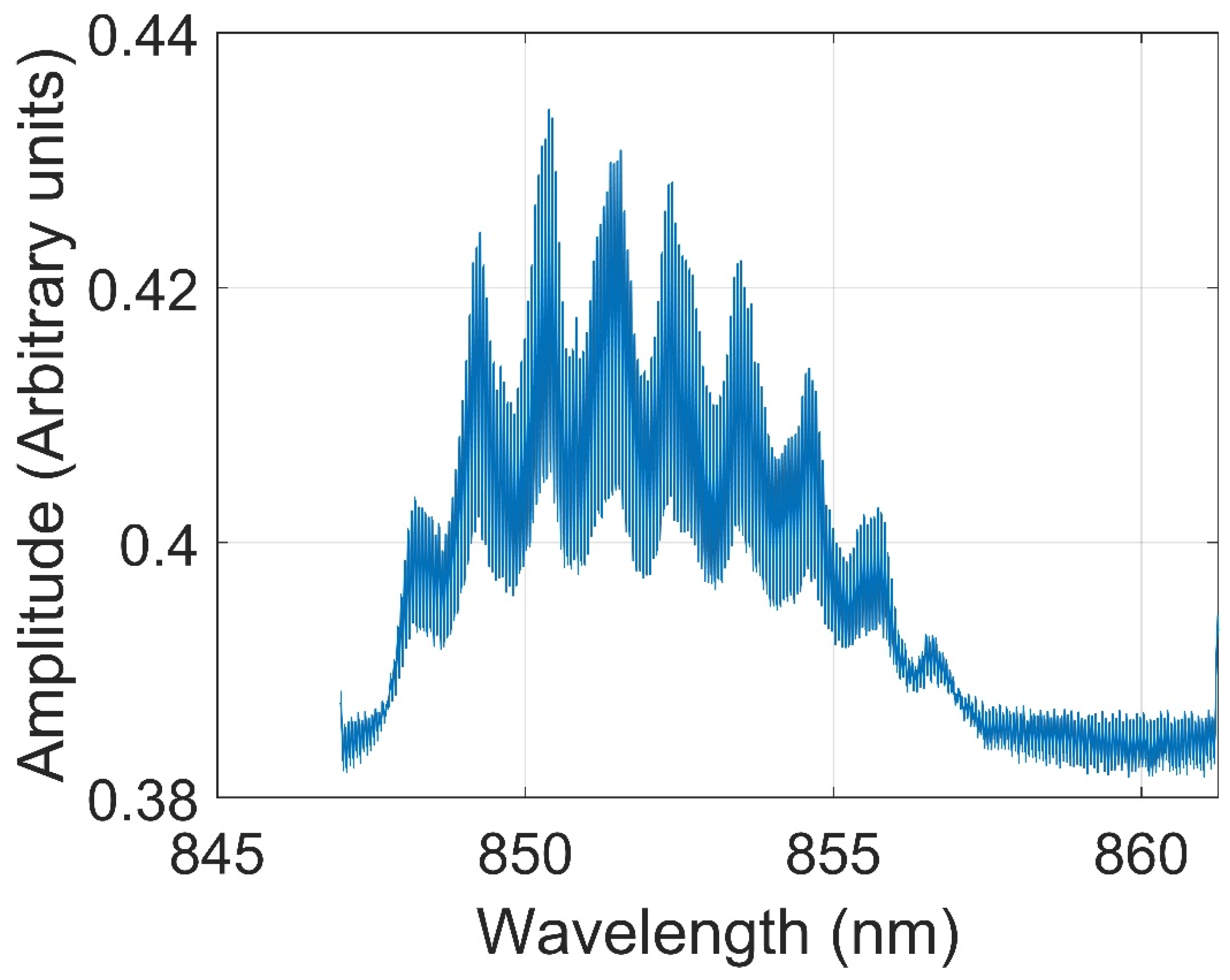
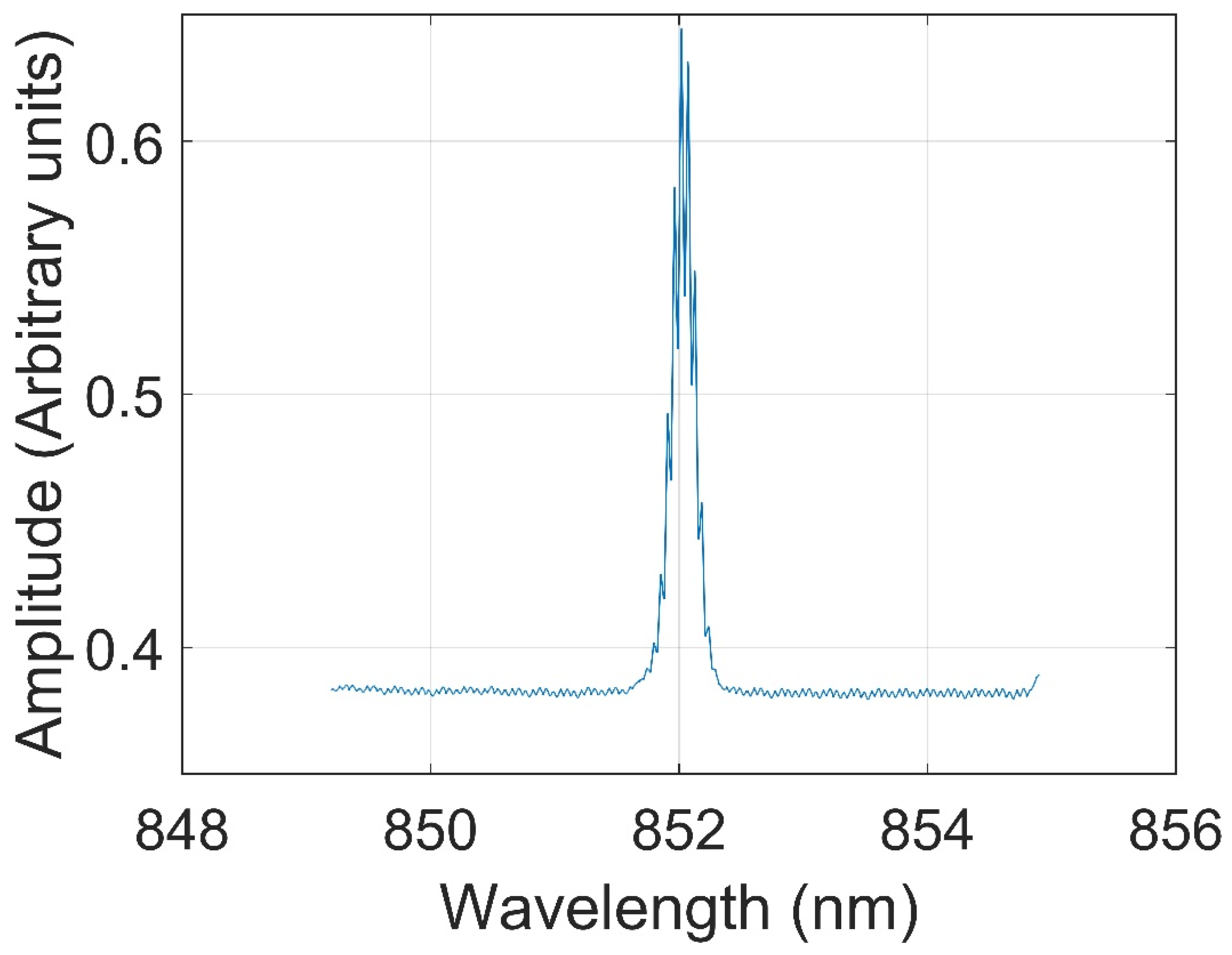
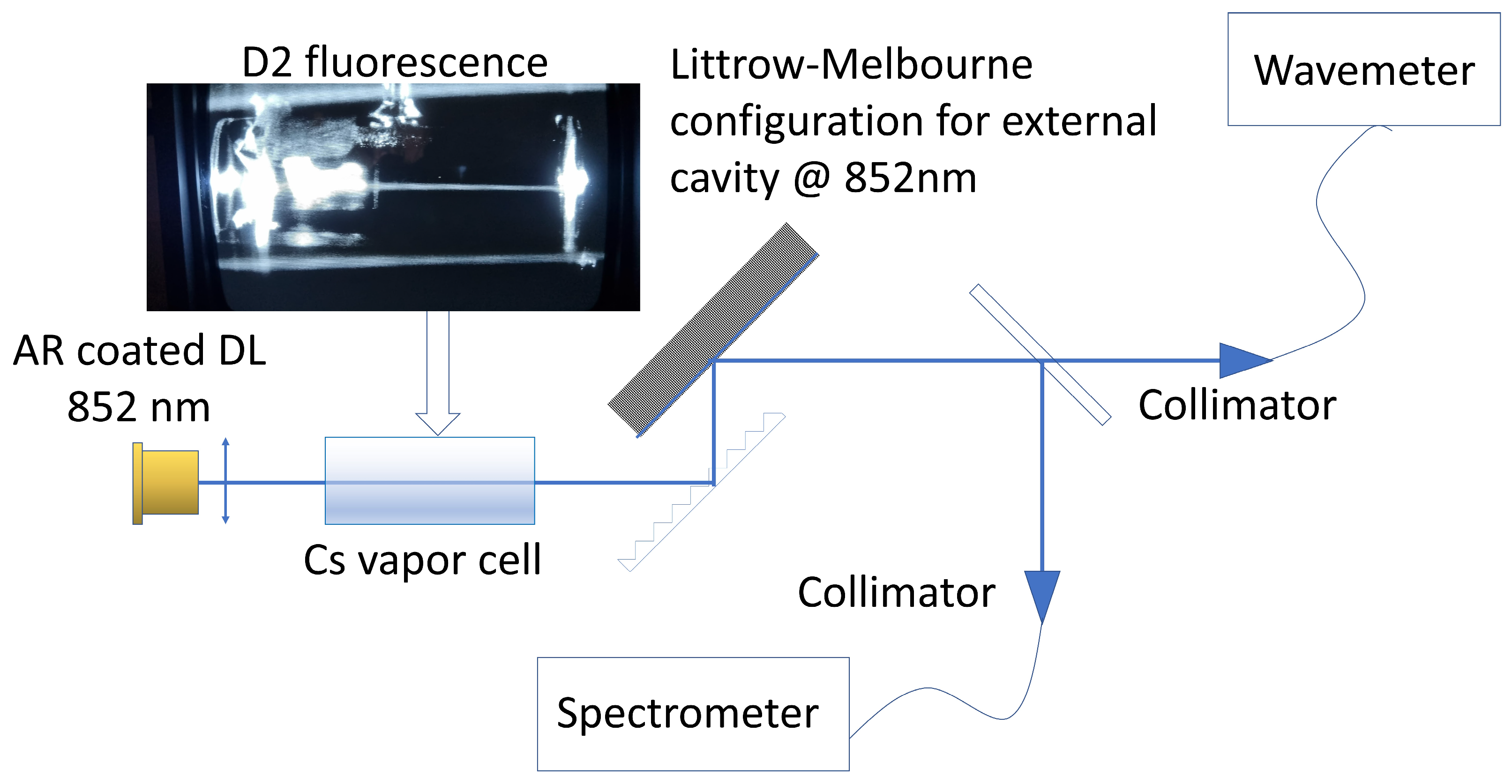
- Figure A1 shows the emission spectrum of Toptica diode laser LD-0860-0080-AR-1 (https://www.toptica.com/fileadmin/Editors_English/14_stocklists/AR-Stock-list.pdf accessed on 28 December 2023). The calibration is 2.35 nm/ms, therefore, the FWHM is approx. 5 nm. The diode is AR coated so there is no front mirror. The tuning range is 840–875. We narrowed and tuned the laser to resonance in the Littrow configuration external cavity. Figure A2 shows the narrowed laser spectrum. The measured linewidth by spectrometer is approx. 0.15 nm which is the spectrometer’s resolution. The real linewidth was therefore measured by the wavemeter and is less than 0.2 pm (less than 60 MHz). For efficient optical pumping the pump-laser linewidth should be in the order of the atomic linewidth and certainly not much smaller to avoid hole burning. The linewidth of the probe laser is similar, and the wavelength is detuned from resonance by several natural linewidths (tens of pico-meter in our case) to avoid absorption and atomic polarization destruction.
- 2.
- The linewidth is narrowed by the Littrow configuration external cavity and not by the Cs atoms or glass cell. Our claim is that, despite the absorption at resonance by Cs atoms, we locked the laser at the desired wavelength with a narrow linewidth, adequate to optical pumping, i.e., in the same order as the natural atomic linewidth. With the cell in the cavity or without it, the linewidth is the same, defined only by the optical cavity.
- 3.
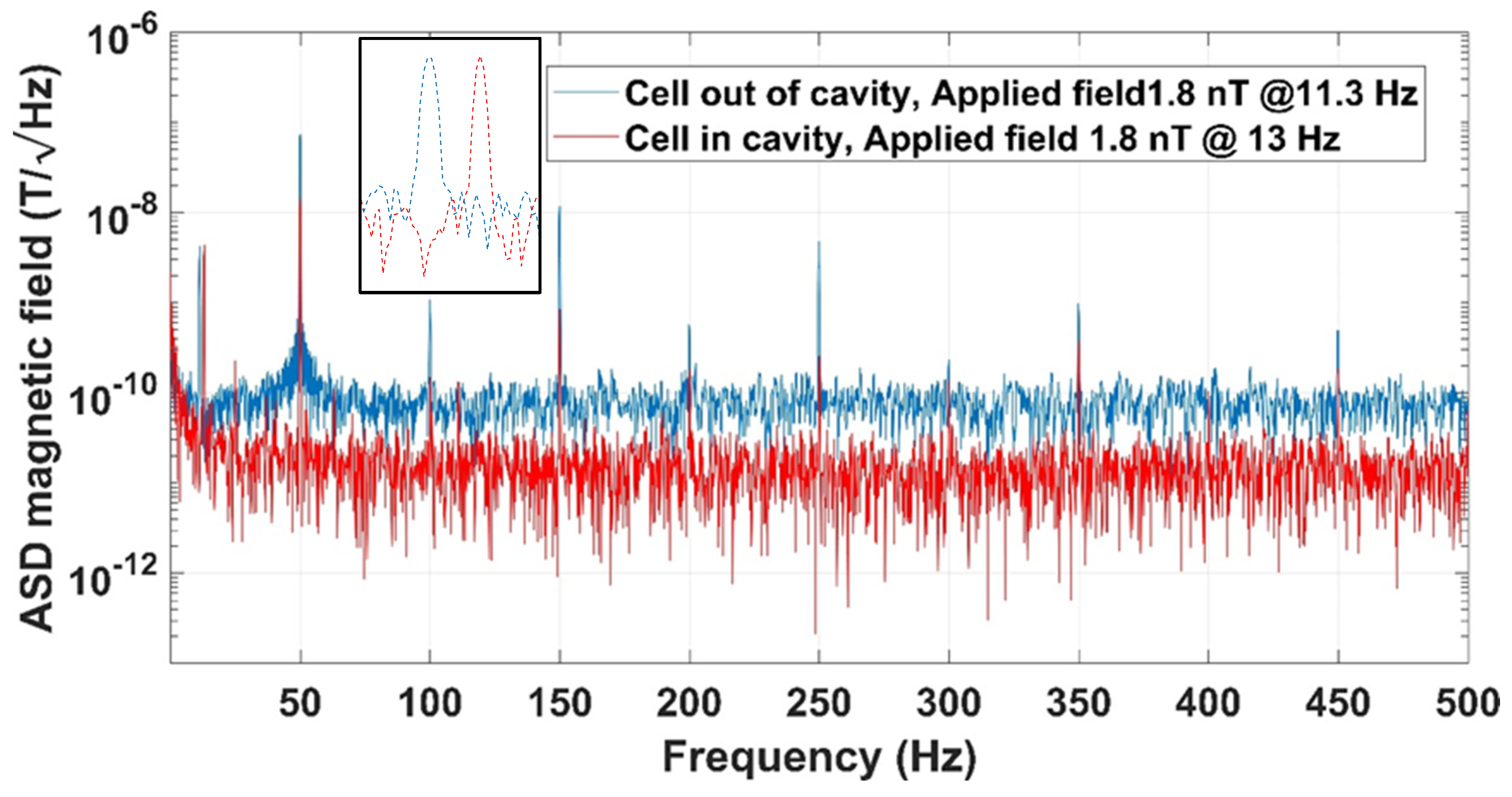
- The maximum bandwidth of our pulsed magnetometer operated at 1 kHz is 500 Hz (as defined by Nyquist frequency), but the magnetometer is sensitive to much higher frequencies. However, its sensitivity decays with frequency and it reaches 3 dB decay at 225 Hz.
- 4.
- The presented pulse magnetometer works unshielded in the earth’s field whose amplitude changes with the latitude. The dynamic range is defined by the range of the ambient field for which minute temporal changes can be measured, and for our magnetometer it is 20–100 µT.
- 5.
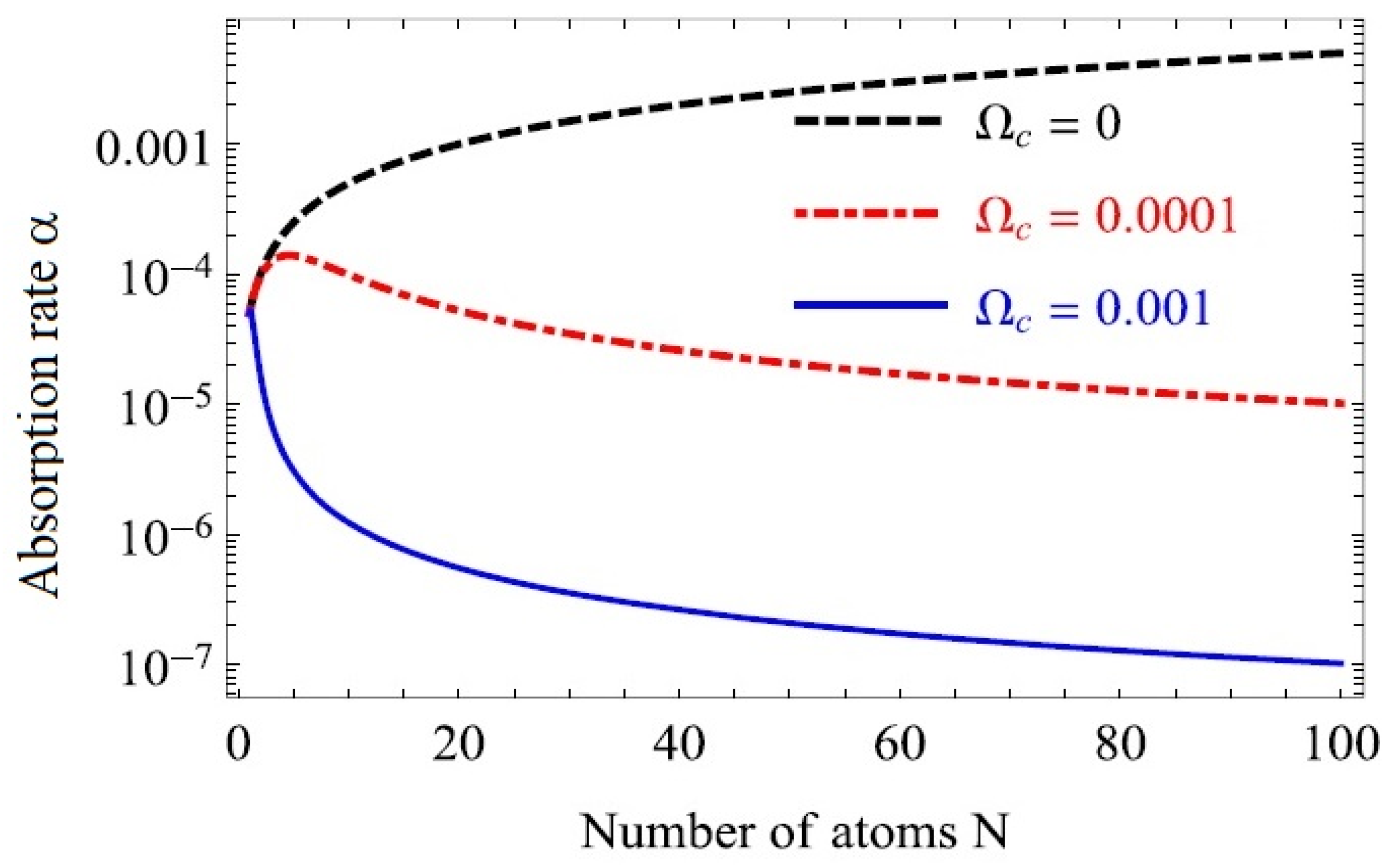
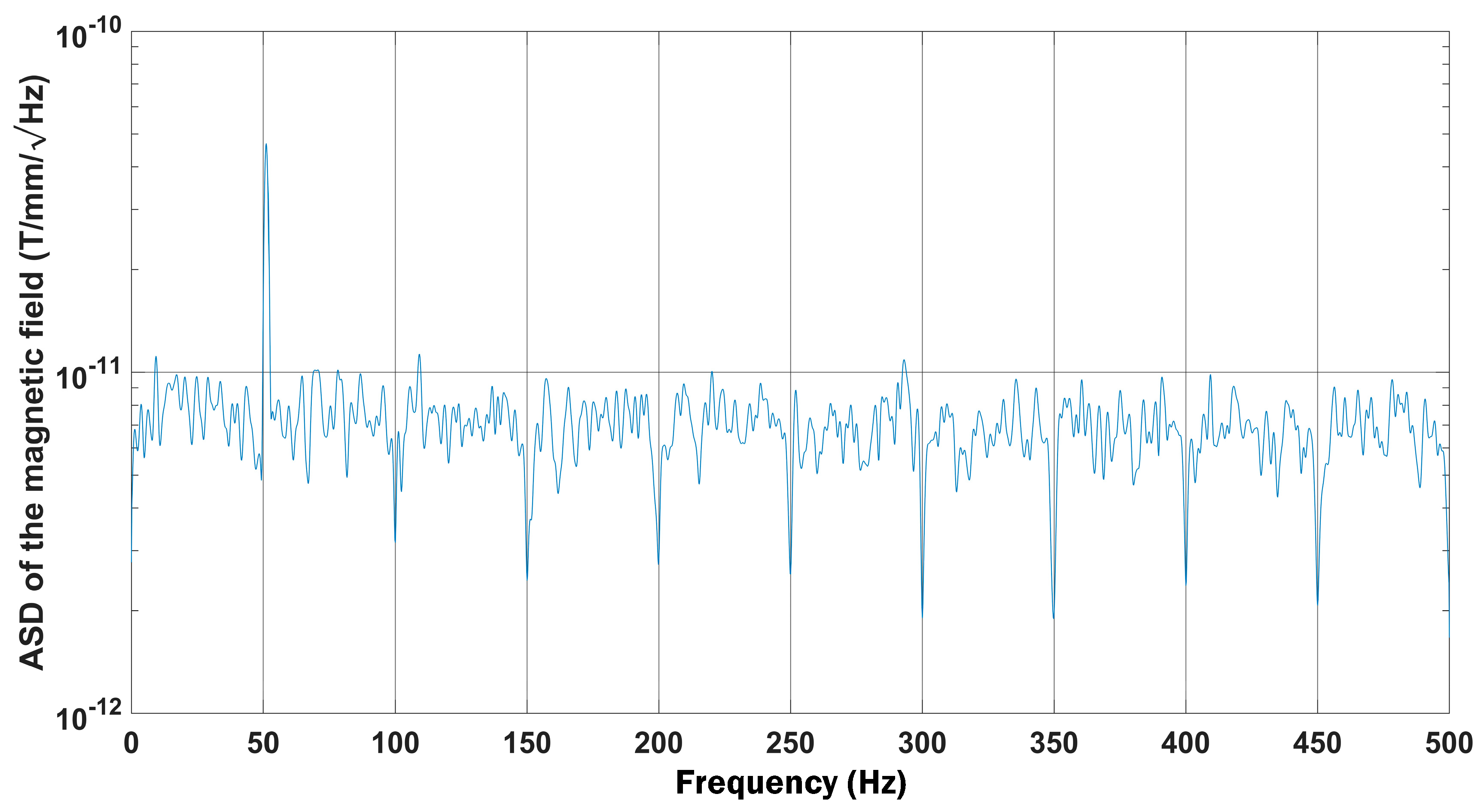
- The sensitivity of the magnetometer is the minimal measured intensity of the minute changes in ambient field, and it is better than 10 pT/√Hz. In our measurements, we applied various magnetic fields at different frequencies (up to 500 Hz), with intensities in the order of 1 nT. These fields are depicted on the background of Earth’s field as shown in Figure 5.
References
- Budker, D.; Romalis, M. Optical magnetometry. Nat. Phys. 2007, 3, 227–234. [Google Scholar] [CrossRef]
- Loh, W.; Stuart, J.; Reens, D.; Bruzewicz, C.D.; Braje, D.; Chiaverini, J.; Juodawlkis, P.W.; Sage, J.M.; McConnell, R. A Brillouin Laser Optical Atomic Clock. arXiv 2020, arXiv:2001.06429. [Google Scholar]
- Zhou, L.; Lin, J.; Xie, Y.M.; Lu, Y.S.; Jing, Y.; Yin, H.L.; Yuan, Z. Experimental quantum communication overcomes the rate-loss limit without global phase tracking. Phys. Rev. Lett. 2023, 130, 250801. [Google Scholar] [CrossRef]
- Azuma, K.; Economou, S.E.; Elkouss, D.; Hilaire, P.; Jiang, L.; Lo, H.K.; Tzitrin, I. Quantum repeaters: From quantum networks to the quantum internet. Rev. Mod. Phys. 2023, 95, 045006. [Google Scholar] [CrossRef]
- Narducci, F.A.A.; TBlack, A.T.; John HBurke, J.H. Advances toward fieldable atom interferometers. Adv. Phys. X 2022, 7, 1946426. [Google Scholar] [CrossRef]
- Bernien, H.; Schwartz, S.; Keesling, A.; Levine, H.; Omran, A.; Pichler, H.; Choi, S.; Zibrov, A.S.; Endres, M.; Greiner, M.; et al. Probing many-body dynamics on a 51-atom quantum simulator. Nature 2017, 551, 579–584. [Google Scholar] [CrossRef]
- Shuker, R.; Koganov, A.G. Photon-induced correlations of quantum systems via an excitation exchange operator. Laser Phys. Lett. 2021, 18, 055205. [Google Scholar] [CrossRef]
- Allred, J.C.; Lyman, R.N.; Kornack, T.W.; Romalis, M.V. High-Sensitivity Atomic Magnetometer Unaffected by Spin-Exchange Relaxation. Phys. Rev. Lett. 2002, 89, 130801. [Google Scholar] [CrossRef]
- Kominis, I.K.; Kornack, T.W.; Allred, J.C.; Romalis, M.V. A sub-femto-tesla multichannel atomic magnetometer. Nature 2003, 422, 596–599. [Google Scholar] [CrossRef] [PubMed]
- Budker, D.; Jackson Kimball, D.F. Optical Magnetometry; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Ben Amar Baranga, A.; Levron, D.; Paperno, E.; Shuker, R. Device and Methodology for Measuring Minute Changes in Ambient Magnetic Field. United States Patent US 10,712,407 B2, 14 July 2020. [Google Scholar]
- Romalis, M.; Dong, H.; Baranga, A. Pulsed Scalar Atomic Magnetometer. United States Patent US 10,852,371 B2, 1 December 2020. [Google Scholar]
- Gerginov, V.; Pomponio, M.; Knappe, S. Scalar Magnetometry Below 100 fT/Hz1/2 in a Microfabricated Cell. IEEE Sens. J. 2020, 20, 12684–12690. [Google Scholar] [CrossRef] [PubMed]
- Ben-Amar Baranga, A.; Gusarov, A.; Koganov, G.A.; Levron, D.; Shuker, R. Optical magnetometer: Quantum resonances at pumping repetition rate of 1/n of the Larmor frequency. J. Appl. Phys. 2020, 128, 174501. [Google Scholar] [CrossRef]
- Limes, M.E.; Foley, E.L.; Kornack, T.W.; Caliga, S.; McBride, S.; Braun, A.; Lee, W.; Lucivero, V.G.; Romalis, M.V. Portable Magnetometry for Detection of Biomagnetism in Ambient Environments. Phys. Rev. Appl. 2020, 14, 011002. [Google Scholar] [CrossRef]
- Campbell, K.; Wang, Y.J.; Savukov, I.; Jau, Y.Y.; Schwindt, P.; Shah, V. Pulsed gradiometry in Earth’s field. In Proceedings of the APS DAMOP, Portland, OR, USA, 1–5 June 2020. [Google Scholar]
- Colombe, Y.; Steinmetz, T.; Dubois, G.; Linke, F.; Hunger, D.; Reichel, J. Strong atom–field coupling for Bose–Einstein condensates in an optical cavity on a chip. Nature 2007, 450, 272–276. [Google Scholar] [CrossRef] [PubMed]
- Koganov, A.G.; Shuker, R. Double dressing by both the number of atoms and the number of photons inside cavity. Results Phys. 2023, 49, 106447. [Google Scholar] [CrossRef]
- Hawthorn, C.J.; Weber, K.P.; Scholten, R.E. Littrow configuration tunable external cavity diode laser with fixed direction output beam. Rev. Sci. Instrum. 2001, 72, 4477–4479. [Google Scholar] [CrossRef]
- Jechow, A.; Raab, V.; Menzel, R.; Cenkier, M.; Stry, S.; Sacher, J. 1 W tunable near diffraction limited light from a broad area laser diode in an external cavity with a line width of 1.7 MHz. Opt. Commun. 2007, 277, 161–165. [Google Scholar] [CrossRef]
- Gusarov, A.; Levron, D.; Baranga, A.; Paperno, E.; Shuker, R. An all-optical scalar and vector spin-exchange relaxation-free magnetometer employing on–off pump modulation. J. Appl. Phys. 2011, 109, 07E507. [Google Scholar] [CrossRef]
- Palmer, C. Diffraction Grating Handbook, 8th ed.; MKS Instruments, Inc.: Rochester, NY, USA, 2020; pp. 122–126. [Google Scholar]
- Brosseau, C. Fundamentals of Polarized Light; John Wiley & Sons Inc.: New York, NY, USA, 1998; pp. 181–209. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ben Amar Baranga, A.; Koganov, G.A.; Levron, D.; Bialolenker, G.; Shuker, R. Quantum Applications of an Atomic Ensemble Inside a Laser Cavity. Photonics 2024, 11, 46. https://doi.org/10.3390/photonics11010046
Ben Amar Baranga A, Koganov GA, Levron D, Bialolenker G, Shuker R. Quantum Applications of an Atomic Ensemble Inside a Laser Cavity. Photonics. 2024; 11(1):46. https://doi.org/10.3390/photonics11010046
Chicago/Turabian StyleBen Amar Baranga, Andrei, Gennady A. Koganov, David Levron, Gabriel Bialolenker, and Reuben Shuker. 2024. "Quantum Applications of an Atomic Ensemble Inside a Laser Cavity" Photonics 11, no. 1: 46. https://doi.org/10.3390/photonics11010046
APA StyleBen Amar Baranga, A., Koganov, G. A., Levron, D., Bialolenker, G., & Shuker, R. (2024). Quantum Applications of an Atomic Ensemble Inside a Laser Cavity. Photonics, 11(1), 46. https://doi.org/10.3390/photonics11010046




