Machine Learning Based Automatic Mode-Locking of a Dual-Wavelength Soliton Fiber Laser
Abstract
1. Introduction
2. Numerical Model and Simulation Results
2.1. Laser Setup and Numerical Model
2.2. Numerical Model
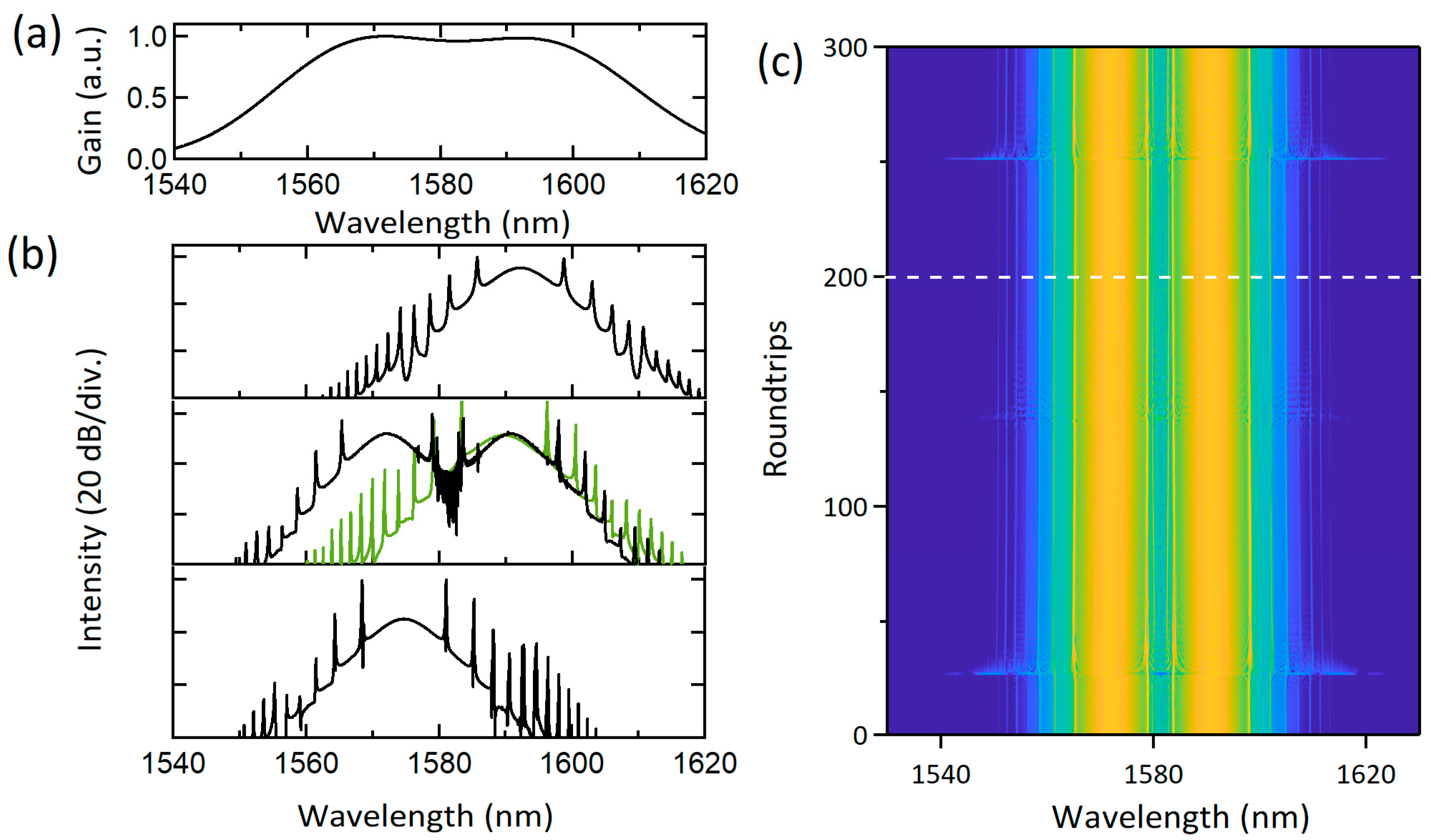
2.3. Impact of Polarization Configurations and the Initial States
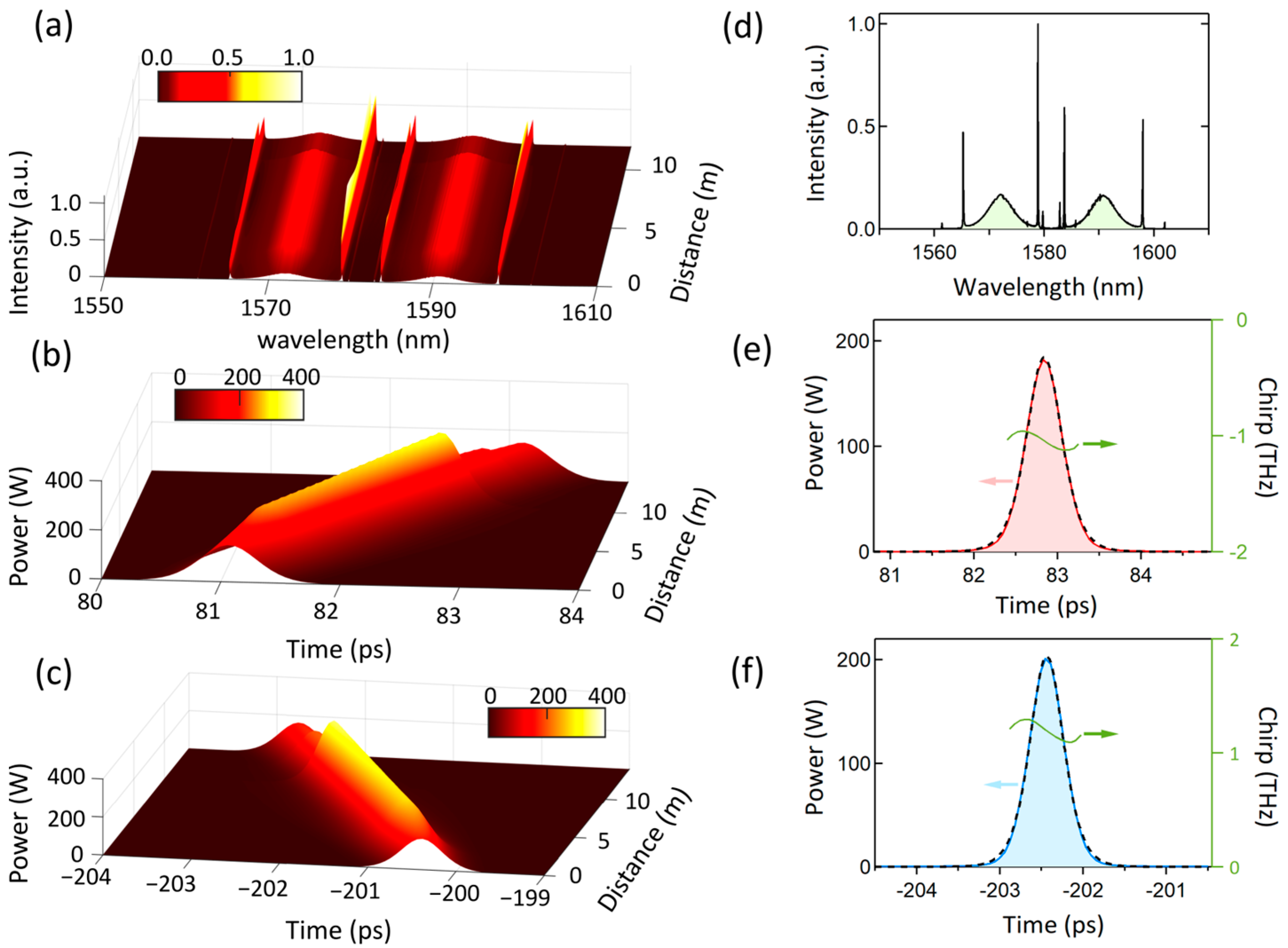
2.4. Pulse Evolution Dynamics of the Mode-Locked Dual-Wavelength Solution
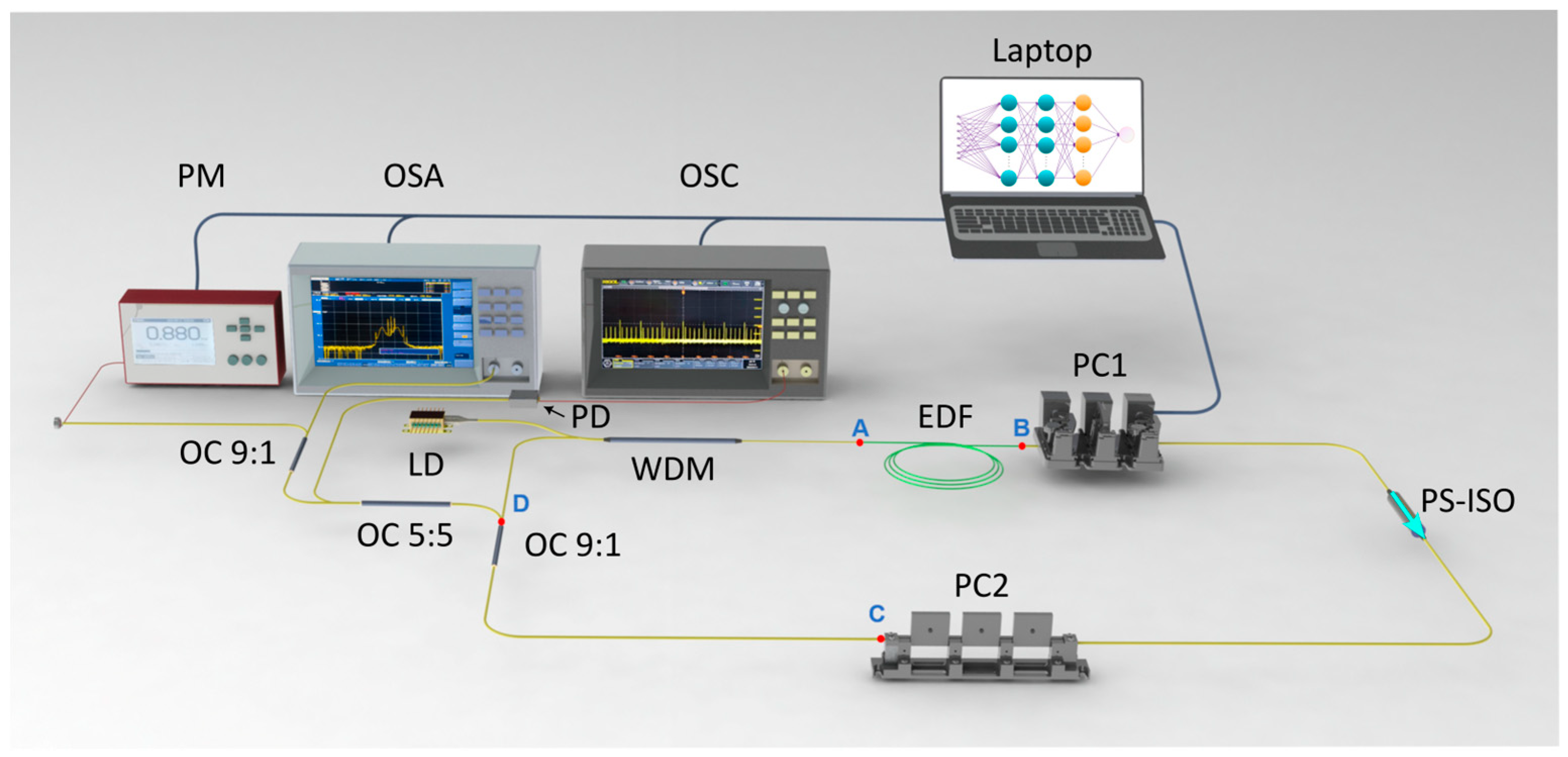
3. Experimental Realization of Automatic Dual-Wavelength Mode-Locking
3.1. Linear Scan of the Wave Plate Angles
3.2. Automatic Mode-Locked Dual-Wavelength Operation
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Coddington, I.; Newbury, N.; Swann, W. Dual-comb spectroscopy. Optica 2016, 3, 414–426. [Google Scholar] [CrossRef]
- Liao, R.; Song, Y.; Liu, W.; Shi, H.; Chai, L.; Hu, M. Dual-comb spectroscopy with a single free-running thulium-doped fiber laser. Opt. Express 2018, 26, 11046–11054. [Google Scholar] [CrossRef]
- Fellinger, J.; Mayer, A.S.; Winkler, G.; Grosinger, W.; Truong, G.-W.; Droste, S.; Li, C.; Heyl, C.M.; Hartl, I.; Heckl, O.H. Tunable dual-comb from an all-polarization-maintaining single-cavity dual-color Yb:fiber laser. Opt. Express 2019, 27, 28062–28074. [Google Scholar] [CrossRef]
- Grelu, P.; Akhmediev, N. Dissipative solitons for mode-locked lasers. Nat. Photonics 2012, 6, 84–92. [Google Scholar] [CrossRef]
- Wei, Y.; Li, B.; Wei, X.; Yu, Y.; Wong, K.K.Y. Ultrafast spectral dynamics of dual-color-soliton intracavity collision in a mode-locked fiber laser. Appl. Phys. Lett. 2018, 112, 081104. [Google Scholar] [CrossRef]
- Liu, M.; Li, T.-J.; Luo, A.-P.; Xu, W.-C.; Luo, Z.-C. “Periodic” soliton explosions in a dual-wavelength mode-locked Yb-doped fiber laser. Photon. Res. 2020, 8, 246–251. [Google Scholar] [CrossRef]
- Liu, R.; Zou, D.; Niu, S.; Song, Y.; Hu, M. Collision-induced Hopf-type bifurcation reversible transitions in a dual-wavelength femtosecond fiber laser. Opt. Express 2023, 31, 1452–1463. [Google Scholar] [CrossRef]
- Pudo, D.; Chen, L.R.; Giannone, D.; Lin, Z.; Bennion, I. Actively mode-locked tunable dual-wavelength erbium-doped fiber laser. IEEE Photon. Technol. Lett. 2002, 14, 143–145. [Google Scholar] [CrossRef]
- Pan, S.; Lou, C. Stable multiwavelength dispersion-tuned actively mode-locked erbium-doped fiber ring laser using nonlinear polarization rotation. IEEE Photon. Technol. Lett. 2006, 18, 1451–1453. [Google Scholar] [CrossRef]
- Zhang, H.; Tang, D.Y.; Wu, X.; Zhao, L.M. Multi-wavelength dissipative soliton operation of an erbium-doped fiber laser. Opt. Express 2009, 17, 12692–12697. [Google Scholar] [CrossRef] [PubMed]
- Luo, Z.C.; Luo, A.P.; Xu, W.C.; Yin, H.S.; Liu, J.R.; Ye, Q.; Fang, Z.J. Tunable Mulitwavelength Passively Mode-locked Fiber Ring Laser Using Intracavity Birefringence-Induced Comb Filter. IEEE Photon. J. 2020, 2, 571–577. [Google Scholar] [CrossRef]
- Luo, X.; Tuan, T.H.; Saini, T.S.; Nguyen, H.P.T.; Suzuki, T.; Ohishi, Y. Tunable and switchable all-fiber dual-wavelength mode locked laser based on Lyot filtering effect. Opt. Express 2019, 27, 14635–14647. [Google Scholar] [CrossRef] [PubMed]
- Guo, Z.; Liu, T.; Peng, J.; Zhu, Y.; Huang, K.; Zeng, H. Self-Started Dual-Wavelength Mode-Locking with Well-Controlled Repetition Rate Difference. J. Light. Technol. 2021, 39, 3575–3581. [Google Scholar] [CrossRef]
- Sharbirin, A.S.; Samion, M.Z.; Ismail, M.F.; Ahmad, H. Ultrafast mode-locked dual-wavelength thulium-doped fiber laser using a Mach-Zehnder interferometric filter. Opto Electron. Rev. 2018, 26, 312–316. [Google Scholar] [CrossRef]
- Latiff, A.A.; Kadir, N.A.; Ismail, E.I.; Shamsuddin, H.; Ahmad, H.; Harun, S.W. All-fiber dual-wavelength Q-switched and mode-locked EDFL by SMF-THDF-SMF structure as a saturable absorber. Opt. Commun. 2017, 389, 29–34. [Google Scholar] [CrossRef]
- Li, R.; Shi, H.; Tian, H.; Li, Y.; Liu, B.; Song, Y.; Hu, M. All-polarization-maintaining dual-wavelength mode-locked fiber laser based on Sagnac loop filter. Opt. Express 2018, 26, 28302–28311. [Google Scholar] [CrossRef] [PubMed]
- Mao, D.; Lu, H. Formation and evolution of passively mode-locked fiber soliton lasers operating in a dual-wavelength regime. J. Opt. Soc. Am. B 2012, 29, 2819–2826. [Google Scholar] [CrossRef]
- Jin, X.; Zhang, M.; Hu, G.; Wu, Q.; Zheng, Z.; Hasan, T. Broad bandwidth dual-wavelength fiber laser simultaneously delivering stretched pulse and dissipative soliton. Opt. Express 2020, 28, 6937–6944. [Google Scholar] [CrossRef]
- Meng, F.; Dudley, J.M. Toward a self-driving ultrafast fiber laser. Light Sci. Appl. 2020, 9, 26. [Google Scholar] [CrossRef]
- Jiang, M.; Wu, H.; An, Y.; Hou, T.; Chang, Q.; Huang, L.; Li, J.; Su, R.; Zhou, P. Fiber laser development enabled by machine learning: Review and prospect. PhotoniX 2022, 3, 16. [Google Scholar] [CrossRef]
- Genty, G.; Salmela, L.; Dudley, J.M.; Brunner, D.; Kokhanovskiy, A.; Kobtsev, S.; Turitsyn, S.K. Machine learning and applications in ultrafast photonics. Nat. Photonics 2021, 15, 91–101. [Google Scholar] [CrossRef]
- Freire, P.; Manuylovich, E.; Prilepsky, J.E.; Turitsyn, S.K. Artificial neural networks for photonic applications—From algorithms to implementation: Tutorial. Adv. Opt. Photonics 2023, 15, 739–834. [Google Scholar] [CrossRef]
- Närhi, M.; Salmela, L.; Toivonen, J.; Billet, C.; Dudley, J.M.; Genty, G. Machine learning analysis of extreme events in optical fibre modulation instability. Nat. Commun. 2018, 9, 4923. [Google Scholar] [CrossRef] [PubMed]
- Mabed, M.; Meng, F.; Salmela, L.; Finot, C.; Genty, G.; Dudley, J.M. Machine learning analysis of instabilities in noise-like pulse lasers. Opt. Express 2022, 30, 15060–15072. [Google Scholar] [CrossRef] [PubMed]
- Zahavy, T.; Dikopoltsev, A.; Moss, D.; Haham, G.I.; Cohen, O.; Mannor, S.; Segev, M. Deep learning reconstruction of ultrashort pulses. Optica 2018, 5, 666–673. [Google Scholar] [CrossRef]
- Valensise, C.M.; Giuseppi, A.; Cerullo, G.; Polli, D. Deep reinforcement learning control of white-light continuum generation. Optica 2021, 8, 239–242. [Google Scholar] [CrossRef]
- Salmela, L.; Tsipinakis, N.; Foi, A.; Billet, C.; Dudley, J.M.; Genty, G. Predicting ultrafast nonlinear dynamics in fibre optics with a recurrent neural network. Nat. Mach. Intell. 2021, 3, 344–354. [Google Scholar] [CrossRef]
- Pu, G.; Zhang, L.; Hu, W.; Yi, L. Automatic mode-locking fiber lasers: Progress and perspectives. Sci. China Inf. Sci. 2020, 63, 160404. [Google Scholar] [CrossRef]
- Andral, U.; Si Fodil, R.; Amrani, F.; Billard, F.; Hertz, E.; Grelu, P. Fiber laser mode locked through an evolutionary algorithm. Optica 2015, 2, 275–278. [Google Scholar] [CrossRef]
- Woodward, R.I.; Kelleher, E.J.R. Towards ‘smart lasers’: Self-optimisation of an ultrafast pulse source using a genetic algorithm. Sci. Rep. 2016, 6, 37616. [Google Scholar] [CrossRef]
- Girardot, J.; Billard, F.; Coillet, A.; Hertz, É.; Grelu, P. Autosetting Mode-Locked Laser Using an Evolutionary Algorithm and Time-Stretch Spectral Characterization. IEEE J. Sel. Top. Quantum Electron. 2020, 26, 1100108. [Google Scholar] [CrossRef]
- Pu, G.; Yi, L.; Zhang, L.; Hu, W. Intelligent programmable mode-locked fiber laser with a human-like algorithm. Optica 2019, 6, 362–369. [Google Scholar] [CrossRef]
- Yan, Q.; Deng, Q.; Zhang, J.; Zhu, Y.; Yin, K.; Li, T.; Wu, D.; Jiang, T. Low-latency deep-reinforcement learning algorithm for ultrafast fiber lasers. Photonics Res. 2021, 9, 1493–1501. [Google Scholar] [CrossRef]
- Li, Z.; Yang, S.; Xiao, Q.; Zhang, T.; Li, Y.; Han, L.; Liu, D.; Ouyang, X.; Zhu, J. Deep reinforcement with spectrum series learning control for a mode-locked fiber laser. Photonics Res. 2022, 10, 1491–1500. [Google Scholar] [CrossRef]
- Girardot, J.; Coillet, A.; Nafa, M.; Billard, F.; Hertz, E.; Grelu, P. On-demand generation of soliton molecules through evolutionary algorithm optimization. Opt. Lett. 2022, 47, 134–137. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Peng, J.; Boscolo, S.; Zhang, Y.; Finot, C.; Zeng, H. Intelligent Breathing Soliton Generation in Ultrafast Fiber Lasers. Laser Photonics Rev. 2022, 16, 2100191. [Google Scholar] [CrossRef]
- Lapre, C.; Meng, F.; Hary, M.; Finot, C.; Genty, G.; Dudley, J.M. Genetic algorithm optimization of broadband operation in a noise-like pulse fiber laser. Sci. Rep. 2023, 13, 1865. [Google Scholar] [CrossRef]
- Pu, G.; Liu, R.; Luo, C.; Song, Y.; Mu, H.; Hu, W.; Hu, M.; Yi, L. Intelligent Single-Cavity Dual-Comb Source with Fast Locking. J. Light. Technol. 2023, 41, 593–598. [Google Scholar] [CrossRef]
- Zhang, Z.X.; Xu, Z.W.; Zhang, L. Tunable and switchable dual-wavelength dissipative soliton generation in an all-normal-dispersion Yb-doped fiber laser with birefringence fiber filter. Opt. Express 2012, 20, 26736–26742. [Google Scholar] [CrossRef]
- Özgören, K.; Ilday, F.Ö. All-fiber all-normal dispersion laser with a fiber-based Lyot filter. Opt. Lett. 2010, 35, 1296–1298. [Google Scholar] [CrossRef]
- Komarov, A.; Leblond, H.; Sanchez, F. Multistability and hysteresis phenomena in passively mode-locked fiber lasers. Phys. Rev. A 2005, 71, 053809. [Google Scholar] [CrossRef]
- Salhi, M.; Leblond, H.; Sanchez, F.; Brunel, M.; Hideur, A. Stability calculations for the ytterbium-doped fibre laser passively mode-locked through nonlinear polarization rotation. J. Opt. A 2004, 6, 774. [Google Scholar] [CrossRef]
- Tang, D.Y.; Zhao, L.M.; Zhao, B.; Liu, A.Q. Mechanism of multisoliton formation and soliton energy quantization in passively mode-locked fiber lasers. Phys. Rev. A 2005, 72, 043816. [Google Scholar] [CrossRef]
- Meng, F.; Lapre, C.; Billet, C.; Sylvestre, T.; Merolla, J.-M.; Finot, C.; Turitsyn, S.K.; Genty, G.; Dudley, J.M. Intracavity incoherent supercontinuum dynamics and rogue waves in a broadband dissipative soliton laser. Nat. Commun. 2021, 12, 5567. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.; Meng, F.; Yan, Q.; Zhang, C.; Jia, Z.; Qin, W.; Qin, G.; Xu, H. Significant enhancement of multiple resonant sidebands in a soliton fiber laser. Photonics Res. 2023, 11, 1847–1860. [Google Scholar] [CrossRef]
- Ulrich, R.; Rashleigh, S.C.; Eickhoff, W. Bending-induced birefringence in single-mode fibers. Opt. Lett. 1980, 5, 273–275. [Google Scholar] [CrossRef]
- Huttner, B.; Reecht, J.; Gisin, N.; Passy, R.; Von der Weid, J.P. Local birefringence measurements in single-mode fibers with coherent optical frequency-domain reflectometry. IEEE Photon. Technol. Lett. 1998, 10, 1458–1460. [Google Scholar] [CrossRef]
- Sergeyev, S.V. Fast and slowly evolving vector solitons in mode-locked fibre lasers. Philos. Trans. Royal Soc. A 2014, 372, 20140006. [Google Scholar] [CrossRef]
- Man, W.S.; Tam, H.Y.; Demokan, M.S.; Wai, P.K.A.; Tang, D.Y. Mechanism of intrinsic wavelength tuning and sideband asymmetry in a passively mode-locked soliton fiber ring laser. J. Opt. Soc. Am. B 2000, 17, 28–33. [Google Scholar] [CrossRef]
- Menyuk, C. Nonlinear pulse propagation in birefringent optical fibers. IEEE J. Quantum Electron. 1987, 23, 174–176. [Google Scholar] [CrossRef]
- Byun, H.; Pudo, D.; Chen, J.; Ippen, E.P.; Kärtner, F.X. High-repetition-rate, 491 MHz, femtosecond fiber laser with low timing jitter. Opt. Lett. 2008, 33, 2221–2223. [Google Scholar] [CrossRef] [PubMed]
- Sergeyev, S.V.; Mou, C.; Rozhin, A.; Turitsyn, S.K. Vector solitons with locked and precessing states of polarization. Opt. Express 2012, 20, 27434–27440. [Google Scholar] [CrossRef] [PubMed]
- Du, W.; Xia, H.; Li, H.; Liu, C.; Wang, P.; Liu, Y. High-repetition-rate all-fiber femtosecond laser with an optical integrated component. Appl. Opt. 2017, 56, 2504–2509. [Google Scholar] [CrossRef] [PubMed]
- Gordon, J.P. Dispersive perturbations of solitons of the nonlinear Schrödinger equation. J. Opt. Soc. Am. B 1992, 9, 91–97. [Google Scholar] [CrossRef]
- Mitchell, M. An Introduction to Genetic Algorithms; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, Q.; Tian, Y.; Zhang, T.; Lv, C.; Meng, F.; Jia, Z.; Qin, W.; Qin, G. Machine Learning Based Automatic Mode-Locking of a Dual-Wavelength Soliton Fiber Laser. Photonics 2024, 11, 47. https://doi.org/10.3390/photonics11010047
Yan Q, Tian Y, Zhang T, Lv C, Meng F, Jia Z, Qin W, Qin G. Machine Learning Based Automatic Mode-Locking of a Dual-Wavelength Soliton Fiber Laser. Photonics. 2024; 11(1):47. https://doi.org/10.3390/photonics11010047
Chicago/Turabian StyleYan, Qi, Yiwei Tian, Tianqi Zhang, Changjian Lv, Fanchao Meng, Zhixu Jia, Weiping Qin, and Guanshi Qin. 2024. "Machine Learning Based Automatic Mode-Locking of a Dual-Wavelength Soliton Fiber Laser" Photonics 11, no. 1: 47. https://doi.org/10.3390/photonics11010047
APA StyleYan, Q., Tian, Y., Zhang, T., Lv, C., Meng, F., Jia, Z., Qin, W., & Qin, G. (2024). Machine Learning Based Automatic Mode-Locking of a Dual-Wavelength Soliton Fiber Laser. Photonics, 11(1), 47. https://doi.org/10.3390/photonics11010047




