Lightning Location Method Using Orthogonal Coded Polarization Optical Time-Domain Reflectometer in Optical Fiber Transmission
Abstract
:1. Introduction
2. Theory and Analysis
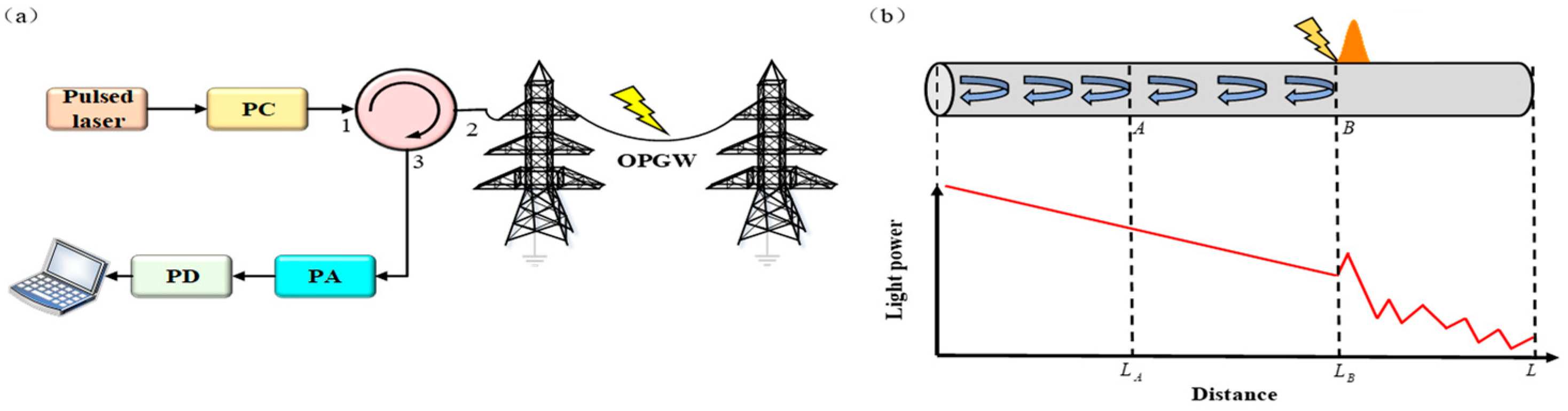
2.1. Principle of POTDR
2.2. Errors in POTDR Lightning Location
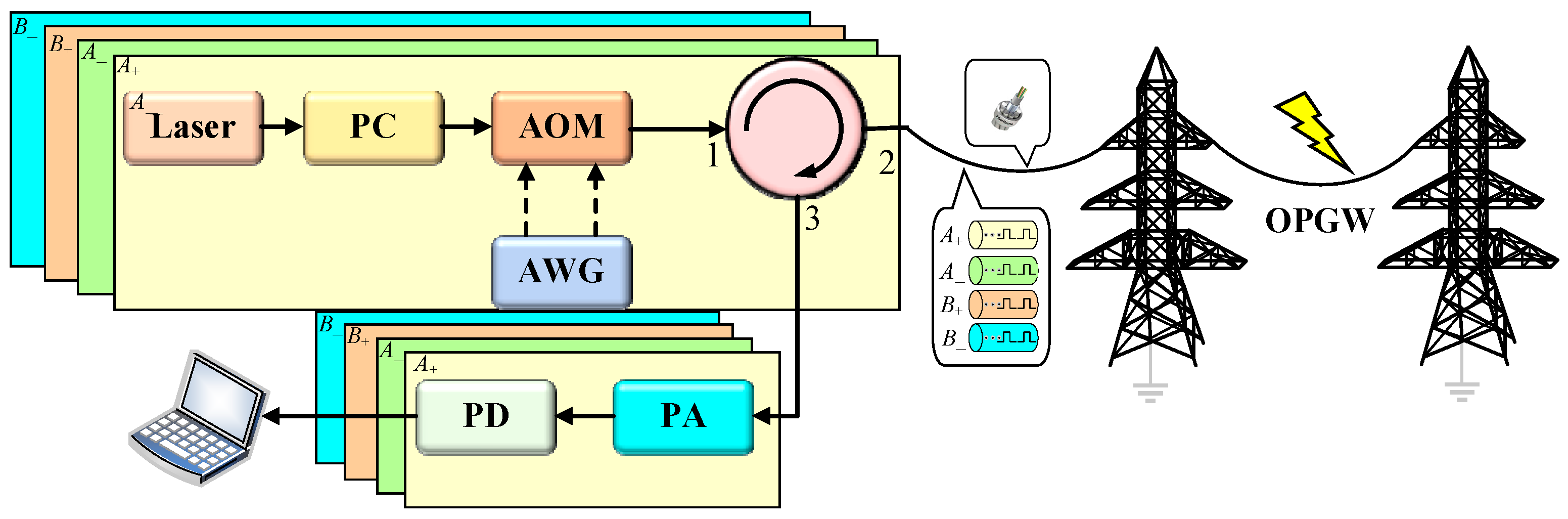
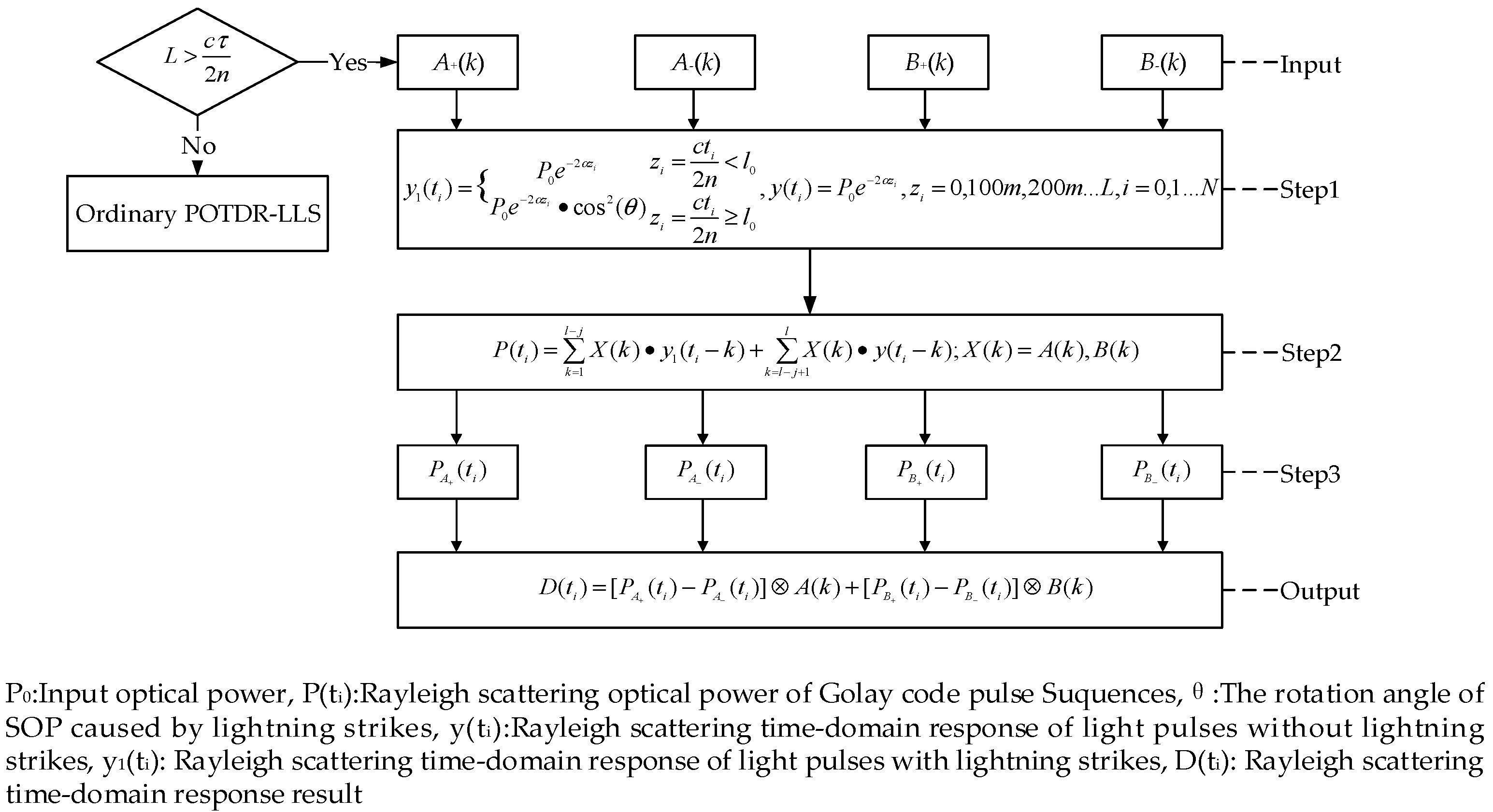
2.3. The Principle of Orthogonal Coded POTDR for Lightning Location
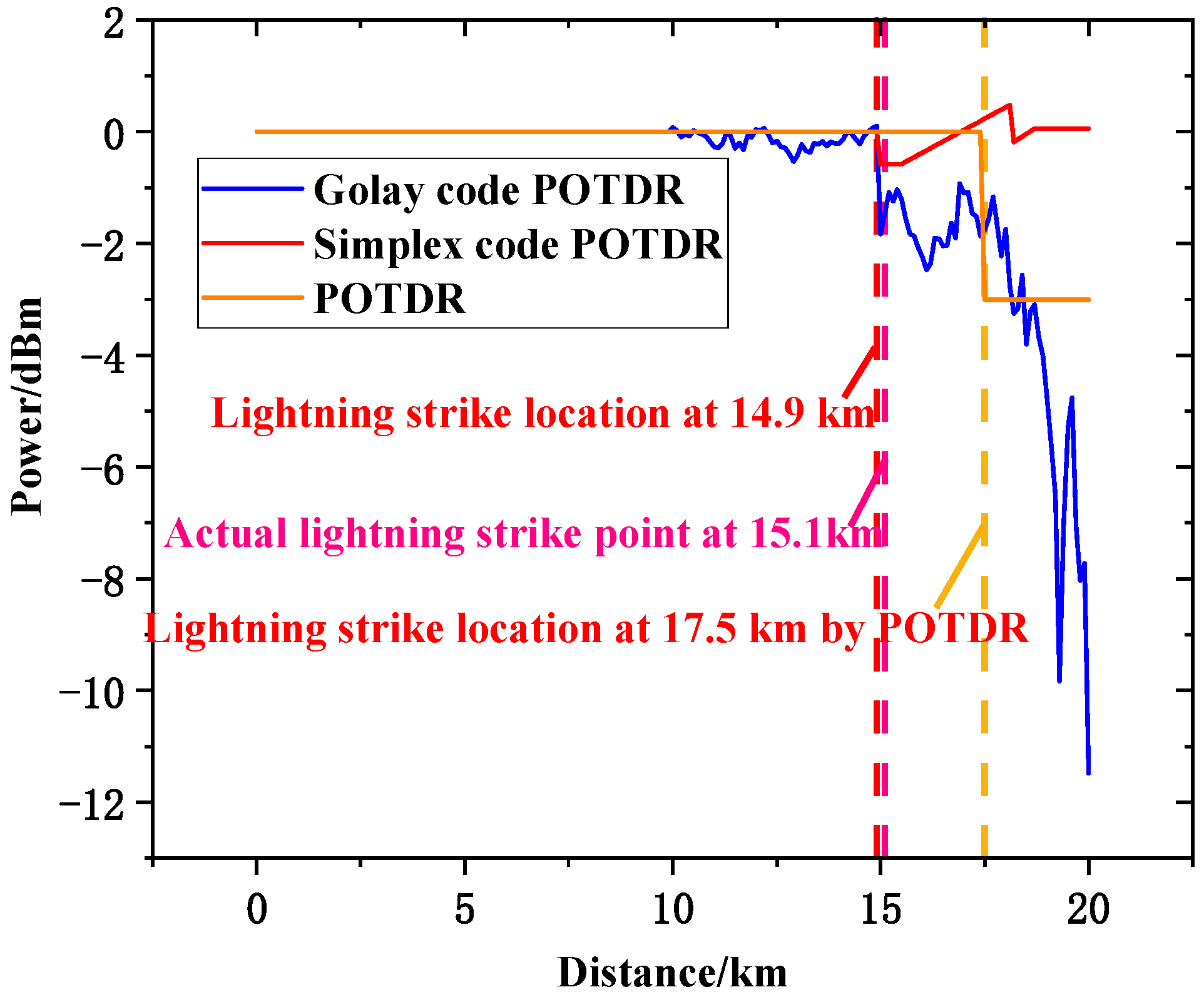
3. Simulation Results and Discussion
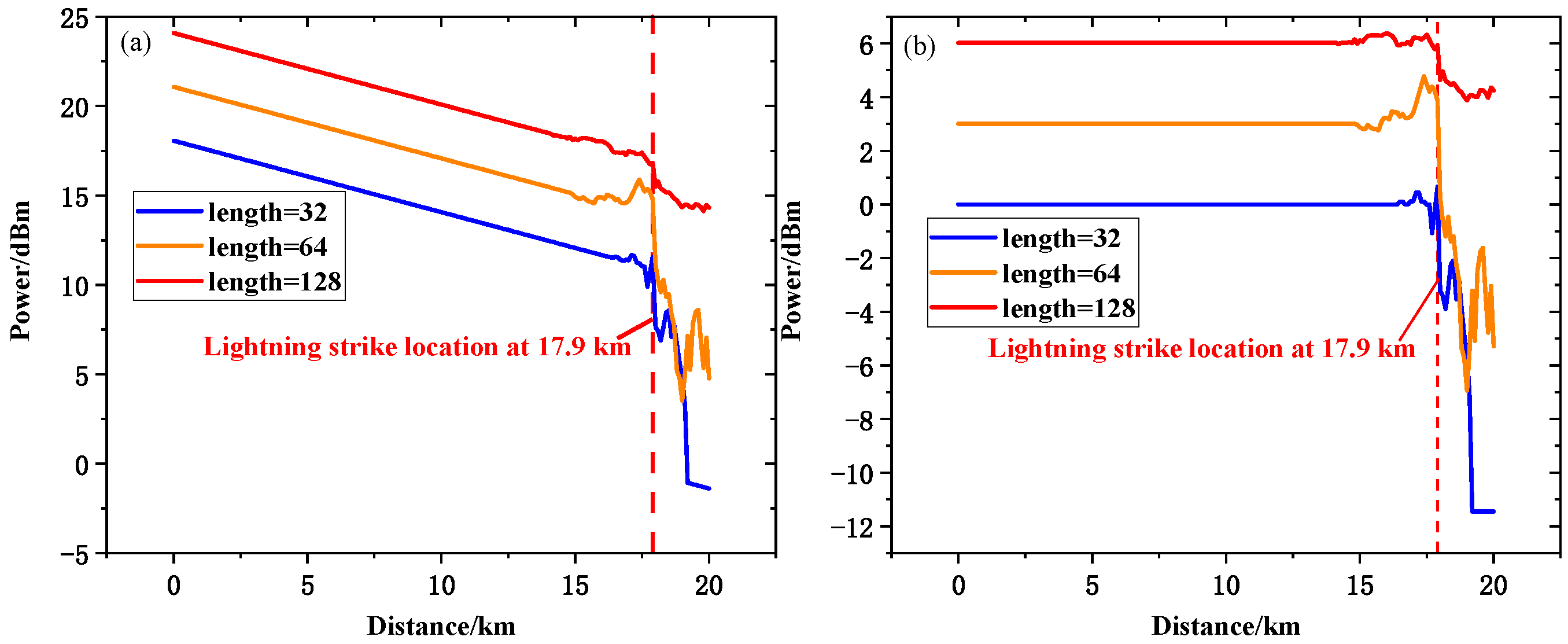
3.1. Simulation of POTDR Lightning Location System Based on Golay Code
3.2. Comparison of Location Accuracy of Different POTDR Lightning Location Schemes
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Krider, E.; Noggle, R.; Gated, M.A.U.A. Wideband Magnetic Direction Finder for Lightning Return Strokes. J. Appl. Meteorol. Clim. 1976, 15, 301–306. [Google Scholar] [CrossRef]
- Rison, W.; Thomas, R.; Krehbiel, P.; Hamlin, T.; Harlin, J. A GPS-based three-dimensional lightning mapping system: Initial observations in central New Mexico. Geophys. Res. Lett. 1999, 26, 3573–3576. [Google Scholar] [CrossRef]
- Chanda, D.; Kishore, N.K.; Sinha, A.K. A wavelet multiresolution-based analysis for location of the point of strike of a lightning overvoltage on a transmission line. Power Deliv. IEEE Trans. Power Deliv. 2004, 19, 1727–1733. [Google Scholar] [CrossRef]
- Hunt, G. Lightning Location System Detections as Evidence: A Unique Bayesian Framework. IEEE Trans. Geosci. Remote Sens. 2021, 59, 1848–1858. [Google Scholar] [CrossRef]
- Qin, Z.; Cheng, Z.; Zhang, Z.; Zhu, J.; Li, F. New method for lightning location using optical ground wire. Chin. Opt. Lett. 2006, 4, 712–714. [Google Scholar]
- Deng, H.; Zhang, R.; Chen, J.; Zhang, H.; Guo, L. Research on Principles and Methods of Lightning Strike Location Based on OPGW Light Polarization State. Insul. Surge Arresters 2018, 2018, 148–153. [Google Scholar]
- Lu, L.; Liang, Y.; Li, B.; Guo, J.; Zhao, H.; Zhang, X. Location of lightning stroke on OPGW by use of distributed optical fiber sensor. In Proceedings of the 2014 International Symposium on Optoelectronic Technology and Application, Beijing, China, 13–15 May 2014; p. 92972I-92972I-6. [Google Scholar]
- Ji, Y.; Shao, J.; Li, S.; Zhou, Q. Study on Distributed OPGW Lightning Strike Location Monitoring System Based on BOTDR. In Proceedings of the 2022 Asia Communications and Photonics Conference (ACP), Shenzhen, China, 5–8 November 2022; pp. 1978–1980. [Google Scholar]
- Lu, L.; Liang, Y.; Li, B.; Guo, J.; Zhao, H.; Zhang, X. Experimental study on location of lightning stroke on OPGW by means of a distributed optical fiber temperature sensor. Opt. Laser Technol. 2015, 65, 79–82. [Google Scholar] [CrossRef]
- Kim, B.; Park, D.; Choi, S. Use of polarization-optical time domain reflectometry for observation of the Faraday effect in single-mode fibers. IEEE J. Quantum Electron. 1982, 18, 455–456. [Google Scholar]
- Rogers, A.J. Polarization-optical time domain reflectometry: A technique for the measurement of field distributions. Appl. Opt. 1981, 20, 1060–1074. [Google Scholar] [CrossRef]
- Ellison, J.G.; Siddiqui, A.S. A fully polarimetric optical time-domain reflectometer. IEEE Photon. Technol. Lett. 1998, 10, 246–248. [Google Scholar] [CrossRef]
- Wulipart, M.; Megret, P.; Blondel, M.; Rogers, A.J.; Defosse, Y. Measurement of the spatial distribution of birefringence in optical fibers. IEEE Photon. Technol.Lett. 2001, 13, 836–838. [Google Scholar] [CrossRef]
- Huang, Z.; Yuan, Y. POTDR based Power Communication Optical Cable Anti External Force Damage Monitoring System. J. Phys. Conf. Ser. 2021, 2005, 012219. [Google Scholar] [CrossRef]
- Charlton, D.; Clarke, S.; Doucet, D.; O’Sullivan, M.; Peterson, D.; Qilson, D.; Wellbrock, G.; Belanger, M. Field measurements of SOP transients in OPGW, with time and location correlation to lightning strikes. Opt. Express 2017, 25, 9689–9696. [Google Scholar] [CrossRef]
- Wang, X.; Hu, J.; Wang, F.; Yong, Y.; Zhang, Y.; Xue, M.; Zhang, X.; Pan, S. Multi-vibration detection by probe pulses with ergodic SOPs in a POTDR system. Opt. Express 2018, 26, 28349–28362. [Google Scholar] [CrossRef]
- van Deventer, M.O. Fundamentals of Bidirectional Transmission over a Single Optical Fiber. Ph.D. Thesis, Technische Universiteit Eindhoven, Eindhoven, The Netherlands, 1994. [Google Scholar]
- Nazarathy, M.; Newton, S.A.; Giffard, R.P.; Moberly, D.S.; Sischka, F.; Trutna, W.R.; Foster, S. Real-Time Long Range Complementary Correlation Optical Time Domain Reflectometer. J. Light. Technol. 1989, 7, 24–38. [Google Scholar] [CrossRef]
- Duckey, L.; Hosung, Y.; Kim, N.Y.; Lee, H.; Park, N. Analysis and Experimental Demonstration of Simplex Coding Technique for SNR Enhancement of OTDR. In Proceedings of the Lightwave Technologies in Instrumentation and Measurement Conference, Palisades, NY, USA, 19–20 October 2004; pp. 118–122. [Google Scholar]
- Park, J.; Bolognini, G.; Lee, D.; Kim, P.; Cho, P.; Pasquale, F.; Park, N. Raman-Based Distributed Temperature Sensor with Simplex Coding and Link Optimization. IEEE Photonic Technol. Lett. 2006, 17, 1879–1881. [Google Scholar] [CrossRef]
- Bolognini, G.; Park, J.; Kim, P.; Lee, D.; Pasquale, F.; Park, N. Performance enhancement of Raman-based distributed temperature sensors using Simplex codes. In Proceedings of the Optical Fiber Communication Conference (Optica Publishing Group, 2006), Anaheim, CA, USA, 5–10 March 2006. paper OTuL1. [Google Scholar]
- Bolognini, G.; Park, J.; Chiuchiarelli, A.; Park, N.; Di Pasquale, F. Improved Performance in Raman-Based Distributed Temperature Sensing with Coded OTDR and Discrete Raman Amplification. In Proceedings of the Optical Fiber Sensors. (Optica Publishing Group, 2006), Cancun, Mexico, 23–27 October 2006. paper ThE45. [Google Scholar]
- Soto, M.A.; Sahu, P.K.; Bolognini, G.; Di Pasquale, F. Brillouin-Based Distributed Temperature Sensor Employing Pulse Coding. IEEE Sens. J. 2008, 8, 225–226. [Google Scholar] [CrossRef]
- Muhammad, S.; Mehmood, H.; Naseem, A.; Abbas, A. Hybrid coding technique for pulse detection in an optical time domain reflectometer. Radio Eng. 2012, 21, 624–663. [Google Scholar]
- Sagues, M.; Piñeiro, E.; Cerri, E.; Minardo, A.; Eyal, A.; Loayssa, A. Two-wavelength phase-sensitive OTDR sensor using perfect periodic correlation codes for measurement range enhancement, noise reduction and fading compensation. Opt. Express 2021, 29, 6021–6035. [Google Scholar] [CrossRef]
- Liao, R.; Tang, M.; Zhao, C.; Wu, H.; Fu, S.; Liu, D.; Shum, P.P. Harnessing oversampling in correlation-coded OTDR. Opt. Express 2019, 27, 1693–1705. [Google Scholar] [CrossRef] [PubMed]
- Tong, F.; Hu, K.; Li, W.; Yu, S.; Lian, W.; Zhao, H.; Wu, B.; Hong, D.; Luo, M.; Hu, Q.; et al. Measurement of optical signal state of polarization in OPGW under lightning strike condition. In Proceedings of the 2024 Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 24–28 March 2024; pp. 1–3. [Google Scholar]
- Zhao, W.; Zhao, J.; Zhang, H.; Gao, J.; Zhang, X. Channel modeling and compensation of ultra-fast spike-shaped RSOP caused by lightning. In Proceedings of the 2021 Asia Communications and Photonics Conference, Shanghai, China, 24–27 October 2021; pp. 1–3. [Google Scholar]
- John, A.; Sadasivan, J.; Seelamantula, C.S. Adaptive Savitzky-Golay Filtering in Non-Gaussian Noise. IEEE Trans. Signal Process. 2021, 69, 5021–5036. [Google Scholar] [CrossRef]
- Zhang, Z.; Bao, X. Distributed optical fiber vibration sensor based on spectrum analysis of Polarization-OTDR system. Opt. Express 2008, 16, 10240–10247. [Google Scholar] [CrossRef] [PubMed]


| Symbol | Meaning | Value |
|---|---|---|
| Optical fiber length | 20 km | |
| Dynamic range | 40 km | |
| Light pulse width | 10 μs | |
| Speed of light in optical fiber | 2 × 108 m/s | |
| Optical signal wavelength | 1550 nm | |
| Golay code length | 32/64/128 | |
| Simplex code length | 127 | |
| Fiber loss | 0.2 dB/km | |
| Rayleigh Backscattering coefficient | 10−7 | |
| rotation of the SOP | 5.1 Mrad/s | |
| Lightning relaxation time | 40 μs | |
| Adjacent codes transmission time interval | 1 μs | |
| 0 | Lightning location | 18.1 km |
| Ar | acquisition rate | 2 Mhz |
| W | laser linewidth | 0.2 nm |
| Wd | detector bandwidth | 20 Mhz |
| Technology | Distance | Location Error | Mismeasurement Rate | Maintenance Cost |
|---|---|---|---|---|
| Orthogonal coded POTDR-LLS | 20 km * | 200 m | low | low |
| GPS-based three-dimensional lightning mapping system [2] | 60 km * | 300 m | high | high |
| Feature extraction of traveling wave signals based on MRA [3] | 100 km * | 1000 m | medium | medium |
| The single ended approach [6] | 50 km * | 166 m | low | high |
| BOTDR-LLS [7] | 0.5 km * | 16 m | high | low |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lian, W.; Su, X.; Li, W.; Wu, B.; Feng, X.; Zhao, H.; Wang, D.; Wu, G.; Liu, L.; Chen, Y.; et al. Lightning Location Method Using Orthogonal Coded Polarization Optical Time-Domain Reflectometer in Optical Fiber Transmission. Photonics 2024, 11, 925. https://doi.org/10.3390/photonics11100925
Lian W, Su X, Li W, Wu B, Feng X, Zhao H, Wang D, Wu G, Liu L, Chen Y, et al. Lightning Location Method Using Orthogonal Coded Polarization Optical Time-Domain Reflectometer in Optical Fiber Transmission. Photonics. 2024; 11(10):925. https://doi.org/10.3390/photonics11100925
Chicago/Turabian StyleLian, Weihua, Xingrui Su, Wei Li, Bin Wu, Xiaofang Feng, Hanqi Zhao, Desong Wang, Guilong Wu, Lin Liu, Yitong Chen, and et al. 2024. "Lightning Location Method Using Orthogonal Coded Polarization Optical Time-Domain Reflectometer in Optical Fiber Transmission" Photonics 11, no. 10: 925. https://doi.org/10.3390/photonics11100925
APA StyleLian, W., Su, X., Li, W., Wu, B., Feng, X., Zhao, H., Wang, D., Wu, G., Liu, L., Chen, Y., & Hu, K. (2024). Lightning Location Method Using Orthogonal Coded Polarization Optical Time-Domain Reflectometer in Optical Fiber Transmission. Photonics, 11(10), 925. https://doi.org/10.3390/photonics11100925





