Analysis on Reducing the Bandwidth of Kelly Sidebands in Mode-Locking Fiber Laser for Narrow Terahertz Signal Generation
Abstract
1. Introduction
2. Model of the Bandwidth of Kelly Sidebands
3. Key Factors Affecting Kelly Sideband Bandwidth
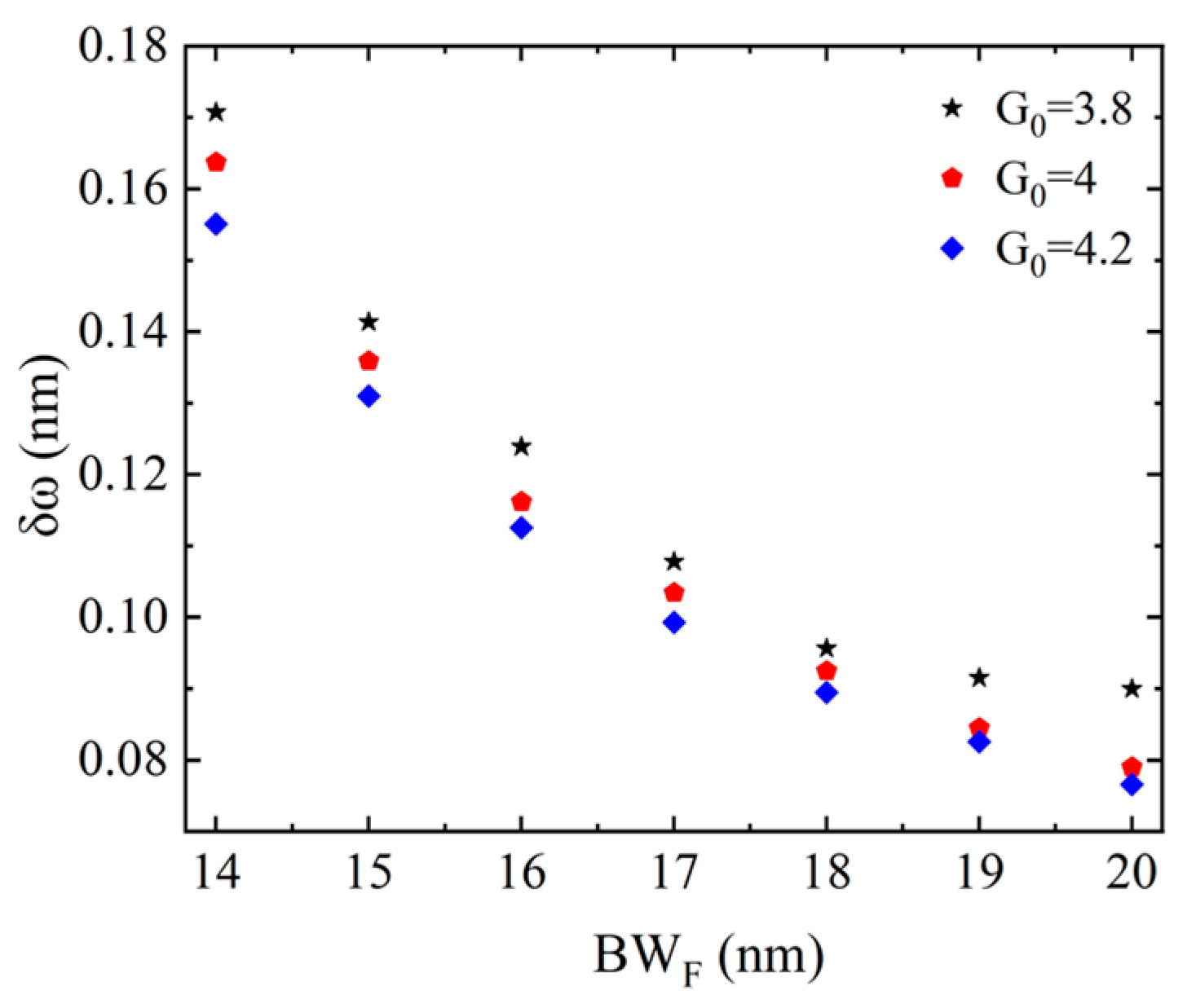
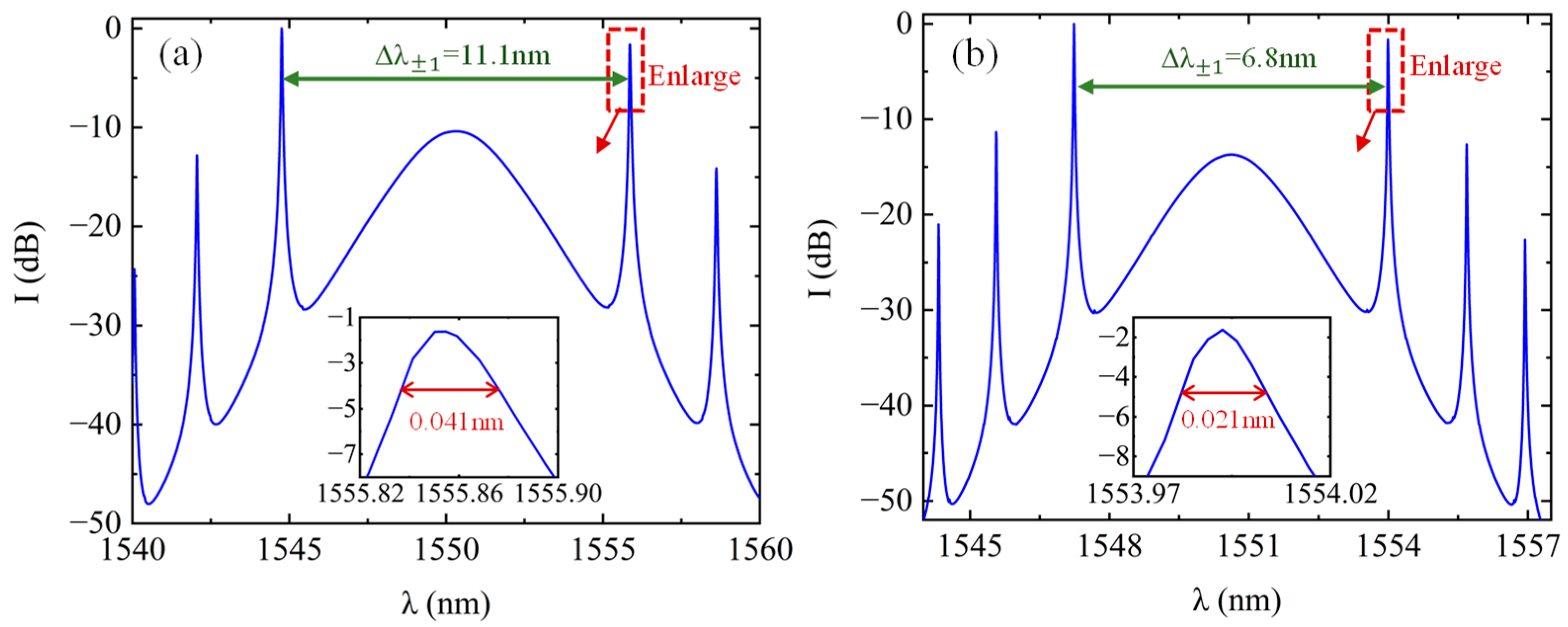
3.1. Influences of Filtering Bandwidth on Bandwidth δω
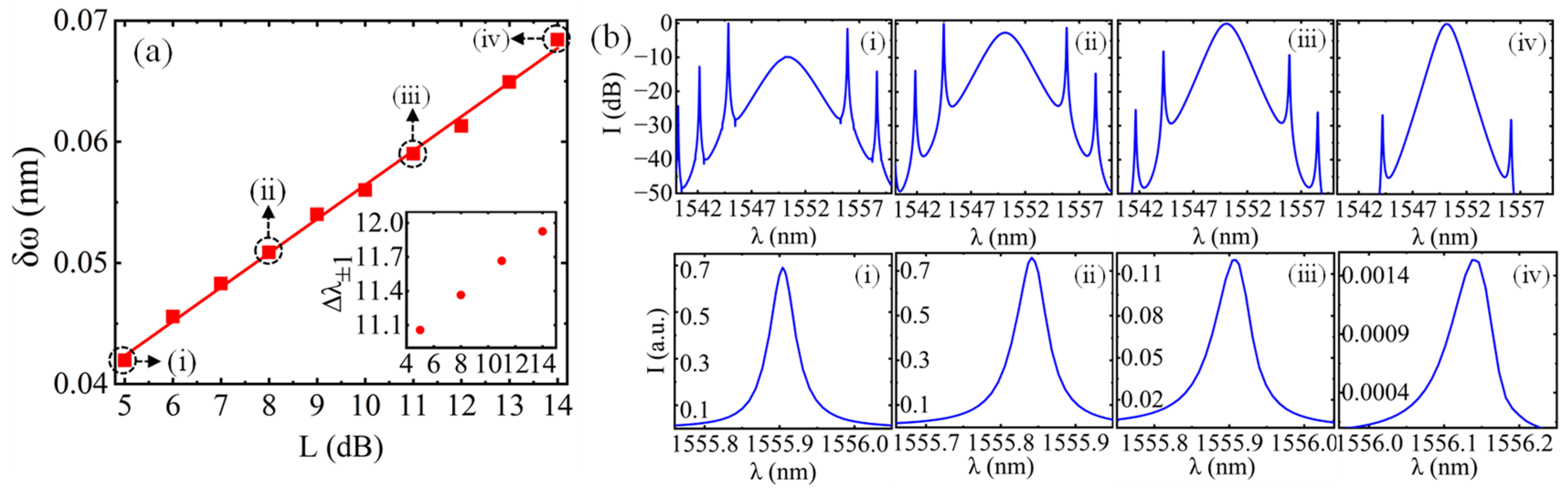
3.2. Influences of Gain Coefficient G0 and Loss L on Bandwidth δω
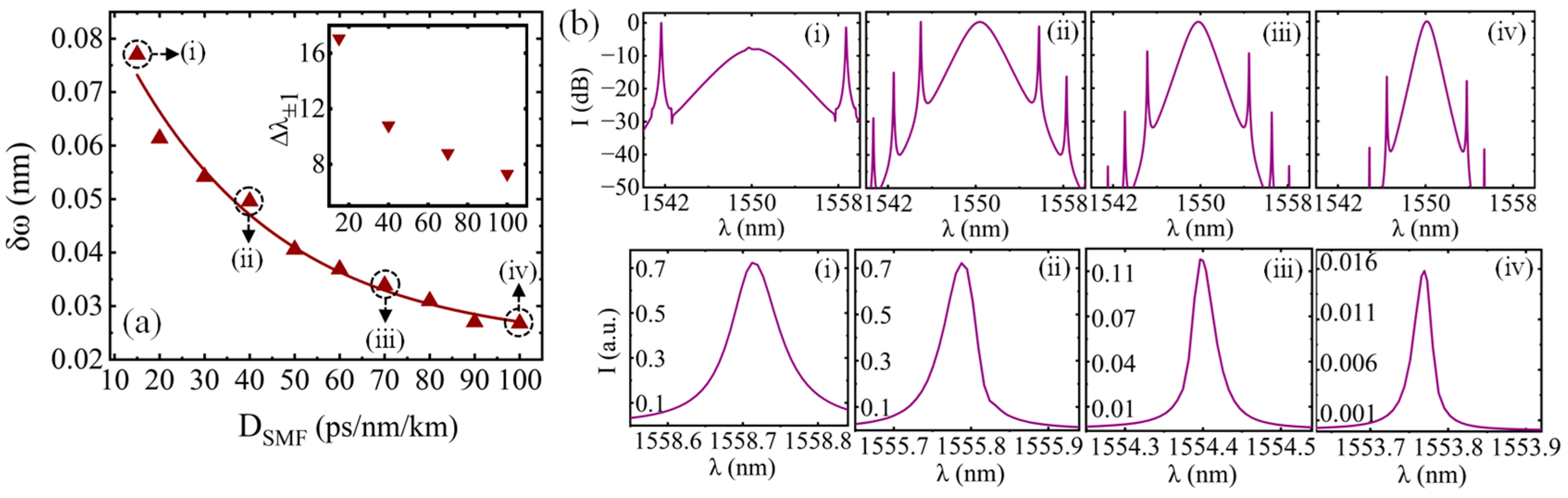
3.3. Influences of Dispersion Parameter on Bandwidth δω
4. Terahertz Signal Generation by Bandwidth-Narrowed Kelly Sidebands
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hebling, J.; Yeh, K.-L.; Hoffmann, M.C.; Nelson, K.A. High-Power THz Generation, THz Nonlinear Optics, and THz Nonlinear Spectroscopy. IEEE J. Sel. Top. Quantum Electron. 2008, 14, 345–353. [Google Scholar] [CrossRef]
- Frühling, U.; Wieland, M.; Gensch, M.; Gebert, T.; Schütte, B.; Krikunova, M.; Kalms, R.; Budzyn, F.; Grimm, O.; Rossbach, J.; et al. Single-shot terahertz-field-driven X-ray streak camera. Nat. Photonics 2009, 3, 523–528. [Google Scholar] [CrossRef]
- Grguraš, I.; Maier, A.R.; Behrens, C.; Mazza, T.; Kelly, T.J.; Radcliffe, P.; Düsterer, S.; Kazansky, A.K.; Kabachnik, N.M.; Tschentscher, T.; et al. Ultrafast X-ray pulse characterization at free-electron lasers. Nat. Photonics 2012, 6, 852–857. [Google Scholar] [CrossRef]
- Pia, S.; Saha, A.; Banerjee, A.; Banerjee, A.; Seteikin, A.Y.; Samusev, I.G. Review on the Evolution of 6G and Terahertz Communication for Highspeed Information Processing. Bull. Russ. Acad. Sci. Phys. 2023, 86, 166–170. [Google Scholar] [CrossRef]
- Zou, F.; Zou, L.; Yang, B.; Ma, Q.; Zou, X.; Zou, J.; Chen, S.; Milosevic, D.; Cao, Z.; Liu, H. Optoelectronic oscillator for 5G wireless networks and beyond. J. Phys. D Appl. Phys. 2021, 54, 423002. [Google Scholar] [CrossRef]
- Pettine, J.; Padmanabhan, P.; Sirica, N.; Prasankumar, R.P.; Taylor, A.J.; Chen, H.-T. Ultrafast terahertz emission from emerging symmetry-broken materials. Light Sci. Appl. 2023, 12, 133. [Google Scholar] [CrossRef] [PubMed]
- Jin, Z.; Guo, Y.; Peng, Y.; Zhang, Z.; Pang, J.; Zhang, Z.; Liu, F.; Ye, B.; Jiang, Y.; Ma, G.; et al. Terahertz Spectral Signatures of Ultrafast Spin Transports in Ferromagnetic Heusler Alloy. Adv. Phys. 2023, 2, 2200049. [Google Scholar] [CrossRef]
- Stigwall, J.; Wiberg, A. Tunable Terahertz Signal Generation by Chirped Pulse Photomixing. IEEE Photonics Technol. Lett. 2007, 19, 931–933. [Google Scholar] [CrossRef]
- Jin, Z.; Peng, Y.; Ni, Y.; Wu, G.; Ji, B.; Wu, X.; Zhang, Z.; Ma, G.; Zhang, C.; Chen, L.; et al. Cascaded Amplification and Manipulation of Terahertz Emission by Flexible Spintronic Heterostructures. Laser Photonics Rev. 2022, 16, 2100688. [Google Scholar] [CrossRef]
- Cai, X.; Xie, T.; Ruan, Q.; Pan, P.; Chen, S.; Luo, J.; Fu, H.; Chen, D.; Gao, S. Continuous-wave THz difference frequency generation based on kHz-linewidth dual-wavelength single-longitudinal-mode Er-doped fiber laser and DAST organic crystal. Opt. Laser Technol. 2022, 150, 107912. [Google Scholar] [CrossRef]
- Tang, M.; Minamide, H.; Wang, Y.; Notake, T.; Ohno, S.; Ito, H. Tunable Terahertz-wave generation from DAST crystal pumped by a monolithic dual-wavelength fiber laser. Opt. Express 2011, 19, 779–786. [Google Scholar] [CrossRef]
- Preußler, S.; Wenzel, N.; Braun, R.-P.; Owschimikow, N.; Vogel, C.; Deninger, A.; Zadok, A.; Woggon, U.; Schneider, T. Generation of ultra-narrow, stable and tunable millimeter- and terahertz-waves with very low phase noise. Opt. Express 2013, 21, 23950–23962. [Google Scholar] [CrossRef] [PubMed]
- Zhao, W.; Shen, M.; Hu, Y.; Wang, Z. Simulation of Terahertz Signal Generation by Dispersion-dependent Kelly Sidebands of Mode-locking Fiber Lasers. Curr. Opt. Photonics 2023, 7, 443–448. Available online: https://opg.optica.org/copp/abstract.cfm?uri=copp-7-4-443 (accessed on 1 November 2024).
- Zhao, W.; Yang, C.; Shen, M. Enhanced Kelly sidebands of mode-locking fiber lasers for efficient terahertz signal generation. Opt. Laser Technol. 2021, 137, 106802. [Google Scholar] [CrossRef]
- Zhao, W.; Yang, C.; Shen, M. A new method for terahertz signal generation using Kelly sidebands of mode-locking fiber laser. Opt. Laser Technol. 2021, 134, 106568. [Google Scholar] [CrossRef]
- Dennis, M.L.; Duling, I.N., III. Intracavity dispersion measurement in mode locked fiber laser. Electron. Lett. 1993, 29, 409–411. [Google Scholar] [CrossRef]
- Zhang, T.; Meng, F.; Yan, Q.; Zhang, C.; Jia, Z.; Qin, W.; Qin, G.; Xu, H. Significant enhancement of multiple resonant sidebands in a soliton fiber laser. Photonics Res. 2023, 11, 1847–1860. [Google Scholar] [CrossRef]
- Smith, N.J.; Blow, K.; Andonovic, I. Sideband generation through perturbations to the average soliton model. J. Light. Technol. 1992, 10, 1329–1333. [Google Scholar] [CrossRef]
- Du, Y.; Shu, X.; Cao, H.; Cheng, P. Dynamics of Dispersive Wave and Regimes of Different Kinds of Sideband Generation in Mode-Locked Soliton Fiber Lasers. IEEE J. Sel. Top. Quantum Electron. 2017, 24, 1101408. [Google Scholar] [CrossRef]
- Weill, R.; Bekker, A.; Smulakovsky, V.; Fischer, B.; Gat, O. Spectral sidebands and multipulse formation in passively mode-locked lasers. Phys. Rev. A At. Mol. Opt. Phys. 2011, 83, 043831. [Google Scholar] [CrossRef]
- Agrawal, G.P. Nonlinear Fiber Optics, 6th ed.; Academic Press: Cambridge, MA, USA, 2019; Chapter 5. [Google Scholar]
- Freude, D. Spectroscopy, 2006; Chapter 2, Page 15. Available online: https://home.uni-leipzig.de/energy/pdf/freuse2.pdf (accessed on 1 November 2024).
- Huang, Q.; Huang, Z.; He, W.; Zhang, X.; Liu, D.; Wang, X.; Leng, Y.; Pang, M. Characterization and Manipulation of Temporal Structures of Dispersive Waves in a Soliton Fiber Laser. J. Light. Technol. 2023, 41, 1545–1551. [Google Scholar] [CrossRef]
- Runge, A.F.J.; Hudson, D.D.; Tam, K.K.K.; de Sterke, C.M.; Blanco-Redondo, A. The pure-quartic soliton laser. Nat. Photonics 2020, 14, 492–497. [Google Scholar] [CrossRef]
- Bacon, D.R.; Madéo, J.; Dani, K.M. Photoconductive emitters for pulsed terahertz generation. J. Phys. D Appl. Phys. 2021, 23, 064001. [Google Scholar] [CrossRef]
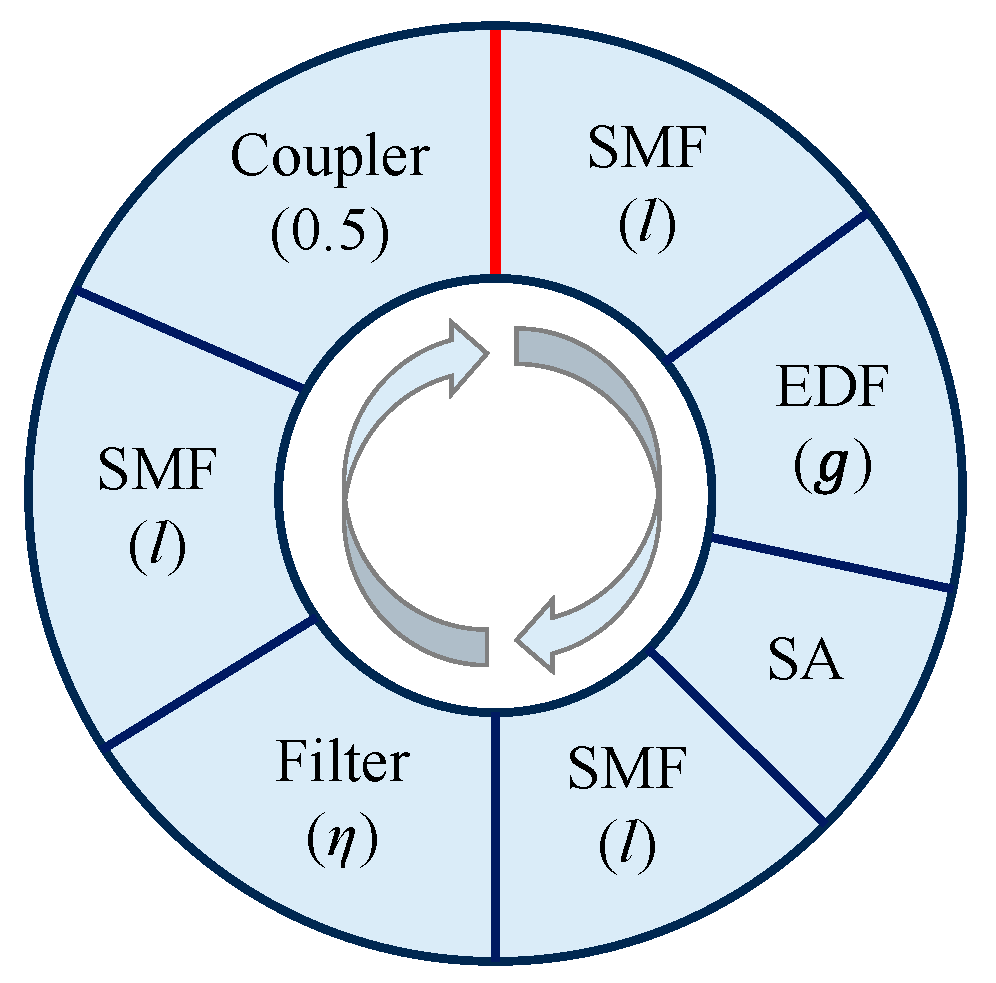



| Parameter | |||
|---|---|---|---|
| X | (a) (m) | (b) [ps/(nm.km)] | G/L (e) |
| SMF | 11 | Related to | |
| EDF | 1.5 | 36 | Related to g |
| Filter | (c) | (d) | |
| 1.0 | Affecting the η value | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, W.; Hu, Y.; Shen, M.; Feng, Q. Analysis on Reducing the Bandwidth of Kelly Sidebands in Mode-Locking Fiber Laser for Narrow Terahertz Signal Generation. Photonics 2024, 11, 1124. https://doi.org/10.3390/photonics11121124
Zhao W, Hu Y, Shen M, Feng Q. Analysis on Reducing the Bandwidth of Kelly Sidebands in Mode-Locking Fiber Laser for Narrow Terahertz Signal Generation. Photonics. 2024; 11(12):1124. https://doi.org/10.3390/photonics11121124
Chicago/Turabian StyleZhao, Weiqian, Youyou Hu, Mingya Shen, and Qiyan Feng. 2024. "Analysis on Reducing the Bandwidth of Kelly Sidebands in Mode-Locking Fiber Laser for Narrow Terahertz Signal Generation" Photonics 11, no. 12: 1124. https://doi.org/10.3390/photonics11121124
APA StyleZhao, W., Hu, Y., Shen, M., & Feng, Q. (2024). Analysis on Reducing the Bandwidth of Kelly Sidebands in Mode-Locking Fiber Laser for Narrow Terahertz Signal Generation. Photonics, 11(12), 1124. https://doi.org/10.3390/photonics11121124





