Automated Characterization of Intrastromal Corneal Cuts Induced by Two Femtosecond Laser Systems Using OCT Imaging
Abstract
1. Introduction
2. Materials and Methods
2.1. Experiment
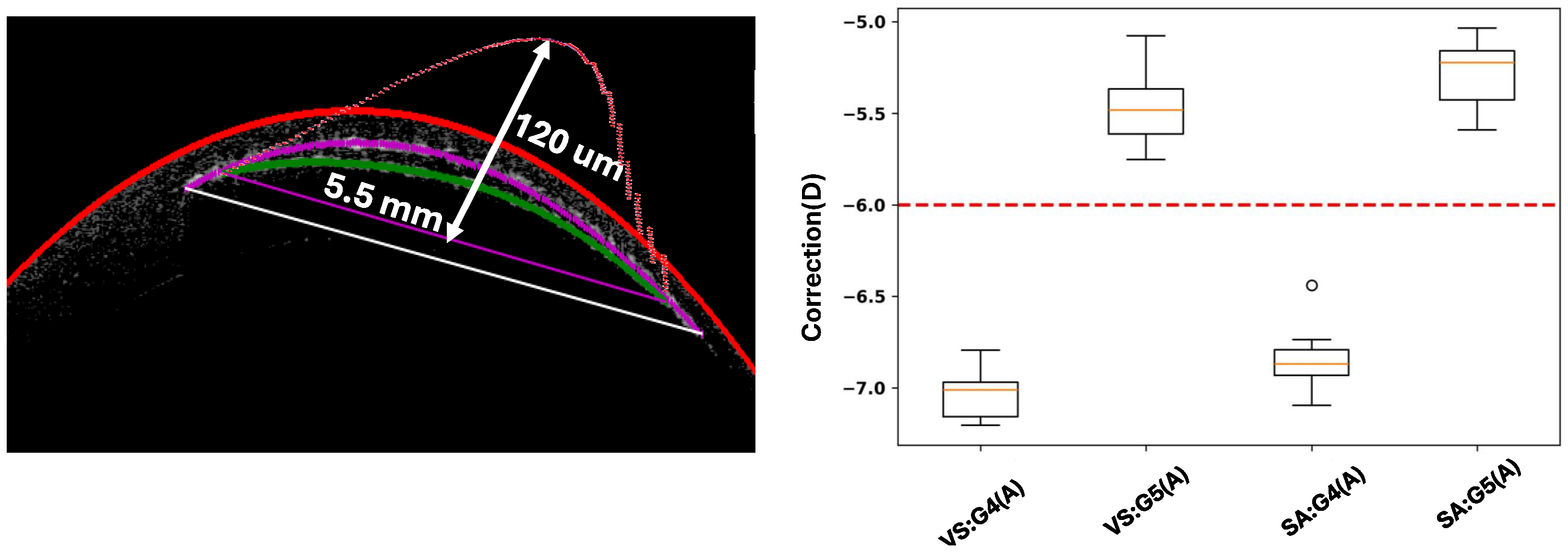
2.2. Image Processing
2.2.1. Bilateral Filtering
2.2.2. Peak Detection
2.2.3. Lenticule Cut Segregation
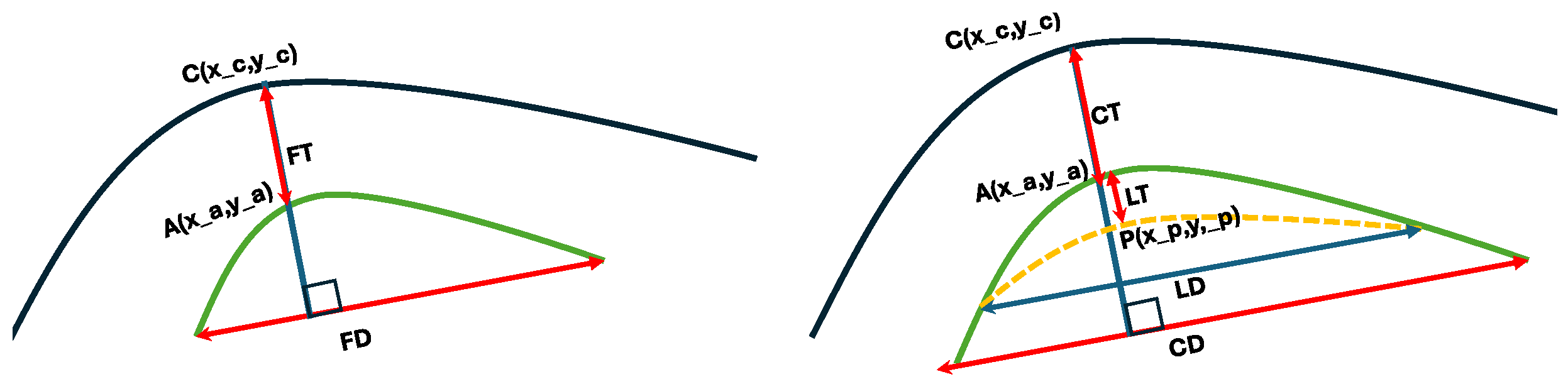
2.2.4. Interlayer Thickness Calculation
- where FT(D), CT(D) and LT(D) stand for flap, lenticule and cap thicknesses (diameters). and specify the cornea, anterior and posterior segments.
- Flap and Cap
- (a)
- Diameter: as straight line from both ends of the effectively segmented substructure (irrespective of whether this is complete or incomplete);
- (b)
- Thickness: as the distance measured along the normal to the straight line from both ends of the effectively segmented substructure (irrespective of whether this is complete or incomplete).
- Lenticule:
- (a)
- Diameter: as straight line from both ends of the effectively segmented substructure (i.e., the cross over or junction between the posterior substructure and the anterior substructure as of the cap);
- (b)
- Thickness: as the distance measured along the normal to the straight line from both ends of the effectively segmented substructure (i.e., the crossover or junction between the posterior substructure and the anterior substructure as of the cap).
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Guidelines and Standards Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| OCT | optical coherent tomography |
| SA | SCHWIND ATOS |
| VS | Zeiss VisuMax 500 |
| CI | confidence interval |
| LD | lenticule diameter |
| FD | flap diameter |
| LT | lenticule thickness |
| CT | cap thickness |
| FT | flap thickness |
References
- Volkan Hurmeric, S.H.Y.; Mutlu, F.M. Optical coherence tomography in cornea and refractive surgery. Expert Rev. Ophthalmol. 2012, 7, 241–250. [Google Scholar] [CrossRef]
- Belin, M.W.; Khachikian, S.S.; McGhee, C.N.J.; Patel, D. New Technology in Corneal Imaging. Int. Ophthalmol. Clin. 2010, 50, 177–189. [Google Scholar] [CrossRef]
- Brass, R. Imaging for the Rest of Us OCT has many uses beyond imaging the macula, including following glaucoma patients and evaluating the anterior segment. Cataract. Refract. Surg. Today Eur. 2011, 79. Available online: http://crstodayeurope.com/wp-content/themes/crste/assets/downloads/crsteuro0511_tp_brass.pdf (accessed on 29 July 2024).
- Ventura, B.V.; Moraes, H.V., Jr.; Kara-Junior, N.; Santhiago, M.R. Role of Optical Coherence Tomography on Corneal Surface Laser Ablation. J. Ophthalmol. 2012, 2012, 676740. [Google Scholar] [CrossRef][Green Version]
- Sridhar, M.S.; Martin, R. Anterior segment optical coherence tomography for evaluation of cornea and ocular surface. Indian J. Ophthalmol. 2018, 66, 367–372. [Google Scholar] [CrossRef] [PubMed]
- Eguchi, H.; Hotta, F.; Kusaka, S.; Shimomura, Y. Intraoperative Optical Coherence Tomography Imaging in Corneal Surgery: A Literature Review and Proposal of Novel Applications. J. Ophthalmol. 2020, 2020, 1497089. [Google Scholar] [CrossRef]
- Marschall, S.; Sander, B.; Mogensen, M.; Jørgensen, T.M.; Andersen, P.E. Optical coherence tomography—Current technology and applications in clinical and biomedical research. Anal. Bioanal. Chem. 2011, 400, 2699–2720. [Google Scholar] [CrossRef]
- Valdes, G.; Romaguera, M.; Serramito, M.; Cerviño, A.; Carracedo, G.G. OCT applications in contact lens fitting. Contact Lens Anterior Eye 2022, 45, 101540. [Google Scholar] [CrossRef]
- Alió, J.; Barrio, J. Atlas of Anterior Segment Optical Coherence Tomography; Essentials in Ophthalmology; Springer International Publishing: Cham, Switzerland, 2020. [Google Scholar]
- Chong, Y.; Azzopardi, M.; Hussain, G.; Recchioni, A.; Gandhewar, J.; Loizou, C.; Giachos, I.; Barua, A.; Ting, D. Clinical Applications of Anterior Segment Optical Coherence Tomography: An Updated Review. Diagnostics 2024, 14, 122. [Google Scholar] [CrossRef]
- Luo, S.; Holland, G.; Mikula, E.; Bradford, S.; Khazaeinezhad, R.; Jester, J.V.; Juhasz, T. Dispersion compensation for spectral domain optical coherence tomography by time-frequency analysis and iterative optimization. Opt. Contin. 2022, 1, 1117–1136. [Google Scholar] [CrossRef]
- Luo, S.; Mikula, E.R.; Khazaeinezhad, R.; Bradford, S.M.; Zhang, F.; Jester, J.V.; Juhasz, T. Evaluating the effect of pulse energy on femtosecond laser trabeculotomy (FLT) drainage channels in human cadaver eyes. Lasers Surg. Med. 2024, 56, 382–391. [Google Scholar] [CrossRef] [PubMed]
- Han, S.B.; Liu, Y.C.; Mohamed-Noriega, K.; Mehta, J.S. Application of Femtosecond Laser in Anterior Segment Surgery. J. Ophthalmol. 2020, 2020, 8263408. [Google Scholar] [CrossRef]
- Steinberg, J.; Mehlan, J.; Mudarisov, B.; Katz, T.; Frings, A.; Druchkiv, V.; Linke, S.J. Safety and Precision of Two Different Flap-morphologies Created During Low Energy Femtosecond Laser-assisted LASIK. J. Ophthalmic Vis. Res. 2023, 18, 3–14. [Google Scholar] [CrossRef]
- Gabric, I.; Bohac, M.; Gabric, K.; Arba Mosquera, S. First European results of a new refractive lenticular extraction procedure—SmartSight by SCHWIND eye-tech-solutions. Eye 2023, 37, 3768–3775. [Google Scholar] [CrossRef]
- Pradhan, K.R.; Arba Mosquera, S. Twelve-month outcomes of a new refractive lenticular extraction procedure. J. Optom. 2023, 16, 30–41. [Google Scholar] [CrossRef]
- Gurnani, B.; Kaur, K. Recent Advances in Refractive Surgery: An Overview. Clin. Ophthalmol. 2024, 18, 2467–2472. [Google Scholar] [CrossRef]
- Zeppieri, M.; Marsili, S.; Enaholo, E.S.; Shuaibu, A.O.; Uwagboe, N.; Salati, C.; Spadea, L.; Musa, M. Optical Coherence Tomography (OCT): A Brief Look at the Uses and Technological Evolution of Ophthalmology. Medicina 2023, 59, 2114. [Google Scholar] [CrossRef]
- Garcia Marin, Y.F.; Alonso-Caneiro, D.; Vincent, S.J.; Collins, M.J. Anterior segment optical coherence tomography (AS-OCT) image analysis methods and applications: A systematic review. Comput. Biol. Med. 2022, 146, 105471. [Google Scholar] [CrossRef]
- Nguyen, T.; Ong, J.; Masalkhi, M.; Waisberg, E.; Zaman, N.; Sarker, P.; Aman, S.; Lin, H.; Luo, M.; Ambrosio, R.; et al. Artificial intelligence in corneal diseases: A narrative review. Contact Lens Anterior Eye 2024, 47, 102284. [Google Scholar] [CrossRef]
- Luo, S.; Holland, G.; Khazaeinezhad, R.; Bradford, S.; Joshi, R.; Juhasz, T. Iridocorneal angle imaging of a human donor eye by spectral-domain optical coherence tomography. Sci. Rep. 2023, 13, 13861. [Google Scholar] [CrossRef]
- Lwowski, C.; Voigt, A.; Van Keer, K.; Kohnen, T. Corneal Lenticule Creation Using a New Solid-State Femtosecond Laser Measured by Spectral Domain OCT in a Porcine Eye Model. Transl. Vis. Sci. Technol. 2022, 11, 20. [Google Scholar] [CrossRef] [PubMed]
- Latz, C.; Asshauer, T.; Rathjen, C.; Mirshahi, A. Femtosecond-Laser Assisted Surgery of the Eye: Overview and Impact of the Low-Energy Concept. Micromachines 2021, 12, 122. [Google Scholar] [CrossRef] [PubMed]
- Heisterkamp, A.; Mamom, T.; Kermani, O.; Drommer, W.; Welling, H.; Ertmer, W.; Lubatschowski, H. Intrastromal refractive surgery with ultrashort laser pulses: In vivo study on the rabbit eye. Graefe’s Arch. Clin. Exp. Ophthalmol. 2003, 241, 511–517. [Google Scholar] [CrossRef] [PubMed]
- Reinstein, D.Z.; Archer, T.J.; Randleman, J.B. Small incision lenticule extraction (SMILE) history, fundamentals of a new refractive surgery technique and clinical outcomes. Eye Vis. 2014, 1, 3. [Google Scholar] [CrossRef]
- Vestergaard, A.H.; Ivarsen, A.; Asp, S.; Hjortdal, J. Femtosecond Lenticule Extraction (FLEx): Clinical Results, Interface Evaluation, and Intraocular Pressure Variation. Investig. Ophthalmol. Vis. Sci. 2017, 53, F327–F332. [Google Scholar] [CrossRef]
- Hjortdal, J.; Ivarsen, A. New Developments in the Lenticule Extraction Procedure. US Ophthalmic Rev. 2014, 7, 20–25. [Google Scholar] [CrossRef]
- Wexler, S.A.; Hall, B. The Accuracy of Flap Thickness and Diameter in LASIK Using a Femtosecond Laser. Clin. Ophthalmol. 2023, 17, 3877–3882. [Google Scholar] [CrossRef]
- Mehrjoo, M.; Pacuraru, A.; Krueger, L.; Beck, F.; Konrad, D. Perioperative Intrastromal Corneal Segmentation after creation of corneal cuts based on Laser Induced Optical Breakdown: A Perspective Study. Manuscript submitted for publication.
- Thorlabs China. GAN111, 2024. Available online: https://www.thorlabs.com/newgrouppage9.cfm?objectgroup_id=8214 (accessed on 29 July 2024).
- Arba Mosquera, S.; Naubereit, P.; Sobutas, S.; Verma, S. Analytical optimization of the cutting efficiency for generic cavitation bubbles. Biomed. Opt. Express 2021, 12, 3819–3835. [Google Scholar] [CrossRef]
- Dishler, J.; Ziebarth, N.M.; Spooner, G.J.R.; Hjortdal, J.; Yoo, S.H. Evaluating Corneal Cut Surface Quality in SMILE. In Small Incision Lenticule Extraction (SMILE): Principles, Techniques, Complication Management, and Future Concepts; Sekundo, W., Ed.; Springer International Publishing: Cham, Switzerland, 2015; pp. 169–177. [Google Scholar] [CrossRef]
- Kristan, J.; Kang, J.J. Neurotrophic keratopathy and refractive surgery. Curr. Opin. Ophthalmol. 2021, 32, 315–318. [Google Scholar] [CrossRef]
- Darzi, S.; Arba Mosquera, S.; Pradhan, K.; Forster, A.; Dick, B.; Taneri, S. Refractive Coupling Effects in Keratorefractive Lenticule Extraction Procedures: A Machine Learning-Assisted Approach. J. Refract. Surg. 2024, 40, e706–e715. [Google Scholar] [CrossRef]
- Tomasi, C.; Manduchi, R. Bilateral filtering for gray and color images. In Proceedings of the Sixth International Conference on Computer Vision (IEEE Cat. No.98CH36271), Bombay, India, 7 January 1998; pp. 839–846. [Google Scholar] [CrossRef]
- Tolimieri, R.; Lu, C.; An, M. Algorithms for Discrete Fourier Transform and Convolution; Springer: Cham, Switzerland, 1997. [Google Scholar]
- Gogola, A.; Jan, N.J.; Lathrop, K.L.; Sigal, I.A. Radial and Circumferential Collagen Fibers Are a Feature of the Peripapillary Sclera of Human, Monkey, Pig, Cow, Goat, and Sheep. Investig. Ophthalmol. Vis. Sci. 2018, 59, 4763–4774. [Google Scholar] [CrossRef] [PubMed]
- Vestri, G.; Versaci, F.; Savini, G. CSO MS-39: Principles and Applications. In Intraocular Lens Calculations; Aramberri, J., Hoffer, K.J., Olsen, T., Savini, G., Shammas, H.J., Eds.; Springer International Publishing: Cham, Switzerland, 2024; pp. 431–442. [Google Scholar] [CrossRef]
- LoPinto, A.; Pirie, C.; Bedenice, D.; Ayres, S. Corneal thickness of eyes of healthy goats, sheep, and alpacas manually measured by use of a portable spectral-domain optical coherence tomography device. Am. J. Vet. Res. 2017, 78, 80–84. [Google Scholar] [CrossRef] [PubMed]
- Radhika, R.; Mahajan, R. An adaptive optimum weighted mean filter and bilateral filter for noise removal in cardiac MRI images. Meas. Sens. 2023, 29, 100880. [Google Scholar] [CrossRef]
- Li, R. An optimal algorithm for bilateral filtering. J. Phys. Conf. Ser. 2023, 2634, 012030. [Google Scholar] [CrossRef]
- Paris, S. A gentle introduction to bilateral filtering and its applications. In Proceedings of the ACM SIGGRAPH 2007 Courses (SIGGRAPH ’07), San Diego, CA, USA, 5–9 August 2007; Association for Computing Machinery: New York, NY, USA, 2007; p. 3-es. [Google Scholar] [CrossRef]
- Gabiger-Rose, A.; Kube, M.; Schmitt, P.; Weigel, R.; Rose, R. Image denoising using bilateral filter with noise-adaptive parameter tuning. In Proceedings of the IECON 2011—37th Annual Conference of the IEEE Industrial Electronics Society, Melbourne, VIC, Australia, 7–10 November 2011; pp. 4515–4520. [Google Scholar] [CrossRef]
- SciPy. 2024. Available online: https://docs.scipy.org/doc/scipy/reference/generated/scipy.signal.find_peaks.html (accessed on 1 October 2024).
- Cox, B.; van der perre, L.; Wielandt, S.; Ottoy, G.; De Strycker, L. High precision hybrid RF and ultrasonic chirp-based ranging for low-power IoT nodes. EURASIP J. Wirel. Commun. Netw. 2020, 2020, 187. [Google Scholar] [CrossRef]
- Okoye, K.; Hosseini, S. Regression Analysis in R: Linear Regression and Logistic Regression. In R Programming: Statistical Data Analysis in Research; Springer Nature: Singapore, 2024; pp. 131–158. [Google Scholar] [CrossRef]
- Nair, P.; Chaudhury, K.N. Fast High-Dimensional Kernel Filtering. IEEE Signal Process. Lett. 2019, 26, 377–381. [Google Scholar] [CrossRef]
- Canny, J.F. A Computational Approach to Edge Detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, PAMI-8, 679–698. [Google Scholar] [CrossRef]
- Lindeberg, T. Scale-Space Theory in Computer Vision; The Springer International Series in Engineering and Computer Science; Springer: New York, NY, USA, 1994. [Google Scholar] [CrossRef]
- Wahba, G. Spline Models for Observational Data; CBMS-NSF Regional Conference Series in Applied Mathematics; Society for Industrial and Applied Mathematics (SIAM): Philadelphia, PA, USA, 1990; Volume 59, p. 169. [Google Scholar] [CrossRef]
- Kehrer, T.; Mosquera, S.A. A simple cornea deformation model. Adv. Opt. Technol. 2021, 10, 433–450. [Google Scholar] [CrossRef]
- Osman, I.M.; Madwar, A.Y. Scanning electron microscopy of human corneal lenticules at variable corneal depths in small incision lenticule extraction cases. Delta J. Ophthalmol. 2016, 17, 109–113. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, Y.; Li, M.; Sun, L.; Zhou, X. Predictability of the Achieved Lenticule Thickness in Small Incision Lenticule Extraction for Myopia Correction. Eye Contact Lens Sci. Clin. Pract. 2018, 44, S410–S413. [Google Scholar] [CrossRef]
- Bohač, M.; Gabrić, I.; Gabrić, K.; Jagić, M.; Arba Mosquera, S. Predictability of the Achieved Lenticule Thickness in Keratorefractive Lenticule Extraction for Myopia Correction. J. Refract. Surg. 2023, 39, 728–735. [Google Scholar] [CrossRef] [PubMed]
- Beer, F.; Wartak, A.; Pircher, N.; Holzer, S.; Lammer, J.; Schmidinger, G.; Baumann, B.; Pircher, M.; Hitzenberger, C.K. Mapping of Corneal Layer Thicknesses With Polarization-Sensitive Optical Coherence Tomography Using a Conical Scan Pattern. Investig. Ophthalmol. Vis. Sci. 2018, 59, 5579–5588. [Google Scholar] [CrossRef] [PubMed]
- Gatinel, D.; Rampat, R.; Dumas, L.; Malet, J. An Alternative Wavefront Reconstruction Method for Human Eyes. J. Refract. Surg. 2020, 36, 74–81. [Google Scholar] [CrossRef] [PubMed]
- Mehrjoo, M.; Gatinel, D.; Malet, J.; Arba Mosquera, S. A Closed-Form Analytical Conversion between Zernike and Gatinel–Malet Basis Polynomials to Present Relevant Aberrations in Ophthalmology and Refractive Surgery. Photonics 2024, 11, 883. [Google Scholar] [CrossRef]
- Langenbucher, A.; Szentmáry, N.; Cayless, A.; Wendelstein, J.; Hoffmann, P. Technical variability of cornea parameters derived from anterior segment OCT fitted with Fringe Zernike polynomials. Graefe’s Arch. Clin. Exp. Ophthalmol. 2024, 262, 505–517. [Google Scholar] [CrossRef]
- Wang, J.; Li, X.; Wang, Z.; Davey, P.G.; Li, Y.; Yang, L.; Lin, M.; Zheng, X.; Bao, F.; Elsheikh, A. Accuracy and reliability of orthogonal polynomials in representing corneal topography. Med. Nov. Technol. Devices 2022, 15, 100133. [Google Scholar] [CrossRef]
- Connor, R.J. Sample Size for Testing Differences in Proportions for the Paired-Sample Design. Biometrics 1987, 43, 207–211. [Google Scholar] [CrossRef]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences, 2nd ed.; Routledge: New York, NY, USA, 1988. [Google Scholar] [CrossRef]
- Gibson, E.; Hu, Y.; Huisman, H.J.; Barratt, D.C. Designing image segmentation studies: Statistical power, sample size and reference standard quality. Med. Image Anal. 2017, 42, 44–59. [Google Scholar] [CrossRef]
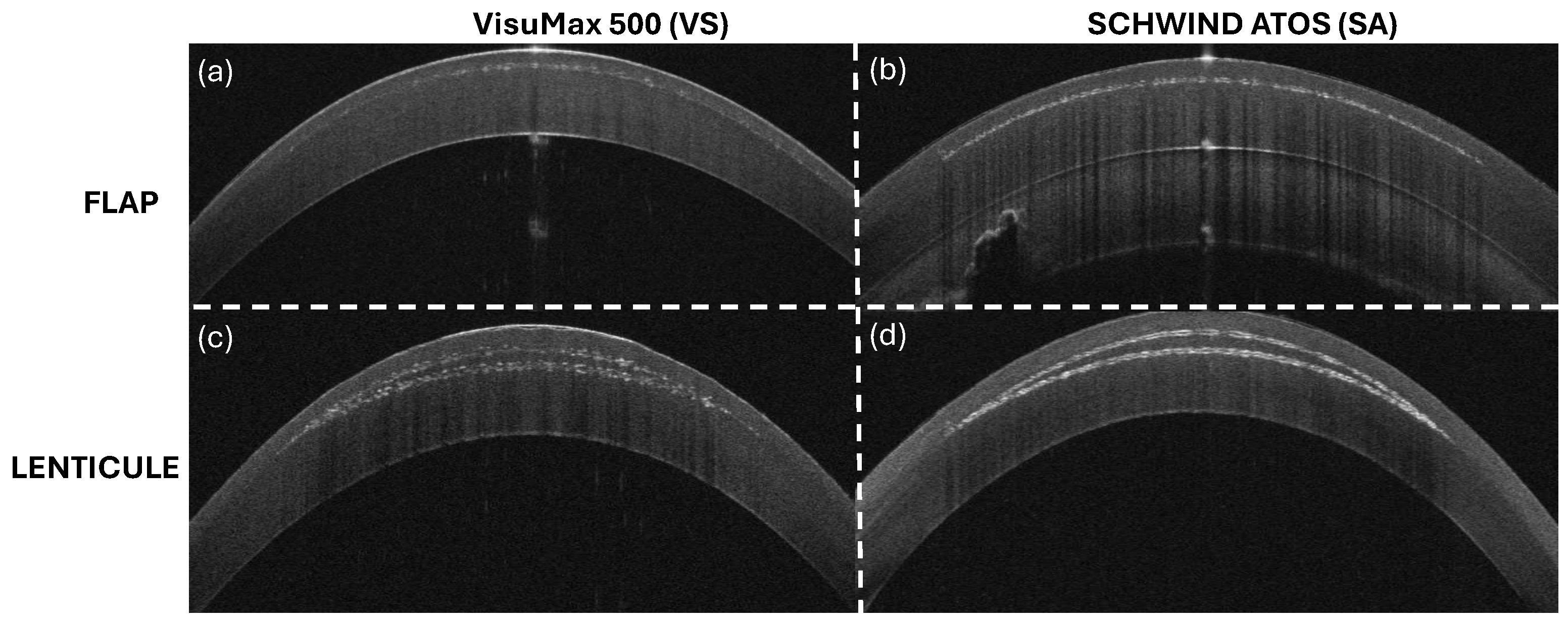
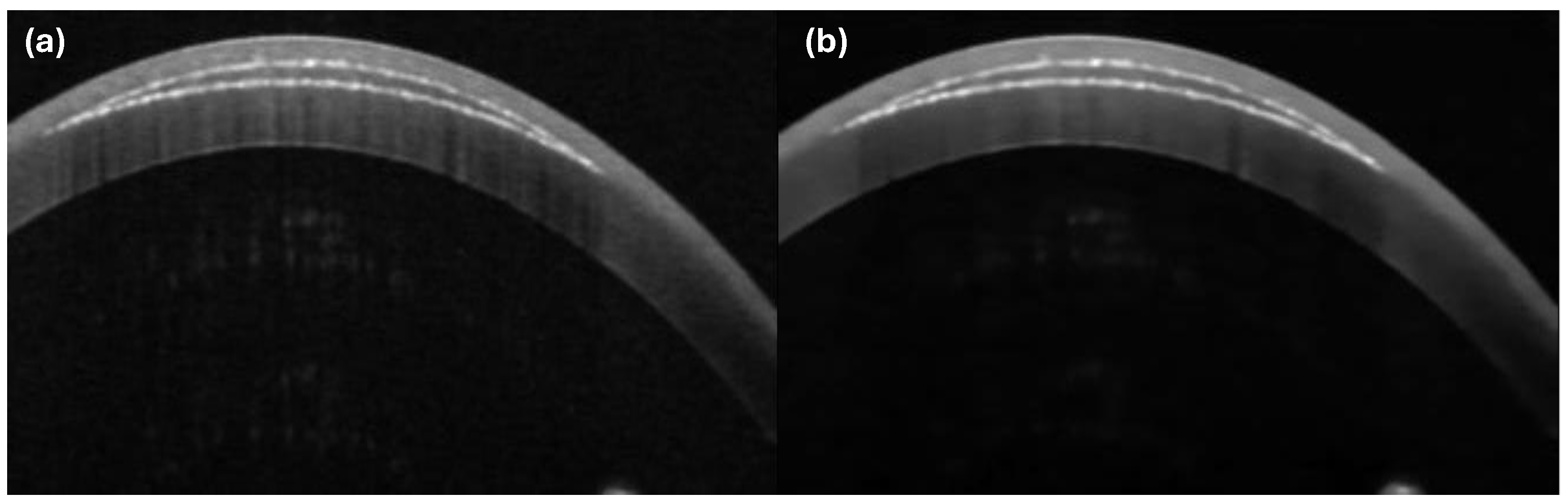


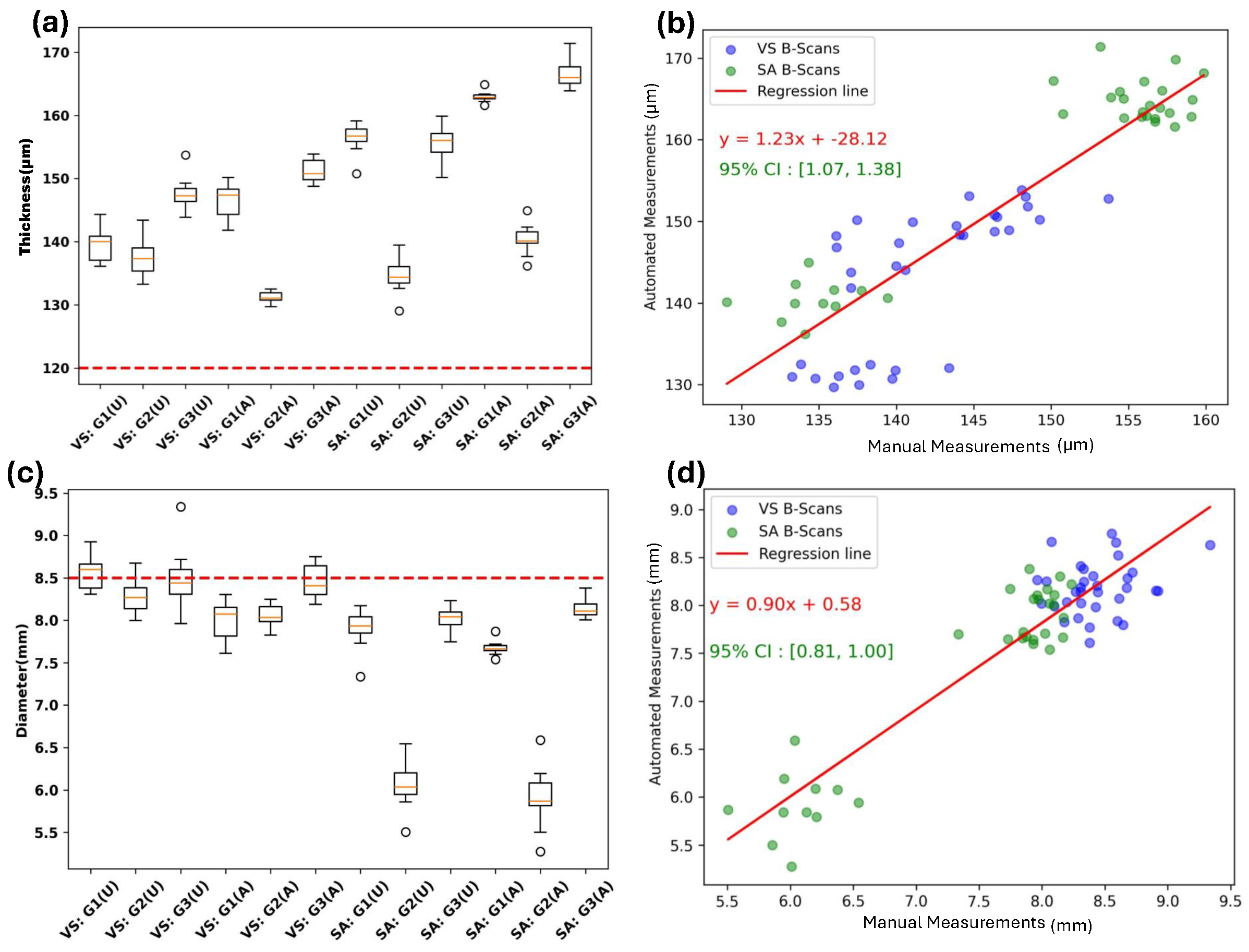


| Parameters | VS | SA |
|---|---|---|
| Energy (anterior and posterior cuts) [nJ] | 115 | 115 |
| Interspot distance [μm] | 4.5 | 4.5 |
| Track distance [μm] | 4.5 | 4.5 |
| Vacuum [mmHg] | 585 | 250 |
| Parameters | Lenticule | Flap |
|---|---|---|
| Lenticule optical zone diameter [mm] | – | |
| Cap diameter [mm] | ||
| Cap thickness [μm] | 120 | 120 |
| Spherical correction [D] | – |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mehrjoo, M.; Khamar, P.; Darzi, S.; Verma, S.; Shetty, R.; Arba Mosquera, S. Automated Characterization of Intrastromal Corneal Cuts Induced by Two Femtosecond Laser Systems Using OCT Imaging. Photonics 2024, 11, 1123. https://doi.org/10.3390/photonics11121123
Mehrjoo M, Khamar P, Darzi S, Verma S, Shetty R, Arba Mosquera S. Automated Characterization of Intrastromal Corneal Cuts Induced by Two Femtosecond Laser Systems Using OCT Imaging. Photonics. 2024; 11(12):1123. https://doi.org/10.3390/photonics11121123
Chicago/Turabian StyleMehrjoo, Masoud, Pooja Khamar, Soodabeh Darzi, Shwetabh Verma, Rohit Shetty, and Samuel Arba Mosquera. 2024. "Automated Characterization of Intrastromal Corneal Cuts Induced by Two Femtosecond Laser Systems Using OCT Imaging" Photonics 11, no. 12: 1123. https://doi.org/10.3390/photonics11121123
APA StyleMehrjoo, M., Khamar, P., Darzi, S., Verma, S., Shetty, R., & Arba Mosquera, S. (2024). Automated Characterization of Intrastromal Corneal Cuts Induced by Two Femtosecond Laser Systems Using OCT Imaging. Photonics, 11(12), 1123. https://doi.org/10.3390/photonics11121123





