Introducing Aberrations into Human Eye Models with High Precision for Objective Visual Quality Evaluation
Abstract
1. Introduction
2. Theory and Methods
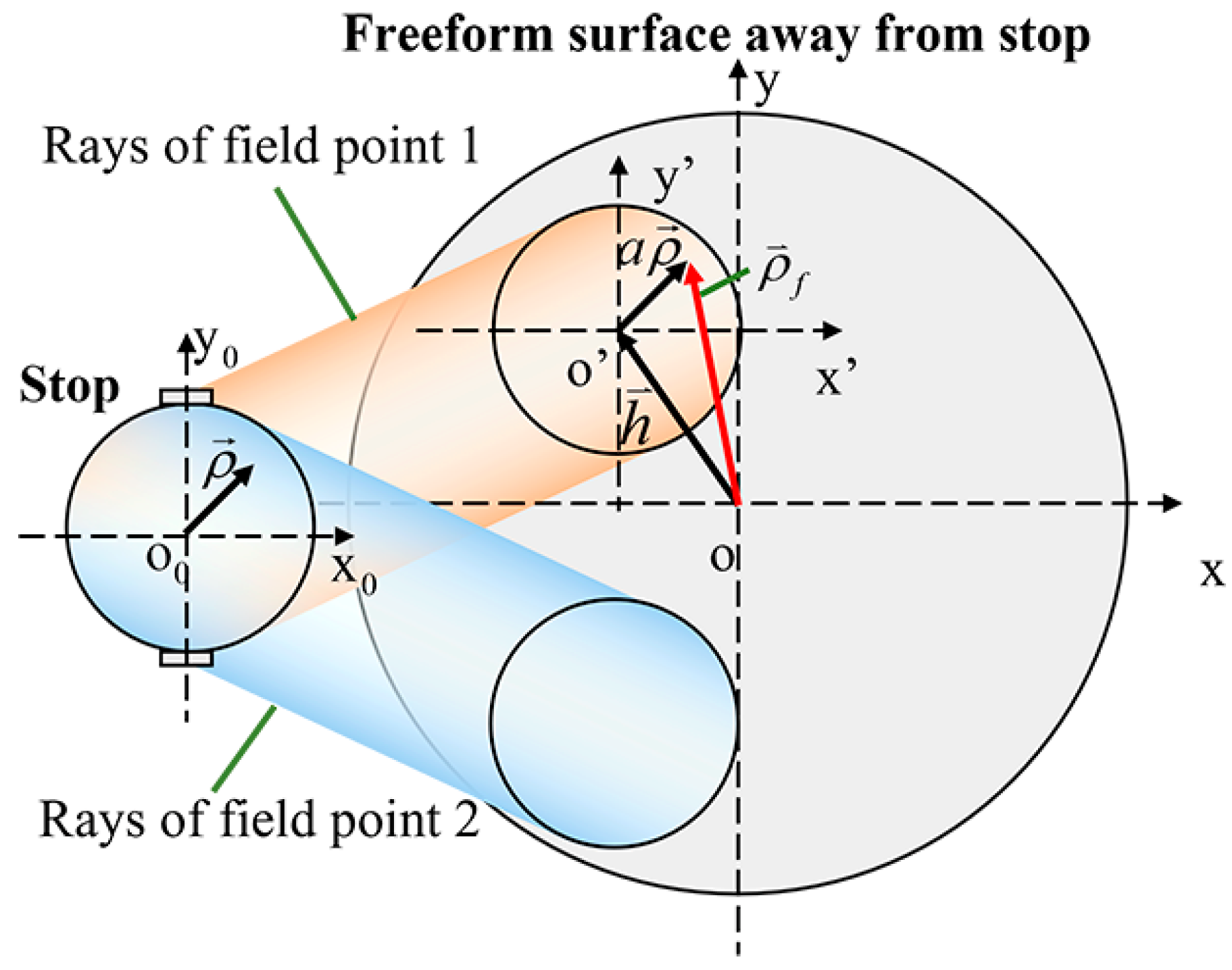
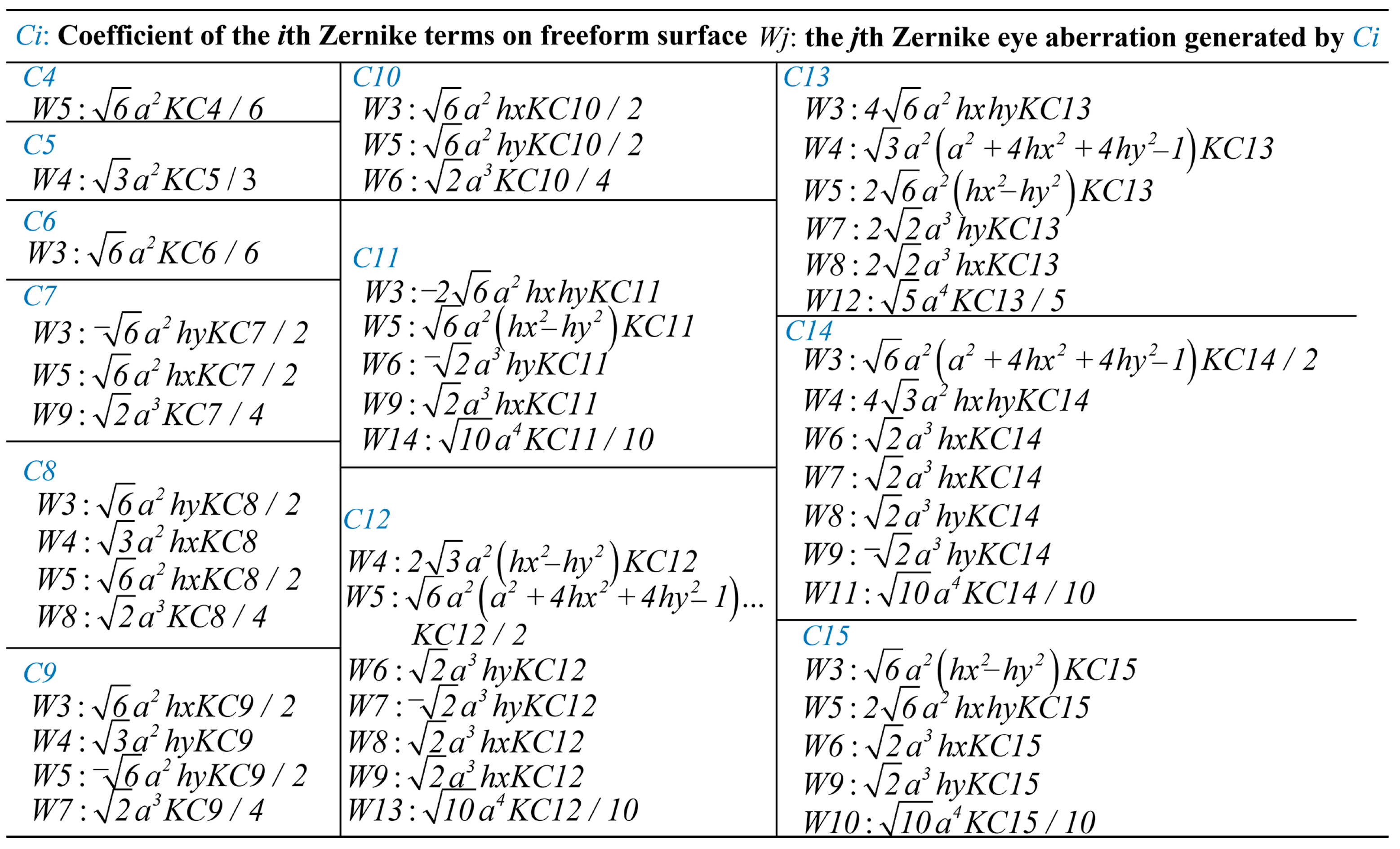
2.1. Eye Aberrations Generated by Surface of Eye Model
2.2. Iterative Method to Accurately Introduce Eye Aberrations into the Eye Model
3. Objective Visual Quality Evaluation of Patients Undergoing Refractive Surgery Using the Proposed Method
4. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Atchison, D.A.; Thibos, L.N. Optical models of the human eye. Clin. Exp. Optom. 2016, 99, 99–106. [Google Scholar] [CrossRef] [PubMed]
- Esteve-Taboada, J.J.; Montes-Mico, R.; Ferrer-Blasco, T. Schematic eye models to mimic the behavior of the accommodating human eye. J. Cataract Refract. Surg. 2018, 44, 627–641. [Google Scholar] [CrossRef] [PubMed]
- Marsack, J.D.; Thibos, L.N.; Applegate, R.A. Metrics of optical quality derived from wave aberrations predict visual performance. J. Vis. 2004, 4, 322–328. [Google Scholar] [CrossRef] [PubMed]
- Villegas, E.A.; Alcon, E.; Artal, P. Impact of positive coupling of the eye’s trefoil and coma in retinal image quality and visual acuity. J. Opt. Soc. Am. A 2012, 29, 1667–1672. [Google Scholar] [CrossRef] [PubMed]
- Niu, S.; Shen, J.; Liao, W.; Liang, C.; Zhang, Y. Study on linear conjugated combination of Zernike modes. Chin. Opt. Lett. 2013, 11, 022201–022203. [Google Scholar] [CrossRef][Green Version]
- Hu, C.; Ravikumar, A.; Hastings, G.D.; Marsack, J.D. Visual interaction of 2nd to 5th order Zernike aberration terms with vertical coma. Ophthalmic Physiol. Opt. 2020, 40, 669–679. [Google Scholar] [CrossRef]
- de Gracia, P.; Dorronsoro, C.; Gambra, E.; Marin, G.; Hernandez, M.; Marcos, S. Combining coma with astigmatism can improve retinal image over astigmatism alone. Vision Res. 2010, 50, 2008–2014. [Google Scholar] [CrossRef]
- Navarro, R.; Santamaría, J.; Bescós, J. Accommodation-dependent model of the human eye with aspherics. J. Opt. Soc. Am. A 1985, 2, 1273–1280. [Google Scholar] [CrossRef]
- El Hage, S.G.; Le Grand, Y. Physiological Optics; Springer: Berlin/Heidelberg, Germany, 1980; pp. 64–66. [Google Scholar]
- Escudero-Sanz, I.; Navarro, R. Off-axis aberrations of a wide-angle schematic eye model. J. Opt. Soc. Am. A 1999, 16, 1881–1891. [Google Scholar] [CrossRef]
- Liou, H.L.; Brennan, N.A. Anatomically accurate, finite model eye for optical modeling. J. Opt. Soc. Am. A 1997, 14, 1684–1695. [Google Scholar] [CrossRef]
- Polans, J.; Jaeken, B.; McNabb, R.P.; Artal, P.; Izatt, J.A. Wide-field optical model of the human eye with asymmetrically tilted and decentered lens that reproduces measured ocular aberrations. Optica 2015, 2, 124–134. [Google Scholar] [CrossRef]
- Tabernero, J.; Kallamata, E.; Velonias, G.; Vera-Diaz, F.A. Individualized modeling for the peripheral optics of the human myopic eye. Biomed. Opt. Express 2023, 14, 2726–2735. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Li, X.; Zhang, L.; Yi, X.; Xing, Y.; Li, K.; Wang, Y. Comparison of wavefront aberrations in the object and image spaces using wide-field individual eye models. Biomed. Opt. Express 2022, 13, 4939–4953. [Google Scholar] [CrossRef] [PubMed]
- Zhao, S.; Wu, H.; Ye, H.; Hu, J.; Hu, M.; Zhang, X. A Multi-Objective Local Optimization Method for Imaging Optical Systems. Photonics 2023, 10, 1218. [Google Scholar] [CrossRef]
- Bauer, A.; Schiesser, E.M.; Rolland, J.P. Starting geometry creation and design method for freeform optics. Nat. Commun. 2018, 9, 1756. [Google Scholar] [CrossRef]
- Zhang, S.; Zhao, X.; Li, D.; Feng, H.; Zhao, S.; Wang, L.; Zhang, X. High-precision analysis of aberration contribution of Zernike freeform surface terms for non-zero field of view. Opt. Express 2024, 32, 3167–3183. [Google Scholar] [CrossRef]
- Fuerschbach, K.; Rolland, J.P.; Thompson, K.P. Theory of aberration fields for general optical systems with freeform surfaces. Opt. Express 2014, 22, 26585–26606. [Google Scholar] [CrossRef]
- Yang, T.; Zhu, J.; Jin, G. Nodal aberration properties of coaxial imaging systems using Zernike polynomial surfaces. J. Opt. Soc. Am. A 2015, 32, 822–836. [Google Scholar] [CrossRef]
- Yang, T.; Cheng, D.; Wang, Y. Aberration analysis for freeform surface terms overlay on general decentered and tilted optical surfaces. Opt. Express 2018, 26, 7751–7770. [Google Scholar] [CrossRef]
- Thibos, L.N.; Applegate, R.A.; Schwiegerling, J.T.; Webb, R. Standards for reporting the optical aberrations of eyes. J. Refract. Surg. 2002, 18, S652–S660. [Google Scholar] [CrossRef]
- Synopsys Inc. Code V Reference Manual; Synopsys Inc.: Sunnyvale, CA, USA, 2012. [Google Scholar]
- Kim, T.I.; Alio Del Barrio, J.L.; Wilkins, M.; Cochener, B.; Ang, M. Refractive surgery. Lancet 2019, 393, 2085–2098. [Google Scholar] [CrossRef] [PubMed]
- Gulmez, M.; Tekce, A.; Kamis, U. Comparison of refractive outcomes and high-order aberrations after small incision lenticule extraction and wavefront-guided femtosecond-assisted laser in situ keratomileusis for correcting high myopia and myopic astigmatism. Int. Ophthalmol. 2020, 40, 3481–3489. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.; Zhang, L.; Ma, J.; Li, M.; Zhang, J.; Zhao, X.; Wang, Y. Comparison of Wavefront-Guided Femtosecond LASIK and Optimized SMILE for Correction of Moderate-to-High Astigmatism. J. Refract. Surg. 2021, 37, 166–173. [Google Scholar] [CrossRef] [PubMed]
- He, X.Y.; He, Q.; Yuan, M.J.; Fang, Z.; Zhang, K.; Zhu, T.P.; Han, W. Evaluation of morphological features: Femtosecond-LASIK flap vs. SMILE cap, and the effects on corneal higher-order aberrations. Graefes Arch. Clin. Exp. Ophthalmol. 2022, 260, 3993–4003. [Google Scholar] [CrossRef]




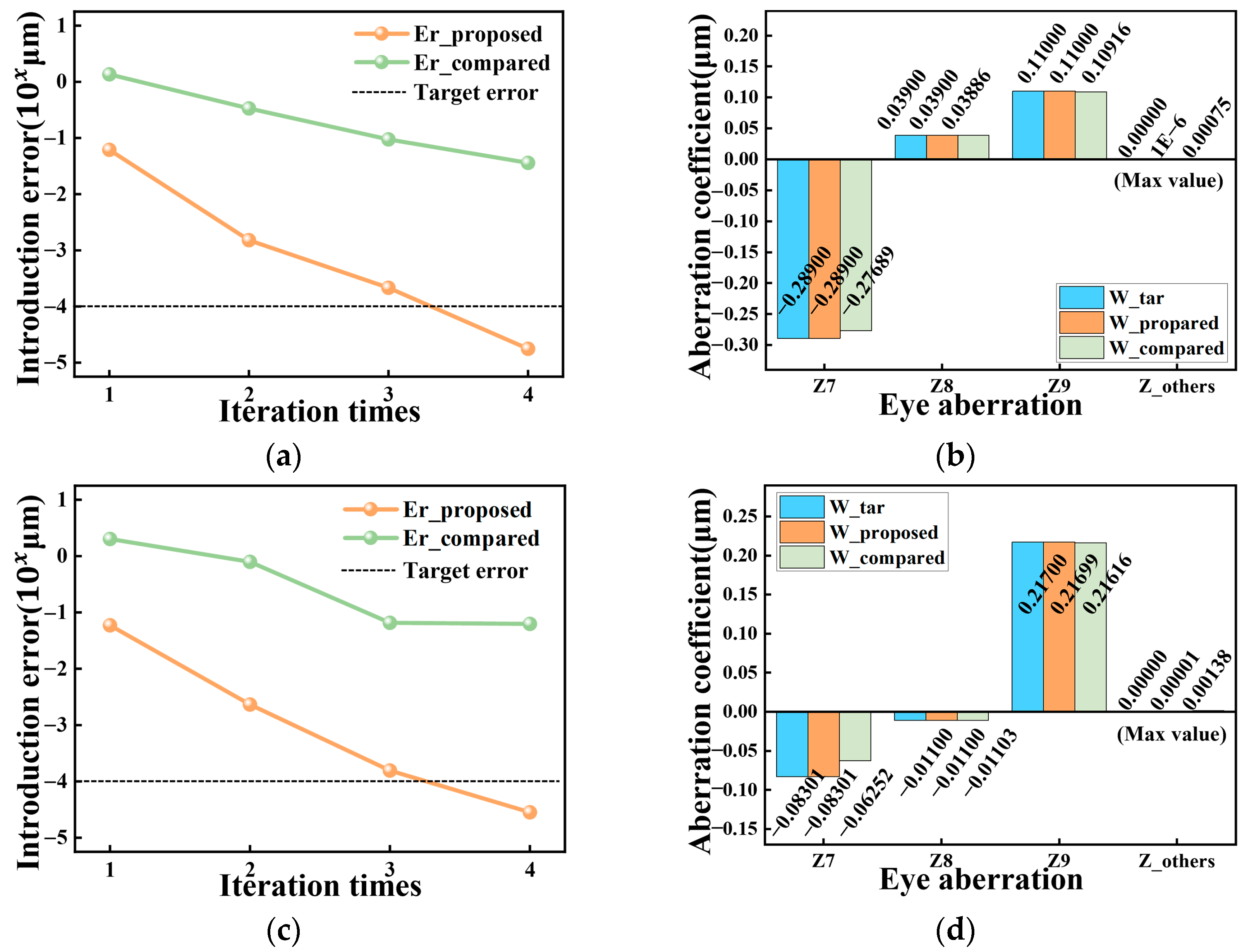

| Surgery | Vertical Coma (μm) | Horizontal Coma (μm) | Spherical Aberration (μm) | HOAs (μm) |
|---|---|---|---|---|
| SMILE | −0.289 | 0.039 | 0.110 | 0.701 ± 0.260 |
| WFG LASIKe | −0.083 | −0.011 | 0.217 | 0.693 ± 0.387 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Zhao, X.; Li, D.; Zhao, X.; Zhang, L.; Wang, Y. Introducing Aberrations into Human Eye Models with High Precision for Objective Visual Quality Evaluation. Photonics 2024, 11, 1146. https://doi.org/10.3390/photonics11121146
Zhang S, Zhao X, Li D, Zhao X, Zhang L, Wang Y. Introducing Aberrations into Human Eye Models with High Precision for Objective Visual Quality Evaluation. Photonics. 2024; 11(12):1146. https://doi.org/10.3390/photonics11121146
Chicago/Turabian StyleZhang, Shuai, Xinheng Zhao, Da Li, Xing Zhao, Lin Zhang, and Yan Wang. 2024. "Introducing Aberrations into Human Eye Models with High Precision for Objective Visual Quality Evaluation" Photonics 11, no. 12: 1146. https://doi.org/10.3390/photonics11121146
APA StyleZhang, S., Zhao, X., Li, D., Zhao, X., Zhang, L., & Wang, Y. (2024). Introducing Aberrations into Human Eye Models with High Precision for Objective Visual Quality Evaluation. Photonics, 11(12), 1146. https://doi.org/10.3390/photonics11121146





