Efficient Second-Harmonic Generation in Thin-Film Lithium Tantalate Through Modal Phase-Matching
Abstract
:1. Introduction
2. Device Structure and Design Results
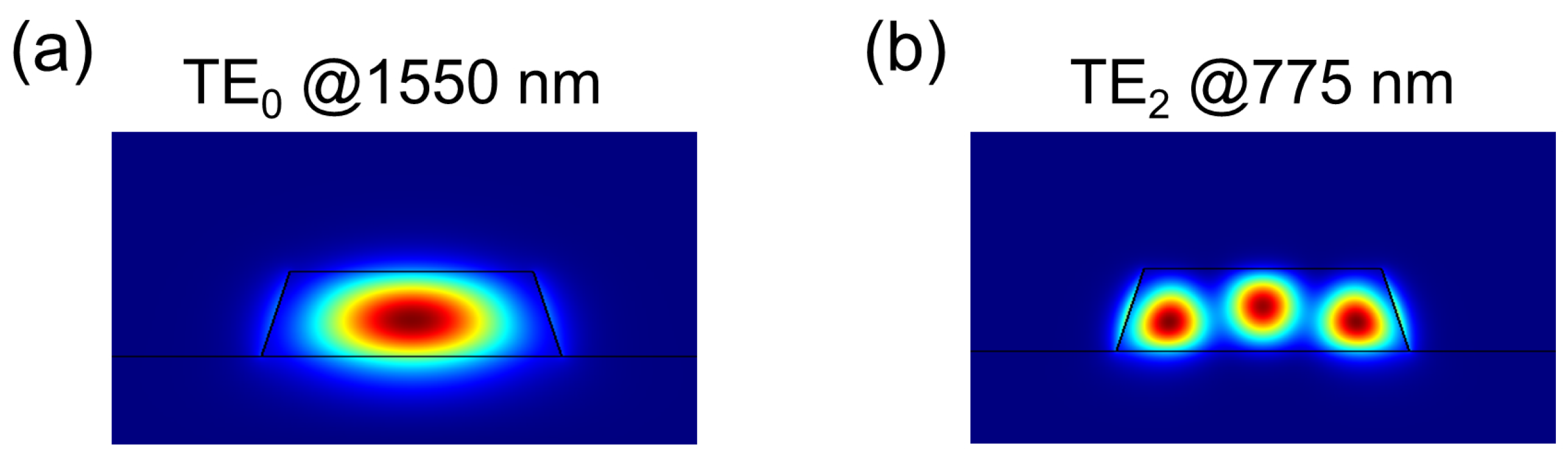
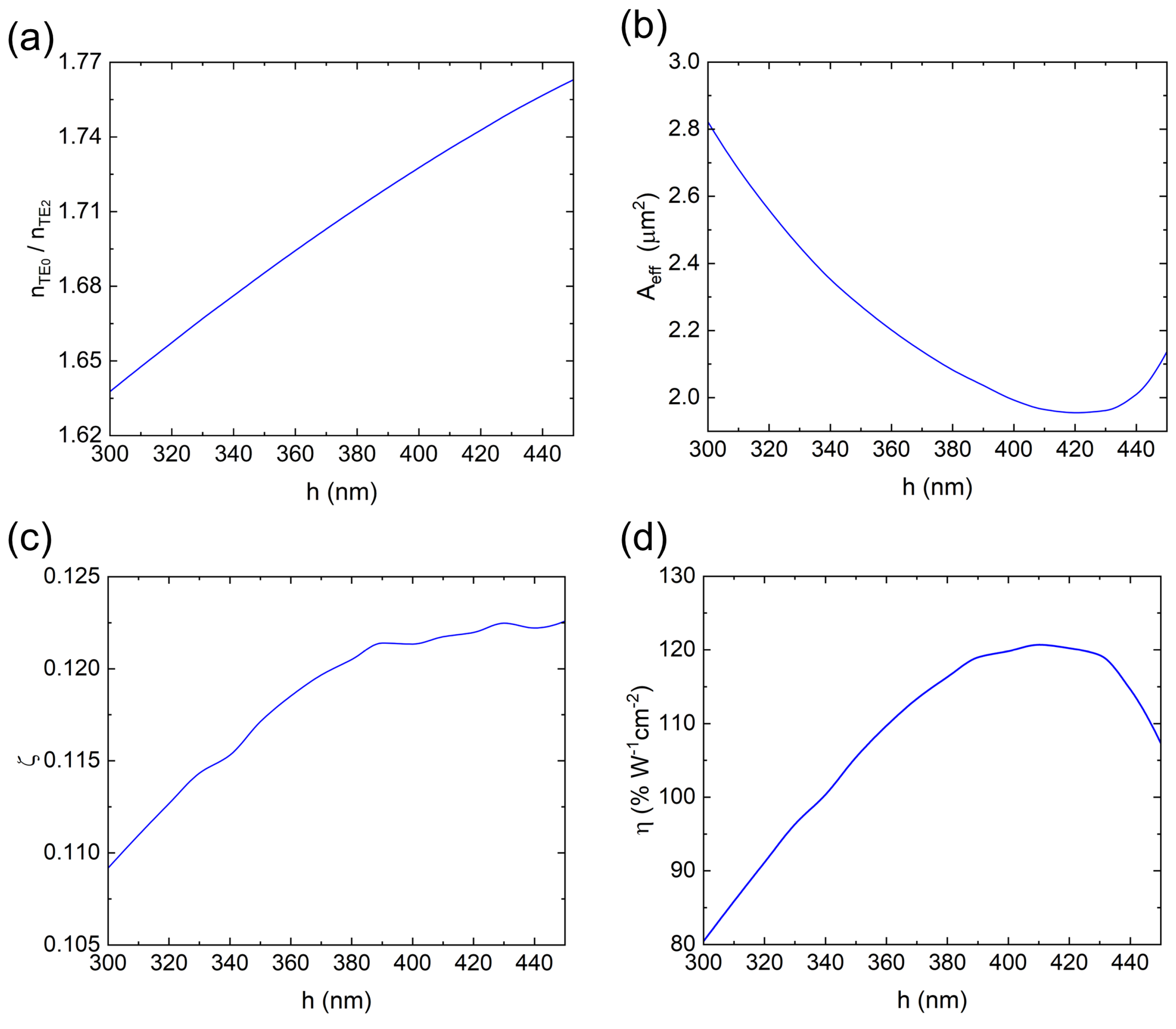
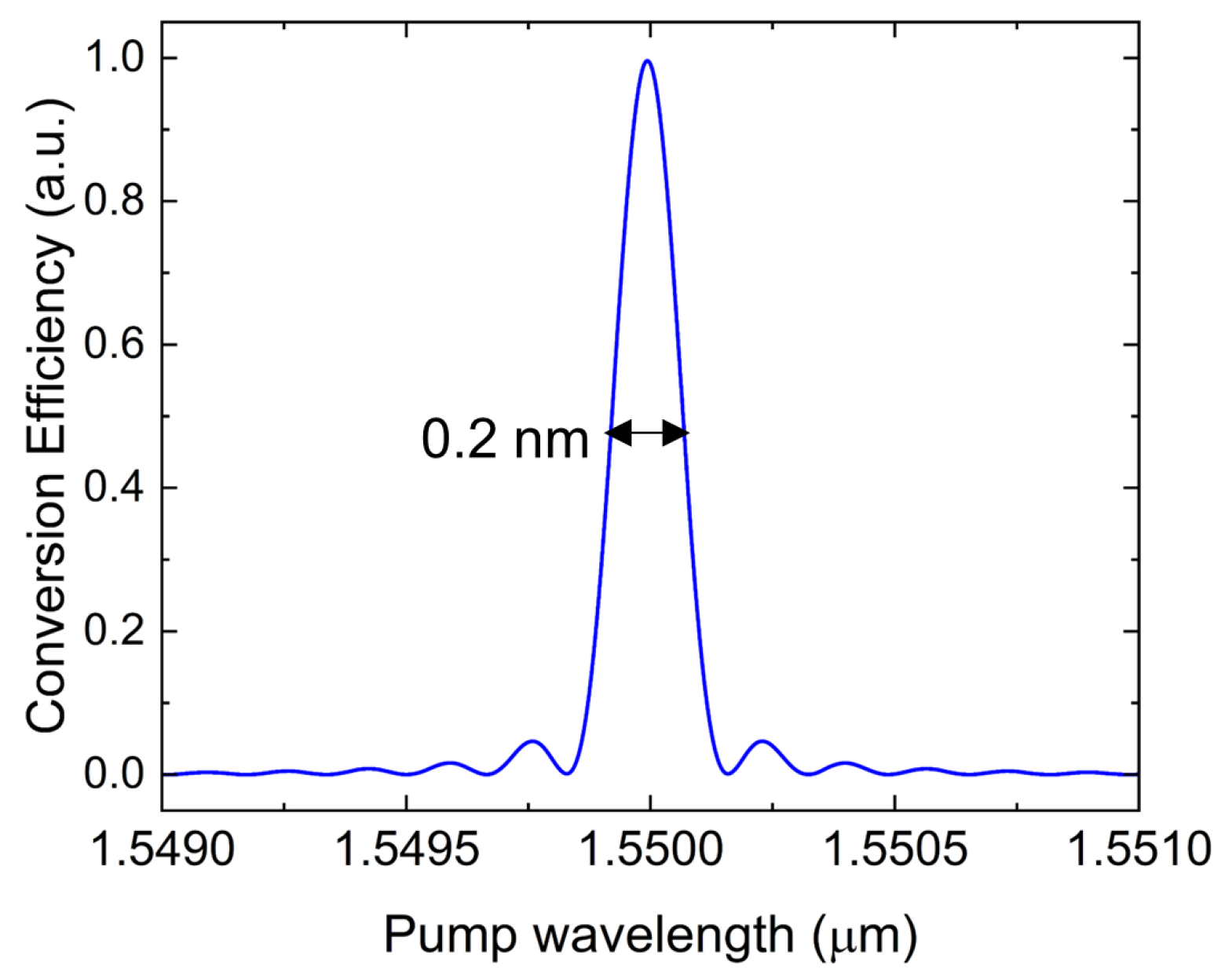
2.1. SHG Based on MPM in TFLN
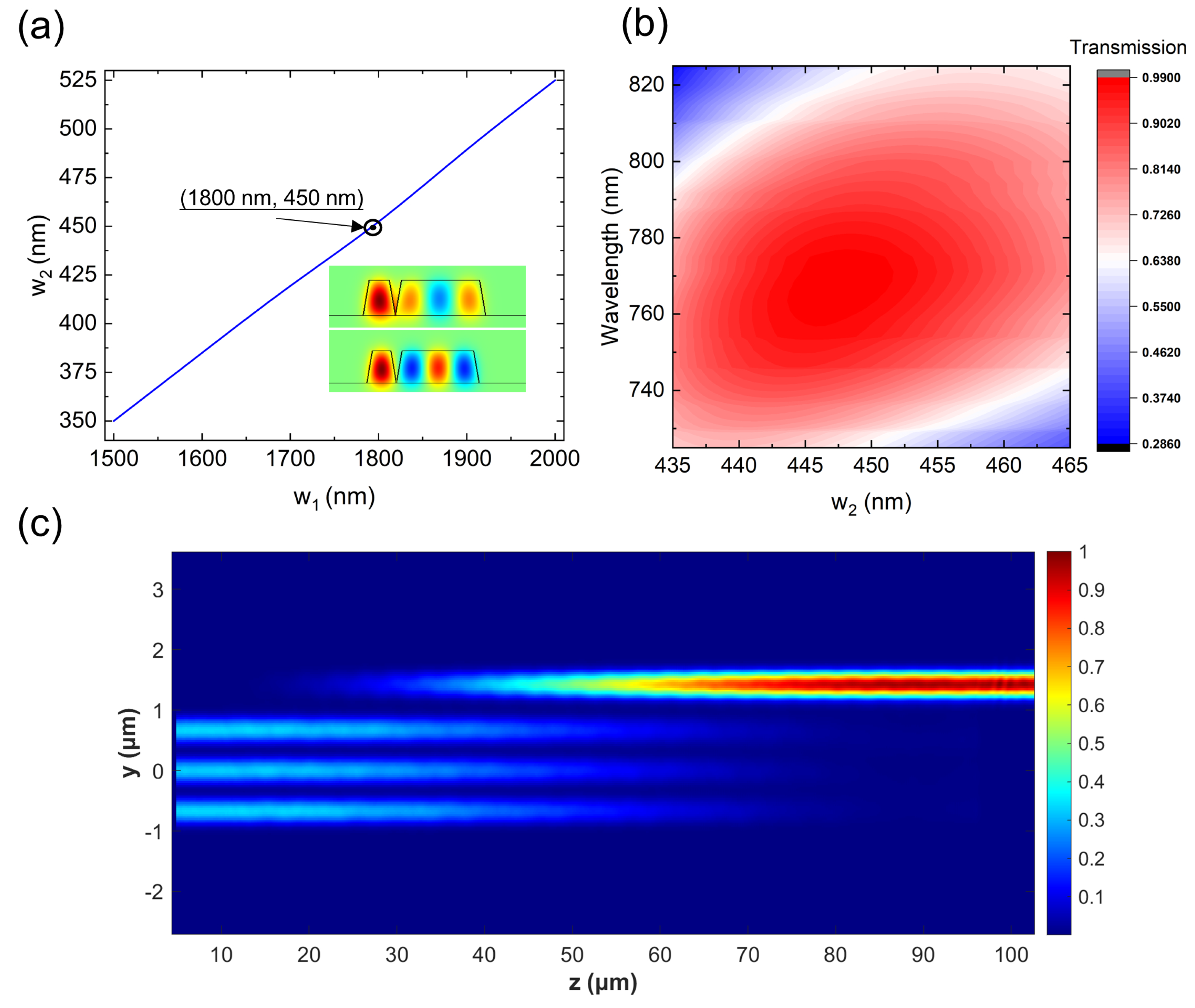
2.2. TE2–TE0 Mode Converter
3. Discussion
4. Conclusion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jundt, D.H. Temperature-dependent Sellmeier equation for the index of refraction. Opt. Lett. 1997, 22, 1553. [Google Scholar] [CrossRef] [PubMed]
- Poberaj, G.; Hu, H.; Soher, W.; Günter, P. Lithium niobate on insulator (LNOI) for micro-photonic devices. Laser Photon. Rev. 2012, 6, 488. [Google Scholar] [CrossRef]
- Meyn, J.P.; Fejer, M. Tunable ultraviolet radiation by second-harmonic generation in periodically poled lithium tantalate. Opt. Lett. 1997, 22, 1214. [Google Scholar] [CrossRef] [PubMed]
- Eknoyan, O.; Yoon, D.; Taylor, H. Low-loss optical waveguides in lithium tantalate by vapor diffusion. Appl. Phys. Lett. 1987, 51, 384. [Google Scholar] [CrossRef]
- Targat, R.L.; Zondy, J.J.; Lemonde, P. 75%-efficiency blue generation from an intracavity PPKTP frequency doubler. Opt. Commun. 2005, 247, 471. [Google Scholar] [CrossRef]
- Zhu, D.; Shao, L.; Yu, M. Integrated photonics on thin-film lithium niobate. Adv. Opt. Photonics 2021, 13, 242. [Google Scholar] [CrossRef]
- Boes, A.; Chang, L.; Langrock, C. Lithium niobate photonics: Unlocking the electromagnetic spectrum. Science 2023, 379, eabj4396. [Google Scholar] [CrossRef]
- Xiao, X.; Liang, S.; Si, J. Performance of LiTaO3 Crystals and Thin Films and Their Application. Crystals 2023, 13, 1233. [Google Scholar] [CrossRef]
- Bruner, A.; Eger, D.; Oron, M.B. Temperature-dependent Sellmeier equation for the refractive index of stoichiometric lithium tantalate. Opt. Lett. 2003, 28, 194. [Google Scholar] [CrossRef]
- Yu, J.; Ruan, Z.; Xue, Y. Tunable and stable micro-ring resonator based on thin-film lithium tantalate. APL Photon. 2024, 9, 036115. [Google Scholar] [CrossRef]
- Wang, C.; Li, Z.; Riemensberger, J. Lithium tantalate photonic integrated circuits for volume manufacturing. Nature 2024, 629, 784. [Google Scholar] [CrossRef] [PubMed]
- Cundiff, S.T.; Ye, J. Colloquium: Femtosecond optical frequency combs. Rev. Mod. Phys. 2003, 75, 325. [Google Scholar] [CrossRef]
- Newman, Z.L.; Maurice, V.; Drake, T. Architecture for the photonic integration of an optical atomic clock. Optica 2019, 6, 680. [Google Scholar] [CrossRef]
- Shen, Y.R. Surface properties probed by second-harmonic and sum-frequency generation. Nature 1989, 337, 519. [Google Scholar] [CrossRef]
- Guo, X.; Zou, C.L.; Schuck, C. Parametric down-conversion photon-pair source on a nanophotonic chip. Light. Sci. Appl. 2017, 6, e16249. [Google Scholar] [CrossRef] [PubMed]
- Rao, A.; Abdelsalam, K.; Sjaardema, T. Actively-monitored periodic-poling in thin-film lithium niobate photonic waveguides with ultrahigh nonlinear conversion efficiency of 4600%W−1cm−2. Opt. Express 2019, 27, 18. [Google Scholar] [CrossRef]
- Luo, R.; He, Y.; Liang, H. Highly tunable efficient second-harmonic generation in a lithium niobate nanophotonic waveguide. Optica 2018, 5, 8. [Google Scholar] [CrossRef]
- Liu, J.; Duan, J.; Zhu, P.; Xia, G.; Hong, Q.; Zhang, K.; Zhu, Z.; Qin, S.; Xu, P. Modal phase-matching in thin-film lithium niobate waveguides for efficient generation of entangled photon pairs. Opt. Express 2024, 32, 23. [Google Scholar] [CrossRef]
- Tovstonog, S.V.; Kurimura, S.; Suzuki, I.; Takeno, K.; Moriwaki, S.; Ohmae, N.; Mio, N.; Katagai, T. Thermal effects in high-power CW second harmonic generation in Mg-doped stoichiometric lithium tantalate. Opt. Express 2008, 16, 15. [Google Scholar] [CrossRef]
- Yan, X.; Liu, Y.; Ge, L.; Zhu, B.; Wu, J.; Chen, Y.; Chen, X. High optical damage threshold on-chip lithium tantalate microdisk resonator. Opt. Lett. 2020, 45, 4100. [Google Scholar] [CrossRef]
- Yan, X.; Xue, M.; Yuan, T.; Wu, J.; Ge, R.; Chen, Y.; Chen, X. Cascaded degenerate four-wave mixing generation in thin-film lithium tantalate microdisk cavity. Phys. Rev. Appl. 2024, 21, 024033. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Xia, G.; Zhu, P.; Zhang, K.; Xu, P.; Zhu, Z. Efficient Second-Harmonic Generation in Thin-Film Lithium Tantalate Through Modal Phase-Matching. Photonics 2024, 11, 1150. https://doi.org/10.3390/photonics11121150
Liu J, Xia G, Zhu P, Zhang K, Xu P, Zhu Z. Efficient Second-Harmonic Generation in Thin-Film Lithium Tantalate Through Modal Phase-Matching. Photonics. 2024; 11(12):1150. https://doi.org/10.3390/photonics11121150
Chicago/Turabian StyleLiu, Jiacheng, Gongyu Xia, Pingyu Zhu, Kaikai Zhang, Ping Xu, and Zhihong Zhu. 2024. "Efficient Second-Harmonic Generation in Thin-Film Lithium Tantalate Through Modal Phase-Matching" Photonics 11, no. 12: 1150. https://doi.org/10.3390/photonics11121150
APA StyleLiu, J., Xia, G., Zhu, P., Zhang, K., Xu, P., & Zhu, Z. (2024). Efficient Second-Harmonic Generation in Thin-Film Lithium Tantalate Through Modal Phase-Matching. Photonics, 11(12), 1150. https://doi.org/10.3390/photonics11121150






