Advances in Soliton Crystal Microcombs
Abstract
1. Introduction
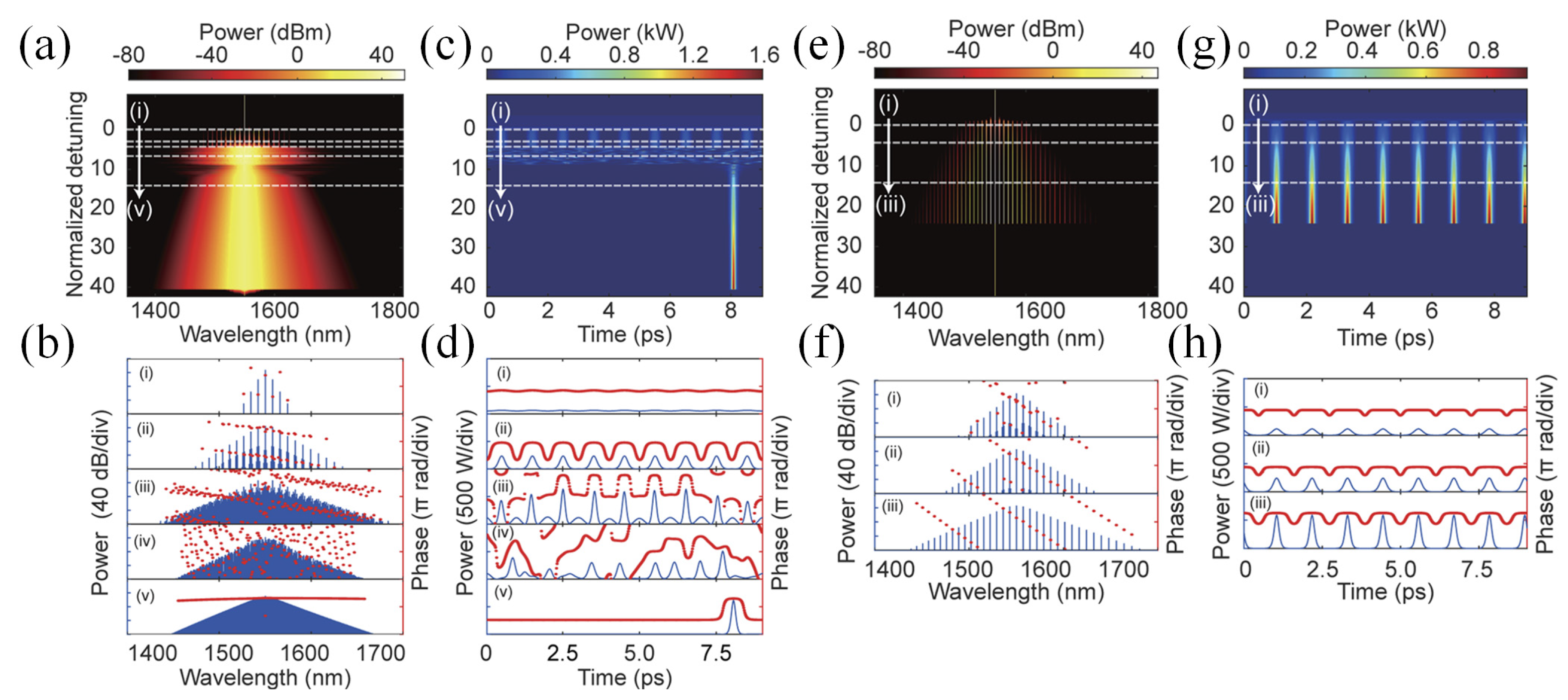
2. Numerical Model of Soliton Microcombs
3. Generating Schemes for Soliton Crystal Microcombs
3.1. Avoided Mode Crossing
3.2. Harmonic Modulation
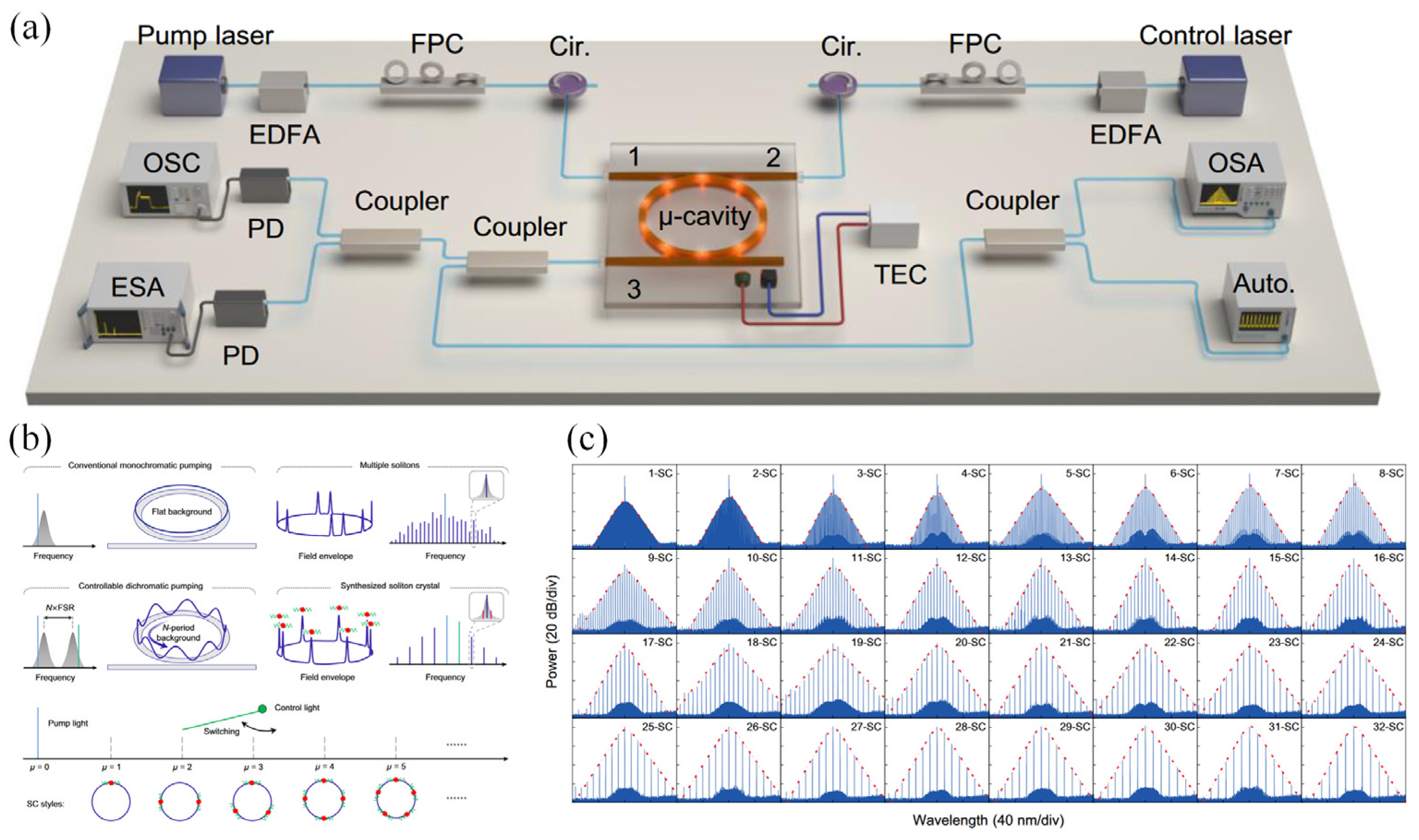
3.3. Bi-Chromatic Pumping
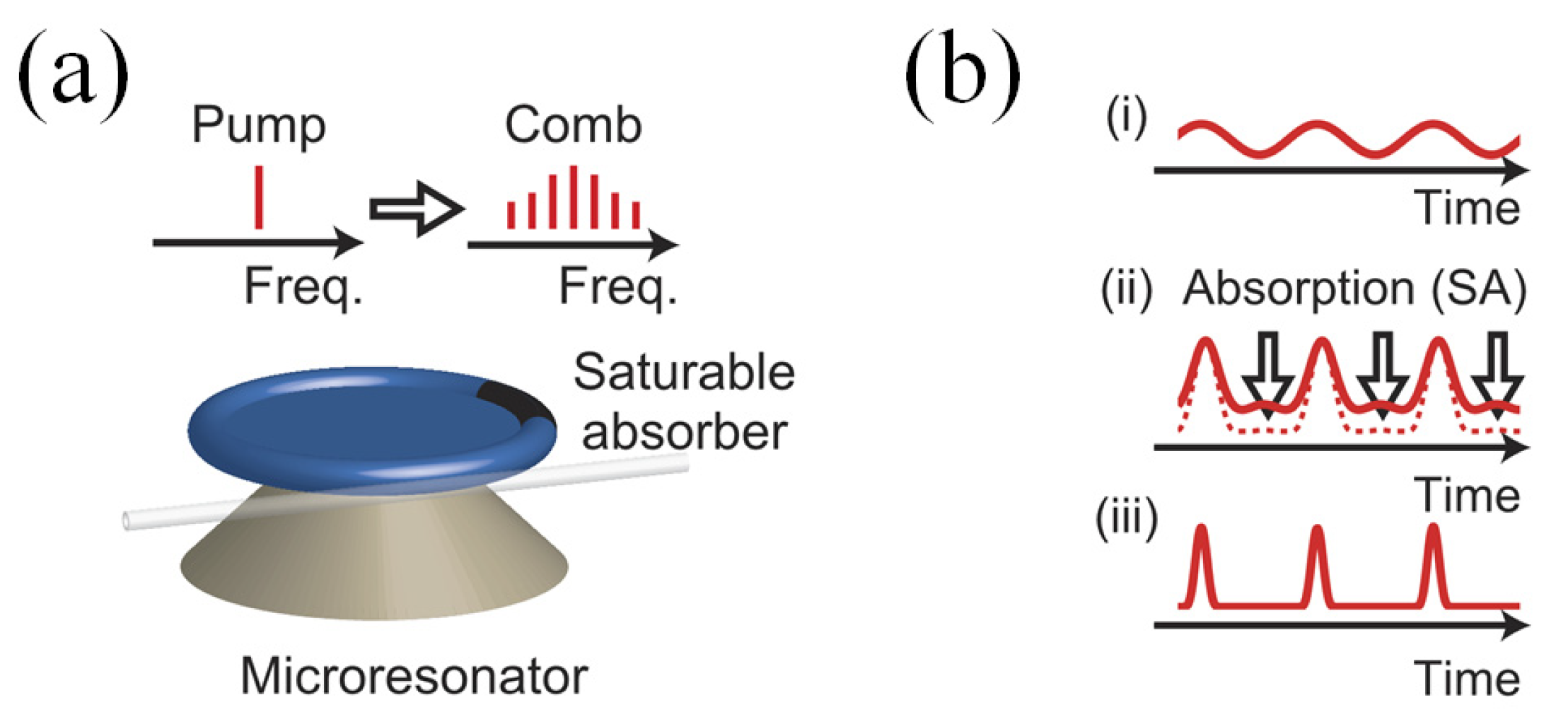
3.4. Saturable Absorber
4. Applications
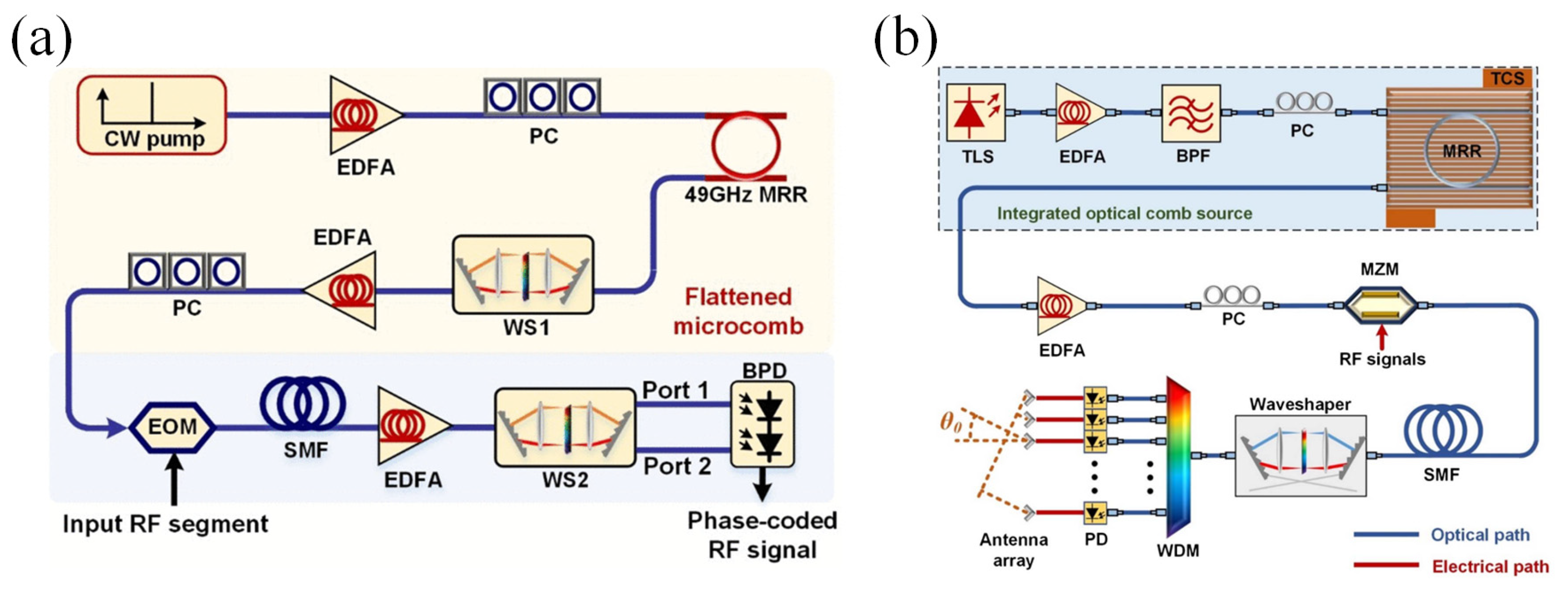
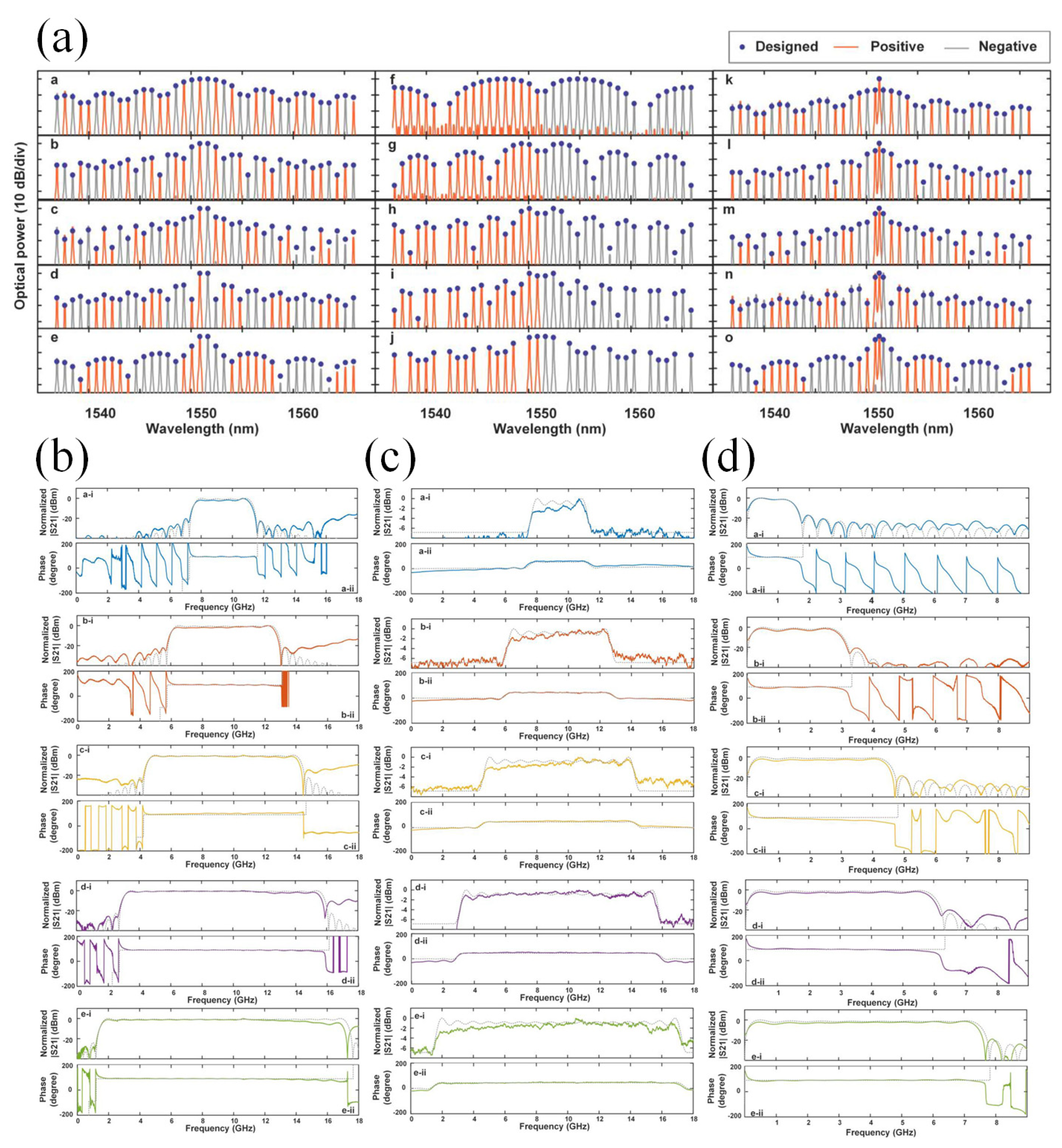
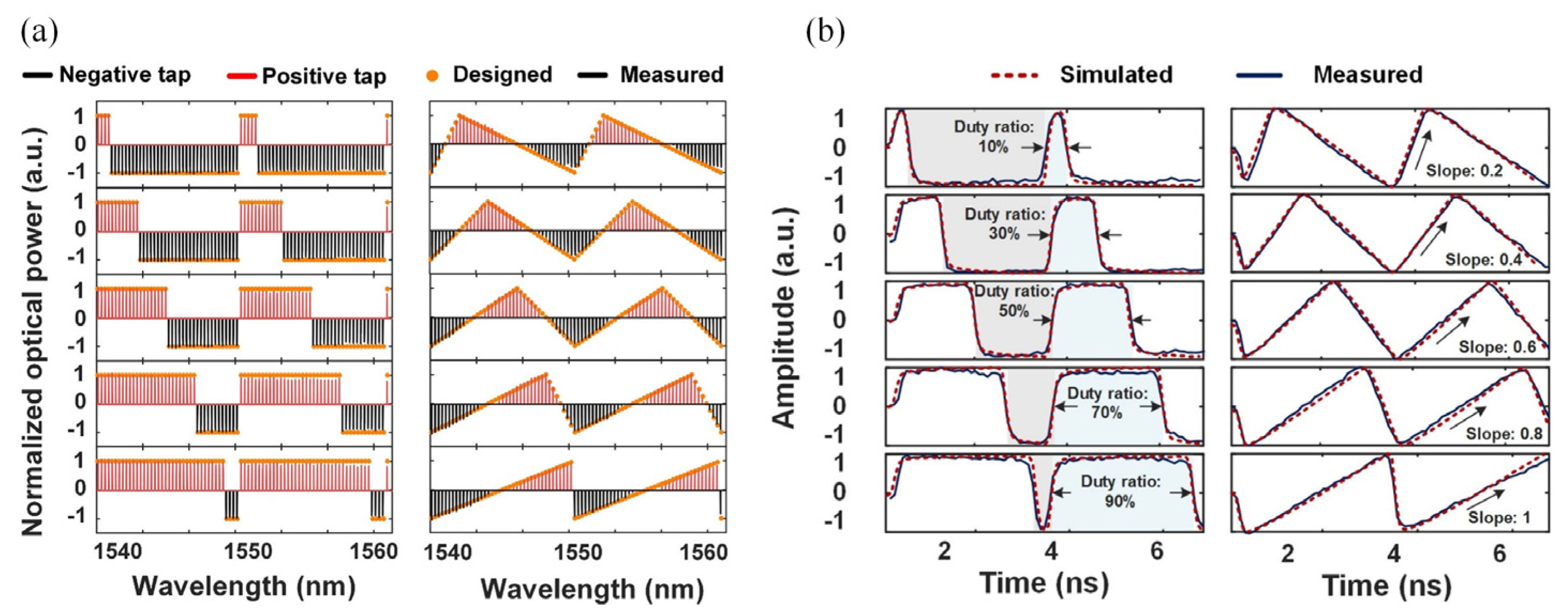
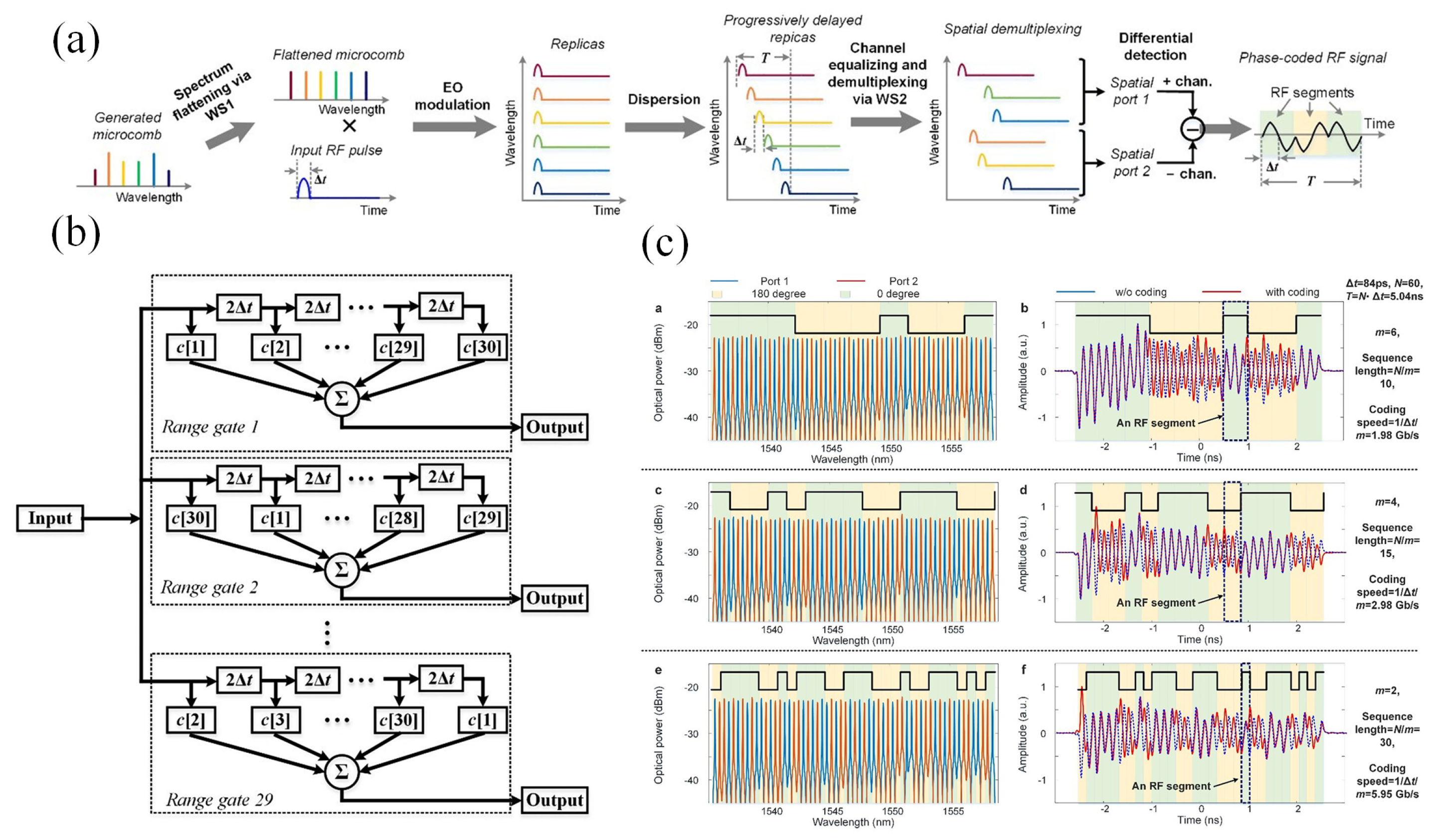
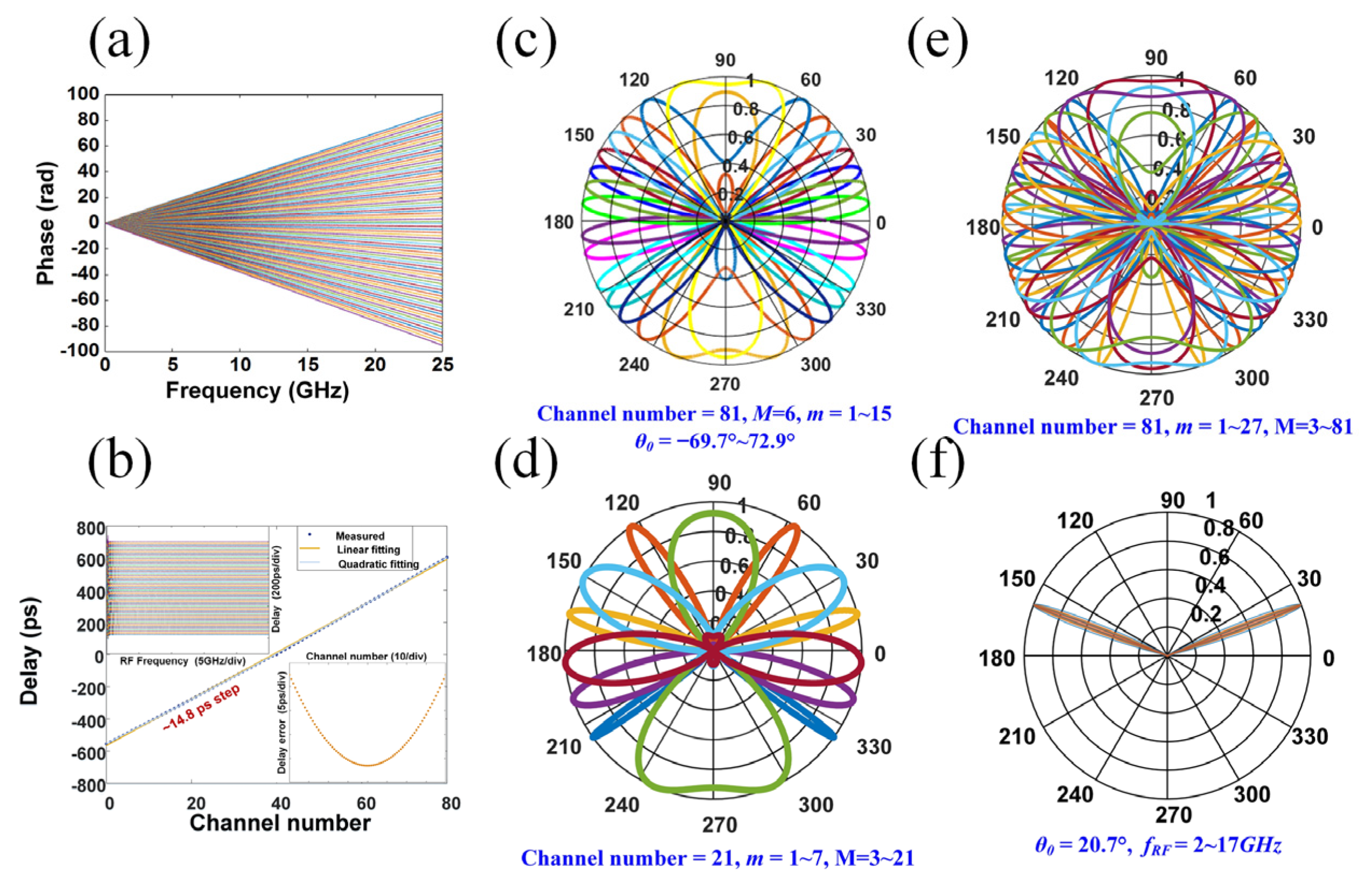
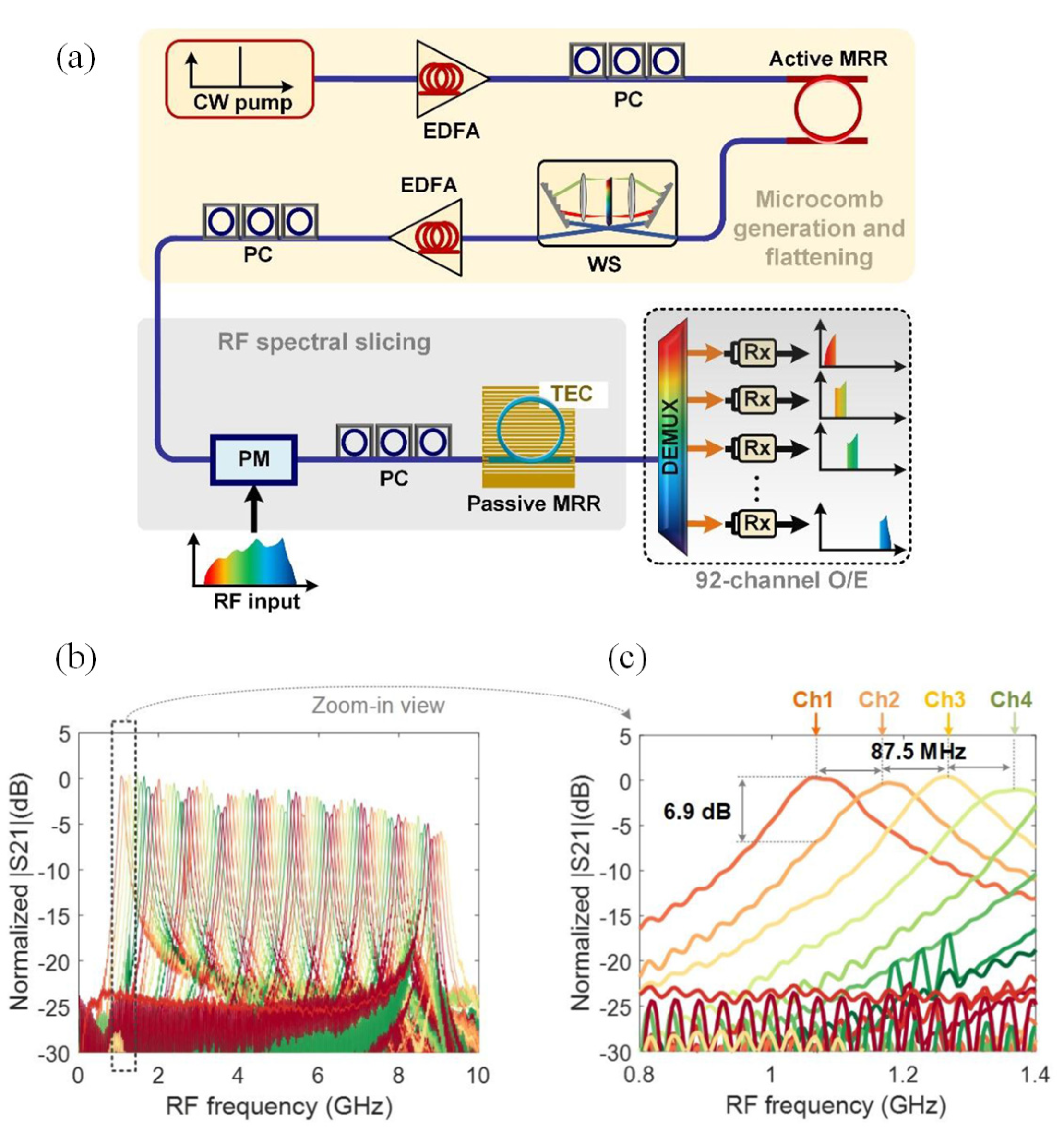
4.1. Microwave Photonics
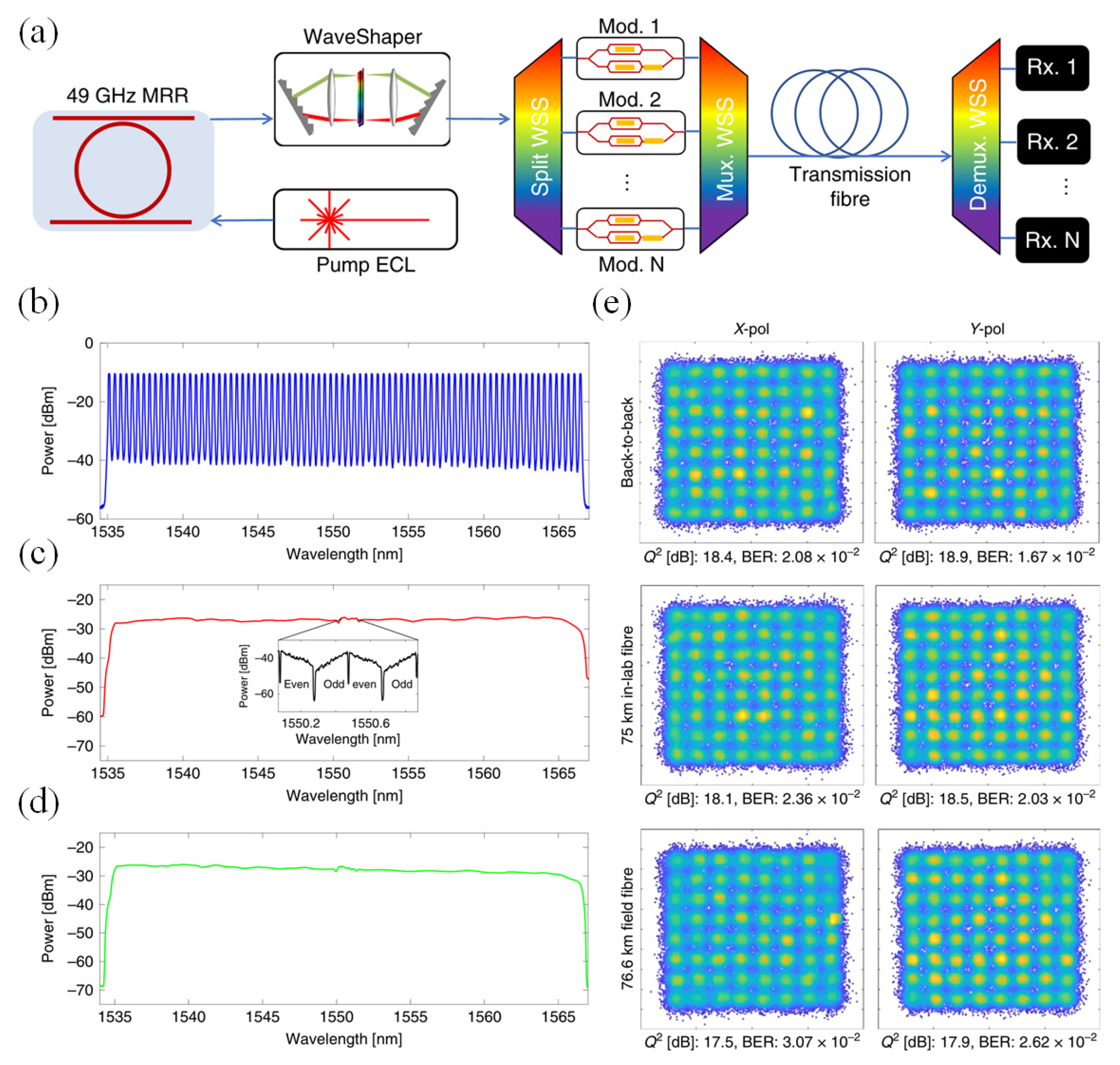
4.2. Optical Communication
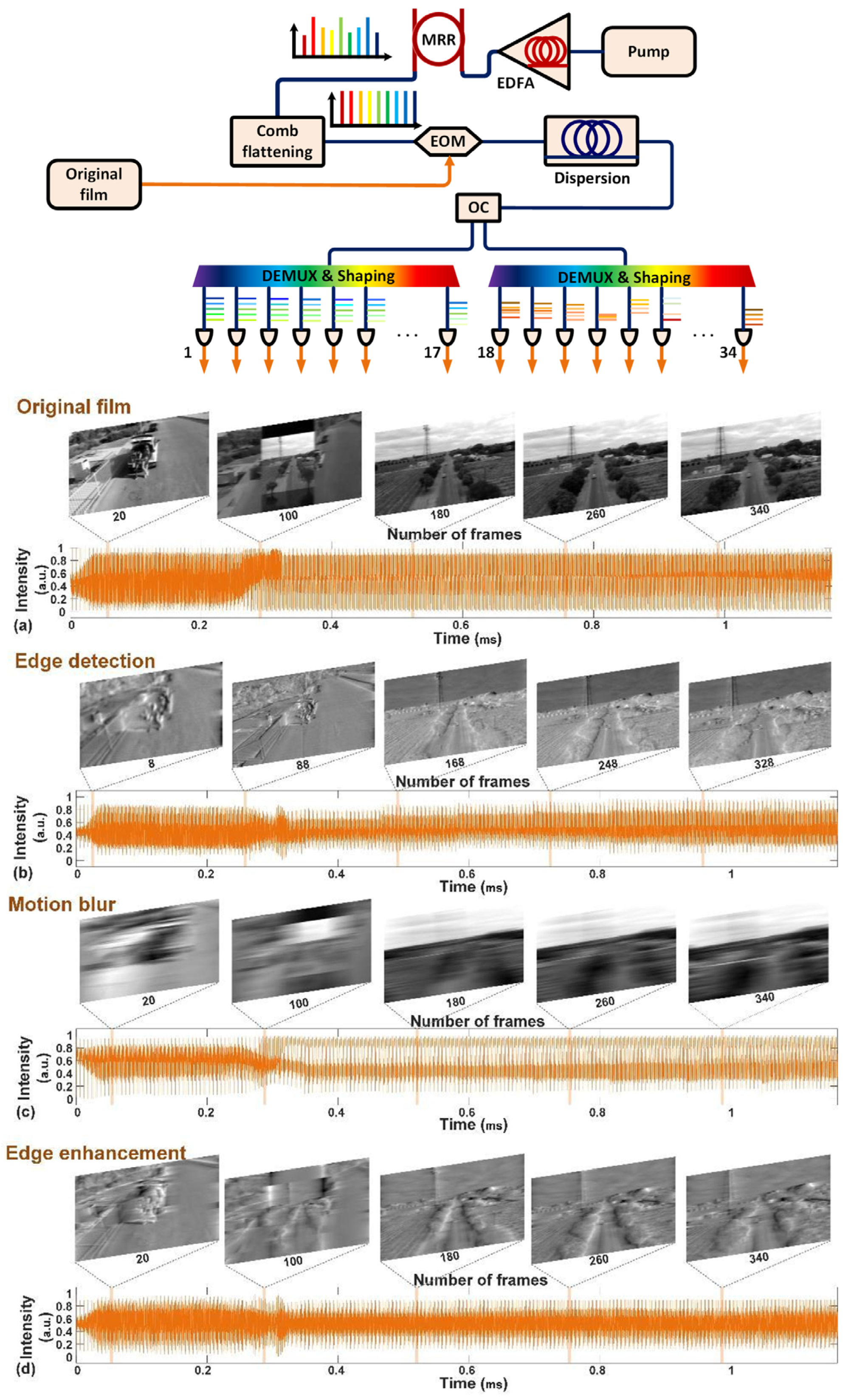
4.3. Photonic Neural Network
5. Challenges and Perspectives
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chang, L.; Liu, S.; Bowers, J.E. Integrated Optical Frequency Comb Technologies. Nat. Photonics 2022, 16, 95–108. [Google Scholar] [CrossRef]
- Kippenberg, T.; Holzwarth, R.; Diddams, S. Microresonator-Based Optical Frequency Combs. Science 2011, 332, 555–559. [Google Scholar] [CrossRef] [PubMed]
- Xiang, C.; Jin, W.; Bowers, J. Silicon nitride passive and active photonic integrated circuits: Trends and prospects. Photonics Res. 2022, 10, A82–A96. [Google Scholar] [CrossRef]
- Yang, Q.; Hu, Y.; Torres-Company, V.; Vahala, K. Efficient microresonator frequency combs. eLight 2024, 4, 18. [Google Scholar] [CrossRef]
- Raja, A.S.; Voloshin, A.S.; Guo, H.; Agafonova, S.E.; Liu, J.; Gorodnitskiy, A.S.; Karpov, M.; Pavlov, N.G.; Lucas, E.; Galiev, R.R.; et al. Electrically pumped photonic integrated soliton microcomb. Nat. Commun. 2019, 10, 680. [Google Scholar] [CrossRef]
- Kippenberg, T.; Gaeta, A.; Lipson, M.; Gorodetsky, M. Dissipative Kerr solitons in optical microresonators. Science 2018, 361, eaan8083. [Google Scholar] [CrossRef]
- Brasch, V.; Geiselmann, M.; Herr, T.; Lihachev, G.; Pfeiffer, M.; Gorodetsky, M.; Kippenberg, T. Photonic chip-based optical frequency comb using soliton Cherenkov radiation. Science 2016, 351, 357–360. [Google Scholar] [CrossRef]
- Liang, W.; Eliyahu, D.; Ilchenko, V.; Savchenkov, A.; Matsko, A.; Seidel, D.; Maleki, L. High spectral purity Kerr frequency comb radio frequency photonic oscillator. Nat. Commun. 2015, 5, 7957. [Google Scholar] [CrossRef]
- Raja, A.S.; Lange, S.; Karpov, M.; Shi, K.; Fu, X.; Behrendt, R.; Cletheroe, D.; Lukashchuk, A.; Haller, I.; Karinou, F.; et al. Ultrafast optical circuit switching for data centers using integrated soliton microcombs. Nat. Commun. 2021, 12, 5867. [Google Scholar] [CrossRef]
- Rizzo, A.; Novick, A.; Gopal, V.; Kim, B.; Ji, X.; Daudlin, S.; Okawachi, Y.; Cheng, Q.; Lipson, M.; Gaeta, A.; et al. Massively scalable Kerr comb-driven silicon photonic link. Nat. Photonics 2023, 17, 781–790. [Google Scholar] [CrossRef]
- Lucas, E.; Brochard, P.; Bouchand, R.; Schilt, S.; Südmeyer, T.; Kippenberg, T. Ultralow-noise photonic microwave synthesis using a soliton microcomb-based transfer oscillator. Nat. Commun. 2020, 11, 374. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Lucas, E.; Raja, A.; He, J.; Riemensberger, J.; Wang, R.; Karpov, M.; Guo, H.; Bouchand, R.; Kippenberg, T. Photonic microwave generation in the X- and K-band using integrated soliton microcombs. Nat. Photonics 2020, 14, 486–491. [Google Scholar] [CrossRef]
- Pavlov, N.; Lihachev, G.; Koptyaev, S.; Lucas, E.; Karpov, M.; Kondratiev, N.; Bilenko, I.; Kippenberg, T.; Gorodetsky, M. Soliton dual frequency combs in crystalline microresonators. Opt. Lett. 2017, 42, 514–517. [Google Scholar] [CrossRef] [PubMed]
- Lucas, E.; Lihachev, G.; Bouchand, R.; Pavlov, N.; Raja, A.; Karpov, M.; Gorodetsky, M.; Kippenberg, T. Spatial multiplexing of soliton microcombs. Nat. Photonics 2018, 12, 699–705. [Google Scholar] [CrossRef]
- Diddams, S.A.; Vahala, K.; Udem, T. Optical Frequency Combs: Coherently Uniting the Electromagnetic Spectrum. Science 2020, 369, eaay3676. [Google Scholar] [CrossRef]
- Yu, M.; Okawachi, Y.; Griffith, A.G.; Picqué, N.; Lipson, M.; Gaeta, A.L. Silicon-Chip-Based Mid-Infrared Dual-Comb Spectroscopy. Nat. Commun. 2018, 9, 1869. [Google Scholar] [CrossRef]
- Stern, L.; Stone, J.R.; Kang, S.; Cole, D.; Suh, M.; Fredrick, C.; Newman, Z.; Vahala, K.; Kitching, J.; Diddams, S. Direct Kerr Frequency Comb Atomic Spectroscopy and Stabilization. Sci. Adv. 2020, 6, eaax6230. [Google Scholar] [CrossRef]
- Suh, M.G.; Yang, Q.F.; Yang, K.Y.; Yi, X.; Vahala, K. Microresonator Soliton Dual-Comb Spectroscopy. Science 2016, 354, 600–603. [Google Scholar] [CrossRef]
- Dutt, A.; Joshi, C.; Ji, X.; Cardenas, J.; Okawachi, Y.; Luke, K.; Gaeta, A.L.; Lipson, M. On-Chip Dual-Comb Source for Spectroscopy. Sci. Adv. 2018, 4, e1701858. [Google Scholar] [CrossRef]
- Newman, Z.L.; Maurice, V.; Drake, T.; Stone, J.R.; Briles, T.C.; Spencer, D.T.; Fredrick, C.; Li, Q.; Westly, D.; Ilic, B.R.; et al. Architecture for the Photonic Integration of an Optical Atomic Clock. Optica 2019, 6, 680. [Google Scholar] [CrossRef]
- Nakamura, T.; Davila-Rodriguez, J.; Leopardi, H.; Sherman, J.A.; Fortier, T.M.; Xie, X.; Campbell, J.C.; McGrew, W.F.; Zhang, X.; Hassan, Y.S.; et al. Coherent Optical Clock Down-Conversion for Microwave Frequencies with 10−18 Instability. Science 2020, 368, 889–892. [Google Scholar] [CrossRef] [PubMed]
- Obrzud, E.; Rainer, M.; Harutyunyan, A.; Anderson, M.; Liu, J.; Geiselmann, M.; Chazelas, B.; Kundermann, S.; Lecomte, S.; Cecconi, M.; et al. A Microphotonic Astrocomb. Nat. Photonics 2019, 13, 31–35. [Google Scholar] [CrossRef]
- Suh, M.-G.; Yi, X.; Lai, Y.-H.; Leifer, S.; Grudinin, I.S.; Vasisht, G.; Martin, E.C.; Fitzgerald, M.P.; Doppmann, G.; Wang, J.; et al. Searching for Exoplanets Using a Microresonator Astrocomb. Nat. Photonics 2019, 13, 25–30. [Google Scholar] [CrossRef] [PubMed]
- Pfeifle, J.; Brasch, V.; Lauermann, M.; Yu, Y.; Wegner, D.; Herr, T.; Hartinger, K.; Schindler, P.; Li, J.; Hillerkuss, D.; et al. Coherent Terabit Communications with Microresonator Kerr Frequency Combs. Nat. Photonics 2014, 8, 375–380. [Google Scholar] [CrossRef]
- Geng, Y.; Zhou, H.; Han, X.; Cui, W.; Zhang, Q.; Liu, B.; Deng, G.; Zhou, Q.; Qiu, K. Coherent optical communications using coherence-cloned Kerr soliton microcombs. Nat. Commun. 2022, 13, 1070. [Google Scholar] [CrossRef]
- Mazur, M.; Suh, M.; Fülöp, A.; Schröder, J.; Torres-Company, V.; Karlsson, M.; Vahala, K.; Andrekson, P. High Spectral Efficiency Coherent Superchannel Transmission with Soliton Microcombs. J. Light. Technol. 2021, 39, 4367–4373. [Google Scholar] [CrossRef]
- Fujii, S.; Tanaka, S.; Ohtsuka, T.; Kogure, S.; Wada, K.; Kumazaki, H.; Tasaka, S.; Hashimoto, Y.; Kobayashi, Y.; Araki, T.; et al. Dissipative Kerr soliton microcombs for FEC-free optical communications over 100 channels. Opt. Express 2022, 30, 1351–1364. [Google Scholar] [CrossRef]
- Fülöp, A.; Mazur, M.; Lorences-Riesgo, A.; Helgason, B.; Wang, P.-H.; Xuan, Y.; Leaird, D.E.; Qi, M.; Andrekson, P.A.; Weiner, A.M.; et al. High-Order Coherent Communications Using Mode-Locked Dark-Pulse Kerr Combs from Microresonators. Nat. Commun. 2018, 9, 1598. [Google Scholar] [CrossRef]
- Marin-Palomo, P.; Kemal, J.; Karpov, M.; Kordts, A.; Pfeifle, J.; Pfeiffer, M.H.P.; Trocha, P.; Wolf, S.; Brasch, V.; Anderson, M.H.; et al. Microresonator-Based Solitons for Massively Parallel Coherent Optical Communications. Nature 2017, 546, 274–279. [Google Scholar] [CrossRef]
- Spencer, D.; Drake, T.; Briles, T.; Stone, J.; Sinclair, L.; Fredrick, C.; Li, Q.; Westly, D.; Ilic, B.; Bluestone, A.; et al. An Optical-Frequency Synthesizer Using Integrated Photonics. Nature 2018, 557, 81–85. [Google Scholar] [CrossRef]
- Vinod, A.; Huang, S.; Yang, J.; Yu, M.; Kwong, D.; Wong, C. Frequency microcomb stabilization via dual-microwave control. Commun. Phys. 2021, 4, 81. [Google Scholar] [CrossRef]
- Huang, S.; Yang, J.; Yu, M.; McGuyer, B.; Kwong, D.; Zelevinsky, T.; Wong, C. A broadband chip-scale optical frequency synthesizer at 2.7 × 10−16 relative uncertainty. Sci. Adv. 2016, 2, 1501489. [Google Scholar] [CrossRef] [PubMed]
- Del’Haye, P.; Coillet, A.; Fortier, T.; Beha, K.; Cole, D.; Yang, K.; Lee, H.; Vahala, K.; Papp, S.; Diddams, S. Phase-coherent microwave-to-optical link with a self-referenced microcomb. Nat. Photonics 2016, 10, 516–520. [Google Scholar] [CrossRef]
- Suh, M.; Vahala, K. Soliton microcomb range measurement. Science 2018, 359, 884–887. [Google Scholar] [CrossRef]
- Trocha, P.; Karpov, M.; Ganin, D.; Pfeiffer, M.; Kordts, A.; Wolf, S.; Krockenberger, J.; Marin-Palomo, P.; Weimann, C.; Randel, S.; et al. Ultrafast optical ranging using microresonator soliton frequency combs. Science 2018, 359, 887–891. [Google Scholar] [CrossRef]
- Wang, X.; Xie, P.; Chen, B.; Zhang, X. Chip-Based High-Dimensional Optical Neural Network. Nano-Micro Lett. 2022, 14, 221. [Google Scholar] [CrossRef]
- Feldmann, J.; Youngblood, N.; Karpov, M.; Gehring, H.; Li, X.; Stappers, M.; Le Gallo, M.; Fu, X.; Lukashchuk, A.; Raja, A.S.; et al. Parallel Convolutional Processing Using an Integrated Photonic Tensor Core. Nature 2021, 589, 52–58. [Google Scholar] [CrossRef]
- Bai, B.; Yang, Q.; Shu, H.; Chang, L.; Yang, F.; Shen, B.; Tao, Z.; Wang, J.; Xu, S.; Xie, W.; et al. Microcomb-Based Integrated Photonic Processing Unit. Nat. Commun. 2023, 14, 66. [Google Scholar] [CrossRef]
- Cheng, J.; Xie, Y.; Liu, Y.; Song, J.; Liu, X.; He, Z.; Zhang, W.; Han, X.; Zhou, H.; Zhou, K.; et al. Human Emotion Recognition with a Microcomb-Enabled Integrated Optical Neural Network. Nanophotonics 2023, 12, 3883–3894. [Google Scholar] [CrossRef]
- He, Z.; Cheng, J.; Liu, X.; Wu, B.; Zhou, H.; Dong, J.; Zhang, X. Microcomb-Driven Optical Convolution for Car Plate Recognition. Photonics 2023, 10, 972. [Google Scholar] [CrossRef]
- Shen, B.; Chang, L.; Liu, J.; Wang, H.; Yang, Q.; Xiang, C.; Wang, R.N.; He, J.; Liu, T.; Xie, W.; et al. Integrated Turnkey Soliton Microcombs. Nature 2020, 582, 365–369. [Google Scholar] [CrossRef] [PubMed]
- Hu, F.; Vinod, A.K.; Wang, W.; Chin, H.-H.; McMillan, J.F.; Zhan, Z.; Meng, Y.; Gong, M.; Wong, C.W. Spatio-Temporal Breather Dynamics in Microcomb Soliton Crystals. Light Sci. Appl. 2024, 13, 251. [Google Scholar] [CrossRef] [PubMed]
- Kippenberg, T.J.; Spillane, S.M.; Vahala, K.J. Kerr-Nonlinearity Optical Parametric Oscillation in an Ultrahigh-Q Toroid Microcavity. Phys. Rev. Lett. 2004, 93, 083904. [Google Scholar] [CrossRef] [PubMed]
- Del’Haye, P.; Schliesser, A.; Arcizet, O.; Wilken, T.; Holzwarth, R.; Kippenberg, T.J. Optical Frequency Comb Generation from a Monolithic Microresonator. Nature 2007, 450, 1214–1217. [Google Scholar] [CrossRef]
- Razzari, L.; Duchesne, D.; Ferrera, M.; Morandotti, R.; Chu, S.; Little, B.E.; Moss, D.J. CMOS-Compatible Integrated Optical Hyper-Parametric Oscillator. Nat. Photonics 2010, 4, 41–45. [Google Scholar] [CrossRef]
- Levy, J.S.; Gondarenko, A.; Foster, M.A.; Turner-Foster, A.C.; Gaeta, A.L.; Lipson, M. CMOS-Compatible Multiple-Wavelength Oscillator for on-Chip Optical Interconnects. Nat. Photonics 2010, 4, 37–40. [Google Scholar] [CrossRef]
- Herr, T.; Brasch, V.; Jost, J.D.; Wang, C.Y.; Kondratiev, N.M.; Gorodetsky, M.L.; Kippenberg, T.J. Temporal Solitons in Optical Microresonators. Nat. Photonics 2014, 8, 145–152. [Google Scholar] [CrossRef]
- Carmon, T.; Yang, L.; Vahala, K.J. Dynamical Thermal Behavior and Thermal Selfstability of Microcavities. Opt. Express 2004, 12, 4742. [Google Scholar] [CrossRef]
- Savchenkov, A.; Matsko, A.; Ilchenko, V.; Solomatine, I.; Seidel, D.; Maleki, L. Tunable Optical Frequency Comb with a Crystalline Whispering Gallery Mode Resonator. Phys. Rev. Lett. 2008, 101, 093902. [Google Scholar] [CrossRef]
- Brasch, V.; Geiselmann, M.; Pfeiffer, M.; Kippenberg, T. Bringing Short-Lived Dissipative Kerr Soliton States in Microresonators into a Steady State. Opt. Express 2016, 24, 29312. [Google Scholar] [CrossRef]
- Joshi, C.; Jang, J.; Luke, K.; Ji, X.; Miller, S.; Klenner, A.; Okawachi, Y.; Lipson, M.; Gaeta, A.L. Thermally Controlled Comb Generation and Soliton Modelocking in Microresonators. Opt. Lett. 2016, 41, 2565. [Google Scholar] [CrossRef] [PubMed]
- Lu, Z.; Wang, W.; Zhang, W.; Chu, S.; Little, B.; Liu, M.; Wang, L.; Zou, C.; Dong, C.; Zhao, B.; et al. Deterministic Generation and Switching of Dissipative Kerr Soliton in a Thermally Controlled Micro-Resonator. AIP Adv. 2024, 9, 025314. [Google Scholar] [CrossRef]
- Wang, X.; Xie, P.; Wang, W.; Wang, Y.; Lu, Z.; Wang, L.; Chu, S.; Little, B.; Zhao, W.; Zhang, W. Program-Controlled Single Soliton Microcomb Source. Photonics Res. 2021, 9, 66–72. [Google Scholar] [CrossRef]
- Zhou, H.; Geng, Y.; Cui, W.; Huang, S.; Zhou, Q.; Qiu, K.; Wei Wong, C. Soliton Bursts and Deterministic Dissipative Kerr Soliton Generation in Auxiliary-Assisted Microcavities. Light Sci. Appl. 2019, 8, 50. [Google Scholar] [CrossRef] [PubMed]
- He, Y.; Yang, Q.-F.; Ling, J.; Luo, R.; Liang, H.; Li, M.; Shen, B.; Wang, H.; Vahala, K.; Lin, Q. Self-Starting Bi-Chromatic LiNbO3 Soliton Microcomb. Optica 2019, 6, 1138–1144. [Google Scholar] [CrossRef]
- Cole, D.C.; Lamb, E.S.; Del’Haye, P.; Diddams, S.A.; Papp, S.B. Silica Soliton Crystals in Kerr Resonators. Nat. Photonics 2017, 11, 671–676. [Google Scholar] [CrossRef]
- Lin, G.; Sun, T. Yttria-Stabilized Zirconia Crystalline Mode Crossing Induced Soliton Frequency Comb Generation in High-Q Yttria-Stabilized Zirconia Crystalline Optical Microresonators. Photonics Res. 2022, 10, 731. [Google Scholar] [CrossRef]
- Wu, L.; Xie, W.; Chen, H.-J.; Colburn, K.; Xiang, C.; Chang, L.; Jin, W.; Liu, J.-Y.; Yu, Y.; Yamamoto, Y.; et al. AlGaAs Soliton Microcombs at Room Temperature. Opt. Lett. 2023, 48, 3853–3856. [Google Scholar] [CrossRef]
- Del’Haye, P.; Coillet, A.; Loh, W.; Beha, K.; Papp, S.; Diddams, S. Phase Steps and Resonator Detuning Measurements in Microresonator Frequency Combs. Nat. Commun. 2015, 6, 5668. [Google Scholar] [CrossRef]
- Niu, R.; Wan, S.; Wang, Z.-Y.; Li, J.; Wang, W.-Q.; Zhang, W.-F.; Guo, G.-C.; Zou, C.-L.; Dong, C.-H. Perfect Soliton Crystals in the High-Q Microrod Resonator. IEEE Photonics Technol. Lett. 2021, 33, 788–791. [Google Scholar] [CrossRef]
- Yao, B.; Huang, S.; Liu, Y.; Vinod, A.; Choi, C.; Hoff, M.; Li, Y.; Yu, M.; Feng, Z.; Kwong, D. Gate-Tunable Frequency Combs in Graphene–Nitride Microresonators. Nature 2018, 558, 410–414. [Google Scholar] [CrossRef] [PubMed]
- Karpov, M.; Pfeiffer, M.H.P.; Guo, H.; Weng, W.; Liu, J.; Kippenberg, T.J. Dynamics of Soliton Crystals in Optical Microresonators. Nat. Phys. 2019, 15, 1071–1077. [Google Scholar] [CrossRef]
- Ali Afridi, A.; Weng, H.; McDermott, M.; Lu, Q.; Guo, W.; Donegan, J.F. Versatile Octave-Spanning Soliton Crystals with High Conversion Efficiency in a Si3N4 Microresonator. Opt. Express 2023, 31, 33191. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.; Zhang, Y.; Zeng, S.; Li, J.; Xie, Y.; Chen, Y.; Yu, S. Low-Noise Kerr Frequency Comb Generation with Low Temperature Deuterated Silicon Nitride Waveguides. Opt. Express 2021, 29, 29557. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Wan, S.; Peng, J.-L.; Wang, Z.-Y.; Niu, R.; Zou, C.-L.; Guo, G.-C.; Dong, C.-H. Thermal Tuning of Mode Crossing and the Perfect Soliton Crystal in a Si3N4 Microresonator. Opt. Express 2022, 30, 13690–13698. [Google Scholar] [CrossRef]
- Boggio, J.M.C.; Bodenmüller, D.; Ahmed, S.; Wabnitz, S.; Modotto, D.; Hansson, T. Low-Loss Silicon Nitride Efficient Kerr Soliton Comb Generation in Micro-Resonator with Interferometric Back-Coupling. Nat. Commun. 2022, 13, 1292. [Google Scholar] [CrossRef]
- Wu, Z.; Gao, Y.; Zhang, T.; Dai, J.; Xu, K. Switching Dynamics of Dissipative Cnoidal Waves in Dual-Coupled Microresonators. Opt. Express 2021, 29, 42369. [Google Scholar] [CrossRef]
- He, Y.; Ling, J.; Li, M.; Lin, Q. Perfect Soliton Crystals on Demand. Laser Photonics Rev. 2020, 14, 1900339. [Google Scholar] [CrossRef]
- Weng, H.; Afridi, A.A.; Liu, J.; Li, J.; Dai, J.; Ma, X.; Zhang, Y.; Lu, Q.; Guo, W.; Donegan, J.F. Near-Octave-Spanning Breathing Soliton Crystal in an AlN Microresonator. Opt. Lett. 2021, 46, 3436. [Google Scholar] [CrossRef]
- Lu, Z.; Chen, H.-J.; Wang, W.; Yao, L.; Wang, Y.; Yu, Y.; Little, B.E.; Chu, S.T.; Gong, Q.; Zhao, W.; et al. Synthesized Soliton Crystals. Nat. Commun. 2021, 12, 3179. [Google Scholar] [CrossRef]
- Xu, B.; Fan, X.; Wang, S.; He, Z. Flat Soliton Microcomb Source. Opto-Electron. Adv. 2022, 5, 210023. [Google Scholar] [CrossRef]
- Wang, W.; Lu, Z.; Zhang, W.; Chu, S.T.; Little, B.E.; Wang, L.; Xie, X.; Liu, M.; Yang, Q.; Wang, L.; et al. Robust Soliton Crystals in a Thermally Controlled Microresonator. Opt. Lett. 2018, 43, 2002. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.; Wu, J.; Shoeiby, M.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Morandotti, R.; Mitchell, A.; Moss, D.J. Reconfigurable Broadband Microwave Photonic Intensity Differentiator Based on an Integrated Optical Frequency Comb Source. APL Photonics 2017, 2, 096104. [Google Scholar] [CrossRef]
- Andrianov, A. All-Optical Manipulation of Elastic Soliton Crystals in a Mode-Locked Fiber Laser. IEEE Photonics Technol. Lett. 2022, 34, 39–42. [Google Scholar] [CrossRef]
- Akhmediev, N.; Soto-Crespo, J.; Grapinet, M.; Grelu, P. Dissipative soliton interactions inside a fiber laser cavity. Opt. Fiber Technol. 2005, 11, 209–228. [Google Scholar] [CrossRef][Green Version]
- Grelu, P.; Akhmediev, N. Dissipative solitons for mode-locked lasers. Nat. Photonics 2012, 6, 84–92. [Google Scholar] [CrossRef]
- Grelu, P.; Belhache, F.; Gutty, F.; Soto-Crespo, J. Phase-locked soliton pairs in a stretched-pulse fiber laser. Opt. Lett. 2002, 27, 966–968. [Google Scholar] [CrossRef]
- Tang, D.; Man, W.; Tam, H.; Drummond, P. Observation of bound states of solitons in a passively mode-locked fiber laser. Phys. Rev. A 2001, 64, 033814. [Google Scholar] [CrossRef]
- Haboucha, A.; Leblond, H.; Salhi, M.; Komarov, A.; Sanchez, F. Analysis of soliton pattern formation in passively mode-locked fiber lasers. Phys. Rev. A 2008, 78, 043806. [Google Scholar] [CrossRef]
- Stratmann, M.; Pagel, T.; Mitschke, F. Experimental observation of temporal soliton molecules. Phys. Rev. Lett. 2005, 95, 143902. [Google Scholar] [CrossRef]
- Krupa, K.; Nithyanandan, K.; Andral, U.; Tchofo-Dinda, P.; Grelu, P. Real-Time Observation of Internal Motion within Ultrafast Dissipative Optical Soliton Molecules. Phys. Rev. Lett. 2017, 118, 243901. [Google Scholar] [CrossRef] [PubMed]
- Herink, G.; Kurtz, F.; Jalali, B.; Solli, D.; Ropers, C. Real-time spectral interferometry probes the internal dynamics of femtosecond soliton molecules. Science 2017, 356, 50–53. [Google Scholar] [CrossRef] [PubMed]
- Kutz, J.; Collings, B.; Bergman, K.; Knox, W. Stabilized pulse spacing in soliton lasers due to gain depletion and recovery. IEEE J. Quantum Electron. 1998, 34, 1749–1757. [Google Scholar] [CrossRef]
- Chembo, Y.K.; Yu, N. Modal Expansion Approach to Optical-Frequency-Comb Generation with Monolithic Whispering-Gallery-Mode Resonators. Phys. Rev. A 2010, 82, 033801. [Google Scholar] [CrossRef]
- Chembo, Y.K.; Yu, N. On the Generation of Octave-Spanning Optical Frequency Combs Using Monolithic Whispering-Gallery-Mode Microresonators. Opt. Lett. 2010, 35, 2696–2698. [Google Scholar] [CrossRef]
- Coen, S.; Randle, H.G.; Sylvestre, T.; Erkintalo, M. Modeling of Octave-Spanning Kerr Frequency Combs Using a Generalized Mean-Field Lugiato–Lefever Model. Opt. Lett. 2013, 38, 37. [Google Scholar] [CrossRef]
- Matsko, A.B.; Savchenkov, A.A.; Liang, W.; Ilchenko, V.S.; Seidel, D.; Maleki, L. Mode-Locked Kerr Frequency Combs. Opt. Lett. 2011, 36, 2845. [Google Scholar] [CrossRef]
- Chembo, Y.K.; Menyuk, C.R. Spatiotemporal Lugiato-Lefever Formalism for Kerr-Comb Generation in Whispering-Gallery-Mode Resonators. Phys. Rev. A 2013, 87, 053852. [Google Scholar] [CrossRef]
- Cole, D.C.; Stone, J.R.; Erkintalo, M.; Yang, K.Y.; Yi, X.; Vahala, K.J.; Papp, S.B. Kerr-Microresonator Solitons from a Chirped Background. Optica 2018, 5, 1304. [Google Scholar] [CrossRef]
- Lu, Z.; Wang, Y.; Zhao, B.; Liu, M.; Wang, W. Perfect Soliton Crystal in a Microcavity via Sub-Harmonic Phase-Modulation Scheme. Jpn. J. Appl. Phys. 2020, 59, 060903. [Google Scholar] [CrossRef]
- Bogaerts, W.; De Heyn, P.; Van Vaerenbergh, T.; De Vos, K.; Kumar Selvaraja, S.; Claes, T.; Dumon, P.; Bienstman, P.; Van Thourhout, D.; Baets, R. Silicon Microring Resonators. Laser Photonics Rev. 2012, 6, 47–73. [Google Scholar] [CrossRef]
- Kumagai, T.; Hirota, N.; Sato, K.; Namiki, K.; Maki, H.; Tanabe, T. Deterministic Generation of a Perfect Soliton Crystal Microcomb with a Saturable Absorber. Opt. Lett. 2022, 47, 1458–1461. [Google Scholar]
- Kumagai, T.; Hirota, N.; Sato, K.; Namiki, K.; Maki, H.; Tanabe, T. Saturable Absorption by Carbon Nanotubes on Silica Microtoroids. J. Appl. Phys. 2018, 123, 233104. [Google Scholar] [CrossRef]
- Tan, M.; Xu, X.; Corcoran, B.; Wu, J.; Boes, A.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Morandotti, R.; Mitchell, A.; et al. RF and Microwave Fractional Differentiator Based on Photonics. IEEE Trans. Circuits Syst. 2020, 67, 2767–2771. [Google Scholar] [CrossRef]
- Tan, M.; Xu, X.; Boes, A.; Corcoran, B.; Wu, J.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Lowery, A.J.; Morandotti, R.; et al. Highly Versatile Broadband RF Photonic Fractional Hilbert Transformer Based on a Kerr Soliton Crystal Microcomb. J. Light. Technol. 2021, 39, 7581–7587. [Google Scholar] [CrossRef]
- Tan, M.; Xu, X.; Boes, A.; Corcoran, B.; Wu, J.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Morandotti, R.; Mitchell, A. Photonic RF Arbitrary Waveform Generator Based on a Soliton Crystal Micro-Comb Source. J. Light. Technol. 2020, 38, 6221–6226. [Google Scholar] [CrossRef]
- Xu, X.; Tan, M.; Wu, J.; Boes, A.; Corcoran, B.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Morandotti, R.; Mitchell, A. Photonic RF Phase-Encoded Signal Generation with a Microcomb Source. J. Light. Technol. 2020, 38, 1722–1727. [Google Scholar] [CrossRef]
- Xu, X.; Wu, J.; Nguyen, T.G.; Moein, T.; Chu, S.T.; Little, B.E.; Morandotti, R.; Mitchell, A.; Moss, D.J. Photonic microwave true time delays for phased array antennas using a 49 GHz FSR integrated optical micro-comb source [Invited]. Photonics Res. 2018, 6, B30–B36. [Google Scholar] [CrossRef]
- Corcoran, B.; Tan, M.; Xu, X.; Boes, A.; Wu, J.; Nguyen, T.; Chu, S.; Little, B.; Morandotti, R.; Mitchell, A.; et al. Ultra-Dense Optical Data Transmission over Standard Fibre with a Single Chip Source. Nat. Commun. 2020, 11, 2568. [Google Scholar] [CrossRef]
- Xu, X.; Tan, M.; Wu, J.; Boes, A.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Morandotti, R.; Moss, D.J. Broadband Photonic RF Channelizer with 92 Channels Based on a Soliton Crystal Microcomb. J. Light. Technol. 2020, 38, 5116–5121. [Google Scholar] [CrossRef]
- Xu, X.; Tan, M.; Corcoran, B.; Wu, J.; Boes, A.; Nguyen, T.; Chu, S.; Little, B.; Hicks, D.G.; Morandotti, R.; et al. 11 TOPS Photonic Convolutional Accelerator for Optical Neural Networks. Nature 2021, 589, 44–51. [Google Scholar] [CrossRef] [PubMed]
- Tan, M. Photonic Signal Processor Based on a Kerr Microcomb for Real-Time Video Image Processing. Commun. Eng. 2023, 2, 94. [Google Scholar] [CrossRef]
- Ambrogio, S.; Narayanan, P.; Tsai, H.; Shelby, R.; Boybat, I.; di Nolfo, C.; Sidler, S.; Giordano, M.; Bodini, M.; Farinha, N.; et al. Equivalent-accuracy accelerated neural-network training using analogue memory. Nature 2018, 558, 60–67. [Google Scholar] [CrossRef] [PubMed]
- Esser, S.; Merolla, P.; Arthur, J.; Cassidy, A.; Appuswamy, R.; Andreopoulos, A.; Berg, D.; McKinstry, J.; Melano, T.; Barch, D.; et al. Convolutional networks for fast, energy-efficient neuromorphic computing. Proc. Natl. Acad. Sci. USA 2016, 113, 11441–11446. [Google Scholar] [CrossRef] [PubMed]
- Graves, A.; Wayne, G.; Eynolds, M.; Harley, T.; Danihelka, I.; Grabska-Barwinska, A.; Colmenarejo, S.; Grefenstette, E.; Amalho, T.; Agapiou, J. Hybrid computing using a neural network with dynamic external memory. Nature 2016, 538, 471–476. [Google Scholar] [CrossRef]
- Xiang, C.; Jin, W.; Terra, O.; Dong, B.; Wang, H.; Wu, L.; Guo, J.; Morin, T.J.; Hughes, E.; Peters, J.; et al. 3D Integration Enables Ultralow-Noise Isolator-Free Lasers in Silicon Photonics. Nature 2023, 620, 78–85. [Google Scholar] [CrossRef]
- Xiang, C.; Guo, J.; Jin, W.; Wu, L.; Peters, J.; Xie, W.; Chang, L.; Shen, B.; Wang, H.; Yang, Q.-F.; et al. High-Performance Lasers for Fully Integrated Silicon Nitride Photonics. Nat. Commun. 2021, 12, 6650. [Google Scholar] [CrossRef]
- Wei, W.-Q.; He, A.; Yang, B.; Wang, Z.-H.; Huang, J.-Z.; Han, D.; Ming, M.; Guo, X.; Su, Y.; Zhang, J.-J.; et al. Monolithic Integration of Embedded III-V Lasers on SOI. Light Sci. Appl. 2023, 12, 84. [Google Scholar] [CrossRef]
- Singh, N.; Lorenzen, J.; Sinobad, M.; Wang, K.; Liapis, A.; Frankis, H.; Haugg, S.; Francis, H.; Carreira, J.; Geiselmann, M.; et al. Silicon Photonics-Based High-Energy Passively Q-Switched Laser. Nat. Photonics 2024, 18, 485–491. [Google Scholar] [CrossRef]
- Snigirev, V.; Riedhauser, A.; Lihachev, G.; Churaev, M.; Riemensberger, J.; Wang, R.; Siddharth, A.; Huang, G.; Möhl, C.; Popoff, Y. Ultrafast Tunable Lasers Using Lithium Niobate Integrated Photonics. Nature 2023, 615, 411–417. [Google Scholar] [CrossRef]
- Sahin, E.; Ooi, K.; Png, C.; Tan, D. Large, scalable dispersion engineering using cladding-modulated Bragg gratings on a silicon chip. Appl. Phys. Lett. 2017, 110, 161113. [Google Scholar] [CrossRef]
- Zhang, K.; Sun, W.; Chen, Y.; Feng, H.; Zhang, Y.; Chen, Z.; Wang, C. A Power-Efficient Integrated Lithium Niobate Electro-Optic Comb Generator. Commun. Phys. 2023, 6, 17. [Google Scholar] [CrossRef]
- Xu, M.; Zhu, Y.; Pittalà, F.; Tang, J.; He, M.; Ng, W.C.; Wang, J.; Ruan, Z.; Tang, X.; Kuschnerov, M.; et al. Dual-Polarization Thin-Film Lithium Niobate in-Phase Quadrature Modulators for Terabit-per-Second Transmission. Optica 2022, 9, 61. [Google Scholar] [CrossRef]
- Xu, M.; He, M.; Zhang, H.; Jian, J.; Pan, Y.; Liu, X.; Chen, L.; Meng, X.; Chen, H.; Li, Z. High-Performance Coherent Optical Modulators Based on Thin-Film Lithium Niobate Platform. Nat. Commun. 2020, 11, 3911. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Shen, J.; Li, J.; Wang, H.; Feng, C.; Zhang, L.; Sun, L.; Xu, J.; Liu, M.; Wang, Y.; et al. High-Speed Electro-Optic Modulation in Topological Interface States of a One-Dimensional Lattice. Light Sci. Appl. 2023, 12, 206. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, M.; Chen, X.; Bertrand, M.; Shams-Ansari, A.; Chandrasekhar, S.; Winzer, P.; Loncar, M. Integrated Lithium Niobate Electro-Optic Modulators Operating at CMOS-Compatible Voltages. Nature 2018, 562, 101. [Google Scholar] [CrossRef]
- Li, M.; Ling, J.; He, Y.; Javid, U.; Xue, S.; Lin, Q. Lithium Niobate Photonic-Crystal Electro-Optic Modulator. Nat. Commun. 2020, 11, 4123. [Google Scholar] [CrossRef]
- Han, C.; Zheng, Z.; Shu, H.; Jin, M.; Qin, J.; Chen, R.; Tao, Y.; Shen, B.; Bai, B.; Yang, F.; et al. Slow-Light Silicon Modulator with 110-GHz Bandwidth. Sci. Adv. 2023, 9, eadi5339. [Google Scholar] [CrossRef]
- Renaud, D.; Assumpcao, D.; Joe, G.; Shams-Ansari, A.; Zhu, D.; Hu, Y.; Sinclair, N.; Loncar, M. Sub-1 Volt and High-Bandwidth Visible to near-Infrared Electro-Optic Modulators. Nat. Commun. 2023, 14, 1496. [Google Scholar] [CrossRef]
- Zhang, Y.; Shao, L.; Yang, J.; Chen, Z.; Zhang, K.; Shum, K.-M.; Zhu, D.; Chan, C.H.; Lončar, M.; Wang, C. Systematic Investigation of Millimeter-Wave Optic Modulation Performance in Thin-Film Lithium Niobate. Photonics Res. 2022, 10, 2380. [Google Scholar] [CrossRef]
- Pan, B.; Liu, H.; Xu, H.; Huang, Y.; Li, H.; Yu, Z.; Liu, L.; Shi, Y.; Dai, D. Ultra-Compact Lithium Niobate Microcavity Electro-Optic Modulator beyond 110 GHz. Chip 2022, 1, 100029. [Google Scholar] [CrossRef]
- Du, Z.; Xiang, C.; Fu, T.; Chen, M.; Yang, S.; Bowers, J.; Chen, H. Silicon nitride chirped spiral Bragg grating with large group delay. APL Photonics 2020, 5, 101302. [Google Scholar] [CrossRef]
- Chen, D.; Zhang, H.; Liu, M.; Hu, X.; Zhang, Y.; Wu, D.; Zhou, P.; Chang, S.; Wang, L.; Xiao, X. 67 GHz Light-Trapping-Structure Germanium Photodetector Supporting 240 Gb/s PAM-4 Transmission. Photonics Res. 2022, 10, 2165. [Google Scholar] [CrossRef]
- Shi, Y.; Zhou, D.; Yu, Y.; Zhang, X. 80 GHz Germanium Waveguide Photodiode Enabled by Parasitic Parameter Engineering. Photonics Res. 2021, 9, 605. [Google Scholar] [CrossRef]
- Shi, Y.; Li, X.; Zou, M.; Yu, Y.; Zhang, X. 103 GHz Germanium-on-Silicon Photodiode Enabled by an Optimized U-Shaped Electrode. Photonics Res. 2024, 12, 1. [Google Scholar] [CrossRef]
- Lischke, S.; Peczek, A.; Morgan, J.; Sun, K.; Steckler, D.; Yamamoto, Y.; Korndörfer, F.; Mai, C.; Marschmeyer, S.; Fraschke, M.; et al. Ultra-Fast Germanium Photodiode with 3-dB Bandwidth of 265 GHz. Nat. Photonics 2021, 15, 925–931. [Google Scholar] [CrossRef]
- Li, L.; Wang, L.; Long, T.; Zhang, Z.; Lu, J.; Chen, B. Ultra-Fast Waveguide MUTC Photodiodes Over 220 GHz. J. Light. Technol. 2024, 14, 7451–7457. [Google Scholar] [CrossRef]
- Wen, P.; Tiwari, P.; Mauthe, S.; Schmid, H.; Sousa, M.; Scherrer, M.; Baumann, M.; Bitachon, B.; Leuthold, J.; Gotsmann, B.; et al. Waveguide Coupled III-V Photodiodes Monolithically Integrated on Si. Nat. Commun. 2022, 13, 909. [Google Scholar] [CrossRef]
- Wu, Q.; Qian, J.; Wang, Y.; Xing, L.; Wei, Z.; Gao, X.; Li, Y.; Liu, Z.; Liu, H.; Shu, H.; et al. Waveguide-Integrated Twisted Bilayer Graphene Photodetectors. Nat. Commun. 2024, 15, 3688. [Google Scholar] [CrossRef]
- Moille, G.; Westly, D.; Orji, N.G.; Srinivasan, K. Tailoring Broadband Kerr Soliton Microcombs via Post-Fabrication Tuning of the Geometric Dispersion. Appl. Phys. Lett. 2021, 119, 121103. [Google Scholar] [CrossRef]
- Murray, C.E.; Tan, M.; Prayoonyong, C.; Zhu, X.; Chu, S.T.; Little, B.E.; Morandotti, R.; Mitchell, A.; Moss, D.J.; Corcoran, B. Investigating the Thermal Robustness of Soliton Crystal Microcombs. Opt. Express 2023, 31, 37749. [Google Scholar] [CrossRef] [PubMed]
- Helgason, O.; Arteaga-Sierra, F.; Ye, Z.; Twayana, K.; Andrekson, P.; Karlsson, M.; Schröder, J.; Torres-Company, V. Dissipative Solitons in Photonic Molecules. Nat. Photonics 2021, 15, 305–310. [Google Scholar] [CrossRef]
- Zhu, E.; Zhao, C. Modulation Instability of Kerr Optical Frequency Combs in Dual-Coupled Optical Cavities. Phys. Rev. A 2022, 105, 013524. [Google Scholar] [CrossRef]
- Helgason, O.; Girardi, M.; Ye, Z.; Lei, F.; Schröder, J.; Torres-Company, V. Surpassing the Nonlinear Conversion Efficiency of Soliton Microcombs. Nat. Photonics 2023, 17, 992–999. [Google Scholar] [CrossRef]
- Gentry, C.M.; Zeng, X.; Popovic, M. Tunable Coupled-Mode Dispersion Compensation and Its Application to on-Chip Resonant Four-Wave Mixing. Opt. Lett. 2014, 39, 5689–5692. [Google Scholar] [CrossRef]
- Xue, X.; Xuan, Y.; Wang, P.; Liu, Y.; Leaird, D.E.; Qi, M.; Weiner, A.M. Normal-dispersion Microcombs Enabled by Controllable Mode Interactions. Laser Photonics Rev. 2015, 9, L23–L28. [Google Scholar] [CrossRef]
- Xu, X.; Ren, G.; Feleppa, T.; Liu, X.; Boes, A.; Mitchell, A.; Lowery, A.J. Self-Calibrating Programmable Photonic Integrated Circuits. Nat. Photonics 2022, 16, 595–602. [Google Scholar] [CrossRef]
- Cohen, L.; Wu, K.; Myilswamy, K.V.; Fatema, S.; Lingaraju, N.B.; Weiner, A.M. Silicon Photonic Microresonator-Based High-Resolution Line-by-Line Pulse Shaping. Nat. Commun. 2024, 15, 7878. [Google Scholar] [CrossRef]
- Zhang, W.; Huang, C.; Peng, H.; Bilodeau, S.; Jha, A.; Blow, E.; Lima, T.; Shastri, B.; Prucnal, P. Silicon Microring Synapses Enable Photonic Deep Learning beyond 9-Bit Precision. Optica 2022, 9, 579. [Google Scholar] [CrossRef]
- Huang, C.; Bilodeau, S.; Lima, T.; Tait, A.N.; Ma, P.Y.; Blow, E.C.; Jha, A.; Peng, H.T.; Shastri, B.J.; Prucnal, P.R. Demonstration of Scalable Microring Weight Bank Control for Large-Scale Photonic Integrated Circuits. APL Photonics 2020, 5, 040803. [Google Scholar] [CrossRef]
- Huang, C.; Fujisawa, S.; de Lima, T.F.; Tait, A.N.; Blow, E.C.; Tian, Y.; Bilodeau, S.; Jha, A.; Yaman, F.; Peng, H.-T.; et al. A Silicon Photonic–Electronic Neural Network for Fibre Nonlinearity Compensation. Nat. Electron. 2021, 4, 837–844. [Google Scholar] [CrossRef]
- Xiang, C.; Liu, J.; Guo, J.; Chang, L.; Wang, R.; Weng, W.; Peters, J.; Xie, W.; Zhang, Z.; Riemensberger, J.; et al. Laser Soliton Microcombs Heterogeneously Integrated on Silicon. Science 2021, 373, 99–103. [Google Scholar] [CrossRef] [PubMed]
- He, M.; Xu, M.; Ren, Y.; Jian, J.; Ruan, Z.; Xu, Y.; Gao, S.; Sun, S.; Wen, X.; Zhou, L.; et al. High-performance hybrid silicon and lithium niobate Mach-Zehnder modulators for 100 Gbit s−1 and beyond. Nat. Photonics 2019, 13, 359–364. [Google Scholar] [CrossRef]
- Sun, S.; He, M.; Xu, M.; Gao, S.; Chen, Z.; Zhang, X.; Ruan, Z.; Wu, X.; Zhou, L.; Liu, L.; et al. Bias-drift-free Mach-Zehnder modulators based on a heterogeneous silicon and lithium niobate platform. Photonics Res. 2020, 8, 1958–1963. [Google Scholar] [CrossRef]
- Shen, X.; Xu, Y.; Dong, Y.; Zhang, B.; Ni, Y. Thin-Film Lithium Niobate-Silicon Nitride Electro-Optic Modulator Based on Embedded Filling Layer. Acta Opt. Sin. 2023, 43, 1413001. [Google Scholar]
- Bioud, Y.A.; Boucherif, A.; Myronov, M.; Soltani, A.; Patriarche, G.; Braidy, N.; Jellite, M.; Drouin, D.; Arès, R. Uprooting defects to enable high-performance III–V optoelectronic devices on silicon. Nat. Commun. 2019, 10, 12353. [Google Scholar] [CrossRef]
- Xu, Y.; Al Sayem, A.; Fan, L.; Zou, C.-L.; Wang, S.; Cheng, R.; Fu, W.; Yang, L.; Xu, M.; Tang, H.X. Bidirectional interconversion of microwave and light with thin-film lithium niobate. Nat. Commun. 2021, 12, 4453. [Google Scholar] [CrossRef]
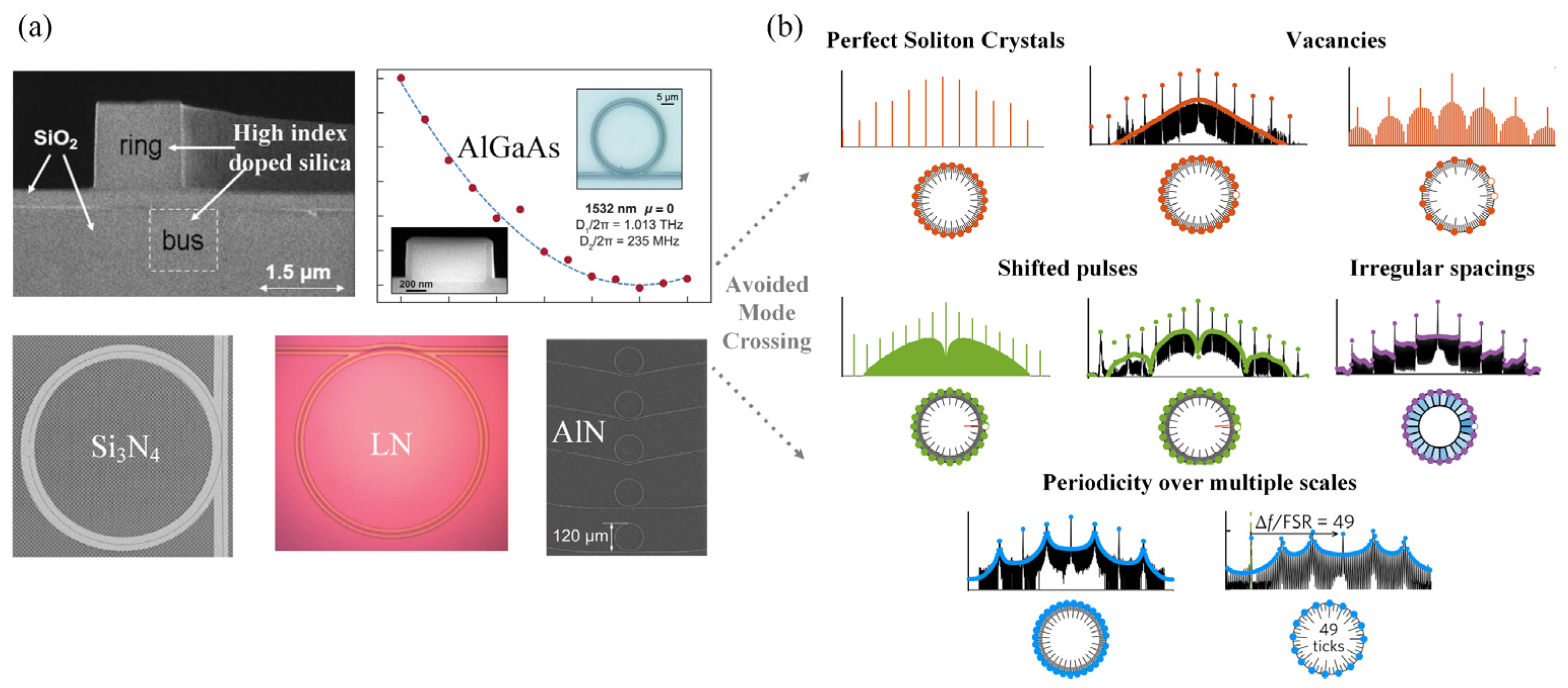



| Material Platform | Structure | FSR (GHz) | Wavelength Range (nm) | Crystal Types | Refs. |
|---|---|---|---|---|---|
| YSZ | microdisk | ~74.5 | 1530–1580 | PSC 1 | [57] |
| AlGaAs | microring | ~1018 | 1400–1700 | PSC | [58] |
| SiO2 | microrod | ~25.6 | 1535–1565 | Defected SC | [59] |
| SiO2 | microdisk | ~26 | 1530–1570 | Multiple SC | [56] |
| SiO2 | microrod | ~60.7 | 1500–1600 | PSC | [60] |
| Graphene–Nitride | microring | ~90 | 1400–1900 | PSC | [61] |
| SiNx | microring | ~200 | 1400–1800 | PSC | [62] |
| LN | microring | ~199.7 | 1480–1640 | PSC | [68] |
| AlN | microring | ~374 | 1150–2300 | PSC | [69] |
| High-Index Doped Silica | microring | ~49 | 1500–1650 | PSC | [70] |
| High-Index Doped Silica | microring | ~48.9 | 1450–1650 | Flat Spectral SC | [71] |
| High-Index Doped Silica | microring | ~48.9 | 1500–1600 | Multiple SC | [72] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Zhang, H.; Song, Y.; Zhu, X.; Murray, C.E.; Bai, Y.; Tan, M.; Chu, S.T.; Moss, D.J.; Xu, X.; et al. Advances in Soliton Crystal Microcombs. Photonics 2024, 11, 1164. https://doi.org/10.3390/photonics11121164
Liu Z, Zhang H, Song Y, Zhu X, Murray CE, Bai Y, Tan M, Chu ST, Moss DJ, Xu X, et al. Advances in Soliton Crystal Microcombs. Photonics. 2024; 11(12):1164. https://doi.org/10.3390/photonics11121164
Chicago/Turabian StyleLiu, Zhihui, Haoran Zhang, Yuhang Song, Xiaotian Zhu, Caitlin E. Murray, Yunping Bai, Mengxi Tan, Sai T. Chu, David J. Moss, Xingyuan Xu, and et al. 2024. "Advances in Soliton Crystal Microcombs" Photonics 11, no. 12: 1164. https://doi.org/10.3390/photonics11121164
APA StyleLiu, Z., Zhang, H., Song, Y., Zhu, X., Murray, C. E., Bai, Y., Tan, M., Chu, S. T., Moss, D. J., Xu, X., & Xu, K. (2024). Advances in Soliton Crystal Microcombs. Photonics, 11(12), 1164. https://doi.org/10.3390/photonics11121164






