Abstract
The utilization of atomic or molecular spectroscopy for frequency locking of single-frequency laser to improve laser frequency stability plays an important role in the experimental investigation of optically pumped atomic magnetometers, atomic clocks, laser cooling and trapping of atoms, etc. We have experimentally demonstrated a technique for frequency stabilization of a single-frequency laser employing the bright state spectroscopy (BSS) with a rubidium atomic vapor cell. By utilizing the counter-propagating dual-frequency 795 nm laser beams with mutually orthogonal linear polarization and a frequency difference of 6.834 GHz, which is equal to the hyperfine splitting of rubidium-87 ground state 5, an absorption-enhanced signal with narrow linewidth at the center of Doppler-broadened transmission spectroscopy is observed when continuous scanning the laser frequency over rubidium-87 D1 transition. This is the so-called BSS. Amplitude of the absorption-enhanced signal in the BSS is much larger compared with the conventional saturation absorption spectroscopy (SAS). The relationship between linewidth and amplitude of the BSS signal and laser beam intensity has been investigated. This high-contrast absorption-enhanced BSS signal has been employed for the laser frequency stabilization. The experimental results show that the frequency stability is with an integration time of 40 s, near one order of magnitude better than that for using the SAS.
1. Introduction
Sub-Doppler spectroscopy is an important method for accurately detecting atomic or molecular resonance lines [1,2,3]. The technique is widely employed in laser frequency locking due to its relative simplicity and reliability. Laser spectroscopy of atoms and molecules is typically conducted by scanning the laser frequency. However, the close-range spectral lines of atomic fine or hyperfine structures are frequently obscured by the Doppler broadening resulting from the thermal motion of the atoms. To circumvent the issue of Doppler broadening when utilizing atomic leaps as a frequency reference, kinds of Doppler-free spectroscopic techniques have been developed, including SAS [4,5,6], polarization spectroscopy [7,8], and modulation transfer spectroscopy [9,10]. In order to obtain dispersion-like signals with a frequency discrimination capability, the SAS needs to be modulated and demodulated by a lock-in amplifier. Polarization spectroscopy can generate dispersion signals by detecting induced birefringence, which can be used directly for frequency locking without additional frequency modulation [11]. Modulation transfer spectroscopy employs external modulation, which avoids the effect on the laser.
The standard configuration for SAS entails the use of two counterpropagating light beams with same frequencies through a gas cell containing atoms or molecules. The beams drive distinct atomic populations, each possessing its own axial velocities, thereby resulting in the generation of transmission peaks on the Doppler background [12]. Recent experiments have been carried out using alkali metal atomic gas cells. Based on coherent population trapping (CPT), the laser frequency locking on Cs atoms has been achieved by utilizing dual-frequency sub-Doppler spectroscopy, with a frequency stability of with integration time of 1 s. The frequency difference between the dual-frequency beams equals the ground-state hyperfine splitting of alkali metals. This has led to the observation of a double-frequency sub-Doppler absorption spectroscopy characterized by high contrast and an inverted sign, which can be leveraged to stabilize laser frequency and enhance its stability further [13,14]. The emergence of this high-contrast inverted sub-Doppler resonance stems from several intricate physical phenomena, including CPT effects between the two hyperfine states of the ground state and a hyperfine state of the excited state, as well as velocity-selective optical pumping effects [15]. Generally speaking, we employ a dual-frequency laser to couple with a three-level system for generating CPT spectroscopy, which are used to lock the microwave frequencies in microwave atomic clocks. However, in this situation, the laser frequency usually cannot be locked. In this paper, we extend this method to Rb atoms to achieve laser frequency locking.
In this paper, we demonstrate the BSS with dual-frequency beam, counterpropagating laser with orthogonal polarizations. First, the interaction between the bright and dark states based on an alkali metal atomic energy level system is theoretically analyzed. Second, the experimental parameters such as microwave frequency, microwave power, and laser power are optimized, the spectral properties in different cases are analyzed, and the laser is frequency locked to this high contrast signal. Finally, the locking effect of a single set of lasers was measured in the time domain, while the frequency stability of the lasers was characterized by the Allan deviation. This frequency locked technology can be applied in experimental studies such as atomic clocks, atomic magnetometers, and laser-cooled atoms to enhance the precision of laser frequencies.
2. Theoretical Analysis
As shown in Figure 1, our model is based on the energy level system of alkali metal atoms, which interacts with the two-frequency pump and probe beams propagating in opposite directions. The linearly polarized two-frequency pump beam makes some atoms enter the CPT dark state. Then, the back-propagating linear polarization probe beam interacts with the dark atom.
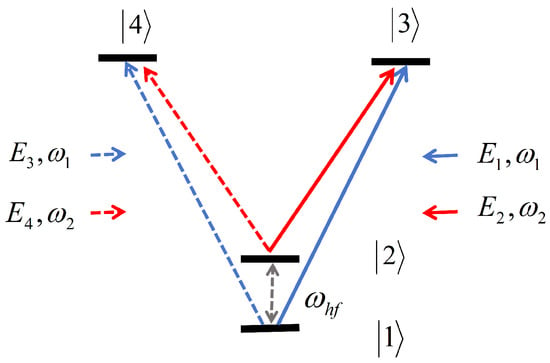
Figure 1.
Alkali metal atomic energy level system. and are the hyperfine states of ground state. and are the excited states of D1 transition.
The pump beam propagates along the z direction, and the electric field of the pump beam and the probe beam can be written as [16]
Here, and are in the same direction as the z axis and correspond to two frequency components and , respectively, while and are backward propagating beams. Since the fields are formed by the reflection of the fields and , they have a certain spatial phase shift, where the relative phase of the two frequencies of the back-propagating beam is denoted by and , respectively.
In Equation (1), is the wave vector, is wavelength, and c is the speed of light in vacuum. In the rotating coordinate system and Raman resonance, when , where is the hyperfine transition frequency of the ground state, the dark state prepared by the pump beam is [17]
In Equation (2), , ; similarly, the dark state prepared by the probe beam is
In Equation (3), . When , , when the two states are parallel or in phase, the atomic absorption decreases (the transmittance of the atomic gas cell increases), that is the saturation absorption transmission peak,
The phase relation is
In this case, and together prepare the dark state, and the ‘competition’ between and does not destroy the CPT effect.
On the contrary, if the two states are orthogonal, i.e., the pump light is prepared in the dark state, and the probe light is prepared in the bright state,
The atomic medium strongly scatters photons from the resonant light field, resulting in a significant increase in the absorption (or transmission reduction) of the atomic vapor cell. This occurs in
In this case, atoms start to absorb intensively and scatter energy from the light field since they are no longer in the dark state.
The sign reversal of the sub-Doppler signal is attributed to the CPT effect. The CPT effect is a quantum interference phenomenon that occurs when atoms interact with coherent light. Two coherent laser beams with a constant phase difference couple the two hyperfine energy levels of the atomic ground state to a common excited state. If the frequency difference between the two laser beams precisely equals the frequency corresponding to the difference between the two hyperfine energy levels of the atom, the atom will be pumped into a coherent superposition state of the two hyperfine energy levels, i.e., a coherent dark state. At this time, there are no atoms in the excited state, and the atom will no longer absorb photons. The atom is “population trapped” on the two hyperfine energy levels of the ground state, manifested as a sharp resonant dark line in its fluorescence spectrum [18]. During the occurrence of optical resonance, atoms within the velocity group exhibit resonance with both lights that are propagating in opposite directions. When the polarizations of the two relevant fields are identical, dark states tend to be rather prevalent. As a consequence, there are a relatively smaller number of atoms capable of absorbing the probe light, thereby enabling the observation of the anticipated saturated absorption signal. In accordance with Equation (6), when the polarization vectors are orthogonal to one another, the atoms that are initially in the dark state within the pump beam will become bright and subsequently be absorbed by the probe light. Under such circumstances, the absorption levels of both beams will increase, and the Lamb dip will experience an inversion.
3. Experimental Setup
The experimental setup is shown in Figure 2, and involves the Doppler effect occurring within a cylindrical gas cell that contained rubidium atoms with natural abundance. The vapor cell has a diameter of 25 mm and a length of 75 mm, without any buffer gas. The vapor cell is placed in a metal magnetic shielded and kept at room temperature. In this experiment, we use a narrow linewidth DBR laser from Photodigm that comes in TO-8 packaging, and can be tuned to the D1 line of rubidium atoms. The laser beam is shaped using the anamorphic prism pair and fully isolated by an optical isolator before being split into two beams using both a half-wave plate and polarization beam splitter 1. One beam is used for subsequent beat note experiments while the other beam connects to an EOPM with fiber input and output. We used a microwave source (Agilent, Model E8257D) to generate a 6.834 GHz RF signal to drive the EOPM. Monitoring of these optical sidebands occurs via a temperature-controlled optical etalon made of fused silica optical glass with specific properties: refractive index of 1.453, thickness of 2.5 mm, coating reflectivity at 98%, and a free spectral range of 40 GHz. To enhance the frequency stability of the microwave source, we employ the Rubidium atomic clock (SRS, Model FS725). Before entering the cell, the beam passes through a half-wave plate and two polarizing beam splitters in order to ensure power control and linear polarization into the cell. Subsequently, upon exiting the cell, the beam traverses a quarter-wave plate, reflects off a 95% reflective mirror surface, and is detected at the output by PD2 for sub-Doppler resonance detection. The presence of a quarter-wave plate between the cell and the mirror guarantees that both backward-propagating beams are polarized orthogonally to each other. The 5% transmitted light is captured by PD1 for CPT signal detection.
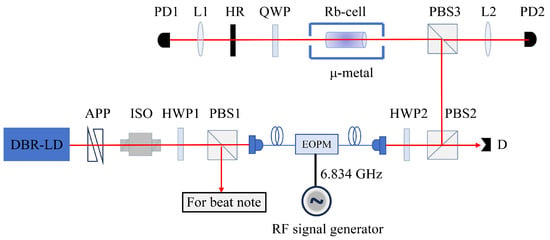
Figure 2.
Experimental setup. APP: anamorphic prism pair; ISO: isolator; HWP: half-wave plate; PBS: polarization beam splitter cube; EOPM: electro-optic phase modulator; L: lens; QWP: quarter-wave plate; HR: high reflectivity mirror (T∼5%); PD: photodiode; D: dump.
4. Experimental Result and Discussions
4.1. Optimization of the Bright-State Spectroscopy Parameters
As shown in Figure 3a, two hyperfine states of the ground state 5 are selected as the lower energy level, and the excited state 5 is used as the upper energy level to construct a -type three-level system. The residual magnetic field inside the one-layer -metal magnetic shielding bucket is lower than 50 nT. The laser is locked to the (F = 2) → ( = 1) transition by the polarization spectroscopy, and the CPT spectroscopy signal is optimized by optimizing the microwave frequency, as shown in Figure 3b. The line width of the CPT spectroscopy is 14.47 ± 0.02 MHz, and its center frequency is about 3.69 MHz out of tune with respect to the ground state frequency, which is due to the Zeeman effect of the magnetic field causes the frequency interval of the ground state hyperfine level to change slightly. By optimizing the microwave power, the amplitudes of the three signals (namely the carrier frequency, the positive first-order sideband, and the negative first-order sideband) are balanced to be the same. An optical etalon of 795 nm wavelength made of fused silica glass with a thickness of 2.5 mm, a free spectral region of about 40 GHz was used as an optical spectrometer, and the transmission spectroscopy of the optical etalon by linear scanning of the laser frequency was as shown in Figure 3c.
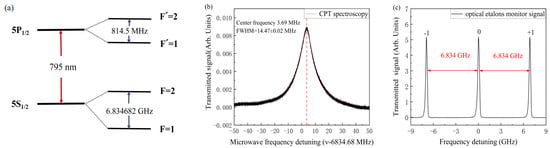
Figure 3.
(a) Relevant energy level diagram of rubidium-87 atoms D1 line; (b) the CPT spectroscopy detected by PD1 in Figure 1 for 6.8 GHz micro-wave frequency optimization; (c) the transmission spectra of the optical etalon for 6.8 GHz micro-wave power optimization. The height of the +1-order and −1-order sideband peaks is roughly equal to that of the carrier peak in center.
Figure 4a shows the BSS. The total laser power through the atomic vapor cell is 900 W. In order to obtain a more favorable signal, we measured the relationship between the spectral line Lorentz signal and the total laser power.
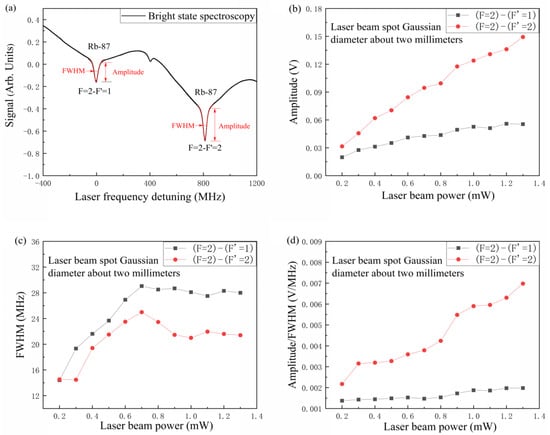
Figure 4.
BSS and parameter optimization. (a) Rubidium 87 with different hyperfine BSS; (b) signal amplitude vs. laser beam power; (c) linewidth vs. laser beam power; (d) amplitude/linewidth vs. laser beam power.
The absorption signal relative to each transition line in the BSS of the D1 line of the rubidium atom is the superposition of a Gaussian line and a Lorentz line. Figure 4b–d illustrates the correlation between the amplitude, linewidth, and amplitude/linewidth of the Lorentz signal and the total laser power incident in the gas chamber. It can be observed that as the laser power increases, the amplitude of the resonance signal rises markedly, and the linewidth increases and then reaches saturation due to power broadening. In fact, there was no significant change in the linewidth of BSS and SAS. In the experiment, a considerable enhancement in the amplitude of the BSS signal was discerned. These observations can be attributed to the optical pumping effect. In traditional SAS, the atomic system is considered to be an open system, which causes the atom to be pumped to another hyperfine ground state and results in a higher effective saturation parameter. Conversely, in the BSS, the atomic system is regarded as being closed, thus preventing the loss of atoms. As shown in Figure 4d, a significant increase in the amplitude of the Lorentz signal and the FWHM ratio (the slope of the frequency differentiation for laser frequency stabilization) was observed in BSS.
4.2. Laser Frequency Locking and Frequency Stability Comparison
In the experiment, PD1 is used to detect the transmission light of the mirror with a transmittance of 5%, and the absorption spectroscopy is observed. The differential signal demodulated by a lock-in amplifier is shown in Figure 5a. From left to right, they are the absorption signals of rubidium-87 (F = 2) → ( = 1) transition, rubidium-87 (F = 2) → ( = 2) transition and rubidium-85. When the 6.8 GHz microwave is turned off, the SAS is detected in the PD2 detector (as shown in Figure 5b), the dashed line is differential signal demodulated by the lock-in amplifier. From left to right, they are the saturation absorption signals of rubidium-87 (F = 2) → ( = 1) transition, crossover, rubidium-87 (F = 2) → ( = 2) transition and rubidium-85 (F = 3) → ( = 2,3) transition. When the 6.8 GHz microwave is turned on, the BSS is detected in the PD2 detector (as shown in Figure 5c), the dashed line is differential signal demodulated by the lock-in amplifier. They are the saturation absorption signal of rubidium-87 (F = 2) → ( = 1), transition crossover and rubidium-87 (F = 2) → ( = 2) transition from left to right. The horizontal axis shows the detuning of the laser frequency and the two optical transition frequencies w = , where is the transition frequency corresponding to the rubidium-87 (F = 2) → ( = 1) transition. The ordinate is a signal power of the photodetector.
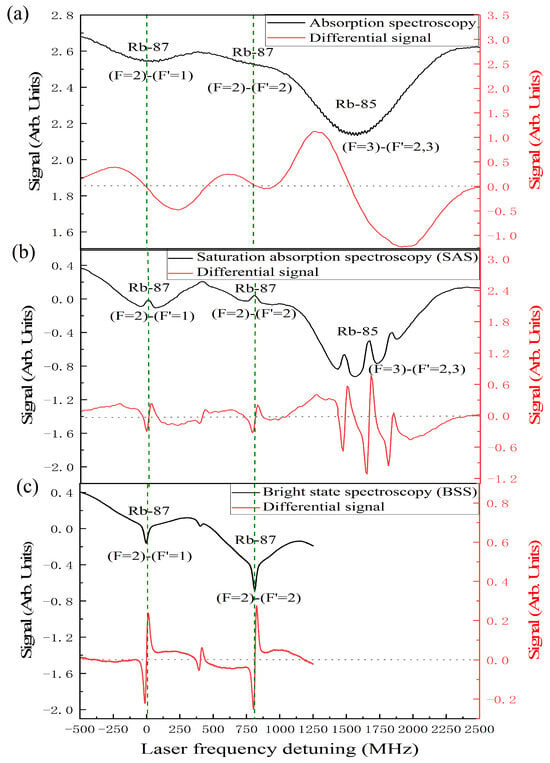
Figure 5.
Atomic absorption signal (black) and differential signal (red). (a) The absorption spectroscopy of the laser beam through the rubidium vapor cell; (b) saturation absorption spectroscopy (SAS); (c) bright state spectroscopy (BSS).
In the experiment, for the frequency fluctuation in the time domain of a single set of 795 nm single-frequency DBR-LD system, the slope of differential signal is used to measure the frequency fluctuation for laser free-running during 25-min, SAS frequency stabilization, and the BSS frequency stabilization, as shown in Figure 6.

Figure 6.
Typical frequency fluctuation. (a) Laser free-running case; (b) laser frequency locked case with the SAS scheme (locked to (F = 2) → ( = 1) transition); (c) laser frequency locked case with the BSS scheme (locked to (F = 2) → ( = 1) transition); (d) laser frequency locked case with the BSS scheme (locked to (F = 2) → ( = 2) transition).
The experimental results show that the free-running frequency fluctuation of the 25-min laser is ±11.16 MHz (as shown in Figure 6a). The laser is locked to rubidium-87 (F = 2) → ( = 1) transition by SAS, and the frequency fluctuation is ±0.94 MHz (as shown in Figure 6b). The laser is locked to rubidium-87 (F = 2) → ( = 1) transition by the BSS, and the frequency fluctuation is ±0.61 MHz (as shown in Figure 6c). The laser is locked to rubidium-87 (F = 2) → ( = 2) transition by the BSS, and the frequency fluctuation is ±0.54 MHz (as shown in Figure 6d). The experimental results show that the BSS frequency stabilization is better than the SAS frequency stabilization.
The laser beat note system can be used to measure the stability of laser frequency. In this experiment, one of the DBR-LDs is used as a reference laser, the other DBR-LD is used as a signal laser. Both lasers are locked to the same transition line in the same way. One of the lasers is frequency shifted by 80 MHz with an acousto-optic modulator (AOM) after locking and the other laser is not frequency shifted. The frequency change of the beat signal is recorded, and then the Allan deviation is used to describe the frequency drift characteristics. The laser beat note system has the characteristics of high precision and high resolution, and has advantages in measuring frequency stability. It is widely used in frequency standards, optical clocks, laser interferometry, and other fields to provide accurate frequency measurement and frequency stability calculation.
Allan deviation is the most common measure of time-domain frequency stability. Overlapping Allan deviation is a commonly used form of Allan deviation , which maximizes the use of a data set by forming all possible overlapping samples at each average time . It can estimate the average time from a set of sample number M frequency measurements, where m is the average factor, is the basic measurement interval, through the expression [19]
The advantage of overlapping Allan deviation is that the number of samples M is more, and the confidence interval is narrower than the original Allan deviation. To some extent, the use of data is more sufficient.
The setup of the beat note experiment is shown in Figure 7. The two lasers in the experiment are Photodigm’s distributed-Bragg-reflector-type laser diode (DBR-LD). DBR-LD#2 outputs a beam of linearly polarized light. Rotating half-wave plate 2 and polarization beam splitter 1 (PBS1) make the output light all pass through PBS1. The output light of DBR-LD#1 is also linearly polarized light. First, the AOM is shifted by 80 MHz, where the AOM is driven by a signal source (SRS, Model SG386). The frequency-shifted light passes through the half-wave plate 1 and the mirror. The half-wave plate is rotated so that the light on PBS1 is completely reflected, and the mirror is adjusted so that the light passing through the two lasers of PBS1 is completely coincident in space. After the two photosynthetic beams, the reflected light and the transmitted light are perpendicular to each other in space. Adjust the other group of half-wave plate 3 and PBS2 to make the two beams after PBS2 have the same polarization state. Then, two beams of light are coupled into the fast photodetector. The two beams of light entering the detector have the same power. The photodetector receives the beat note signal of the mixed frequency light of the two beams. After low-pass filtering, the second harmonic and higher harmonics of 80 MHz are filtered to avoid the influence of these harmonics on the frequency counting measurement. The output electrical signal is sent to the frequency counter (KeySight, Model 53220A) for frequency counting after the low noise amplifier.

Figure 7.
Beat note experimental setup. L: lens; AOM: acousto-optic modulator; HR: high reflectivity mirror; HWP: half-wave plate; PBS: polarization beam splitter; P: P-polarized light; S: S-polarized light; LPF: low pass filter; AMP: amplifier; D: dump.
In the experiment, in order to make the measurement results more reliable, the signal source (SRS, Model SG386), as well as the RF microwave source and the frequency counter use the rubidium clock (SRS, Model FS725) as the external reference signal. The stability of the 1 s interrogation time of the rubidium clock is , and the stability of the 100 s interrogation time is . It can provide a good external reference signal for the signal source and frequency counter, which is helpful to the accuracy of the experimental results.
The frequency stability Allan deviation results are shown in Figure 8. In the free-running regime, the frequency stability is with integration time of 1 s and with integration time of 40 s. Both lasers are locked to the rubidium-87 (F = 2) → ( = 1) transition with SAS, the frequency stability is with integration time of 1 s and with integration time of 40 s. Both lasers are locked to the rubidium-87 (F = 2) → ( = 1) transition with the BSS, the frequency stability is with integration time of 1 s and with integration time of 40 s. The frequency stability is nearly an order of magnitude higher than that of the SAS. Both lasers are locked to the rubidium-87 (F = 2) → ( = 2) transition with the BSS, the frequency stability is with integration time of 1 s, and the frequency stability is with integration time of 40 s. The frequency stability is further improved compared with the BSS locked to the rubidium-87 (F = 2) → ( = 1) transition.

Figure 8.
The overlapping Allan deviation values are calculated from the beat note data. The two lasers in free-running case, the locked cases with the same hyperfine transition as the reference using the SAS scheme and the BSS scheme, respectively.
The bandwidth of the frequency locking system has an important influence on the frequency locking effect, which is mainly reflected in the locking time and frequency tracking ability. The bandwidth of the frequency locking system determines the time of the system from the loss of lock state to the stable lock state. The bandwidth also affects the ability of the frequency locking system to track frequency changes. Wider bandwidth allows faster tracking of frequency changes as the system responds more quickly to external disturbances or signal changes. In this experiment, there are many factors that limit the bandwidth of the feedback loop, such as current modulation port, adder, detector, PID locking loop, etc. The decrease in frequency stability on a higher time scale in the experiment is limited by the bandwidth of the locking loop.
5. Conclusions
In this experiment, the technique of locking the laser frequency by BSS with rubidium atomic vapor cell based on the opposite transmission of dual-frequency orthogonally polarized light field is demonstrated. The laser frequency fluctuations for the free running case, the frequency stabilizing cases with SAS scheme and with BSS scheme have been measured and compared. At the same time, the frequency stability is characterized by Allan deviation through the beat note of two lasers. When the laser is locked to rubidium-87 (F = 2) → ( = 1) transition with BSS, the frequency stability is with integration time of 40 s, which is an order of magnitude better than the SAS case ( @40 s). This method can be further used in the field of quantum precision measurement to improve the measurement accuracy, such as atomic magnetometer, atomic clock and so on.
Author Contributions
Conceptualization, J.W.; methodology, J.W.; validation, J.Z. and Y.Y.; investigation, J.Z., Y.Y., L.Z. and Y.L.; data curation, J.Z.; writing—original draft preparation, J.Z.; writing—review and editing, J.W.; supervision, J.W.; project administration, J.W.; funding acquisition, J.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work is partially supported by the National Key R&D Program of China (Grant No. 2021YFA1402002), the National Natural Science Foundation of China (Grant No. 12474483) and the Fundamental Research Program of Shanxi Province (Grant No. 202403021211013).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data underlying the results presented in this paper are not publicly available at this time, but may be obtained from the authors upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Butcher, R.J. Sub-Doppler laser spectroscopy. Opt. Quantum Electron. 1993, 25, 79. [Google Scholar] [CrossRef]
- Long, D.A.; Fleisher, A.J.; Plusquellic, D.F.; Hodges, J.T. Multiplexed sub-Doppler spectroscopy with an optical frequency comb. Phys. Rev. A 2016, 94, 061801. [Google Scholar] [CrossRef] [PubMed]
- de Oliveira, V.S.; Silander, I.; Rutkowski, L.; Soboń, G.; Axner, O.; Lehmann, K.K.; Foltynowicz, A. Sub-Doppler optical-optical double-resonance spectroscopy using a cavity-enhanced frequency comb probe. Nat. Commun. 2024, 15, 161. [Google Scholar] [CrossRef] [PubMed]
- Hänsch, T.W.; Shahin, I.S.; Schawlowänsch, A.L. High-resolution saturation spectroscopy of the sodium D lines with a pulsed tunable dye laser. Phys. Rev. Lett. 1971, 27, 707. [Google Scholar] [CrossRef]
- Hänsch, T.W.; Levenson, M.; Schawlow, A. Complete hyperfine structure of a molecular iodine line. Phys. Rev. Lett. 1971, 26, 946. [Google Scholar] [CrossRef]
- Pappas, P.G.; Burns, M.M.; Hinshelwood, D.D.; Feld, M.S.; Murnickänsch, D.E. Saturation spectroscopy with laser optical pumping in atomic barium. Phys. Rev. A 1980, 21, 1955. [Google Scholar] [CrossRef]
- Wieman, C.; Hänsch, T.W. Doppler-free laser polarization spectroscopy. Phys. Rev. Lett. 1976, 36, 1170. [Google Scholar] [CrossRef]
- Haroche, S.; Hartmann, F. Theory of saturated-absorption line shapes. Phys. Rev. A 1972, 6, 1280. [Google Scholar] [CrossRef]
- Kunz, P.D.; Heavner, T.P.; Jefferts, S.R. Polarization-enhanced absorption spectroscopy for laser stabilization. Appl. Opt. 2013, 52, 8048. [Google Scholar] [CrossRef] [PubMed]
- Negnevitsky, V.; Turner, L.D. Wideband laser locking to an atomic reference with modulation transfer spectroscopy. Opt. Express 2013, 21, 3103. [Google Scholar] [CrossRef] [PubMed]
- Shirley, J.H. Modulation transfer processes in optical heterodyne saturation spectroscopy. Opt. Lett. 1982, 7, 537. [Google Scholar] [CrossRef] [PubMed]
- MacAdam, K.B.; Steinbach, A.; Wieman, C. A narrow-band tunable diode laser system with grating feedback, and a saturated absorption spectrometer for Cs and Rb. Am. J. Phys. 1992, 60, 1098. [Google Scholar] [CrossRef]
- Hafiz, M.A.; Coget, G.; Clercq, E.D.; Boudot, R. Doppler-free spectroscopy on the Cs D1 line with a dual-frequency laser. Opt. Lett. 2016, 41, 2982. [Google Scholar] [CrossRef] [PubMed]
- Brazhnikov, D.; Petersen, M.; Coget, G.; Passilly, N.; Maurice, V.; Gorecki, C.; Boudot, R. Dual-frequency sub-Doppler spectroscopy: Extended theoretical model and microcell-based experiments. Phys. Rev. A 2019, 99, 062508. [Google Scholar] [CrossRef]
- Li, Q.; Yun, P.; Yang, T.; Hao, Q.; Zhang, S.; Gu, S. Noise suppression by differential detection of simultaneous electromagnetically induced transparency and absorption in counterpropagating bichromatic light. New J. Phys. 2023, 25, 103039. [Google Scholar] [CrossRef]
- Taichenachev, A.V.; Yudin, V.I.; Velichansky, V.L.; Kargapoltsev, S.V.; Wynands, R.; Kitching, J.; Hollberg, L. High-contrast dark resonances on the D1 line of alkali metals in the field of counterpropagating waves. JETP Lett. 2004, 80, 236. [Google Scholar] [CrossRef]
- Hafiz, M.A.; Brazhnikov, D.; Coget, G.; Taichenachev, A.; Yudin, V.; Clercq, E.D.; Boudot, R. High-contrast sub-Doppler absorption spikes in a hot atomic vapor cell exposed to a dual-frequency laser field. New J. Phys. 2017, 19, 073028. [Google Scholar] [CrossRef]
- Breschi, E.; Kazakov, G.; Lammegger, R.; Mileti, G.; Matisov, B.; Windholz, L. Quantitative study of the destructive quantum-interference effect on coherent population trapping. Phys. Rev. A 2009, 79, 063837. [Google Scholar] [CrossRef]
- Riley, W.J.; Howe, D.A. Handbook of Frequency Stability Analysis; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2008.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).