CO2 Measurement under Different Pressure and Vibration Conditions Using Tunable Diode Laser Absorption Spectroscopy
Abstract
:1. Introduction
2. Theory and Method
2.1. Lambert–Beer Law
2.2. Experimental Setup
3. Results
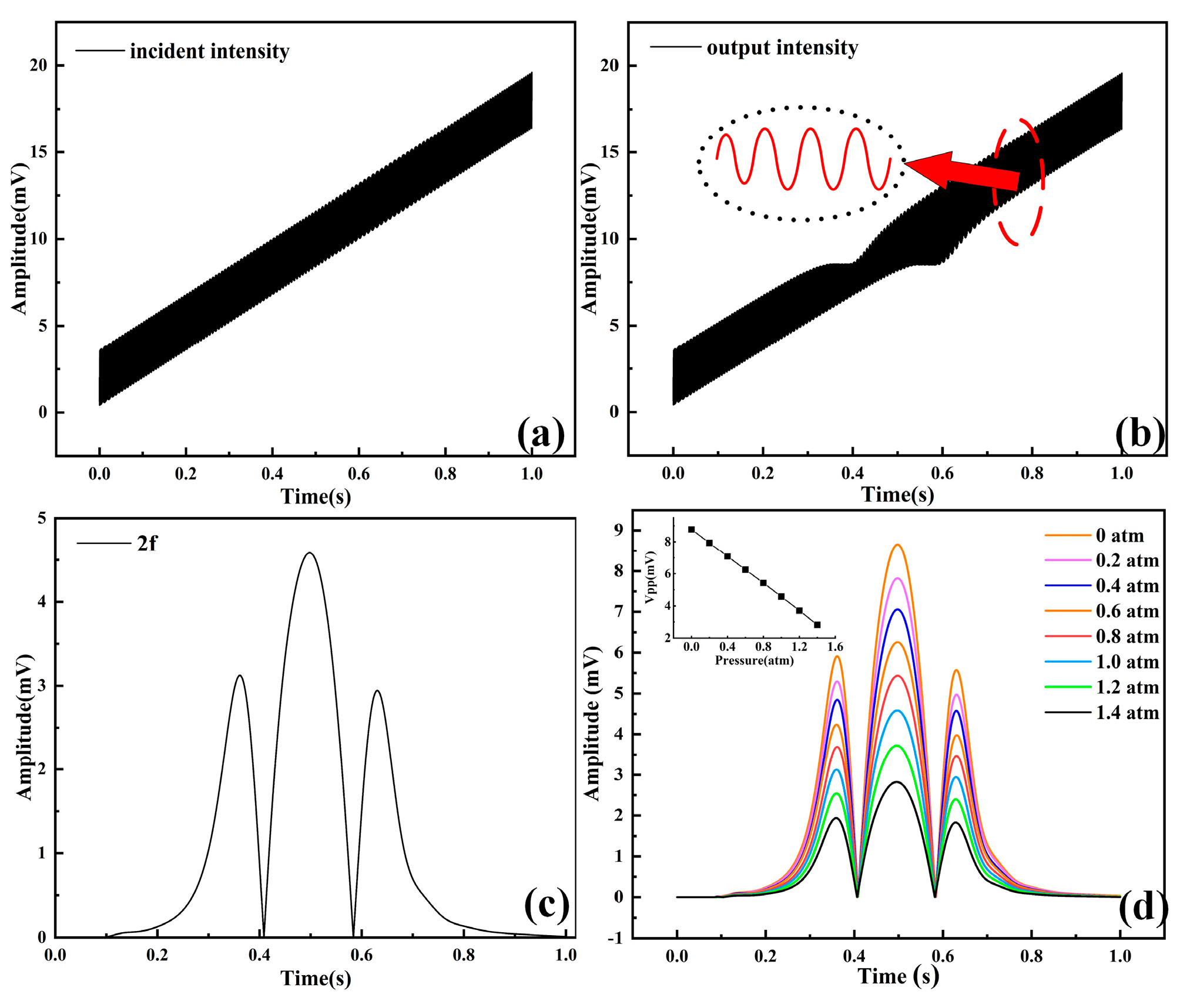
3.1. Determination of Main Parameters
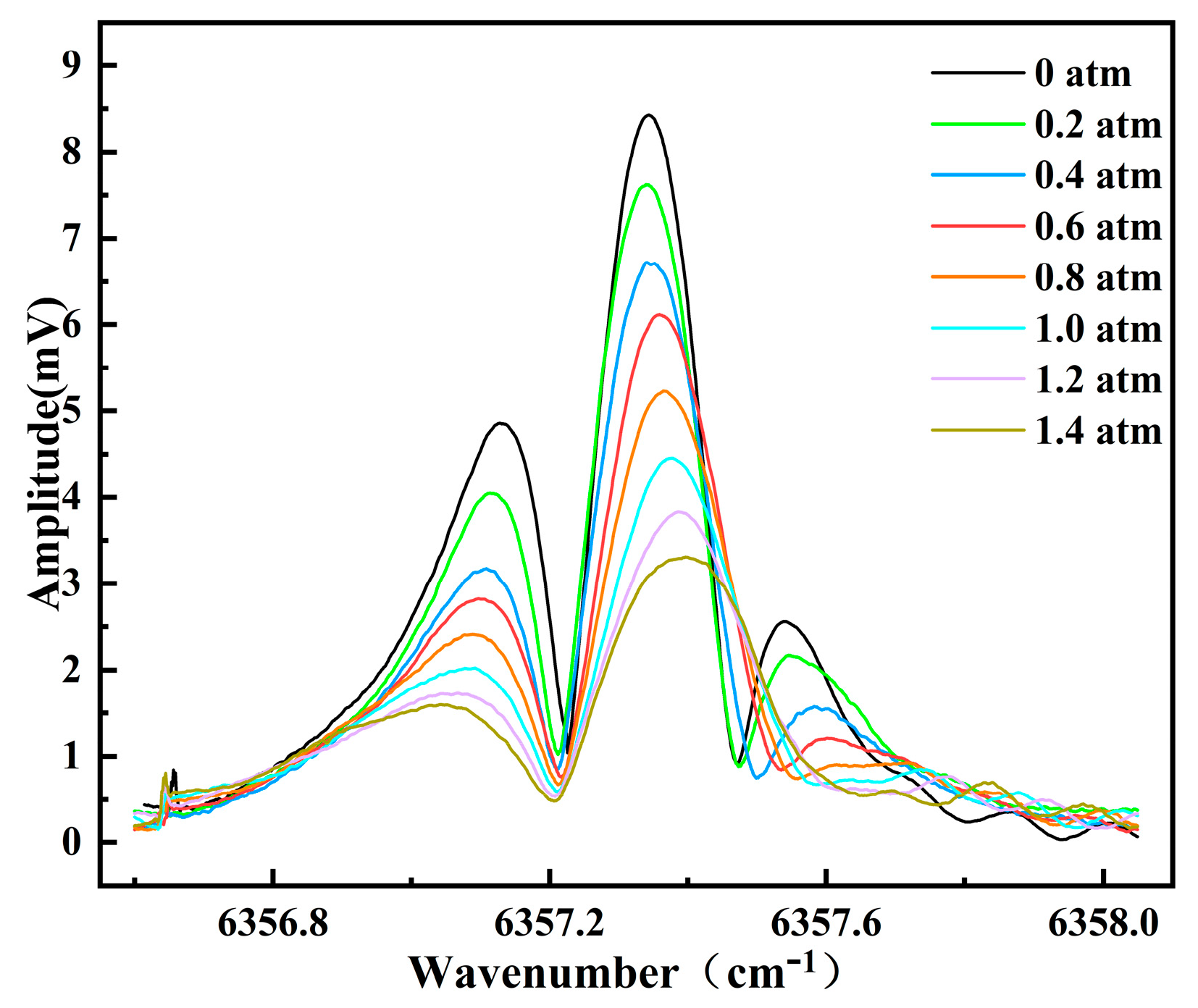
3.2. Pressure Testing
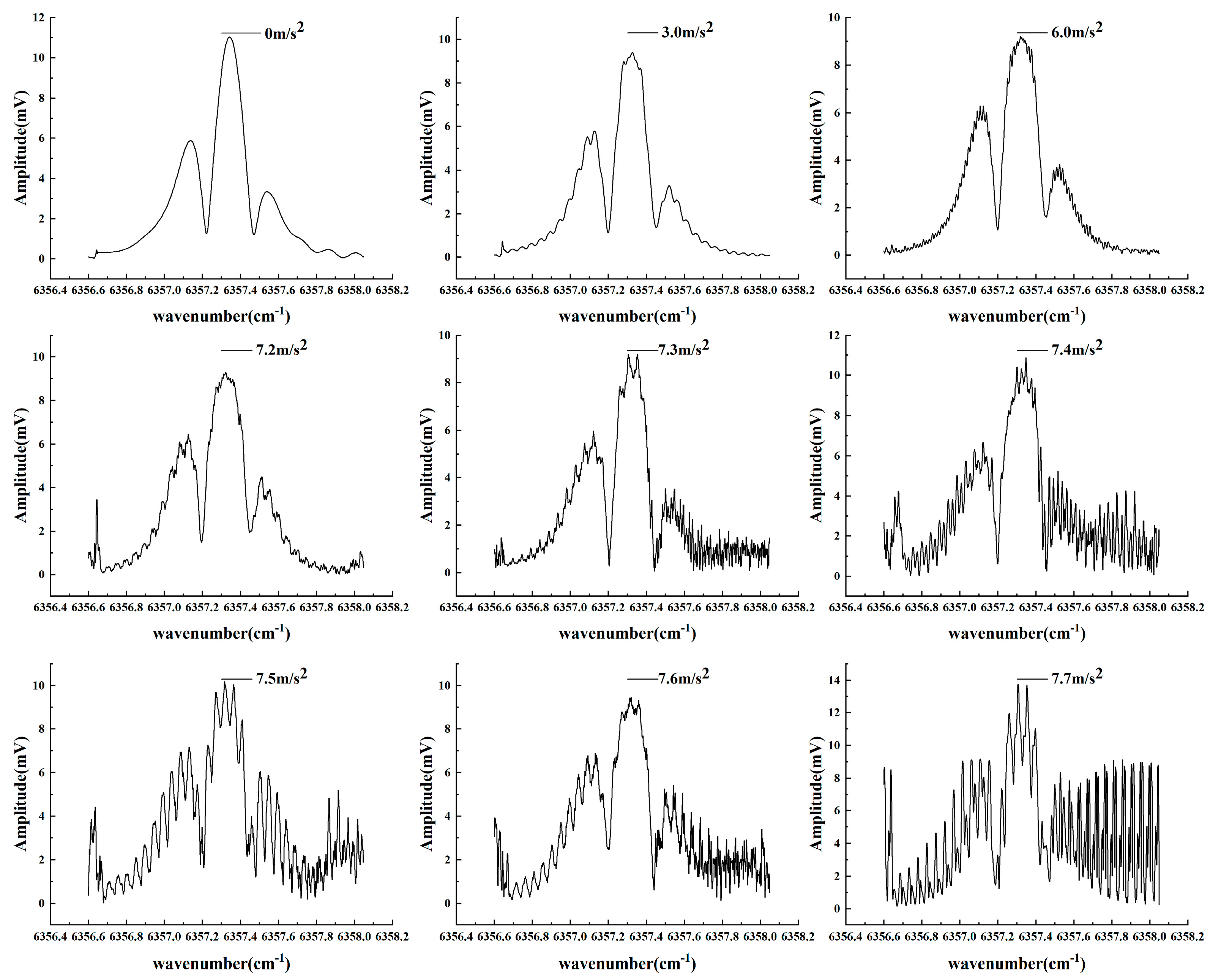
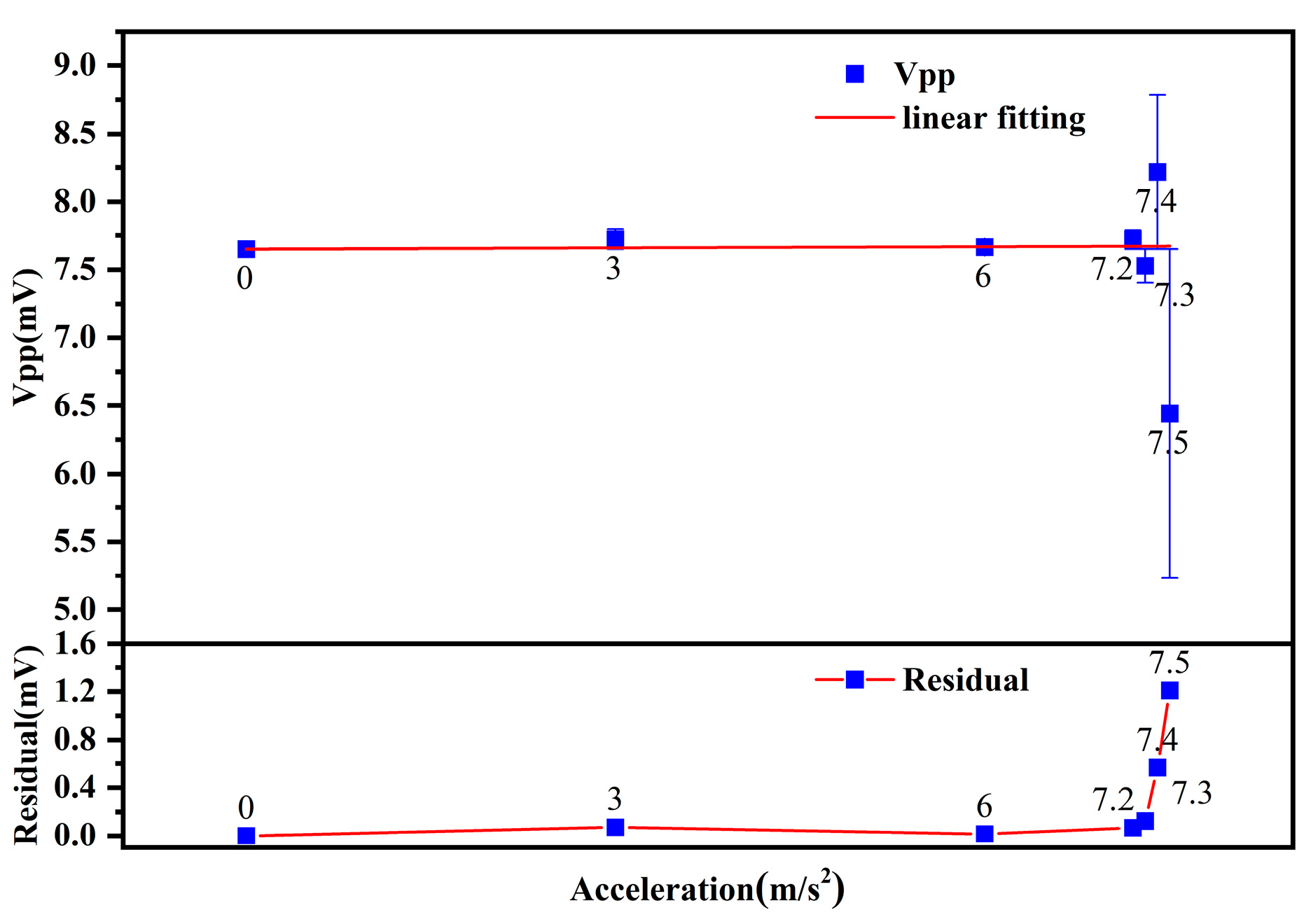
3.3. Vibration Testing
4. Discussion
4.1. Analysis of Pressures
4.2. Analysis of Vibrations
4.3. The Combined Effects of Pressures and Vibrations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mahamuni, G.; Rutherford, J.; Davis, J.; Molnar, E.; Posner, J.D.; Seto, E.; Korshin, G.; Novosselov, I. Excitation–Emission Matrix Spectroscopy for Analysis of Chemical Composition of Combustion Generated Particulate Matter. Environ. Sci. Technol. 2020, 54, 8198–8209. [Google Scholar] [CrossRef] [PubMed]
- Weiser, V.; Eisenreich, N. Fast Emission Spectroscopy for a Better Understanding of Pyrotechnic Combustion Behavior. Propellants Explos. Pyrotech. 2005, 30, 67–78. [Google Scholar] [CrossRef]
- Makowiecki, A.S.; Hoghooghi, N.; Strong, E.F.; Cole, R.K.; Ycas, G.; Giorgetta, F.R.; Lapointe, C.B.; Glusman, J.F.; Daily, J.W.; Hamlington, P.E.; et al. Mid-infrared dual frequency comb spectroscopy for combustion analysis from 2.8 to 5 µm. Proc. Combust. Inst. 2021, 38, 1627–1635. [Google Scholar] [CrossRef]
- Brackmann, C.; Bood, J.; Afzelius, M.; Bengtsson, P.E. Thermometry in internal combustion engines via dual-broadband rotational coherent anti-Stokes Raman spectroscopy. Meas. Sci. Technol. 2004, 15, R13. [Google Scholar] [CrossRef]
- Bolshov, M.A.; Kuritsyn, Y.A.; Romanovskii, Y.V. Tunable diode laser spectroscopy as a technique for combustion diagnostics. Spectrochim. Acta Part B At. Spectrosc. 2015, 106, 45–66. [Google Scholar] [CrossRef]
- Lee, J.; Bong, C.; Yoo, J.; Bak, M.S. Combined use of TDLAS and LIBS for reconstruction of temperature and concentration fields. Opt. Express 2020, 28, 21121–21133. [Google Scholar] [CrossRef] [PubMed]
- Du, J.; Yin, C.; Deng, J.; Wang, W.; Cai, C. Study on influence of temperature and pressure in TDLAS trace CO detection. In Proceedings of the 2017 IEEE 2nd Information Technology, Networking, Electronic and Automation Control Conference (IT-NEC), Chengdu, China, 15–17 December 2017; pp. 213–217. [Google Scholar]
- Al-Manea, A.; Buttsworth, D.; Saleh, K.; Malpress, R.; Leis, J. Measurement of turbulent supersonic steam jet flow characteristics using TDLAS. Flow Meas. Instrum. 2022, 87, 102212. [Google Scholar] [CrossRef]
- Buchholz, B.; Afchine, A.; Ebert, V. Rapid, optical measurement of the atmospheric pressure on a fast research aircraft using open-path TDLAS. Atmos. Meas. Tech. 2014, 7, 3653–3666. [Google Scholar] [CrossRef]
- Lanzinger, E.; Jousten, K.; Kühne, M. Partial pressure measurement by means of infrared laser absorption spectroscopy. Vacuum 1998, 51, 47–51. [Google Scholar] [CrossRef]
- Deng, J.; Chen, W.-L.; Wang, W.-F.; He, Y.; Zhang, B.-L. Study on Online Detection Method of Methane Gas in Coal Mine Based on TDLAS Technology; Springer: Singapore, 2019; pp. 318–332. [Google Scholar]
- Burkle, S.; Walter, N.; Wagner, S. Laser-based measurements of pressure broadening and pressure shift coefficients of combustion-relevant absorption lines in the near-infrared region. Appl. Phys. B-Lasers Opt. 2018, 124, 121. [Google Scholar] [CrossRef]
- Cai, T.D.; Gao, G.Z.; Wang, M.R.; Wang, G.S.; Gao, X.M. Measurements of CO2 Concentration at High Temperature and Pressure Environments Using Tunable Diode Laser Absorption Spectroscopy. Spectrosc. Spect. Anal. 2014, 34, 1769–1773. [Google Scholar]
- Cai, T.D.; Gao, G.Z.; Wang, M.R.; Wang, G.S.; Liu, Y.; Gao, X.M. High-Pressure Measurements of Temperature and CO2 Concentration Using Tunable Diode Lasers at 2 μm. Appl. Spectrosc. 2016, 70, 474–484. [Google Scholar] [CrossRef] [PubMed]
- Li, C.L.; Wu, Y.F.; Qiu, X.B.; Wei, J.L.; Deng, L.H. Pressure-Dependent Detection of Carbon Monoxide Employing Wavelength Modulation Spectroscopy Using a Herriott-Type Cell. Appl. Spectrosc. 2017, 71, 809–816. [Google Scholar] [CrossRef] [PubMed]
- Li, N.; Lu, X.J.; Weng, C.S. Laser intensity and absorbance measurements by tunable diode laser absorption spectroscopy based on non-line fitting algorithm. Acta Phys. Sin. Ch. Ed. 2018, 67, 057801. [Google Scholar]
- Nwaboh, J.A.; Werhahn, O.; Ortwein, P.; Schiel, D.; Ebert, V. Laser-spectrometric gas analysis: CO2–TDLAS at 2 µm. Meas. Sci. Technol. 2013, 24, 015202. [Google Scholar] [CrossRef]
- Witzel, O.; Klein, A.; Meffert, C.; Wagner, S.; Kaiser, S.; Schulz, C.; Ebert, V. VCSEL-based, high-speed, in situ TDLAS for in-cylinder water vapor measurements in IC engines. Opt. Express 2013, 21, 19951–19965. [Google Scholar] [CrossRef] [PubMed]
- Pogány, A.; Ott, O.; Werhahn, O.; Ebert, V. Towards traceability in CO2 line strength measurements by TDLAS at 2.7 µm. J. Quant. Spectrosc. Radiat. Transf. 2013, 130, 147–157. [Google Scholar] [CrossRef]
- Gordon, I.E.; Rothman, L.S.; Hill, C.; Kochanov, R.V.; Tan, Y.; Bernath, P.F.; Birk, M.; Boudon, V.; Campargue, A.; Chance, K.V.; et al. The HITRAN2016 molecular spectroscopic database. J. Quant. Spectrosc. Radiat. 2017, 203, 3–69. [Google Scholar] [CrossRef]
- Zhang, R.; Li, C.R.; Wang, Y.; Bai, W. Research on modulation frequency and scanning frequency parameters selection of TDLAS system. In Proceedings of the International Conference on Industrial Technology EDEP, Beijing, China, 11–12 June 2016; pp. 1–6. [Google Scholar]
- Li, H.; Liu, J.; He, Y.; He, J.; Yao, L.; Xu, Z.Y.; Chen, J.Y.; Yuan, S.; Kan, R.F. Simulation and analysis of second-harmonic signal based on tunable diode laser absorption spectroscopy. Spectrosc. Spectr. Anal. 2013, 33, 881–885. [Google Scholar]







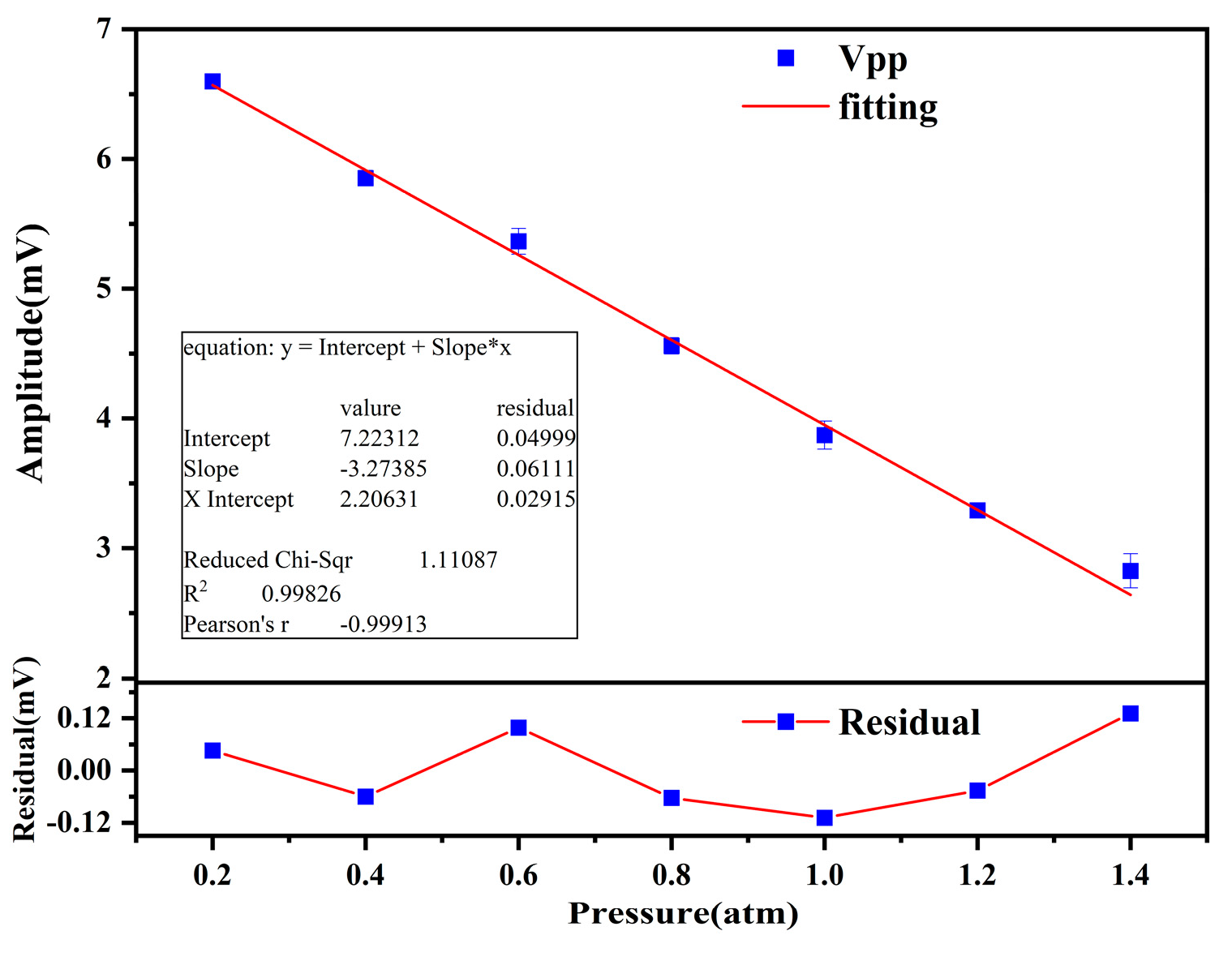

| Pressure (atm) | Residual (mV) | Relative Error (%) |
|---|---|---|
| 0.2 | 0.04602 | 0.697 |
| 0.4 | −0.06005 | 1.026 |
| 0.6 | 0.09862 | 1.838 |
| 0.8 | −0.06305 | 1.383 |
| 1.0 | −0.10879 | 2.811 |
| 1.2 | −0.04619 | 1.404 |
| 1.4 | 0.1312 | 4.645 |
| Acceleration (m/s2) | SNR | Residual |
|---|---|---|
| 3.0 | 28.5646 | 0.07225 |
| 6.0 | 28.2636 | 0.01474 |
| 7.2 | 23.5769 | 0.06814 |
| 7.3 | 18.3290 | 0.12298 |
| 7.4 | 4.8184 | 0.56725 |
| 7.5 | 13.7239 | 1.20948 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ban, D.; Li, N.; Zheng, Y.; Xue, C. CO2 Measurement under Different Pressure and Vibration Conditions Using Tunable Diode Laser Absorption Spectroscopy. Photonics 2024, 11, 146. https://doi.org/10.3390/photonics11020146
Ban D, Li N, Zheng Y, Xue C. CO2 Measurement under Different Pressure and Vibration Conditions Using Tunable Diode Laser Absorption Spectroscopy. Photonics. 2024; 11(2):146. https://doi.org/10.3390/photonics11020146
Chicago/Turabian StyleBan, Deyue, Nan Li, Yongqiu Zheng, and Chenyang Xue. 2024. "CO2 Measurement under Different Pressure and Vibration Conditions Using Tunable Diode Laser Absorption Spectroscopy" Photonics 11, no. 2: 146. https://doi.org/10.3390/photonics11020146




