Abstract
The reflection and transmission spectra of a metamaterial formed by omega-shaped elements with pre-calculated optimal parameters on a silicon substrate have been recorded in the terahertz range at oblique incidence for the s- and p-polarizations of the incident wave. The spectra were interpreted within the dipole radiation theory of electromagnetic waves. Both measurement results and analysis provide evidence supporting the presence of a pronounced polarization anisotropy impact in the reflection and transmission of the metamaterial. The potential of these materials to be utilized in the development of devices that control the polarization properties of THz radiation across a wide spectral range is examined.
1. Introduction
The advancements of next-generation high-speed communication systems, commonly referred to as 6G and non-contact spectroscopic systems, have caused growing attention to the practical applications of radiation using ever-increasingly high frequencies, such as the terahertz (THz) range. Consequently, there is an increasing focus on the development of techniques and technologies aimed at controlling the properties of THz radiation [1,2,3,4]. The selected spectral range additionally offers favorable prospects for the experimental modeling of compact radiation control devices intended for application in other ranges. This is due to the fact that the fabrication of prototypes and models for experimental THz devices does not require highly precise nanoscale technological procedures, which may be essential for devices operating in the optical range. In contrast to radio band devices operating at centimeter wavelengths, the model devices will exhibit relatively compact dimensions.
In recent times, there has been considerable research focused on artificial media with negative values of dielectric permittivity and magnetic permeability (ε < 0 and μ < 0). These media have great potential for manipulating the amplitude, spectral, and angular characteristics of THz radiation. Media that possess a negative value for one of the parameters are commonly referred to as ε-negative or μ-negative, denoted as ENG and MNG accordingly [5,6]. The genuine metamaterial, devoid of any analogs in the environment, is recognized as a binegative medium (BNG), which possesses both parameters in the negative. The latter option has the potential to offer the highest degree of flexibility in designing compact devices for controlling radiation parameters with unique functionality [7]. From our perspective, this option is particularly appealing for further investigation. One potential application, among others, for metamaterials is their utilization as polarization converters for electromagnetic waves across various spectral ranges. These polarizers may consist of variously shaped elements, such as helices with different numbers of turns, split rings oriented in different ways, and classical or rectangular omega-shaped elements [8,9,10,11,12,13,14,15,16,17,18,19,20]. The polarizers function predominantly within the microwave and, to a lesser degree, THz frequency ranges. The development of wave polarizers in the THz range is thus a relevant task. This paper considers a metamaterial formed by aluminum omega elements arranged on a silicon substrate. While each omega element has a classical shape, its geometrical parameters, specifically the ratio between the length of straight arms and the radius of the turn, are pre-optimized considering the wavelength of the electromagnetic field. The specified optimization leads to strong polarization selectivity of the omega-elements, i.e., to their fundamentally distinct excitation by waves of various polarization. The novelty of this paper consists of demonstrating the strong polarization selectivity of the metamaterial with respect to oblique incident terahertz waves of various polarizations. Furthermore, the scientific novelty arises from analyzing the polarization of the reflected wave, which can be either linearly polarized or circularly polarized, depending on the frequency and polarization of the incident wave. The experimental part of this research is also innovative, as it implements an optical scheme to investigate a metamaterial under oblique incidence of terahertz radiation while also allowing for the manipulation of its polarization.
An in-depth analysis of our findings in relation to the results of previous studies [7,8,9,10,11,12,13,14,15,16,17,18,19,20] will be conducted separately in the near future. The advantages of the optical scheme we have proposed include the use of a metamaterial with only one layer of omega elements, which simplifies the fabrication process and decreases costs while also diminishing the wave absorption losses. Additionally, the benefits encompass the utilization of the reflected wave, which exhibits a significant intensity even for a single layer of metallic omega elements, instead of the wave that has passed through the metamaterial. The utilization of classical-shaped omega elements, which have been empirically demonstrated to be effective in creating metamaterials and for which deposition techniques on various substrates are well acknowledged, provides an additional advantage.
2. Fabrication of an Experimental Sample
The authors previously conducted calculations and experimental investigations on omega-elements that possess an optimal shape within the microwave range of 2.55 to 3.8 GHz [21,22]. Omega particles of this nature demonstrate a harmonious combination of electric and magnetic characteristics, rendering them potentially valuable components for metamaterials and metasurfaces. The authors conducted a study in [23,24] to investigate the transition from the microwave to the THz region. That study involved the modeling of a single omega-shaped element and a metasurface composed of these resonators in the field of a THz wave. The present paper describes the findings of an empirical investigation conducted on an omega-shaped element and a metamaterial based on this element, whereby the properties of the latter were optimized specifically for THz radiation. This research focuses on the advancement and examination of the spectral-polarization properties of an omega-structured metamaterial. The constituent elements of this metamaterial are designed to possess equivalent importance in terms of both dielectric permittivity and magnetic permeability. It is demonstrated that the metamaterial based on an array of omega-elements with a pre-calculated optimal shape exhibits polarization-selective properties and can perform the functions of an effective converter of electromagnetic wave polarization in the THz range. The methodology for determining the optimal parameters of omega elements as the basis for electromagnetic wave polarization transducers has been detailed in the authors’ publications [21,22,23,24] and is summarized following Formula (4).
The metamaterial was fabricated using aluminum elements arranged in the shape of the Greek letter Ω, which were positioned in a rectangular array on the surface of a silicon substrate. All elements in the array exhibited the same orientation. Figure 1 displays the omega-shaped element parameters along with a microscopically captured image of the material surface.
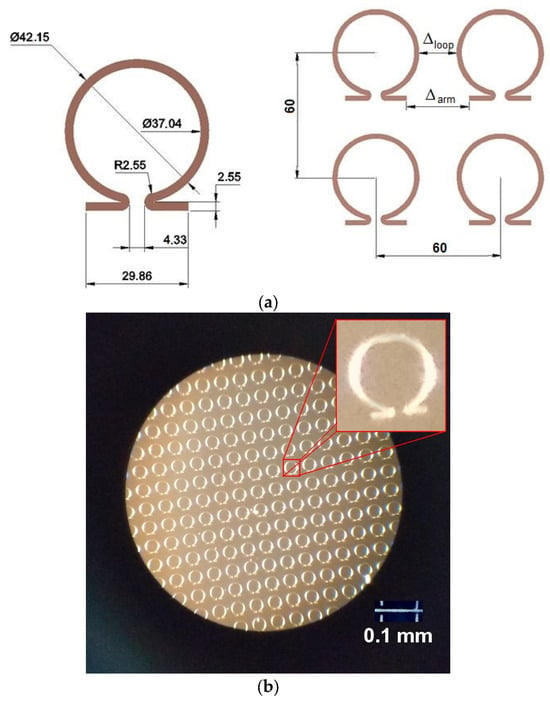
Figure 1.
(a) Omega-shaped element parameters for the THz range, denoted in micrometers; (b) a microscopic photograph of the metamaterial, revealing a single element.
Silicon substrate of 100 mm industrial size have been filled with omega-shaped elements almost completely. Step of placement of elements was 60 μm in both directions of square lattice. Scale of 0.1 mm is shown at the photo of Figure 1b.
The omega-shaped element consists of two main components, namely a split ring resonator (SRR [6]) and a linear dipole that is electrically interconnected to form a single system. A notable distinction from the structure suggested in [7] is the substantial electrical connection observed between the components of the element. This kind of connection can result in the emergence of radiation polarization conversion effects when combined with polarization-dependent spectral filtering. The dimensions of the element determine its resonance properties for both components of the electromagnetic field of THz radiation.
It is noteworthy that the omega-shaped elements constitute a metasurface due to the exceedingly thin nature of their layer. The term “metamaterial” is employed to emphasize the existence of a substrate that is significantly thicker than the omega-shaped element layer.
3. Experiment and Discussion of Results
In order to investigate the polarization and spectral properties of a metamaterial formed by omega-shaped elements on a silicon substrate, THz radiation path of a pulse terahertz spectrometer was built accordingly to sketch represented in Figure 2.
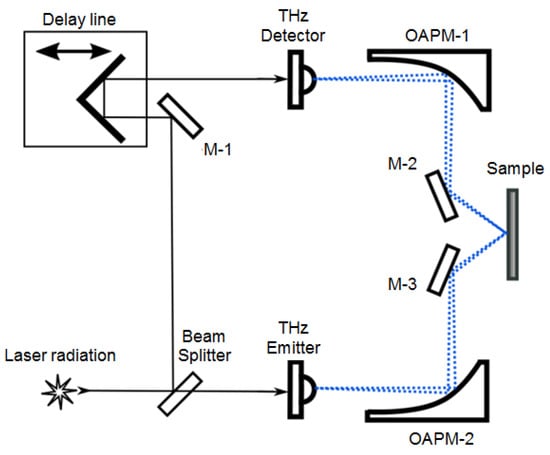
Figure 2.
Schematic of the THz spectrometer (M-1, M-2, and M-3 are the metal mirrors; OAPM-1, OAPM-2 are the parabolic mirrors). Solid black lines show the path of propagation of laser radiation. The blue dotted lines indicate the path of propagation of THz radiation with weak divergence.
THz radiation illuminated a circular area of ~6 mm diameter during spectral measurements. Thus, in interaction with the radiation, a group of omega-shaped elements was involved in quantity of about 11,300 elements. The terahertz radiation has been formed in quite collimated beam, because of off-axis parabolic mirrors OAPM-1, 2 (Figure 2) were chosen to only compensate initial divergence of the beam.
The sensitivity to polarization is a significant characteristic shown by photoconductive antennas employed in THz spectrometer sources and radiation receivers. This sensitivity enables the detector to function as a polarization analyzer. In this particular scenario, the orientation of the antennas is such that the electric field vector is aligned with the horizontal plane. This alignment corresponds to the plane of the schematic diagram in Figure 2 and also agrees with the p-polarization of incidence radiation. To convert the alignment to s-polarization, it was made possible to rotate the assembly, including mirrors 3-2 and 3-3, along with the sample holder. The radiation will be displaced off the plane. Here, the sample will be positioned beneath the mirrors. As a result, the plane of the metamaterial will be aligned in parallel to the polarization plane of the THz radiation. The polarization of the THz wave, in this case, is perpendicular to the plane of incidence. A more detailed description of the spectrometer set-up can be found in [25].
The study focused on examining changes in the spectral composition of THz radiation reflected from a metamaterial. The investigation specifically looked at how these changes were influenced by the orientation of the symmetry axis of the omega-shaped element in relation to the projection of the radiation polarization direction onto the plane of the metamaterial. The system of designations for rotation angles that have been adopted is explained in Figure 3.
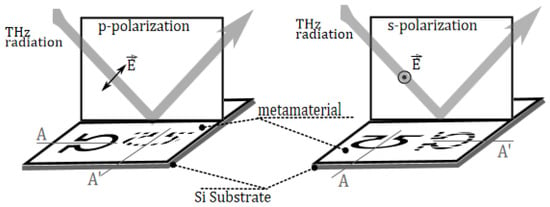
Figure 3.
Orientation of the symmetry axis of omega-shaped elements A and A’ with respect to the polarization of THz radiation with angle values of 0° and 90°, accordingly.
The standard representation of the metamaterial in Figure 3 consists of a single omega element. The element represented in the schematic by a dashed line signifies the alteration in the orientation of its symmetry axis A as the metamaterial undergoes rotation around an axis perpendicular to its surface for π/2 to reach position A’. The measurement of the rotation angle of the symmetry axis of the omega-shaped element is conducted with respect to the electric field vector of the incident wave. Therefore, the zero value of the angle corresponds to the position of the symmetry axis inside the plane of oscillations of the electric vector of THz radiation that is directed towards the sample. At an angle of 90 degrees, the symmetry axis of the omega-shaped element is orthogonal to the electric vector of the incident wave, while the “arms” of the omega-shaped element are situated within the plane of oscillations of the electric vector of the incident THz radiation. The designations and nomenclature frequently employed for the components of the electric field vector of the wave are and . The numerical values within the notations of the dependencies depicted in the schematics presented below are representative of the rotation angles expressed in degrees.
Time-domain spectrometers are conventionally used to perform a point-by-point measurement of the current in a photoconductive antenna (PCA) detector induced by the electrical component of the THz pulse field. The current is proportional to the field strength and recorded as a function of delay time. The waveform length was 140 ps, and the delay line scanning step was chosen to be ~0.075 ps. The indicated parameters correspond to a spectral resolution of ~0.008 THz and a frequency range of up to 7.5 THz after the Fourier transform. The excess range width is justified by the possibility of determining the position of the pulse on the time scale more accurately. Accordingly, visual control of the sample positioning is ensured during the waveform recording. Also, it is possible to estimate the average refractive index, as well as to choose parameters for data preprocessing before the Fourier transform. The selected waveform duration and corresponding spectral resolution are sufficient and meet the measurement requirements.
The high transparency and relatively large refractive index of the Si substrate, equal to an average of 3.5, cause the appearance of several echo pulses in the waveform. Echoes are produced by reflections in the plane-parallel silicon layer. As a result, the spectrum after the Fourier transform is distorted by the so-called Fabry-Perot effect [26]. Moreover, components of the transmission spectrum are added to the reflection spectrum. The information about these components is carried by echo pulses passing twice through the metasurface layer. Figure 4 demonstrates an example of the waveform and preprocessing results.
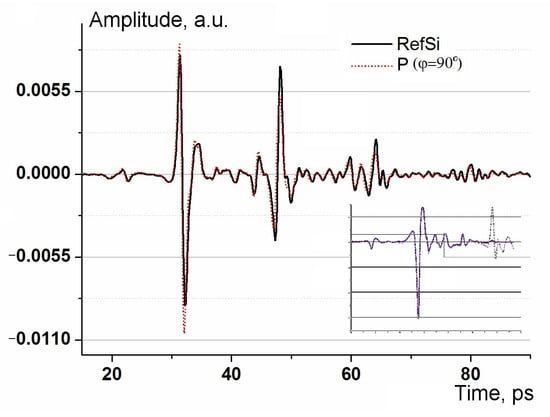
Figure 4.
View of the typical waveform for the metamaterial and for the silicon substrate (RefSi). The blue curve in the inset illustrates the application of window function.
It is notable that the reflectivity of the matrix is higher than that of the Si substrate. Therefore, we used the reflection from the aluminum plate as a reference signal. The weak peak is visible on the waveform at 23 ps is caused by the design of the emitter and is compensated in the Fourier transform by a symmetrical analog that is formed in the detector antenna. To suppress the Fabry-Perot effects, we used the window function proposed in [27].
This function is smooth and its derivatives are smooth as well. Compared to the common window functions, such as Hann, Hanning, etc., it introduces less attenuation near the peak due to a wider and flatter top. The result of applying the window function is presented in the inset of Figure 4. Here, the solid line shows the result of applying the window function, while the suppressed echo signal is indicated by the dotted line. The resulting spectra retained a small residual modulation, which did not prevent the correct analysis of polarization-dependent spectral changes.
The reflection from a thin aluminum plate, that was fixed in the holder instead of the sample, was used as a reference signal. Figure 5 illustrates families of characteristic reflection spectra.
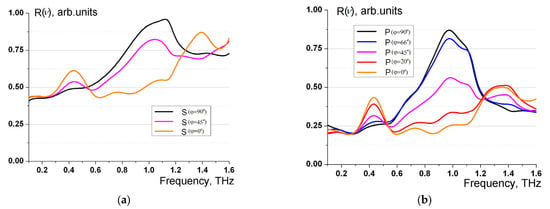
Figure 5.
Reflection spectra of a metamaterial formed by omega-shaped elements on a silicon substrate for s- (a) and p-polarization (b) of the incident wave.
It is necessary to note that it is max resolution, not a result of applying some common criteria. Fabry-Perot effect with no waveform processing looks in such a way we can suppose a relatively narrow peak at ~400 GHz. Both other peaks seem to be wider. Applying a window of 40 ps full width leads to a resolution of 0.025 THz. Peak width remains the same as shown in the manuscript, but Fabry-Perot became too large to be published. So twice less resolution of 50 GHz was chosen. We tried some deconvolution procedures to remove the effect also. The first peak really appeared to be sharpened, but the result was too noisy. Moving the window smooth procedure with 10 points averaging leads to the result that appears to be very similar to the presented one.
Certainly, any kind of preprocessing removes some valuable information, and we hope that we found a correct trade-off between information loss and presentation quality for quality (not quantitative) analysis.
The acquired experimental outcomes are explicable in light of the theory of dipole radiation of electromagnetic waves [28]. The dipole radiation theory is applicable because the dimensions of each omega-shaped element are considerably smaller than the wavelength of the electromagnetic field. In the dipole approximation, the electric field intensity of the wave emitted by an omega-shaped element has the following form:
Here, is the radius-vector from the center of the omega-element to the observation point; is the vacuum permeability; is the distance from the center of the omega-element to the observation point; is the unit vector of the wave normal; c is the speed of light in vacuum; is the dipole moment of the omega-shaped element, is the magnetic moment of the omega-shaped element (two dots above the vectors denote the second derivative of these vector quantities).
A more general approach to calculating the electric field intensity of the emitted wave in Formula (2) requires that the multipole moments be taken into account as well. As an example, such a modern field as nanophotonics of the all-dielectric structures can be cited, whereas the interplay between electric and magnetic Mie dipole-like and higher-order multipoles leads to a variety of phenomena and applications [29,30]. However, the metamaterial under consideration consists of metallic omega-elements of classical shape. Within these elements, the condition of half-wave resonance with standard distribution of electric current and electric charge is realized. Therefore, the dipole moments, both dielectric and magnetic, considered in Formula (2), play a key role when compared to the moments of higher orders and are the primary contributors to the radiated field.
According to Equation (2), it can be deduced that an omega-shaped element exhibits efficient wave radiation when it experiences a substantial induction of electric dipole moment and/or magnetic moment . The metamaterial under investigation uses omega-shaped elements that possess pre-calculated parameters, which are characterized by the simultaneous excitation of both electric dipole moment and magnetic moment, with the absolute values of both moments satisfying the following relation with a certain degree of accuracy.
Therefore, the omega-shaped element can be regarded as a bianisotropic particle exhibiting both electric and magnetic properties. Formula (3) is verified by both theoretical calculations and modeling. It is satisfied precisely for omega-elements with the geometrical parameters outlined in this paper, provided that waves with a frequency of about 1 THz are used. In the event that a modification to the frequency of electromagnetic waves becomes necessary due to experimental conditions, Formula (3) will be satisfied using updated parameters of the omega-element. New optimal parameters for the omega elements necessary to achieve a different frequency of the electromagnetic field can be calculated using a universal technique described in the publications authored by [21,22,23,24] and previously tested in the microwave range.
As stated before, the omega-shaped element can be regarded as a bianisotropic particle that possesses both dielectric and magnetic properties. Bianisotropic properties, also known as crossing properties, are fully manifested if they can be activated by both electric and magnetic fields of the incident wave. Therefore, omega-structures are known to necessitate an oblique incidence of electromagnetic waves. This allows the magnetic field vector to penetrate the omega-shaped element loop and excite an electric current. Under the action of both fields of the incident wave, the induced electric dipole moment of the omega-shaped element is oriented along its arms, i.e., lies in the plane of the metasurface, whereas the excited magnetic moment is orthogonal to the omega-shaped element turn, i.e., perpendicular to the metasurface. Hence, according to Formula (2), the wave reflected from the metasurface can exhibit elliptic polarization, considering the phase shift between the oscillations of the electric dipole moment and the magnetic moment equal to . Regarding the omega-shaped element with optimal parameters, the integrated use of Formulas (2) and (3) demonstrates that at an angle of incidence equal to , the polarization properties of this element manifest themselves in the most pronounced form, including the possible emergence of a reflected wave with circular polarization. In this regard, this paper empirically examines the most effective angle of oblique incidence, which is determined to be .
The omega-shaped element exhibits the most effective excitation when its “arms” are aligned with the plane of oscillation of the electric field vector of the incident wave, specifically in the case of . Here, the displacement of conduction electrons along the “arms” is accompanied by the appearance of electric current within the coil. Specifically, both the electric dipole moment and magnetic moment are induced simultaneously. The plots of reflection coefficients in Figure 4 for these cases of effective activation of the omega-shaped element at are denoted as and . It can be deduced from Figure 5 that the wave reflection coefficients attain their maximum values precisely in the cases indicated as and . In the case of , the “arms” of the omega-shaped element are parallel to the incident wave vector . In the case involving , the “arms” of the omega-shaped element are situated within the plane of oscillations of the incident wave vector . Throughout the experiment, the angle between the symmetry axis of the omega-shaped element and the plane of oscillation of the incident wave electric vector takes the values of 90, 66, 45, 20 and 0 degrees. It is possible to consider the component of the electric vector of the incident wave parallel to the “arms” of the omega-shaped element, which is equal to , , where is the incidence angle of the wave on the surface of the metamaterial. As the angle decreases, there is a corresponding decrease in the component , resulting in an ensuing decrease in the reflection coefficient. Figure 5 illustrates precisely this behavior of reflection coefficients for incident waves with s- and p-polarizations.
Thus, the experimental findings relating to the reflection coefficients, which are displayed in Figure 5, are consistent with the outcomes of the theoretical analysis.
Additionally, the frequency dependence of the reflection coefficients for s- and p-polarization of the incident wave, as depicted in Figure 5, is noteworthy. The resonant nature of the metamaterial reflection spectra can be attributed to the enhanced excitation of each omega-shaped element at a certain frequency, which is related to the geometrical parameters of the omega-shaped element. The resonant excitation of the omega-shaped element occurs when its full length in the straightened state is approximately equal to half the wavelength of the electromagnetic field: . Consequently, the resonant frequency satisfies the relation as follows:
Here, is the full length of the omega-shaped element in the straightened state, l is the omega-shaped element arm length, is the coil radius of the omega-shaped element.
The gap width and the width of the metal strip are approximately 3–6% relative to the full length of the omega-shaped element in the rectified state and the diameter of its turn (see Figure 1a). Consequently, both the gap width and the metal strip width exhibit negligible impact on the position of the resonant frequency. According to Formula (4), it is the arm length and the radius of the omega-shaped element turn that determine the value of the resonance frequency in the first approximation.
Since the half-wave resonance condition is satisfied, the electric current distribution in the omega-shaped element is well-known, which is confirmed by both theoretical calculations and modeling. The current distribution is characterized by the maximum value of electric current density centrally in the omega-shaped element and a monotonic decrease in current density towards the ends of the element. As a result, the current density becomes zero at the ends of the arms of the omega-shaped element.
The authors’ publications [21,22,23,24] outline the approach for determining the optimal parameters of omega-shaped elements as the basis for electromagnetic wave polarization transducers. This methodology consists of the following stages. First, when designing a metamaterial, it is important to ascertain the specific operating frequency (wavelength) that the potential device will require. It is imperative to utilize Formula (4) to calculate the ratio between the arm length l of the omega-shaped element and the radius of its turn r. This relation will not be sufficient to definitively establish the values of the two unknown quantities. Secondly, it is necessary to calculate the electric dipole moment p and the magnetic moment m of the omega-shaped element. Here one should use the electric current and charge distribution within the omega-particle, which can be determined through numerical or analytical modeling based on the half-wave resonance condition. The values of the p and m moments are to be expressed in terms of l and r element parameters. Thirdly, it is necessary to substitute the values of p and m into Formula (4) and thereby obtain the second relation between l and r, which is missing for the calculation of two unknowns. Fourth, the determination of two unknown quantities l and r is necessary, which are directly related to the operating frequency of the polarization transducer. Finally, one should select the optimal position of the metamaterial with respect to the incident wave vector, as well as choose the preferred polarization of the incident wave.
The metamaterial under investigation uses omega-shaped elements with mean parameters l = 12.8 μm, = 19.8 μm. Therefore, based on Equation (4), it can be concluded that the resonance frequency is = 1.0 THz, which is approximately equal to the maximum frequency of the reflection coefficients in Figure 5. These coefficients are obtained at the angles between the symmetry axis of the omega-shaped element and the plane of oscillation of the electric vector of the incident wave . At these specific angles , the omega-shaped elements are activated predominantly by the electric vector of the incident wave, resulting in the fulfilment of relation (4). When the angle between the symmetry axis of the omega-shaped element and the plane of oscillation of the electric vector of the incident wave assumes values of , it can be observed that the omega-shaped elements are mostly excited by the magnetic field vector of the incident wave. In this instance, the electric current originates primarily in the coil of the omega-shaped element, with its arms not contributing, which results in another resonant frequency formula.
By employing Formula (5), the resonance frequency is determined to be THz. The frequency obtained is roughly equivalent to the frequency of the second maximum of the reflection coefficients shown in Figure 5.
Figure 5a,b demonstrate that the metamaterial exhibits also the local maximum reflection for terahertz waves near the frequency range of 0.4–0.45 THz. The analysis of the incident wave polarization for this reflection peak reveals that this maximum is excited by the magnetic field of the incident wave. Unlike the resonance frequencies described by Formulas (4) and (5), which characterize the activation of a single omega-shaped element, the low-frequency reflection peak being discussed is the result of the collective excitation of multiple omega-shaped elements. In order to analyze the mutual influence of neighboring omega-shaped elements in the metamaterial, it is necessary to consider the distance between the arms of two adjacent omega-shaped elements and the distance between the turns (loops) of two adjacent omega-shaped elements . From Figure 1a it is evident that μm, μm. Given that the inequality is satisfied, it is anticipated that there will be a more pronounced coupling between the loops of adjacent elements compared to the coupling between the arms of adjacent elements. Since the turns are predominantly excited by the magnetic field, the resonance for the frequency range of 0.4–0.45 THz is initiated by the magnetic field of the incident wave. This fact is illustrated in Figure 5a,b. In order to consider the electric current distribution, without loss of generality, it is possible to conditionally distinguish three neighboring omega-elements in the metasurface. The modeling reveals that the magnetic moment vector and the magnetic field vector of the wave coincide in the central omega-shaped element near the resonance frequency. This occurs due to the fact that the magnetic moment within the central omega-shaped element is excited primarily by the magnetic field of the incident wave. Herewith, the electric current in the central omega-shaped element generates a right-handed system with the magnetic field vector of the incident wave. Both the magnetic field of the incident wave and the field of the central omega-element exert an influence on the adjacent elements within the group being studied. When exposed to this field, the magnetic moments that are opposite in direction to the magnetic field of the incident wave become activated in the omega-elements positioned on either side of the central one. Consequently, the distribution of the electric current in the group of omega-shaped elements (central and two neighboring ones) corresponds to three half-waves. In other words, the eigenmode is excited, for which the total length of three neighboring omega-shaped elements is approximately equal to three half-waves of the electromagnetic field.
Considering the previously stated, the resonant frequency in this case can be determined using the following formula:
The calculation by Formula (6) generates a value of THz, which closely aligns with the experimental values (see Figure 5a,b).
Undoubtedly, the reflection coefficients of terahertz waves from a metamaterial can be accurately computed using Finite Element Analysis software packages such as COMSOL. Formulas (4)–(6) represent basic relations that allow approximating the position of frequency maxima in the reflection spectrum of the metamaterial. Despite the simplicity of the qualitative approach employed here, Formulas (4)–(6) are unquestionably valuable for predicting the frequency-polarization characteristics of the metamaterial during the design phase. Peaks experimentally observed in the reflection spectrum may exhibit a frequency shift relative to the values calculated by Formulas (4)–(6). For the frequency , this shift reaches approximately 17%. This frequency shift may arise from various factors, including the presence of a substrate, the mutual influence of omega-shaped elements within the metamaterial, oblique wave incidence, etc. The forthcoming research will employ the Finite Element Analysis software package to precisely determine the value of the frequency shift and maxima position in the reflection spectrum. This process will require time and a substantial expansion of this paper’s length in order to present the findings.
Hence, the frequency dependence of reflection coefficients displayed in Figure 5, including the occurrence of three main maxima, correlates with the findings of the theoretical study.
The incidence angle of radiation on the metamaterial is not accounted for in Formulas (4)–(6). Experimental studies performed at normal incidence of THz waves on the metamaterial confirm the presence of three main maxima in the reflection spectra at the same frequency values , , and as well as notable polarization anisotropy in the reflection coefficients.
It is essential to consider a significant distinction between the reflected waves at s- and p-polarization of the incident wave, which arises from the different polarization of the reflected radiation. According to Equation (2), when a wave with s-polarization is incident on a metamaterial, the resulting reflected radiation is likewise linearly polarized and comprises only an s component. When the incident wave is p-polarized, the reflected radiation demonstrates an elliptical polarization that closely resembles circular polarization.
Additionally, an investigation into the transmission of THz radiation through the metamaterial was conducted. Figure 6 illustrates families of characteristic transmission spectra.
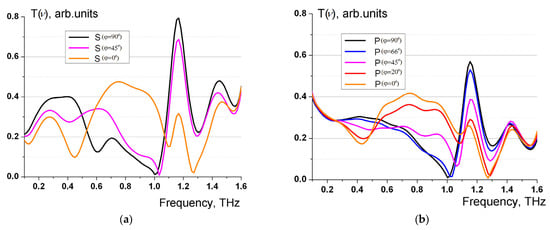
Figure 6.
Transmission spectra of a metamaterial formed by omega-shaped elements on a silicon substrate for s-polarization (a) and p-polarization (b) of the incident wave.
When constructing the spectra, standard normalization to the wave intensity in the absence of metamaterial was performed. The transmission spectra exhibit a resonant nature and demonstrate an almost total lack of the transmitted wave in close proximity to the frequency for the cases , , , , as well as in the vicinity of the frequency for the cases , , . The analysis reveals that the spectra are close to the frequency dependence of the reflection coefficients presented in Figure 5. The joint analysis of Figure 5a,b and Figure 6a,b provides conclusive evidence of the frequency-selective properties of the metamaterial with strictly defined maxima of reflection and corresponding minima within the transmission of terahertz waves. When conducting a joint analysis of the figures, it is important to investigate the resonant nature of wave transmission and reflection in relation to their polarization and frequency. At the same time, it should be considered that the reflection and transmission spectra were collected via different normalization methods, which are generally accepted. Therefore, further research will concentrate on conducting a thorough comparison of the numerical values of the R and T coefficients and verification of the relation , with A representing the absorption coefficient of the metamaterial.
4. Conclusions
The reflection and transmission spectra of a metamaterial formed by omega-shaped elements with pre-calculated optimal parameters on a silicon substrate have been recorded in the terahertz range at oblique incidence for the s- and p-polarizations of the incident wave. The spectra were interpreted within the dipole radiation theory of electromagnetic waves. The obtained measurement findings indicate a significant polarization anisotropy of reflection and transmission of the metamaterial formed by omega elements on a silicon substrate, which can be used to control THz radiation. One of the potential practical applications of the device under consideration could be exemplified by wireless communication systems. Subsequent investigations should focus on controlling the ellipticity coefficient of terahertz radiation and monitoring the ellipticity. An evaluation ought to be performed to compare the advantages of the proposed optical layout with a more conventional configuration of half-wave and quarter-wave plates, including the comparison of the bandwidth of the frequencies used.
Author Contributions
Conceptualization, A.V.L. and I.V.S.; methodology, I.V.S., A.L.S. and M.A.P.; investigation, A.L.S., M.A.P., G.V.S. and A.Y.K.; writing—original draft preparation, A.V.L., I.V.S. and S.A.K.; writing—review and editing, A.V.L., I.V.S. and S.A.K.; visualization, A.Y.K.; supervision, A.V.L., I.V.S. and S.A.K.; project administration, A.L.S. All authors have read and agreed to the published version of the manuscript.
Funding
The research was conducted as part of the State Research Program titled “Photonics and Electronics for Innovations”.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Acknowledgments
The authors wish to thank Tatyana Lozovskaya, a senior teacher, for her help in translating this article. The research was carried out within the framework of the State Research Program “Photonics and electronics for innovation”, the subprogram “Opto- and microwave electronics” and the Belarussian Republican Foundation for Basic Research (project F22KITG-021).
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Han, S.; Pitchappa, P.; Wang, W.; Srivastava, Y.K.; Rybin, M.V.; Singh, R. Extended bound states in the continuum with symmetry-broken terahertz dielectric metasurfaces. Adv. Opt. Mater 2021, 9, 2002001. [Google Scholar] [CrossRef]
- Liu, D.; Yu, X.; Wu, F.; Xiao, S.; Itoigawa, F.; Ono, S. Terahertz high-Q quasi-bound states in the continuum in laser-fabricated metallic double-slit arrays. Opt. Express 2021, 29, 24779–24791. [Google Scholar] [CrossRef]
- Liu, B.; Peng, Y.; Jin, Z.; Wu, X.; Gu, H.; Wei, D.; Zhu, Y.; Zhuang, S. Terahertz ultrasensitive biosensor based on wide-area and intense light-matter interaction supported by QBIC. Chem. Eng. J. 2023, 462, 142347. [Google Scholar] [CrossRef]
- Peng, Y.; Shi, C.; Zhu, Y.; Gu, M.; Zhuang, S. Terahertz spectroscopy in biomedical field: A review on signal-to-noise ratio improvement. PhotoniX 2020, 1, 12. [Google Scholar] [CrossRef]
- Chen, H.T.; Padilla, W.J.; Zide, J.M.; Gossard, A.C.; Taylor, A.J.; Averitt, R.D. Active terahertz metamaterial devices. Nature 2006, 444, 597–600. [Google Scholar] [CrossRef]
- Pendry, J.B.; Holden, A.J.; Robbins, D.J.; Stewart, W.J. Magnetism from conductors and enhanced nonlinear phenomena. IEEE Trans. Microw. Theory Tech. 1999, 47, 2075–2084. [Google Scholar] [CrossRef]
- Xu, T.; Lin, Y.S. Tunable Terahertz Metamaterial Using an Electric Split-Ring Resonator with Polarization-Sensitive Characteristic. Appl. Sci. 2020, 10, 4660–4668. [Google Scholar] [CrossRef]
- Cheng, Z.; Cheng, Y. A multi-functional polarization convertor based on chiral metamaterial for terahertz waves. Opt. Commun. 2019, 435, 178–182. [Google Scholar] [CrossRef]
- Sun, B.; Yingying, Y. Optical refractive index sensor based on the conjugated bilayer Γ-shaped chiral metamaterials. Optik 2019, 182, 587–593. [Google Scholar] [CrossRef]
- Yu, Y.; Sun, B. Analysis of giant circular dichroism metamaterial based on conductive coupling. Optik 2019, 182, 1046–1052. [Google Scholar] [CrossRef]
- Mirzamohammadi, F.; Nourinia, J.; Ghobadi, C.; Majidzadeh, M. A bi-layered chiral metamaterial with high-performance broadband asymmetric transmission of linearly polarized wave. AEU—Int. J. Electron. Commun. 2019, 98, 58–67. [Google Scholar] [CrossRef]
- Cheng, Y.Z.; Nie, Y.; Cheng, Z.Z.; Wang, X.; Gong, R.Z. Asymmetric chiral metamaterial circular polarizer based on twisted split-ring resonator. Appl. Phys. B 2014, 116, 129–134. [Google Scholar] [CrossRef]
- Sakellari, I.; Yin, X.; Nesterov, M.L.; Terzaki, K.; Xomalis, A.; Farsari, M. 3D chiral plasmonic metamaterials fabricated by direct laser writing: The twisted omega particle. Adv. Opt. Mater. 2017, 5, 1700200. [Google Scholar] [CrossRef]
- Stojanović, D.B.; Beličev, P.P.; Radovanović, J.; Milanović, V. Numerical parametric study of chiral effects and group delays in Ω element based terahertz metamaterial. Phys. Lett. A 2019, 383, 1816–1820. [Google Scholar] [CrossRef]
- Liu, D.J.; Xiao, Z.Y.; Ma, X.L.; Xu, K.K.; Tang, J.Y.; Wang, Z.H. Broadband asymmetric transmission and polarization conversion of a linearly polarized wave based on chiral metamaterial in terahertz region. Wave Motion 2016, 66, 1–9. [Google Scholar] [CrossRef]
- Liu, D.J.; Xiao, Z.Y.; Ma, X.L.; Wang, Z.H. Broadband asymmetric transmission and multi-band 90° polarization rotator of linearly polarized wave based on multi-layered metamaterial. Opt. Commun. 2015, 354, 272–276. [Google Scholar] [CrossRef]
- Vehmas, J.; Hrabar, S.; Tretyakov, S. Omega transmission lines with applications to effective medium models of metamaterials. J. Appl. Phys. 2014, 115, 134905. [Google Scholar] [CrossRef]
- Asadchy, V.S.; Díaz-Rubio, A.; Tretyakov, S.A. Bianisotropic metasurfaces: Physics and applications. Nanophotonics 2018, 7, 1069–1094. [Google Scholar] [CrossRef]
- Mazanov, M.; Yermakov, O.; Deriy, I.; Takayama, O.; Bogdanov, A.; Lavrinenko, A.V. Photonic spin Hall effect: Contribution of polarization mixing caused by anisotropy. Quantum Rep. 2020, 2, 489–500. [Google Scholar] [CrossRef]
- Yermakov, Y.; Hurshkainen, A.A.; Dobrykh, D.A.; Kapitanova, P.V.; Iorsh, I.V.; Glybovski, S.B.; Bogdanov, A.A. Experimental observation of hybrid TE-TM polarized surface waves supported by a hyperbolic metasurface. Phys. Rev. B 2018, 98, 195404. [Google Scholar] [CrossRef]
- Semchenko, I.V.; Khakhomov, S.A.; Podalov, M.A.; Tretyakov, S.A. Radiation of circularly polarized microwaves by a plane periodic structure of Ω elements. J. Commun. Technol. Electron. 2007, 52, 1002–1005. [Google Scholar] [CrossRef]
- Semchenko, I.V.; Khakhomov, S.A.; Samofalov, A.L.; Podalov, M.A.; Songsong, Q. The effective optimal parameters of metamaterial on the base of omega-elements. In Recent Global Research and Education: Technological Challenges; Advances in Intelligent Systems and Computing; Jablonski, R., Szewczyk, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2017; Volume 519, pp. 3–9. [Google Scholar]
- Balmakou, A.; Podalov, M.; Khakhomov, S.; Stavenga, D.; Semchenko, I. Ground-plane-less bidirectional terahertz absorber based on omega resonators. Opt. Lett. 2015, 40, 2084–2087. [Google Scholar] [CrossRef]
- Semchenko, I.; Khakhomov, S.; Samofalov, A.; Podalov, M.; Solodukha, V.; Pyatlitski, A.; Kovalchuk, N. Omega-structured substrate-supported metamaterial for the transformation of wave polarization in THz frequency range. In Recent Advances in Technology Research and Education: Proceedings of the 16th International Conference on Global Research and Education Inter-Academia, Iasi, Romania, 25–28 September 2017; Springer: Berlin/Heidelberg, Germany, 2018; Volume 660, pp. 72–80. [Google Scholar]
- Khodasevich, M.A.; Lyakhnovich, A.V.; Eriklioglu, H. Chocolate Sample Classification by Principal Component Analysis of Preprocessed Terahertz Transmission Spectra. J. Appl. Spectrosc. 2022, 89, 251–255. [Google Scholar] [CrossRef]
- Fastampa, R.; Pilozzi, L.; Missori, M. Cancellation of Fabry-Perot interference effects in terahertz time-domain spectroscopy of optically thin samples. Phys. Rev. A 2017, 95, 063831. [Google Scholar] [CrossRef]
- Lyon, D.A. The discrete Fourier transform, part 4: Spectral leakage. J. Object Technol. 2009, 8, 23–34. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. The Classical Theory of Fields, 4th ed.; Pergamon Press: Oxford, UK, 1975; Volume 2, 402p. [Google Scholar]
- Kivshar, Y. All-dielectric meta-optics and non-linear nanophotonics. Natl. Sci. Rev. 2018, 5, 144–158. [Google Scholar] [CrossRef]
- Staude, I.; Pertsch, T.; Kivshar, Y.S. All-dielectric resonant meta-optics lightens up. ACS Photonics 2019, 6, 802–814. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).