Spatial Relation Awareness Module for Phase Unwrapping
Abstract
1. Introduction
- Path-following approach: several proposed methods include the quality guided path algorithm, which determines the unwrapping path using a quality map or reliability criteria [9,10,11], and the branch cut algorithm [12], which imposes constraints on the unwrapping path to traverse line segments connecting two endpoints.
- Minimum norm approach: An approach to phase unwrapping by minimizing the norm between the gradient of the wrapping phase and the unwrapping phase. Phase unwrapping using the least-squares method [13] is the most typical minimum norm approach.
- We demonstrated that the performance of phase unwrapping can be improved by applying the proposed module SRAM, which takes into account the continuity of phase and the relationships between pixels, to the encoder–decoder model.
- The SRAM proposed in this study is easy to implement, highly reusable, and can be applied to a wide range of encoder–decoder models.
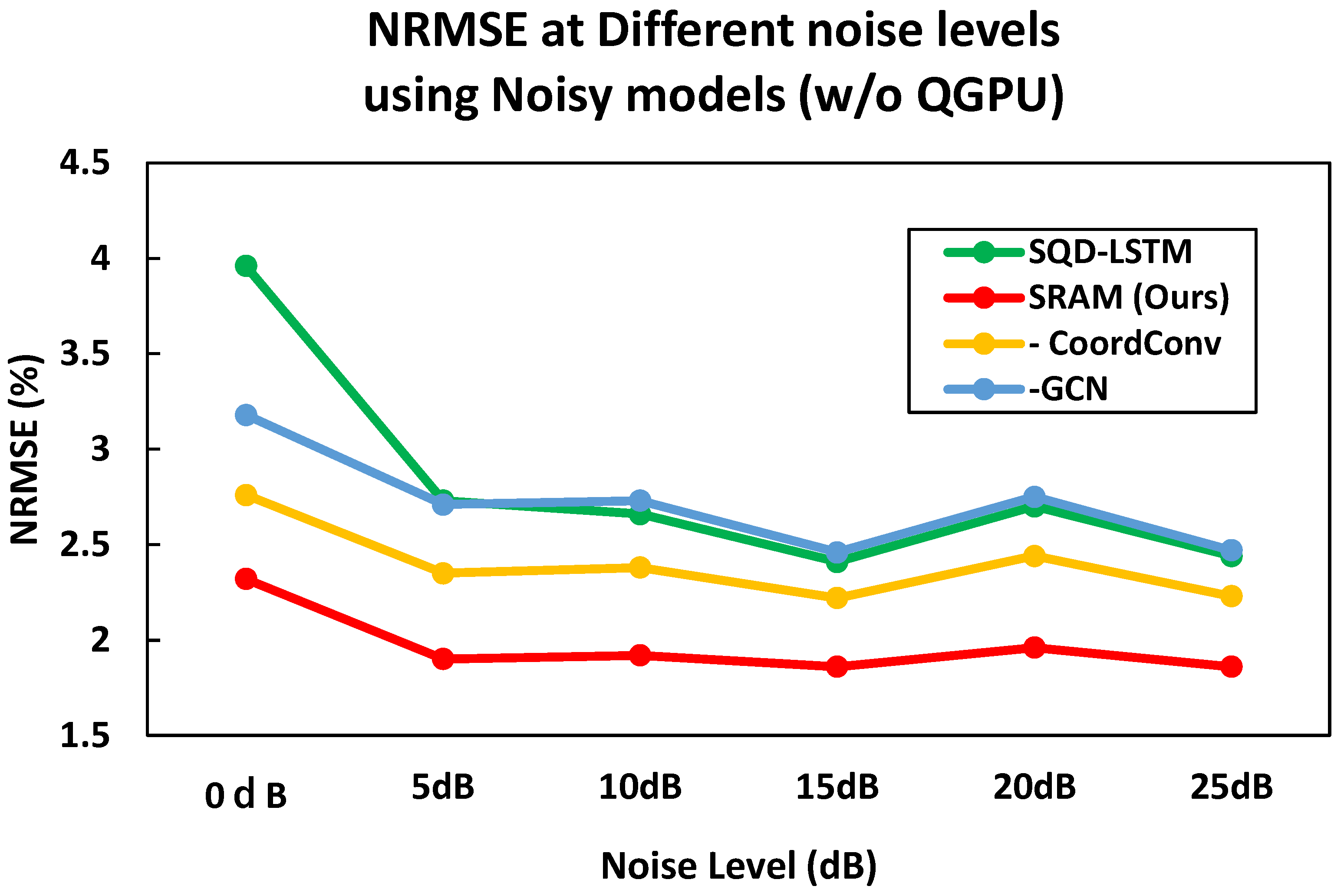
- In terms of the performance of phase unwrapping on wrapped phases containing noise, the proposed method achieved a 4.98% improvement in normalized root mean square error (NRMSE) compared to the conventional method, quality-guided phase unwrapping (QGPU) [9]. Furthermore, it outperformed the CNN-based method, spatial quad-directional long short term memory (SQD-LSTM) [8], by 0.65%.
2. Related Work
2.1. Quality-Guided Phase Unwrapping Algorithm
2.2. CNN Approach
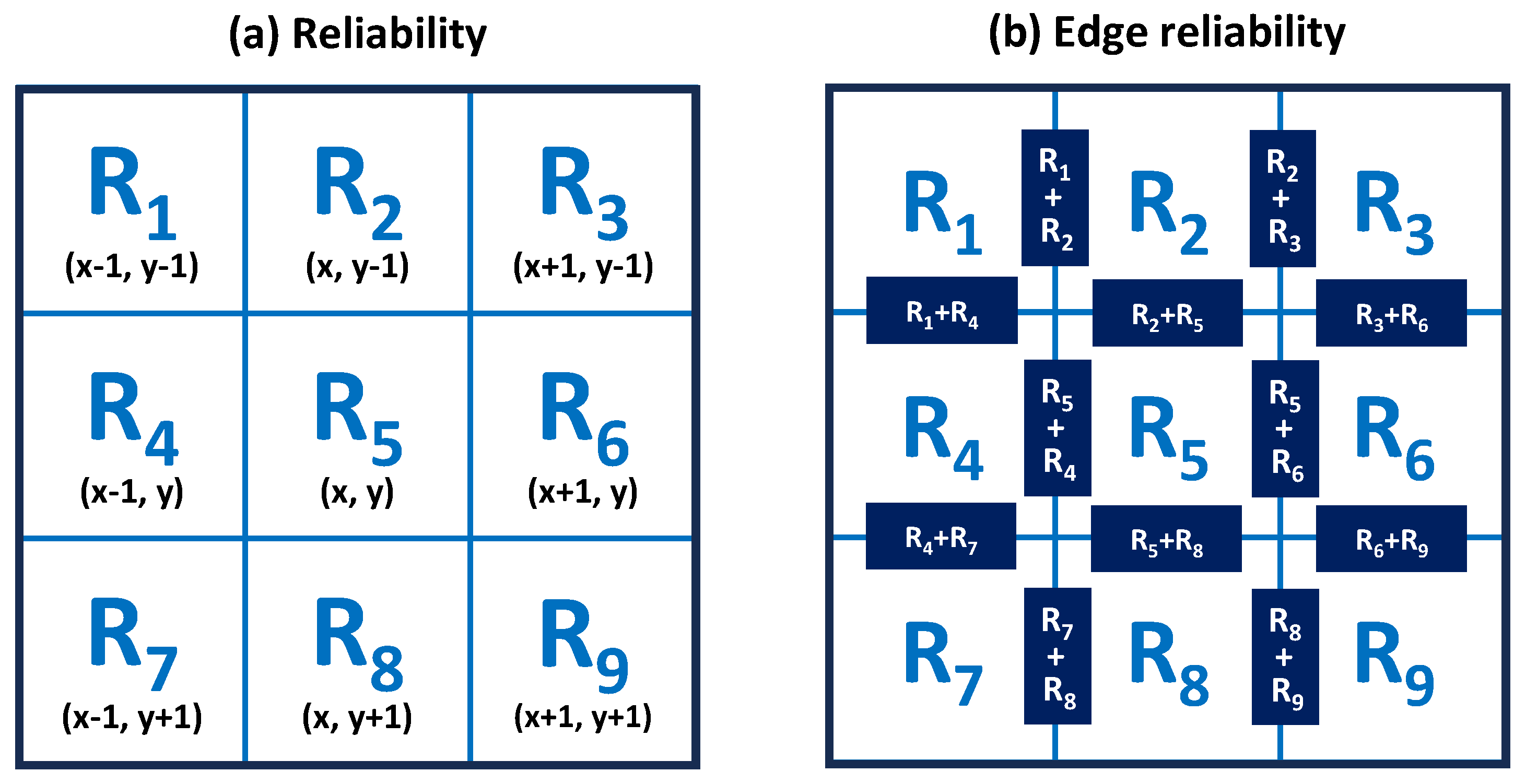
3. Proposed Method
4. Results
4.1. Data Generation
4.2. Implementation Details
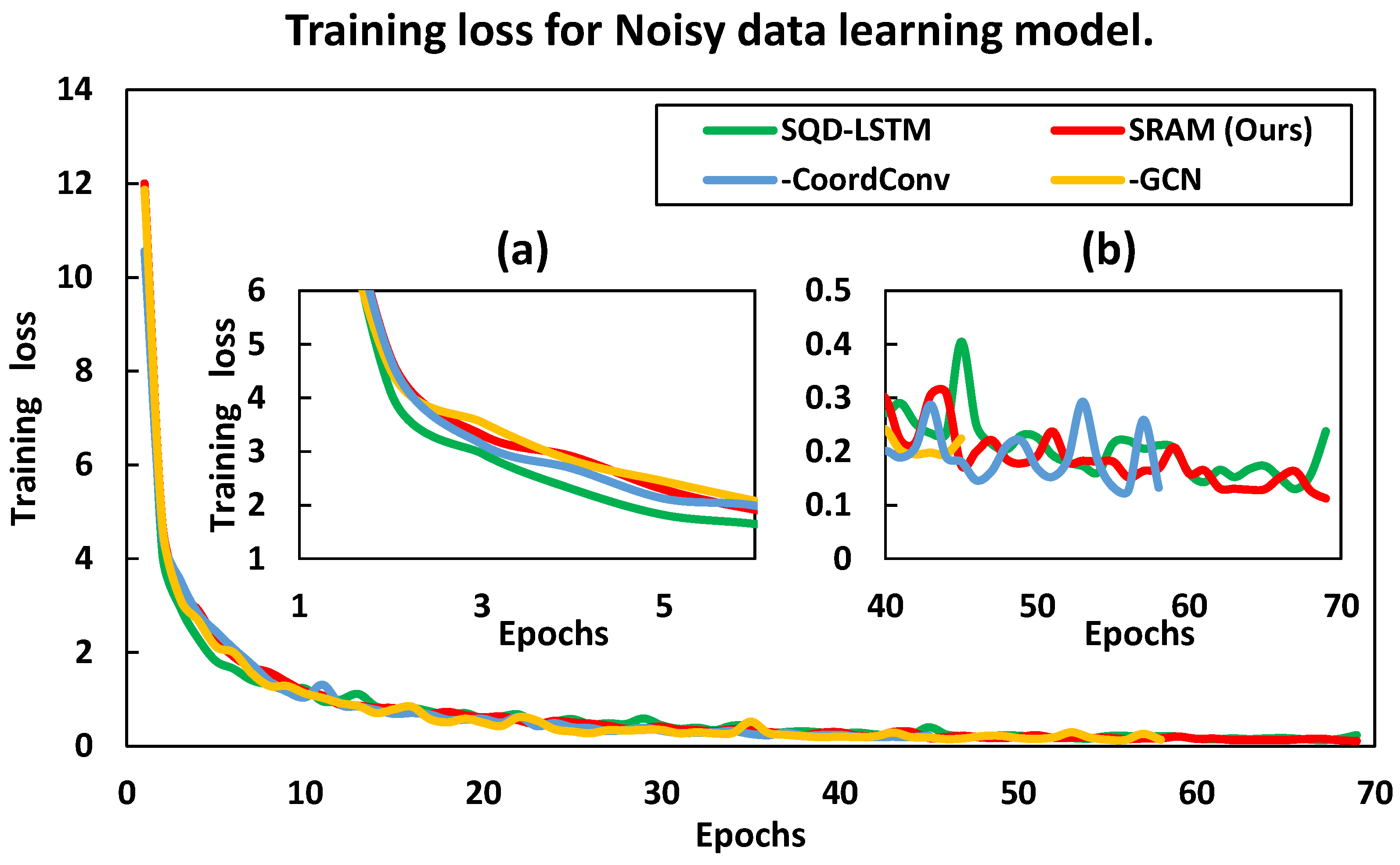
4.3. Quantitative Evaluation
- SRAM (Ours): a proposed CNN model employing SRAM for skip connection.
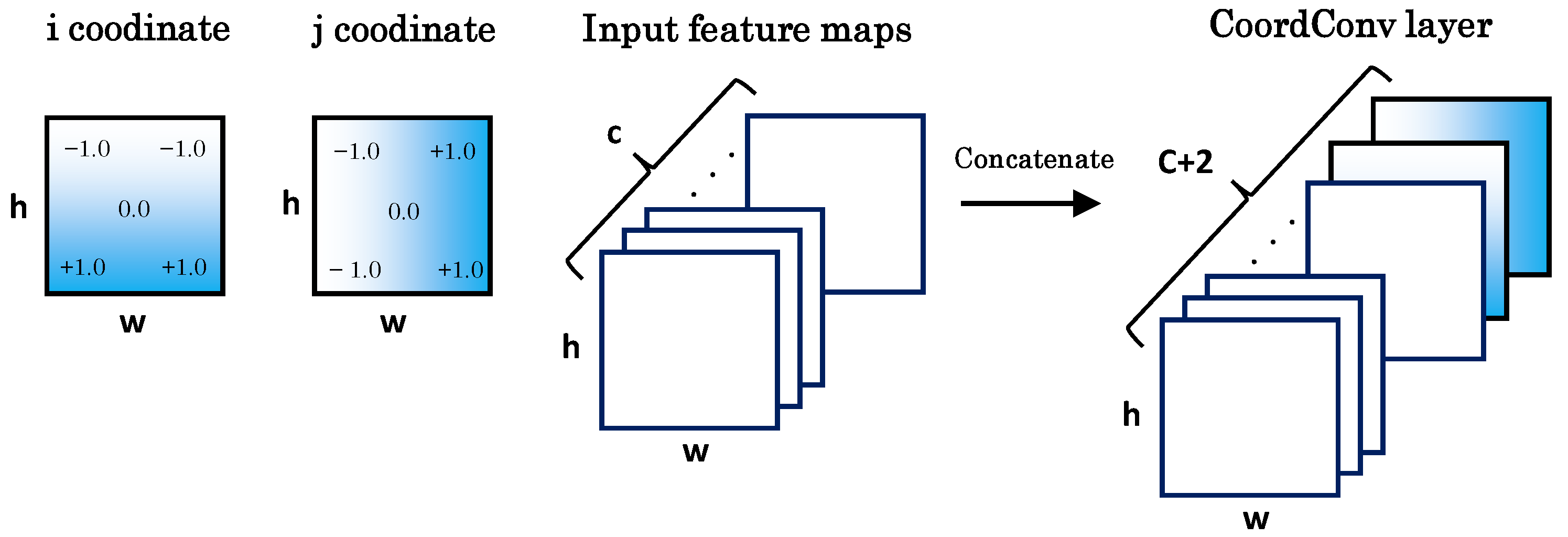
- −CoordConv: An ablation model that removes CoordConv [26] from the proposed SRAM. In other words, a model in which only GCNs are applied to skip connections.
- −GCN: An ablation model that removes GCN [25] from the proposed SRAM. In other words, a model in which only CoordConv is applied to skip connections.
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dong, J.; Liu, T.; Chen, F.; Zhou, D.; Dimov, A.; Raj, A.; Cheng, Q.; Spincemaille, P.; Wang, Y. Simultaneous phase unwrapping and removal of chemical shift (SPURS) using graph cuts: Application in quantitative susceptibility mapping. IEEE Trans. Med. Imaging 2014, 34, 531–540. [Google Scholar] [CrossRef]
- Goldstein, R.M.; Zebker, H.A.; Werner, C.L. Satellite radar interferometry: Two-dimensional phase unwrapping. Radio Sci. 1988, 23, 713–720. [Google Scholar] [CrossRef]
- Gorthi, S.S.; Rastogi, P. Fringe projection techniques: Whither we are? Opt. Lasers Eng. 2010, 48, 133–140. [Google Scholar] [CrossRef]
- Waghmare, R.G.; Sukumar, P.R.; Subrahmanyam, G.S.; Singh, R.K.; Mishra, D. Particle-filter-based phase estimation in digital holographic interferometry. J. Opt. Soc. Am. A 2016, 33, 326–332. [Google Scholar] [CrossRef] [PubMed]
- Itoh, K. Analysis of the phase unwrapping algorithm. Appl. Opt. 1982, 21, 2470. [Google Scholar] [CrossRef] [PubMed]
- Ghiglia, D.C.; Pritt, M.D. Two-Dimensional Phase Unwrapping: Theory, Algorithms, and Software, 1st ed.; Wiely-Interscience: Hoboken, NJ, USA, 1998. [Google Scholar]
- Spoorthi, G.; Gorthi, R.K.S.S.; Gorthi, S. PhaseNet 2.0: Phase unwrapping of noisy data based on deep learning approach. IEEE Trans. Image Process. 2020, 29, 4862–4872. [Google Scholar] [CrossRef]
- Perera, M.V.; De Silva, A. A joint convolutional and spatial quad-directional LSTM network for phase unwrapping. In Proceedings of the ICASSP 2021—2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, ON, Canada, 6–11 June 2021; pp. 4055–4059. [Google Scholar]
- Lei, H.; Chang, X.Y.; Wang, F.; Hu, X.T.; Hu, X.D. A novel algorithm based on histogram processing of reliability for two-dimensional phase unwrapping. Optik 2015, 126, 1640–1644. [Google Scholar] [CrossRef]
- Zhao, M.; Huang, L.; Zhang, Q.; Su, X.; Asundi, A.; Kemao, Q. Quality-guided phase unwrapping technique: Comparison of quality maps and guiding strategies. Appl. Opt. 2011, 50, 6214–6224. [Google Scholar] [CrossRef] [PubMed]
- Herráez, M.A.; Burton, D.R.; Lalor, M.J.; Gdeisat, M.A. Fast two-dimensional phase-unwrapping algorithm based on sorting by reliability following a noncontinuous path. Appl. Opt. 2002, 41, 7437–7444. [Google Scholar] [CrossRef]
- Huang, Q.; Zhou, H.; Dong, S.; Xu, S. Parallel branch-cut algorithm based on simulated annealing for large-scale phase unwrapping. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3833–3846. [Google Scholar] [CrossRef]
- Pritt, M.D.; Shipman, J.S. Least-squares two-dimensional phase unwrapping using FFT’s. IEEE Trans. Geosci. Remote Sens. 1994, 32, 706–708. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Hinton, G.; Deng, L.; Yu, D.; Dahl, G.E.; Mohamed, A.r.; Jaitly, N.; Senior, A.; Vanhoucke, V.; Nguyen, P.; Sainath, T.N.; et al. Deep neural networks for acoustic modeling in speech recognition: The shared views of four research groups. IEEE Signal Process. Mag. 2012, 29, 82–97. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- LeCun, Y.; Bengio, Y. Convolutional networks for images, speech, and time series. Handb. Brain Theory Neural Netw. 1995, 3361, 1995. [Google Scholar]
- Pohlen, T.; Hermans, A.; Mathias, M.; Leibe, B. Full-resolution residual networks for semantic segmentation in street scenes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4151–4160. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–7 October 2015; Springer: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- Wang, K.; Li, Y.; Kemao, Q.; Di, J.; Zhao, J. One-step robust deep learning phase unwrapping. Opt. Express 2019, 27, 15100–15115. [Google Scholar] [CrossRef]
- Zhang, T.; Jiang, S.; Zhao, Z.; Dixit, K.; Zhou, X.; Hou, J.; Zhang, Y.; Yan, C. Rapid and robust two-dimensional phase unwrapping via deep learning. Opt. Express 2019, 27, 23173–23185. [Google Scholar] [CrossRef]
- Zhang, J.; Tian, X.; Shao, J.; Luo, H.; Liang, R. Phase unwrapping in optical metrology via denoised and convolutional segmentation networks. Opt. Express 2019, 27, 14903–14912. [Google Scholar] [CrossRef]
- Chen, L.C.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-decoder with atrous separable convolution for semantic image segmentation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 801–818. [Google Scholar]
- Peng, C.; Zhang, X.; Yu, G.; Luo, G.; Sun, J. Large kernel matters–improve semantic segmentation by global convolutional network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4353–4361. [Google Scholar]
- Liu, R.; Lehman, J.; Molino, P.; Petroski Such, F.; Frank, E.; Sergeev, A.; Yosinski, J. An intriguing failing of convolutional neural networks and the coordconv solution. Adv. Neural Inf. Process. Syst. 2018, 31. [Google Scholar]
- Xie, X.; Tian, X.; Shou, Z.; Zeng, Q.; Wang, G.; Huang, Q.; Qin, M.; Gao, X. Deep learning phase-unwrapping method based on adaptive noise evaluation. Appl. Opt. 2022, 61, 6861–6870. [Google Scholar] [CrossRef]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. Segnet: A deep convolutional encoder-decoder architecture for image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Available online: https://docs.opencv.org/3.4/df/d3a/group__phase__unwrapping.html (accessed on 15 January 2024).
- Available online: https://github.com/Laknath1996/DeepPhaseUnwrap/ (accessed on 15 January 2024).
- Azuma, C.; Ito, T.; Shimobaba, T. Adversarial domain adaptation using contrastive learning. Eng. Appl. Artif. Intell. 2023, 123, 106394. [Google Scholar] [CrossRef]



| Dataset | Noise (dB) | Number of Images | |
|---|---|---|---|
| Train | Test | ||
| Noisy | [0, 5, 10, 20, 60] | 1000 | 1000 |
| Noise Free | None | 1000 | 1000 |
| Method | NRMSE | Computational Time (ms) | |||
|---|---|---|---|---|---|
| Noise Free | Noisy | Noise Free | Noisy | 0 (dB) | |
| QGPU [9] | 0.00% | 7.08% | 12.33 | 14.68 | 243.12 |
| SQD-LSTM [8] | 2.19% | 2.75% | 42.26 | 42.60 | 42.22 |
| SRAM (Ours) | 1.65% | 2.10% | 44.86 | 45.05 | 44.81 |
| −CoordConv | 2.12% | 2.33% | 44.89 | 45.06 | 45.11 |
| −GCN | 1.87% | 2.39% | 42.18 | 42.37 | 42.03 |
| Noise Level (dB) | ||||||
|---|---|---|---|---|---|---|
| 0 | 5 | 10 | 15 | 20 | 25 | |
| QGPU [9] | 25.56% | 4.50% | 1.81% | 0.91% | 0.54% | 0.27% |
| SQD-LSTM [8] | 3.96% | 2.73% | 2.66% | 2.41% | 2.70% | 2.44% |
| SRAM (Ours) | 2.32% | 1.90% | 1.92% | 1.86% | 1.96% | 1.86% |
| −CoordConv | 2.76% | 2.35% | 2.38% | 2.22% | 2.44% | 2.23% |
| −GCN | 3.18% | 2.71% | 2.73% | 2.46% | 2.75% | 2.47% |
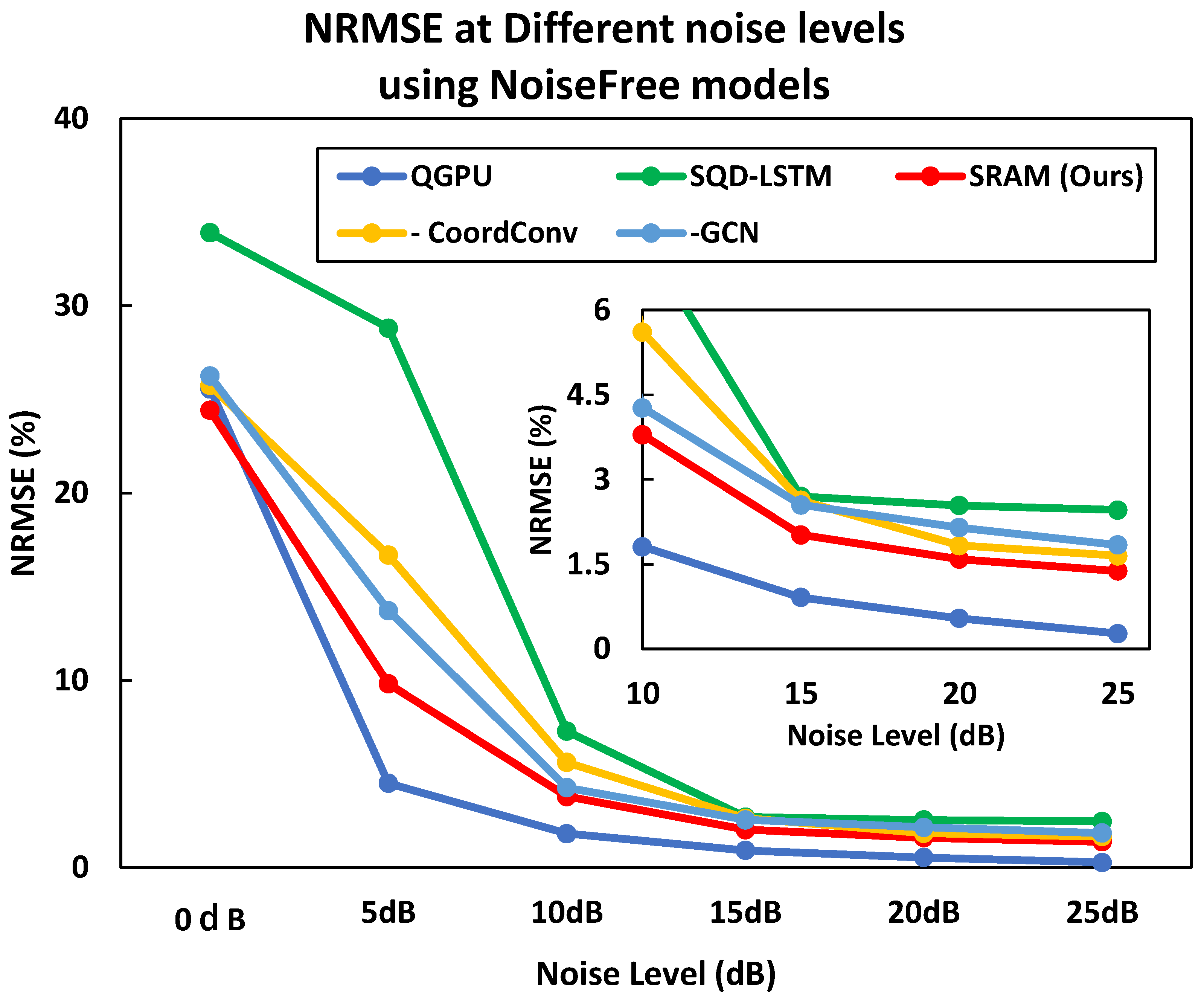
| Noise Level (dB) | ||||||
|---|---|---|---|---|---|---|
| 0 | 5 | 10 | 15 | 20 | 25 | |
| QGPU [9] | 25.56% | 4.50% | 1.81% | 0.91% | 0.54% | 0.27% |
| SQD-LSTM [8] | 33.90% | 28.81% | 7.28% | 2.70% | 2.54% | 2.46% |
| SRAM (Ours) | 24.42% | 9.81% | 3.79% | 2.02% | 1.59% | 1.38% |
| −CoordConv | 25.74% | 16.68% | 5.61% | 2.63% | 1.83% | 1.65% |
| −GCN | 26.25% | 13.72% | 4.27% | 2.55% | 2.15% | 1.84% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Azuma, C.; Ito, T.; Shimobaba, T. Spatial Relation Awareness Module for Phase Unwrapping. Photonics 2024, 11, 175. https://doi.org/10.3390/photonics11020175
Azuma C, Ito T, Shimobaba T. Spatial Relation Awareness Module for Phase Unwrapping. Photonics. 2024; 11(2):175. https://doi.org/10.3390/photonics11020175
Chicago/Turabian StyleAzuma, Chiori, Tomoyoshi Ito, and Tomoyoshi Shimobaba. 2024. "Spatial Relation Awareness Module for Phase Unwrapping" Photonics 11, no. 2: 175. https://doi.org/10.3390/photonics11020175
APA StyleAzuma, C., Ito, T., & Shimobaba, T. (2024). Spatial Relation Awareness Module for Phase Unwrapping. Photonics, 11(2), 175. https://doi.org/10.3390/photonics11020175





