Study on the Generation of 1.9 μm Mode Superposition Conversion Laser by Double-End Off-Axis Pumping
Abstract
:1. Introduction
2. Theoretical Analysis
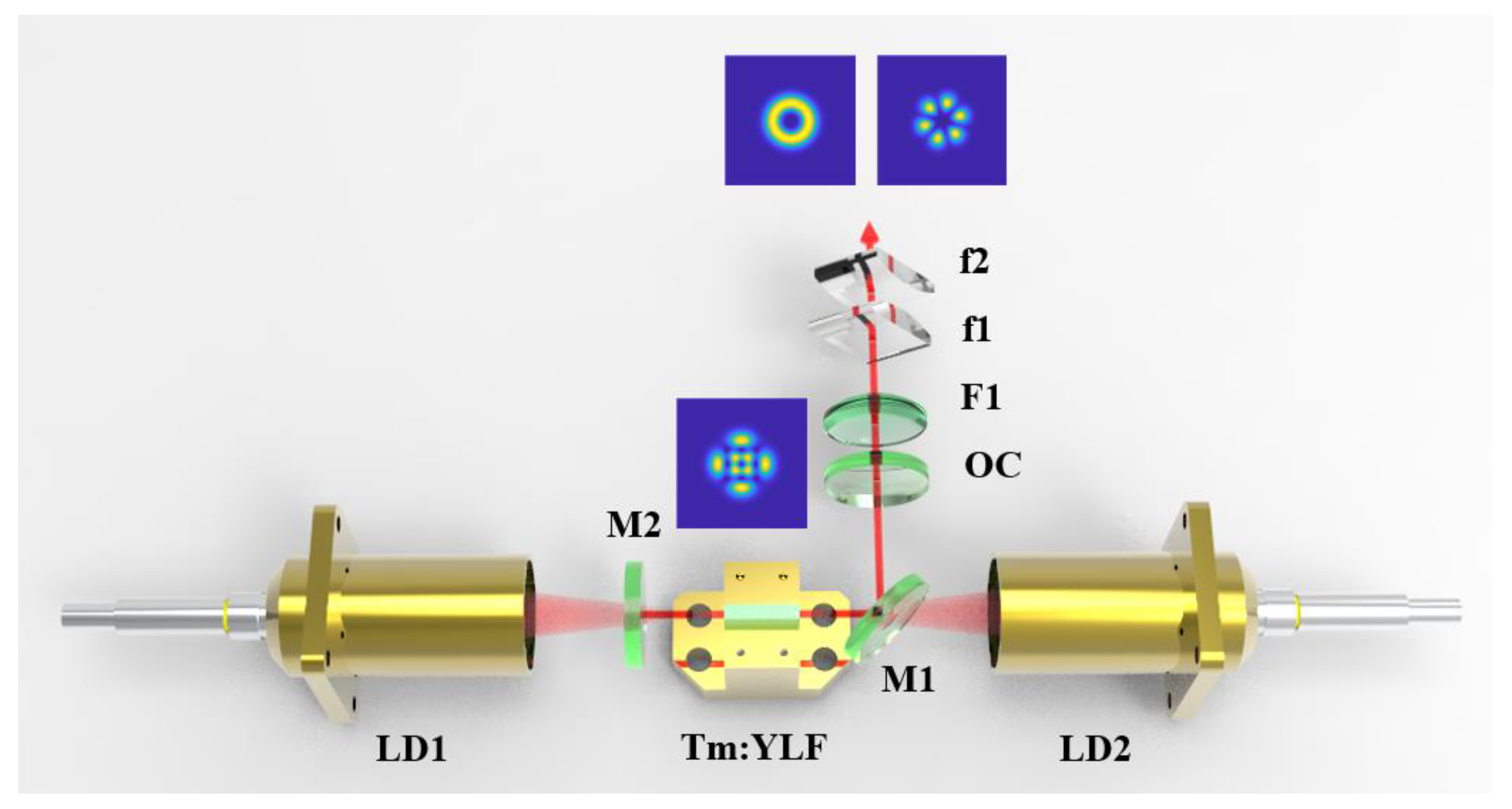
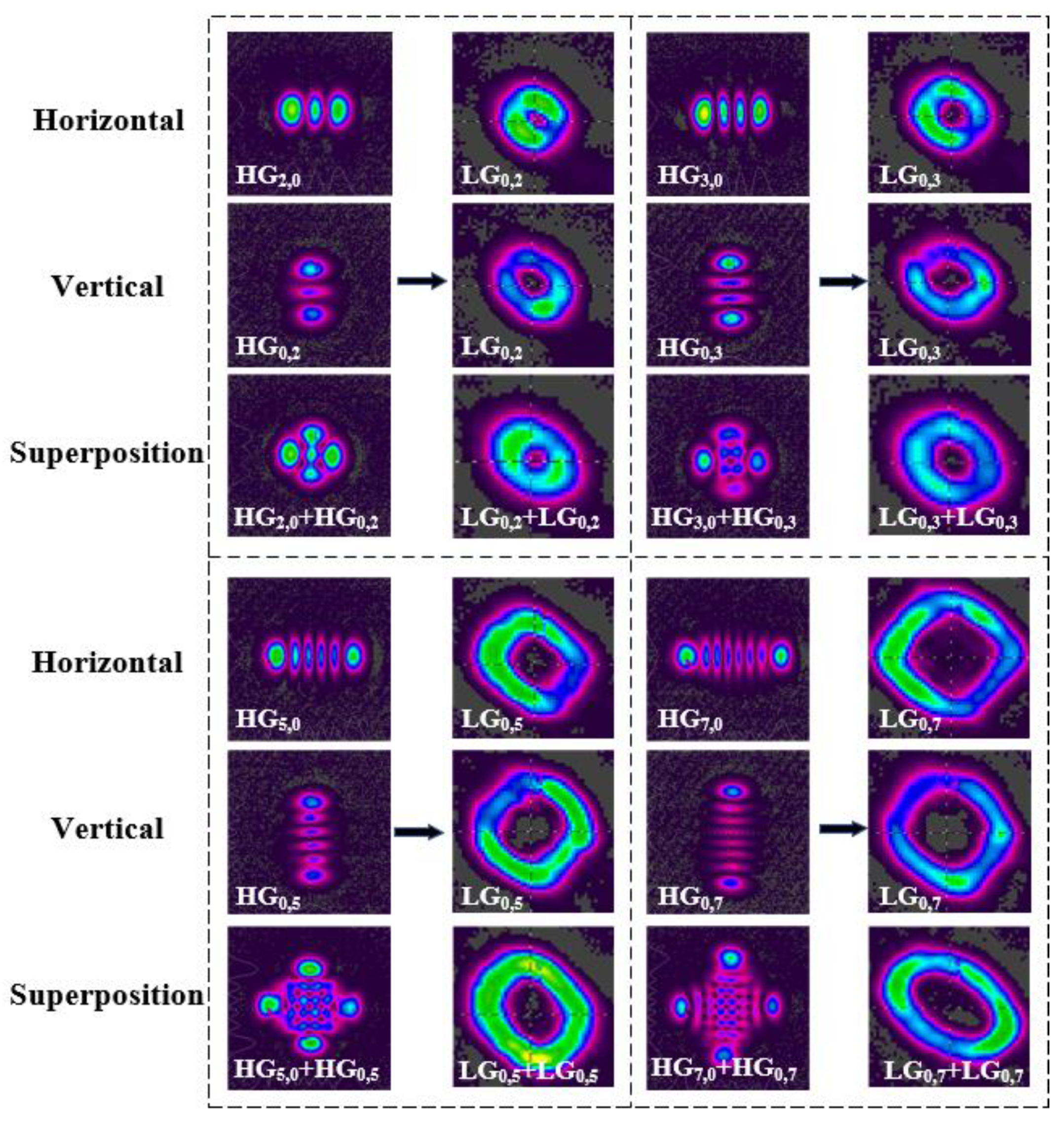
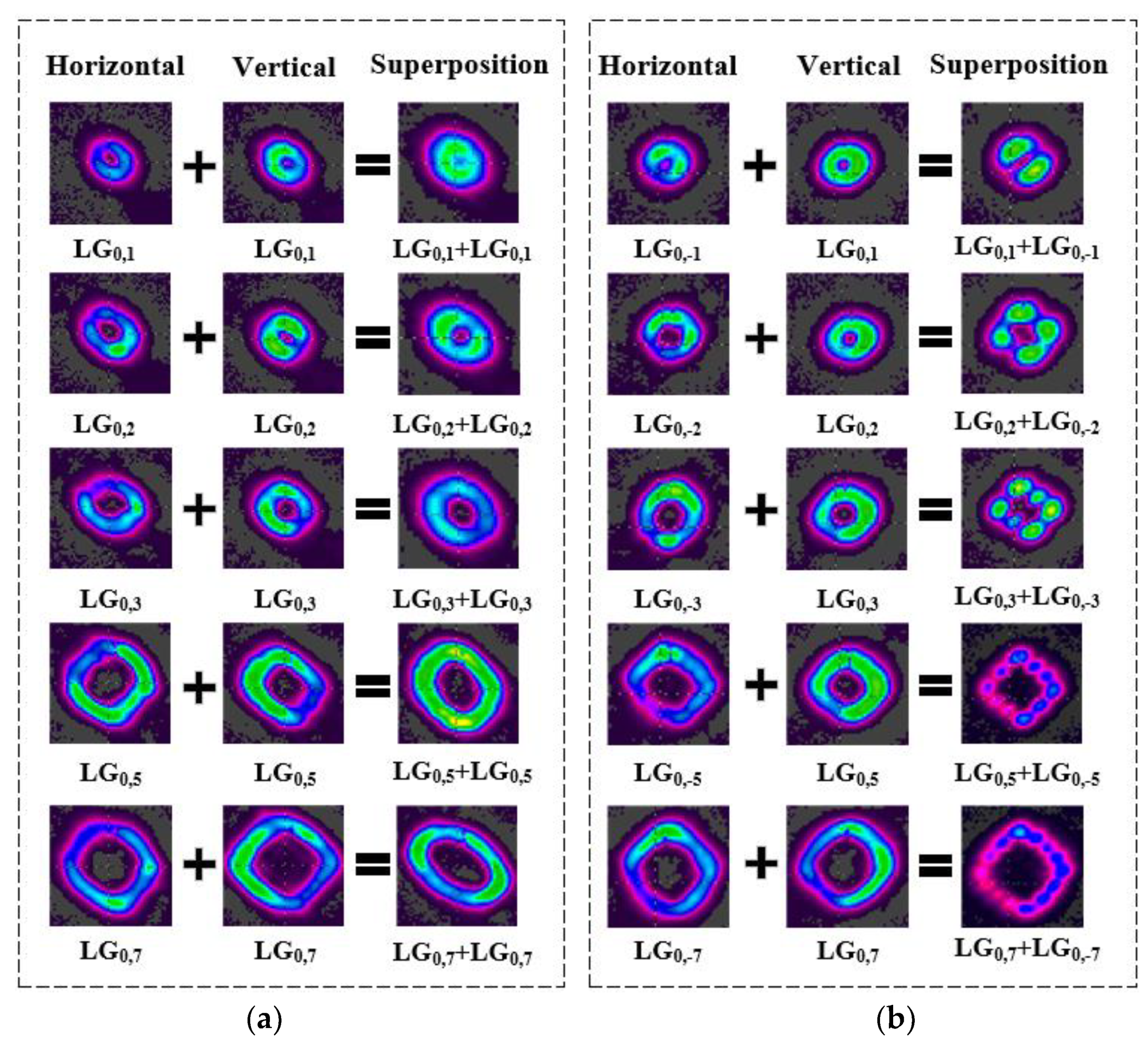
3. Experimental Apparatus and Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Curtis, J.E.; Grier, D.G. Structure of optical vortices. Phys. Rev. Lett. 2003, 90, 133901. [Google Scholar] [CrossRef]
- Rosales-Guzm’an, C.; Trichili, A.; Dudley, A.; Ndagano, B.; Ben Salem, A.; Zghal, M.; Forbes, A. Optical communications beyond orbital angular momentum. In Proceedings of the Optical Engineering + Applications, San Diego, CA, USA, 28 August–1 September 2016. [Google Scholar]
- Simpson, N.B.; Dholakia, K.; Allen, L.; Padgett, M.J. Mechanical equivalence of spin and orbital angular momentum of light: An optical spanner. Opt. Lett. 1997, 22, 52–54. [Google Scholar] [CrossRef]
- Gao, C.; Gao, M.-W.; Weber, H. Generation and application of twisted hollow beams. Optik 2004, 115, 129–132. [Google Scholar] [CrossRef]
- Rjeb, A.; Guerra, G.; Issa, K.; Fathallah, H.A.; Chebaane, S.; Machhout, M.; Palmieri, L.; Galtarossa, A. Inverse-raised-cosine fibers for next-generation orbital angular momentum systems. Opt. Commun. 2020, 458, 124736. [Google Scholar] [CrossRef]
- Tamburini, F.; Anzolin, G.; Umbriaco, G.; Bianchini, A.; Barbieri, C. Overcoming the Rayleigh criterion limit with Orbital Angular Momentum of light. Phys. Rev. Lett. 2006, 97, 163903. [Google Scholar] [CrossRef]
- Xie, Z.; Lei, T.; Li, F.; Qiu, H.; Zhang, Z.; Wang, H.; Min, C.; Du, L.; Li, Z.; Yuan, X. Ultra-broadband on-chip twisted light emitter for optical communications. Light Sci. Appl. 2018, 7, 18001. [Google Scholar] [CrossRef]
- Krenn, M.; Fickler, R.; Fink, M.; Handsteiner, J.; Malik, M.; Scheidl, T.; Ursin, R.; Zeilinger, A. Twisted light communication through turbulent air across Vienna. arXiv 2014, arXiv:1402.2602. [Google Scholar]
- Mukai, T.; Mukai, S.; Noguchi, K. Is water-ice the carrier of the 3μm-absorption in infrared objects? Astrophys. Space Sci. 1978, 53, 77–84. [Google Scholar] [CrossRef]
- Esterowitz, L.; Hoffman, C.A. Laser-Tissue/Water Interaction of the Erbium 2.9 μm Laser. In Proceedings of the Cambridge Symposium-Fiber/LASE ’86, Cambridge, MA, USA, 18–26 August 1986. [Google Scholar]
- Wang, J. Advances in communications using optical vortices. Photonics Res. 2016, 4, B14–B28. [Google Scholar] [CrossRef]
- Willner, A.E.; Huang, H.; Yan, Y.; Ren, Y.; Ahmed, N.; Xie, G.; Bao, C.; Li, L.; Cao, Y.; Zhao, Z.; et al. Optical communications using orbital angular momentum beams. Adv. Opt. Photonics 2015, 7, 66–106. [Google Scholar] [CrossRef]
- Gibson, G.M.; Courtial, J.; Padgett, M.J.; Vasnetsov, M.V.; Pas’ko, V.A.; Barnett, S.M.; Franke-Arnold, S. Free-space information transfer using light beams carrying orbital angular momentum. Opt. Express 2004, 12, 5448–5456. [Google Scholar] [CrossRef] [PubMed]
- Lerner, V.E.; Shwa, D.; Drori, Y.; Katz, N. Shaping Laguerre-Gaussian laser modes with binary gratings using a digital micromirror device. Opt. Lett. 2012, 37, 4826–4828. [Google Scholar] [CrossRef]
- Mirhosseini, M.; Magaña-Loaiza, O.S.; Chen, C.; Rodenburg, B.; Malik, M.; Boyd, R.W. Rapid generation of light beams carrying orbital angular momentum. Opt. Express 2013, 21, 30196–30203. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Yan, Y.; Arbabi, A.; Xie, G.; Liu, C.; Zhao, Z.; Ren, Y.; Li, L.; Ahmed, N.; Willner, A.J.; et al. Orbital angular momentum beams generated by passive dielectric phase masks and their performance in a communication link. Opt. Lett. 2017, 42, 2746–2749. [Google Scholar] [CrossRef] [PubMed]
- Beijersbergen, M.W.; Coerwinkel, R.P.C.; Kristensen, M.; Woerdman, J.P. Helical-wavefront laser beams produced with a spiral phaseplate. Opt. Commun. 1994, 112, 321–327. [Google Scholar] [CrossRef]
- Ren, Y.; Li, M.F.; Huang, K.; Wu, J.; Gao, H.; Wang, Z.; Li, Y.-m. Experimental generation of Laguerre-Gaussian beam using digital micromirror device. Appl. Opt. 2010, 49, 1838–1844. [Google Scholar] [CrossRef]
- Chen, Y.; Fang, Z.-X.; Ren, Y.; Gong, L.; Lu, R. Generation and characterization of a perfect vortex beam with a large topological charge through a digital micromirror device. Appl. Opt. 2015, 54, 8030–8035. [Google Scholar] [CrossRef]
- Beijersbergen, M.W.; Allen, L.; Veen, H.E.L.O.v.d.; Woerdman, J.P. Astigmatic laser mode converters and transfer of orbital angular momentum. Opt. Commun. 1993, 96, 123–132. [Google Scholar] [CrossRef]
- Abramochkin, E.G.; Volostnikov, V.G. Beam transformations and nontransformed beams. Opt. Commun. 1991, 83, 123–135. [Google Scholar] [CrossRef]
- Vaity, P.; Singh, R.P. Self-healing property of optical ring lattice. Opt. Lett. 2011, 36, 2994–2996. [Google Scholar] [CrossRef]
- Naidoo, D.; Ait-Ameur, K.; Brunel, M.; Forbes, A. Intra-cavity generation of superpositions of Laguerre–Gaussian beams. Appl. Phys. B 2012, 106, 683–690. [Google Scholar] [CrossRef]
- Szatkowski, M.; Masajada, J.; Augustyniak, I.; Nowacka, K. Generation of composite vortex beams by independent Spatial Light Modulator pixel addressing. Opt. Commun. 2020, 463, 125341. [Google Scholar] [CrossRef]
- Shen, Y.; Meng, Y.; Fu, X.; Gong, M. Wavelength-tunable Hermite-Gaussian modes and an orbital-angular-momentum-tunable vortex beam in a dual-off-axis pumped Yb: CALGO laser. Opt. Lett. 2018, 43, 291–294. [Google Scholar] [CrossRef]
- Huang, X.; Xu, B.; Cui, S.; Xu, H.; Cai, Z.; Chen, L. Direct Generation of Vortex Laser by Rotating Induced Off-Axis Pumping. IEEE J. Sel. Top. Quantum Electron. 2018, 24, 1601606. [Google Scholar] [CrossRef]
- Uren, R.; Beecher, S.J.; Smith, C.R.; Clarkson, W.A. Method for Generating High Purity Laguerre–Gaussian Vortex Modes. IEEE J. Quantum Electron. 2019, 55, 1700109. [Google Scholar] [CrossRef]
- Liu, J.-L.; Lin, J.; Chen, X.-y.; Yu, Y.; Wu, C.; Jin, G. A 1.9 μm Tm: YLF external cavity mode conversion vortex laser based on LD off-axis pump. Opt. Commun. 2021, 482, 126596. [Google Scholar] [CrossRef]
- Ding, Y.; Yang, J.; Chen, D.; Dong, J. Rectangular Beam Pumped Raman Microchip Laser for Generating Multiwavelength High-Order Hermite–Gaussian Lasers and Vortex Lasers. Ann. Der Phys. 2022, 534, 2200095. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, J.-L.; Liu, M.; Li, R.; Zhang, L.; Chen, X.-Y. An Orbital-Angular-Momentum- and Wavelength-Tunable 2 μm Vortex Laser. Photonics 2022, 9, 926. [Google Scholar] [CrossRef]
- Sun, Y.; Liu, J.-L.; Li, C.; Zhao, X.; Chen, X. Study on the effect of pump beam on the purity of high-order HG mode in off-axis pumped Tm: YLF laser. Infrared Phys. Technol. 2023, 135, 104954. [Google Scholar] [CrossRef]
- Chen, X.-Y.; Yang, X.-N.; Chen, B.; Liu, J.-L. Study on 1.9 μm structured lasers based on Ince–Gaussian modes superposition with multi-modulation by different directions off-axis dual-end-pump. Opt. Commun. 2022, 530, 129020. [Google Scholar] [CrossRef]
- Pratesi, R.; Ronchi, L.A. Generalized Gaussian beams in free space. J. Opt. Soc. Am. 1977, 67, 1274–1276. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Kovalev, A.A. Hermite-Gaussian modal laser beams with orbital angular momentum. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 2014, 31, 274–282. [Google Scholar] [CrossRef]
- Ando, T.; Matsumoto, N.; Ohtake, Y.; Takiguchi, Y.; Inoue, T. Structure of optical singularities in coaxial superpositions of Laguerre-Gaussian modes. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 2010, 27, 2602–2612. [Google Scholar] [CrossRef] [PubMed]
- Anguita, J.A.; Herreros, J.; Djordjevic, I.B. Coherent Multimode OAM Superpositions for Multidimensional Modulation. IEEE Photonics J. 2014, 6, 7900811. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Chen, X.; Sun, Y.; Liu, J.; Jin, G. Study on the Generation of 1.9 μm Mode Superposition Conversion Laser by Double-End Off-Axis Pumping. Photonics 2024, 11, 210. https://doi.org/10.3390/photonics11030210
Li C, Chen X, Sun Y, Liu J, Jin G. Study on the Generation of 1.9 μm Mode Superposition Conversion Laser by Double-End Off-Axis Pumping. Photonics. 2024; 11(3):210. https://doi.org/10.3390/photonics11030210
Chicago/Turabian StyleLi, Chao, Xinyu Chen, Ye Sun, Jingliang Liu, and Guangyong Jin. 2024. "Study on the Generation of 1.9 μm Mode Superposition Conversion Laser by Double-End Off-Axis Pumping" Photonics 11, no. 3: 210. https://doi.org/10.3390/photonics11030210
APA StyleLi, C., Chen, X., Sun, Y., Liu, J., & Jin, G. (2024). Study on the Generation of 1.9 μm Mode Superposition Conversion Laser by Double-End Off-Axis Pumping. Photonics, 11(3), 210. https://doi.org/10.3390/photonics11030210



