Barium Chalcogenide Crystals: A Review
Abstract
1. Introduction
2. Crystal Growth
2.1. Ternary Chalcogenides
2.2. Quaternary Chalcogenides
3. Characterization
3.1. Crystallographic Data
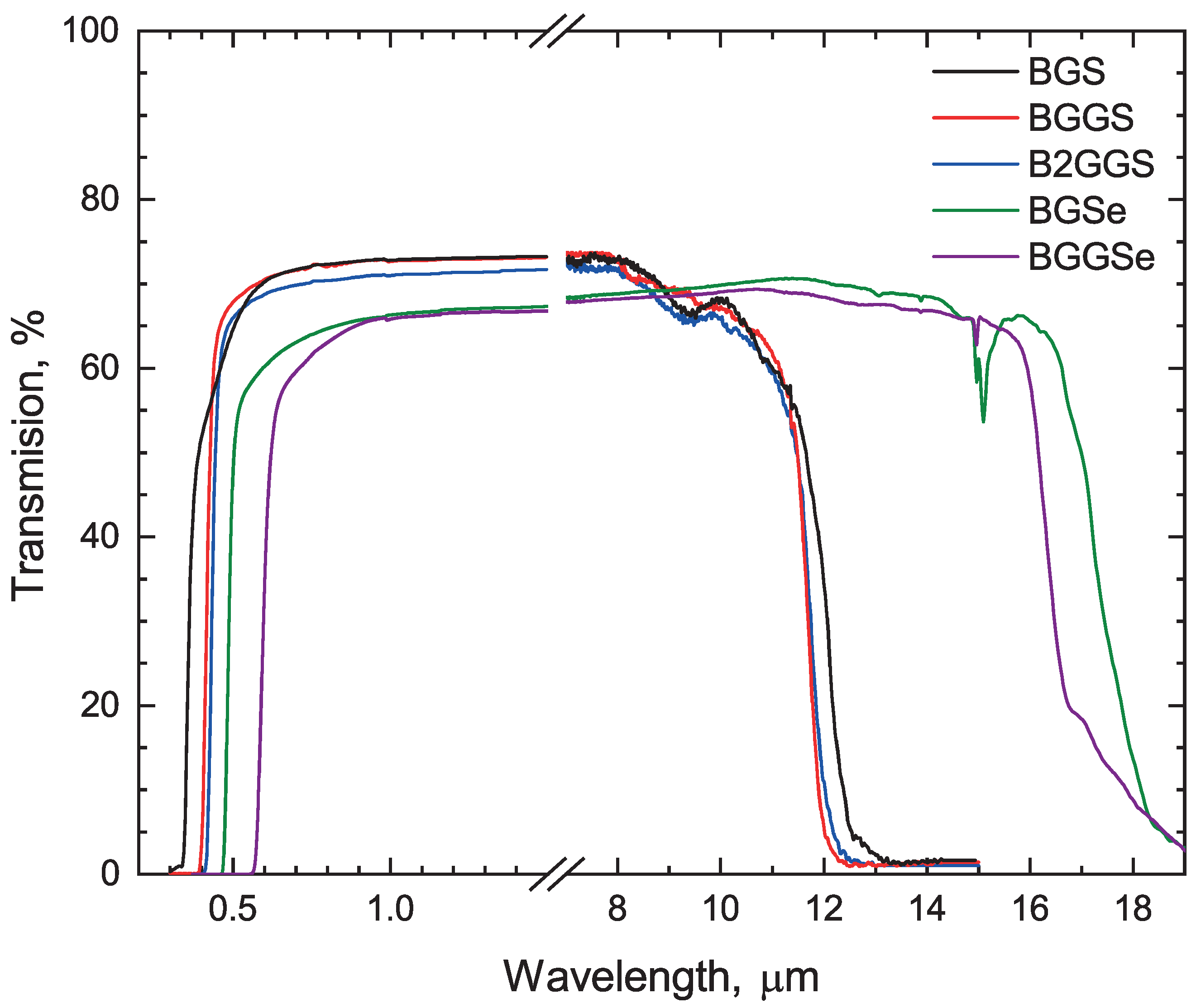
3.2. Optical Properties
3.3. Dispersion Characteristics
3.4. Nonlinear Optical Characteristics
| Crystal | Effective Nonlinearity Expressions | d, pm/V |
|---|---|---|
| BGS | x-y: ; y-z: ; x-z, ; x-z, ; | = ; ; ; @532 nm [51] |
| BGSe | x-y: ; x-y: ; y-z, ; x-z, ; x-z, ; x-z, ; x-z, ; | ; ; ; ; ; @532 nm [76] |
| BGGS | ; ; | ; No data |
| BGGSe | ; ; ; @5.3 m [78] | |
| B2GGS | ; | = = = =13; @1.86 m [57] |
3.5. Thermophysical Characteristics
3.6. Mechanical Characteristics
4. LIDT
5. Frequency Down-Conversion to the Mid-IR Range
5.1. BGS
5.2. BGSe
| Crystal Type, (, ) | Device Type | Length, mm | Pump Source | Pulse Duration and Rep. Rate | Tuning Range | Energy/Power |
|---|---|---|---|---|---|---|
| BGS I type (9.2°, 0°) [111] | OPO | 14.1 | Nd:YAG, 1064 nm | 8 ns 100 Hz | 5.5-7.3 m | 0.5 mJ @6.2 m |
| BGS I type (12.5°, 0°) [113] | OPA | 15 | 30 ps 10 Hz | 6.3–8.8 m | 66 J @6.3 m | |
| BGS I type (13.1°, 0°) [112] | OPA | 8.3 | Yb:KGd(WO), 1028 nm | 180 fs 100 Hz | 7.6–11.5 m | 59 mW @10 m 81 mW @8 m. |
| BGSe-I type (45°, 0°) [114] | OPO | 11.8 | Nd:YLF, 1053 nm | 15 ns 100 Hz | 2.9–9.3 m | 4–10 J @4–5 m |
| BGSe-I type (45°, 0°) [107] | OPO | 11.8 | 2.6–10.4 m | 45 J @3.3 m | ||
| BGSe-II type (33°, 90°) [114] | OPO | 10 | 5–5.4 m | 14 J @8.1 m | ||
| BGSe-I type (46°, 0°) [90] | OPO | 14.6 | Nd:YAG, 1064 nm | 8 ns 10 Hz | 2.7–17 m | 3.7 mJ @7.2 m |
| BGSe-II type (33.5°, 90°) [90] | OPO | 13.6 | 3.6–9.6 m | 4.7 mJ @5.3 m | ||
| BGSe-I type (53.4°, 0°) [116] | OPO | 18.8 | 8 ns 10 Hz | 4.1–4.5 m | 1.92 mJ @4.3 m | |
| BGSe-I type (54.7°, 0°) [117] | OPO | 17.3 | 16 ns 10 Hz | 3.1–5.2 m | 2.56 mJ @4.1 m | |
| BGSe-I type (53.2°, 0°) [118] | OPO | 10 | 6.7 ns 10 Hz | 1.03 mJ @4.3 m | ||
| BGSe-I type (55.9°, 0°) [89] | OPO | 16 | 11.4 ns 20 Hz | 3.6–3.8 m | 21.5 mJ @3.8 m | |
| BGSe-I type (42.5°, 0°) [119] | OPO | 15 | 10 ns 10 Hz | 8–14 m | 1.05 mJ @11 m | |
| BGSe-I type (56.3°, 0°) [120] | OPO | 15 | 13 ns 1 Hz | ±5 nm | 0.49 mJ @3.5 m | |
| BGSe-I type (55.3°, 0°) [121] | OPO | 15 | 11.6 ns 300 Hz | 3.2–4.2 m | 1.03 W @3.7 m | |
| BGSe-I type (42.5°, 0°) [122] | OPO | 16 | 13.6 ns 250 Hz | 3.42–4.73 m | 1.3 mJ @4.1 m | |
| BGSe-I type (53.2°, 0°) [123] | OPO | 15 | 13.7 ns 500 Hz | 1.52 mJ @4.4 m | ||
| BGSe-I type (56.3°, 0°) [124] | OPO | 13 ns 1 Hz | 2.76–4.64 m | |||
| BGSe-I type (47.1°, 0°) [125] | OPO | 25 | 18 ns 10 Hz | 6.8 mJ @6.45 m | ||
| BGSe-I type (46°, 0°) [115] | DFG | 14.6 | OPO, 1.85 + 2.51 m | 8 ns 10 Hz | 7–8.2 m | 711 J @7 m |
| BGSe I type (40.8°, 0°) [103] | OPO | 30 | Ho:YAG, 2091 nm | 27 ns 500 Hz | 4.3–5.2 m | 1.47 mJ @4.4 m |
| BGSe-II type (6°, 90°) [104] | OPO | 30 | 16 ns 1 kHz | 8–9 m | 314 J @8.9 m | |
| BGSe-II type (23.5°, 90°) [126] | OPO | 33 | 29.3 ns 1 kHz | 3.82–4 m | 520 J @3.94 m | |
| BGSe-I type (40.8°, 0°) [127] | OPO | 30 | 28 ns 1 kHz | 4.5–5.3 m | 1.8 mJ @4.5 m | |
| BGSe-I type (39.4°, 0°) [128] | OPO | 31 | Cr, Er:YSGG, 2.79 m | 21 ns 10 Hz | 5.6–9.5 m | 3.5 mJ @5 m |
| BGSe-I type (45°, 0°) [129] | DFG | 8 | Yb:YAG, 1030 nm | 2 ps 10 Hz | 6.5–8.6 m | 60 J @7 m |
| BGSe I type (54.7°, 0°) [108] | OPA | 8 | Nd:YAG, 1064 nm | 30 ps 10 Hz | 3–5 m | 830 J @3.9 m |
| BGSe I type (44°, 0°) [67] | OPA | 8 | 6.4–11 m | 38 J @11 m | ||
| BGSe-I type (40.2°, 0°) [82] | OPA | 10 | 8–14 m | 140–230 J | ||
| BGSe-I type (47°, 0°) [130] | OPA | 10 | Yb:KGW, 1030 nm | 290 fs 50 kHz | 3.7–17 m | 10 mW @16 m |
| BGSe [131] | OPA | 1 | Yb:YAG, 1.03 m + 1.15–1.8 m | 550 fs 10 kHz | 2.5–10 m | 6 J @3 m |
| BGSe-I type (67°, 0°) [132] | DFG | 15 | Ti:sapphire, 730–970 nm | CW | 3.2–7.92 m | 1.41 W @5 m |
| BGGSe II type (27.5°, 0°) [133] | OPO | 9.3 | cascaded OPO, 1.85 + 2.51 m | 8 ns 10 Hz | 4.4–13 m | 750 J @8 m |
| BGGSe II type (27.5°, 0°) [134] | OPO | 9.3 | cascaded OPO, 1.95 + 2.55 m | 8 ns 100 Hz | 6.6–11.3 m | 1.45 mJ @8.2 m |
| BGGSe I type (25°, 30°) [135] | DFG | 2.6 | mode-locked Er:fiber oscillator | 59 fs 100 MHz | 5.8–8.5 m | 21 pJ |
| BGGSe I type (30°, 28°) [136] | DFG | 4.4 | SPOPOs, 1035 nm | 130 fs 40 MHz | up to 10 m | 54 mW |
5.3. BGGSe
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Abbreviations
| LIDT | Laser-induced damage threshold |
| mid-IR | Mid-infrared |
| HF laser | Hydrogen fluoride laser |
| DF laser | Deuterium fluoride laser |
| QCL | Quantum cascade laser |
| OPO | Optical parametric oscillator |
| DFG | Difference frequency generator |
| OPA | Optical parametric amplifier |
| AGS | Silver thiogallate, AgGaS2 |
| AGSe | Silver selenogallate, AgGaSe2 |
| ZGP | Zinc germanium phosphide, ZnGeP2 |
| LGT | LiGaTe2 |
| LGS | LiGaS2 |
| BGS | BaGa4S7 |
| BGSe | BaGa4Se7 |
| BGGS | BaGa2GeS6 |
| BGGSe | BaGa2GeSe6 |
| B2GGS | Ba2Ga8GeS16 |
| PPLN | Periodically poled lithium niobate |
| PPKTP | Periodically poled potassium titanyl phosphate |
| PPKTA | Periodically poled potassium titanyl arsenate |
| PBN | Pyrolytic boron nitride |
| VHN | Vickers hardness number |
| CW | Continuous wave |
| VBG | Volume Bragg grating |
References
- Rothman, L.; Gordon, I.; Babikov, Y.; Barbe, A.; Chris Benner, D.; Bernath, P.; Birk, M.; Bizzocchi, L.; Boudon, V.; Brown, L.; et al. The HITRAN2012 molecular spectroscopic database. J. Quant. Spectrosc. Radiat. Transf. 2013, 130, 4–50. [Google Scholar] [CrossRef]
- Harren, F.J.; Mandon, J.; Cristescu, S.M. Photoacoustic Spectroscopy in Trace Gas Monitoring. In Encyclopedia of Analytical Chemistry; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2012. [Google Scholar] [CrossRef]
- Schilt, S.; Thévenaz, L.; Niklès, M.; Emmenegger, L.; Hüglin, C. Ammonia monitoring at trace level using photoacoustic spectroscopy in industrial and environmental applications. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2004, 60, 3259–3268. [Google Scholar] [CrossRef]
- Kistenev, Y.V.; Borisov, A.V.; Kuzmin, D.A.; Penkova, O.V.; Kostyukova, N.Y.; Karapuzikov, A.A. Exhaled air analysis using wideband wave number tuning range infrared laser photoacoustic spectroscopy. J. Biomed. Opt. 2017, 22, 017002. [Google Scholar] [CrossRef]
- Litvinova, K.S.; Rafailov, I.E.; Dunaev, A.V.; Sokolovski, S.G.; Rafailov, E.U. Non-invasive biomedical research and diagnostics enabled by innovative compact lasers. Prog. Quantum Electron. 2017, 56, 1–14. [Google Scholar] [CrossRef][Green Version]
- Ventura, A.; Slimen, F.B.; Lousteau, J.; White, N.; Masoudi, A.; Janicek, P.; Poletti, F. Flexible Mid-IR fiber bundle for thermal imaging of inaccessible areas. Opt. Express 2019, 27, 20259–20272. [Google Scholar] [CrossRef] [PubMed]
- Aleĭnikov, V.S.; Belyaev, V.P.; Devyatkov, N.D.; Klimenko, V.I.; Mamedli, L.D.; Masychev, V.I.; Sysoev, V.K. Applications of a carbon monoxide laser in surgery. Sov. J. Quantum Electron. 1983, 13, 1304. [Google Scholar] [CrossRef]
- Edwards, G.S.; Pearlstein, R.D.; Copeland, M.L.; Hutson, M.S.; Latone, K.; Spiro, A.; Pasmanik, G. 6450 nm wavelength tissue ablation using a nanosecond laser based on difference frequency mixing and stimulated Raman scattering. Opt. Lett. 2007, 32, 1426–1428. [Google Scholar] [CrossRef]
- Romann, A.; Sigrist, M.W. Photoacoustic gas sensing employing fundamental and frequency-doubled radiation of a continuously tunable high-pressure CO2 laser. Appl. Phys. B 2002, 75, 377–383. [Google Scholar] [CrossRef]
- Ionin, A.A.; Guo, J.; Zhang, L.M.; Xie, J.J.; Andreev, Y.M.; Kinyaevsky, I.O.; Klimachev, Y.M.; Kozlov, A.Y.; Kotkov, A.A.; Lanskii, G.V.; et al. Mode-locked CO laser frequency doubling in ZnGeP2 with 25% efficiency. Laser Phys. Lett. 2011, 8, 723. [Google Scholar] [CrossRef]
- Patel, B.C.M.; Rickwood, K.R. Morphological changes induced by short pulse hydrogen fluoride laser radiation on dental hard tissue and restorative materials. Lasers Surg. Med. 1997, 21, 1–6. [Google Scholar] [CrossRef]
- Sorokina, I.T. Broadband Mid-Infrared Solid-State Lasers. In Mid-Infrared Coherent Sources and Applications; Ebrahim-Zadeh, M., Sorokina, I.T., Eds.; Springer: Dordrecht, The Netherlands, 2008; pp. 225–260. [Google Scholar] [CrossRef]
- Tacke, M. New developments and applications of tunable IR lead salt lasers. Infrared Phys. Technol. 1995, 36, 447–463. [Google Scholar] [CrossRef]
- Genner, A.; Martín-Mateos, P.; Moser, H.; Lendl, B. A Quantum Cascade Laser-Based Multi-Gas Sensor for Ambient Air Monitoring. Sensors 2020, 20, 1850. [Google Scholar] [CrossRef] [PubMed]
- Sherstov, I.; Kolker, D.; Vasiliev, V.; Pavlyuk, A.; Miroshnichenko, M.; Boyko, A.; Kostyukova, N.; Miroshnichenko, I. Laser photo-acoustic methane sensor (7.7 µm) for use at unmanned aerial vehicles. Infrared Phys. Technol. 2023, 133, 104865. [Google Scholar] [CrossRef]
- Kostyukova, N.Y.; Kolker, D.B.; Zenov, K.G.; Boyko, A.A.; Starikova, M.K.; Sherstov, I.V.; Karapuzikov, A.A. Mercury thiogallate nanosecond optical parametric oscillator continuously tunable from 4.2 to 10.8 µm. Laser Phys. Lett. 2015, 12, 095401. [Google Scholar] [CrossRef]
- Malara, P.; Maddaloni, P.; Gagliardi, G.; Natale, P.D. Combining a difference-frequency source with an off-axis high-finesse cavity for trace-gas monitoring around 3 µm. Opt. Express 2006, 14, 1304–1313. [Google Scholar] [CrossRef] [PubMed]
- Basov, N.G.; Ionin, A.A.; Kotkov, A.A.; Kurnosov, A.K.; McCord, J.E.; Napartovich, A.P.; Seleznev, L.V.; Turkin, N.G.; Hager, G.D. Pulsed laser operating on the first vibrational overtone of the CO molecule in the 2.5–4.2-µm range: 1. Multifrequency lasing. Quantum Electron. 2000, 30, 771. [Google Scholar] [CrossRef]
- Witteman, W.J. The CO2 Laser; Springer: Berlin/Heidelberg, Germany, 1987; p. 311. [Google Scholar] [CrossRef]
- Budilova, O.; Ionin, A.; Kinyaevskiy, I.; Klimachev, Y.; Kotkov, A.; Kozlov, A. Ultra-broadband hybrid infrared laser system. Opt. Commun. 2016, 363, 26–30. [Google Scholar] [CrossRef]
- Boreysho, A.S. High-power mobile chemical lasers. Quantum Electron. 2005, 35, 393. [Google Scholar] [CrossRef]
- Mirov, S.B.; Moskalev, I.S.; Vasilyev, S.; Smolski, V.; Fedorov, V.V.; Martyshkin, D.; Peppers, J.; Mirov, M.; Dergachev, A.; Gapontsev, V. Frontiers of Mid-IR Lasers Based on Transition Metal Doped Chalcogenides. IEEE J. Sel. Top. Quantum Electron. 2018, 24, 1601829. [Google Scholar] [CrossRef]
- Bewley, W.W.; Canedy, C.L.; Kim, C.S.; Kim, M.; Merritt, C.D.; Abell, J.; Vurgaftman, I.; Meyer, J.R. Continuous-wave interband cascade lasers operating above room temperature at λ= 4.7–5.6 µm. Opt. Express 2012, 20, 3235–3240. [Google Scholar] [CrossRef]
- Li, L.; Ye, H.; Jiang, Y.; Yang, R.Q.; Keay, J.C.; Mishima, T.D.; Santos, M.B.; Johnson, M.B. MBE-grown long-wavelength interband cascade lasers on InAs substrates. J. Cryst. Growth 2015, 425, 369–372. [Google Scholar] [CrossRef]
- Vitiello, M.S.; Scalari, G.; Williams, B.; Natale, P.D. Quantum cascade lasers: 20 years of challenges. Opt. Express 2015, 23, 5167–5182. [Google Scholar] [CrossRef] [PubMed]
- Vodopyanov, K. Pulsed Mid-IR Optical Parametric Oscillators. In Solid-State Mid-Infrared Laser Sources; Sorokina, I.T., Vodopyanov, K.L., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; pp. 144–183. [Google Scholar] [CrossRef]
- Jackson, A.; Ohmer, M.; LeClair, S. Relationship of the second order nonlinear optical coefficient to energy gap in inorganic non-centrosymmetric crystals. Infrared Phys. Technol. 1997, 38, 233–244. [Google Scholar] [CrossRef]
- Ammann, E.O.; Yarborough, J.M. Optical parametric oscillation in proustite. Appl. Phys. Lett. 1970, 17, 233–235. [Google Scholar] [CrossRef]
- Hanna, D.; Luther-Davies, B.; Rutt, H.; Smith, R.; Stanley, C. Q-switched laser damage of infrared nonlinear materials. IEEE J. Quantum Electron. 1972, 8, 317–324. [Google Scholar] [CrossRef]
- Angell, M.J.; Emerson, R.M.; Hoyt, J.L.; Gibbons, J.F.; Eyres, L.A.; Bortz, M.L.; Fejer, M.M. Growth of alternating (100)/(111)-oriented II-VI regions for quasi-phase-matched nonlinear optical devices on GaAs substrates. Appl. Phys. Lett. 1994, 64, 3107–3109. [Google Scholar] [CrossRef]
- Ye, H.; Kumar, S.C.; Wei, J.; Schunemann, P.G.; Ebrahim-Zadeh, M. Singly-resonant pulsed optical parametric oscillator based on orientation-patterned gallium phosphide. Opt. Lett. 2018, 43, 2454–2457. [Google Scholar] [CrossRef] [PubMed]
- Fan, Y.X.; Eckardt, R.C.; Byer, R.L.; Route, R.K.; Feigelson, R.S. AgGaS2 infrared parametric oscillator. Appl. Phys. Lett. 1984, 45, 313–315. [Google Scholar] [CrossRef]
- Boyko, A.A.; Kostyukova, N.Y.; Marchev, G.M.; Pasiskevicius, V.; Kolker, D.B.; Zukauskas, A.; Petrov, V. Rb:PPKTP optical parametric oscillator with intracavity difference-frequency generation in AgGaSe2. Opt. Lett. 2016, 41, 2791–2794. [Google Scholar] [CrossRef]
- Antipov, O.; Eranov, I.; Kositsyn, R. 10-W mid-IR optical parametric oscillators based on ZnGeP2 elements pumped by a fibre-laser-pumped Ho: YAG Laser. Experimental and numerical study. Quantum Electron. 2017, 47, 601. [Google Scholar] [CrossRef]
- Yudin, N.N.; Khudoley, A.; Zinovev, M.; Slyunko, E.; Podzyvalov, S.; Kuznetsov, V.; Gorodkin, G.; Kumeysha, P.; Lysenko, A.; Kalsin, A.; et al. Experimental Investigation of Laser Damage Limit for ZPG Infrared Single Crystal Using Deep Magnetorheological Polishing of Working Surfaces. Crystals 2024, 14, 32. [Google Scholar] [CrossRef]
- Bairamov, B.H.; Rud’, V.Y. Properties of Dopants in ZnGeP2, CdGeAs2, AgGaS2 and AgGaSe2. MRS Bull. 1998, 23, 41–44. [Google Scholar] [CrossRef]
- Yudin, N.; Zinoviev, M.; Kuznetsov, V.; Slyunko, E.; Podzvalov, S.; Voevodin, V.; Lysenko, A.; Kalsin, A.; Shaimerdenova, L.; Baalbaki, H.; et al. Effect of Dopants on Laser-Induced Damage Threshold of ZnGeP2. Crystals 2023, 13, 440. [Google Scholar] [CrossRef]
- Vodopyanov, K.L.; Maffetone, J.P.; Zwieback, I.; Ruderman, W. AgGaS2 optical parametric oscillator continuously tunable from 3.9 to 11.3 µm. Appl. Phys. Lett. 1999, 75, 1204–1206. [Google Scholar] [CrossRef]
- Lippert, E.; Rustad, G.; Arisholm, G.; Stenersen, K. High power and efficient long wave IR ZnGeP2 parametric oscillator. Opt. Express 2008, 16, 13878–13884. [Google Scholar] [CrossRef]
- Antipov, O.; Novikov, A.; Eranov, I.; Kolker, D. High-efficiency oscillations at 1940 nm and 2070 nm in diode-pumped Tm:Lu2O3 ceramics lasers and their OPO frequency converision. In Proceedings of the 2014 International Conference Laser Optics, St. Petersburg, Russia, 30 June–4 July 2014; p. 1. [Google Scholar] [CrossRef]
- Das, S. Optical parametric oscillator: Status of tunable radiation in mid-IR to IR spectral range based on ZnGeP2 crystal pumped by solid state lasers. Opt. Quantum Electron. 2019, 51, 70. [Google Scholar] [CrossRef]
- Beasley, J.D. Thermal conductivities of some novel nonlinear optical materials. Appl. Opt. 1994, 33, 1000–1003. [Google Scholar] [CrossRef]
- Eckardt, R.C.; Fan, Y.X.; Byer, R.L.; Marquardt, C.L.; Storm, M.E.; Esterowitz, L. Broadly tunable infrared parametric oscillator using AgGaSe2. Appl. Phys. Lett. 1986, 49, 608–610. [Google Scholar] [CrossRef]
- Isaenko, L.I.; Yelisseyev, A.P. Recent studies of nonlinear chalcogenide crystals for the mid-IR. Semicond. Sci. Technol. 2016, 31, 123001. [Google Scholar] [CrossRef]
- Tyazhev, A.; Vedenyapin, V.; Marchev, G.; Isaenko, L.; Kolker, D.; Lobanov, S.; Petrov, V.; Yelisseyev, A.; Starikova, M.; Zondy, J.J. Singly-resonant optical parametric oscillation based on the wide band-gap mid-IR nonlinear optical crystal LiGaS2. Opt. Mater. 2013, 35, 1612–1615. [Google Scholar] [CrossRef]
- Morimoto, T.; Sono, N.; Miyamoto, T.; Kida, N.; Okamoto, H. Generation of a carrier-envelope-phase-stable femtosecond pulse at 10 µm by direct down-conversion from a Ti:sapphire laser pulse. Appl. Phys. Express 2017, 10, 122701. [Google Scholar] [CrossRef]
- Kinyaevskiy, I.; Koribut, A.; Seleznev, L.; Klimachev, Y.; Dunaeva, E.; Ionin, A. Frequency conversion of a chirped Ti:sapphire laser pulse to 11.4 µm wavelength with SrMoO4 Raman shifter and LiGaS2 DFG crystal. Opt. Laser Technol. 2024, 169, 110035. [Google Scholar] [CrossRef]
- Isaenko, L.; Dong, L.; Yelisseyev, A.; Lobanov, S.; Korzhneva, K.; Gromilov, S.; Sukhih, A.; Pugachev, A.; Vedenyapin, V.; Kurus, A.; et al. A new nonlinear optical crystal Li0.81Ag0.19InSe2 with balanced properties for efficient nonlinear conversion in the mid-IR region. J. Alloys Compd. 2023, 969, 172382. [Google Scholar] [CrossRef]
- Isaenko, L.; Dong, L.; Kurus, A.; Lin, Z.; Yelisseyev, A.; Lobanov, S.; Molokeev, M.; Korzhneva, K.; Goloshumova, A. LixAg1-xGaSe2: Interplay Between Lithium and Silver in Mid-Infrared Nonlinear Optical Chalcogenides. Adv. Opt. Mater. 2022, 10, 2201727. [Google Scholar] [CrossRef]
- Lin, X.; Zhang, G.; Ye, N. Growth and Characterization of BaGa4S7: A New Crystal for Mid-IR Nonlinear Optics. Cryst. Growth Des. 2009, 9, 1186–1189. [Google Scholar] [CrossRef]
- Badikov, V.; Badikov, D.; Shevyrdyaeva, G.; Tyazhev, A.; Marchev, G.; Panyutin, V.; Noack, F.; Petrov, V.; Kwasniewski, A. BaGa4S7: Wide-bandgap phase-matchable nonlinear crystal for the mid-infrared. Opt. Mater. Express 2011, 1, 316–320. [Google Scholar] [CrossRef]
- Badikov, V.; Badikov, D.; Shevyrdyaeva, G.; Tyazhev, A.; Marchev, G.; Panyutin, V.; Petrov, V.; Kwasniewski, A. Phase-matching properties of BaGa4S7 and BaGa4Se7: Wide-bandgap nonlinear crystals for the mid-infrared. Phys. Status Solidi RRL Rapid Res. Lett. 2011, 5, 31–33. [Google Scholar] [CrossRef]
- Yao, J.; Mei, D.; Bai, L.; Lin, Z.; Yin, W.; Fu, P.; Wu, Y. BaGa4Se7: A New Congruent-Melting IR Nonlinear Optical Material. Inorg. Chem. 2010, 49, 9212–9216. [Google Scholar] [CrossRef]
- Yin, W.; Feng, K.; He, R.; Mei, D.; Lin, Z.; Yao, J.; Wu, Y. BaGa2MQ6 (M = Si, Ge; Q = S, Se): A new series of promising IR nonlinear optical materials. Dalton Trans. 2012, 41, 5653–5661. [Google Scholar] [CrossRef]
- Lin, X.; Guo, Y.; Ye, N. BaGa2GeX6(X=S, Se): New mid-IR nonlinear optical crystals with large band gaps. J. Solid State Chem. 2012, 195, 172–177. [Google Scholar] [CrossRef]
- Badikov, V.V.; Badikov, D.V.; Laptev, V.B.; Mitin, K.V.; Shevyrdyaeva, G.S.; Shchebetova, N.I.; Petrov, V. Crystal growth and characterization of new quaternary chalcogenide nonlinear crystals for the mid-IR: BaGa2GeS6 and BaGa2GeSe6. Opt. Mater. Express 2016, 6, 2933–2938. [Google Scholar] [CrossRef]
- Badikov, V.; Badikov, D.; Shevyrdyaeva, G.; Laptev, V.; Melnikov, A.; Chekalin, S. Optical and generation characteristics of new nonlinear Ba2Ga8GeS16 and Ba2Ga8(GeSe2)S14 crystals for the mid-IR range. Quantum Electron. 2022, 52, 296. [Google Scholar] [CrossRef]
- Badikov, V.V.; Badikov, D.V.; Shevyrdyaeva, G.S.; Kato, K.; Umemura, N.; Miyata, K.; Panyutin, V.L.; Petrov, V. Crystal growth and characterization of a new quaternary hexagonal nonlinear crystal for the mid-IR: Ba2Ga8GeS16. J. Alloys Compd. 2022, 907, 164378. [Google Scholar] [CrossRef]
- The optical properties of the nonlinear crystal BaGa4Se7. Opt. Mater. 2020, 99, 109564. [CrossRef]
- Schunemann, P.G.; Zawilski, K.T. Horizontal Gradient Freeze Growth of Barium Thio- and Selleno-gallates for Mid-Infrared Frequency Conversion. In High-Brightness Sources and Light-Driven Interactions; Optica Publishing Group: Massachusetts, NW, USA, 2018; p. MT2C.7. [Google Scholar] [CrossRef]
- Schunemann, P.G.; Zawilski, K.T. Seeded growth of BaGa4S7 and BaGa4Se7 for mid-IR frequency conversion. In Optica Advanced Photonics Congress 2022; Optica Publishing Group: Massachusetts, NW, USA, 2022; p. AM6A.2. [Google Scholar] [CrossRef]
- Liu, B.W.; Zeng, H.Y.; Zhang, M.J.; Fan, Y.H.; Guo, G.C.; Huang, J.S.; Dong, Z.C. Syntheses, Structures, and Nonlinear-Optical Properties of Metal Sulfides Ba2Ga8MS16 (M = Si, Ge). Inorg. Chem. 2015, 54, 976–981. [Google Scholar] [CrossRef] [PubMed]
- ANSI/IEEE Std. 176-1987; IEEE Standard on Piezoelectricity. IEEE: Piscataway, NJ, USA, 1988. [CrossRef]
- Petrov, V.; Badikov, V.V.; Badikov, D.V.; Kato, K.; Shevyrdyaeva, G.S.; Miyata, K.; Mero, M.; Wang, L.; Heiner, Z.; Panyutin, V.L. Barium nonlinear optical crystals for the mid-IR: Characterization and some applications. J. Opt. Soc. Am. B 2021, 38, B46–B58. [Google Scholar] [CrossRef]
- Jiang, S.; Wan, S.; Luo, W.; Li, B.; Yao, J. The structural origin of the 15 µm residual absorption in the BaGa4Se7 crystal. J. Mater. Chem. C 2022, 10, 649–654. [Google Scholar] [CrossRef]
- Kato, K.; Badikov, V.V.; Miyata, K.; Petrov, V. Refined Sellmeier equations for BaGa4S7. Appl. Opt. 2021, 60, 6600–6603. [Google Scholar] [CrossRef]
- Yang, F.; Yao, J.Y.; Xu, H.Y.; Zhang, F.F.; Zhai, N.X.; Lin, Z.H.; Zong, N.; Peng, Q.J.; Zhang, J.Y.; Cui, D.F.; et al. Midinfrared Optical Parametric Amplifier With 6.4–11 μm Range Based on BaGa4Se7. IEEE Photonics Technol. Lett. 2015, 27, 1100–1103. [Google Scholar] [CrossRef]
- Boursier, E.; Segonds, P.; Ménaert, B.; Badikov, V.; Panyutin, V.; Badikov, D.; Petrov, V.; Boulanger, B. Phase-matching directions and refined Sellmeier equations of the monoclinic acentric crystal BaGa4Se7. Opt. Lett. 2016, 41, 2731–2734. [Google Scholar] [CrossRef]
- Kato, K.; Miyata, K.; Petrov, V. Phase-matching properties of BaGa4Se7 for SHG and SFG in the 0.901 10.5910 m range. Appl. Opt. 2017, 56, 2978–2981. [Google Scholar] [CrossRef]
- Zhai, N.; Li, C.; Xu, B.; Bai, L.; Yao, J.; Zhang, G.; Hu, Z.; Wu, Y. Temperature-Dependent Sellmeier Equations of IR Nonlinear Optical Crystal BaGa4Se7. Crystals 2017, 7, 62. [Google Scholar] [CrossRef]
- Kato, K.; Miyata, K.; Petrov, V. Refined Sellmeier and thermo-optic dispersion formulas for BaGa4Se7. Opt. Mater. Express 2023, 13, 1852–1858. [Google Scholar] [CrossRef]
- Kato, K.; Umemura, N.; Badikov, V.V.; Badikov, D.V.; Petrov, V. Temperature-dependent phase-matching properties of BaGa2GeS6 in the 0.767–10.5910 µm spectral range. Appl. Opt. 2022, 61, 10774–10777. [Google Scholar] [CrossRef]
- Kato, K.; Miyata, K.; Badikov, V.V.; Petrov, V. Phase-matching properties of BaGa2GeSe6 for three-wave interactions in the 0.778-10.5910 µm spectral range. Appl. Opt. 2018, 57, 7440–7443. [Google Scholar] [CrossRef] [PubMed]
- Kato, K.; Miyata, K.; Okamoto, T.; Badikov, V.V.; Petrov, V. Thermo-optic dispersion formula for BaGa2GeSe6. Appl. Opt. 2019, 58, 9709–9711. [Google Scholar] [CrossRef] [PubMed]
- Kato, K.; Badikov, V.V.; Umemura, N.; Miyata, K.; Petrov, V. Phase-matching properties of Ba2Ga8GeS16. J. Opt. Soc. Am. B 2023, 40, A17–A20. [Google Scholar] [CrossRef]
- Guo, F.; Boursier, E.; Segonds, P.; Na, A.P.; Debray, J.; Badikov, V.; Panyutin, V.; Badikov, D.; Petrov, V.; Boulanger, B. Second-order nonlinear optical coefficients of the monoclinic crystal BaGa4Se7. Opt. Lett. 2022, 47, 842–845. [Google Scholar] [CrossRef] [PubMed]
- Boursier, E.; Segonds, P.; Debray, J.; Inácio, P.L.; Panyutin, V.; Badikov, V.; Badikov, D.; Petrov, V.; Boulanger, B. Angle noncritical phase-matched second-harmonic generation in the monoclinic crystal BaGa4Se7. Opt. Lett. 2015, 40, 4591–4594. [Google Scholar] [CrossRef] [PubMed]
- Kato, K.; Badikov, V.V.; Wang, L.; Panyutin, V.L.; Mitin, K.V.; Miyata, K.; Petrov, V. Effective nonlinearity of the new quaternary chalcogenide crystal BaGa2GeSe6. Opt. Lett. 2020, 45, 2136–2139. [Google Scholar] [CrossRef]
- Sheik-bahae, M.; Said, A.A.; Stryland, E.W.V. High-sensitivity, single-beam n2 measurements. Opt. Lett. 1989, 14, 955–957. [Google Scholar] [CrossRef] [PubMed]
- Mero, M.; Wang, L.; Chen, W.; Ye, N.; Zhang, G.; Petrov, V.; Heiner, Z. Laser-induced damage of nonlinear crystals in ultrafast, high-repetition-rate, mid-infrared optical parametric amplifiers pumped at 1 μm. In Pacific Rim Laser Damage 2019: Optical Materials for High-Power Lasers; Shao, J., Jitsuno, T., Rudolph, W., Eds.; International Society for Optics and Photonics—SPIE: Cergy-Pontoise, France, 2019; Volume 11063, p. 1106307. [Google Scholar] [CrossRef]
- Mero, M.; Petrov, V.; Heiner, Z. Progress in ultrafast, mid-infrared optical parametric chirped pulse amplifiers pumped at 1 μm. In Nonlinear Frequency Generation and Conversion: Materials and Devices XIX; Schunemann, P.G., Schepler, K.L., Eds.; International Society for Optics and Photonics—SPIE: Cergy-Pontoise, France, 2020; Volume 11264, p. 112640F. [Google Scholar] [CrossRef]
- Yang, F.; Yao, J.Y.; Guo, Y.W.; Yuan, L.; Bo, Y.; Peng, Q.J.; Cui, D.F.; Wu, Y.C.; Xu, Z.Y. High-energy continuously tunable 8–14 µm picosecond coherent radiation generation from BGSe-OPA pumped by 1064 nm laser. Opt. Laser Technol. 2020, 125, 106040. [Google Scholar] [CrossRef]
- Guo, Y.; Zhou, Y.; Lin, X.; Chen, W.; Ye, N. Growth and characterizations of BaGa4S7 crystal. Opt. Mater. 2014, 36, 2007–2011. [Google Scholar] [CrossRef]
- Yao, J.; Yin, W.; Feng, K.; Li, X.; Mei, D.; Lu, Q.; Ni, Y.; Zhang, Z.; Hu, Z.; Wu, Y. Growth and characterization of BaGa4Se7 crystal. J. Cryst. Growth 2012, 346, 1–4. [Google Scholar] [CrossRef]
- Exner, G.; Susner, M.A.; Murray, J.; Grigorov, A.; Siebenaller, R.; Conner, B.S.; Rowe, E.; Guha, S.; Petrov, V. Thermo-mechanical properties of BaGa2GeS(e)6 nonlinear optical crystals. Opt. Mater. Express 2023, 13, 1335–1344. [Google Scholar] [CrossRef]
- Wu, J.; Huang, W.; Liu, H.g.; He, Z.; Chen, B.; Zhu, S.; Zhao, B.; Lei, Y.; Zhou, X. Investigation of the Thermal Properties and Crystal Growth of the Nonlinear Optical Crystals AgGaS2 and AgGaGeS4. Cryst. Growth Des. 2020, 20, 3140–3153. [Google Scholar] [CrossRef]
- Aggarwal, R.L.; Fan, T.Y. Thermal diffusivity, specific heat, thermal conductivity, coefficient of thermal expansion, and refractive-index change with temperature in AgGaSe2. Appl. Opt. 2005, 44, 2673–2677. [Google Scholar] [CrossRef]
- Wei, J.; Murray, J.; Badikov, V.V.; Petrov, V.; Guha, S. Thermal Properties of the Trigonal Quaternary Nonlinear Crystals BaGa2GeS6 and BaGa2GeSe6. In Proceedings of the Conference on Lasers and Electro-Optics, San Jose, CA, USA, 9–14 May 2021; Optica Publishing Group: Massachusetts, NW, USA, 2021; p. STu1C.4. [Google Scholar] [CrossRef]
- Zhang, Y.; Zuo, Y.; Li, Z.; Wu, B.; Yao, J.; Shen, Y. High energy mid-infrared laser pulse output from a BaGa4Se7 crystal-based optical parametric oscillator. Opt. Lett. 2020, 45, 4595–4598. [Google Scholar] [CrossRef] [PubMed]
- Kostyukova, N.Y.; Boyko, A.A.; Badikov, V.; Badikov, D.; Shevyrdyaeva, G.; Panyutin, V.; Marchev, G.M.; Kolker, D.B.; Petrov, V. Widely tunable in the mid-IR BaGa4Se7 optical parametric oscillator pumped at 1064 nm. Opt. Lett. 2016, 41, 3667–3670. [Google Scholar] [CrossRef]
- Exner, G.; Grigorov, A.; Badikov, V.; Petrov, V. Hardness and Young’s modulus of BaGa4S7 and BaGa4Se7 nonlinear optical crystals. Opt. Mater. 2022, 133, 112994. [Google Scholar] [CrossRef]
- Gupta, R.C.; Varshney, P.; Pravesh.; Lal, M.; Kumar, D.; Singh, K.; Verma, A. Mechanical stability parameters of chalcogenides and pnictides based optoelectronic materials. Chalcogenide Lett. 2023, 20, 101–112. [Google Scholar] [CrossRef]
- ISO 21254-1:2011; Lasers and Laser-Related Equipment—Test Methods for Laser-Induced Damage Threshold—Part 1: Definitions and General Principles. International Organization for Standardization: Geneva, Switzerland, 2011.
- Demos, S.G.; Hoffman, B.N.; Carr, C.W.; Cross, D.A.; Negres, R.A.; Bude, J.D. Mechanisms of laser-induced damage in absorbing glasses with nanosecond pulses. Opt. Express 2019, 27, 9975–9986. [Google Scholar] [CrossRef]
- Liu, G.; Kuang, D.; Song, L.; Xu, C.; Yan, C. Mechanism in damage variation of nanosecond laser-induced damage of germanium sheets in vacuum. Opt. Laser Technol. 2023, 157, 108663. [Google Scholar] [CrossRef]
- Stuart, B.C.; Feit, M.D.; Rubenchik, A.M.; Shore, B.W.; Perry, M.D. Laser-Induced Damage in Dielectrics with Nanosecond to Subpicosecond Pulses. Phys. Rev. Lett. 1995, 74, 2248–2251. [Google Scholar] [CrossRef]
- Wood, R. Laser induced damage thresholds and laser safety levels. Do the units of measurement matter? Opt. Laser Technol. 1998, 29, 517–522. [Google Scholar] [CrossRef]
- Manenkov, A.A.; Prokhorov, A.M. Laser-induced damage in solids. Sov. Phys. Uspekhi 1986, 29, 104. [Google Scholar] [CrossRef]
- Bliss, E.S. Pulse duration dependence of laser damage mechanisms. Opto-Electron. 1971, 3, 99–108. [Google Scholar] [CrossRef]
- Erushin, E.Y.; Kostyukova, N.Y.; Boyko, A.A.; Baranova, E.; Verbovaty, D.; Badikov, D. Issledovaniye luchevoy stoykosti serosoderzhashchikh kristallov bariyevykh khal’kogenidov. In Proceedings of the XIX International Youth Conference on Luminescence and Laser Physics, Irkutsk, Russia, 3–8 July 2023; p. 85. [Google Scholar]
- Zhao, X.; Li, C.; Bai, J.; Wang, Z.; Yao, J.; Tan, R.; Xu, X. Recalibration of the nonlinear optical coefficients of BaGa4Se7 crystal using second-harmonic-generation method. Opt. Lett. 2021, 46, 5894–5897. [Google Scholar] [CrossRef]
- Kostyukova, N.Y.; Boyko, A.A.; Eranov, I.D.; Antipov, O.L.; Kolker, D.B.; Kostyukov, A.I.; Erushin, E.Y.; Miroshnichenko, I.B.; Badikov, D.V.; Badikov, V.V. Laser-induced damage threshold of the nonlinear crystals BaGa4Se7 and BaGa2GeSe6 at 2091 nm in the nanosecond regime. J. Opt. Soc. Am. B 2020, 37, 2655–2659. [Google Scholar] [CrossRef]
- Yuan, J.H.; Li, C.; Yao, B.Q.; Yao, J.Y.; Duan, X.M.; Li, Y.Y.; Shen, Y.J.; Wu, Y.C.; Cui, Z.; Dai, T.Y. High power, tunable mid-infrared BaGa4Se7 optical parametric oscillator pumped by a 2.1 µm Ho:YAG laser. Opt. Express 2016, 24, 6083–6087. [Google Scholar] [CrossRef] [PubMed]
- Zhao, B.; Chen, Y.; Yao, B.; Yao, J.; Guo, Y.; Wang, R.; Dai, T.; Duan, X. High-efficiency, tunable 8-9 µm BaGa4Se7 optical parametric oscillator pumped at 2.1 µm. Opt. Mater. Express 2018, 8, 3332–3337. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Q.; Hao, J.; Liu, H.; Yao, J.; Li, Z.; Liu, J.; Mak, K.F. Broadband, few-cycle mid-infrared continuum based on the intra-pulse difference frequency generation with BGSe crystals. Opt. Express 2020, 28, 37903–37909. [Google Scholar] [CrossRef]
- Kostyukova, N.Y.; Boyko, A.A.; Erushin, E.Y.; Kostyukov, A.I.; Badikov, V.V.; Badikov, D.V.; Kolker, D.B. Laser-induced damage threshold of BaGa4Se7 and BaGa2GeSe6 nonlinear crystals at 1053 nm. J. Opt. Soc. Am. B 2019, 36, 2260–2265. [Google Scholar] [CrossRef]
- Kolker, D.B.; Kostyukova, N.Y.; Boyko, A.A.; Badikov, V.V.; Badikov, D.V.; Shadrintseva, A.G.; Tretyakova, N.N.; Zenov, K.G.; Karapuzikov, A.A.; Zondy, J.J. Widely tunable (2.6–10.4 µm) BaGa4Se7 optical parametric oscillator pumped by a Q-switched Nd:YLiF4 laser. J. Phys. Commun. 2018, 2, 035039. [Google Scholar] [CrossRef]
- Yang, F.; Yong Yao, J.; Yan Xu, H.; Feng, K.; Long Yin, W.; Qin Li, F.; Yang, J.; Feng Du, S.; Jun Peng, Q.; Yuan Zhang, J.; et al. High efficiency and high peak power picosecond mid-infrared optical parametric amplifier based on BaGa4Se7 crystal. Opt. Lett. 2013, 38, 3903–3905. [Google Scholar] [CrossRef] [PubMed]
- Boyko, A.A.; Eryshin, E.Y.; Kostyukova, N.Y.; Kolker, D.B.; Kostyukov, A.I.; Miroshnichenko, I.B.; Badikov, D.V.; Badikov, V.V. Laser-Induced Damage Threshold of dark yellow phase BaGa4Se7 Crystal at 1053 nm. In Proceedings of the 2020 International Conference Laser Optics (ICLO), St. Petersburg, Russia, 2–6 November 2020; p. 1. [Google Scholar] [CrossRef]
- Erushin, E.; Kostyukova, N.; Boyko, A.; Loginova, A.; Safaraliev, G.; Shevyrdyaeva, G.; Badikov, D. Ba2Ga8GeS16: New nonlinear optical crystals with high laser-induced damage threshold for parametric down-conversion in mid-IR. Appl. Phys. B 2023, 130, 10. [Google Scholar] [CrossRef]
- Tyazhev, A.; Kolker, D.; Marchev, G.; Badikov, V.; Badikov, D.; Shevyrdyaeva, G.; Panyutin, V.; Petrov, V. Midinfrared optical parametric oscillator based on the wide-bandgap BaGa4S7 nonlinear crystal. Opt. Lett. 2012, 37, 4146–4148. [Google Scholar] [CrossRef]
- Heiner, Z.; Petrov, V.; Mero, M. Efficient, sub-4-cycle, 1-µm-pumped optical parametric amplifier at 10 µm based on BaGa4S7. Opt. Lett. 2020, 45, 5692–5695. [Google Scholar] [CrossRef]
- Zhang, J.J.; Yang, F.; Yang, S.D.; Fang, S.H.; Wang, X.J.; Peng, Q.J.; Ye, N.; Xu, Z.Y. Tunable mid-IR optical parametric amplifier pumped at 1064 nm based on a wideband-gap BaGa4S7 crystal. Infrared Phys. Technol. 2020, 111, 103571. [Google Scholar] [CrossRef]
- Kostyukova, N.; Bobylev, A.; Boyko, A.; Zenov, K.; Shadrintseva, A.; Tretyakova, N.; Badikov, V.; Kolker, D. Wide tunable BaGa4Se7 optical parametric oscillator pumped by Nd:YLF laser. In Proceedings of the 2016 International Conference Laser Optics (LO), St. Petersburg, Russia, 27 June–1 July 2016; p. R8-39. [Google Scholar] [CrossRef]
- Boyko, A.A.; Kostyukova, N.Y.; Badikov, V.; Badikov, D.; Panyutin, V.; Shevyrdyaeva, G.; Pasiskevicius, V.; Zukauskas, A.; Marchev, G.M.; Kolker, D.B.; et al. Intracavity difference-frequency mixing of optical parametric oscillator signal and idler pulses in BaGa4Se7. Appl. Opt. 2017, 56, 2783–2786. [Google Scholar] [CrossRef]
- He, Y.; Xu, D.; Yao, J.; Wang, Y.; Guo, Y.; Zhu, X.; Yan, C.; Tang, L.; Li, J.; Zhong, K.; et al. Intracavity-Pumped, Mid-Infrared Tandem Optical Parametric Oscillator Based on BaGa4Se7 Crystal. IEEE Photonics J. 2019, 11, 1300109. [Google Scholar] [CrossRef]
- Xu, W.T.; Wang, Y.Y.; Xu, D.G.; Li, C.; Yao, J.Y.; Yan, C.; He, Y.X.; Nie, M.T.; Wu, Y.C.; Yao, J.Q. High-pulse-energy mid-infrared optical parametric oscillator based on BaGa4Se7 crystal pumped at 1.064 µm. Appl. Phys. B 2017, 123, 80. [Google Scholar] [CrossRef]
- Kang, M.; Deng, Y.; Yan, X.; Zeng, X.; Guo, Y.; Yao, J.; Zeng, F.; Zheng, J.; Zhou, K.; Qu, C.; et al. A compact and efficient 4.25 μm BaGa4Se7 optical parametric oscillator. Chin. Opt. Lett. 2019, 17, 121402. [Google Scholar] [CrossRef]
- Xu, D.; Zhang, J.; He, Y.; Wang, Y.; Yao, J.; Guo, Y.; Yan, C.; Tang, L.; Li, J.; Zhong, K.; et al. High-energy, tunable, long-wave mid-infrared optical parametric oscillator based on BaGa4Se7 crystal. Opt. Lett. 2020, 45, 5287–5290. [Google Scholar] [CrossRef] [PubMed]
- Bian, J.; Kong, H.; Ye, Q.; Yao, J.; Guo, L.; Sun, X. Narrow-linewidth BaGa4Se7 optical parametric oscillator. Chin. Opt. Lett. 2022, 20, 041901. [Google Scholar] [CrossRef]
- Liu, G.; Zhang, Z.; Li, C.; Meng, J.; Li, T.; Zhao, Z.; Cong, Z.; Yao, J.; Liu, Z. Comparison of a high-power 3.75 µm BaGa4Se7 OPO based on a plane-parallel resonator and an unstable resonator with a Gaussian reflectivity mirror. Appl. Opt. 2022, 61, 7330–7335. [Google Scholar] [CrossRef] [PubMed]
- He, Y.; Yan, C.; Chen, K.; Xu, D.; Li, J.; Zhong, K.; Wang, Y.; Yao, R.; Yao, J.; Yao, J. High Repetition Rate, Tunable Mid-Infrared BaGa4Se7 Optical Parametric Oscillator Pumped by a 1 μm Nd:YAG Laser. Appl. Sci. 2022, 12, 7197. [Google Scholar] [CrossRef]
- Kang, M.; Deng, Y.; Yao, J.; Zhu, Q. High Power and Efficient 4.43 μm BaGa4Se7 Optical Parametric Oscillator Pumped at 1064 nm. Photonics 2022, 9, 105. [Google Scholar] [CrossRef]
- Ye, Q.; Kong, H.; Bian, J.; Yao, J.; Wang, E.; Wu, Y.; Xu, H.; Wen, K.; Hu, Y. Widely tunable and high resolution mid-infrared laser based on BaGa4Se7 optical parametric oscillator. Front. Optoelectron. 2023, 16, 26. [Google Scholar] [CrossRef]
- Wen, N.; Shen, Y.; Wen, Y.; Wang, E.; Yao, J.; Fang, Y.; Gao, H.; Bo, Y.; Chen, Z.; Peng, Q. A Stable and Compact Mid-IR at 6.45 μm Exceeding 6 mJ of Pulse Energy BaGa4Se7 Optical Parametric Oscillator. Appl. Sci. 2023, 13, 6413. [Google Scholar] [CrossRef]
- Liu, G.; Chen, Y.; Li, Z.; Yang, K.; Yao, B.; Yao, J.; Wang, R.; Yang, C.; Mi, S.; Dai, T.; et al. High-beam-quality 2.1 mkm pumped mid-infrared type-II phase-matching BaGa4Se7 optical parametric oscillator with a ZnGeP2 amplifier. Opt. Lett. 2020, 45, 3805–3808. [Google Scholar] [CrossRef]
- Yang, K.; Liu, G.; Li, C.; Yao, B.; Yao, J.; Chen, Y.; Mi, S.; Duan, X.; Dai, T. Research on performance improvement technology of a BaGa4Se7 mid-infrared optical parametric oscillator. Opt. Lett. 2020, 45, 6418–6421. [Google Scholar] [CrossRef] [PubMed]
- Hu, S.; Wang, L.; Guo, Y.; Cheng, T.; Wu, X.; Wang, Z.; Wu, H.; Yao, J.; Wu, Y.; Jiang, H. High-conversion-efficiency tunable mid-infrared BaGa4Se7 optical parametric oscillator pumped by a 2.79 μm laser. Opt. Lett. 2019, 44, 2201–2203. [Google Scholar] [CrossRef] [PubMed]
- Jelínek, M.; Kubeček, V.; Novák, O.; Huynh, J.; Cimrman, M.; Chyla, M.; Smrž, M.; Mocek, T.; Smetanin, S.N.; Grechin, S.G.; et al. Difference Frequency Generation in BaGa4Se7 Tunable in a 6.5–8.5 µm Range with a Peak Power of 30 MW Pumped by 1.03 µm, 1.8 ps Laser. In Optica High-brightness Sources and Light-Driven Interactions Congress 2022; Optica Publishing Group: Massachusetts, NW, USA, 2022; p. JTh4A.15. [Google Scholar] [CrossRef]
- Tian, K.; Wang, W.; Li, C.; Wan, Z.; Hu, B.; He, L.; Xiang, M.; Yao, J.; Wu, H.; Liang, H. Ultrabroad (3.7–17 µm) tunable femtosecond optical parametric amplifier based on BaGa4Se7 crystal. Opt. Lett. 2022, 47, 5973–5976. [Google Scholar] [CrossRef] [PubMed]
- Lukošiūnas, J.; Kananavičius, R.; Danilevičius, R.; Januškevičius, R.; Schunemann, P.G.; Michailovas, A. Efficient high resolution broadband SFG spectrometer utilizing BGSe nonlinear crystal covering 2.5–10 µm spectral range. In Laser Congress 2023 (ASSL, LAC); Optica Publishing Group: Massachusetts, NW, USA, 2023; p. ATh2A.4. [Google Scholar] [CrossRef]
- Sun, M.G.; Cao, Z.S.; Yao, J.Y.; Ma, H.L.; Guo, Y.W.; Gao, X.M.; Rao, R.Z.; Wu, Y.C. Continuous-wave difference-frequency generation based on BaGa4Se7 crystal. Opt. Express 2019, 27, 4014–4023. [Google Scholar] [CrossRef]
- Boyko, A.; Badikov, V.; Shevyrdyaeva, G.; Badikov, D.; Pasiskevicius, V.; Zukauskas, A.; Petrov, V. Intracavity-pumped, cascaded optical parametric oscillator based on BaGa2GeSe6. In High-Brightness Sources and Light-Driven Interactions; Optica Publishing Group: Massachusetts, NW, USA, 2018; p. MW2C.3. [Google Scholar] [CrossRef]
- Chen, W.; Wang, L.; Divliansky, I.B.; Pasiskevicius, V.; Mhibik, O.; Moelster, K.M.; Zukauskas, A.; Glebov, L.B.; Petrov, V. Narrowband, intracavity-pumped, type-II BaGa2GeSe6 optical parametric oscillator. Opt. Express 2024, 32, 1728–1735. [Google Scholar] [CrossRef]
- Elu, U.; Maidment, L.; Vamos, L.; Steinle, T.; Haberstroh, F.; Petrov, V.; Badikov, V.; Badikov, D.; Biegert, J. Few-cycle mid-infrared pulses from BaGa2GeSe6. Opt. Lett. 2020, 45, 3813–3815. [Google Scholar] [CrossRef]
- Stibenz, G.; Beutler, M.; Rimke, I.; Badikov, V.; Badikov, D.; Petrov, V. Femtosecond mid-IR difference-frequency generation in BaGa2GeSe6 from a 40 MHz optical parametric oscillator pumped at 1035 nm. In Conference on Lasers and Electro-Optics; Optica Publishing Group: Massachusetts, NW, USA, 2018; p. STh4F.5. [Google Scholar] [CrossRef]
- Ionin, A.A.; Badikov, D.V.; Badikov, V.V.; Kinyaevskiy, I.O.; Klimachev, Y.M.; Kotkov, A.A.; Kozlov, A.Y.; Sagitova, A.M.; Sinitsyn, D.V. Sum frequency generation of multi-line slab radio frequency discharge carbon monoxide laser system with intracavity nonlinear BaGa2GeSe6 crystal. Opt. Lett. 2018, 43, 4358–4361. [Google Scholar] [CrossRef]

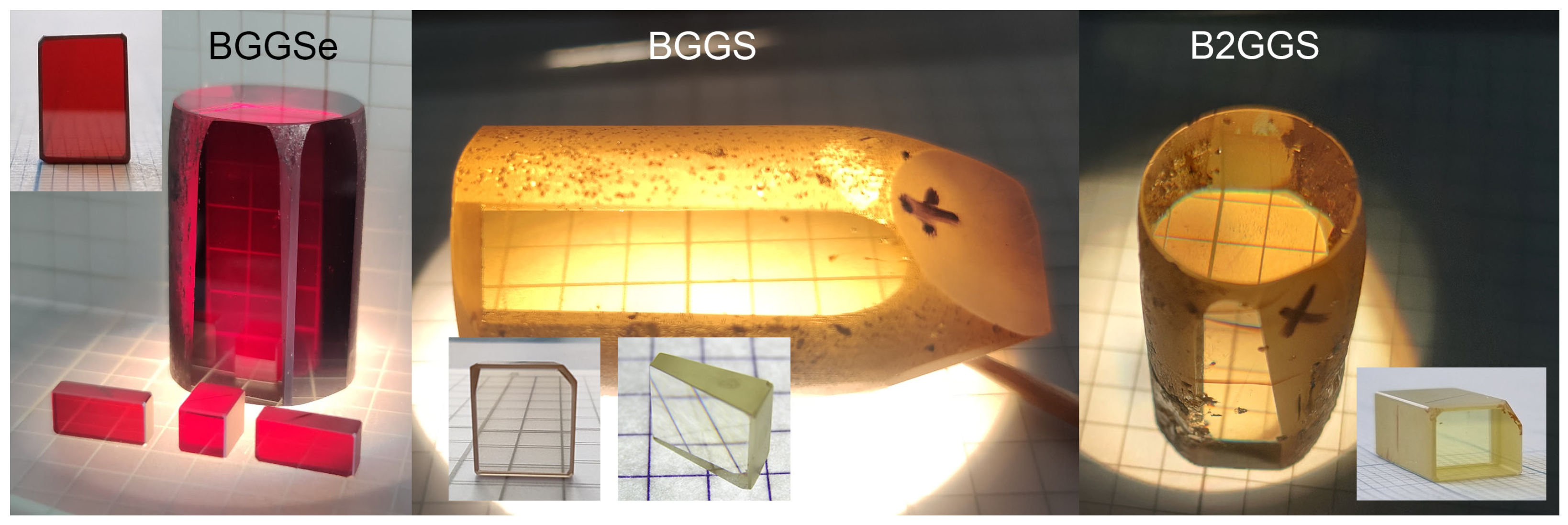
| Crystal | Lattice Parameters |
|---|---|
| BGS | a = 6.237 Å, b = 14.774 Å, c = 5.934 Å [61] (using the convention c < a < b [63]) |
| BGSe | a = 7.6252 Å; b = 6.5114 Å; c = 14.702 Å;
= 121.24° [50] a = 14.702 Å, b = 6.5114 Å, c = 7.6252 Å, = 121.24° [61] (using the convention c < a, b—monoclinic axis [63]) |
| BGGS | a = 9.5967 Å; c = 8.671 Å [55] |
| BGGSe | a = 10.0438 Å; c = 9.114 Å [55] |
| B2GGS | a = 10.886 Å, c = 11.915 Å [62] |
| Crystal | Measurement Conditions | n2·10−14, cm2/W | , cm/GW |
|---|---|---|---|
| BGS | 1.053 m; 5.1 ns; 100 Hz; 700 MW/cm2; 2.03 mm long; | 0.85 | Not observed |
| 1.028 m; 180 fs; 100 Hz and 100 kHz; 8 GW/cm2; o- and e-pol., 4.8 mm long; [80] | 0.72–0.83 | Not observed | |
| 1.028 m; 180 fs; 100 Hz and 100 kHz; 2.3 GW/cm2; o- and e-pol., 8.3 mm long; [81] | 1.0 | Not observed | |
| BGSe | 1.053 m; 5.1 ns; 100 Hz; 245 MW/cm2; o- and e-pol.; 2.31 mm long | 1.55–1.81 | Not observed |
| 1.064 m; 30 ps; 10 Hz; occurs at 1.3 GW/cm2; 4 mm long; [82] | No data | Observed | |
| BGGS | 1.053 m; 5.1 ns; 100 Hz; 700 MW/cm2; 2.05 mm long | 0.78 | Not observed |
| BGGSe | 1.053 m; 5.1 ns; 100 Hz; 245 MW/cm2; o- and e-pol.; 2.04 mm long | 7.4–14 | 1.3–2.2 |
| B2GGS | 1.053 m; 5.1 ns; 100 Hz; 700 MW/cm2; 2.6 mm long | 1.93 | Not observed |
| Crystal | Thermal Conductivity, Wm−1K−1 | Thermal Diffusivity, mm2s−1 | Thermal Expansion, 10−6K−1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a | b | c | a | b | c | a | b | c | ||||
| BGS [83] | 1.46 | 1.58 | 1.68 | @323 K | 0.74 | 0.80 | 0.93 | @323 K | No data | No data | No data | |
| 1.54 | 1.46 | 1.52 | @373 K | 0.66 | 0.72 | 0.82 | @373 K | |||||
| 1.57 | 1.45 | 1.44 | @423 K | 0.64 | 0.68 | 0.78 | @423 K | |||||
| BGSe [84] | 0.74 | 0.64 | 0.56 | @298 K | 0.50 | 0.42 | 0.38 | @298 K | 9.24 | 10.76 | 11.70 | @293–573 K |
| BGGS [85] | 0.91 | 1.10 | @298 K | 1.10–0.6 | 0.9–0.5 | @184–473 K | 12.1 | 6.93 | @300 K | |||
| BGGSe [85] | 0.63 | 0.76 | @298 K | 0.8–0.4 | 0.65–0.35 | @ 184–473 K | 12.2 | 3.84 | @300 K | |||
| B2GGS | No data | No data | No data | No data | No data | No data | No data | No data | No data | |||
| Crystal | Hardness, GPa | Hardness VHN, kg/mm2 | Young’s Modulus, GPa | Temperature, K | Thermal Drift, nm/s | |
|---|---|---|---|---|---|---|
| BGS [91] | 6.00 | 556 | 80.0 | 291.75 | 0.26 | |
| BGSe [91] | 3.63 | 336 | 57.6 | 289.85 | 0.33 | |
| BGGS [85] | a-cut | 4.99 | 463 | 65.1 | 293.7 | 0.3 |
| c-cut | 4.66 | 432 | 71.3 | 294.5 | 0.17 | |
| BGGSe [85] | a-cut | 4.10 | 380 | 53.5 | 294.2 | 0.19 |
| c-cut | 4.25 | 394 | 61.1 | 294.2 | 0.14 | |
| B2GGS | No data | No data | No data | No data | No data | |
| Wavelength | 10 m | 2 m | 1 m | ||
|---|---|---|---|---|---|
| Pulse Duration | ns | ns | fs | ns | ps |
| BGS | 52.4 J/cm2 (9.58 m, 100 ns, 1 Hz) [83] | 10 J/cm2 (2.1 m, 15 ns, 1 Hz) * [83] | 2.4 J/cm2 (1.064 m, 15 ns, 1 Hz) [50] 3.7/2.9 J/cm2 (1.064 m, 14/1 ns, 0.1/0.5 kHz) [51] 7.4/6.4 J/cm2 (1.053 m, 5.1 ns, 0.1/1 kHz) [100] | ||
| BGSe | 36.6 J/cm2 (10.6 m, 100 ns, 1 Hz) [101] | 4.8/3.3/2.1 J/cm2 (2.091 m, 15 ns, 2/5/10 kHz) [102] 2.46 J/cm2 (2.091 m, 15 ns, 0.5 kHz) * [103] 1.37 J/cm2 (2.091 m, 15 ns, 0.5 kHz) * [104] | 81 GW/cm2 (2.4 m, 28 fs, 69 MHz) [105] | 2/1.4/1.1 J/cm2 (1.053 m, 5.1 ns, 0.1/0.5/1 kHz) * [106] 2.9/2.9/2.6 J/cm2 (1.053 m, 8.3 ns, 0.1/0.15/0.2 kHz) * [107] 1.4/1 J/cm2 (1.064 m, 14/1 ns, 0.1/0.5 kHz) [90] 5.6 J/cm2 (1.064 m, 5 ns, 1 Hz) [84] | 0.18 J/cm2 (1.064 m, 30 ps, 10 Hz) [108] |
| Doped BGSe | 6.6/5.1/2.5 J/cm2 (2.091 m, 15 ns, 2/5/10 kHz) [102] | 2.5/2.3/2.3/2 J/cm2 (1.053 m, 5.1 ns, 0.1/0.5/1/2 kHz) * [109] | |||
| BGGS | 14 J/cm2 (10.6 m, 100 ns, 1 Hz) [56] | 6.8/7 J/cm2 (1.053 m, 5.1 ns, 0.1/1 kHz) [100] | |||
| B2GGS | 6.9/7 J/cm2 (1.053 m, 5.1 ns, 0.1/1 kHz) [110] | ||||
| BGGSe | 11 J/cm2 (10.6 m, 100 ns, 1 Hz) [56] | 6.5/4.3/2.7 J/cm2 (2.091 m, 15 ns, 2/5/10 kHz) [102] | 1.9/1.6/1.3 J/cm2 (1.053 m, 5.1 ns, 0.1/0.5/1 kHz) * [106] | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kostyukova, N.; Erushin, E.; Boyko, A.; Shevyrdyaeva, G.; Badikov, D. Barium Chalcogenide Crystals: A Review. Photonics 2024, 11, 281. https://doi.org/10.3390/photonics11030281
Kostyukova N, Erushin E, Boyko A, Shevyrdyaeva G, Badikov D. Barium Chalcogenide Crystals: A Review. Photonics. 2024; 11(3):281. https://doi.org/10.3390/photonics11030281
Chicago/Turabian StyleKostyukova, Nadezhda, Evgenii Erushin, Andrey Boyko, Galina Shevyrdyaeva, and Dmitry Badikov. 2024. "Barium Chalcogenide Crystals: A Review" Photonics 11, no. 3: 281. https://doi.org/10.3390/photonics11030281
APA StyleKostyukova, N., Erushin, E., Boyko, A., Shevyrdyaeva, G., & Badikov, D. (2024). Barium Chalcogenide Crystals: A Review. Photonics, 11(3), 281. https://doi.org/10.3390/photonics11030281





