Hybrid Graphene–Silicon Arrayed Waveguide Gratings for On-Chip Signal–Frequency Conversion
Abstract
:1. Introduction
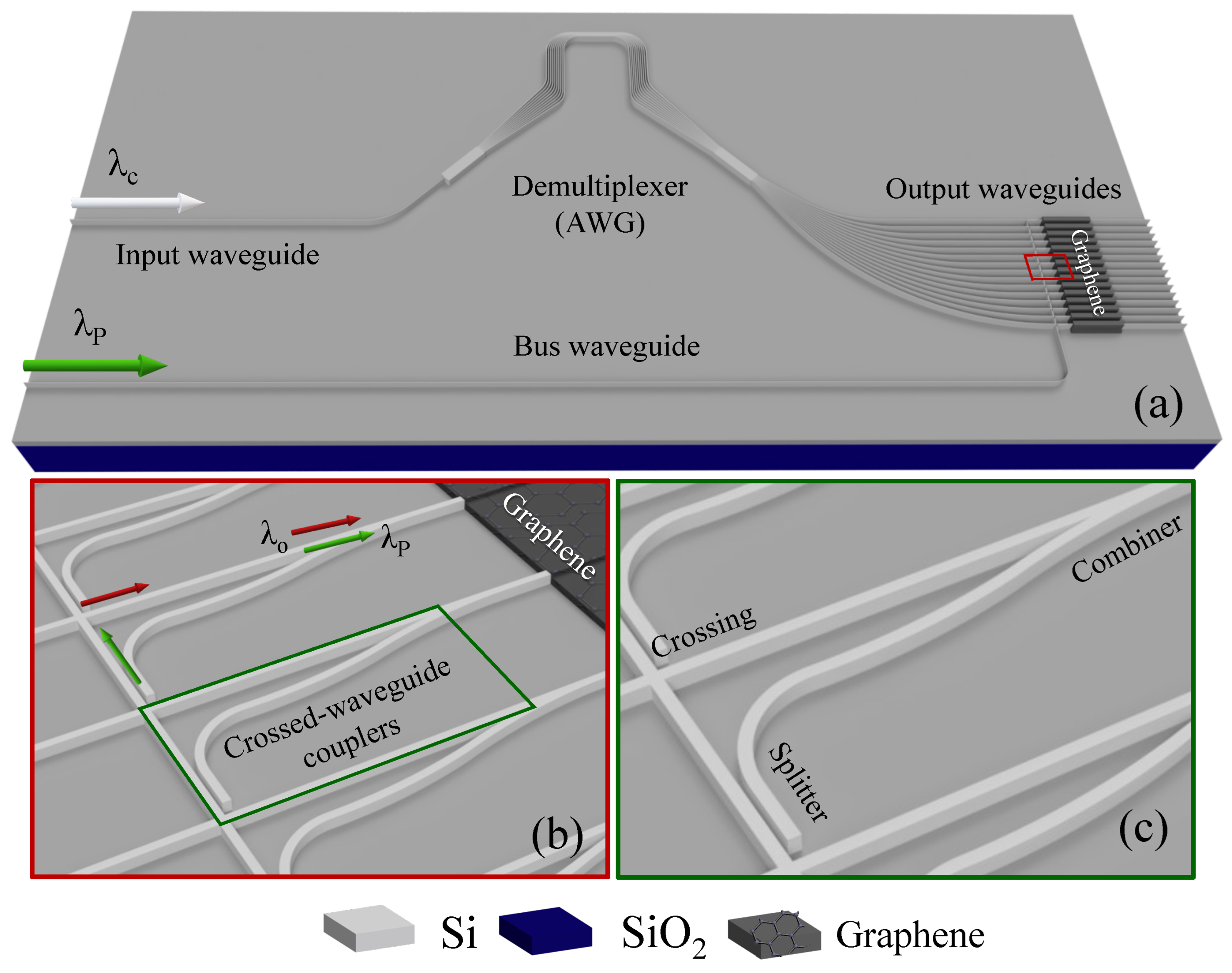
2. Concept
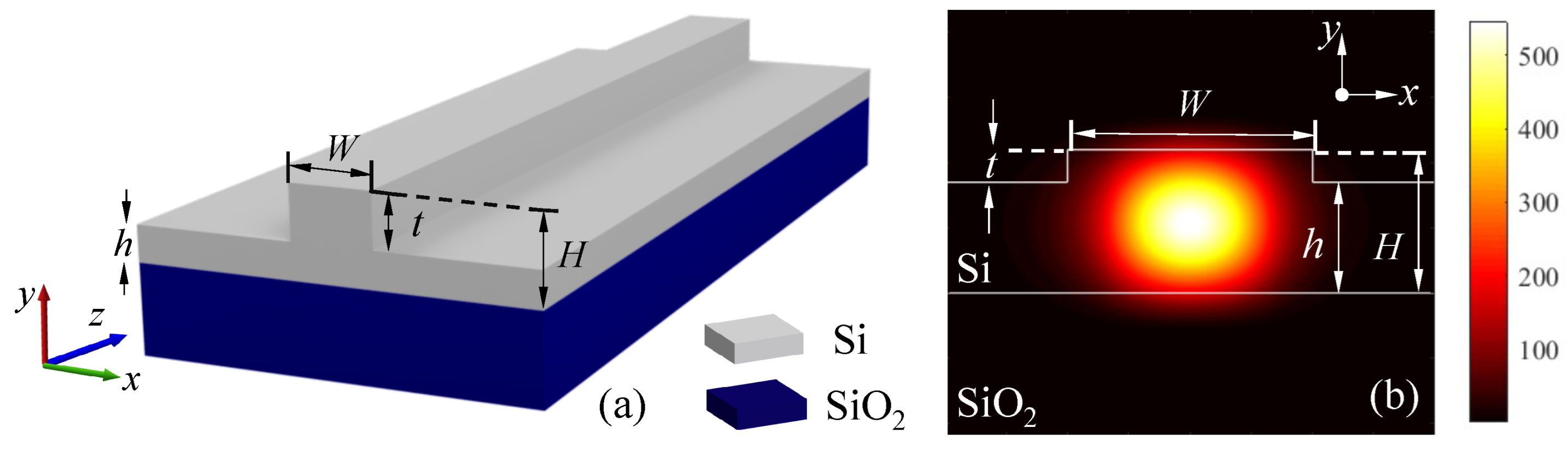
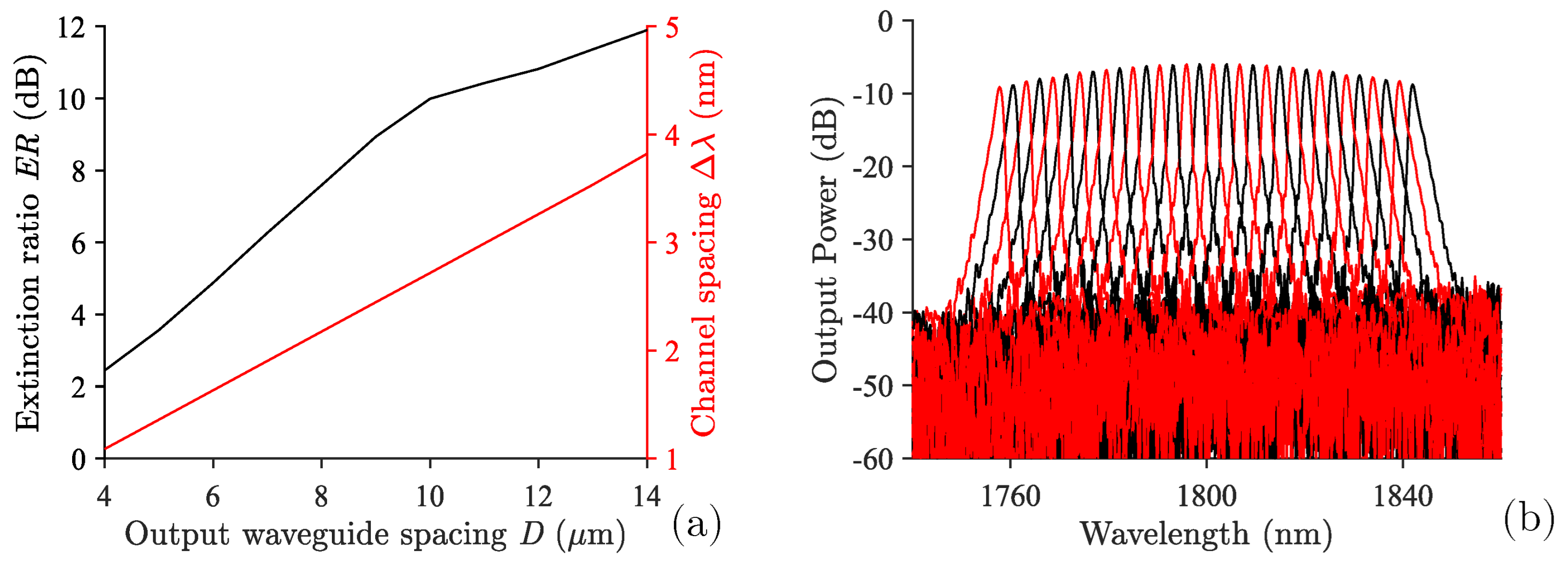
3. Design and Simulation of the Silicon Circuit
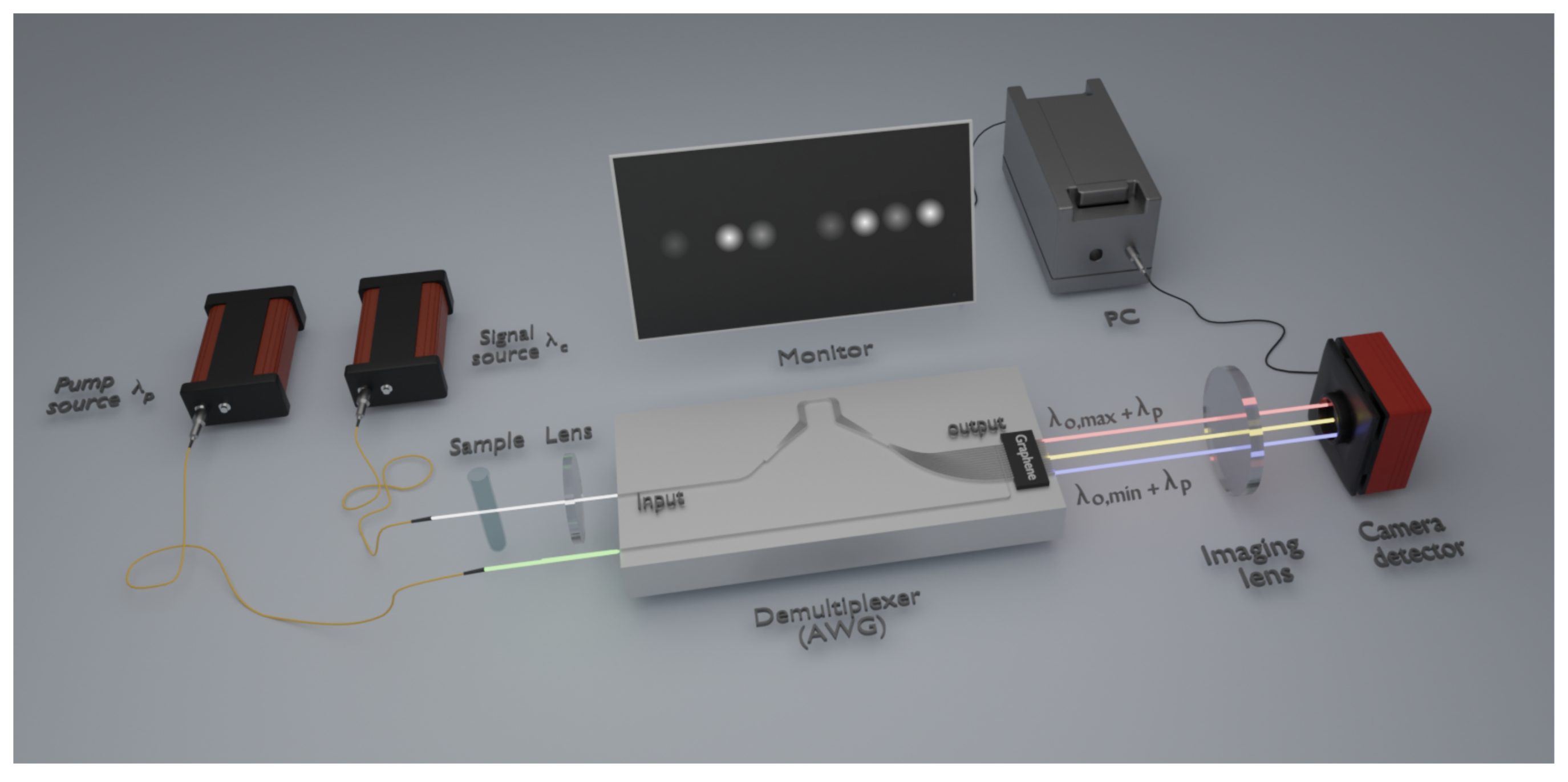
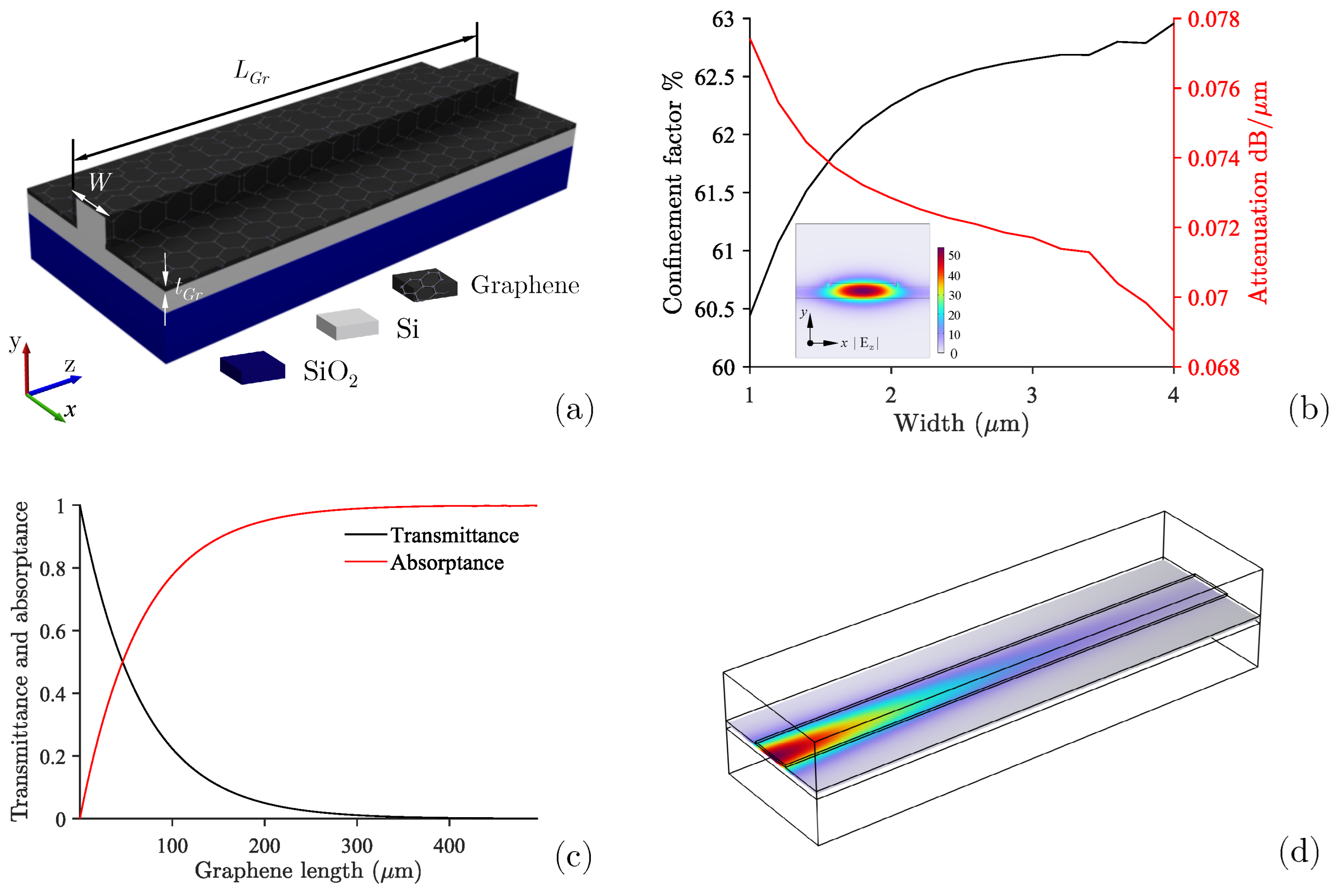
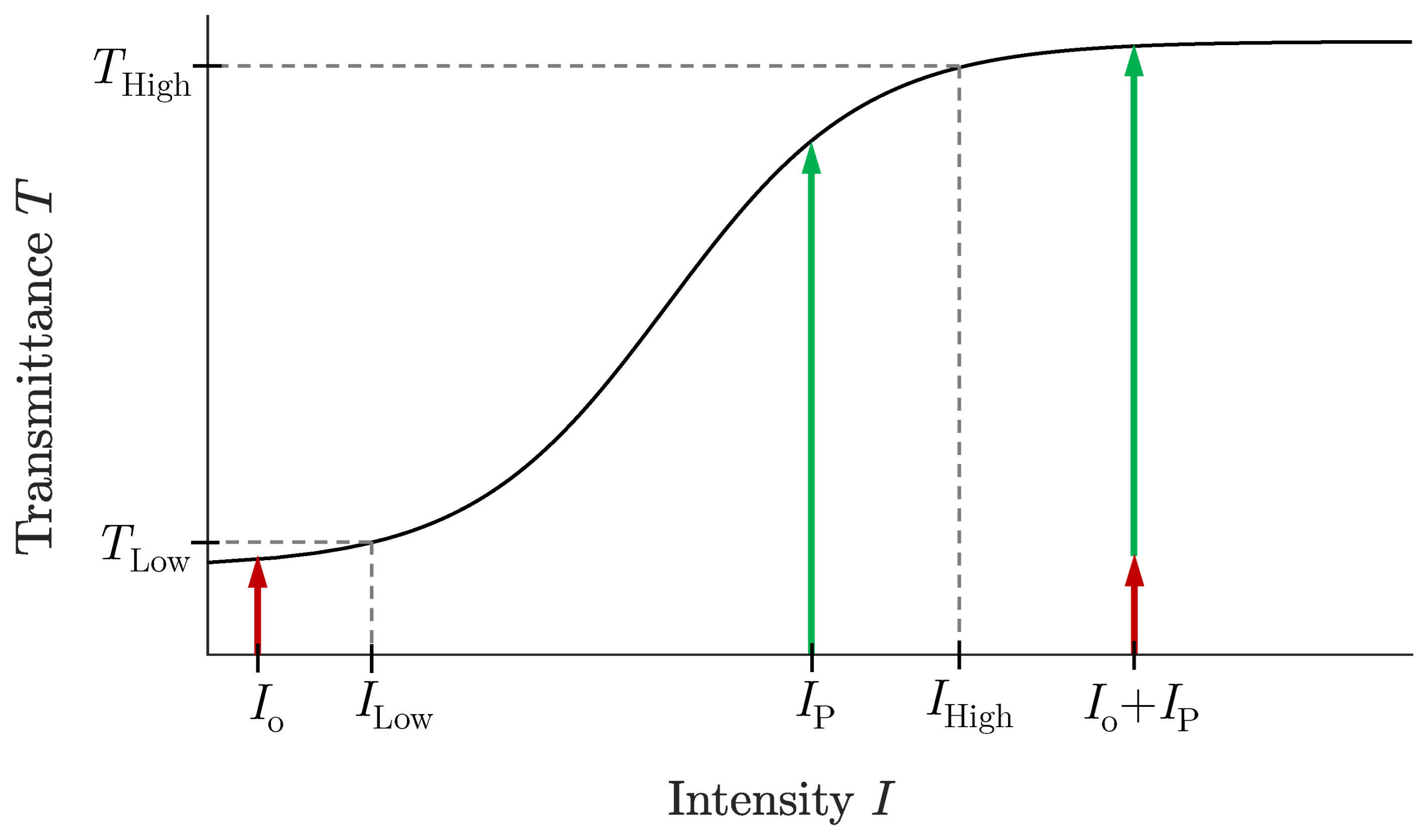
4. Silicon–Graphene Operation for Spectrometry
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ismail, N.; Choo-Smith, L.P.; Wörhoff, K.; Driessen, A.; Baclig, A.; Caspers, P.; Puppels, G.; De Ridder, R.; Pollnau, M. Raman spectroscopy with an integrated arrayed-waveguide grating. Opt. Lett. 2011, 36, 4629–4631. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Yeh, Y.C.; Ladasky, J.; Farhoodfar, A.; Schmidt, D. Single chip AWG-based Raman spectroscopy for continuous glucose monitoring. In Proceedings of the Optical Diagnostics and Sensing XVI: Toward Point-of-Care Diagnostics, San Francisco, CA, USA, 13–18 February 2016; SPIE: Bellingham, WA, USA, 2016; Volume 9715, pp. 216–221. [Google Scholar]
- Akca, B.; Chang, L.; Sengo, G.; Wörhoff, K.; Pollnau, M.; de Ridder, R.; Nguyen, V.D.; Kalkman, J.; van Leeuwen, T. Integrated AWG spectrometer for on-chip optical coherence tomography. In Proceedings of the 15th European Conference on Integrated Optics (ECIO), Cambridge, UK, 7–9 April 2010; IEEE Photonics Society: Piscataway, NJ, USA, 2010. [Google Scholar]
- Ybanez, N.; Bogaerts, W.; Hens, Z.; Baets, R. On-chip arrayed waveguide grating interrogated silicon-on-insulator microring resonator-based gas sensor. IEEE Photonics Technol. Lett. 2011, 23, 1505–1507. [Google Scholar]
- Weng, S.; Yuan, P.; Zhuang, W.; Zhang, D.; Luo, F.; Zhu, L. SOI-based multi-channel awg with fiber bragg grating sensing interrogation system. Photonics 2021, 8, 214. [Google Scholar] [CrossRef]
- Kee, J.S.; Poenar, D.P.; Neužil, P.; Yobaş, L.; Chen, Y. Design and fabrication of Poly (dimethylsiloxane) arrayed waveguide grating. Opt. Express 2010, 18, 21732–21742. [Google Scholar] [CrossRef] [PubMed]
- Martens, D.; Subramanian, A.Z.; Pathak, S.; Vanslembrouck, M.; Bienstman, P.; Bogaerts, W.; Baets, R.G. Compact silicon nitride arrayed waveguide gratings for very near-infrared wavelengths. IEEE Photonics Technol. Lett. 2014, 27, 137–140. [Google Scholar] [CrossRef]
- Schauwecker, B.; Przyrembel, G.; Kuhlow, B.; Radehaus, C. Small-size silicon-oxynitride AWG demultiplexer operating around 725 nm. IEEE Photonics Technol. Lett. 2000, 12, 1645–1646. [Google Scholar] [CrossRef]
- Tippinit, J.; Pélisset, S.; Baah, M.; Kuittinen, M.; Roussey, M. Titanium Dioxide AWG for the Visible. In Proceedings of the 2020 Photonics North (PN), Niagara Falls, ON, Canada, 26–28 May 2020; IEEE: Piscataway, NJ, USA, 2020; p. 1. [Google Scholar]
- Nikbakht, H.; van Someren, B.; Hammer, M.; Akca, B.I. Weak optical modes for high-density and low-loss photonic circuits. APL Photonics 2023, 8, 056107. [Google Scholar] [CrossRef]
- Tang, X.; Zheng, Y.; Liu, J.; Duan, J.A. Optimization Method for Center Frequency Accuracy of High-Channel-Count Arrayed Waveguide Grating in Dense Wavelength Division Multiplexing Systems. Photonics 2023, 10, 1178. [Google Scholar] [CrossRef]
- Zou, J.; Sun, F.; Wang, C.; Zhang, M.; Wang, J.; Lang, T.; Wang, X.; Le, Z.; He, J.J. Silicon-based arrayed waveguide gratings for WDM and spectroscopic analysis applications. Opt. Laser Technol. 2022, 147, 107656. [Google Scholar] [CrossRef]
- Zou, J.; Xia, X.; Chen, G.; Lang, T.; He, J.J. Birefringence compensated silicon nanowire arrayed waveguide grating for CWDM optical interconnects. Opt. Lett. 2014, 39, 1834–1837. [Google Scholar] [CrossRef]
- Zou, J.; Ma, X.; Xia, X.; Wang, C.; Zhang, M.; Hu, J.; Wang, X.; He, J.J. Novel wavelength multiplexer using (N + 1) × (N + 1) arrayed waveguide grating and polarization-combiner-rotator on SOI platform. J. Light. Technol. 2021, 39, 2431–2437. [Google Scholar] [CrossRef]
- Pathak, S.; Dumon, P.; Van Thourhout, D.; Bogaerts, W. Comparison of AWGs and echelle gratings for wavelength division multiplexing on silicon-on-insulator. IEEE Photonics J. 2014, 6, 1–9. [Google Scholar] [CrossRef]
- Ye, T.; Fu, Y.; Qiao, L.; Chu, T. Low-crosstalk Si arrayed waveguide grating with parabolic tapers. Opt. Express 2014, 22, 31899–31906. [Google Scholar] [CrossRef] [PubMed]
- Stanton, E.J.; Volet, N.; Bowers, J.E. Silicon arrayed waveguide gratings at 2.0-μm wavelength characterized with an on-chip resonator. Opt. Lett. 2018, 43, 1135–1138. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Bhat, S.; Tessema, N.; Kraemer, R.; Napoli, A.; Delrosso, G.; Calabretta, N. Ultrawide-band Low Polarization Sensitivity 3-μm SOI Arrayed Waveguide Gratings. J. Light. Technol. 2022, 40, 3432–3441. [Google Scholar] [CrossRef]
- Nair, R.R.; Blake, P.; Grigorenko, A.N.; Novoselov, K.S.; Booth, T.J.; Stauber, T.; Peres, N.M.; Geim, A.K. Fine structure constant defines visual transparency of graphene. Science 2008, 320, 1308. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Xing, Z.; Chen, X.; Cheng, Z.; Li, X.; Liu, T. Recent progress in waveguide-integrated graphene photonic devices for sensing and communication applications. Front. Phys. 2020, 8, 37. [Google Scholar] [CrossRef]
- Li, H.; Anugrah, Y.; Koester, S.J.; Li, M. Optical absorption in graphene integrated on silicon waveguides. Appl. Phys. Lett. 2012, 101, 111110. [Google Scholar] [CrossRef]
- Marini, A.; Cox, J.; De Abajo, F.G. Theory of graphene saturable absorption. Phys. Rev. B 2017, 95, 125408. [Google Scholar] [CrossRef]
- Liu, M.; Yin, X.; Ulin-Avila, E.; Geng, B.; Zentgraf, T.; Ju, L.; Wang, F.; Zhang, X. A graphene-based broadband optical modulator. Nature 2011, 474, 64–67. [Google Scholar] [CrossRef]
- Liu, M.; Yin, X.; Zhang, X. Double-layer graphene optical modulator. Nano Lett. 2012, 12, 1482–1485. [Google Scholar] [CrossRef] [PubMed]
- Luo, S.; Wang, Y.; Tong, X.; Wang, Z. Graphene-based optical modulators. Nanoscale Res. Lett. 2015, 10, 199. [Google Scholar] [CrossRef] [PubMed]
- Oya, M.; Kishikawa, H.; Goto, N.; Yanagiya, S.i. All-optical switch consisting of two-stage interferometers controlled by using saturable absorption of monolayer graphene. Opt. Express 2012, 20, 27322–27330. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Lv, J.; Lin, B.; Cao, Y.; Yi, Y.; Zhang, D. Graphene-assisted polymer waveguide optically controlled switch using first-order mode. Polymers 2021, 13, 2117. [Google Scholar] [CrossRef] [PubMed]
- Muntaha, S.T.; Hokkanen, A.; Harjanne, M.; Cherchi, M.; Suopajärvi, P.; Karvinen, P.; Pekkarinen, M.; Roussey, M.; Aalto, T. 3D Printed Lenses for Vertical Beam Collimation of Optical Phased Arrays. 3D Print. Addit. Manuf. 2023. ahead of Print. [Google Scholar] [CrossRef]
- Optiwave. OptiMode User’s Reference; Optiwave: Ottawa, ON, Canada, 2013; Volume 3.1. [Google Scholar]
- Optiwave. WDM Phasar Technical Background and Tutorials; Optiwave Systems Inc.: Ottawa, ON, Canada, 2000. [Google Scholar]
- Liu, L.; Dai, D.; Dainese, M.; Wosinski, L.; He, S. Compact arrayed waveguide grating demultiplexers based on amorphous silicon nanowires. In Proceedings of the Nanophotonics, Uncasville, CO, USA, 26–28 April 2006; Optica Publishing Group: Washington, DC, USA, 2006; p. NWB5. [Google Scholar]
- Przyrembel, G.; Kuhlow, B.; Solehmainen, K.; Aalto, T.; Heimala, P. Design and fabrication of arrayed waveguide grating multiplexers on silicon-on-insulator platforms. Opt. Eng. 2007, 46, 094602. [Google Scholar] [CrossRef]
- Cheben, P.; Schmid, J.; Delâge, A.; Densmore, A.; Janz, S.; Lamontagne, B.; Lapointe, J.; Post, E.; Waldron, P.; Xu, D.X. A high-resolution silicon-on-insulator arrayed waveguide grating microspectrometer with sub-micrometer aperture waveguides. Opt. Express 2007, 15, 2299–2306. [Google Scholar] [CrossRef] [PubMed]
- Li, K.; Yuan, P.; Lu, L.; Dong, M.; Zhu, L. PLC-based arrayed waveguide grating design for fiber Bragg grating interrogation system. Nanomaterials 2022, 12, 2938. [Google Scholar] [CrossRef]
- Multiphysics, C. Graphene Metamaterial Perfect Absorber; COMSOL: Stockholm, Sweden, 2022. [Google Scholar]
- Falkovsky, L.A. Optical properties of graphene. J. Phys. Conf. Ser. 2008, 129, 012004. [Google Scholar] [CrossRef]
- Teng, D.; Wang, K.; Li, Z. Graphene-coated nanowire waveguides and their applications. Nanomaterials 2020, 10, 229. [Google Scholar] [CrossRef]
- Deng, S.; Yetisen, A.K.; Jiang, K.; Butt, H. Computational modelling of a graphene Fresnel lens on different substrates. RSC Adv. 2014, 4, 30050–30058. [Google Scholar] [CrossRef]
- Bao, Q.; Zhang, H.; Ni, Z.; Wang, Y.; Polavarapu, L.; Shen, Z.; Xu, Q.H.; Tang, D.; Loh, K.P. Monolayer graphene as a saturable absorber in a mode-locked laser. Nano Res. 2011, 4, 297–307. [Google Scholar] [CrossRef]
- Takahashi, M.; Ueda, W.; Goto, N.; Yanagiya, S. Saturable absorption by vertically inserted or overlaid monolayer graphene in optical waveguide for all-optical switching circuit. IEEE Photonics J. 2013, 5, 6602109. [Google Scholar] [CrossRef]
- Vasquez, A.; Samolis, P.; Zeng, J.; Sander, M.Y. Micro-structuring, ablation, and defect generation in graphene with femtosecond pulses. OSA Contin. 2019, 2, 2925–2934. [Google Scholar] [CrossRef]

| Parameter | Notation | Value |
|---|---|---|
| Waveguide effective index | 3.08 | |
| Cladding effective index | 2.84 | |
| Number of array waveguides | N | 180 |
| Number of output waveguides | 32 | |
| Diffraction orders | m | 12 |
| Free spectral range | 150.00 nm | |
| Output waveguide separation | D | 4.00 μm |
| Array waveguide separation | 4.00 μm | |
| Free propagation region length | f | 3780.00 μm |
| Array waveguide length increment | 7.03 μm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tippinit, J.; Kuittinen, M.; Roussey, M. Hybrid Graphene–Silicon Arrayed Waveguide Gratings for On-Chip Signal–Frequency Conversion. Photonics 2024, 11, 302. https://doi.org/10.3390/photonics11040302
Tippinit J, Kuittinen M, Roussey M. Hybrid Graphene–Silicon Arrayed Waveguide Gratings for On-Chip Signal–Frequency Conversion. Photonics. 2024; 11(4):302. https://doi.org/10.3390/photonics11040302
Chicago/Turabian StyleTippinit, Janvit, Markku Kuittinen, and Matthieu Roussey. 2024. "Hybrid Graphene–Silicon Arrayed Waveguide Gratings for On-Chip Signal–Frequency Conversion" Photonics 11, no. 4: 302. https://doi.org/10.3390/photonics11040302
APA StyleTippinit, J., Kuittinen, M., & Roussey, M. (2024). Hybrid Graphene–Silicon Arrayed Waveguide Gratings for On-Chip Signal–Frequency Conversion. Photonics, 11(4), 302. https://doi.org/10.3390/photonics11040302





