Adaptive Optics Methods to Rat Eye Properties: Impact of Pupil Diameter on Wavefront Detection
Abstract
1. Introduction
2. Simulation
2.1. Rat Eye Model and Optical Simulation
2.2. Simulation Results
3. Wavefront Detection Experiments
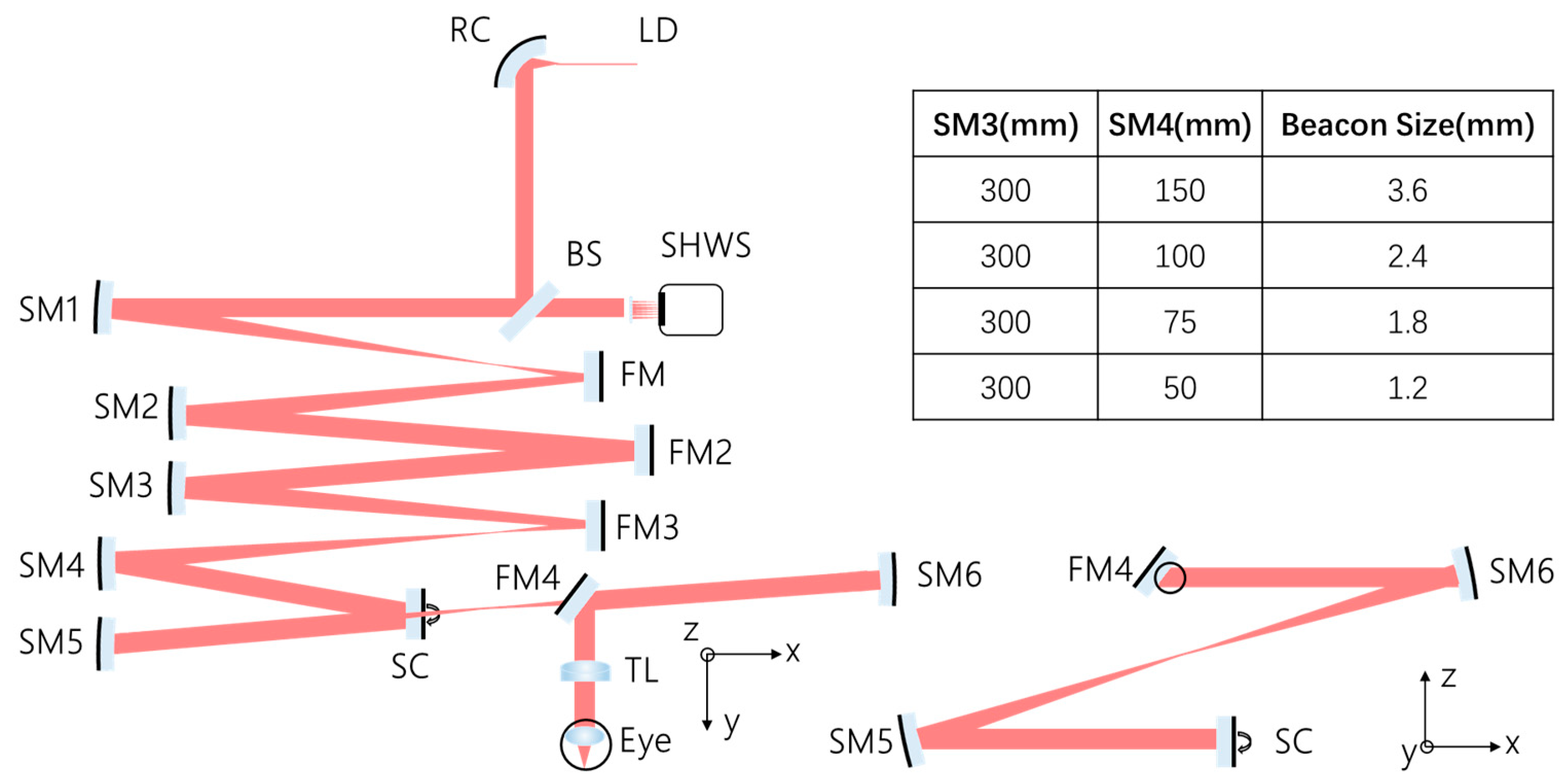
3.1. Optical System and Wavefront Detection
3.2. Animal Preparation
3.3. Wavefront Sensing and Aberration Analysis
4. Results
4.1. Wavefront Sensing
4.2. Zernike Coefficients
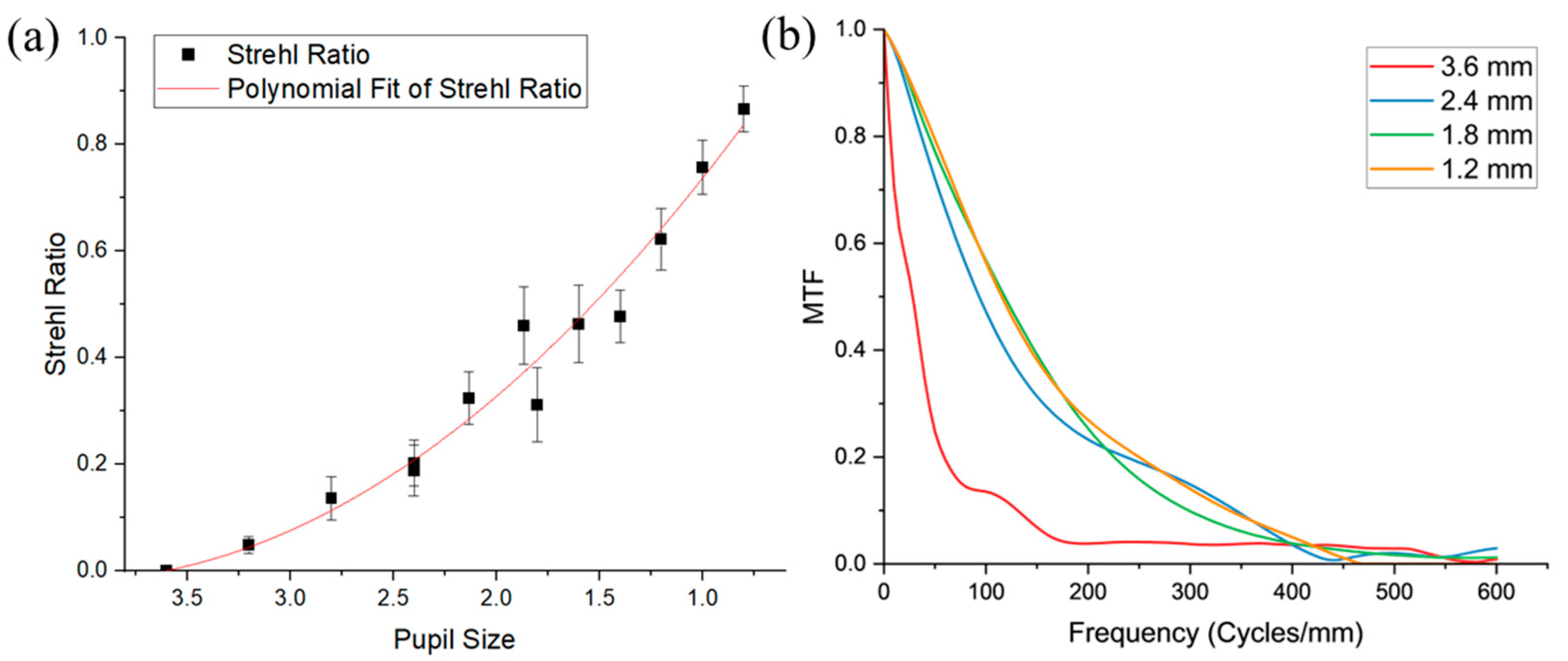
4.3. Strehl Ratio and Modulation Transfer Functions
5. Discussion
5.1. Simulation
5.2. Wavefront Detection
5.3. Comparison of Wavefront Measurement for the Human, Mouse, and Rat Eye
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Garcia-Valenzuela, E.; Shareef, S.; Walsh, J.; Sharma, S.C. Programmed Cell Death of Retinal Ganglion Cells during Experimental Glaucoma. Exp. Eye Res. 1995, 61, 33–44. [Google Scholar] [CrossRef] [PubMed]
- Medeiros, F.A.; Zangwill, L.M.; Bowd, C.; Vessani, R.M.; Susanna, R.; Weinreb, R.N. Evaluation of Retinal Nerve Fiber Layer, Optic Nerve Head, and Macular Thickness Measurements for Glaucoma Detection Using Optical Coherence Tomography. Am. J. Ophthalmol. 2005, 139, 44–55. [Google Scholar] [CrossRef] [PubMed]
- Berisha, F.; Feke, G.T.; Trempe, C.L.; McMeel, J.W.; Schepens, C.L. Retinal Abnormalities in Early Alzheimer’s Disease. Investig. Ophthalmol. Vis. Sci. 2007, 48, 2285. [Google Scholar] [CrossRef] [PubMed]
- Safi, H.; Safi, S.; Hafezi-Moghadam, A.; Ahmadieh, H. Early Detection of Diabetic Retinopathy. Surv. Ophthalmol. 2018, 63, 601–608. [Google Scholar] [CrossRef] [PubMed]
- Roorda, A. Applications of Adaptive Optics Scanning Laser Ophthalmoscopy. Optom. Vis. Sci. 2010, 87, 260–268. [Google Scholar] [CrossRef] [PubMed]
- Williams, D.R. Imaging Single Cells in the Living Retina. Vis. Res. 2011, 51, 1379–1396. [Google Scholar] [CrossRef] [PubMed]
- Roorda, A.; Duncan, J.L. Adaptive Optics Ophthalmoscopy. Annu. Rev. Vis. Sci. 2015, 1, 19–50. [Google Scholar] [CrossRef] [PubMed]
- Burns, S.A.; Elsner, A.E.; Sapoznik, K.A.; Warner, R.L.; Gast, T.J. Adaptive Optics Imaging of the Human Retina. Prog. Retin. Eye Res. 2019, 68, 1–30. [Google Scholar] [CrossRef] [PubMed]
- Akyol, E.; Hagag, A.M.; Sivaprasad, S.; Lotery, A.J. Adaptive Optics: Principles and Applications in Ophthalmology. Eye 2021, 35, 244–264. [Google Scholar] [CrossRef]
- Vorontsov, M.; Shmalgauzen, V. The Principles of Adaptive Optics; Moscow Izdatel Nauka: Moscow, Russia, 1985. [Google Scholar]
- He, Y.; Bao, M.; Chen, Y.; Ye, H.; Fan, J.; Shi, G. Accuracy Characterization of Shack–Hartmann Sensor with Residual Error Removal in Spherical Wavefront Calibration. Light Adv. Manuf. 2023, 4, 393–403. [Google Scholar] [CrossRef]
- Lu, J.; Li, H.; He, Y.; Shi, G.; Zhang, Y. Superresolution in Adaptive Optics Confocal Scanning Laser Ophthalmoscope. Acta Phys. Sin. 2011, 60, 34207. [Google Scholar] [CrossRef]
- Atas, M.C.D.; Landicho, L.M.T.; Lobo, A.D.; Orubia, C.J.L.; Silverio, A.C.O.; Aquino, A.U.; Amado, T.M.; Puno, J.C.V.; Quijano, J.F.C.; Arago, N.M. Development of Wavefront Sensor Using Shack-Hartmann Principle. In Proceedings of the 2019 IEEE 11th International Conference on Humanoid, Nanotechnology, Information Technology, Communication and Control, Environment, and Management (HNICEM), Laoag, Philippines, 29 November–1 December 2019; IEEE: Toulouse, France; pp. 1–5. [Google Scholar] [CrossRef]
- Liu, L.; Wu, Z.; Qi, M.; Li, Y.; Zhang, M.; Liao, D.; Gao, P. Application of Adaptive Optics in Ophthalmology. Photonics 2022, 9, 288. [Google Scholar] [CrossRef]
- Bird, M.; Kisilak, M.; Campbell, M. Optical Quality of the Rat Eye. Investig. Ophthalmol. Vis. Sci. 2007, 48, 2759. [Google Scholar]
- Zhou, X.; Bedggood, P.; Metha, A. Limitations to Adaptive Optics Image Quality in Rodent Eyes. Biomed. Opt. Express 2012, 3, 1811. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Geng, Y.; Greenberg, K.P.; Wolfe, R.; Gray, D.C.; Hunter, J.J.; Dubra, A.; Flannery, J.G.; Williams, D.R.; Porter, J. In Vivo Imaging of Microscopic Structures in the Rat Retina. Investig. Ophthalmol. Vis. Sci. 2009, 50, 5872. [Google Scholar] [CrossRef] [PubMed]
- Andrews, I. Wavefront Assessment and Correction of the Rat Eye for Two Photon Excitation Therapies. Master’s Thesis, University of Waterloo, Waterloo, ON, Canada, 2016. [Google Scholar]
- Jian, Y.; Xu, J.; Gradowski, M.A.; Bonora, S.; Zawadzki, R.J.; Sarunic, M.V. Wavefront Sensorless Adaptive Optics Optical Coherence Tomography for in Vivo Retinal Imaging in Mice. Biomed. Opt. Express 2014, 5, 547. [Google Scholar] [CrossRef] [PubMed]
- Wahl, D.J.; Jian, Y.; Bonora, S.; Zawadzki, R.J.; Sarunic, M.V. Wavefront Sensorless Adaptive Optics Fluorescence Biomicroscope for in Vivo Retinal Imaging in Mice. Biomed. Opt. Express 2016, 7, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Jayabalan, G.S.; Wu, Y.-K.; Bille, J.F.; Kim, S.; Mao, X.W.; Gimbel, H.V.; Rauser, M.E.; Fan, J.T. In Vivo Two-Photon Imaging of Retina in Rabbits and Rats. Exp. Eye Res. 2018, 166, 40–48. [Google Scholar] [CrossRef] [PubMed]
- Glickstein, M.; Millodot, M. Retinoscopy and Eye Size. Science 1970, 168, 605–606. [Google Scholar] [CrossRef] [PubMed]
- Geng, Y.; Schery, L.A.; Sharma, R.; Dubra, A.; Ahmad, K.; Libby, R.T.; Williams, D.R. Optical Properties of the Mouse Eye. Biomed. Opt. Express 2011, 2, 717. [Google Scholar] [CrossRef]
- Chaudhuri, A.; Hallett, P.E.; Parker, J.A. Aspheric Curvatures, Refractive Indices and Chromatic Aberration for the Rat Eye. Vis. Res. 1983, 23, 1351–1363. [Google Scholar] [CrossRef] [PubMed]
- Campbell, M.C.W.; Hughes, A. An Analytic, Gradient Index Schematic Lens and Eye for the Rat Which Predicts Aberrations for Finite Pupils. Vis. Res. 1981, 21, 1129–1148. [Google Scholar] [CrossRef] [PubMed]
- Delori, F.C.; Webb, R.H.; Sliney, D.H. Maximum Permissible Exposures for Ocular Safety (ANSI 2000), with Emphasis on Ophthalmic Devices. J. Opt. Soc. Am. A 2007, 24, 1250. [Google Scholar] [CrossRef] [PubMed]
- Thibos, L.N.; Applegate, R.A.; Schwiegerling, J.T.; Webb, R. Standards for Reporting the Optical Aberrations of Eyes. J. Refract. Surg. 2002, 18, S652–S660. [Google Scholar] [CrossRef] [PubMed]
- Liang, J.; Grimm, B.; Goelz, S.; Bille, J.F. Objective Measurement of Wave Aberrations of the Human Eye with the Use of a Hartmann–Shack Wave-Front Sensor. J. Opt. Soc. Am. A 1994, 11, 1949. [Google Scholar] [CrossRef]



| Surface | n (@735 nm) | Radius of Curvature (mm) | Thickness (mm) | Conic Constant |
|---|---|---|---|---|
| Ant cornea | −2.965 | 0.796 | ||
| 1.3776 | 0.26 | |||
| Post cornea | −2.705 | 0.407 | ||
| 1.3303 | 0.62 | |||
| Ant lens | −2.34 | 0.181 | ||
| Core lens | 1.486 (n0 in Equation (1)) | 3.71 | ||
| Post lens | 2.34 | 0.268 | ||
| 1.3302 | 1.39 | |||
| ILM | 3.624 | |||
| 0.17 | ||||
| OLM | 1.3302 | 3.624 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kong, W.; Huang, J.; He, Y.; Shi, G. Adaptive Optics Methods to Rat Eye Properties: Impact of Pupil Diameter on Wavefront Detection. Photonics 2024, 11, 359. https://doi.org/10.3390/photonics11040359
Kong W, Huang J, He Y, Shi G. Adaptive Optics Methods to Rat Eye Properties: Impact of Pupil Diameter on Wavefront Detection. Photonics. 2024; 11(4):359. https://doi.org/10.3390/photonics11040359
Chicago/Turabian StyleKong, Wen, Jiangjie Huang, Yi He, and Guohua Shi. 2024. "Adaptive Optics Methods to Rat Eye Properties: Impact of Pupil Diameter on Wavefront Detection" Photonics 11, no. 4: 359. https://doi.org/10.3390/photonics11040359
APA StyleKong, W., Huang, J., He, Y., & Shi, G. (2024). Adaptive Optics Methods to Rat Eye Properties: Impact of Pupil Diameter on Wavefront Detection. Photonics, 11(4), 359. https://doi.org/10.3390/photonics11040359





