Synergy between AI and Optical Metasurfaces: A Critical Overview of Recent Advances

Abstract

The interplay between two paradigms, artificial intelligence (AI) and optical metasurfaces, nowadays appears obvious and unavoidable. AI is permeating literally all facets of human activity, from science and arts to everyday life. On the other hand, optical metasurfaces offer diverse and sophisticated multifunctionalities, many of which appeared impossible only a short time ago. The use of AI for optimization is a general approach that has become ubiquitous. However, here we are witnessing a two-way process—AI is improving metasurfaces but some metasurfaces are also improving AI. AI helps design, analyze and utilize metasurfaces, while metasurfaces ensure the creation of all-optical AI chips. This ensures positive feedback where each of the two enhances the other one: this may well be a revolution in the making. A vast number of publications already cover either the first or the second direction; only a modest number includes both. This is an attempt to make a reader-friendly critical overview of this emerging synergy. It first succinctly reviews the research trends, stressing the most recent findings. Then, it considers possible future developments and challenges. The author hopes that this broad interdisciplinary overview will be useful both to dedicated experts and a general scholarly audience.

1. Introduction

Nowadays, there is probably no literate person who has not at least heard about artificial intelligence (AI) [1,2,3]. With the number of its practical applications steadily rising, many people have already been in contact with at least some form of AI—be it in a modern smartphone with built-in AI chips [4,5], the Internet [6] and Internet of Things [7], public services [8], or even domestic appliances in smart homes [9]. Generative AI already has natural conversations with people [10] and generates art (paints and draws pictures or generates them in a photorealistic 3D manner, composes music, writes fiction, creates animations or concept art, etc.) [11]. Other kinds of AI perform different optimizations, including those of design and production of goods, telecommunications [12] and traffic [13], sensing [14], aerospace [15] but also basically all branches of engineering [16,17,18], industry [19], customer services [20], banking and finance [21] including the stock market [22], but also cryptocurrencies and blockchain technology [23], education [24], robotics [25], military [26] and, obviously, scientific research [27]. It appears that practically no area of humanity is left entirely without AI. The range is extremely wide and expanding at a furious and ever accelerating pace. Its significance is becoming overwhelming and cannot be overestimated.

Even those who are not really aware what AI actually is often have very strong opinions either for or, quite often, against it and even, although relatively rarely, with a balanced approach [11]. While prejudices and partialities do not have (and must not have) anything in common with science, ethical questions do have [28] and the appearance of both, as well as the related controversies, show the depth to which AI has already penetrated our lives—with strong potentials to drastically increase that role in future. A new information revolution is not coming—whether we are ready or not, it is already here, all set to change almost every facet of our lives.

Another paradigm with direct and important connections with AI is photonics, more specifically metaphotonics [29,30,31,32,33], which deals with all-optical structures and devices with their properties exceeding the natural ones, and which, albeit basically in its infancy, already manages to extend far beyond the conventional optics. The lion’s share of metaphotonics belongs to metasurfaces, ultrathin (quasi-2D) optical structures that in a majority of cases are fully compatible with the planar fabrication technologies used in conventional microelectronics.

Metasurfaces are applicable in a large number of practical areas, including displays, sensors and detectors technologies, and many other state-of-the art devices and systems that find their usability in optical telecommunications, medicine, homeland security, power industry and many other fields of fundamental importance. Contrary to AI, which is a buzzword known to practically everyone, metasurfaces and metaphotonics generally are mostly known to experts only, their usefulness nevertheless stretching far beyond their almost non-existent popularity among average citizens. They also exhibit strongly disruptive potentials and may bring about revolutionary changes in communication technologies, computing, general data management and processing, and many other fields—after all, they do promise all-optical circuitry with speeds approaching that of light in an optical medium (i.e., frequencies in the order of hundreds of terahertz), far exceeding those met in modern microelectronics, all the while requiring a fraction of the existing power consumption and, in spite of some beliefs even spread among some experts, offering a packaging density at nanoscale, comparable to the modern VLSI [34]. They have the potential to deliver us computers and communications vastly superior and orders of magnitude faster compared to those produced today.

The metaphotonic components are already being designed, optimized, produced and even applied utilizing AI. Such a situation has been expectable and, in a way, unavoidable from both scientific and engineering points of view. A disruptive technology such as AI has already improved so many different areas, including our everyday lives. Why would it not be used to improve another disruptive technology?

What sets the AI–metasurface relation apart from numerous other areas is that their connection goes both ways. AI is indeed used to make metasurfaces better but some metasurfaces are used to make some types of AI better. Thus, these two fields are in a quite peculiar kind of synergy since there is two-way feedback between them. Metasurfaces that simultaneously represent AI chips are already produced, and there is a potential to use the existing feedback between the two to iteratively and actively improve both simultaneously. Thus, the result is merging the multifunctionalities of artificial metamaterials with artificial intelligence [35]. This text is dedicated to the state of the art of the two paradigms and to the existing synergy between them. It attempts at the same time to offer some critical observations, to clarify some less than unambiguous terms that often end up getting mixed up and even to speculate about some possible further directions.

The manuscript is organized as follows. After mentioning the broad context of the topic and stressing its importance in Section 1, the definitions and classifications pertinent to the field of metasurfaces are given and some of the most important classes of those structures and their building blocks are broadly overviewed in Section 2. Artificial intelligence for metaphotonics is overviewed in Section 3. After introductory remarks, the methods of direct design including surrogate modeling and simulation are considered in that part of the text. Section 4 considers the opposite direction of enhancement and deals with metasurface-based AI structures and methods that go toward implementing photonics-based AI hardware in the form of metasurfaces. Section 5 gives a short discussion of potential benefits but at the same time the related challenges, as well as a very broad outlook over possible future research directions, while Section 6 offers a speculative consideration of some possible new structures whose implementation would further strengthen the existing AI–metasurface synergy. Section 7 outlines some of the existing safety concerns and possible ethical questions. Section 8 concludes the text, presenting its main contributions in some detail. Figure 1 shows a simplified schematic presentation of the utilized methodology and some of the main contributions of this treatise.

This treatise is dedicated to a strongly multidisciplinary and very wide field. Thus, when writing it, one of the goals was to keep the text friendly and comprehensible to as wide an audience as possible at different levels of expertise and within different disciplines. In other words, the text attempts to obey the famous Simplicity Principle often attributed to Einstein that “Everything should be made as simple as possible, but not simpler.” To that end, efforts have been made to use here style and language as clear and accessible as possible, while not sacrificing scientific accuracy, width and precision. Hopefully, this manuscript, regarded within the vast body of the existing literature, can assure a reader-friendly approach while still enabling readers to stay updated with the most recent developments and possible future directions.

2. Metasurfaces and Metaphotonics

2.1. Introduction: From Optical Metamaterials to Metasurfaces and General Metaphotonics

Officially, negative refractive index metamaterials have been first theoretically proposed in electromagnetics as early as in 1967, when Victor Veselago published his paper on artificial structures that can simultaneously have negative values of relative dielectric permittivity and of relative magnetic permeability, and concluded that such materials would have an effective refractive index below zero [36]. However, the concepts related to negative refraction had actually appeared much earlier, as early as in 1944, when a textbook by L.I. Mandelshtam was published describing backward propagation of waves and negative refraction [37].

For some time, materials with negative refraction were denoted as left-handed materials (LHMs), but this term has since been abandoned because it brought confusion regarding the terminology related to chiral materials that has been in standard use in chemistry since Lord Kelvin introduced the term “chirality” in 1894 (the left-handedness and right-handedness of molecules were observed even earlier, in 1812), i.e., long before negative index materials were even discovered. The most often used term today is negative refractive index metamaterials (NRMs), closely followed by double negative materials (DNGs).

For a few decades, Veselago’s paper was a theoretical curiosity until John Pendry proposed in 1999 practical structures that enabled experimental fabrication of NRMs [38]. The first experimental NRM structures were fabricated in 2001 for the microwave range [39]. Further works led to the observation of different unexpected and often counter-intuitive properties of NRMs. The wavevector and Poynting vector are antiparallel in NRMs, the Doppler effect and Snell’s law are reversed (the latter means that a light beam impingent at the interface between two materials, one of them with positive refractive index and the other with negative, will refract under the same side it came from), Čerenkov radiation and the Doppler shift are reversed in NRM, the Goos–Hänchen shift is negative for reflection from NRM. There are many more such phenomena [40].

The explosive growth of research dedicated to metamaterials soon resulted in two generalizations. The first one was related to their electromagnetic properties, since it has been observed that the effective refractive index (and actually the permittivity and permeability) can be tailored to reach any desired value, not only negative. Thus, metamaterials with extremely high [41] and extremely low (near-zero) [42] refractive index were produced, as well as those with extreme values of permittivity or permeability (e.g., [43]). The next step was a generalization of metamaterials to any structures that ensure the engineering of their effective properties and support propagation of some kind of waves. Thus, a path to acoustic metamaterials has been paved [44]. Other useful newly introduced classes were thermal metamaterials [45,46] that control heat flow and mechanical metamaterials [47,48,49] enabling the design of structures with mechanical properties exceeding the natural ones. A currently valid general definition of a metamaterial is that it represents an artificial structure with subwavelength functional building blocks (meta-atoms) tailored to have one or more effective properties that are seldom or never observed in nature.

Since the electromagnetic metamaterial conceptualization, there have been different practical problems related to them. In their general 3D form they are extremely difficult to manufacture, especially for shorter wavelengths, and they suffer heavy absorption losses. The problems have been the most difficult in the optical range, where the wavelengths are the shortest. A solution was to make metamaterials ultrathin (with deeply subwavelength thickness), i.e., planar, and to build their meta-atoms on such a flat surface. When introduced, such 2D metamaterials were first termed metafilms [50] and then metasurfaces [51].

Besides their obvious organic interweaving with general metamaterials, the roots of metasurfaces can be traced back to several fields. Among others, these include computer-generated surface holograms in optics and frequently selective surfaces in microwave and antenna theory [52].

2.1.1. Some Properties of Optical Metasurfaces

Optical metasurfaces [53,54] are defined here as artificial ultrathin (quasi-2D) planar structures with ordered, quasi-ordered or disordered subwavelength patterns of building blocks (the so-called meta-atoms) strongly interacting with incoming visible, ultraviolet or infrared radiation in different manners, while strongly modifying it.

The introduction of practical metasurfaces had an additional benefit in that it made their fabrication compatible with the planar technologies routinely used in microelectronics and microelectromechanical systems (MEMSs). At the same time, this approach ensured significantly lower optical absorption losses since the structure thickness has been minimized; thus, the optical paths have become vastly shorter. Such architecture nevertheless ensured extremely strong light–matter interaction, both in transmissive and reflective mode. Additional advantages of metasurfaces are their advanced integrability and low insertion losses. A decisive step in the development of metasurfaces has been made when the seminal paper by Yu et al. appeared [55], dedicated to generalized laws of reflection and refraction in optical metasurfaces derived from Fermat’s principle. It proved the possibility of obtaining abrupt instead of the usual gradual phase changes. The distance along the lateral direction of metasurfaces needed for such changes was in the order of a single wavelength. This discovery has had profound consequences since the phase discontinuities it introduced ensured great flexibility in optical beam steering, shaping and focusing, and thus resulted in a vast number of novel possible practical uses. This quickly brought the rapid subsequent development of the field of metasurface theory and applications.

As far as materials for metasurfaces are concerned, one can choose for their plasmonic parts conductors based on free electrons, e.g., noble metals (most usual gold and silver), aluminum, different alloys including alkali–noble intermetallic compounds, transparent conductive oxides like ITO (indium tin oxide), AZO (aluminum-zinc-oxide), GZO (gallium-zinc-oxide), some 2D materials like graphene or MXenes, etc. [56,57]. Conductive meta-atoms behave as 2D arrays of nanoantennas, i.e., they represent resonant electric dipoles ensuring a strong optical response. However, their overall absorption losses remain quite high, in spite of the minuscule depth of the metasurfaces.

Another approach is to use all-dielectric meta-atoms with resonant electric and magnetic dipoles, which also ensures a strong response but keeps losses low. To this end, high relative dielectric permittivity dielectrics are used. Convenient for this role are semiconductors which in this case are approximately regarded as lossless dielectrics with a high real part of the refractive index, since their absorption losses are low due to an extremely short optical path at nanoscale, in spite of the imaginary part of their refractive index being far from negligible.

In some types of metasurfaces, special functional materials are used, not because of their values of refractive index and their role in the basic optical functionalities of the structures themselves, but because of their ability to impart specific additional properties to metasurfaces. This is the case with, e.g., nonlinear optical materials, quantum structures, phase-change materials, etc.

Table 1. Summary of different materials used to obtain metasurfaces with specific properties.

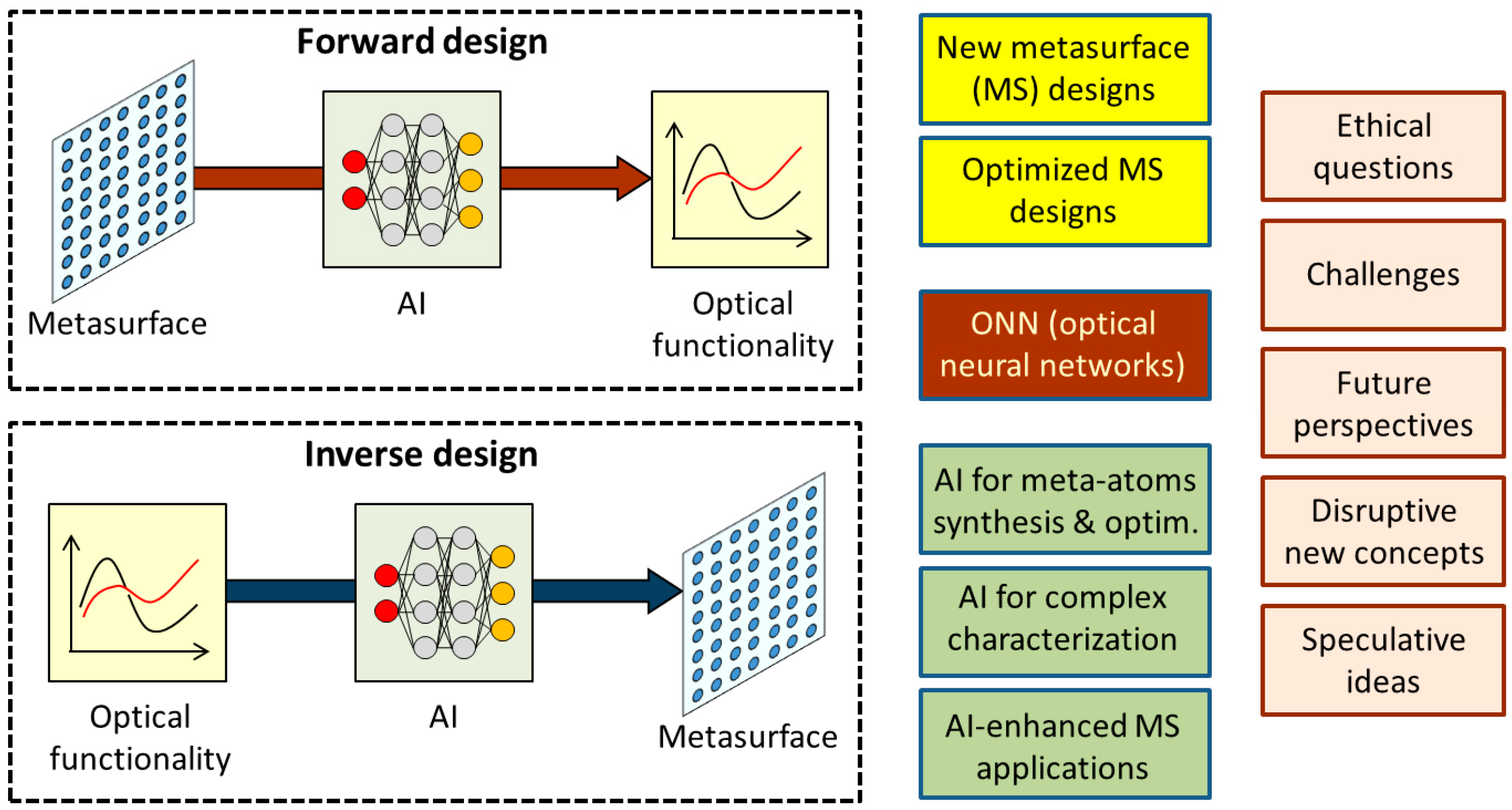
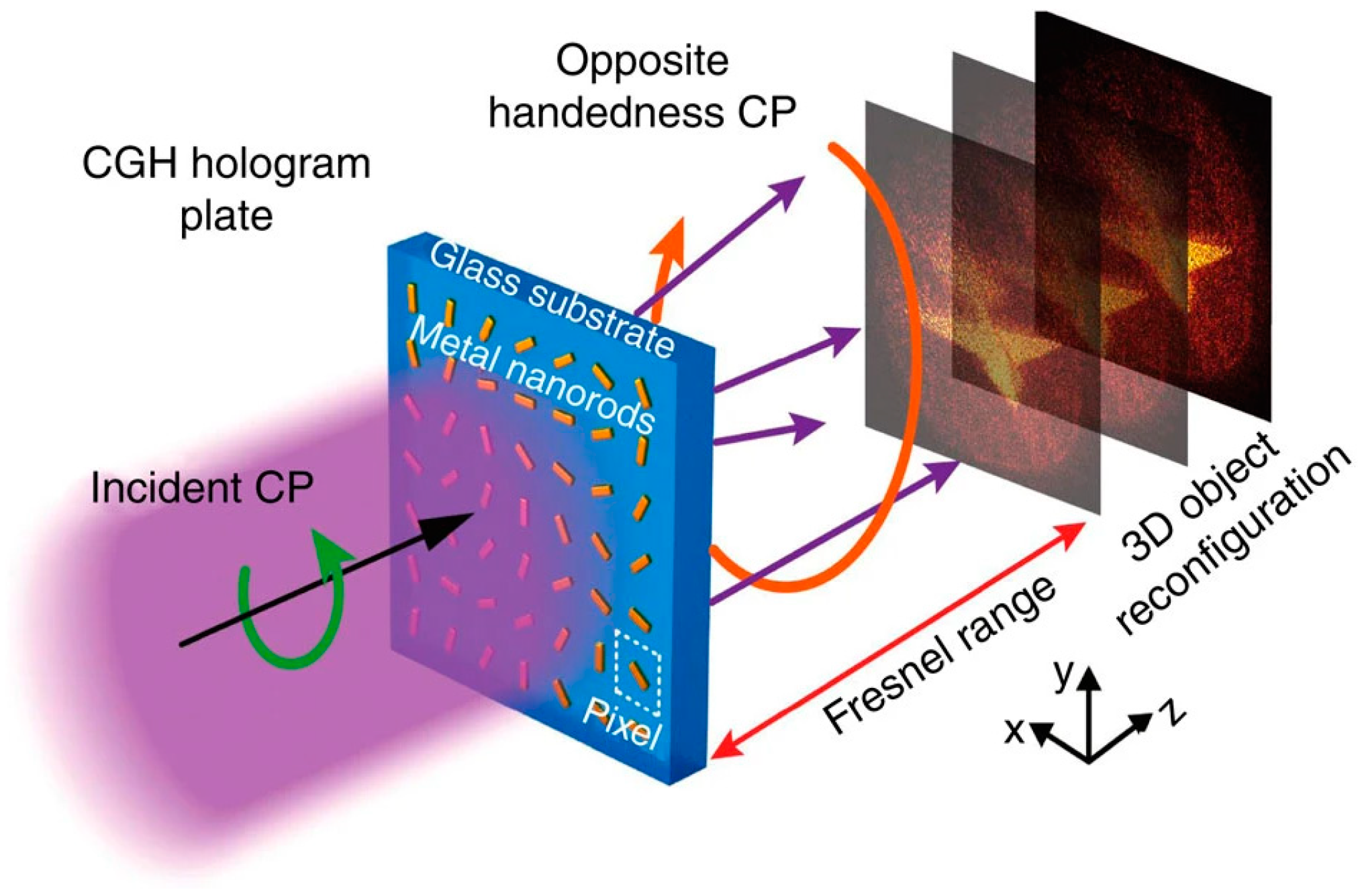
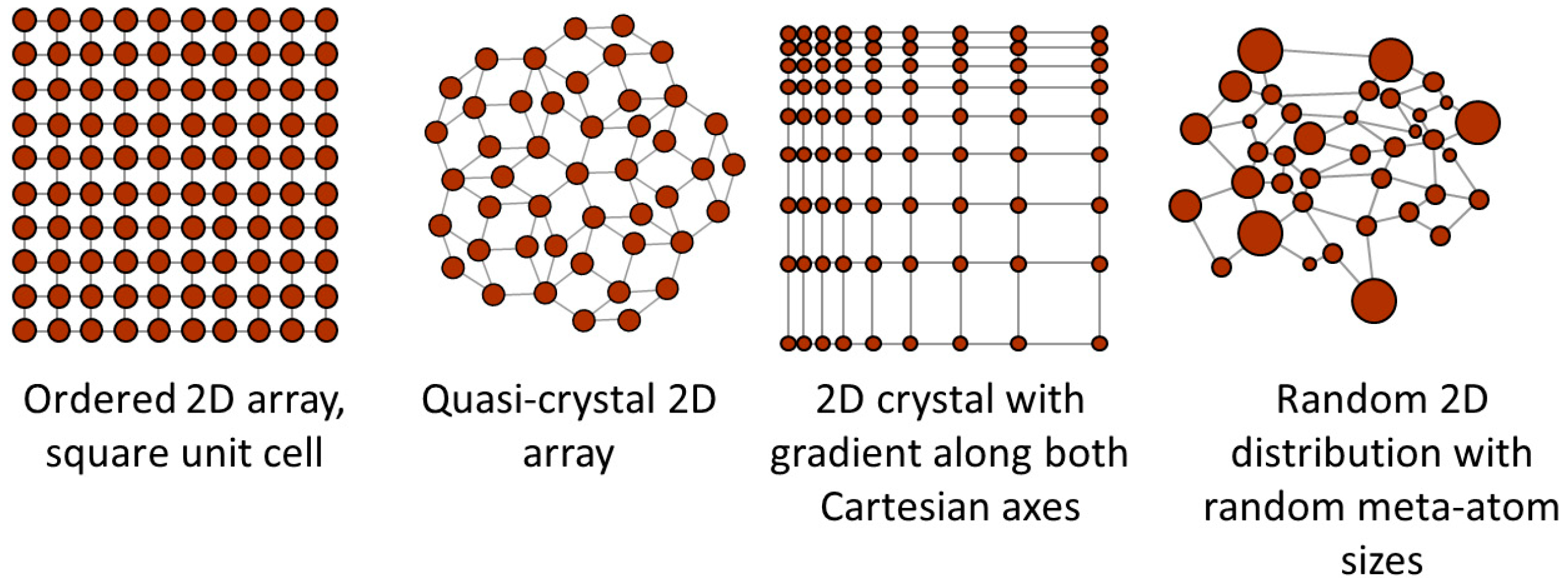
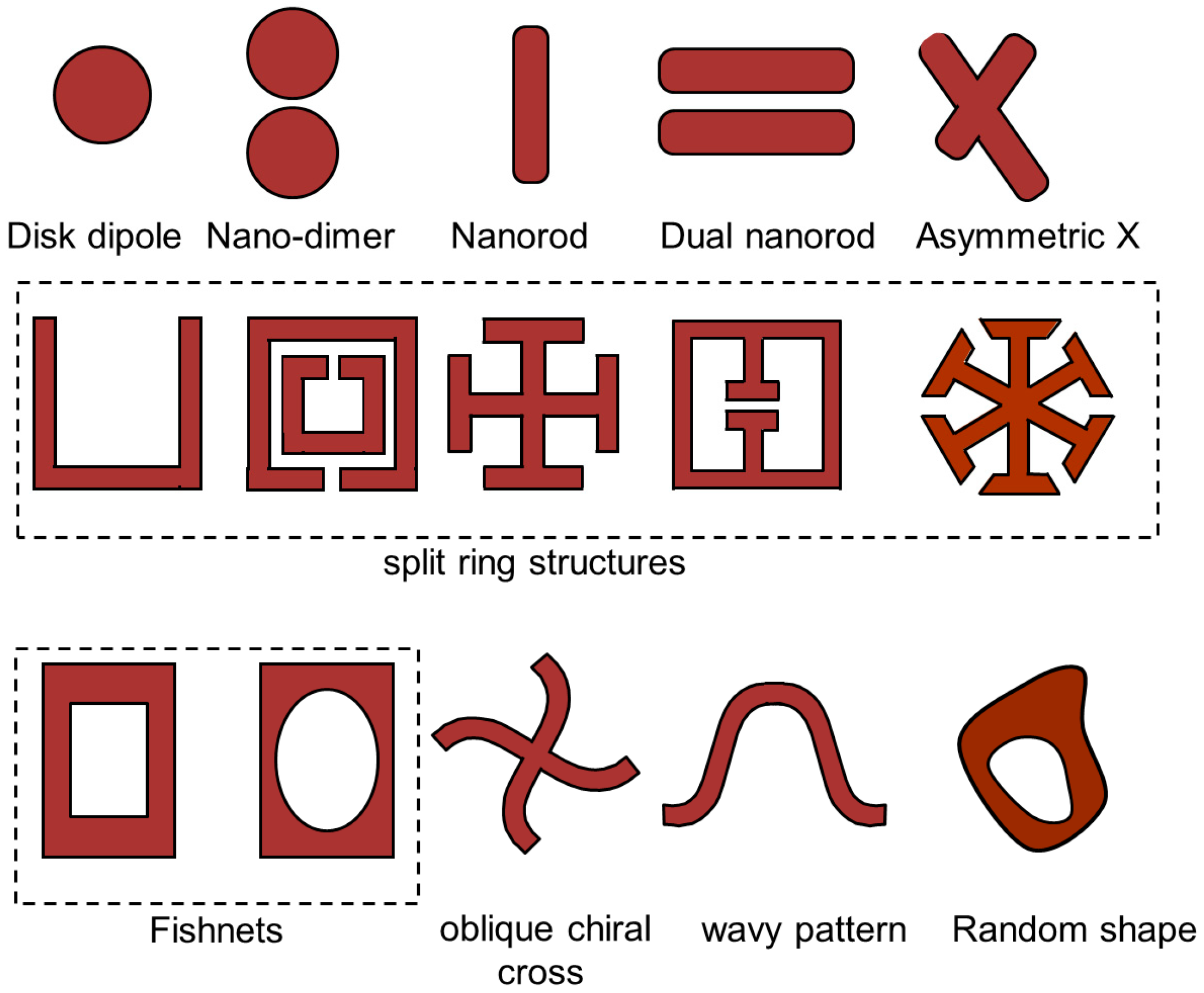
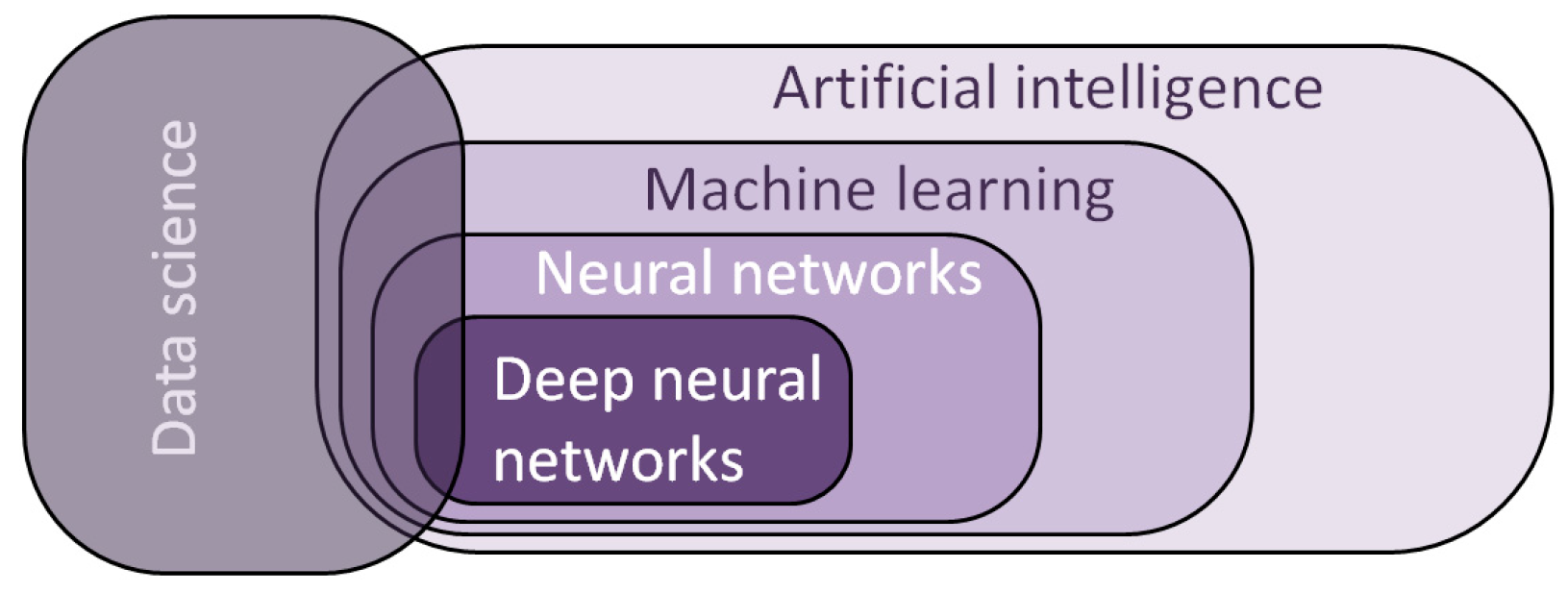
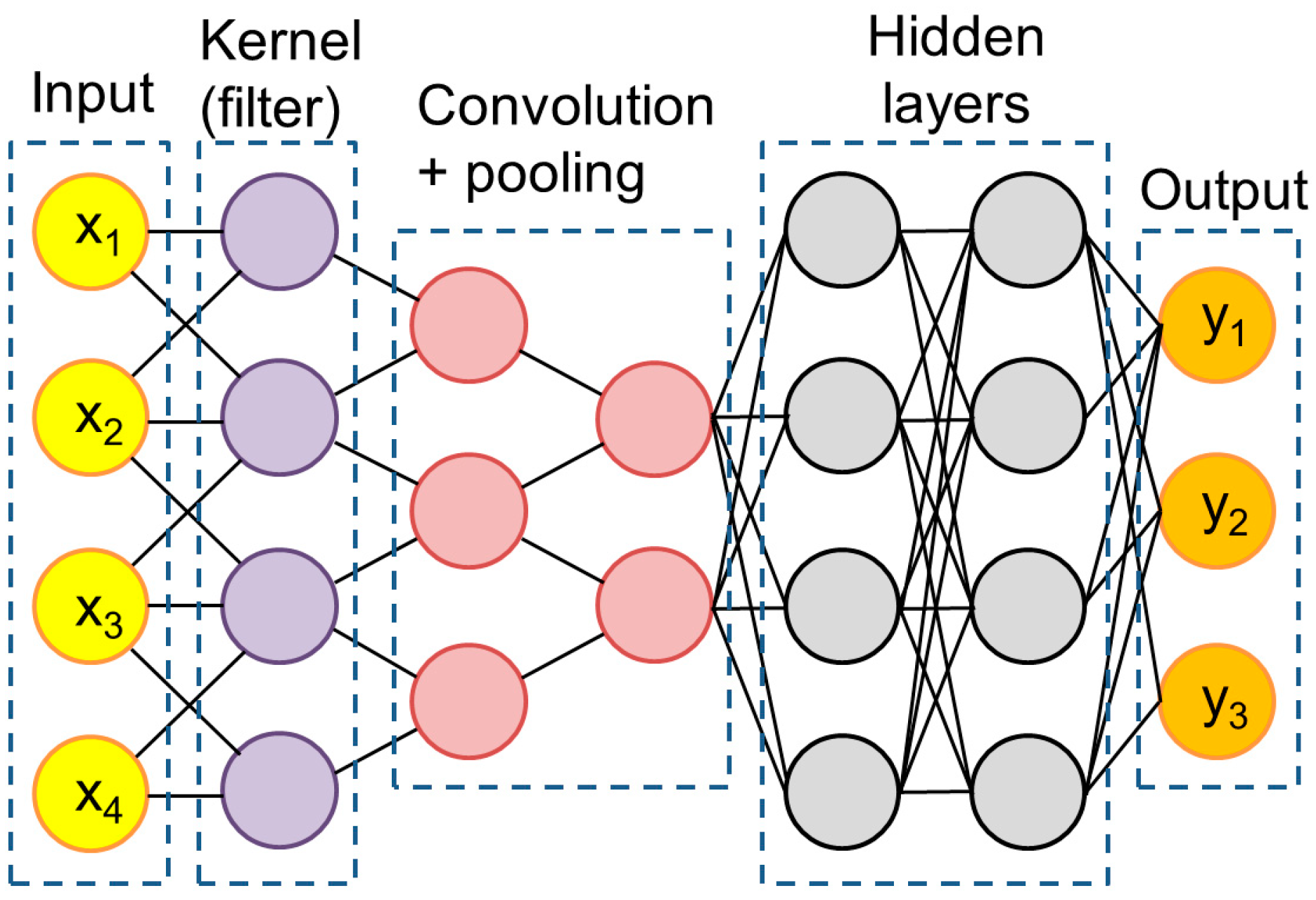
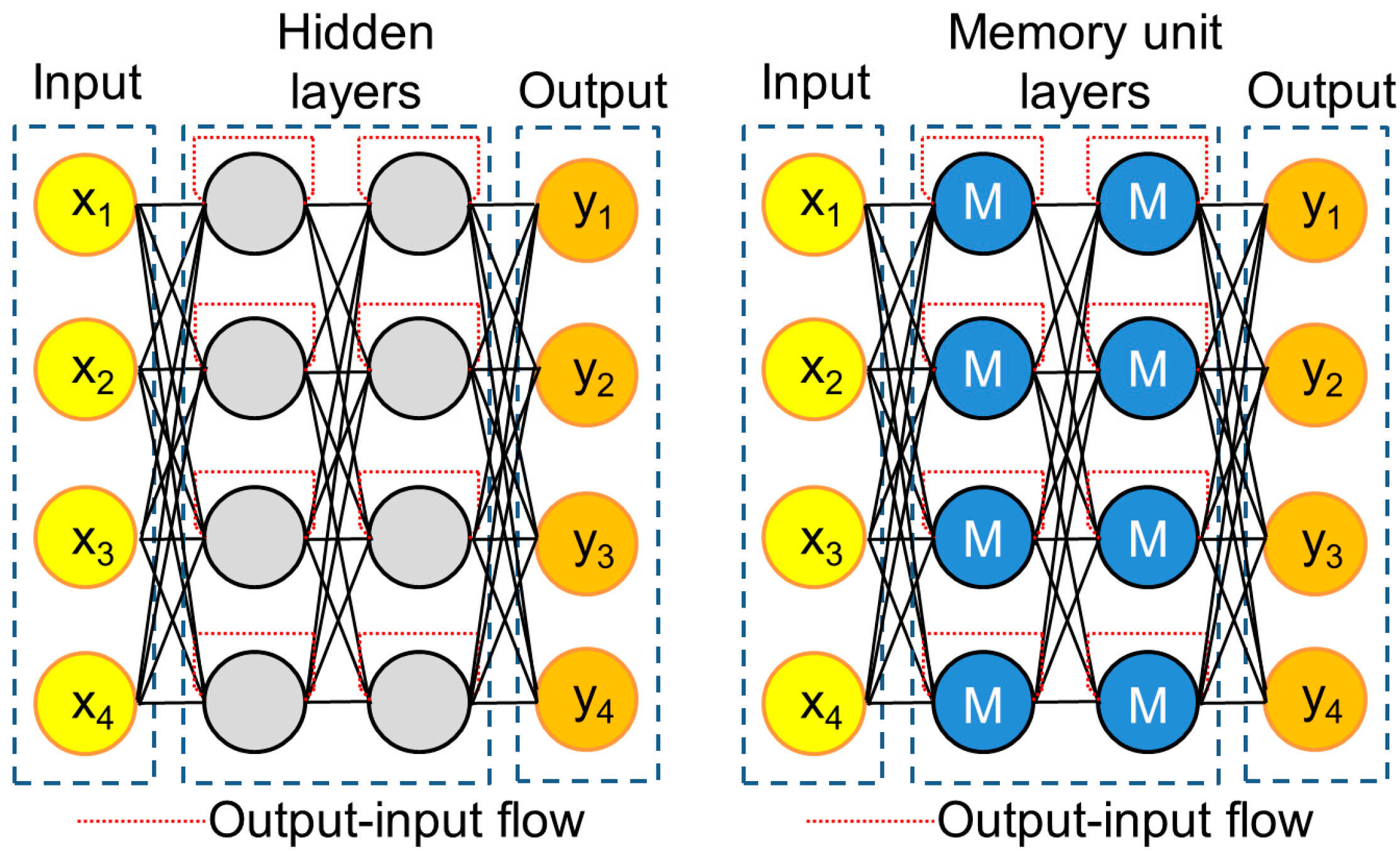
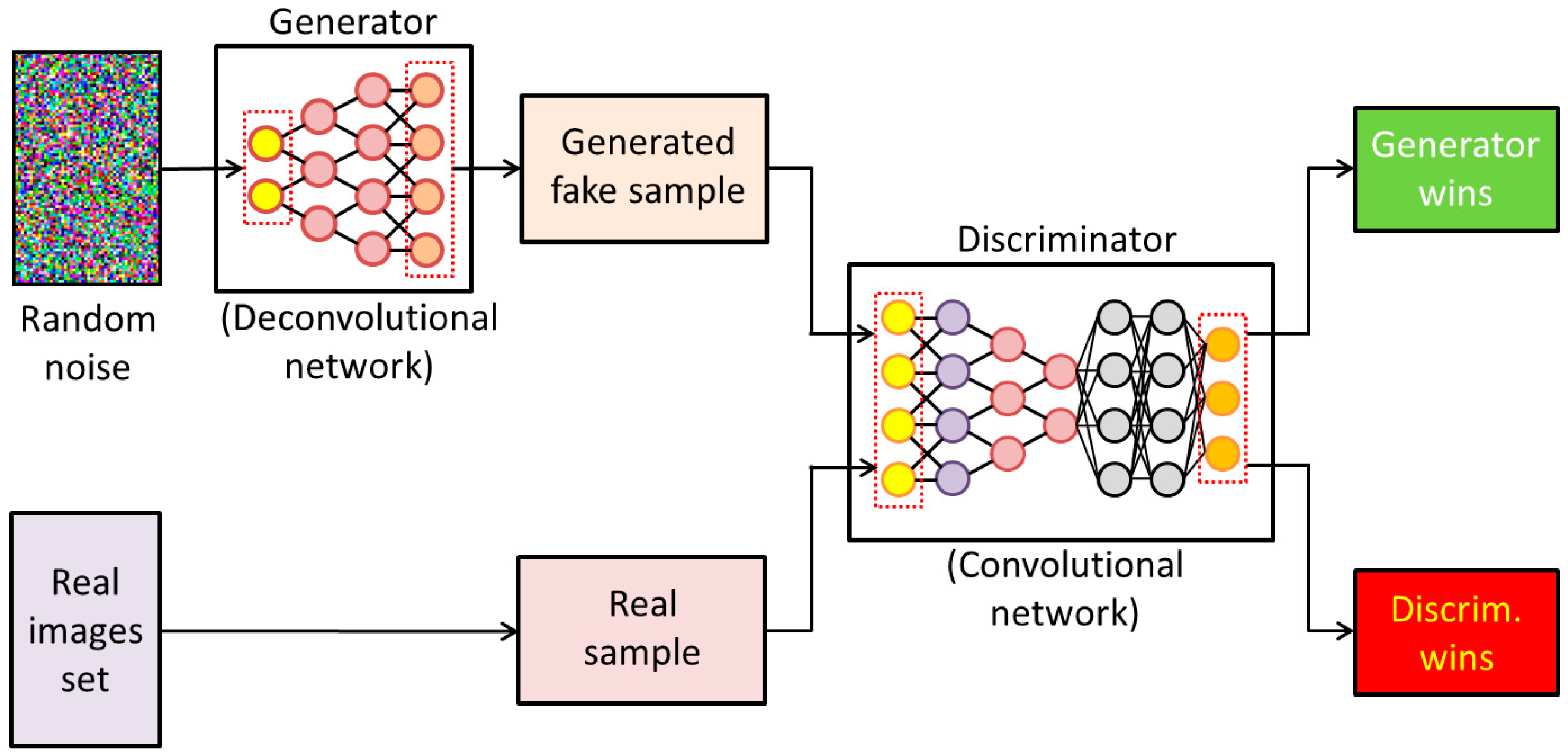
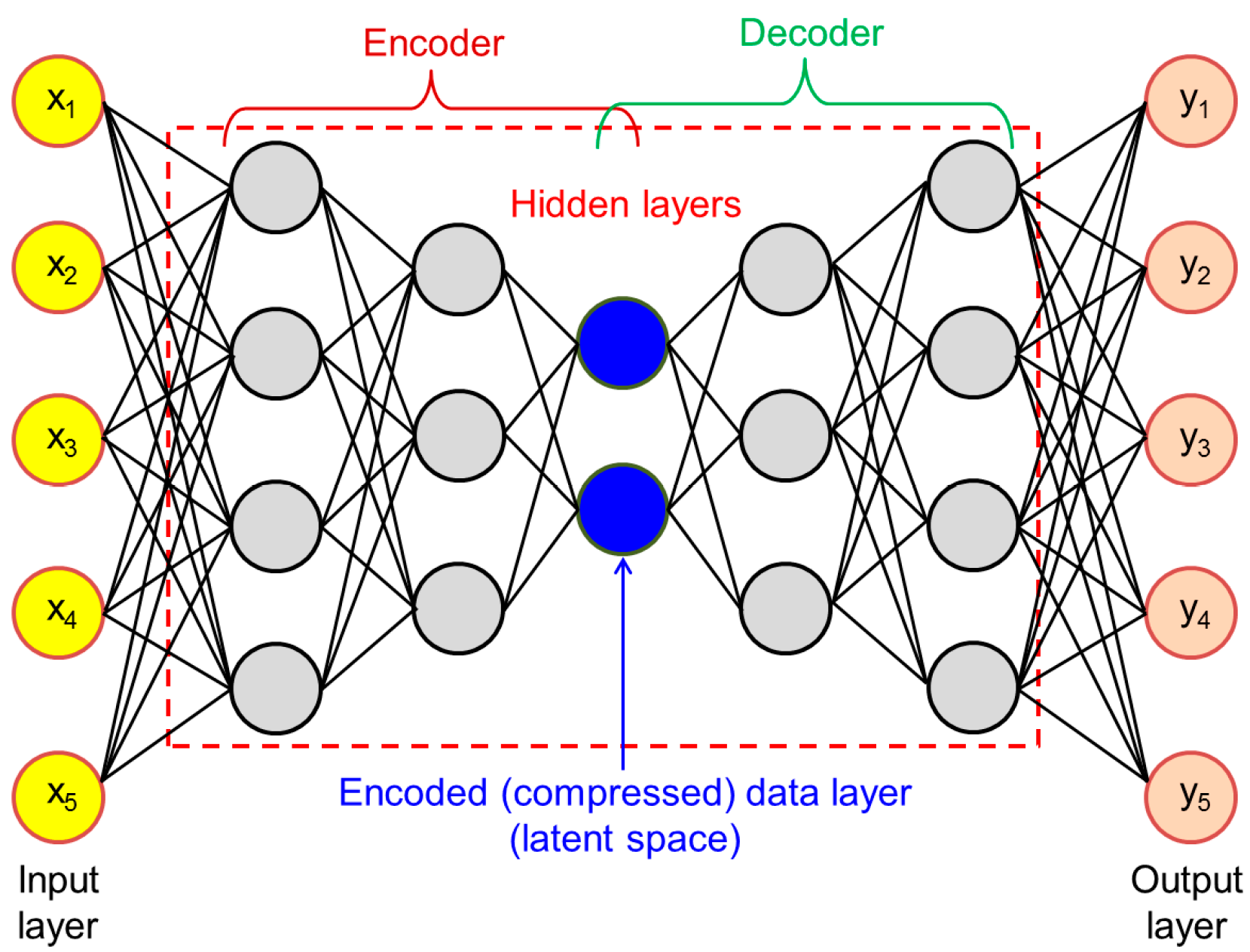
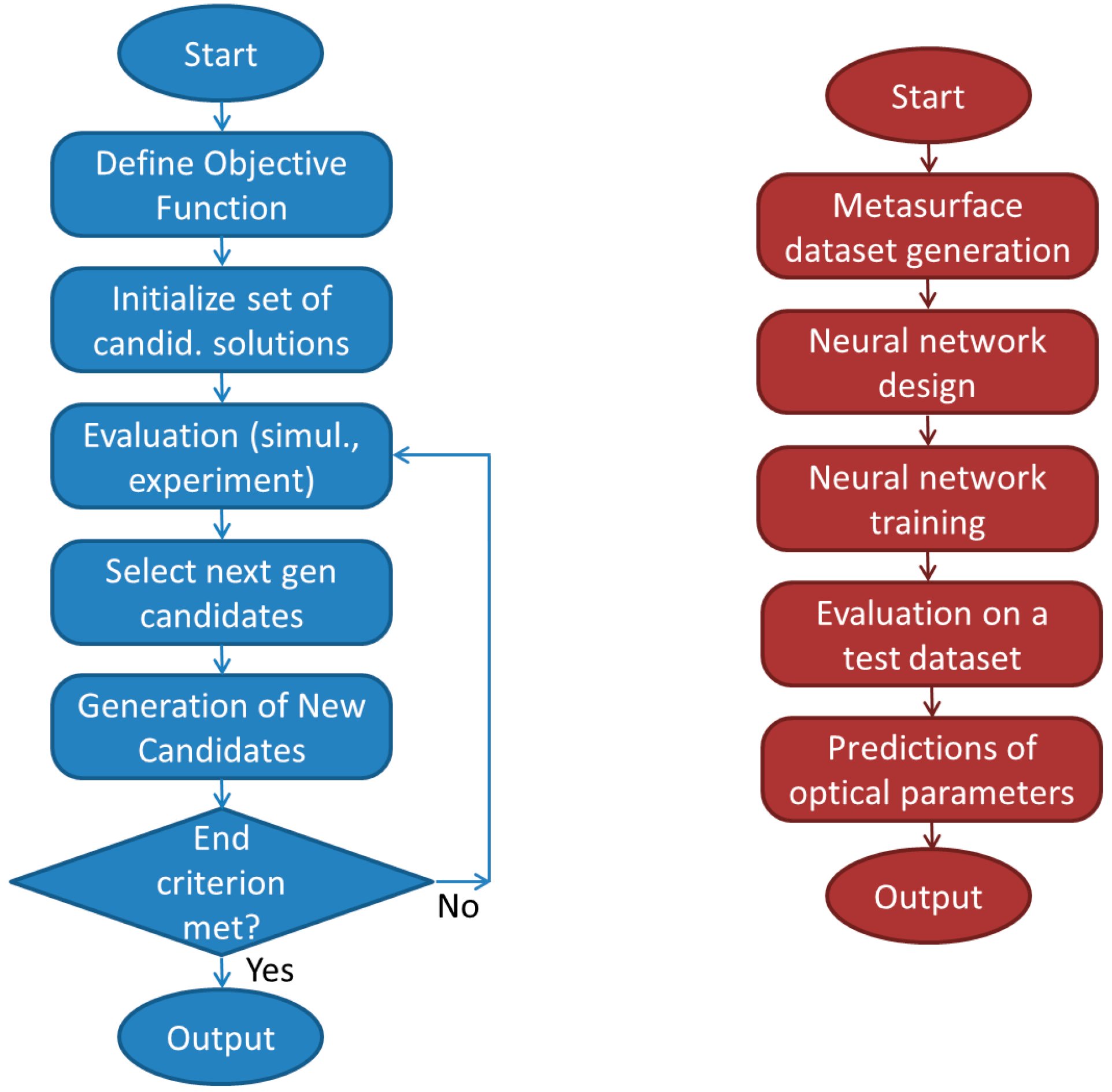
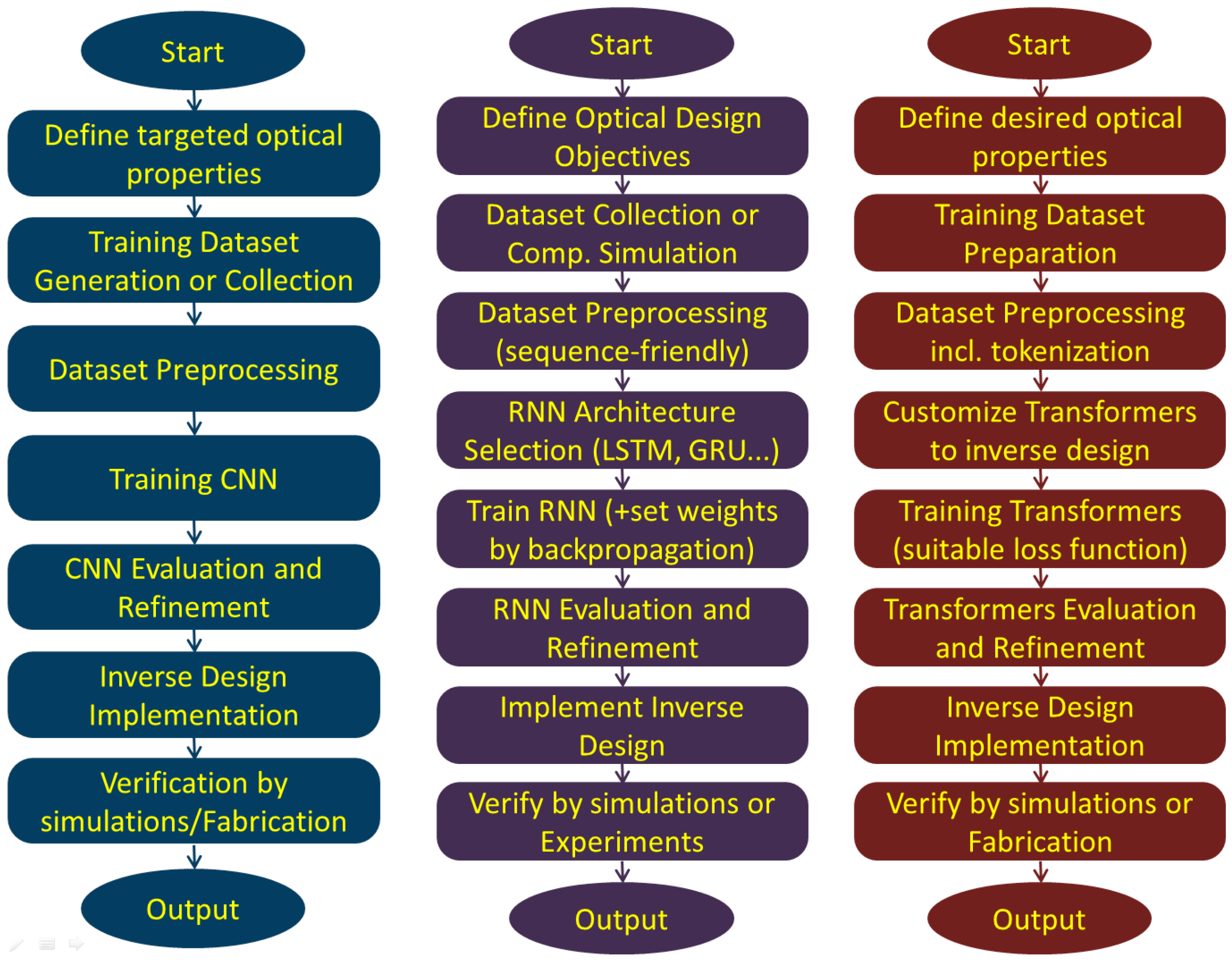
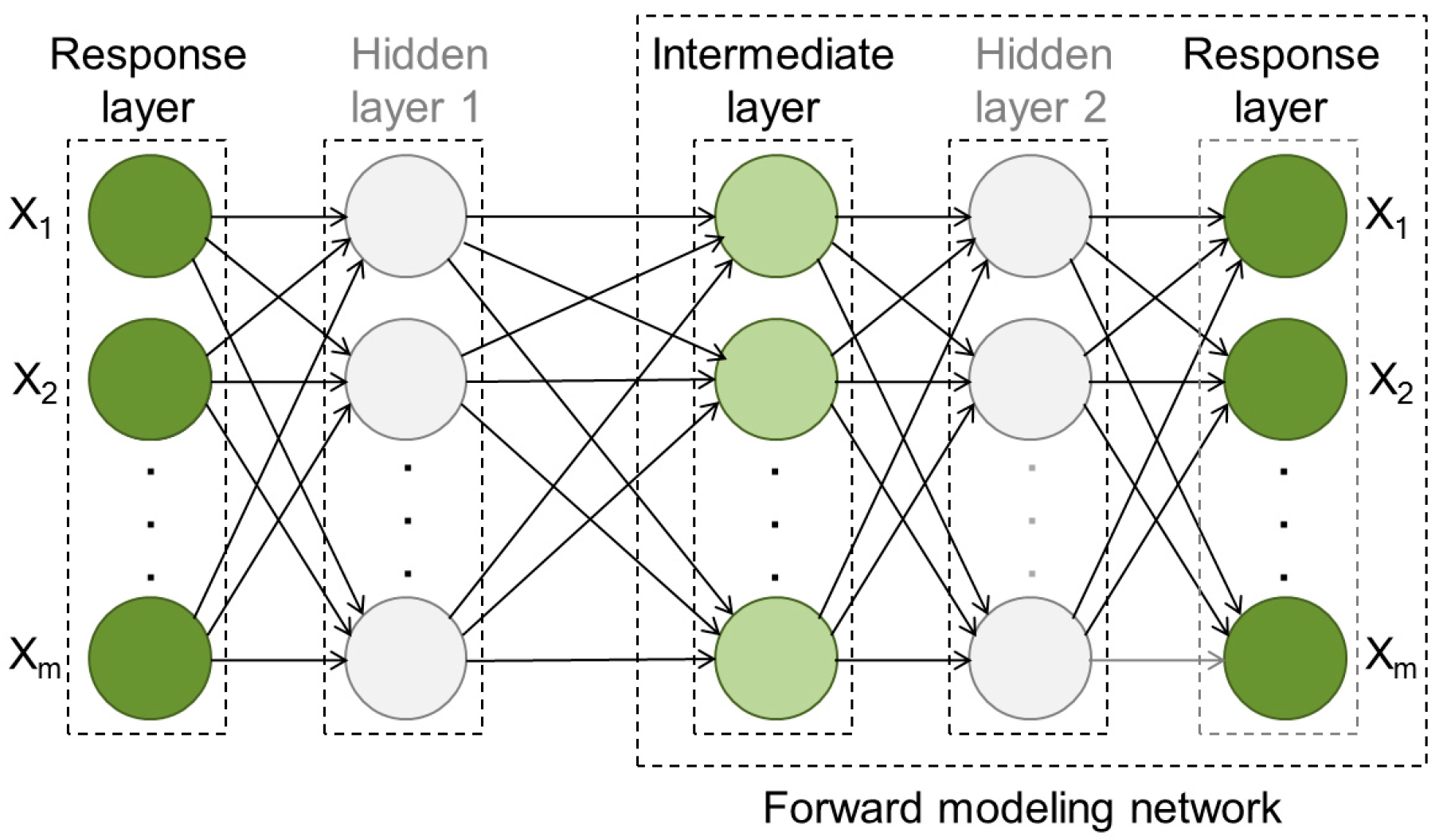
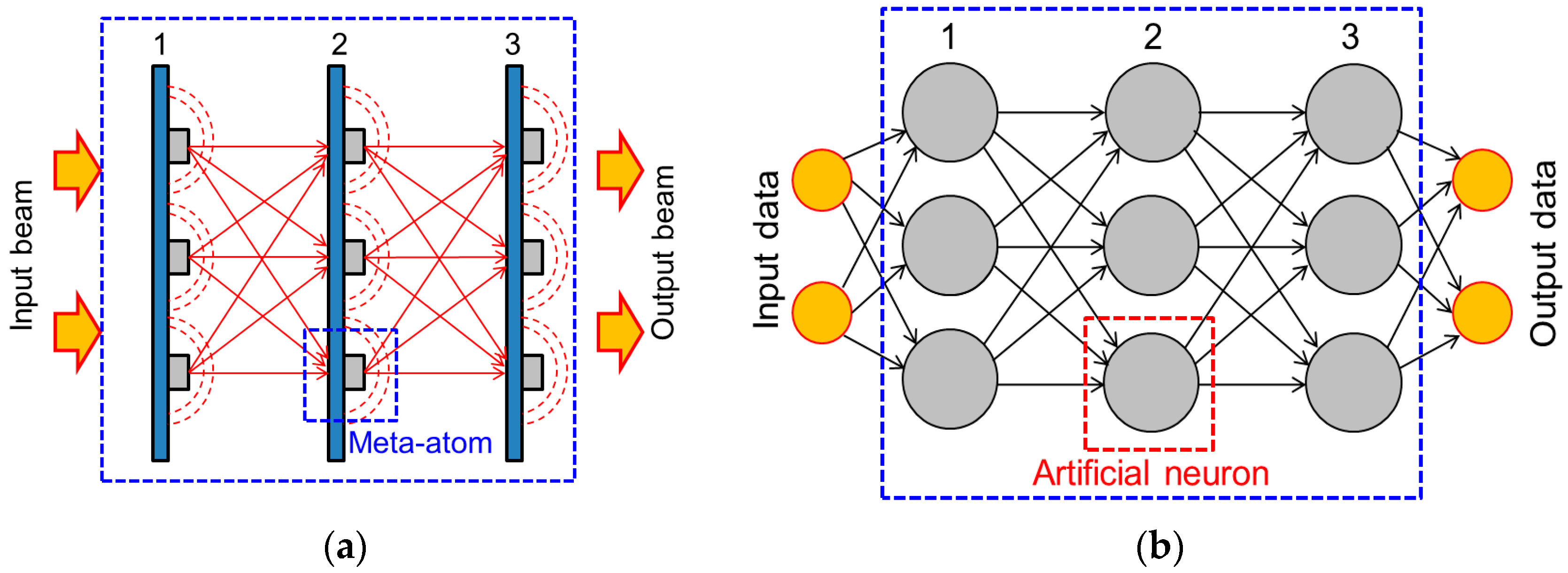
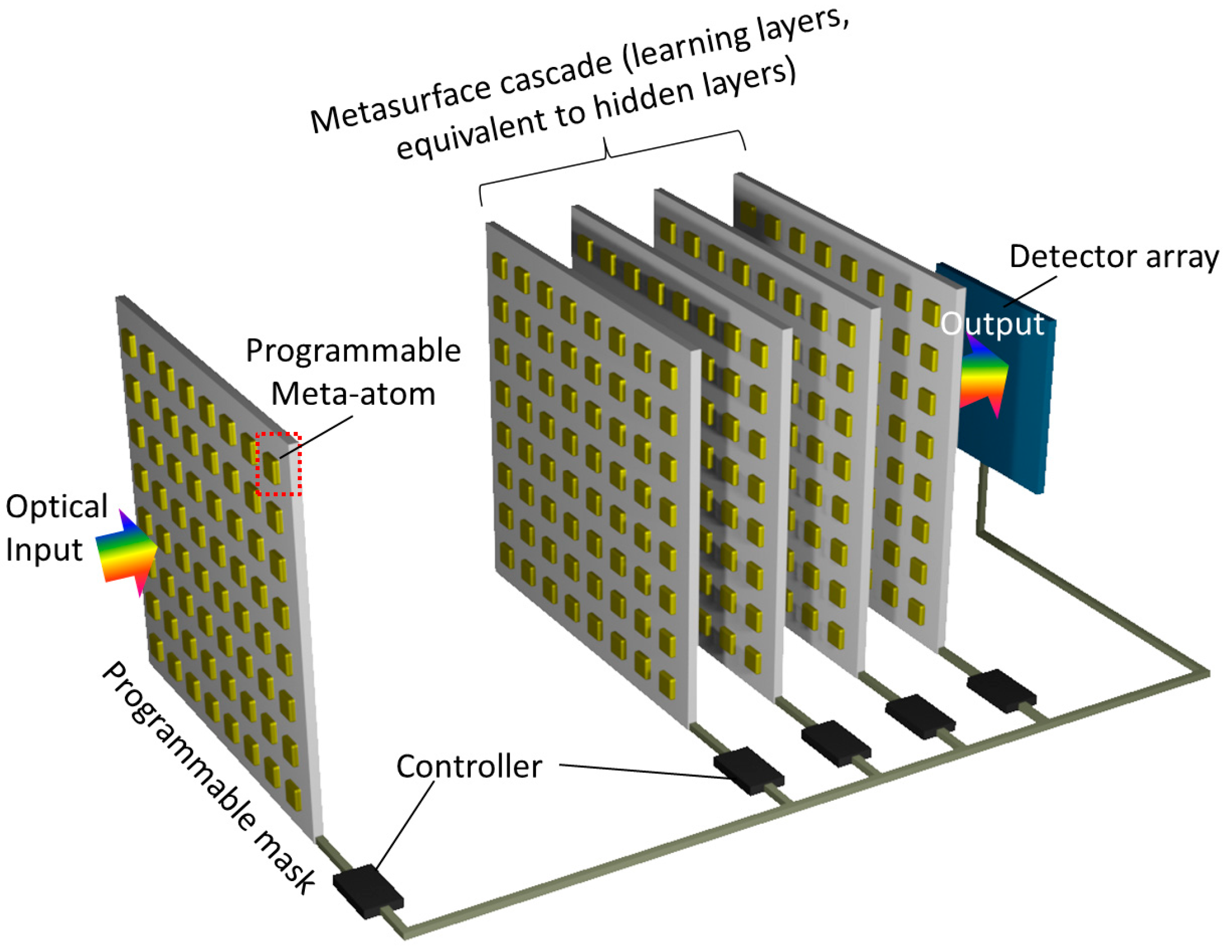
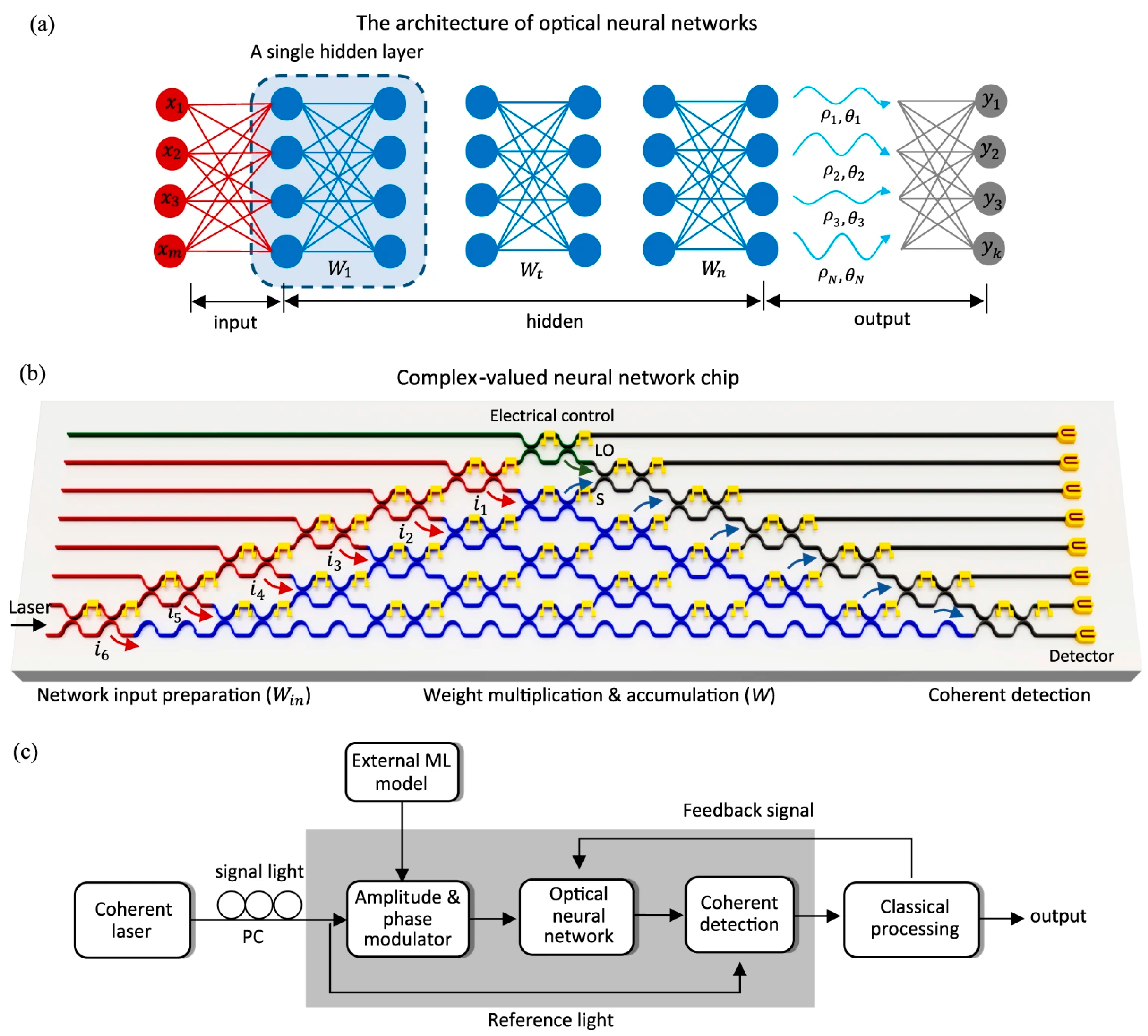
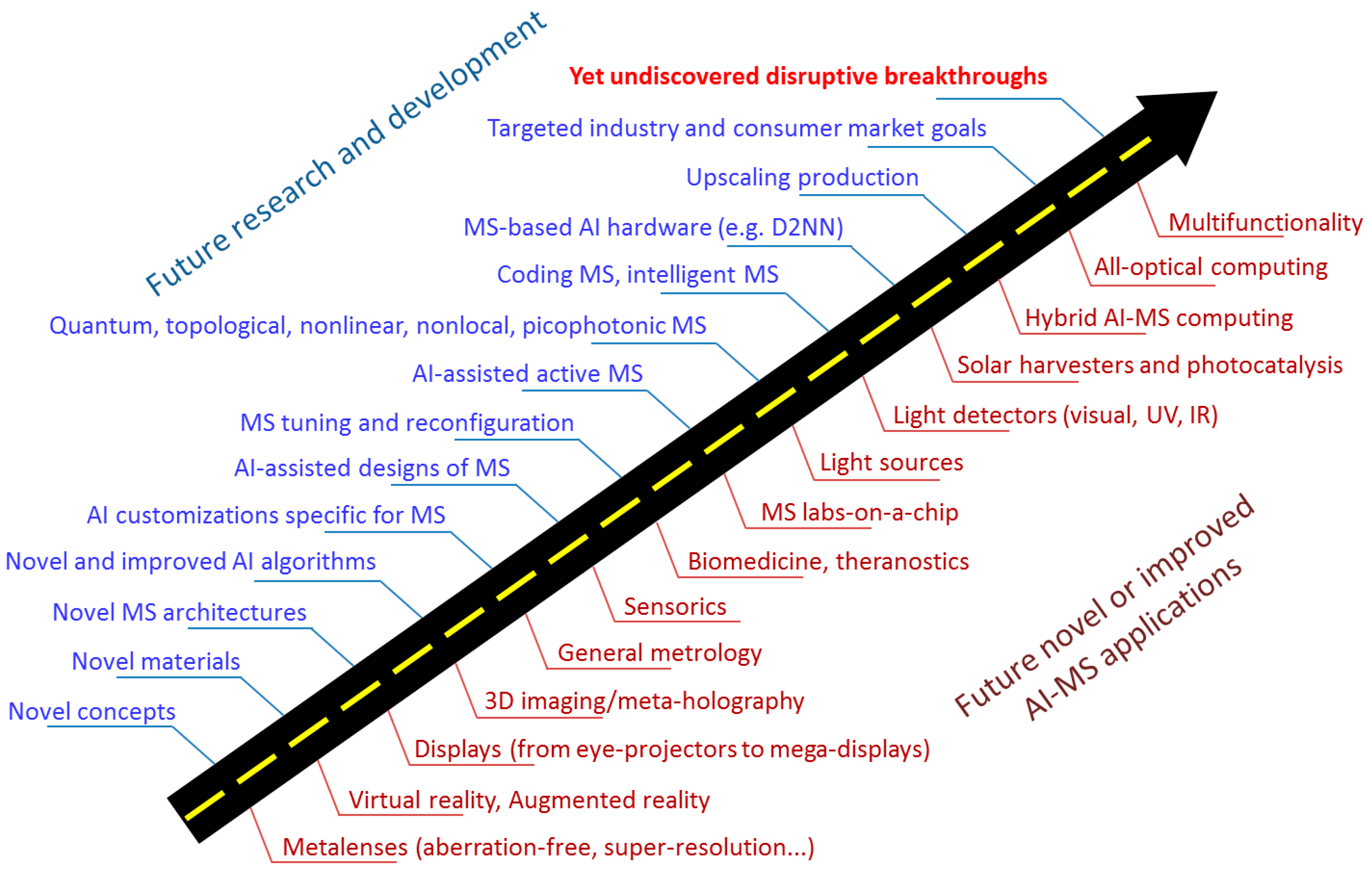
Metasurface Material	Role	Examples, Advantages and Disadvantages
Conductive parts of plasmonic structures (Drude-type free electron conductors)	Basic material for all plasmonic metasurfaces	Noble metals, aluminum, different alloys including alkali–noble intermetallics, transparent conductive oxides, refractory plasmonic materials, highly doped semiconductors, 2D materials like graphene or MXenes Advantage: extremely high field localizations Disadvantage: high losses
High-refractive index dielectric	Basic material for all all-dielectric and plasmonic metasurfaces	Lossless dielectrics like polymers, copolymers, ceramics; ultrathin semiconductors Advantages: near-zero losses, localizations of EM field Disadvantage: weaker localizations than with conductors
Special functional materials	Materials introducing additional multifunctionalities to metasurfaces, e.g., nonlinear optical behavior, quantum properties, tunability in real time, etc.	Nonlinear optical materials, quantum structures, phase-change materials, LCD and many more Advantage: additional multifunctionalities Disadvantage: complex operational requirements depending on function (very high fields for nonlinear, cryogenic temperatures for quantum materials, etc.)

summarizes the different materials used to fabricate various types of metasurfaces.

It is readily observable that the classification of materials shown in Table 1 does not conform to the classification usually met in the literature on metasurfaces and, more generally, on plasmonics. Very often, one meets three items in such literature: pure metals, pure dielectrics and their mixtures (e.g., [58,59,60]). However, while noble metals (most often silver and gold) are indeed the most frequently used conductors in metasurfaces and general plasmonics, they are by no means the only conductive building blocks to ensure plasmonic resonance. Within the last decade, a large number of alternative free-electron conductors have emerged in the literature, many of them offering advantages over noble metals (like lower losses, plasma frequencies in different frequency ranges, quasi-2D geometry and similar). The column “Examples” in Table 1 presents a short list of the most often met plasmonic materials, both traditional and alternative. It may be said that an organized quest for such materials has been started by the seminal paper [56] in which some of the conductive materials mentioned in Table 1 were proposed (although there have been prior publications which proposed similar alternative plasmonic materials, e.g., [61,62,63]). All of the materials listed in the first line of Table 1 have a negative value of dielectric permittivity ε in at least some part of the spectrum and their conductivity is based on the electron conductivity that can be described by the classical Drude model [64]. Further, plasmonic structures cannot function without at least some dielectric since a simple surface plasmon polariton will be formed at an interface between negative (ε < 0) and positive permittivity material (ε > 0), i.e., they are hybrid structures by definition, not some solid blocks (or sheets) of metal—this makes separate mentioning of hybrid metal–dielectric structures superfluous. Thus, Table 1 can be observed as a critical re-examination of the customary metasurface material classification. It must be said, however, that some sources do present materials for metasurfaces correctly. For instance, an approach similar to the one presented in Table 1 has been published in a review by Choudhuri et al. [65] in ample detail. Naturally, there are differences, especially regarding the viable semiconductors for low-loss structures and the multifunctional materials.

Since their introduction, the circle of the fields of light control using metasurfaces has been steadily expanding. Through different mechanisms, these methods ensure an almost total control over the main parameters of light flow, including the phase, amplitude, polarization, dispersion, wavefront form, even frequency (through utilizing nonlinear functional materials) and quantum states (e.g., single or entangled photons, Fock states, squeezed states, superposition, etc.). This has resulted in the development of meta-optics and metaphotonics, in which different and sometimes wildly varying fields converge.

2.1.2. Uses of Optical Metasurfaces

Some examples of practical applications of metasurfaces proposed so far include advanced cameras [66], microscopes [67], telescopes [68] and other imaging systems, including those with super-resolution [69] (exceeding Abbe diffraction limit); contact lenses [70], virtual reality [71] and augmented reality [72] headsets and other kinds of eyewear; antireflective structures [73]; superabsorbers [74]; light concentrators [75] (achieving exceptionally large photonic densities of states that some authors call “anomalous” [76]); highly reflective metasurfaces [77]; nonreciprocal (one-way) transmission structures [78]; different metasurface-based displays (like novel OLED, LED or simple LED) [79]; different kinds of metasurface-based nanoplasmonic sensors [80] and detectors [81]; LIDAR [82]; optical data storage [83]; solar energy harvesting structures and devices [84]; light sources like laser [85] and LED [86]; micro- and nanophotolithographic systems [87] (proximity-field nanopatterning); spectroscopy [88,89]; high-power lasers for material machining [90]; lasers for medical applications [91] (including theranostics and surgery); meta-holograms [92]; holographic 3D displays [93]; fiber-optical communication systems (different optical components like optical waveguides [94], beam shapers [95] and steerers [96], multiplexers and demultiplexers [97], integrated nanophotonic components for on-chip communication [98]); and many more.

As an illustration, Figure 2 shows a meta-hologram structure and its image reconfiguration procedure. The hologram is made of in-plane nanorods with various orientations on a thin glass plate.

As far as the more advanced applications are concerned, some of them include optofluidic devices [100] for microreactors encompassing photocatalysis [101], lab-on-chip technologies [102]; optical tweezers for micro- and nanoparticle trapping and manipulation [103]; optical levers for atomic force microscopy [104]; biomedical imaging [105], e.g., optical coherence tomography [106], terahertz imaging [107]; super-resolution microscopy beyond the Abbe diffraction limit [108] including the use of superlenses and hyperlenses [109]; nonlinear optical devices for frequency conversion [110]; quantum optics [33] for quantum computing [111] and quantum cryptography [112]; stealth coatings [113]; optical cloaking devices (invisibility shields) [114,115], nonreciprocal cloaking (cloak that hides objects from the outside viewpoint but permits looking from the object outward) [116]; camouflage into virtual objects (electromagnetic illusions) [117,118]; and general transformation optics [119] (including its applications in, e.g., astrophysical all-optical simulation and the related models in other fields [120]).

All of the above-listed principles and applications are metasurface-based building blocks of the wider field of metaphotonics. It is a short cross-section of the state of the art presented for illustrative purposes only, i.e., without systematization, while the real number of applications, patents and research teams is hard even to guess since it increases on a daily basis.

2.2. Classifications of Optical Metasurfaces

Optical metasurfaces may be classified into a number of groups according to several criteria, which include their (multi)functionalities, their architecture, the optical transformations they perform, the possibility of their dynamic control through reconfigurability, their applications, etc. Many metasurfaces belong to more than one class, which is the natural consequence of the complexity and multifunctionality of some of them.

The following text presents some possible metasurface classification tables organized according to different criteria, including those listed above but not limited to them. Based on the previous paragraph, the reader should bear in mind that some types of metasurfaces can appear in more than one table.

The most obvious classification is according to the geometry of metasurfaces. It may be conducted in dependence on the distribution of meta-atoms on the surface, on the cross-section profile of the surface or on the shape of the meta-atoms themselves.

Table 2. Metasurface classification according to the distribution of meta-atoms on it.

Meta-Atom Distribution	Summary of Description
Periodic Metasurfaces	The distribution forms a regular pattern, similar to those in natural crystals but in 2D form. Meta-atoms are arranged in unit cells that can be square, rectangular, triangular, hexagonal, etc. [121]. Various orders of diffracted light are possible. Advantages: Easy to design due to pattern simplicity. Batch fabrication compatible with standard planar technologies. Useful for various applications, from beam shaping and steering to 2D lensing. Disadvantage: Not suitable for any applications where non-periodic distribution of meta-atoms is needed.
Aperiodic Metasurfaces	Regular 2D patterns are still present, but the distances and relative locations among them are determined in accordance with various aperiodic sequences and no unit cell can be defined. Examples include Cantor sequences along one or both axes, Thue–Morse, Fibonacci, etc. [122]. Advantage: Almost arbitrary wavefront modulation. Disadvantage: Technological difficulties to produce.
Quasiperiodic Metasurfaces	The pattern of the distribution of meta-atoms in quasi-periodic metasurfaces [123] is ordered but not periodic and instead it follows that encountered in quasi-crystals (e.g., distributions like in the famous Penrose tiling [124]—actually, Penrose-distributed meta-atoms on metasurfaces were reported in [125]; a vast number of different geometries, including, e.g., dendritic nanostructures [126] were also used). Advantages: Can create unique diffraction effects and generate complex light fields resulting in multifunctional metasurfaces, superabsorbers, etc. Disadvantage: Complex fabrication for larger areas.
Gradient Metasurfaces (Metagratings)	The distribution of meta-atoms or of their dimensions is spatially varying, thus ensuring a position-dependent optical response. Other material parameters can be graded as well (e.g., gradient refractive index—GRIN) [127]. Advantage: Enables reaching a gradient in the phase, amplitude or polarization of the optical signal, thus, e.g., facilitating beam steering and focusing [128,129]. Disadvantage: Complex fabrication for larger areas.
Random Metasurfaces	Meta-atoms are randomly distributed here. This randomness may range from a slight disorder to quasi-randomly generated distributions to fully random ones. Advantages: Random metasurfaces can find different applications, e.g., in light scattering enhancement, speckle reduction and improved light absorption (of importance for photodetection including solar cells and generally superabsorbers [130]). Disadvantage: Complex fabrication for larger areas, problems with repeatability.
Dynamically Reconfigurable Metasurfaces	It is possible to use external stimuli to tailor the properties of these metasurfaces. They represent almost a class of their own and play an important role in AI–metasurface synergy. Various stimuli can be used to reconfigure them. An example is elastomer-based metasurfaces where the distribution of meta-atoms is achieved by applying external mechanical force in an arbitrary manner [131]. Advantage: Ensures the production of tunable structures of interest for applications where dynamic changes are essential. Disadvantage: Complex fabrication, mostly related to integrating tuning material and bringing stimulus to the desired position.

shows some possible cases of meta-atom spatial distributions on different types of metasurfaces, without any pretensions to generality.

Figure 3 presents several possible distributions of meta-atoms on a metasurface for illustration purposes only, without any claims to generality.

Table 3. Geometrical classification of metasurfaces based on the cross-sectional geometry of the entire metasurface.

Cross-Section Profile	Summary of Description
Fully plasmonic cross-section	These metasurfaces are composed in their entirety of plasmonic conductors (in a majority of cases noble metals but alternative materials include those quoted in Table 1). The full plasmonic layer metastructures include extraordinary optical transmission (EOT) sheets [132] which may be topologically continuous [133]. These structures may be single- or multilayer and one or more plasmonic materials may be alternating between the layers. Advantage: Extremely high field enhancements and localizations, convenient for, e.g., nonlinear optical materials. Disadvantage: Very high absorption losses, hindering or fully obstructing some applications.
All-dielectric cross-section	These metasurfaces are composed in their entirety of dielectrics with a high refractive index that are either lossless or extremely low-loss at optical frequencies [128,134]. May be single- or multilayer. Advantage: Low losses. Disadvantage: Much lower field enhancements and localizations than with plasmonic materials.
Hybrid plasmonic conductor–dielectric metasurfaces	These metasurfaces combine in a single structure plasmonic conductors with dielectrics [135]. This ensures the simultaneous use of plasmonic and dielectric resonances. In this manner, decreased losses are obtained in parallel with strong field localizations. A large part of the existing plasmonic metasurfaces are actually built with such a geometry. Advantage: A controllable manner to decrease losses and simultaneously obtain strong field localizations, convenient for many applications (e.g., negative refractive index metasurfaces, superabsorbers). Disadvantages: Complex control of properties; many such structures nevertheless have high losses.
Metal–insulator–metal (MIM) sandwich structures	The cross-section of this type of hybrid cross-section metasurfaces consists of a top and bottom metal layer with a dielectric spacer between them [136]. The top and bottom layer may consist of conductive nanoantennas/meta-atoms or nano-apertures, like in, e.g., superabsorbers [74,137], or may be continuous. The spacer may be continuous or riddled with apertures. The usual abbreviation “MIM” is actually misleading, since any plasmonic conductor can be used as the “M” part, not only metals. Advantage: Convenient for introducing different signal modes and for high-performance optical waveguides. Disadvantage: Losses in the plasmonic parts.
Insulator–metal–insulator (IMI) sandwich structures	A reversal of the above structure, since two dielectric parts are on the outside and a conductive layer is in the middle. Advantage: Described as one of the simplest and nearest to ideal plasmonic waveguides [138]. Disadvantage: Its waveguiding properties lag behind those of MIMs.
General multilayer metasurfaces	Multilayer metasurfaces are obtained by stacking a larger number of subwavelength layers. Each of them may have a different geometry and composition. Advantages: Successive processing of optical signals can be obtained. This layout offers a higher degree of design freedom and is thus often used for metaphotonics-based AI [110]. Besides this, it ensures functionalities like broadband operation. Complex frequency dispersions are obtainable by a single structure, including those allowing for negative group velocity modes with simple free space coupling without a need for couplers. Disadvantage: Rather complex structures.
3D Metasurfaces	The term 3D metasurfaces at first glance appears to be contradictio in adjecto since basically it could be understood as a 2D object having three dimensions. Actually, these are flat metastructures organized to form a hollow and layer-built 3D, like a house of cards. One of the methods to obtain them is origami deformation or “bulking” [139]. Advantage: Sophisticated functionalities are obtainable like symmetry breaking to achieve chirality switching [139] or for fabrication of metasurface-based cloaking devices [140]. Disadvantage: Not actually 2D metasurfaces but only containing them as their main building blocks.

shows a classification of metasurfaces based on the cross-sectional geometry of the entire metasurface.

Figure 4 shows several simple cross-sections of plasmonic metasurfaces. Figure 4a shows a fully plasmonic cross-section, for instance metallic. Figure 4b is an all-dielectric lossless cross-section. Figure 4c shows a three-layer metal–insulator–metal (MIM) sandwich structure (any plasmonic material may be used instead of metal). Figure 4d is an insulator–metal–insulator (IMI) sandwich structure (the same remark is valid as above). Finally, Figure 4e represents a multilayer alternating plasmonic–dielectric structure. Obviously, a multilayer structure may consist of two or more alternating plasmonic materials, or, in an analogous fashion, two or more alternating dielectric layers. The thickness of different layers may vary, as well as their composition. Additionally, their composition may be graded along the surface or perpendicularly to it.

Table 4. Some often-used meta-atom geometries.

Meta-Atom Type	Summary of Description
Rod-shaped meta-atoms	The cross-section of these meta-atoms may vary; it can be cylindrical, hemicylindrical (in both cases, the base shape may be either circular, elliptical or arbitrary curvilinear), rectangular, triangular, etc. Typically, they lie in the metasurface plane. The rod length may also vary and thus the aspect ratio too. Advantages: They can support electric and magnetic resonance and be used to control light polarization and phase. Simpler control of in-plane coupling; good directionality. Disadvantage: Low interaction with out-of-plane components.
Pillar shape	Actually a rod shape, but either assuming its perpendicular position with respect to the planar surface or tilted under some angle; both represent an extension beyond planar geometries. The same comment regarding their base is valid as for the rod form but other forms can also be used, like X-shaped base, Y or V-shaped, etc. Advantages: Supporting electric and magnetic resonances and controlling light polarization and phase. Disadvantages: Increased fabrication complexity; requires additional fab steps to control integration with the metasurface.
Spherical shape	Obtained by depositing nanoscale spherules on the planar surface that may adhere with only a small part to it or be more or less embedded (up to full immersion, an example for which would be plasmonic spheres embedded into a dielectric metasurface body). Advantage: Excellent isotropic properties, thus useful for omnidirectional applications. Disadvantage: Rather poor anisotropic properties and directionality.
Ellipsoids	A variation of the above type but with ellipsoids instead of spherules. Advantage: Better polarization control than that of spherical meta-atoms. Disadvantage: More complex to fabricate than spherical meta-atoms.
Disk shape	Most often with a circular or elliptical base, its diameter being much larger than its height. Advantage: Simple to fabricate by planar technologies and thus relatively low-cost, very popular for many metasurface applications. Disadvantage: Rather poor performance in controlling complex optical signals having components in 3D.
Other 3D forms	For instance, pyramids, nano-cubes, different polyhedra and actually any existing nanoparticle shape including the highly complex ones; they may protrude from the plane or be partially or fully embedded into the metasurface, their orientation providing directive or omnidirectional properties. Advantage: In many cases useful for complex optical interactions and multi-directional functions. Disadvantage: Fabrication may be complex and costly, although it may be alleviated or avoided if self-assembled nanoparticles are used.
Asymmetric meta-atoms	Planar forms like X, Y and V with unequal sides; introduce strong anisotropy. Advantages: Simple planar fabrication; convenient for obtaining anisotropic response, applicable for fine polarization conversion and control; tailorable directionality; may be useful for asymmetric scattering of light, control of circular dichroism, etc. Disadvantage: Can be difficult to optimize for certain functionalities.
Complex shapes	Stars, crosses, various G-shapes, L-shapes, spirals with circular, rectangular, triangular forms, U-shapes, T-shapes, twisted crosses and actually any imaginable and fabricable planar nano-geometry. Advantages: Readily fabricated by planar technologies; highly tailorable and flexible design and thus applicable for a wide range of different wave manipulations, offering extensive design flexibility; some of them are convenient for chiral response. Disadvantages: Can be complex for design and simulations; may have poor scalability.
Split-ring resonators	Single or multiple planar rings with single or multiple splits in each of their rings; historically, the earliest form that ensured experimental implementation of negative effective permeability. Advantages: Useful for applications requiring resonant response; can be helpful to obtain magnetic responses at optical frequencies; assisting to achieve negative magnetic permeability at non-optical lower frequencies (e.g., microwave). Disadvantage: Resonant response makes them poorly usable for broadband applications.
Complementary structures	Apertures shaped in the form of any of the meta-atom geometries mentioned in this table, function according to Babinet principle. Advantage: Through inverting the field distribution (optical to electrical and electrical to optical) of their solid counterparts complement and enhance the optical field distribution control. Disadvantage: Complex design and fabrication, complex tuning to desired frequency dispersion.
Fishnet structures	Ordered arrays of nanoholes that are circular or rectangular in a majority of cases, although other aperture geometries sometimes appear. Complementary to solid cylindrical structures. Advantages: Have advanced optical properties that made fishnet the principal geometry of extraordinary optical transmission arrays and of fishnet metamaterial (the latter being historically the first structures to reach negative refractive index in the visible spectral range); generally useful for the enhancement of different optical properties. Disadvantage: Relatively complex fabrication.
Chiral structures	Twisted or helical rods, planar spirals or helices, asymmetric split rings and generally any asymmetric meta-atoms. Advantages: Such structures enable the metasurface to make a distinction between the two kinds of circularly polarized light, the left-handed (LH) and the right-handed (RH) ones; can modify light polarization in manners unattainable by non-chiral meta-atoms, ensuring, e.g., light polarization rotation, conversion between linear and circular polarization, control over circular dichroism, enantioselective sensing and general chiroptical applications. Disadvantage: Relatively complex structures requiring highly accurate geometry control.
Arbitrary (freeform) shapes	Typically implemented in planar geometry lying within the metasurface plane. The shapes can have literally any form, although after being optimized at least some of them tend to assume geometrical forms encountered in living organisms. Advantage: Ensure maximum design freedom when performing AI optimization of meta-atom forms for targeted applications tailored for complex and very specific optical requirements. Disadvantages: Design may be computationally demanding, especially for complex shapes. Usually require AI optimization. Fabrication can also be challenging.

deals with the fundamental building blocks of metasurfaces, the meta-atoms, and presents some of the most often met classes of their geometries. A comprehensive list of shapes is impossible to make as it is literally endless. Just random shapes may have any imaginable form and complexity. Also, there are variations of each of the types, both in their overall sizes (which more often than not vary within a single metasurface) and the specific way the geometry is implemented (for instance, split ring resonators may have different shapes and layouts, with varying number of splits and shapes and numbers of rings).

For the reason of brevity, Table 4 only shows a choice of simpler canonical shapes. Obviously, not just any arbitrary shape will be convenient for a given application. Thus, it is usual to perform targeted optimization of the meta-atom geometries, which can be performed by AI methods. One of the approaches to such an optimization of metasurfaces is presented by Whiting et al. [141]. Additionally, they generated a meta-atom library using their 3D surface contour method for its design. As an illustration, Figure 5 shows some selected types of 2D meta-atoms (planar nanoantennas), without any attempts at either completeness or systematic presentation.

A meta-atom is the basic part of a metasurface unit cell. However, in some situations, one needs a more complex ordered group of meta-atoms to attain an optical functionality. Such groups are known as supercells [142,143]. An example of a simple supercell is shown in Figure 6. The illustration is rendered based on a paper by Guo et al. [144] which considers ordered 2D arrays of such complex multi-meta-atom cells for the formation of metasurfaces with space–time phase modulation for nonreciprocal function.

Figure 7 shows three well-known single- or multilayer metasurfaces with nano-apertures playing the role of complementary “meta-atoms”. All three structures are presented with square unit cells. For the sake of clarity, only four unit cells are shown for each example. The top and bottom surfaces are plasmonic material (gold color). The middle spacer, in the cases where it exists, is a lossless dielectric (grey color). An extraordinary optical transmission [132] surface is shown in Figure 7a. A negative effective refractive index metasurface with “fishnet” geometry [145,146] is shown in Figure 7b. A plasmonic superabsorber [137] structure is shown in Figure 7c. In this last structure, nano-apertures only exist in the top surface, while the dielectric spacer and the bottom plasmonic surfaces are without holes. The cross-section profiles of (b) and (c) are of the MIM type.

Table 5. Optical metasurface classification according to their basic role.

Metasurface Functionality	Summary of Properties
Phase control	Crucial for the basic metasurface functions; by phase modification from 0 to 2π one ensures complete control over wavefront; the main approaches are geometric phase control (the Pancharatnam–Berry type) [147], Huygens’ metasurfaces [148] and phase shift in gradient metasurfaces [129], as well as resonant phase shift, transmission and reflection (scattering parameters) phase control and polarization state phase control. Advantages: Accurate and complete light wavefront control; crucial for beam shaping and steering, meta-holography and a majority of other applications. Disadvantage: Challenging design and fabrication due to mandatory high precision.
Amplitude control	Control over the value of scattering parameters (reflectance, transmittance) and absorptance/emittance. Advantages: Ensures adjustment of light intensity distribution; convenient for numerous uses in imaging and spatial light modulation. Disadvantage: The system efficiency may be decreased due to optical losses.
Polarization control	Creation of planar polarizers, polarization converters, wave plates, etc. Advantages: Enables light polarization conversion and general manipulation with it; useful for numerous practical applications. Disadvantage: Operating conditions and the system geometry may limit the efficiency of control.
Dispersion control	Control of pulse shaping and chromatic aberration correction. Advantages: Managing the manner that light at different wavelengths propagates through the system; convenient for broadband optical systems; very useful for imaging and flat lenses. Disadvantages: Complex design and fabrication.
Direction control	Control of light beam direction without moving parts; may be regarded as a subset of phase control. Advantages: Able to steer beams dynamically; useful for various applications like LIDAR and optical communications. Disadvantage: Challenging steering precision control.
Frequency control	Control over upconversion, downconversion and frequency mixing, e.g., through the use of nonlinear optical materials and ultra-strong light localization immanent to plasmonic metasurfaces. Advantages: Enables tuning the operating frequency; useful for different spectrum-related applications like dynamic spectral filtering. Disadvantages: External control, if any, makes the design and fabrication more challenging; high fields are often necessary; increased risk of unreliable operation and failure.
Quantum properties control	Control of light–matter interplay at the quantum level with the final goal of incorporating quantum information functionalities, including quantum computing and quantum cryptography. Advantage: Ability to manipulate quantum states of light, thus applicable for quantum computing, quantum cryptography. Disadvantages: A need for cryogenic operating temperatures; complex fabrication.
Multiple parameter control	Simultaneous control over two or more of the above-listed functional parameters in a single highly compact system. Advantages: Useful for multiplexing applications, fine tuning of optical parameters and extending the functionality ranges. Disadvantage: The system has to be much more complex than a single-parameter one; design and fabrication are more complex; the need to adjust several parameters at the same time often necessitates performance compromises.

presents a classification of optical metasurfaces according to their basic role (or roles, if they are multiple). Only the fundamental functions are given. The listed control methods may be applied to either passive or active metasurfaces.

2.3. Advanced and Specialized Metasurfaces

Table 6. Some advanced optical metasurfaces.

Metasurface Type	Summary of Properties
Nonlinear metasurfaces	Metasurfaces with built-in nonlinear optical materials, offering nonlinear functionalities. Advantages: Introducing nonlinear optics functionalities like frequency control; ensuring a wealth of new semiconductor-like properties of optical materials. Disadvantage: High field intensities needed.
Topological metasurfaces	Metasurfaces mimicking the topology of condensed matter physics systems including topological insulators and edge modes. Advantage: Topological properties ensure high quality light manipulation able to avoid defects and disorder in metasurface material. Disadvantage: Complex fabrication procedures.
Quantum metasurfaces	Metasurfaces with built-in quantum mechanical materials, offering quantum functionalities. Advantage: Ability to manipulate quantum states of light, thus applicable for quantum computing, quantum cryptography. Disadvantage: Needs cryogenic operating temperatures; complex fabrication with low tolerance to inaccuracies.
Tunable metasurfaces	Metasurfaces whose optical parameters can be adjusted to desired values using external stimuli. Advantages: Enable dynamic control of their optical properties by a control signal, thus adaptable to different changeable environments and varying operating conditions; convenient for many advanced applications. Disadvantages: The integration of tuning mechanisms and their external control increases the complexity of the system; the speed of the tuning mechanisms often can be inadequate, as well as their reliability.
Digital coding metasurfaces	Metasurfaces designed and applied based on the principles of digital signal processing. Advantage: Programmable control over optical waves, useful for a wide range of applications, including optical computing, communications, LIDAR, etc. Disadvantage: Complex design and complex optimization; depending on mechanisms used, the efficiency and operation speed may be low.
Intelligent metasurfaces	Tunable metasurfaces that ensure wave–information–matter interaction, ensuring autonomous response. Advantages: Integration of sensing and computing abilities, highly adaptable, usable in adaptability in smart applications. Disadvantages: Complex design and fabrication; power consumption may be high.
Neuromorphic metasurfaces	Intelligent metasurfaces based on the principles of neuromorphic computing, their artificial neurons mimicking human ones to a certain degree. Advantages: Applicability in novel generation of optical computing, high speed. Disadvantages: Very complex design and fabrication; currently still under development and thus with significant functional inadequacies; problems with scalability and system integration.

presents in brief some advanced types of metasurfaces. Most of these are applicable in reconfigurable systems related to advanced AI metaphotonics.

In the following text, some advanced or specialized metasurfaces of interest for AI–metaphotonics synergy are dealt with in some more detail. The accent is put on the structures whose use capitalizes on the strengths and advantages of their relation with AI. Thus, a large part is dedicated to adaptive metasurfaces and a smaller one to passive. This is of special importance for the AI–metasurface synergy. The reader should be aware that some of the described types of metasurfaces may partly overlap functionally and that some metasurfaces may at the same time belong to more than a single type (for instance, a quantum metasurface may simultaneously be tunable, etc.).

2.3.1. Topological Metasurfaces

Topological metasurfaces utilize the concepts of topological physics developed in the field of condensed matter science and apply them to metasurfaces [149]. Their basic principles are inspired by the concepts of topological insulators (structures that act as insulators in their bulk but conduct along their edges). The states along a topological insulator volume are called the edge states.

A metasurface equivalent of topological structures from condensed matter physics is a metasurface whose geometry and topological properties are used to create passageways for light through the structure traveling along the edge states and circumventing the bulk of topological insulators altogether. In this way, the chance for backscattering due to defects and disorder is avoided—optical modes travel along the edge states losslessly, fully circumventing defects. Thus, the optical topological structures are introduced with the prime intent of utilizing the principles of topological order to manipulate optical modes to make them insensitive to defects.

Technically, topological metasurfaces are produced in such a manner that optical topological phases are fabricated within the metasurface, together with the edge optical states/modes which help the light avoid scattering due to disorder and imperfections in the material. Thus, mimicking the topological insulators and their edge modes helps the optical modes avoid scattering on defects and imperfections and propagate losslessly. The state of the art in the field is active topological metasurfaces that include nonlinear structures and reconfigurable ones [150].

2.3.2. Meta-Holograms

Holography ensures complete control over wavefronts, since it enables full engineering of all of its defining parameters, including obtaining arbitrary phase, amplitude and polarization. Since its discovery by Denis Gabor in 1948 [151] who observed that the interference of two waves kept full information about the amplitude and phase of the beam scattered by an object, it has retained its popular image in the media as the method to obtain 3D pictures (actually interferograms), even films. The 3D image of the object recorded in a hologram is reconstructed by diffracting a coherent readout beam from the surface of the holographic interferogram.

Meta-holograms [152], actually metasurface-based computer-generated holograms, are superior to conventional holograms, since they have subwavelength building blocks with nanoscale precision; thus, their geometrical and material parameters offer a much higher performance than conventional holograms. Compared to traditional holograms, meta-holograms provide much higher spatial resolutions, lower noise and ultrahigh accuracy of the reconstructed images, while undesired diffraction orders are eliminated and large space–bandwidth products are ensured, as well as extended viewing angles.

Another advantage of meta-holography of interest for AI–metaphotonics synergy is the possibility of fabricating tunable/reconfigurable meta-holograms [153,154], thus ensuring dynamic control over their optical parameters without permanently altering the meta-hologram. An example of intelligent coding meta-holograms is analyzed by Liu et al. [155]. Tunable meta-holograms have also opened pathways to their use in adaptive optics, switchable imaging and advanced 3D displays [156], and, on the other hand, for optical traps [157] and quantum optics [158,159].

2.3.3. Nonreciprocal Metasurfaces

Nonreciprocal metasurfaces are structured in such a manner that they break Lorentz reciprocity [110]. In that manner, light propagating in different directions will exhibit different properties. The most well-known nonreciprocal structures are those with asymmetric transmission, which means that light propagating in one direction will have one value of optical transmission, while that going in the opposite direction will have another value. An optical diode would be an illustration of such nonreciprocal behavior. Ideally, it would transmit 100% of light in one direction and 0% in the opposite direction, reflecting 100%. Another illustration is an optical isolator, which would also ideally transmit 100% in one direction, but both its transmission and reflection in the opposite direction would be 0%, where 100% of the light in the back direction would end up being fully absorbed or transformed into a different mode, or with its frequency being changed to a different value.

Several approaches to the fabrication of nonreciprocal metasurfaces have been proposed [160]. Among them are those that introduce spatiotemporal modulation in the metasurface [161], nonlinear coupled Fano metasurfaces [162], the use of unilateral edge states in topological metasurfaces [163], Faraday rotation-enhancing plasmonic and dielectric metasurfaces [164], nonlinear metasurfaces whose values of refractive index are intensity-dependent [110], the use of plasmonic “meta-weaves” within the framework of sector-way propagation [165], a checkerboard combination of adjacent all-passive nonlinear electromagnetic “diodes” and chiral elements [166], drift-biased and magnetically biased graphene metasurfaces [167], etc.

Tunable and reconfigurable nonreciprocal structures are among the hot topics in the field of AI–metasurface synergy. Some examples include manipulation with transmitting and receiving channels in nonreciprocal surfaces that has been dealt with in 2024 [168], nonreciprocal magnetic metasurfaces for phase modulation in 2023 [169] and many more.

The most convenient approaches to nonreciprocal metasurfaces appear to be those that do not require external biasing. The use of nonlinear materials can be problematic due to the intensity of necessary optical fields and the related excessive optical power dissipation. Finally, a significant challenge is the efficiency of nonreciprocal light propagation, which in some of the quoted approaches can be quite low. One could expect that novel architectures could help solve the existing hurdles.

2.3.4. Quantum Metasurfaces

Quantum metasurfaces help manipulate quantum level light–matter interactions [170,171]. Within their structure, they include functional materials that ensure operations over quantum states of light. Through quantum states of light (e.g., single photons, entangled photons, squeezed states and Fock states), related to the particle properties of light (as determined by its dual particle/wave nature), they ensure their application in quantum computing, quantum cryptography and quantum noise suppression needed for measurement accuracy improvement and signal-to-noise reduction. The introduction of these interesting and potentially very useful effects to the field of metasurfaces opens a lot of pathways for further research and applications [33].

Hybrid metasurfaces with surface plasmon modes efficiently coupled with quantum emitters represent a novel development in the field [171]. The said coupling maximizes the local density of photon states at the quantum emitter, thus significantly enhancing the spontaneous emission rate, whose low value may easily be of the most problematic segments in quantum emission. It can also help with two other observed problems, namely the broad emission spectrum appearing as a consequence of phonon-mediated decoherence and the non-directionality of emission occurring to the electric dipole nature of quantum emitters which are both improved due to the plasmonic resonance in the hybrids.

A big challenge with compact structures exhibiting and utilizing quantum effects is a necessity for very low cryogenic operating temperatures (down to tens of microkelvins). Actually, the increase in the operating temperatures ideally to room temperature remains a significant obstacle to a widespread utilization of quantum metasurfaces and to bringing applications like quantum computers and quantum cryptography to everyday use. Therefore, it is not surprising that the questions how to maintain quantum coherence and minimize quantum noise at elevated temperatures are among the main challenges related to quantum metasurfaces.

The methods proposed to elevate the operating temperatures proposed so far include robust quantum emitters that ensure coherent quantum properties at increased temperatures. Some structures proposed to perform this feat include certain kind of defects in wide-bandgap semiconductors that ensure quantum emission at room temperature. Such effects have been observed with silicon defects in silicon carbide and with nitrogen vacancies in diamond crystals. Experimentally, an introductory key step toward the room temperature operation of imaging of quantum emitters in solid state has been demonstrated by Huang et al. in 2019 [172]. They manufactured a metasurface on a diamond substrate that incorporated nitrogen vacancy centers (known to contain electron spins manipulable at room temperature). The metasurface on diamond served as a metalens to collect single photons emitted from the said vacancies.

Further proposed pathways to the elevation of the operating temperature of quantum metasurfaces include rethinking their structure to reduce phonon interactions causing decoherence and thermal quenching of quantum emission at elevated temperatures. Hybridizing metasurface structures to include host materials or nanostructures exhibiting greater robustness to temperature variations could also prove itself to be a viable method. Another pathway is an enhancement of the Purcell effect and generally of light–matter interactions. Finally, some quantum materials, like 2D structures, prove themselves more robust to temperature variations.

Other challenges related to quantum metasurfaces are currently the need for the efficient scalable integration of quantum emitters into metasurfaces without impairing the quantum properties. Improved nanofabrication with highly accurate orientation and positioning of quantum elements must be achieved for this purpose. Spatial uniformity in the order of nanometers and quantitative stability of quantum properties like quantum efficiency and operating wavelengths are difficult to maintain across macroscopic areas of metasurfaces. However, these technological problems are not dissimilar to those having been encountered before with some nanoplasmonic structures. Since these have been successfully solved, it may be carefully said that the future of this field appears promising.

Tunable and configurable quantum metasurfaces were reported in some recent publications [173,174]. This research could help in paving the way for quantum effects in intelligent metasurfaces.

2.3.5. Tunable Metasurfaces

Tunable metasurfaces are those that allow their optical properties to be adjusted (tailored) after their fabrication through the application of external stimuli. Their importance in AI-based control is high and this is the reason why relatively more space is dedicated to them here. Two distinct groups can be discerned among such metasurfaces. One of them includes statically tuned structures, where one performs a longer-term or permanent modification with a goal to, e.g., adjust with high accuracy (“finely tune”) the targeted static optical properties through post-fabrication processing. Thus, the accent here is on an ability to reach a passive optimized state in a stable manner. The term may sound slightly misleading, since some of such “static” changes can actually be implemented repeatedly—just not on a real-time basis—so that they actually represent switching between different stationary operating modes. This is the reason why some authors prefer to use the term switchable for it instead of tunable [175]. Another one, much more important in practical situations and within the context of the AI–metasurface relationship, represents dynamic/active tuning that may occur with different speeds, from relatively slow ones to those in real time, which often implies very high speeds. A prerequisite for both groups is a measurable optical response of the metastructure configuration to an external stimulus.

Basically, there are two main subclasses of dynamically tunable geometries: spatially variable ones and temporally variable ones. While these will have to overlap to a certain degree, the main point of such differentiation will be their main physical target, be it spatial or temporal change or both together.

The goal of the first one is a modified spatial arrangement after tuning, while its duration is of less consequence (bear in mind that it does not mean of no consequence, since the period of reconfiguration will influence the overall performance and speed of the setup). This kind of adjustment process is significant for, e.g., metalenses with variable focal lengths or even with an ability to discern variable images, depending on the application requirements and the built-in spectral or multiplexing abilities of the lenses.

In contrast to the case of spatial tuning, in temporal tuning the accent is on the reconfiguration/switching speed and its synchronization with the system clock and dynamics. The main role of this kind of tuning is a real-time modulation convenient for work within synchronized systems (e.g., communications). Modulation can be carried out between different functional states, like phase switching or polarization tuning, amplitude modulation, etc. It requires different tunable materials and, in general, fast switching mechanisms.

Particular approaches to tuning will be related to the applicable physical tuning mechanisms. Obviously, they will also depend on the particular functional materials built into the metasurfaces that support the concrete kind of tuning.

Modulation mechanisms used with tunable/active metasurfaces can be divided into several distinct ones that actively modify the complex refractive index of metasurfaces, each with its own set of advantages and disadvantages. The following list presents some of the most important and most often met.

• Optical modulation is the fastest method of tuning metasurfaces, its ultrafast speeds even reaching the femtosecond to picosecond range. The control signal in this case is a light beam, so the system is all-optical, including both the hardware and the modulating signal. Typically, nonlinear optical effects are used (although they are not the only convenient mechanism). The external light beam intensity, spectral distribution or polarization are used to control the properties of the functional material of the metasurface.

The most usually applied functional materials for this type of tuning are nonlinear optical materials like, e.g., barium borate, lithium niobate, lithium iodate, different organic molecules, etc. [176,177]. Generally, such materials include plasmonic conductors, semiconductors, dielectrics and hybrid structures. Additionally, the presence of plasmonic conductors strongly enhances nonlinear effects in metasurfaces due to the plasmonic localization of the electromagnetic field and its creation of field hotspots [178]. Thus, such synergy between plasmonics and optical nonlinearity in hybrid metasurfaces enhances the metasurface performance and generates novel functionalities impossible to achieve with any of the mentioned components separately.

Some of the nonlinear phenomena used for metasurface tuning include second harmonic generation [179], third harmonic generation [180], higher harmonic generation [181], optical-parametric oscillation [182], optical rectification [183], four-wave mixing in metasurfaces [184], etc. Related nonlinear phenomena also have great importance, like the optical Kerr effect (a third-order nonlinear process of refractive index changes with the light intensity) [185] and the effects related to it like, e.g., self-focusing, self-phase-modulation, soliton formation [186], two-photon photochromism [187] and many more.

All-optical modulation methods of metasurfaces without nonlinear optical materials include the thermal effects of plasmonic phenomena due to extreme light localizations in hotspots; hybrid systems in which one uses embedding of materials with strong light–matter interaction into metasurfaces (examples would be the use of quantum structures in 2D single-atom or single-molecule planar materials like graphene or MXenes) where their interaction with the external control light beam results in all-optical effects; finally, there are structural changes in linear phase-change materials induced by external light beam, where either all-optically induced phase switching happens, or structural deformations are caused, including molecular reorientation. The creation of such all-optical modulation phenomena currently represents a significant challenge.

2.

Electric field modulation is probably the oldest and most well-established method for dynamically tuning the optical properties of metasurfaces [188]. It uses an external electric field to modify the complex refractive index (i.e., including absorption), and the structural characteristics of both the metasurface with its meta-atoms and of their surroundings. There are several mechanisms that are used for this purpose, depending on the functional materials used. One can use electro-optic materials like, e.g., lithium niobate or III-V semiconductors like gallium arsenide. The applied electric field can act through the Pockels effect, causing a linear response, or the Kerr effect, causing quadratic changes. Among the advantages of this method is that it is fast, while the technology of the incorporation of electro-optic materials, structures and even devices is mature, well-known and not only compatible with planar processes but directly belonging to them. Another approach is the use of 2D materials like graphene, transition metal carbides, nitrides or carbonitrides—MXenes (e.g., Ti₃C₂, Mo₂C, Ti₄N₃ and a lot more), or transition metal dichalcogenides—TMD (e.g., MoS₂, WS₂, etc.). Electric field changes charge carrier concentration in 2D materials, thus modifying their conductivity and the optical parameters related to it. This alternative approach also ensures a very fast response. One can make transistor structures enhanced with 2D materials, thus ensuring a further degree of control. Liquid crystals (nematic, cholesteric, columnar and smectic) are also an often-met group of materials when tuning metasurfaces by electric field. Their refractive index is thus changed, as well as the orientation of their molecules. One can tune the phase, amplitude and polarization of optical waves, but the speed is lower than that attained with, e.g., 2D materials or electro-optic setups. The next group are transparent conductive oxides (TCOs), where maybe the best known and most often used are indium tin oxide (ITO) and aluminum-doped zinc oxide (AZO). In these plasmonic materials, the electric field modifies both their carrier concentration and their plasma frequency. An example of the use of TCO in metasurfaces is gate-tunable field effect transistors (FETs) incorporating ITO or AZO, as described in the paper by Shirmanesh et al. [188]. In their ITO-gated FET they achieved simultaneously in the same device both dynamic light beam steering and its reconfigurable focusing. The next group is multiple quantum wells supporting intersubband transitions which, besides their optical and electric properties being controlled, also offer quantum effects. An example is multiple quantum wells based on III-V semiconductors which have been used for beam steering by metasurfaces through applying the quantum-confined Stark effect [189].

3.

Thermal tuning [190]. Many optical materials will have their complex refractive index dependent on temperature (the thermo-optic effect). In metasurfaces, this effect will be local because of their heterogeneous structure in which each constituent material has its own thermo-optic coefficient. In addition to that, if semiconductors or plasmonic materials are used, a temperature increase will result in a charge concentration increase, thus strongly affecting not only their refractive index but the plasmon resonance frequency and thus the whole spectral dispersion.

Another thermal effect is thermal expansion at elevated temperatures, which will also include geometry reconfiguration. Finally, in the case that thermally switchable phase-change materials are used, their internal structure will be switched. For instance, vanadium oxide transits from an insulator to a metallic material at 68 °C, which strongly affects its optical behavior. Thermal tuning of metasurfaces was described in [191].

4.

Phase-change materials—PCMs (e.g., vanadium oxide, chalcogenide glasses and especially Ge₂Sb₂Te₅ (GST), an optical material used in rewritable optical disks) are also used for tunable metasurfaces. A group of their own, their phase transitions can be switched thermally, optically and sometimes electrically. The manners in which these phase transitions influence the optical properties of metasurfaces are the complex refractive index change (including absorptive losses) and electrical conductivity. For instance, VO₂ switches from an insulator to a conductor with a temperature change. A rich and multifunctional use of PCM, or, more precisely, of GST in reconfigurable metasurfaces obtained by femtosecond laser pulses was described in [192]. Electrically tunable PCMs were presented in [193].

5.

Structural modifications through mechanical deformations as a tuning method for optical metasurfaces [194] mean the application of mechanical forces to modify meta-atom geometry (their overall shape and/or structure, including their height and width) or parts or even the whole metasurface through rearranging the relative position of meta-atoms on the metasurface (the distance among the elements is changed, thus modifying the periodicity of the unit cells or supercells). Both approaches modify the near-field interactions between meta-atoms. The mechanical forces can be applied directly (by stretching, pressing or straining the whole metasurface) or indirectly, by integration with some kind of actuators, for instance MEMS [195] or NEMS devices (nano-mechanical reconfiguration of metasurfaces) [196] or even microfluidic structures, whose microchannels can influence the metasurface geometry by applying pressure. Mechanical deformations can generally be local (acting with precision on some specific point or points, like for instance by pressurized fluidics) or global (using a flexible substrate for metasurfaces that can be stretched or compressed, e.g., an elastomeric material, and then applying mechanical force to it to modify its overall shape; another global method is shifting two distinct metasurface blocks in parallel) [15]. The resulting changes in the geometric parameters will affect the overall optical behavior of the metasurface. Flexible metasurfaces can also be bended or twisted, making out-of-plane deformations that influence the optical properties.

6.

Optofluidic modulation [197]. This includes microfluidic and nanofluidic changes. This approach represents manipulation with fluids at the microscale and possibly even nanoscale that changes the refractive index of the area around the structure by introducing their own, thus altering the optical properties of the metasurface. This ensures dynamic control of the metasurface electromagnetic response. A problem is a low speed, limited by the optofluidic kinetics.

7.

Chemical modulation [198]. Microchannel tubes filled with chemicals can be interwoven with the metasurface structure. The chemicals are used to modify the complex refractive index of the metasurface. Simple water or ethanol solutions can be used. If necessary, the chemical can be replaced by another.

8.

Hydrogenation/dehydrogenation cycle of transition metals [175]. If one exposes transition metal to hydrogen, a metal hydride is formed through the process of hydrogenation. The obtained material is a dielectric and its optical parameters are dramatically modified in that manner. The return to the previous metallic state is done by simply exposing the hydride to oxygen and thus performing dehydrogenation and resetting the optical parameters to their original value. This tuning method represents a switching process.

9.

Magnetic fields can be used in metasurface tuning when applied to magneto-optical materials, thus increasing Faraday rotation in Fano-resonant structures. A metasurface composed of ferrite rods and metallic foils was tuned by a magnetic field through adjusting the thickness of its ferrite rods, thus obtaining metasurfaces with different gradients of the rod thickness [199].

10.

Hybridized (multistimuli) modulation encompasses the cases when two or more of the above-listed methods are simultaneously used. These allow one to enter the tuning ranges unattainable by any single method. In addition to that, new functionalities are achievable. Zou et al. [200] introduced the concept of multistimuli metasurfaces and illustrated it by describing a liquid crystal on silicon metasurface which is at the same time responsive to electric and thermal activation and modulation. Copolymer metasurfaces with dual sensitivity to optical and thermal modulation were also described [201]. Simultaneous electric and magnetic tuning was presented by Izdebskaya et al. [202].

In-depth reviews of different tuning and modulation mechanisms for metasurfaces have been presented by Badloe et al. in 2021 [175] and by Yang et al. in 2022 [203]. They both systematically considered details of the selected approaches in a comprehensive manner. Some of the above-considered methods, however, were not handled in either of the two papers.

2.3.6. Digital Coding Metasurfaces

Digital coding metasurfaces [204,205] (often denoted only as “digital metasurfaces” or “coding metasurfaces”) represent a subclass of metasurfaces designed utilizing the principles of digital signal processing. They consist of subwavelength-sized meta-atoms that are also termed “pixels”, analogously to digital screens or bitmap images. Each of these meta-pixels can be designed with its own set of parameters, enabling it to cause a targeted discrete amount of phase shift (and sometimes amplitude change) of the input optical beam. Thus, a function not dissimilar to digital signal processing is obtained, but massively spatially parallelized.

Most often, the processing is binary, where zero corresponds to the digital bit of light “off”, i.e., phase shift being adjusted to 0 by the corresponding meta-pixel, while the “on” state corresponds to the meta-pixel assigning a phase shift of π to the optical bit. On the other hand, metasurfaces enable the designer to use a multi-level approach, where more than two discrete levels are applied (e.g., phase shifts of 0, π/2, π and 3π/2 will represent a four-level system—a quaternary digital metasurface). Thus, the phase is digitally modulated into a desired number of levels and in a manner with a desired degree of phase control precision. On the other hand, this can be further used to tune the phase profile at the output, and through such control to adjust the beam direction and actually the complete wavefront, but also to achieve, e.g., polarization control.

2.3.7. Intelligent Metasurfaces

Intelligent metasurfaces represent an advanced subclass of tunable metasurfaces [35,206,207,208]. They elevate the dynamic adjustability to the next level in the sense that they ensure its smart application by incorporating building blocks that ensure an automated response, thus enabling simultaneous control over the incoming raw signal (light or other type of electromagnetic wave), information (processing) and matter (typically nonlinear materials and generally a multifunctional material). To be able to achieve that purpose, they are conceptualized as fully active platforms that may at the same time incorporate sensors, signal feedback blocks and computational elements. The computational elements may have the form of embedded electronic devices that ensure signal processing in real time of both measured outputs or adequate control signals. The most complex autonomous operation can be ensured by using AI, most often machine learning. The latter ensures the integration of photonics with AI in optical nanostructures [208]. The intelligent metasurfaces may also use all-optical nonlinear computational elements and may perform different mathematical operations from basic arithmetics to differentiation and integration [209]. Some advantages of the latter are rather obvious—their speed will be much higher because the signals used are photons; also, the optical metasurface architecture will ensure massive parallelism of signals. The advantage of electronic devices is in their mature technology and all kinds of necessary components that are readily and widely available at an industrial level.

The properties of meta-atoms belonging to an intelligent metasurface are actively and autonomously reprogrammable through its merging with functional materials and by monitoring devices and procedures coupled with control mechanisms or algorithms.

Ding et al. proposed a metasurface-based quantum logic operator convenient for optical quantum computing on a large scale [210]. They implemented it as an all-optical diffractive neural network with spatial and polarization multiplexing that performs four principal quantum logic operations (Pauli-X, Pauli-Y, Pauli-Z and Hadamard gates). The network is based on a single hidden layer (actually a metasurface). Intelligent metasurfaces can also be built in the form of meta-holograms [155].

2.3.8. Neuromorphic Metasurfaces

Neuromorphic (brain-inspired) computing [211] represents the use of devices and architectures that mimic the structure and functions of the brain, in that way vastly improving information processing. Its main advantages over the conventional von Neumann architectures are that it offers a vast improvement of computing speed and complexity, while at the same time attaining much lower power consumption. Itself being an important paradigm in science and engineering, its use as a base for AI systems has been a subject of intensive research in recent years [212]. Among a plethora of different ways to implement neuromorphic hardware, electronics appears to be the most often used nowadays [212] (analog, mixed analog–digital and, less often, fully digital architectures that utilize various hardware devices, including standard transistor-based VLSI circuitry, but also memristors, spintronics, threshold switches, superconducting devices, etc.; very often, a hybrid method is applied where at least a part of the system is simulated in software). However, an increasingly important approach to neuromorphic computing is the use of optical metasurfaces [213] and other nanophotonics-based methods [214]. Among the wave-based approaches there is the use of nonlinear wave operations that include rogue waves, solitons, dispersion shock waves, etc. [215]. As well as in nonlinear neuromorphic metasurfaces, they can be implemented in other different physical environments that include polaritonics, Bose–Einstein condensates and even hydrodynamics [215].

Early approaches to optics-based neuromorphic computing (e.g., [216]) already noted many advantages of the all-optical approach over that based on electronics. However, a problem had been observed at that time with the minimum necessary dimensions of the building blocks of optical systems, which were of the order of hundreds of micrometers (compared to tens of micrometers in neuromorphic microelectronics and tens of nanometers in spintronics and superconductive devices [211]). The advances in plasmonic metasurfaces effectively eliminated the problem, since plasmonic circuitry has in the meantime been proven able to reach high packaging densities comparable to those of VLSI [34]. At that, one can observe that nanoplasmonics still keeps evolving and developing, while electronics is a quite mature field, with the end of Moore’s law being anticipated more and more frequently [217]. Most of the advantages of plasmonic metasurfaces are due to the extreme localizations of electromagnetic fields they exhibit.

The advantages of plasmonic neuromorphic metasurfaces over other types of neuromorphic architectures all stem from the inherent properties of all-optical circuitry [218]. A vastly augmented computing speed is one of the main beneficial properties of general neuromorphic hardware in its electronic-device-based form. In all-optical architectures, this is brought to an even higher level since their speed is determined by the light speed within the optical medium of the metasurface, a trait electronic devices cannot match. Metasurface-based all-optical implementations of neuromorphic architecture further strongly improve literally all the other benefits of neuromorphic devices as listed in the first paragraph of this subsection. They include much low power consumption (metasurfaces are, more often than not, fully passive and do not need any bias power worth mentioning; even when nonlinear materials are used, they can be brought to their operating point using plasmonic hotspot formations at extremely low overall levels of optical energy), very high speeds (the speed of light in metasurface materials will be obviously lower than that in vacuum but still much higher than that of electrons) and massive parallelization of processed data, both through spatial and wavelength multiplexing.

Figure 8 shows a simplified representation of a Huygens metasurface-based neuromorphic coder. A stack of metasurfaces is used, each with pillar-composed reliefs. The widths of pillars vary and each point hit by a light beam serves as a Huygens source spreading the signal further, thus modifying its phase and amplitude. A metasurface scatters the light in a manner corresponding to neural computing. The resulting signal after the end of the array is passed represents the coded output. The illustration is based on the diffractive neural networks presented by Lin et al. [219] modified by Wu et al. into a neuromorphic structure [220] to reduce the complexity of nanofabrication of the metasurface stack (phase delay is tuned by changing the lateral dimensions of the scatterers instead of the thickness of the material, the latter being postulated in the above-cited paper by Lin et al. [219]).

In their 2023 paper, Liu et al. considered their concept of photonic meta-neurons [221]. The authors state that their structures optically emulate biological neurons by using optical metasurfaces that modulate optical signals by applying high-dimensional and hierarchical processing to them.

3. AI for Metaphotonics

3.1. Introductory Remarks

It is a historical curiosity that the main developments in the metamaterials/metasurfaces field have been occurring almost in parallel with those in artificial intelligence, so that the main breakthroughs that have led to the linking of these two paradigms and the birth of their synergy literally appear as if they were meant to be merged. A graphical presentation of some parallel developments in the two areas since 2007 has been published in 2022 in a paper by Chen et al. [222], although the main discoveries in both fields had come much earlier. Another such diagram, given for a wider period of parallel developments in AI and metamaterials/metasurfaces, can be found in the in-depth review of information metasurfaces and intelligent metasurfaces by Ma et al. [206]. Their diagram work stresses the key developments in both fields since the very beginnings in the nineteen-forties until the publication of their paper.

The conventional approach to designing nanophotonics is to use some of the numerical simulation methods, for instance, Finite Elements Method (FEM), Finite Difference Time Domain (FDTD), Finite Difference Frequency Domain (FDFD), Rigorous Coupled Wave Analysis (RCWA), finite integration technique (FIT), generalized multipole technique, volume integral equation (VIE) methods, discontinuous Galerkin time domain (DGTD), Green’s functions method, etc. [223,224], and start from the geometry and materials to accurately determine scattering parameters and other optical properties. However, these methods are computationally expensive, especially when dealing with complex structures, and in some cases a non-negligible time is necessary even on supercomputers. A need for faster methods was obvious. One possible solution was to utilize AI methods.

AI methods represent an alternative approach to the design of metasurfaces in that they can learn from the exactly calculated examples. Upon a finished training, they are able to solve novel problems belonging to the same class in a much shorter time based on the data they learned from accurate simulations.

Mostly, two large groups of AI methods have been utilized to design and optimize meta-atoms and metasurfaces. The first group is metaheuristic methods, while the other is machine learning (ML) procedures (itself consisting of two subgroups, exact mathematical approaches and the use of neural networks). Hybrid solutions among all of these have also been met.

AI methods are often (but not always) observed as “black box methods”, not offering the user insight into the reasoning why some solutions have been preferred over others [225,226]—although many teams are currently dedicating their efforts to make the logic behind the results offered by AI more transparent and explainable [227,228,229]. Whatever the final solution of the black box controversy could be, machine learning methods have proven themselves immensely useful and are very often applied. An illustration of the strong current interest in such methods is visible from the fact that some review articles dedicated to the use of AI optimization in metamaterials and nanophotonics generally have already appeared in 2024 (for instance [230,231,232]). The following subsection briefly presents a classification of the AI methods available for metasurface design and optimization.

3.2. Overview of Some AI Optimization and Design Methods

This subsection broadly overviews and classifies some AI methods that could be used in meta-atom, meta-unit cell, supercell and full metasurface design and optimization. Generally, the methods can be categorized into three main groups, namely general heuristic methods, neural networks (NN) and complex approaches (e.g., hybrids of two or more heuristics and/or NN; multi-objective methods also belong to this group and are of special interest for metasurfaces). Each of these groups branches into further subgroups.

3.2.1. General Heuristic Methods

As far as the heuristic methods are concerned, these methods (that basically represent approximate algorithms) can be further divided into (1) heuristics in the strict sense of the word, i.e., “basic” heuristics, (2) metaheuristics and (3) hyper-heuristics (the highest-level approach that explores basic heuristics or metaheuristics, combines them or their parts and selects the most convenient ones to generate the optimal algorithms). Other heuristic methods that represent hybrids with other optimization methods have also been introduced, like matheuristics (hybrid of metaheuristics with exact mathematical optimization), learnheuristics (hybrid of metaheuristics with machine learning), etc. A sophisticated general classification of heuristics has been reviewed by Juan et al. in 2023 [233]. Figure 9 shows a block diagram representing the basic classification.

Basic heuristics themselves include a number of approaches. Some of them are Approximation Algorithms [234], Branch And Bound Algorithm [235], Constraint Satisfaction [236], Constructive Algorithms [237], Cutting Plane Algorithm [238], Divide and Conquer Algorithm [239], Greedy Algorithms [240], Hill Climbing [241], Iterative Improvement [242], Local Search Algorithms [243], etc.

Metaheuristic algorithms [244,245] represent iterative methods using an underlying “basic” heuristic procedure to smartly combine higher-level strategies for exploring the search space, avoid local optima and find an approximation for the global optimum. Metaheuristics are mimicking various natural or sociological phenomena (e.g., animal or human collective behavior, their physiological processes and plant behavior, but also mathematical procedures, physical, astrophysical and chemical phenomena, etc.) [246]. This mimicking is the reason why these algorithms are often designated as metaphor-based. The number of metaheuristic methods is huge and is still increasing. A 2023 publication by Ma et al. [247] analyzed a list of more than 500 metaheuristics and benchmarked many of them.

This paragraph very briefly summarizes some of the more important metaheuristics with an accent on those most often used in metasurface design and optimization. A classification can be made based on the number of units considered to be population-based or single-solution based. Another classification of metaphor-based algorithms can be made by grouping underlying metaphors into Evolutionary Algorithms, Swarm Intelligence Algorithms, those mimicking animal or human physiological processes, their sociological behavior, botanical processes, mathematical procedures, physical and chemical phenomena, geological, astrophysical, etc. Each of these can be further subdivided and in many cases these subdivisions can be further categorized into different groups. So, Evolutionary Algorithms can be subdivided into Genetic Algorithm, Memetic Algorithm and Differential Evolution; Swarm Intelligence Algorithms are especially numerous and they can be further divided into animal behavior, human sociology and anthropology, human and animal physiology, and plant physiology and processes. Finally, there are natural science-based algorithms that include chemistry, physics, geology, astrophysics and even mathematics. Figure 10 depicts this abbreviated taxonomy. A gentle introduction with more in-depth details on this topic can be found in [248].

Some prominent Swarm Intelligence Algorithms include Particle Swarm Optimization [249], Ant Colony Optimization [250], Gray Wolf Optimizer [251], Whale Optimization Algorithm [252], Bat Algorithm [253], Firefly Algorithm [254], Cuckoo Search Algorithm [255], Orca Predation Algorithm [256], Starling Murmuration Optimizer [257], etc.

According to the number of journal publications, Swarm Intelligence Algorithms represent the largest part of all metaheuristics, with nearly 50% of all and almost 70% of all bio-inspired ones [247]. Out of those, Particle Swarm Optimization by itself is the most applied Swarm Intelligence Algorithm. The most published algorithm among all metaheuristics is Differential Evolution. Simulated annealing, Artificial Immune System and Ant Colony Optimization are among the top few. A detailed analysis of these ratings can be found in the mentioned in-depth analysis [247].

The most often met metaheuristics in metasurface design and optimization reflect this overall situation. These seem to be Evolutionary Algorithms and Particle Swarm Optimization.

As far as hyper-heuristics are concerned, if this classification skips hybrid algorithms like the ones where hyper-heuristics are formed by merging metaheuristics with machine learning, the most prominent approaches seem to be Selection Hyper-heuristics [258] and Generation Hyper-heuristics [259], with Ensemble Hyper-heuristics as a subclass of the latter. Figure 11 summarizes this classification.

3.2.2. Machine Learning Based on Direct Mathematical Procedures

Machine learning generally represents a wide range of algorithms and tools able to process large datasets in various ways with the ultimate goal to “learn” from them and improve themselves over this process [260,261,262]. ML plays an extremely important role in modern data processing and belongs to the wider field of AI. A wide array of tools belong to ML, that can be roughly divided into exact mathematical procedures and various kinds of neural networks. The latter further includes deep neural networks as its most advanced and most well-known subgroup.

Figure 12 shows the described classification, together with the relative relations between the subgroups. It also shows their relative relation to general data science.

All machine learning methods can be divided into four general groups, the supervised learning groups, the unsupervised learning groups, semi-supervised and reinforcement learning.

Supervised learning denotes machine learning algorithms trained using previously labeled data within a given dataset, i.e., for which there is a need for human inference. The model learns a function that maps input data to output based on the learnt pairs of input–output data. The output prediction processes are task-oriented for supervised learning. The most common tasks of this type of machine learning are regression (data fitting, for continuous target variables) and classification (data separation according to the learned function, for discrete target variables).

Unsupervised learning algorithms are trained using unlabeled data. This is a data-driven process that does not have the need for human intervention. It is mostly used for the clustering and association of data within a dataset. Unsupervised learning recognizes meaningful structures, identifies trends, performs data grouping and generally performs data exploration.

Semi-supervised learning algorithms represent a combination of supervised and unsupervised learning. Typically, a training procedure observes a small amount of labeled data mixed with a much larger amount of unlabeled data. It can perform their classification and clustering. Semi-supervised learning is very convenient to detect outliers like, for instance, in fraud detection. In other words, this is both a task-driven and data-driven process.

Reinforcement learning algorithms are based on the concept of awards and penalties. This is an environment-based approach in which typically four elements are introduced: Agent, Environment, Policy and Rewards. The purpose of the algorithm is to enable agents to autonomously evaluate behavior within the given environment and to determine its optimum. Reinforcement learning is the most sophisticated of the four main groups of machine learning; however, it is not very convenient for simple and straightforward tasks. The most common tasks of this type of machine learning are control and classification.

Table 7. Four main classes of machine learning algorithms.

Learning Name	Approach	Label	Main Application Subgroups
Supervised	Task driven	Labeled	Classification, regression
Unsupervised	Data driven	Unlabeled	Associations, clustering
Semi-supervised	Task and data driven	Labeled and unlabeled	Classification, clustering
Reinforcement	Environment driven	N.A. (reward-based)	Control, classification

shows the four listed classes of machine learning algorithms. The kind of approach describing each one of them is presented, as well as if the data is labeled or not and the two main groups of applications for each class (actually, the number of applications per class can be—and often is—larger).

Table 8. Main application subgroups of machine learning with lists of names of some of their mathematical algorithms. No neural network algorithms are presented.

Classification	Regression	Clustering	Association	Dimensionality Reduction	Reinforcement
(Types: Binary, Multiclass, Multi-label)	(May overlap with classification methods)	(Partitioning, Constraint-, Density-, Grid-, Model-based)	(Discovering relationships of interest)	(Includes feature learning)	(Trial and error learning in an interactive environment)
Adaptive boosting	Least absolute shrinkage	K-means clustering	AIS association rule	Principal component analysis	Monte Carlo methods
Naive Bayes	Linear regression	Gaussian mixture	SETM	Analysis of variance	Quality learning (Q-Learning)
Linear discriminant analysis	Multiple linear regression	Mean-shift clustering	A priori	Chi square	State–Action– Reward–State– Action (SARSA)
Logistic regression	Polynomial regression	Agglomerative hierarchical clustering	Equivalence Class Clustering and bottom- up Lattice Traversal	t-Distributed Stochastic Neighbor Embedding	Temporal Difference (TD) Learning
K-nearest neighbors	Selection operator regression	Density-based spatial clustering of Applications with Noise	Frequent-pattern growth	Model-based selection
Decision tree			ABC-Rule Miner	Pearson correlation
Random forest			Frequent pattern growth	Recursive feature elimination
Gradient-boosted trees				Principal component analysis
Extreme gradient boosting				Variance threshold
Rule-based classification
Stochastic gradient descent

presents six main application subgroups of machine learning with the names of some of the most popular mathematical algorithms for all of them. Each of these subgroups belongs to the four main groups listed in the previous table. No neural network algorithms are presented in this table. They are treated further in their own separate subdivision.

3.2.3. Machine Learning Based on Deep Neural Networks

Neural networks (NN) as a whole are based on algorithms mimicking the data processing of living neurons. Probably the most popular and definitively the most powerful machine learning methods nowadays are those based on deep neural networks (DNN). They have even been called the core technology of artificial intelligence [263].

The basic unit in DNN and generally in NN that corresponds to a single neuron is the artificial neuron. It is a software unit having a large number of inputs x₁I₂, …, x_i, …, x_N, each of them being multiplied by some weight function w_i, while the middle unit performs the summation Σ of all inputs and applies an activation function (transfer function, e.g., Sigmoid, Hyperbolic Tangent, Rectified Linear Unit, Soft-max, Heaviside step function, etc.) f to the sum. The signal y obtained represents the output function. Thus, the artificial neuron mimics the data processing architecture of a natural neuron. Figure 13 is a schematic presentation of an artificial neuron. Other names used for an artificial neuron are node (usually drawn in schematic presentations as an empty circle), unit or simply neuron. If the activation function of a node is a simple Heaviside step function, then the often-used name for this node is perceptron.

When using the term perceptron, one has to be careful because the word also denotes the simplest, single-layer neural network architecture, capable of performing linear classification. Such a dual, context-dependent use for the same term may be a source of some confusion, since both meanings are simultaneously met in the literature. However, as mentioned, the contexts and levels are different (micro, where it denotes the simplest building block of neural networks with only a single artificial neuron, but also macro, denoting the simplest neural network, with only a single layer, but which may contain a larger number of artificial neurons). A perceptron network (macro form) can be also built of a larger number of layers, in which case it is denoted as a multilayer perceptron (MLP) network.

The basic artificial neural network (ANN) is built from at least three layers of nodes: an input layer, one (or more) hidden layers and an output layer (Figure 14) [264]. If an NN has a low number of hidden layers (typically one) then it is denoted as a shallow neural network. If the number of hidden layers is larger (from several to tens, even hundreds) the network is deep. The ANN is viewed as the prototype neural network since it is the simplest NN that can be built in both the shallow and the deep mode. It is now recognized that, while a shallow NN can solve some simple linear problems, the deep NNs are the architecture of choice when dealing with complex problems, which includes the design of metasurfaces, where in some cases complexities may be extreme.

An ANN uses a training algorithm also sometimes denoted as an optimizer. These algorithms are necessary to modify such neural network hyperparameters as learning rate or weights. A large number of optimizers is used. Among the more well-known ones are methods like Broyden–Fletcher–Goldfarb–Shanno (BFGS) quasi-Newton algorithm, Levenberg–Marquardt, Resilient Back-Propagation, Incremental Back-Propagation, Batch Back-Propagation, Gradient Descent, Stochastic Gradient Descent, Mini-Batch Gradient Descent, Gradient Descent Momentum, Nesterov Accelerated Gradient, Variable Learning Rate Gradient Descent, Conjugate Gradient with Powell/Beale Restarts, Polak–Ribiére Conjugate Gradient, Fletcher–Powell Conjugate Gradient, Scaled Conjugate Gradient, Variable Learning Rate Gradient Descent, Adagrad, Adadelta, Adaptive Moment Estimation (Adam), Bayesian Regularization, One Step Secan, etc. [265,266]. Metaheuristics can also be used for ANN training (for instance, genetic algorithms, PSO, etc. [267].

Since the hidden layers are the processing part and the heart of an NN, a larger number of hidden layers typically (but not always) means more sophisticated functionalities. In practical situations, which are strongly dependent on a particular ANN application, the number of hidden layers may range from several to tens and in extreme cases up to more than hundreds. As an example, the currently popular ResNet 152 convolutional neural network architecture [268] that has been, among many other purposes, used for the design of nonlinear optical diffraction patterns has 152 hidden layers. The raw information about the hidden layer number comes with a caveat, however, since the larger number does not always guarantee a better performance and the practical applications often disprove the point of view “deeper is better”. As an illustration, in the attention-mechanism-based approaches like Transformer Neural Networks [269], it has been observed that highly effective models are achievable with relatively modest network depths. Another word of warning is due here, since the “largest number” of hidden layers in a DNN is hard to define unequivocally, as it will often depend on how one defines a “layer” in different architectures.

Yet another ambiguity should be clarified here. The term “artificial neural network” (ANN), besides denoting the prototype neural network as described above, can also be used as an umbrella term for basically all other types of neural networks, including convolutional neural networks (CNNs), recurrent neural networks (RNNs), generative adversarial networks (GANs), Transformer Networks (TN), etc., because they are all built on the same underlying principle of the artificial neuron.

Table 9. Deep neural network classification into four main groups of ML based on supervision level.

Supervised	Unsupervised (Generative)	Semi-Supervised	Reinforcement
Convolutional Neural Network (CNN)	Generative Adversarial Network (GAN)	Deep Transfer Learning (DTL)	Deep Reinforcement Learning (DRL)
Recurrent Neural Network (RNN)	Autoencoder	Hybrid Deep Neural Network	Generalized Reinforcement Learning-based Deep Neural Network
Deep Belief Network (DBN)	Variational Autoencoder (VAE)	Graph stochastic neural network (GSNN)	Policy Gradient Networks
Physics-Informed Neural Network (PINN)	Self-organizing Map (SOM) (Kohonen Map)		Actor–Critic Networks
Transformer Neural Network (TNN)	Restricted Boltzmann machine (RBM)		Soft Actor–Critic (SAC)
Multilayer Perceptron (MLP)			Deep Deterministic Policy Gradient (DDPG)
Long Short-Term Memory Network (LSTM)			Twin Delayed DDPG (TD3)
Radial Basis Function (RBF)
Gated Recurrent Unit (GRU)

gives its contribution to NN taxonomy by showing a classification of some popular DNNs into the four main groups of ML based on their supervision level. One must be careful when performing such classification, because there are DNNs that do not belong solely to a single group. For instance, Fully Connected Neural Networks (FCNNs) [270], also known as dense networks, can be applied to all four groups, because these DNNs are adaptable and thus can be utilized in different manners, as determined by a specific goal. A similar point of view is generally valid for stochastic neural networks [271], since one can introduce stochasticity into NNs belonging to any of the four main groups.

Considering details of all the quoted DNNs would vastly surpass the scope of this overview. Thus, only a few of them that are of current interest for metasurface design and evaluation will be touched upon here purely as the most prominent examples.

Convolutional Neural Network (CNN)

Convolutional Neural Networks (CNNs) [213,272,273,274] are a class of supervised deep neural networks. They are built biomimetically, their inspiration being the visual cortex of animals. They are used with vast success in image analysis, being built to be adaptive and to automatically recognize the spatial hierarchies of image features. Because of that, they are very useful in general image recognition and the detection and classification of their objects. Their usefulness in the design of metasurfaces is rather obvious, since metasurfaces themselves can be observed as images of meta-atom shapes on a planar substrate.

There are several typical blocks in CNN architecture. The key ones are the convolutional layers which actually perform the convolution operations. They apply kernels (filters) to input images. In this manner, they create the spatial feature map of these images, including the edges of shapes they contain. CNNs learn the kernels automatically during the training process. After performing the convolution, an activation function is applied. Typically, this function is the Rectified Linear Unit—ReLU, a nonlinear activation function which returns the value of 0 if its input is negative and keeps all the existing positive values unchanged. Thus, it actually performs a rectifying role. The nonlinearity thus introduced allows the CNN to learn more complex representations of the processed image data. The next step is downsampling. This is done in pooling layers, and its goal is to decrease the computational load necessary for processing images. It reduces the feature map dimensionality while keeping its crucial information untouched. A regular fully connected multilayer ANN structure is connected after several convolutional and pooling layers. It performs the complex reasoning tasks of the CNN like feature classification. A logistic layer may follow the last fully connected layer, just before the output layer. Its task is to determine the probabilities for every input being in each of the determined classes. Figure 15 shows a simplified scheme of CNN architecture. The ReLU activation function is implied, while the logistic layer is not shown.

When used for the design of metasurfaces, CNNs are most convenient to automatically recognize periodic patterns and optimize them. Thus, they can make the design more efficient by improving some optical parameters like scattering or absorption.

Recurrent Neural Network (RNN)

Recurrent neural networks (RNNs) [275,276] are a class of supervised neural networks whose task is to deal with data sequences and to recognize patterns in these sequences or time series of data. They are often used in language processing and speech recognition. Their use in photonic design was dealt with in the paper by Ma et al. [277] where it has been shown that RNNs are convenient to model spectra in the temporal domain caused by different resonant modes. A consideration of the use of RNNs in inverse design in photonics has been considered in [278] and in metasurfaces in [279].

The characteristic features of RNNs are that they are able to use an internal memory when processing data sequences and to ensure bidirectional flow of information between nodes, i.e., in some cases the output of given nodes will subsequently affect the input of these same nodes. In other words, RNNs are characterized by their hidden nodes being cyclically interconnected. This kind of temporal dynamic behavior enables information to persist in RNNs over time. Thus, these NNs effectively exhibit memory capabilities and are enabled to learn sequences in this manner.

Confusion often occurs when recurrent neural networks are mixed up with the similarly named recursive neural networks (where the same set of weights is applied recursively over their input). Although the abbreviation for the latter is RvNN, both types of NN are often denoted as RNN.

Since challenges have been observed when training RNNs (like the vanishing gradient problem or exploding gradient problem that appears with backpropagated errors), several modifications of RNNs have been introduced to tackle these challenges. The most well-known among a number of the proposed ones are Long Short-Term Memory (LSTM) and Gated Recurrent Unit (GRU). Many different versions of RNNs exist but their description would be out of scope of this treatise. As an illustration, Figure 16 presents simplified node-maps of the standard RNN (left) and Long Short-Term Memory (LSTM) (right).

In the design of metasurfaces, RNNs are most convenient to predict the time evolution of an optical response. This property makes them applicable to optimize metasurfaces for various dynamic environments.

Transformer Neural Network (TNN)

Transformer Neural Networks (TNNs) [280,281] belong to supervised deep neural networks. They were first introduced in the seminal conference paper “Attention is All You Need” by Vaswani et al. in 2017 [282]. They presented a drastically disruptive approach to the manner sequences were processed by CNNs and by their modifications LSTMs and GRUs. The consequence was that it became the foundation of a majority of modern NN systems in natural language processing. Transformer NNs do not process data in a sequential manner. Compared to CNNs, LSTNs and GRUs, Transformers are able to parallelly process entire sequences. A reduction in training times stemming from it compared to the earlier sequential methods is obvious.

The Transformer architecture includes an encoder and decoder. The encoder introduces the input sequence and generates its fixed-size vector representation. The decoder uses self-attention and cross-attention, and generates the output sequence based on the vector representation by the decoder.

It can be seen from this description that there are several fundamental blocks of the Transformer model. The core one is the self-attention mechanism that computes the attention scores (or weights) by comparing each element in the input sequence with every other element. In other words, this sublayer enables each position in a given sequence to lend its attention to all positions in the previous layer by being applied to the encoder output and decoder input. This ensures the possibility that the model catches complex relationships and interdependences among the sequence data. The advantage is that the mutual distance between data in a sequence is not a factor like in, e.g., RNNs, i.e., the model functions at long distances. The attention mechanism is applied to the output of the encoder and the input of the decoder.

The attention mechanism is further enhanced by introducing cross-attention. This splits the self-attention mechanism into multiple “heads”, thus enabling parallel attendance to information located at different positions. Since Transformers do not perform sequential data processing, they encode positions together with data instead. In that way, the knowledge about the position in a sequence is retained. Each sublayer has a residual connection around it. This is followed by normalization. Finally, each layer has a feed-forward neural network. Both encoder and decoder consist of multilayers of self-attention and feedforward neural networks.

Although primarily dedicated to dealing with sequential data like language processing, but using massive parallelism, Transformer networks are useful in the inverse design of metasurfaces. An example is the work of Huang, Feng and Cai [281], published in 2024. Another example from the same year is for SERS-based metasurfaces, as published by Cai et al. [280]. When designing metasurfaces, TNNs drastically improve both the accuracy and efficiency of a multifunctional approach in the usually large design spaces. This is a consequence of their parallelism, enhancing their ability to focus on the most important and most influential parameters.

Generative Adversarial Network (GAN)

The generative adversarial network (GAN) [155,283,284,285,286] is an unsupervised generative deep neural network. Although unsupervised operation is basic for this type of DNN, GANs have been successfully applied in semi-supervised and reinforcement learning. GANs are designed to solve generative modeling problems, i.e., to generate new data based on the learned training examples that mimic real data, and ultimately are indistinguishable from them. To this end, a GAN is built in two parts, the generator DNN and the discriminator DNN, that are pitted against each other during training (the generator–discriminator “game”). The generator attempts to generate fake data that look as close to real as possible, while the discriminator’s task is to find out which data are fake and thus help the generator to improve its subsequent attempts. The training ends when the discriminator becomes unable to distinguish between fake and reaIta, which means that the generator has reached the point at which it produces data with a satisfactory level of quality. A simplified flow chart of GAN architecture is shown in Figure 17.

Different objective functions can be used for GANs, depending among other things on which generator–discriminator adversarial game is used for training. These games include the original minimax game, maximum likelihood game or non-saturating game. Problems may appear during training, and the most challenging are mode collapse (if the generator learns to make only a low number or small variety of samples), non-convergence (if instabilities/oscillations occur) or vanishing gradients (the discriminator performs too well in too short a time, thus hindering the generator from learning with sufficient quality). A number of modified versions of GANs exist, among them Wasserstein GAN, Conditional GAN, InfoGAN, Integral Probability Metrics, etc. [284].

GANs are typically used to generate realistic images and other data and to achieve image super-resolution (processing low resolution originals to enhance their resolution). Since they are related to images, they are naturally applicable to metasurfaces. When designing metasurfaces, they facilitate rapid prototyping through the creation of new design variations by the adversarial approach, thus iteratively improving the design parameters and reaching the optimum properties and performance. A number of related journal papers were published dedicated to that topic [155,283,287,288].

Autoencoder

An autoencoder [289,290,291] is an unsupervised neural network. Its main task is to learn as efficiently as possible encoding of the input data, usually with a goal either to reduce the dimensionality of the dataset or learn its features to achieve more efficient ways to represent them and use them, e.g., in classification tasks. The task is typically achieved by encoding the input from a high-dimensional form to a lower-dimensional code (and thus compress it to latent-space representation). The subsequent step is to decode such data to make the output containing reconstructed data maximally similar to the original input. Thus, autoencoders are trained by minimizing the reconstruction loss (the differences between the original input and the decoded output). Because of that, the autoencoder neural networks consist of two main blocks, the encoder and the decoder. During the training process the weights of the encoder and decoder are adjusted to minimize the mismatch between the input and the output. Thus, the main goal of autoencoders is to render complex data using the minimum amount of code while at the same time minimizing (ideally: fully avoiding) compression losses.

A number of autoencoder variants exist, createI either as improvements of the basic form or as solutions to reach specific properties and extend the applicability fields. These include Variational Autoencoder, Denoising Autoencoder, Convolutional Autoencoder, Deep Autoencoder, Sparse Autoencoder, Contractive Autoencoder, Undercomplete Autoencoder, etc. Figure 18 shows a node map of an autoencoder of a deep network type.

Among other fields, autoencoders have been used in image processing (like denoising, dimensionality reduction), analysis (feature learning to be utilized for classification, detection of outliers) and generation of new images based on the learned training data. These peculiarities make them convenient for use in nanophotonics, especially in 2D. When used in metasurface design, they compress and decompress the design parameters, which improves the efficiency of design space exploration. Their ability of dimensional reduction makes them very convenient to efficiently use a minimal data input to reach optimal structuring and configuration. They have been applied in numerous metasurface designs [205,292,293].

Other Types of NN

Many other important types of neural networks are also used to design metasurfaces, besides those well established and chosen to be presented above. Some of them include physics-informed neural networks [294], Invertible Neural Networks [295], Siamese Neural Networks [296], Memory-Augmented Neural Networks for Meta-Learning Models [297], Neuro-Symbolic Networks [298], Capsule Networks [299], Graph Neural Networks (GNNs) [240,300], Neural Ordinary Differential Equations [301], even the recent and potentially very powerful Quantum Neural Networks [302,303] (with subdivision to Quantum versions of classical neural networks, Hybrid Quantum–Classical Neural Networks and Quantum-Inspired Neural Networks). The alternative NN types at the beginning of this list have been introduced recently and they already display numerous desirable traits, meaning that it may well be that their high potentials could be widely used in the future. The text below briefly mentions two NN algorithms that in the opinion of the writer of these lines merit special interest in the world of metasurfaces.

Physics-informed neural networks (PINN)

PINNs [304] are artificial neural networks that embed in their code the knowledge of general physical laws, under the condition that these laws are describable by partial differential equations (PDEs) which are usually nonlinear. The inclusion of PDEs in the learning process enables easier machine learning in PINNs and thus finding the right solutions with a vastly smaller amount of training data. The method was first introduced in 2017 by Raissi, Perdikaris and Karniadakis [304] (the cited paper is from 2019, but the proposal by the team first appeared in 2017 in arXiv). The same team published very soon afterwards a review on PINNs in Nature Reviews Physics [294] which received about 3000 citations in a very short period of time, proving the expected usefulness of this physics-augmented approach in the eyes of the scientific community. PINNs readily accept the Maxwell equations/Helmholtz equation, which makes them very convenient to work with metasurfaces. This ensures at the same time much faster calculation and higher accuracy. Examples of the use of PINNs with metasurfaces include the papers [305,306,307,308] and many more.

Invertible Neural Networks (INNs)

Invertible Neural Networks are unsupervised neural network algorithms convenient for the machine learning of probabilistic models. They are reversible by design. That is to say, if their output is known, one can unequivocally recover their input. This property allows them to be used for finding simple and quick solutions in all fields where inverse problems are met. The most important trait of an INN is its architecture consisting of layers with an invertible design, which ensures the inversion of the INN function. Since the knowledge of the Jacobian determinant of the transformation is necessary to peIform proper iIversion, t”e IN’ architecture also ensures a fast and efficient computation of that determinant.

Historically, the pivotal publications that introduced this approach are two arXiv texts by Dinh et al., one from 2014 that introduced the framework for learning invertible transformations, based on learning a nonlinear deterministic transformation that maps the data to a latent space and make it conform to a factorized distribution [309]. Another one was from 2016 and it further advanced the approach through a demonstration of a scalable and practical process of training deep invertible networks [310].

Owing to their invertibility, INNs can be used in optical metasurfaces to perform the dual task of forward and inverse modeling, thus ensuring the usability of these networks in design and surrogate simulation. For instance, in 2023, Wang et al. used an INN for metasurface design and evaluation [295]. The use of INNs in related fields has been illustrated by Fung et al. by carrying out the inverse design of 2D MoS₂ for memristive neuromorphic applications [311].

3.2.4. Hybrid ML Models

Hybrid approaches include the simultaneous use of two or more methods with the goal of leveraging their individual strengths at the same time. The hybrid methods make use of the complementary strengths of their constitutive blocks to tackle the extremely complex nature of metasurface problems which often include highly interconnected and complicated inter-relationships among different parameters, are inherently nonlinear and have high-dimensional design spaces.

This text assumes that there are six main groups of methods that can be hybridized. They encompass (1) neural networks, (2) other machine learning techniques, (3) heuristics (including basic heuristics, metaheuristics and hyper-heuristics), (4) exact mathematical models (these may be physics-based or operation-research-related, including tree and forest methods, dynamic programming and constraint programming), (5) fuzzy logic and (6) statistical techniques, including statistical machine learning. Any combinations are possible among almost any members of the six quoted groups (inter-hybridization), as well as within the same group (intra-hybridization). Some of the above methods can be modified to be usable for multi-objective optimization and these multi-objective approaches can also be included into hybridization schemes. The topic of multi-objective optimization is covered in the following subsection.

One of the obvious and often-chosen paths is the hybridization of neural networks with metaheuristics. An example of this path is a procedure where a metaheuristic approach explores global optimization by mimicking natural processes, while NN models, trained on data from simulations or experiments, perform pattern recognition, generative operations, data-driven predictions, surrogate simulations, etc., thus reducing the overall computational load and improving accuracy.

Another frequent method is hybridization between neural networks and exact mathematical procedures. One very important class of this has already been considered in this text, in the part on physics-informed neural networks where an artificial neural network algorithm is hybridized with nonlinear partial differential equations, which vastly accelerates and streamlines the generation of learning datasets.

Further, one can use hybrids of two or more neural networks, combining their individual strengths to resolve the problems encountered when modeling a specific metasurface. An example would be a combination of a CNN (processing structural information) and dense NN (correlating the structures under consideration with their optical parameters). Another example is autoencoder–CNN combinations (the first one generates a compact encoding of the metasurface structure, while CNN then calculates its optical properties).

Another possibility is the hybridization of two or more heuristic algorithms, including any of the basic heuristic, metaheuristic or hyper-heuristic approaches. Some of these approaches may be efficient in local search, while the advantages of others are related to global search. This is largely covered by hyper-heuristic procedures which can generate their own meta-procedures built from parts of usual metaheuristics like genetic algorithms, particle swarm algorithms and many more.

The ability of hybrid ML models to combine different AI architectures enables them to solve complex tasks in metasurface design. Thus, these methods are convenient for, e.g., simultaneously optimizing multiple parameters or ensuring metasurface optimal function under widely varying operating conditions.

3.2.5. Multi-Objective Optimization

In many situations, problems have more than one objective function. Such functions often pose conflicting or competing requests. They must be simultaneously optimized. The solution of such a problem is known as multi-objective optimization [312] (also known as Multi-Criteria Optimization, Multi-Attribute Optimization, Vector Optimization and Pareto Optimization). The solution space in this case is multimodal. Solving a multi-objective problem generally means determining a set of solutions with some kind of trade-off between its objectives. The best possible multi-objective trade-off solution set is denoted as Pareto set (a set with Pareto-optimal solutions). No other solutions exist that perform better than the Pareto set for one solution without being worse in another solution. Expectedly, multi-objective algorithms are much more complex than single-objective algorithms.

Some examples of multi-objective (MO) metaheuristics include MO Genetic Algorithm [313], MO Differential Evolution [314], MO Particle Swarm Optimization [315], MO Ant Colony Optimization [316], MO Artificial Immune System [317] and many more. The field of MO metaheuristics is huge. The repository of publications and software dedicated solely to Evolutionary Algorithms [318] contains more than 10,000 books, articles, presentations, dissertations and software items. The interested reader is also directed to a book on MO Evolutionary Algorithms [319] with its in-depth approach.

Artificial Neural Networks are also being used for multi-objective optimization [320]. The use of MO NN-based surrogate modeling is used in [321] for situations when the problem includes uncertainty problems. Related to surrogate models in MO, Gaussian processes were described as great tools to generate them [322]. Another large group are MO Reinforcement Learning Methods [323,324].

The multi-objective optimization methods are a natural choice for the design of metasurfaces, since as a rule this kind of design simultaneously poses multiple objectives. Thus, MOs are almost ideal for optimizing the performance of a whole metasurface system by balancing its trade-offs. An example would be simultaneously optimizing metasurface diffraction efficiency, bandwidth and angular dependency.

3.3. AI and First-Principles Analysis for Metasurfaces through Surrogate Modeling

As mentioned in Section 3.1, it has been customary for a long time to approach the design of electromagnetic structures, devices and systems and their interaction with electromagnetic fields starting from the first principles (ab initio) through solving Maxwell equations for a given set of boundary conditions directly, i.e., without relying on empirical data or simplifications of the models. Since this is an extremely complex task that does not allow analytical solutions except in a handful of very basic cases, numerical methods have soon become the approach of choice. The simulation techniques quoted in Section 3.1 include FEM, FDTD, FDFD, RCWA, FIT, generalized multipole technique, VIE, DGTD, generalized multipole technique, Green’s functions method, etc.

As said in Section 3.1, all the simulation methods quoted in the previous paragraph are computationally expensive. On the other hand, as a rule, first-principles calculations dedicated to modeling meta-atoms and metasurfaces are extremely complex and thus computationally demanding, while the analysis of their whole design space is often next to impossible for similar reasons.

This subsection considers an alternative method to direct simulations that ensures much faster first-principles analysis—the use of surrogate modeling [325] by applying AI for this purpose [222]. To obtain a surrogate model, the user first trains a chosen network with the already existing data from simulations obtained using some of the above-quoted techniques. A lower amount of training data is sufficient if a physics-informed neural network is used. After such training, a wide enough design space will be defined and the neural network will be able to deliver an approximate solution of the first-principles problem—or multitudinous solutions, if the problem definition allows it. What AI has learned from data generated by ab initio optical simulations will predict the output results for new designs much faster than the above-mentioned traditional simulation methods. This leads to high acceleration of the calculation cycle, often thousands of times faster, in many cases even more. The described role in accelerating calculations is probably the most important trait of AI-based surrogate modeling.

Besides rapid predictions through surrogate models, there are other AI contributions related to the first-principles analysis. Among them are complex multi-objective optimization tasks that readily search large parameter spaces, often finding parameter sets that would otherwise be missed because of the overwhelming computational power needed for similar searches using conventional methods. Ab initio calculation enhancement by DNN can also help correct systematic errors in the conventional simulation tools themselves. Another useful application of this approach is that it may bring completely novel meta-atom and metasurface designs using generative neural networks. Related to this is predictive modeling, where AI models will anticipate how design changes of meta-atoms/metasurfaces will modify the output performance of the system, thus saving still more computational time.

Regarding examples of the helpfulness of AI-assisted ab initio calculations, one can quote Zhang et al. [326] who used two types of AI, genetic algorithms and deep neural networks (“Predicting NN”), to analyze a large number of meta-atoms, thus obtaining the desired absorption enhancement of a metasurface, while at the same time achieving four orders of magnitude faster calculations. Kuhn, Repän and Rockstuhl [327] designed core–multi-shell particles for light scatterers and used their surrogate model to calculate scattering parameters with a speed about four orders of magnitude higher than when applying classical Mie theory. Pestourie et al. [328] published in 2023 their “physics-enhanced deep-surrogate” ab initio method for the solution of various physical problems based on partial differential equations which they exemplified by analyzing complex meta-atoms. They showed that their system reduced the need for training data by at least a factor of 100.

One can see that AI-assisted ab initio modeling represents an excellent choice to calculate complex meta-atoms and metasurfaces with large degrees of freedom. Besides offering vastly higher speeds compared to traditional simulations, it ensures different complex multi-objective optimizations, partially or even fully new designs (as long as they are generated within the DNN object space), even error corrections of the initial simulation code.

3.4. Forward Design of Metasurfaces

The forward design of metasurfaces using AI actually takes the traditional path and its input data are the metasurface geometry and composition. This includes the information on all the building blocks, i.e., the size, shape, building materials and spatial arrangement of the meta-atoms, as well as the geometry—e.g., the profile—and composition of the metasurface host itself. The output data are the optical properties, like the spectral dispersions of scattering parameters (reflectivity and transmissivity), absorption, phase shift, polarization and actually any parameters that will ensure designing metasurfaces with tailored functionalities.

The point where this kind of design differs from the traditional, simulation-based forward designs is that AI ensures the prediction of output parameters that were not numerically simulated previously, obtained using sample-based learning. One of the approaches will be surrogate modeling. The accurate prediction process is crucial in obtaining metasurfaces with functionalities tailored to targeted practical applications.

The main AI methods used in forward design are metaheuristics and deep neural networks (DNNs). Their approaches to exploring the tremendously large and vastly multidimensional design spaces are based on their own peculiarities and differ between themselves.

3.4.1. Forward Design Using Metaheuristics

Among metaheuristic algorithms, the most often used ones in the forward design of metasurfaces are Particle Swarm Optimization (PSO), Genetic Algorithms (GAs) and simulated annealing (SA). Hybrids of two or more metaheuristic procedures have also been applied. For instance, in 2023, Xu et al. [329] used a hybrid metaheuristic approach by combining Particle Swarm Optimization (PSO) with a Genetic Algorithm (GA) to forward design several different beamsplitters based on multilayer metagratings.

The generic process flow when applying heuristics in the forward design of metasurfaces can be outlined in several steps. (1) Defining objective function. This step is performed to quantitatively relate the geometry/material with the targeted optical behavior and to ensure a comparison among different designs. (2) Initialization of candidate solutions. A larger number of competing metasurface designs is defined for varying parameter sets. (3) Evaluation based on the defined objective function. The function can be defined using analytic models (in rather simple cases), numerical simulations like, e.g., FEM or FDTD or by directly measuring experimental results. (4) Candidate selection. Candidates to be kept for the next generation are selected among the existing ones according to the evaluation results obtained in step (3). Different selection mechanisms may be used for that purpose, including but not limited to proportional selection (roulette wheel, stochastic universal sampling), tournament selection, rank-based selection and truncation selection (elitism). (5) Operators are applied to the existing sets to create new candidates that will replace those rejected during selection step (4). Depending on the specific metaheuristics used they may be velocity and position update in particle swarms, crossover or mutation in genetic algorithms, etc. (6) Iterative process. Depending on whether the termination criterion is fulfilled (e.g., satisfactory solution reached or maximum number of iterations exceeded), the optimization procedure is either finished or returned to evaluation, selection and generation step on repeating. (7) Process output. The set of fully optimized design parameters for a forward-designed metasurface is reached.

The simplified flowchart of the described generic metaheuristic procedure is presented in Figure 19 left. Bear in mind that many specific metaheuristics exhibit different process flows, sometimes even drastically different, so the flowchart in the figure should be understood as an illustrative example only.

3.4.2. Forward Design Using Deep Neural Networks

Among deep neural networks that have been used in the forward design of metasurfaces, it is worth mentioning convolutional neural networks, then recurrent NNs and generative adversarial networks. The generic process flow when applying DNNs in the forward design of metasurfaces can be outlined in several main steps. (1) Dataset preparation. After choosing a starting geometry and photonic materials, one usually uses numerical simulations or experimental results, although in some situations analytical calculations may be utilized as well. Typically, several metasurface designs are considered. (2) Neural network choice/design. A NN architecture (most often convolutional, although a number of other DNNs are used, including generative ones) is designed based on its capability and convenience to learn the relationship between the geometrical/material design of the metasurface and the resulting optical responses; in many situations physics-informed NNs are used because quite large datasets are needed for proper learning procedures and PINNs enable a significant decrease in the dataset size since they define a general form of dependencies. (3) Training. The designed NN is trained on the predefined design dataset. It is based on minimizing the difference between the optical properties the NN predicted and the real ones. Gradient-based optimization algorithms are typically used for this purpose (e.g., stochastic gradient descent). (4) Evaluation. A part of the datasets separated from the learning ones is used to apply the NN after the learning procedure and assess the achieved accuracy of the prediction, as well as its general advantages and disadvantages. After evaluation and the learning process have been successfully finished and tested, the NN is ready for exploitation. (5) Prediction. The use of the NN for repeated rapid determination of the optical properties of a larger number of new metasurface designs by the trial-and-error method until the targeted optical properties are reached with a satisfactory accuracy. This approach can be regarded as surrogate modeling (or metamodeling) since it gives a parameter set without a need for either full simulation or experimental implementation. Surrogate modeling is generally a very useful and often utilized approach in AI design and the optimization of metasurfaces.

A simplified flowchart of the described procedure is presented in Figure 17 right. It does not encompass the use of PINNs or similar solutions, but serves as a generic representation of NN-based forward design.

Based on the considerations presented in this subsection, one can see that both metaheuristics and DNNs have their own advantages and disadvantages. Among the main strengths of metaheuristics are their power to perform accurate optimizations needing only relatively modest-sized datasets, contrary to DNNs which require large collections of data. On the other hand, DNNs are vastly faster once their training is finished and are able to perform very complex mappings between the metasurface designs and the targeted optical behavior. This is the reason why hybrid approaches are often used, combining at the same time the strengths of metaheuristics and DNNs.

3.5. Inverse Design of Metasurfaces

Inverse design of metasurfaces starts from the desired output optical function(s) or performance and determines the optimal structure or parameters that ensure it and that are related to the design and optimization of separate meta-atoms, their unit cells, their supercells (if any) and the overall properties of the metasurface [330]. Such optimization problems are highly complex because the relationship between the design space (geometry and materials) and the objective space (the desired optical function and performance from which the optimization is started) is typically both nonlinear and high-dimensional. Because of that complexity, the role of AI is crucial in this field. Inverse design is in many cases more efficient than forward design since its prime target is the desired output (the required optical properties).

There are two techniques utilized for the inverse design of metasurfaces. They include Topology Optimization [331], iterative changes in the design space with a goal of determining the optimum material distribution that satisfies the targeted objectives and constraints, and Adjoint Method [332], an optimization technique calculating the gradient of the objective function with respect to the design parameters.

Regarding the mentioned gradient of the objective function, two general approaches are applied in inverse design, the gradient-based (as used in the Adjoint Method) and gradient-free one (for Topology Optimization). As its name suggests, the gradient-based approach needs the derivation of gradients of the objective function with respect to each of the design parameters to guide the search for optimal solutions. Obviously, the basic requirement is that the gradients of the objective function exist and are either easily calculated or approximated, which directly defines the efficiency and the applicability of the method itself. It is most convenient for this approach if the objective function is smooth. In some cases, the method may happen to be sensitive to the choice of the initial and boundary conditions and may get stuck in some of the local optima. The positive property of the gradient approach is its convergence speed. One can conclude that gradient-based approach efficiently explores well-defined design spaces and deals well with higher dimensionalities.

The gradient-free approach does not depend on the derivatives of the objective function. This makes it particularly convenient for the cases when the derivatives of the objective function do not exist in the whole domain or some of its parts—i.e., when the function is discontinuous or non-differentiable. It is also the method of choice when the objective function is noisy. Finally, it is convenient in situations when the derivatives are either difficult or impossible to compute. The price to pay is that the methods belonging to this approach are often computationally expensive (requiring more function evaluations to converge) and slower than the gradient-based ones. The gradient-free methods especially tend to slow down as the dimensionality of the design space increases. Here, one can conclude that the gradient-free approach works efficiently for broader exploration when the design space is highly complex and interactions are less predictable, but deals less well with higher dimensionalities.

3.5.1. Metaheuristics for Inverse Design of Metasurfaces

Metaheuristic methods belong to gradient-free approaches. Among a great multitude of methods in this group, it appears that those most frequently met in inverse design are genetic algorithms, a few of the particle swarm algorithms, simulated annealing (multi-objective forms are preferred) and hybrid approaches combining the advantages of two or more metaheuristic or hyper-heuristic methods.

Although metaheuristics have been utilized to perform the inverse design and optimization of metasurfaces, they were less used for that purpose, that frequency decreasing over time. The reason is that compared to neural networks their computational costs are often formidable (hours and even days for metaheuristics versus seconds for DNNs). Also, one usually has to resort to the intensive use of numerical simulations in parallel with metaheuristics [333].

In spite of the mentioned problems related to the inverse design of metasurfaces using heuristics, some teams nevertheless use algorithms belonging to that gradient-free approach. A good example is a Science article published in 2023 by Xiong et al. [334] in which a combination of a genetic metaheuristic algorithm and an iterative Fourier transform algorithm were used to design a metasurface-based holographic memory storage medium with significantly increased memory capacity. The enhancement has been attained through a cross-talk decrease enabled, paradoxically at first glance, by deliberately introducing engineered noise. Another recent example is the work of Digani et al. [335] who utilized several metaheuristic methods (GA, PSO, SA) to search for global optima on non-smooth search spaces with high irregularities and with more than 60 optimization parameters, and concluded that PSO offered the best performance. Jin et al. [336] used a segmented hierarchical Evolutionary Algorithm to inverse design meta-holograms using large pixels to speed up the procedure.

3.5.2. Deep Learning NN for Inverse Design of Metasurfaces

Deep learning neural networks belong to gradient-based approaches. They represent the largest and most often used group of AI procedures for the inverse design of metasurfaces. The DNNs themselves have been briefly presented in subdivision 3.2.3. of this text, so in this subdivision just some DNN flowcharts are shown specifically tailored for the inverse design of metasurfaces.

The most often met DNN type for the said purpose is definitely the convolutional neural networks. At the start of a CNN inverse procedure, a targeted optical function (or a set of several such functions) is defined. Then, a dataset is generated consisting of metasurface structures paired with their optical responses. The full set of optical responses for each structure can be obtained by “brute force” numerical simulations, by experiments or by combining the simulations with surrogate modeling. Surrogate models [337] help cover a much wider variety of metasurface designs. The next step is preprocessing the dataset to prepare it for training the CNN. This means making three separate sets, one each for training, validation and testing. Possibly, this step may include dataset normalization as well as its enhancement to boost its diversity and the number of units. CNN training follows, which includes the optimization of network weights and biases using a gradient descent optimization algorithm (or, in hybrid systems, some metaheuristic procedures). The training result is the predictive model to be further used in the inverse procedure (CNN learns to predict the optical response for a metasurface structure unknown to it). The performance of the trained CNN is further evaluated on the specifically pre-defined test set for its accuracy and generalization capabilities, in other words, based on its performance metrics. In this step the CNN refinements can be performed by fine-tuning its hyperparameters, the CNN architecture itself or the applied training process. Only at this point can the inverse design start by giving an input (desired optical response) to predict the adequate CNN to generate such a response. During this stage, additional refinements and optimizations of the algorithm may be carried out. As the final step, the CNN output metasurface structure may be verified by “brute force” physics-based simulations or experimental works. The described process flow is shown as a flowchart in Figure 20 left.

The basic form of flowchart for the RNN inverse design of metasurfaces is similar to that of CNNs. The differences are related to the nature of the RNN and include the following: after performing the dataset collection/generation, it may be necessary to structure the data so as to stress its sequential or time-dependent properties. For instance, they may reflect the temporal changes in the optical field during its interaction with the metasurface. A similar consideration is valid for the preprocessing stage, where, besides the steps performed for CNN, it may be necessary to modify the data to a sequence form. Further, when selecting and designing a convenient RNN architecture, one should consider alternative designs besides the basic one, for instance Long Short-Term Memory (LSTM) or Gated Recurrent Unit (GRU), since it may be essential for some inverse designs to be able to capture long-time data dependencies, especially in tunable, reconfigurable and generally higher-complexity metasurface systems and interactions. It may be necessary to design the RNN to accept electromagnetic field evolution. When training the RNN, besides the usual steps as seen in the CNN process flow, one may wish to utilize a loss function that reflects with accuracy the difference between the network’s predictions and the actual data, where the RNN’s weights are tuned through backpropagation. The flowchart of the RNN is shown in Figure 20 Middle.

Similar consideration of the flow process organization is valid for the Transformer Neural Network method. While in principle its flowchart is similar to those of CNNs or RNNs, there are particularities of TNNs at some critical points that must be taken into account. For the data preprocessing step, it is crucial to perform data normalization and encoding in a Transformer-friendly form. This may require altering spatial designs into sequences or performing the tokenization of physical properties (encoding them as smaller units). When designing and adjusting Transformers, an appropriate architecture should be chosen (the standard Transformer model or some of its variants optimized for the specificities of the metasurface under consideration). When training a Transformer procedure, one should choose a suitable loss function quantifying the difference between the predicted and the actual designs. It is to be optimized by the gradient-descent-based approach. The Transformer flowchart is shown in Figure 20 right.

The next topic of consideration is generative models for the inverse design of metasurfaces. Flowcharts for both GANs and for autoencoders appear rather similar to that for CNNs. The differences in the GAN case are in key details belonging to some of the items of the flowcharts. These include data conversion into a format convenient for the GAN during data preprocessing and selection of an appropriate GAN architecture during the GAN design step. The same step includes setting the generator to output metasurface structural designs while the discriminator should evaluate the performance of both generated and real designs. The training step itself proceeds in a manner standard for GAN, i.e., by alternately updating the generator and discriminator.

In the case of autoencoders, one of the main differences is in the training step, since the NNs should learn to minimize the reconstruction loss when dealing with the starting dataset. A mean squared error is convenient for the loss function, while binary cross-entropy is appropriate if the data are binary. In the generative inverse design, latent space optimization is carried out by exploring it and determining the representations that most closely correspond to targeted electromagnetic responses and then generating the corresponding metasurface structures using the decoder. All other steps basically coincide with those of CNNs.

The rest of this subsection considers some publication examples where the authors utilized DNNs for the inverse design of metasurfaces. All five main listed groups of inverse methods are exemplified. Naturally, only select cases are presented among a vast number of pertinent works.

CNNs: Lin et al. considered the use of a CNN as a high numerical accuracy tool for the inverse design of plasmonic metasurfaces [272]. They demonstrated an accuracy of ±8 nm for the critical metasurface geometrical parameters. In 2024, Kiani et al. [338] utilized two CNN networks, one of them trained by transfer learning for dataset computing acceleration, for the inverse design of tunable metasurfaces based on graphene. They generated a large starting dataset, with about 54,000 metasurface structures.

RNNs: Wang et al. designed an all-dielectric optical metasurface using the Long Short-Term Memory (LSTM) version of the recurrent neural network [339]. The team used that approach to design a metasurface-based subtractive color filter. Tang et al. utilized a physics-informed recurrent neural network to forecast the temporal dynamics of optical resonances [275]. They also determined the corresponding resonance frequencies. For this purpose, they acquired a fraction of the sequence as the input. They utilized this approach in another 2D structures field, that of graphene plasmonics.

Transformers: Huang, Feng and Cai used Transformer Neural Networks for the inverse design of graphene-based terahertz metasurfaces [281]. They utilized a modified and enhanced version of the Transformer network together with conditional generative adversarial neural networks. They used their generative AI to obtain graphene metasurface images directly from the targeted THz multi-resonant absorption spectra. Chen et al. published in 2024 their results on the inverse design of all-dielectric (and thus ultra-low-loss) surface-enhanced Raman scattering (SERS) metasurfaces [280]. The design exhibits quasi-bound states in the continuum (Q-BIC) with a large Rabi splitting, thus ensuring a SERS enhancement factor of about 10 million. Their results have shown a superior performance compared to conventional metal-containing SERS structures.

GANs: Liu et al. presented the use of a generative neural network to perform the inverse design of a metasurface [340]. The team developed a generative adversarial network (GAN) consisting of three parts, a simulator, a generator and a critic, all three actually being convolutional neural networks. When initiating their design from the desired optical spectrum, the generative network takes a candidate pattern from a user-defined set of patterns that matches most closely the initial spectrum. Kiani, Kiani and Zolfaghari used a conditional GAN integrated with Gramian angular fields for the inverse design of multifunctional metasurfaces for the microwave range [341]. Jafar-Zanjani et al. performed the inverse design of active metasurfaces for telecommunication wavelengths [287].

Autoencoders: Tanriover et al. [342] developed a whole end-to-end framework enabling the inverse design of freeform meta-atoms for dielectric metasurfaces using a generative network of the autoencoder type. Importantly, their approach not only included a generated library of freeform shapes but also took into account nanofabrication constraints. Naseri and Hum used a variational autoencoder to generate dual- and triple-layer electromagnetic metasurfaces [343].

3.5.3. Hybrid Approach to the Inverse Design of Metasurfaces

An approach to improve the design of metasurfaces is to use the hybrid methods, as described in Subdivision 3.2.4. It appears that at the moment of writing this treatise this method is gaining in popularity. To exemplify this promising branch of investigation, both deep learning and heuristic optimization were used by Li et al. in 2023 for the inverse design of a multifunctional metasurface [344]. Also in 2023, Panda et al. [345] used a combination of metaheuristics and deep neural networks for simultaneous structure–material design. They applied their approach in the design of phase-change material tunable metasurfaces.

In the field of metasurface holograms, Zhu et al. utilized a deep learning algorithm coupled with an evolutionary metaheuristic optimizer to obtain several meta-systems [346]. These included a meta-hologram with space/polarization/wavelength multiplexing, a beam generator with polarization multiplexing and dual function, and a second-order differentiator intended for all-optical computing.

Jafar-Zanjani et al. utilized conditional generative adversarial networks to carry out the inverse design of active metasurfaces based on transparent conductive oxides [287]. At the same time, they used multi-objective evolutionary metaheuristics to generate the training dataset.

Kudishev et al. [347] used a combination of the topology optimization method with their adversarial autoencoder generative neural network (itself a combination of a variational autoencoder and a generative adversarial network) to perform the inverse design of optimized thermal emitter metasurfaces. They drastically improved the hybrid-method optimization process compared to the one using only topology optimization, with 4900 times faster computational time and final device efficiencies of about 98%, as compared to 92%.

3.6. Bidirectional Design

Besides using forward and inverse design separately, a viable approach is to include them both simultaneously in the solution of the same problem (end-to-end, i.e., bidirectional). For this purpose, one can form an iterative procedure that utilizes both methods of solution at the same time. This can start from the forward design with some set of initial conditions and then forward and inverse procedures can be iteratively applied until the targeted result is reached.

The use of combined forward surrogate modeling and inverse design through the use of deep learning neural networks in a single tandem architecture has been described by Liu et al. [348] (Figure 21). This approach has been proposed within the context of the fundamental property of the nonuniqueness of electromagnetic modeling solutions, in this case stemming from data inconsistency in inverse scattering problems. This bidirectional (end-to-end) approach has been used since in various problems in photonics [349].

Zhu et al. proposed, and both numerically and experimentally implemented an approach to the AI-based design of metasurfaces that utilizes a tandem (bidirectional) deep neural network together with an iterative algorithm [350]. Their procedure enabled them to obtain accurate quantitative field distributions, not just qualitative ones. Other interesting works based on tandem neural networks include those that handle dielectric metasurfaces by applying a pre-trained autoencoder [292], deal with the nonuniqueness problem with a metasurface-based invisibility cloak [351], optimize nanostructure color design in a truncated cone silicon metasurface [352], etc. Du et al. proposed a deep neural network model [353] consisting of a forward design part (a transposed convolutional network with dense layers for the fast determination of a metasurface optical response) and an inverse design part (convolutional neural networks with dense layers) that can automatically build a metasurface structure based on the optical response(s).

4. Metaphotonics-Based AI Hardware

4.1. Optical Neural Networks

The seminal paper by Lin et al. published in Science journal proposed fabricating optical chips with structurally and functionally built-in deep learning neural networks [219], with the intention of further using them in object classification, all-optical image analysis, feature detection and as the key part of novel camera designs. The authors do not explicitly use the term “metasurfaces” and write “multiple layers of diffractive surfaces” instead. As mentioned before in this text, such an approach offers a lot of advantages over electronics-based DNNs, including processing at light speed, vastly decreased energy consumption and the possibility of batch production using basically the same planar technologies as in microelectronic industry.

Although the concept of DNNs implemented as active optical metasurface hardware appears deceptively simple, its full implementation poses formidable obstacles. A consequence is that, nowadays, several years after the introduction of the concept and in spite of the appearance of hundreds of relevant, strong and influential pertinent publications, the field is still in its infancy.

If one considers the structure of a vast majority of the publications on metaphotonics-based AI, it is readily observed that they mostly cover the field of deep learning neural networks implemented in the form of different metasurface-based architectures. The absence of almost all other competing AI-based design and optimization approaches in the literature is striking—even more so when one remembers that many of the approaches not used in this hardware integration of AI into metasurfaces are readily applied in the design of metasurfaces themselves.

The reason for this seemingly counterintuitive situation becomes apparent if one considers a neural network deep learning system and compares its architecture to that of an optical metasurface [209,232]. Figure 22a shows a multilayer consisting of three optical metasurfaces in transmission configuration where a meta-atom serves as a diffractive optical source; Figure 22b shows a corresponding node map of a deep learning neural network. The analogy between the two architectures is striking, as seen by comparing Figure 22a,b.

It is readily observed that the architecture of deep learning neural networks shares an architectural, conceptual and functional similarity with transmissive stacks of metasurfaces. Both have integrated arrays of basic functional elements (artificial neurons in neural networks and meta-atoms in metasurfaces). These functional elements interact with inputs (electronic data in case of conventional neural networks, light in metasurface stacks). Stacks of metasurfaces play the role of hidden layers in conventional neural networks. Both neural networks and metasurface stacks generate a targeted output through complex processing. Thus, the optical structure of an optical metasurface is analogous to the computational structure of a neural network. This analogy goes even further, as it enables the implementation of different functionalities since the response of each separate meta-atom can be adjusted in a manner similar to tuning weights in a neural network. This allows for the dynamic tailoring of the targeted properties and an increased degree of freedom when determining the output signal in such tunable systems.

The name for the presented neural networks that is often met in the literature is deep learning optical neural networks (DONNs) or simply Optical Neural Networks (ONNs) [354,355]. To stress that a DONN operation is based on diffractive optics, the notation D²NN is used [219]. The observed similarity facilitates the design of metasurfaces using neural networks, but also the integration and implementation of neural network functionalities into optical metasurfaces.

4.2. A very Short History

The field of optical neural networks is actually (and unsurprisingly) older than that of metasurfaces. Numerous treatises on ONN have been published long before the very concept of metasurfaces was first presented. Some examples include almost prophetic publications from the previous century [356,357]. Instead of metasurfaces that did not even exist at the time, discrete optical components were utilized, together with standard nonlinear optical materials.

The first book dedicated to the topic, as far as the author of this text knows, was published in 2013 [358], just two years after the seminal article on the generalized laws of reflection and refraction [55] appeared in Science and started the snowballing-turn-avalanche of metasurface-oriented research. In this way, older works ensured a solid foundation to be built upon immediately after the metasurfaces experienced the mentioned game-changing research boost.

As mentioned at the start of Section 4.1, the beginnings of metasurface-based AI hardware were marked by the work of Lin et al. 2018 [219]. The further explosive growth and extension of intelligent metasurfaces to different fields has ensued (see subdivisions 2.3.7. and 2.3.8. for further details), and is continuing to expand and generalize in this very moment.

Reviews dedicated to photonic metasurface-based neural networks have been regularly appearing throughout the whole period. Some of those that have appeared in recent years include [359,360,361].

4.3. Metasurfaces with Hardware-Integrated Optical Neural Networks

One of the pioneering experimental works with optical neural networks on chip was presented by Shen et al. in 2017 in Nature Photonics [362]. They proposed, theoretically described and experimentally fabricated an ONN with two hidden layers. The architecture of their ONN was based on a cascaded array of programmable Mach–Zehnder interferometers on a Si photonic integrated circuit. Each layer consisted of an optical interference unit that enabled the multiplication of optical matrices and an optically nonlinear unit for nonlinear activation. Their experimental ONN consisted of 56 Mach–Zehnder interferometers and was trained for vowel recognition.

One must mention here again the seminal work of Lin et al. from 2018 [219]. Based on the mentioned publication and that of Liu et al. 2022 [363], Figure 23 shows a schematic presentation of an intelligent metasurface-based optical neural network. A stack of externally tunable (to the level of each separate meta-atom) learning metasurfaces is the optical version of the hidden layer array of a conventional neural network. Controllers may be utilizing some of the external tuning mechanisms mentioned in Section 2.3.5 (e.g., phase-change materials or electronic real-time control through field-programmable gate arrays—FPGAs).

Luo et al. described in 2022 a multitask D²NN classifier with polarization multiplexing and with a density of more than 6 million meta-atoms per square millimeter; the signal parallelization is calculated by multiplying this number by the number of polarization channels. Signals are read out by a CMOS imager in this combined optoelectronic active structure [364].

The same team leader with most of the authors from the work cited in the previous paragraph proposed in 2023 a novel all-optical neural meta-transformer [365] whose meta-atoms make use of structural birefringence and polarization rotation to ensure complete control over the tailoring of full Fourier components, in this manner ensuring arbitrary control of all learnable parameters in diffractive optical neural computing.

Also in 2023, Jian et al. proposed the concept of a metasurface-based hardware implementation of an analog recurrent neural network for mechanical (acoustic) vibrations [276]. This represents expanding the area of DNN metasurfaces beyond wave electromagnetics.

Zhang et al. proposed the implementation of an optical neural network for complex-value (instead of real-value) operations in the form of an optical neural chip [359]. To this end, they utilized the possibility of optical systems to use both phase and magnitude in order to perform complex arithmetics. The approach was to apply optical interferometry. Using their optical chip, they obtained a performance exceeding many real-valued counterparts. Figure 24 shows the composition of their complex-valued optical neural network.

Wu et al. presented Ge₂Sb₂Te₅ phase-change-material-controllable programmable metasurfaces functioning as optical analogs of convolutional neural networks [144]. They described them as a promising hardware accelerator for machine learning that utilizes the advantages of high speed and low power dissipation related to its light-based properties.

Liu et al. described another optical hardware implementation of deep neural network they termed programmable artificial intelligence machine [363]. For this purpose, they based their diffractive DNN on a multi-stack array of digital coding metasurfaces, each of the meta-atoms in the stack acting as an optical artificial neuron and being controlled by two amplifier chips. The authors developed a reinforcement learning algorithm for ML within their system. They have shown that their concept can be used for coders–decoders in communication, image classification and general multi-beam focusing.

In their 2023 paper, Sun et al. presented a review of diffractive deep neural networks [366], including their history starting from the seminal work of Lin et al. [219]. They further focused on diffractive optical neural networks based on holographic optical elements with free space interconnections. They also reviewed nonlinear D²NN and possible applications of the diffractive deep neural networks.

In 2024, Matuszewski, Prystupiuk and Opala reviewed scenarios under which all-optical computing may exceed the microelectronic and optoelectronic ones from the points of view of scalability and power consumption [367]. They concluded that electronic circuits, optoelectronic and all-optical ones share similar performance issues from the points of view of memory access and data acquisition costs, while the all-optical systems have a potential to exceed the other two in large neural networks, especially if the generative approach is used.

Also in 2024, a review by Khonina et al. [368] of different types of optical neural networks was published. It considers photonic AI networks for imaging and computing purposes, and includes various types like photonic versions of feedforward neural networks (FNNs) and recurrent neural networks (RNNs) together with their subset reservoir computing (RC), convolutional neural networks (CNNs), spiking neural networks (SNNs) and photonic Ising machines (PIMs). Not all of these have been implemented in metasurface form and some of them currently only exist as massive prototypes on optical tables. They are mentioned here for the sake of completeness and because the implementation of all of them in the metasurface form appears a natural continuation of their development.

5. Discussion, Challenges and Outlook

5.1. Selected General Issues

This text considered some aspects of the AI–metasurface synergy. Its goal was to illustrate at least some of the enormously useful breakthroughs and advances it procreated. Based on that, it appears that the main advantages of the concept of optical AI-enhanced metasurfaces are

• Their miniaturization, especially regarding their minuscule thickness and the dimensions of their meta-atoms;
• The possibility to tailor them at will, including their spatiotemporal tunability, bringing an almost infinite number of novel light processing functionalities;
• The possibility to impart them intelligent functionalities, which brings an enormous number of novel potential applications;
• High speed, high parallelization and low power consumption.

It could be said that the future from the point of view of the state of the art of the existing AI–metasurface synergy appears bright—and looks brighter every day. If the situation and condition in science do not drastically change, undoubtedly the existing synergy will continue to bring us more and more potent novel solutions. It appears that no observable fundamental limitations that could mean the end of such a winning streak lie in front of us. This means that the main risks that could stop the research are in human nature or, to be more specific, in the way future society positions itself toward artificial intelligence. However, this is both outside of the scientific domain and thus out of the grasp of researchers.

A few cautionary words came from Molesky et al. [369], whose advice was to conduct research on the ultimate performance of metasurfaces and general nanophotonic devices. In their opinion, with which the writer of these lines wholeheartedly agrees, one of the prime tasks in the field should be the establishment of the theoretical limits of the achievable performance. Such a task would undoubtedly depend on a particular intended functionality, the desired device size, and the available starting materials and their physics.

Regarding the achievable performance and the possible long-term directions of the synergy, one should mention that some works with AI optimization in nanophotonics brought the researchers to structures almost uncannily resembling biological ones, met in different organisms, as observed in, e.g., [370]. In other words, a kind of inadvertent biomimetics or in silico evolution could be awaiting the AI–metasurface researchers. Some teams already made use of that photonics–biology relationship and utilized it to research advanced nanophotonic structures. Among the examples are biological morphological structures based on Turing patterns utilizing the reaction–diffusion principle, as described in his seminal paper “The chemical basis of morphogenesis” [371]. Such structures, which are widespread throughout the living world, have been used to produce optical metasurfaces [372] and other nanopatterned functional photonic structures [373].

5.2. Usefulness of AI in Material Science in Metasurface Synthesis, Optimization, Characterization and Applications

AI is of great practical value for the material science aspect of work with optical metasurfaces across its various stages. To illustrate this, its role in the synthesis, optimization, characterization and applications of optical metasurfaces is summarized here.

While synthesizing meta-atoms, AI can be of crucial importance for predicting the results of various material synthesis methods. This is essential when selecting the most convenient and most effective approaches to fabricate structures with specifically defined properties. While doing so, AI not only speeds up the initial and the hardest steps of synthesis, but also ensures the advancement of metasurface synthesis technologies and facilitates their tailoring. It also takes into account multiple factors as well as their trade-offs, which is all of great importance for this part of the procedure.

At this stage, AI also performs the optimization of process conditions by analyzing the production flow for the chosen initial conditions and returns the most convenient synthesis parameters, e.g., environmental ones like humidity, pressure, temperature and external illumination, but also process information like optimum chemical compositions and ratios. Throughout the process, multiple design objectives can be targeted simultaneously. Such an approach brings researchers closer to the intended results in a shorter period of time, while at the same time increasing yields and making the synthesis “greener”. Similar optimization is also carried out when choosing the most convenient meta-atom design, both in the sense of the form and the optical functionalities.

The role of AI in characterization is to ensure the simultaneous analysis of multiple data regardless of the characterization technique used, for instance, considering whole optical spectra in sensing applications instead of single-wavelength measured values. This not only ensures richer and more accurate data processing with the simultaneous recognition of a larger number of constituents or analytes, but also drastically increases the speed of data analysis. The only bottleneck here is the training procedure of the AI which does take time before a procedure is to be used for the first time but this also can be at least partly avoided by utilizing physics-informed neural networks. AI in characterization can also be useful for prediction of various properties (both structural and functional) of the synthesized metasurfaces and of their building blocks, further speeding up the characterization stage.

Finally, AI has at least a double role in the application stage. One of them is the metasurface behavior prediction for various operating conditions. Another is direct control over the metasurface functionality itself. This is used for tunable and reconfigurable systems, where AI will perform the real-time control of metasurface performance by adjusting the tuning mechanism properties in dependence on the external commands or environmental conditions of interest for the metasurface operation.

5.3. Challenges

5.3.1. Inherent Uncertainty of AI Algorithms

This subsection deals with some foreseeable challenges in the field. Among them are the inherent uncertainty of AI algorithms [374], which may be either a result of external causes (included in the training data fed to the algorithm) or may be related to the AI algorithm itself (model uncertainty). If erroneous results are obtained in a critical application (e.g., metasurfaces used to extract medical data of importance for patient survival or metaphotonics used in machine vision systems for autonomous (self-driving) vehicles) then possible erroneous results may be life-threatening. This is why the uncertainty factor is a challenging task for future research—not because it is unsolvable but because its critical nature requires a very accurate approach, ideally with a zero chance of failure.

5.3.2. Lab-to-Fab Upscaling

The next important challenge is upscaling the fabrication of lab-designed prototypes to the industry level. One of the problems here is a very high cost of nanofabrication, since many optical systems are currently produced in a sequential manner, for instance, using ion beam technology which is very difficult to switch to batch fabrication. The modern ULSI (Ultra-Large-Scale Integration) microelectronics industry shows that the problem of the batch production of planar structures with nanoscale resolution is definitely solvable but may require extremely high entry costs.

An additional but related issue is that the metasurface designs themselves must be fabricable, which is achievable by incorporating the fabrication constraints directly into the inverse design algorithm [375], similar to the method applied in the conventional custom integrated circuit design. Another obstacle in this area is how to perform the upscale to allow for larger and even more complex systems, since the complexity of metasurface-based systems can be—and already often is—formidable.

The system footprint is one of the challenges facing both the designers and the manufacturers. Typically, a small metasurface footprint will be readily achievable by the use of nanoscale planar or NEMS technologies. Problems will arise when the producers desire to fabricate large format metasurfaces (like those for macroscopic displays, be it, e.g., OLED or meta-holographic 3D displays) since in that case one deals with typical multiscale problems both during the design stage and fabrication.

Continuing research in this direction is of crucial importance to a more widespread use of AI–metasurface systems. Obviously, it would signify their much wider adoption by industry and business.

5.3.3. Free-Space Scattering Losses

One of the current problems is the optical signal degradation in free-space-interconnected diffractive optical neural networks. A conventional neural network requires standard computing hardware, while a DONN requires a stack of planar structures (i.e., a cascade) that have the role of hidden layers, often with free-space coupling, which hampers its functionality since each additional layer in the cascade contributes its own reflective and scattering losses to the total output signal; thus, the signal loses its power quickly with an increase in the number of the layers.

A problem related to that is that free-space interconnection typically implies inter-layer distances of a few centimeters, which is detrimental to the compactness of the systems and loses one of its important advantages over electronic circuitry. One could speculate that a possible solution to both of these problems could be the application of dense sandwich architecture with superlens coupling or other near-field effects among the metasurface layers brought at much smaller distances or, alternatively, the use of high-permittivity dielectric spacers for layer immersion that would significantly decrease interlayer distances in the multilayers of diffractive neural networks.

Future research in this area would be of strategic importance. It could lead to a giant step towards more widespread use of all-optical AI, with many consequences like an optical computing development boost.

5.3.4. Noise in Optical Metasurfaces

The next very important challenge is a consequence of the existence of noise mechanisms (widely regarded as statistical fluctuations of some system parameters). They can be very detrimental in many systems, for instance, in sensing metasurfaces they will define the ultimate limit of sensitivity. Noise mechanisms can be roughly divided into the fundamental noises and technology-related (fabrication-induced, also denoted as geometry-related) ones.

Fundamental noise mechanisms in metasurfaces are caused by unavoidable physical processes related to the very operation principles of these metaphotonic structures. They include quantum noise [376], which can be further divided into (1) quantum fluctuations of the electromagnetic field, also known as vacuum noise or zero-point noise [377,378]; (2) photon shot noise [379], caused by the discrete nature of light, that is, its quantization into photons; (3) quantum mechanical uncertainty in building materials of metasurface; and (4) nonlinear quantum noise [380], i.e., stochastic fluctuations in nonlinear materials built into metasurfaces; all of these are directly related to quantum processes. Other fundamental mechanisms are optical thermal (Johnson–Nyquist) noise [381] (temperature-related stochastic fluctuations of material electromagnetic response, observable as random changes of refractive index) and optical flicker (1/f or “pink”) noise [382] (although it can be technology related too; the main cause of the optical flicker noise are low-frequency fluctuations of charge carrier concentration over time, defects/traps in metasurface material and material surface states). Adsorption–desorption noise [383] is also often included among fundamental noise sources. It arises through the stochastic adsorption and desorption of molecules (e.g., gases or liquids) on the metasurface (which obviously must be surrounded by some kind of ambient medium).

Geometry-related (fabrication-induced) noise is actually caused by the random deviations produced from the designed ones. This may be either due to imperfections/inaccuracies of nanoscale fabrication or the design failing to encompass the design rules that would take into account limitations of a particular fabrication technology. In both situations, the result is some kind of stochastic geometry disorder that may consist either in the basic metasurface materials or remnants of auxiliary materials used during production—like, e.g., excess oxide or photoresist remaining after lithographic mask removal. The fab-induced imperfections may include variations in meta-atoms’ shape, size or location, but also overall roughness of surfaces and built-in material imperfections like unplanned scattering centers within material, impurities or defects. Papers dealing with this kind of noise include, e.g., [384] (researching general disorder introduced by fabrication imperfections into nanophotonic structures) or [385] (considering disorder introduced by fabrication imperfections into metasurfaces).

Problems with metasurface performance caused by the presence of any of the listed noise mechanisms include a decrease in precision (of extreme importance for meta-holograms, beam shapers and steerers, various types of flat lenses, AR and VR systems and many more), degradation of data transfer through signal-to-noise decrease (of importance for practically all metasurfaces that handle data, including but not limited to ONNs and generally intelligent metasurfaces, but also critical in different sensor and detector applications), instability over time (thus reducing the reliability of basically all metasurfaces), limiting capabilities of quantum metasurfaces (damaging, e.g., cryptographic and optical computing applications), etc.

A number of methods were proposed to mitigate the undesirable consequences of noise. Many of them are made similar to those already being used in electronic systems. Among the most important ones are advanced signal processing and filtering after the optical signal has already passed through the metasurface(s). Another approach is real-time noise control and compensation though the incorporation of dedicated active elements like phase-change materials. It could be possible to keep under control at least some of the many types of optical noise through the development of novel metasurface materials (including nanocomposites) with noise-generating mechanisms inherently generating lower noise levels. A careful refining of fabrication methods in the future should result in decreasing a majority of technology-related mechanisms. This is connected with the lab-to-fab upscaling of manufacturing processes and must be solved simultaneously. Finally, quantum applications of metasurfaces require their own set of mitigation techniques. Besides the obvious controls over cryogenic temperatures, special approaches to noise decrease like quantum squeezed states and quantum entanglement could be helpful.

One has to stress that the role of stochastic fluctuations will strongly depend on a particular system. In some metasurfaces it will completely disable certain functions or at least pose the limits of operation, while in other its importance will be next to nothing. In certain systems, noise may even be a blessing in disguise, since it may lead to a performance enhancement and be engineered to enable a desired functionality. A 2023 Science paper by Xiong et al. [334] considers an intriguing scenario where, paradoxically at first glance, noise actually increases the capacity of holographic mass-media storage metasurfaces. This is carried out by improving polarization multiplexing through introducing two kinds of engineered noise, one of them correlated with least-squares estimation and another non-correlated (with fully random distribution). The method is also applicable to other types of metasurfaces as well, including those used for optical displays with high-resolution data and for cryptography.

There are actually a number of situations where the stochastic nature of noise can be used in a beneficial way. Besides stochastic resonance in metasurfaces where engineered noise amplifies weak optical signals under certain conditions, there are some other approaches as well. Speckle patterns, generated by coherent light interference on random surface roughness, actually carry a lot of information about the scattering metasurface, which can be useful in sensing, imaging or data encoding. Engineered thermal emission, which actually represents a free-space continuation of Johnson–Nyquist noise [386], can be tailored to match the bandgap of thermophotovoltaic metasurfaces, thus improving their conversion efficiency. Metasurface random roughness can be used to create more efficient built-in random lasers, thus ensuring unique lasing characteristics. Last but not least, quantum noise in metasurfaces for quantum cryptography can be used to enhance their quantum key distribution protocols.

Future research in this field would serve several important goals. First, it would augment the function of many AI–metasurface systems and, by removing an important roadblock, even bring about some that cannot currently exist or are stuck in the midst of their development. Second, with better understanding of the mechanisms, a larger number of new situations could be discovered where noise mechanisms are actually beneficial. Last but not least, this research would help define the ultimate performance of metasurface-based devices and systems, which was defined as one of the strategic goals earlier in this treatise.

5.3.5. DONN Metasurfaces and Optical Nonlinearity

The following consideration specifically regards challenges related to diffractive-metasurface-integrated neural networks. One of them is that, while at a first glance their mathematical functions appear very similar to those of conventional deep neural networks, there is one exceedingly significant difference. One should remember that, to solve optimization problems, both types of structures basically have to solve equation systems, i.e., to perform vector–matrix multiplication, which they successfully do. However, they need activation functions and real-life activation functions are usually nonlinear. This is not a problem for conventional non-optical neural networks but the metasurface-implemented DONNs will be linear, which will sharply limit their functionality. A deceptively simple and obvious way to overcome this deficiency in optical structures is to utilize nonlinear optical materials. However, the nonlinear response of the available materials is very weak (thus requiring extremely strong electromagnetic fields to reach usable values) and difficult to control. The methods that have been proposed until now to overcome this deficiency succeeded only partially (e.g., Zou et al. 2019, [387]; Xu et al. 2022, [388]). In 2023, Wang et al. proposed a nonlinear multilayer ONN encoder that used a commercial image intensifier for its optical-to-optical nonlinear activation function [354]. Many other attempts have been made in this direction. One could state that using plasmonic hotspots coinciding with nonlinear optical materials alleviates the problem due to the extraordinarily strong localizations of electromagnetic fields such hotpots create, thus upping the level of nonlinear effects. Generally, however, it may be said that the quoted engineering problem still poses a number of challenges. This is currently a lively field of research with the potential to bring dramatic and even strategic changes in the future.

5.3.6. Multitasking with DONN Metasurfaces

Among the limitations of diffractive neural network metasurfaces is that in principle they represent single-task systems, while multitasking in the sense of performing multifunctional operations simultaneously may often be problematic [364,389,390]. That could appear paradoxical, since multiplexing is actually vastly less complex to implement in optical systems than in electronic ones—after all, a metaphotonics designer can multiplex a signal’s amplitude, phase, wavelength or polarization, contrasted to signals in electronics which are typically processed sequentially, by time division multiplexing. However, the problem of how to make a metastructure perform different functions with different multiplexed signals remains. The multitasking processing problem is the hardest for passive metasurfaces, which, once trained, will continue performing the same task in the same manner interminably. The situation is somewhat better with tunable and reconfigurable structures, and the best situation is with intelligent coding metasurfaces. However, even in the best situations, at least part of the problem will remain. A possible solution has been presented by Cheng et al. in 2024 [391]. They proposed the concept of a reconfigurable photonic computing architecture they named “Lifelong Learning Optical Neural Network (L²ONN).” They are inspired by the concept of neuromorphic optical metasurfaces (subdivision 2.3.8. in this paper). They claim that their system can learn through an incremental procedure tens of tasks in a single photonic model and apply them simultaneously. Wavelength multiplexing is applied to that end. Lifelong learning capacity and the avoidance of “forgetting” is achieved by using multi-spectral parallelism and spatial sparsity of phase-change-material-based filters. Rather than mimicking electronic DNNs, the system is conceptualized to imitate the human thought processes of both remembering and forgetting. Since all of this is quite new (the paper has been published a week before writing this text) it remains yet to be seen how efficient and widespread the L²ONN will be.

The presented considerations of challenges that AI–metasurface synergy faces are limited, since they do not analyze other problems like the necessity for large and high-quality training datasets, and, probably even more important, the methods of interpretation of AI-optimized metasurface designs, like the avoidance of the “black box problem” of the opaqueness of the conclusion methods of NNs and the creation of optimized designs understandable to humans. The latter problem is touched upon in Section 7.

5.3.7. Particular Challenges

This subsection briefly mentions numerous concrete challenges related to already existing or potential applications. Basically, all applications listed in Section 2.1.2. pose their own limitations or roadblocks that will undoubtedly lead to their further research and development. There are many other applications that are not even mentioned there. For a vastly more detailed recent list of challenges systematized over different fields of metasurfaces research one could consult the excellent, systematic and quite long article written as a roadmap for optical metasurfaces [392]. One must mention that even for those metasurfaces not explicitly mentioned as a part of AI–metasurface synergy it is valid that at least their design is amply supported by AI, most often through inverse procedures, without which most of them could not have been produced.

Since this is not a roadmap article, but rather a friendly and comprehensible intro into an increasingly popular paradigm for a wide audience at different levels of expertise and within different disciplines, a systematic consideration of application-related challenges does not belong to it. Instead of it, the author chose to quote just two classes of applications for illustration purposes only.

One of the selected typical groups are metalenses, which are extremely popular in a large number of diverse applications. The challenges and roadblocks defining the basis for the potential research of metalenses are their restricted focusing efficiency, general image quality, ways to reach a trade-off between their different parameters, the decrease in or full removal of different image aberrations, the problem of metalens size upscaling, the introduction of multifunctionality, methods of imparting novel or improved properties, optimization for various novel applications and many more. The circle is ever expanding.

An example of a multifunctional metalens is shown in Figure 25. It illustrates the tailorable structuring of quantum emission utilizing such a metalens. Details are given in the figure caption.

The second example is metasurface-based chemical sensors and biosensors. Challenges in this application field include selectivity increase, sensitivity enhancement, constituent materials choice, surface functionalization, response speed, recognition of multiple analytes, device miniaturization, avoidance of detrimental effects of noise (especially the adsorption–desorption-based one), sample handling, material biocompatibility, possibility of endoscopic use, reusability of a single sensor over an extended period of time (non-disposability), cost-effectiveness and much more.

The subsection on challenges is concluded by a few words on some cutting-edge emerging research subjects related to AI–metasurface synergy. Illustrations of some more exotic doors leading to largely unexplored and often unexpected challenges include metasurface use in picophotonics (a research field dealing with light interaction with deeply subatomic objects or events, whose dimensions are in the picometer scale, i.e., beyond thermal fluctuations [394]), Poincaré beams which are spatially polarized light beams carrying both orbital and spin angular momentum [395], metasurface-based time crystals which actually represent quasi-2D photonic structures whose electromagnetic properties are spatially uniform but temporally periodical [396] and many more.

5.4. Perspectives (Possible Research Directions to Overcome Challenges)

The arrival of the metasurface paradigm and its synergy with the even more impactful paradigm of AI brought an explosion of different novel research results and practical applications. The already existing diversification of metasurfaces is readily seen from Subdivision 2.1.2. of this text. One cannot see a reason why this trend would not continue in the foreseeable future, even if some overly restrictive legislatures with repercussions against AI were to be brought in some countries. It is probable that such lawmaking would mostly handle safety-related issues and thus it is hard to see a reason why they would completely tear down the successful synergy that is already proving itself lucrative to many industries, while avoiding a vast majority of safety problems. An additional motive against such a self-destructive decision is that AI–metasurface synergy aligns extremely well with the existing environmental roadmaps and policies. After all, metasurfaces promise not only to spend vastly less energy than electronics, but they also ensure much more efficient solar harvesting and keep introducing display and illumination systems with strongly decreased power consumption. Thus, they are able to contribute to sustainability and green technologies, and fight global warming.

Another perspective is that the very versatility of AI–metasurface synergy should be sufficient to result in continued attention and funding for their research, development and industrial production. It goes even further, since these two paradigms could easily merge with other paradigms, integrating themselves with other technologies and creating hybrids with enhanced or completely new functionalities that are yet untapped.

Meanwhile, the nanotechnologies that ensured the physical existence of the both paradigms are continuing to get refined and grow at an accelerated pace. The same is valid for the theoretical models and computational tools in both of the fields.

This consideration of possible future development does not (and obviously cannot) take into account some possibly even more disruptive positive breakthroughs but, based on the already existing trends, it must not dismiss their potential and actually very probable appearance. After all, just a few years ago it was difficult or even impossible to predict the advancements brought to everyday life by the advent of generative AI. Similar reasoning is valid for most of the metasurface-based practical applications. Both paradigms bring quantum leaps within themselves.

Taking into account the above consideration, it is hard to imagine a near future in which AI–metasurface synergy stops continuing its rapid advancement. Even more, the already ongoing research will probably result in numerous useful novelties. It is hard to anticipate the future but, if the modern trends are to be continued, then further progress and even evolution of the field appear very likely.

A roadmap of some expected future developments in the AI–metasurface (AI-MS) synergy field is shown in Figure 26, intended to better visualize different oncoming novelties in the field. Because of the sheer quantity and extensiveness of new developments, it is impossible even to attempt to encompass at least the main part of the most significant ones. Thus, the figure represents illustrative examples of some of the key developments. The top side represents the roadmap of some expected future scientific developments in the AI-MS synergy field, while the bottom side of the roadmap shows some of the expected future novel or improved AI-MS applications.

It was planned that this text offers a much wider overview of at least some of the particular possible developments. However, the writer decided against it. The reason for this decision is that, while writing this manuscript, a high-profile open-access treatise appeared online (at the very end of February 2024) in ACS Photonics, entitled “Roadmap for Optical Metasurfaces” [392] and written by 43 authors, many of whom are luminaries of the nanophotonics field generally and of metasurfaces particularly, including people who created the field itself. The publication was so fresh that at the moment of writing this text no bibliographic data were available for it on the publisher’s website. The text itself is structured as an ultimate guide for the possible development directions of the metasurface paradigm in the days ahead, as seen through the eyes of many of those who gave the birth to the field (although not all of them, since it would be logistically impossible). The absence of Prof. Federico Capasso from the author list (who does appear in the Acknowledgments, though) is probably the most noticeable non-inclusion.

In the view of the previous paragraph, a rather short insight into some particular perspectives of AI–metasurface synergy research is given here as an illustration of the vast potentials still hidden within the field. The two classes quoted in Challenges are dealt with. One of them has already been analyzed in the above-mentioned roadmap article although some additional information is included here, while the other regretfully remained practically unmentioned in it.

(1) Perspectives and possible future research for metalenses include further technology improvement for enhancing image quality [397] and introducing novel methods of metalens characterization [398]. Upscaling metalenses and extending their diameter is also an attractive research direction, since this would make them available in many novel applications. A possible direction is combining them with other different metasurfaces to augment current functionalities and introduce new ones (such new functionalities could include bound states in continuum or Fano resonances).

Among possible directions for future works in this field it was suggested to integrate metalenses into existing photonic systems, thus replacing conventional optics. Alternatively, one could integrate them with conventional optical components needing a correction of their aberrations. Further integration with AI would also be beneficial to enhance the functionality of metalenses and even include active behavior [399].

As far as the potential metalens applications are concerned, one could envision their improved use in virtual reality systems [400], augmented reality [401] or machine vision [402], or as AI-controllable multifocal metalenses [403]. More exotic applications include using metalenses in nonlinear optics [404], in quantum photonics [33] and analog optical computers [405], different kinds of novel displays [397] like novel nano-pixelate LED displays, 3D displays, bionic displays, intelligent displays, etc.

(2) Perspectives and possible future research for metasurface-based chemical sensors and biosensors (see e.g., [406]) include the works on their applicability in rapid multianalyte sensing systems assisted by AI [407], thus ensuring at the same time vastly increased selectivity and readout speed. Another important current field of practical work is sensor cost reduction [408]. A wide topic of current research is materials convenient for biosensors. As an illustration, in [409], the use of nonlinear optical materials is considered for biosensor enhancement, together with the simultaneous use of AI. Various methods of sensitivity enhancement [410] represent one of the most important research fields regarding metasurface sensors (as well as sensors generally) and it will probably be continuously performed as long as sensors themselves are used. Future topics also include device miniaturization, sample handling and sensor reusability (non-disposability), as well as never-ending investigation of the effects of noise, especially of adsorption–desorption-based fluctuations. A figure schematically representing a MS-based selective metasensor of molecules is shown in Figure 27.

Potential applications include low-cost sensors combined with cellphones transmitting patient data directly to clinical centers [411] (wearable self-testing systems), advanced lab-on-a-chip systems using metasurface-based biosensors [412], MS platforms for the sensing of biomarkers of different kinds of malignant tumors, viral diseases and neurodegenerative issues [413] and generally precision medicine.

A few examples of possible subjects of emerging research unrelated to the above-described two fields include, without any particular order, generators of stable and well-designed topological fields [414], noninvasive single-shot high frame rate image sensors with sub-Brownian resolution [394], superoscillatory lenses focusing light beyond the diffraction limit [415], metasurface-based vortex beam generators [416], etc. Obviously, this is only a tiny illustrative fraction of a vast body of ongoing research to give one a taste of oncoming things. Many other AI–metasurface-related topics will be open in the next period—and some of them are probably starting to open right now but one has to wait for the first publications. All of this belongs to a future we have yet to see.

6. Speculative Consideration of Some Possible Alternative Directions

This part of the text speculates on some possible development directions of the AI–metasurface synergy that have not been implemented so far and that some people could even describe as far-fetched. Yet, no obvious fundamental physical or material limitations are blocking their achievement. The problems to overcome, while quite significant and even formidable, belong to the fields of engineering and technology. To illustrate some possible directions, two exemplary conceptual problems are given. They are very far from being the only ones within the very rich current stream of solutions that are constantly being created and enriched, and actually there are multitudinous approaches within the ever-extending collection of possible pathways.

6.1. Alternative All-Optical Hardware Implementations: Metaheuristics on a Metasurface

It is readily imaginable that under certain conditions it could be possible to extend the metasurface-based (and generally metaphotonics-based) hardware implementations of AI beyond the currently used deep learning optical neural networks (DONN or D²ONN) to other approaches from the huge pool of available AI methods and procedures. Besides the previously mentioned genetic algorithms and particle swarm procedures from the rich pool of metaheuristic methods, hyper-heuristic methods come to mind, as well as the multitudinous hybrid and multi-objective algorithms. However, as far as the author of this text knows, direct hardware integration of other AI algorithms besides neural networks into optical metasurfaces has not been explicitly documented in the open literature yet. This is for a good reason, because hardware integration of, e.g., metaheuristic algorithms into metasurfaces poses formidable challenges.

To perform an optical hardware implementation of a metaheuristic algorithm, the metasurface would necessitate dynamically reconfiguring itself whenever it receives feedback about its optimization performance for a given iteration cycle. Luckily, mechanisms for altering the metasurface structure through real-time tuning of its meta-atoms are known (as outlined in Subdivision 2.3.5). Nevertheless, such feats are much more complex than the application of DONNs or the use of static metasurfaces.

One of the problems is the solution evaluation and feedback of the obtained results back to the iterative metaheuristic loop. As is well known, metaheuristic optimization requires the performance evaluation for each generation (iterative step) of solutions and the use of the obtained information to decide whether to continue the search or to deliver the final solution set. Implementing this in hardware would necessitate integrated sensors and feedback loops that could assess the metasurface optical properties and tune them according to the obtained results for the current generation, a task that drastically increases the complexity of potential optical metaheuristic hardware.

Yet another layer of complexity is the necessary sophisticated control systems. The iterative nature of metaheuristic algorithms would require complex control systems capable of executing the above-mentioned steps of algorithm logic, of adequately tailoring the metasurface/meta-atoms and, probably most importantly, processing feedback from the evaluation mechanisms. All components mentioned in the present system description have to be integrated into a compact and efficient metasurface package. It is speculated here that the necessary control and feedback systems needed for the hardware integration of metaheuristic algorithms into a metasurface or a cascade of metasurfaces could eventually actually be achieved through careful application of general optical metasurface-based analog computing [405,417,418,419].

Since the optimization properties of metaheuristics are used in this very moment in both forward and inverse design, an optical hardware implementation of their algorithms would be a welcome addition to the already rich toolbox of metasurface design. Finally, a similar consideration would be valid for hardware implementation of various alternative machine learning algorithms other than diffractive neural networks and metaheuristics.

6.2. Self-Evolving Intelligent Metasurfaces

This subsection is dedicated to the hypothetical concept of a self-improving all-optical metasurface system that integrates AI both in the design/optimization process and the operational functionality of the metasurface hardware. In such a system, positive feedback and interaction would be ensured between the all-optical AI–metasurface block and its all-optical AI–metasurface optimizer. Such a hypothetical combination could improve itself iteratively and ensure the autonomous enhancement of each of these two main building blocks, thus becoming self-evolving. Such an approach could significantly reduce the design iteration time, discover novel design paradigms that might not be intuitive to human designers, and adapt to new requirements or constraints in real time, as soon as they emerge. The mentioned feedback loop would ensure that the AI “designer” part not only designs the metasurface but also continuously learns from its performance in real-world applications, using this data to feed further design improvements. This could lead to a system that evolves over time, becoming more efficient, versatile or capable of handling a broader range of tasks.

A vast number of challenges would need to be addressed before the realization of such a self-evolving system. Sensing and actuation would need to be fully integrated with it, since a truly adaptive metasurface would obligatorily have means to sense its performance and the ability to reconfigure itself based on this feedback. The devices integrated directly with the metasurface could be photonic, but also electronic and generally of any other available type. The real-time decision making and metasurface tailoring would have to be very fast. While the signals themselves are transmitted at the speed of light in the given medium, the whole approach might need to utilize novel computational architectures or leverage emerging technologies such as photonic computing. An additional problem would be how to ensure that the AI algorithms used for both design and operational adaptation are efficient, reliable and capable of making sound decisions in a wide range of scenarios. As mentioned, photonic computing could be an answer to this requirement to algorithmic efficiency and robustness. Solving of the mentioned problems would probably need the development of novel materials and technology procedures that would satisfy the stringent requirements of the architecture of the described system.

The tasks and challenges facing the proposed concept would be formidable, to say the least. However, the goal of self-improving and self-evolving photonic systems, if achieved, would be extremely disruptive, with potentials to transform not only the field of metasurfaces, but also AI and general computing, communications, sensing and much more, so it might just be worth the price.

7. Possible Risks and Ethical Questions

The potential main concerns of using AI to design and optimize metaphotonics and nanophotonics generally are related to the following: (1) metaphotonics is currently being used (or considered to be used soon) in numerous key areas including telecommunications, computing, transportation, most of the existing fields of engineering, biomedicine and healthcare (especially the branches dealing directly and in real time with patients), environmental protection, homeland security, etc. (2) Many AI systems use a stochastic approach to converge to their solutions and while their reliability can be—and usually is—very high, errors are possible and sometimes unavoidable. (3) One cannot neglect the possibilities of malevolent external attacks, e.g., by hacker organizations, meddling third parties generally, including hostile groups or even rogue countries’ government organizations, which could even be using their own AIs specially optimized to cause the greatest possible damage at the weakest points. In theory, even the internal functions and the intrinsic architecture of AI metadevices themselves may be sensitive to malevolent attacks in the case of tunable and reconfigurable metasurfaces. This kind of risk increases with the complexity of the metadevices, currently reaching its peak with intelligent and autonomous structures.

Any disruptions to the strategic systems quoted in point (1) of the previous paragraph could result in undesired and largely unforeseeable consequences, and, in cases where large and strategic systems are involved, such disruption could potentially lead to catastrophic consequences. This is not to say that the risks outweigh the numerous benefits—actually, it currently appears that it is quite the opposite. The take-home message is that even in seemingly impenetrable and intrinsically safe systems there is a necessity for serious and high-quality risk management, depending on what could be at stake.

Another kind of problem is connected with quite a different subject, that of human psychology. Any systems that ultimately function as a “black box”—i.e., without human insight into the logic behind its decision making or without being at least partly explainable, will be poised to cause skepticism and distrust. This will be especially valid if AI should bring life-or-death decisions, for instance in biomedicine in cases where the discovery and treatment of potentially life-threatening conditions are included, in road traffic where self-driven vehicles could cause loss of lives, AI-controlled air transport or, the worst of all, in military applications where AI-built or controlled systems could do enormous damage (e.g., if using attack drones or intelligent missiles) [226]. In spite of the useful efforts to introduce the explainable artificial intelligence (XAI) [229,420], some degree of distrust and even blind hatred and fear may always be expected to linger in the world in which some persons keep continuing their crusades even against such well-proven and life-saving solutions like, e.g., MMR vaccines.

8. Conclusions

The main contributions of this treatise on the AI–metasurface synergy include

• An attempt to disclose an easy-to-follow overview of snapshots of the most recent and most interesting developments in as systematic yet simple a manner as achievable (bearing in mind that full generality would have been literally impossible at this level of diversification and sophistication in the field).
• Presentation of some particularities of metamaterials, metasurfaces and metaphotonics, from the very roots of the fields to the contemporary breakthroughs, with the accent on the latest trends.
• Presentation of some particularities of AI of interest for the AI–metasurface synergy, again starting from the field roots and ending with the latest trends.
• Consideration of the use of AI for the design and optimization of metasurfaces (including forward, inverse and bidirectional end-to-end approaches), often with possible solutions proposed.
• Consideration of metasurfaces used for the hardware implementation of AI in the form of diffractive optical neural networks, again with proposals of selected likely solutions to some of the current challenges.
• Critical re-examination of certain subtopics, including the clarification of some ambiguities often met in nomenclature.
• Inclusion of certain fields of importance seldom touched upon within the context of AI–metasurface synergy, for instance, the fundamental and fabrication-induced mechanisms of noise and their main detrimental effects, but also their beneficial uses.
• A consideration of certain speculative ideas and approaches that could be rather useful in the foreseeable future and may be of interest to those scholars grappling with certain current open problems in the field, as well to many of those with general interest in some potential future solutions.
• A general consideration of the challenges and advantages in the field.
• An examination of possible safety risks and ethical questions related to the field.
• An offer of a different and alternative perspective to a frequently analyzed and reviewed field.
• A consideration that is organized to be maximally reader-friendly towards an interdisciplinary and multidisciplinary audience, to this end offering as simple an approach as reasonable.

As a final conclusion it may be made that the main drawback of practically all implementations of AI–metasurface synergy is their novelty or, rather, their underdevelopment as a logical consequence of that novelty. The field is still in its infancy and a lot of work has yet to be carried out. The results achieved until now are more than encouraging but they represent only the tip of an iceberg of what has to be developed further. Paradoxically, at the same time, this drawback appears to be the main advantage of all-optical meta-circuitry. If in a rather short period of time such a huge number of doors and research directions have been opened, one could extrapolate (carefully and with maximum caution) what could be expected in the coming years. This developmental boost should be contrasted with the quite mature field of electronics where the end of Moore’s law is being announced more and more loudly and frequently. Luckily, a viable alternative appears to be right in front of us and it seems that it is coming in quite bright light.