Tunable Near-Infrared Transparent Bands Based on Cascaded Fabry–Perot Cavities Containing Phase Change Materials
Abstract
:1. Introduction
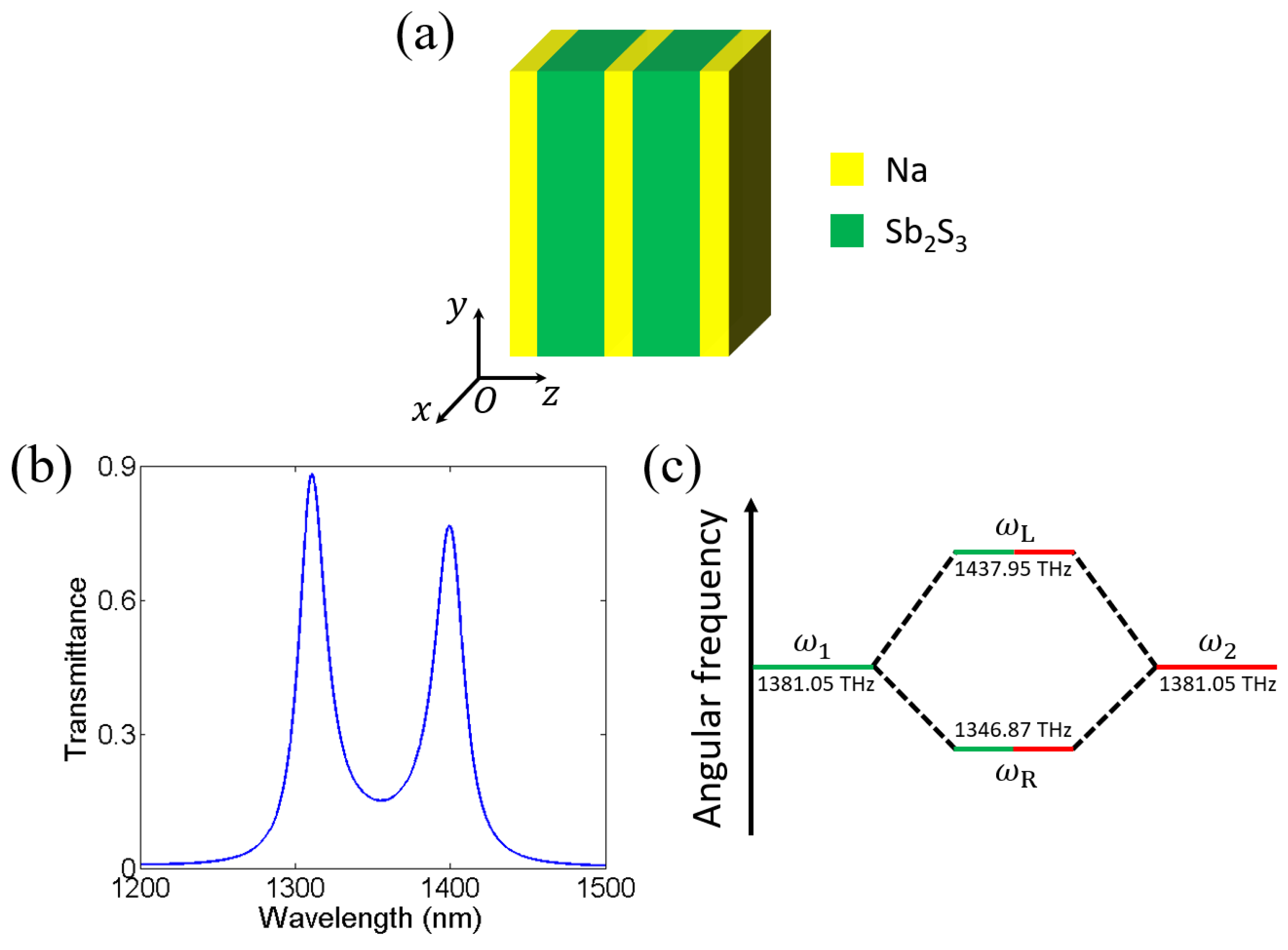
2. Tunable Near-Infrared Transparent Bands Based on Cascaded Fabry–Perot Cavities
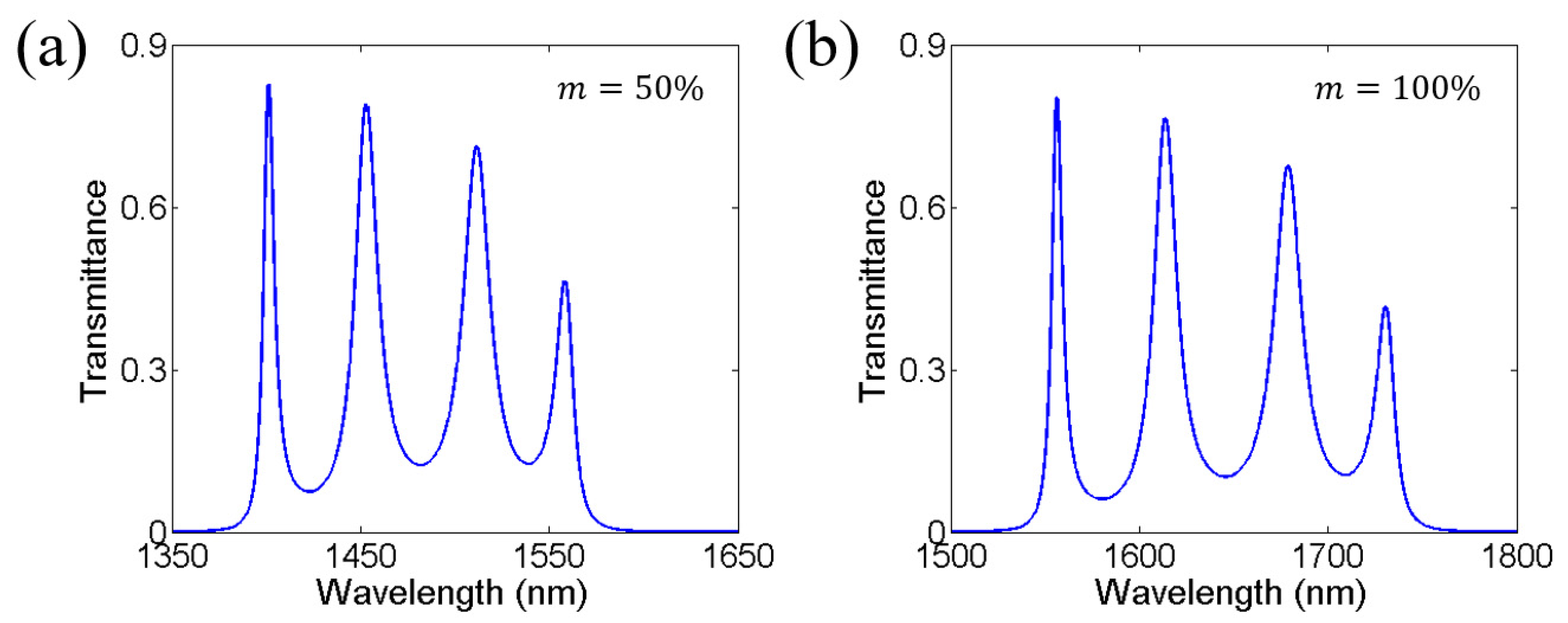
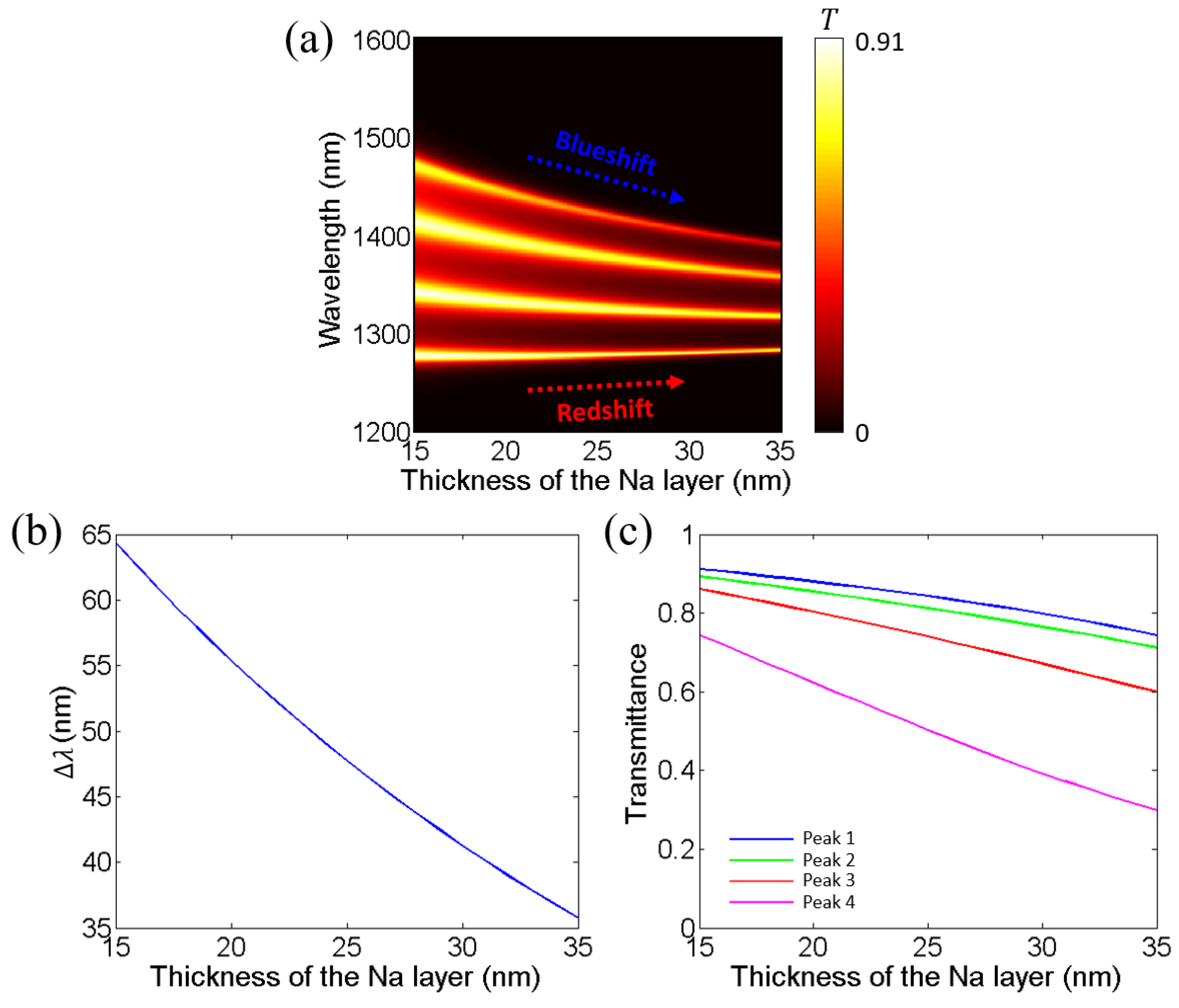
3. Effects of Layer Thickness and Incident Angle on Near-Infrared Transparent Bands and Mode Coupling
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Miroshnichenko, A.E.; Flach, S.; Kivshar, K.S. Fano resonances in nanoscale structures. Rev. Mod. Phys. 2010, 82, 2257–2298. [Google Scholar] [CrossRef]
- Zangeneh-Nejad, F.; Fleury, R. Topological Fano resonances. Phys. Rev. Lett. 2019, 122, 014301. [Google Scholar] [CrossRef] [PubMed]
- Wu, F.; Qi, X.; Qin, M.; Luo, M.; Long, Y.; Wu, J.; Sun, Y.; Jiang, H.; Liu, T.; Xiao, S.; et al. Momentum mismatch driven bound states in the continuum and ellipsometric phase singularities. Phys. Rev. B 2024, 109, 085436. [Google Scholar] [CrossRef]
- Marburger, J.H.; Felber, F.S. Theory of a lossless nonlinear Fabry–Perot interferometer. Phys. Rev. A 1978, 17, 335–342. [Google Scholar] [CrossRef]
- Stadt, H.; Muller, J.M. Multimirror fabry–perot interferometers. J. Opt. Soc. Am. A 1985, 2, 1363–1370. [Google Scholar] [CrossRef]
- Zuo, C.; Wu, K.; Shi, J.; Guang, D.; Wu, X.; Yu, B. Ultrasensitive temperature sensor based on cascading a polarization mode interferometer with a Fabry–Perot interferometer. Opt. Laser Technol. 2024, 168, 109910. [Google Scholar] [CrossRef]
- Zhang, H.-Y.; Gao, Y.; Zhang, Y.-P.; Wang, S.-F. Independently tunable multichannel terahertz filters. Chin. Phys. B 2011, 20, 094101. [Google Scholar] [CrossRef]
- Moiseev, S.G.; Glukhov, I.A.; Dadoenkova, Y.S.; Bentivegna, F.F. Polarization-selective defect mode amplification in a photonic crystal with intracavity 2D arrays of metallic nanoparticles. J. Opt. Soc. Am. B 2019, 36, 1645–1652. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, D.; Zhang, H.-F. Realization of double Fano resonances with a InSb-doped Fabry–Perot cavity. Results Phys. 2022, 35, 105417. [Google Scholar] [CrossRef]
- Gryga, M.; Ciprian, D.; Gembalova, L.; Hlubina, P. One-dimensional photonic crystal with a defect layer utilized as an optical filter in narrow linewidth LED-based sources. Crystals 2023, 13, 93. [Google Scholar] [CrossRef]
- Li, S.; Feng, G.; Liu, Y.; Wu, M.; Zhao, X.; Sun, F.; Gan, Z.; Chen, Z.; Yang, Y. Omnidirectional near-infrared narrowband filters based on defective mirror-symmetry one-dimensional photonic crystals containing hyperbolic metamaterials. Opt. Laser Eng. 2024, 176, 108107. [Google Scholar] [CrossRef]
- Wu, J.; Zeng, R.; Liang, J.; Huang, D.; Dai, X.; Xiang, Y. Spin-dependent and tunable perfect absorption in a Fabry–Perot cavity containing a multi-Weyl semimetal. Opt. Express 2023, 31, 30079–30091. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.G.; Liu, W.; Yao, H.Y.; Liang, L.J.; Yan, X.; Zong, M.J.; Gao, S.; Huang, C.C.; Qiu, F.; Feng, Z.W.; et al. Broad/narrowband switchable terahertz absorber based on Dirac semimetal and strontium titanate for temperature sensing. Appl. Opt. 2024, 63, 1306–1312. [Google Scholar] [CrossRef] [PubMed]
- Uphoff, M.; Brekenfeld, M.; Rempe, G.; Ritter, S. Frequency splitting of polarization eigenmodes in microscopic Fabry–Perot cavities. New J. Phys. 2017, 17, 013053. [Google Scholar] [CrossRef]
- Wu, F.; Chen, M.; Xiao, S. Wide-angle polarization selectivity based on anomalous defect mode in photonic crystal containing hyperbolic metamaterials. Opt. Lett. 2022, 47, 2153–2156. [Google Scholar] [CrossRef] [PubMed]
- Villa, F.; Lopez-Rios, T.; Regalado, L.E. Electromagnetic modes in metal-insulator-metal structures. Phys. Rev. B 2001, 63, 165103. [Google Scholar] [CrossRef]
- Li, Z.; Butun, S.; Aydin, K. Large-area, lithography-free super absorbers and color filters at visi1ble frequencies using ultrathin metallic films. ACS Photonics 2015, 2, 183–188. [Google Scholar] [CrossRef]
- Lv, J.; Chen, D.; Du, Y.; Wang, T.; Zhang, X.; Li, Y.; Zhang, L.; Wang, Y.; Jordan, R.; Fu, Y. Visual detection of thiocyanate based on Fabry–Perot etalons with a responsive polymer brush as the transducer. ACS Sens. 2020, 5, 303–307. [Google Scholar] [CrossRef] [PubMed]
- Taal, A.J.; Lee, C.; Choi, J.; Hellenkamp, B.; Shepard, K.L. Toward implantable devices for angle-sensitive, lens-less, multifluorescent, single-photon lifetime imaging in the brain using Fabry–Perot and absorptive color filters. Light Sci. Appl. 2022, 11, 24. [Google Scholar] [CrossRef] [PubMed]
- Shu, S.; Li, Z.; Li, Y.Y. Triple-layer Fabry–Perot absorber with near-perfect absorption in visible and near-infrared regime. Opt. Express 2013, 21, 25307–25315. [Google Scholar] [CrossRef]
- Zhao, D.; Meng, L.; Gong, H.; Chen, X.; Chen, Y.; Yan, M.; Li, Q.; Qiu, M. Ultra-narrow-band light dissipation by a stack of lamellar silver and alumina. Appl. Phys. Lett. 2014, 104, 221107. [Google Scholar] [CrossRef]
- Kocer, H.; Butun, S.; Li, Z.; Aydin, K. Reduced near-infrared absorption using ultra-thin lossy metals in Fabry–Perot cavities. Sci. Rep. 2015, 5, 8157. [Google Scholar] [CrossRef]
- Li, Z.; Palacios, E.; Butun, S.; Kocer, H.; Aydin, K. Omnidirectional, broadband light absorption using large-area, ultrathin lossy metallic film coatings. Sci. Rep. 2015, 5, 15137. [Google Scholar] [CrossRef] [PubMed]
- Mirshafieyan, S.S.; Luk, T.S.; Guo, J. Zeroth order Fabry–Perot resonance enabled ultra-thin perfect light absorber using percolation aluminum and silicon nanofilms. Opt. Mater. Express 2016, 6, 1032–1042. [Google Scholar] [CrossRef]
- Sreekanth, K.V.; Ouyang, Q.; Han, S.; Yong, K.T.; Singh, R. Giant enhancement in Goos-Hänchen shift at the singular phase of a nanophotonic cavity. Appl. Phys. Lett. 2018, 112, 161109. [Google Scholar] [CrossRef]
- Liu, F.; Shi, H.; Zhu, X.; Dai, P.; Lin, Z.; Long, Y.; Xie, Z.; Zhou, Y.; Duan, H. Tunable reflective color filters based on asymmetric Fabry–Perot cavities employing ultrathin Ge2Sb2Te5 as a broadband absorber. Appl. Opt. 2018, 57, 9040–9045. [Google Scholar] [CrossRef]
- Chen, W.; Liu, J.; Ma, W.Z.; Yu, G.X.; Chen, J.Q.; Cai, H.Y.; Yang, C.F. Numerical study of multilayer planar film structures for ideal absorption in the entire solar spectrum. Appl. Sci. 2020, 10, 3276. [Google Scholar] [CrossRef]
- Liu, C.; Wang, G.; Zhang, L.; Fan, F.; Zhang, X.; Fu, Y.; Wang, T. Dynamic color display with viewing-angle tolerance based on the responsive asymmetric Fabry–Perot cavity. ACS Appl. Mater. Interfaces 2022, 14, 7200–7207. [Google Scholar] [CrossRef] [PubMed]
- Scalora, M.; Bloemer, M.J.; Pethel, A.S.; Dowling, J.P.; Bowden, C.M.; Manka, A.S. Transparent, metallo-dielectric, one-dimensional, photonic band-gap structures. J. Appl. Phys. 1998, 83, 2377–2383. [Google Scholar] [CrossRef]
- Bloemer, M.J.; Scalora, M. Transmissive properties of Ag/MgF2 photonic band gaps. Appl. Phys. Lett. 1998, 72, 1676–1678. [Google Scholar] [CrossRef]
- Kee, C.-S.; Kim, K.; Lim, H. Optical resonant transmission in metal-dielectric multilayers. J. Opt. A Pure Appl. Opt. 2004, 6, 22–25. [Google Scholar] [CrossRef]
- Zhang, J.-L.; Jiang, H.-T.; Shen, W.-D.; Liu, X.; Li, Y.-Y.; Gu, P.-F. Omnidirectional transmission bands of one-dimensional metal-dielectric periodic structures. J. Opt. Soc. Am. B 2008, 25, 1474–1478. [Google Scholar] [CrossRef]
- Zhang, M.C.; Allen, T.W.; Drobot, B.; McFarlane, S.; Meldrum, A.; DeCorby, R.G. Transparency and stability of Ag-based metal-dielectric multilayers. Appl. Opt. 2013, 52, 7479–7485. [Google Scholar] [CrossRef]
- Briones, E.; Sanchez, S.; Vergara, C.; Briones, J. Reflective color filters based on SiO2/Cu multilayer stacks. J. Appl. Phys. 2023, 134, 083101. [Google Scholar] [CrossRef]
- Belyaev, V.; Zverev, N.; Abduev, A.; Zotov, A. E-wave interaction with the one-dimensional photonic crystal with weak conductive and transparent materials. Coatings 2023, 13, 712. [Google Scholar] [CrossRef]
- Bikbaev, R.G.; Maksimov, D.N.; Pankin, P.S.; Chen, K.P.; Timofeev, I.V. Critical coupling vortex with grating-induced high Q-factor optical Tamm states. Opt. Express 2021, 29, 4672–4680. [Google Scholar] [CrossRef]
- Wu, F.; Wu, X.; Xiao, S.; Liu, G.; Li, H. Broadband wide-angle multilayer absorber based on a broadband omnidirectional optical Tamm state. Opt. Express 2021, 29, 23976–23987. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Zheng, G. Excitation of Hybrid Waveguide-Bloch surface states with Bi2Se3 plasmonic material in the near-infrared range. Micromachines 2022, 13, 1020. [Google Scholar] [CrossRef]
- Wu, F.; Li, X.; Fan, X.; Lin, L.; Taya, S.A.; Panda, A. Wide-angle absorption based on angle-insensitive light slowing effect in photonic crystal containing hyperbolic metamaterials. Photonics 2022, 9, 181. [Google Scholar] [CrossRef]
- Huang, C.H.; Wu, C.H.; Bikbaev, R.G.; Ye, M.J.; Chen, C.W.; Wang, T.J.; Timofeev, I.V.; Lee, W.; Chen, K.P. Wavelength-and angle-selective photodetectors enabled by graphene hot electrons with Tamm plasmon polaritons. Nanomaterials 2023, 13, 693. [Google Scholar] [CrossRef]
- Barone, P.W.; Baik, S.; Heller, D.A.; Strano, M.S. Near-infrared optical sensors based on single-walled carbon nanotubes. Nat. Mater. 2015, 4, 86–92. [Google Scholar] [CrossRef] [PubMed]
- Hakkel, K.D.; Petruzzella, M.; Ou, F.; Klinken, A.; Pagliano, F.; Liu, T.; Veldhoven, R.P.J.; Fiore, A. Integrated near-infrared spectral sensing. Nat. Commun. 2022, 13, 103. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Zhang, C.; Hu, J.; Han, H. Dual-band refractive index sensor with cascaded asymmetric resonant compound grating based on bound states in the continuum. Opt. Express 2023, 31, 13959–13969. [Google Scholar] [CrossRef] [PubMed]
- Wu, F.; Liu, T.; Xiao, S. Polarization-sensitive photonic bandgaps in hybrid one-dimensional photonic crystals composed of all-dielectric elliptical metamaterials and isotropic dielectrics. Appl. Opt. 2023, 62, 706–713. [Google Scholar] [CrossRef] [PubMed]
- Wang, E.W.; Yu, S.-J.; Phan, T.; Dhuey, S.; Fan, J.A. Arbitrary achromatic polarization control with reconfigurable metasurface systems. Laser Photonics Rev. 2023, 17, 2200926. [Google Scholar] [CrossRef]
- She, Y.; Liu, D.; Li, J.; Yao, M.; Zheng, Y.; Wu, F. Tunable wide-angle high-efficiency polarization selectivity based on a one-dimensional photonic crystal containing elliptical metamaterials. Phys. Lett. A 2024, 494, 129299. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, J.; Mao, Y.-F.; Chen, J.; Wang, S.; Chen, H.-Z.; Zhang, Y.; Wang, S.-Y.; Chen, X.; Li, T.; et al. Stable, high-performance sodium-based plasmonic devices in the near infrared. Nature 2020, 581, 401–405. [Google Scholar] [CrossRef] [PubMed]
- Rawashdeh, A.; Lupa, S.; Welch, W.; Yang, A. Sodium surface lattice plasmons. J. Phys. Chem. C 2021, 125, 25148–25154. [Google Scholar] [CrossRef]
- Delaney, M.; Zeimpekis, I.; Lawson, D.; Hewak, D.W.; Muskens, O.L. A new family of ultralow loss reversible phase-change materials for photonic integrated circuits: Sb2S3 and Sb2Se3. Adv. Funct. Mater. 2020, 30, 2002447. [Google Scholar] [CrossRef]
- Jana, S.; Sreekanth, K.V.; Abdelraouf, O.A.M.; Lin, R.; Liu, H.; Teng, J.; Singh, R. Aperiodic Bragg reflectors for tunable high-purity structural color based on phase change material. Nano Lett. 2024, 24, 3922–3929. [Google Scholar] [CrossRef]
- Liu, T.; Zhang, D.; Liu, W.; Yu, T.; Wu, F.; Xiao, S.; Huang, L.; Miroshnichenko, A.E. Phase-change nonlocal metasurfaces for dynamic wave-front manipulation. Phys. Rev. Appl. 2024, 21, 044004. [Google Scholar] [CrossRef]
- Yeh, P. Optical Waves in Layered Media; Wiley: Hoboken, NJ, USA, 1988. [Google Scholar]
- Hu, J.; Liu, W.; Xie, W.; Zhang, W.; Yao, E.; Zhang, Y.; Zhan, Q. Strong coupling of optical interface modes in a 1D topological photonic crystal heterostructure/Ag hybrid system. Opt. Lett. 2019, 44, 5642–5645. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.; Yao, E.; Xie, W.; Liu, W.; Li, D.; Lu, Y.; Zhan, Q. Strong longitudinal coupling of Tamm plasmon polaritons in graphene/DBR/Ag hybrid structure. Opt. Express 2019, 27, 18642–18652. [Google Scholar] [CrossRef] [PubMed]
- Gao, H.; Li, P.; Yang, S. Tunable multichannel optical absorber based on coupling effects of optical Tamm states in metal-photonic crystal heterostructure-metal structure. Opt. Commun. 2020, 457, 124688. [Google Scholar] [CrossRef]
- Pankin, P.S.; Sutormin, V.S.; Gunyakov, V.A.; Zelenov, F.V.; Tambasov, I.A.; Masyugin, A.N.; Volochaev, M.N.; Baron, F.A.; Chen, K.P.; Zyryanov, V.Y.; et al. Experimental implementation of tunable hybrid Tamm-microcavity modes. Appl. Phys. Lett. 2021, 119, 161107. [Google Scholar] [CrossRef]
- Jena, S.; Tokas, R.B.; Thakur, S.; Udupa, D.V. Rabi-like splitting and refractive index sensing with hybrid Tamm plasmon-cavity modes. J. Phys. D Appl. Phys. 2022, 55, 175104. [Google Scholar] [CrossRef]
- Xu, W.-H.; Chou, Y.-H.; Yang, Z.-Y.; Liu, Y.-Y.; Yu, M.-W.; Huang, C.-H.; Chang, C.-T.; Huang, C.-Y.; Lu, T.-C.; Lin, T.-R.; et al. Tamm plasmon-polariton ultraviolet lasers. Adv. Photonics Res. 2022, 3, 2100120. [Google Scholar] [CrossRef]
- Liu, Q.; Zhao, X.; Li, C.; Zhou, X.; Chen, Y.; Wang, S.; Lu, W. Coupled Tamm plasmon polaritons induced narrow bandpass filter with ultra-wide stopband. Nano Res. 2022, 15, 4563–4568. [Google Scholar] [CrossRef]
- Qin, K.; Deng, X.-H.; Zhang, P.; Guo, F.; Song, Y.; Tao, L.; Yuan, J. Tunable multiband THz perfect absorber due to the strong coupling of distributed Bragg reflector cavity mode and Tamm plasma polaritons modes based on MoS2 and graphene. Opt. Commun. 2024, 550, 129947. [Google Scholar] [CrossRef]
- Kaienburg, P.; Klingebiel, B.; Kirchartz, T. Spin-coated planar Sb2S3 hybrid solar cells approaching 5% efficiency. Beilstein J. Nanotechnol. 2018, 9, 2114–2124. [Google Scholar] [CrossRef]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
She, Y.; Zhong, K.; Tu, M.; Xiao, S.; Chen, Z.; An, Y.; Liu, D.; Wu, F. Tunable Near-Infrared Transparent Bands Based on Cascaded Fabry–Perot Cavities Containing Phase Change Materials. Photonics 2024, 11, 497. https://doi.org/10.3390/photonics11060497
She Y, Zhong K, Tu M, Xiao S, Chen Z, An Y, Liu D, Wu F. Tunable Near-Infrared Transparent Bands Based on Cascaded Fabry–Perot Cavities Containing Phase Change Materials. Photonics. 2024; 11(6):497. https://doi.org/10.3390/photonics11060497
Chicago/Turabian StyleShe, Yuchun, Kaichan Zhong, Manni Tu, Shuyuan Xiao, Zhanxu Chen, Yuehua An, Dejun Liu, and Feng Wu. 2024. "Tunable Near-Infrared Transparent Bands Based on Cascaded Fabry–Perot Cavities Containing Phase Change Materials" Photonics 11, no. 6: 497. https://doi.org/10.3390/photonics11060497
APA StyleShe, Y., Zhong, K., Tu, M., Xiao, S., Chen, Z., An, Y., Liu, D., & Wu, F. (2024). Tunable Near-Infrared Transparent Bands Based on Cascaded Fabry–Perot Cavities Containing Phase Change Materials. Photonics, 11(6), 497. https://doi.org/10.3390/photonics11060497






