Four-Fold, Cross-Phase Modulation Driven UV Pulse Compression in a Thin Bulk Medium
Abstract
:1. Introduction
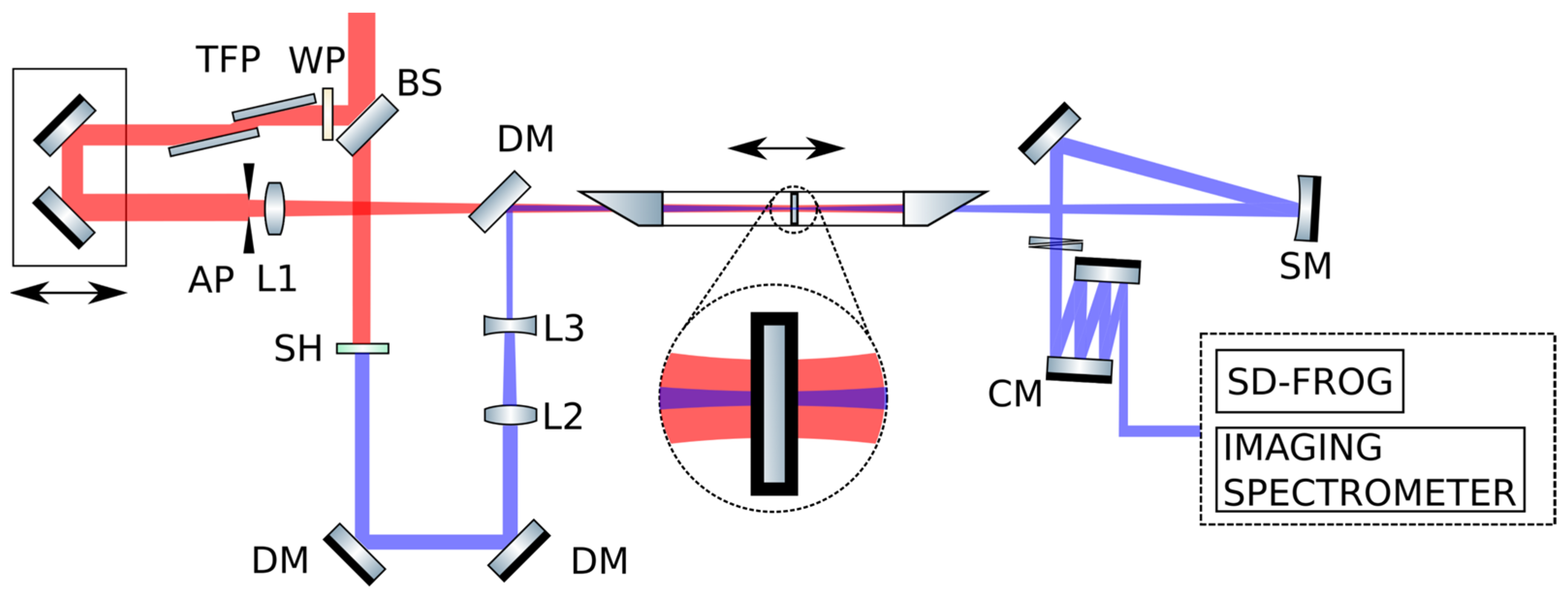
2. Materials and Methods
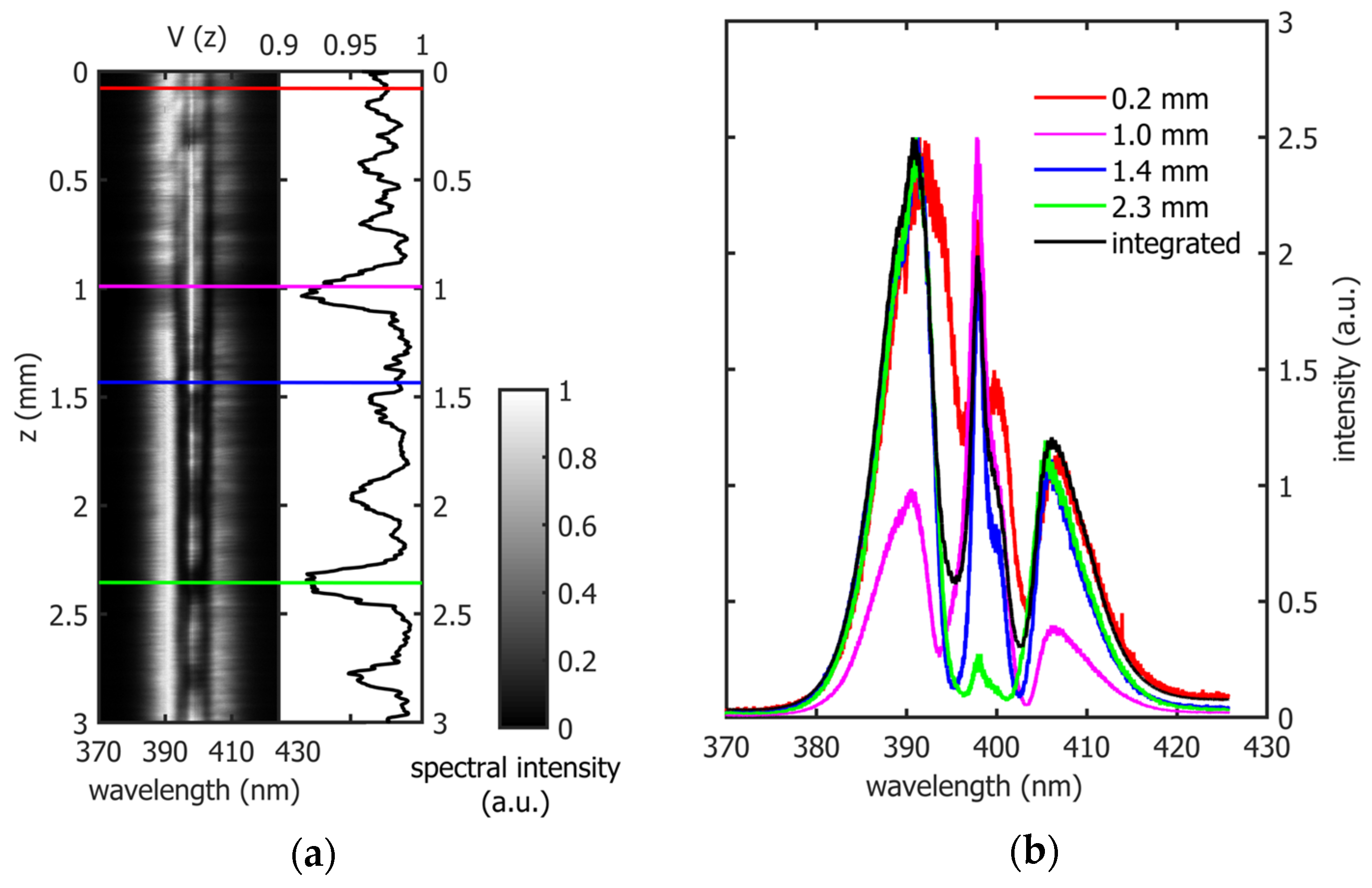
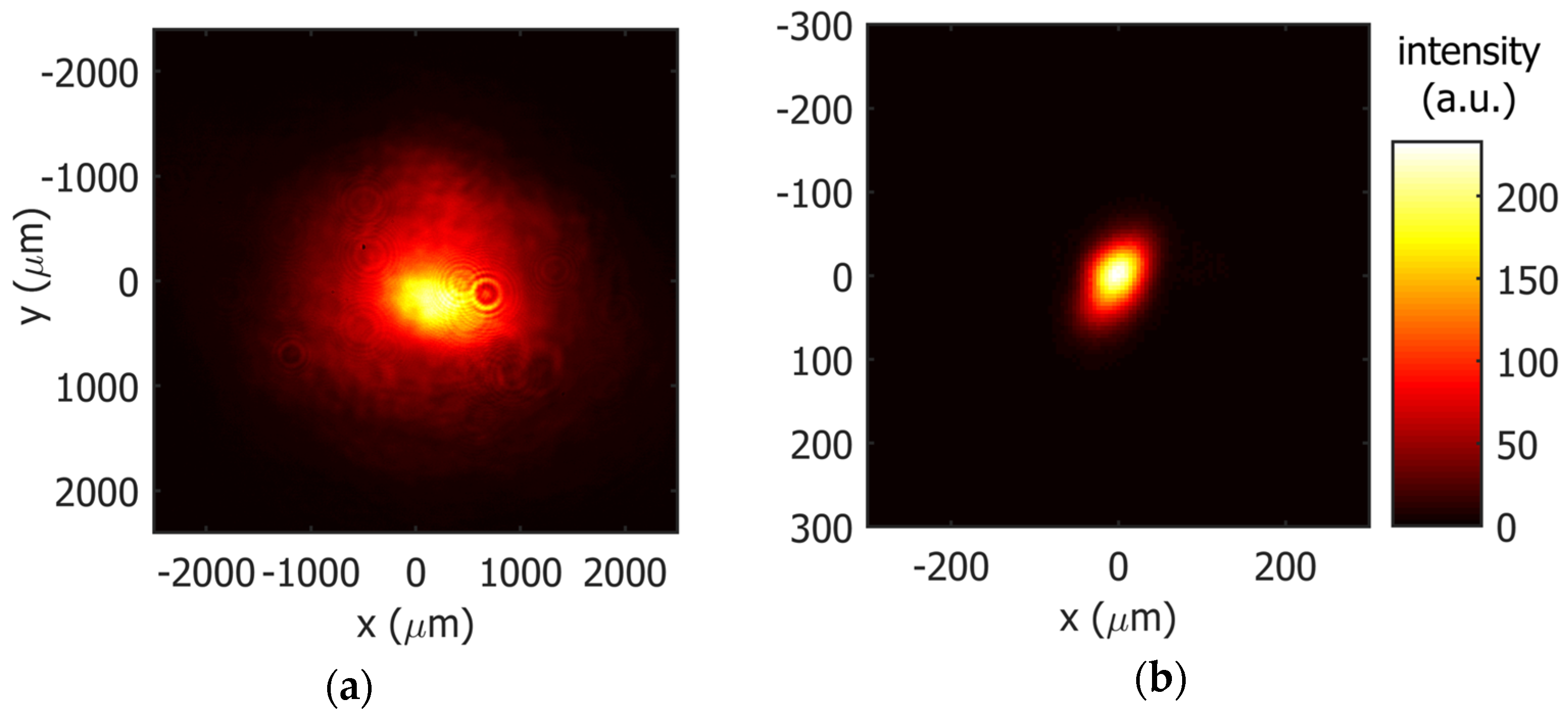
3. Results
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chergui, M. Ultrafast Molecular Photophysics in the Deep-Ultraviolet. J. Chem. Phys. 2019, 150, 070901. [Google Scholar] [CrossRef] [PubMed]
- Cannizzo, A. Ultrafast UV Spectroscopy: From a Local to a Global View of Dynamical Processes in Macromolecules. Phys. Chem. Chem. Phys. 2012, 14, 11205–11223. [Google Scholar] [CrossRef]
- Popmintchev, D.; Hernández-García, C.; Dollar, F.; Mancuso, C.; Pérez-Hernández, J.A.; Chen, M.-C.; Hankla, A.; Gao, X.; Shim, B.; Gaeta, A.L.; et al. Ultraviolet Surprise: Efficient Soft X-ray High-Harmonic Generation in Multiply Ionized Plasmas. Science 2015, 350, 1225–1231. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Xu, Y.; Ulonska, S.; Robinson, J.S.; Ranitovic, P.; Kaindl, R.A. Bright High-Repetition-Rate Source of Narrowband Extreme-Ultraviolet Harmonics beyond 22 eV. Nat Commun 2015, 6, 7459. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, T.; Ribič, P.R. Shortening the Pulse Duration in Seeded Free-Electron Lasers by Chirped Microbunching. Opt. Express OE 2019, 27, 30875–30892. [Google Scholar] [CrossRef] [PubMed]
- Galli, M.; Wanie, V.; Lopes, D.P.; Månsson, E.P.; Trabattoni, A.; Colaizzi, L.; Saraswathula, K.; Cartella, A.; Frassetto, F.; Poletto, L.; et al. Generation of Deep Ultraviolet Sub-2-Fs Pulses. Opt. Lett. 2019, 44, 1308. [Google Scholar] [CrossRef]
- Reiter, F.; Graf, U.; Schultze, M.; Schweinberger, W.; Schröder, H.; Karpowicz, N.; Azzeer, A.M.; Kienberger, R.; Krausz, F.; Goulielmakis, E. Generation of Sub-3 Fs Pulses in the Deep Ultraviolet. Opt. Lett. OL 2010, 35, 2248–2250. [Google Scholar] [CrossRef] [PubMed]
- Durfee, C.G.; Backus, S.; Kapteyn, H.C.; Murnane, M.M. Intense 8-Fs Pulse Generation in the Deep Ultraviolet. Opt. Lett. 1999, 24, 697. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Okamura, K.; Kida, Y.; Teramoto, T.; Kobayashi, T. Clean Sub-8-Fs Pulses at 400 Nm Generated by a Hollow Fiber Compressor for Ultraviolet Ultrafast Pump-Probe Spectroscopy. Opt. Express OE 2010, 18, 20645–20650. [Google Scholar] [CrossRef] [PubMed]
- Nagy, T.; Simon, P. Generation of 200-μJ, Sub-25-Fs Deep-UV Pulses Using a Noble-Gas-Filled Hollow Fiber. Opt. Lett. 2009, 34, 2300. [Google Scholar] [CrossRef] [PubMed]
- Xiao, F.; Fan, X.; Wang, L.; Zhang, D.; Wu, J.; Wang, X.; Zhao, Z. Generation of Intense Sub-10 Fs Pulses at 385nm. Chinese Phys. Lett. 2020, 37, 114202. [Google Scholar] [CrossRef]
- Hu, F.; Wang, Z.; Yao, Q.; Cao, W.; Zhang, Q.; Lu, P. Clean Hundred-µJ-Level Sub-6-Fs Blue Pulses Generated with Helium-Assisted Solid Thin Plates. Opt. Lett. OL 2023, 48, 2555–2558. [Google Scholar] [CrossRef] [PubMed]
- Canhota, M.; Weigand, R.; Crespo, H.M. Simultaneous Measurement of Two Ultrashort Near-Ultraviolet Pulses Produced by a Multiplate Continuum Using Dual Self-Diffraction Dispersion-Scan. Opt. Lett. 2019, 44, 1015. [Google Scholar] [CrossRef] [PubMed]
- Travers, J.C.; Grigorova, T.F.; Brahms, C.; Belli, F. High-Energy Pulse Self-Compression and Ultraviolet Generation through Soliton Dynamics in Hollow Capillary Fibres. Nat. Photonics 2019, 13, 547–554. [Google Scholar] [CrossRef]
- Agrawal, G.P.; Baldeck, P.L.; Alfano, R.R. Temporal and Spectral Effects of Cross-Phase Modulation on Copropagating Ultrashort Pulses in Optical Fibers. Phys. Rev. A 1989, 40, 5063–5072. [Google Scholar] [CrossRef] [PubMed]
- Matsubara, E.; Yamane, K.; Sekikawa, T.; Yamashita, M. Generation of 2.6 Fs Optical Pulses Using Induced-Phase Modulation in a Gas-Filled Hollow Fiber. J. Opt. Soc. Am. B JOSAB 2007, 24, 985–989. [Google Scholar] [CrossRef]
- Jiang, Y.; Messerschmidt, J.P.; Scheiba, F.; Tyulnev, I.; Wang, L.; Wei, Z.; Rossi, G.M. Ultraviolet Pulse Compression via Cross-Phase Modulation in a Hollow-Core Fiber. Optica OPTICA 2024, 11, 291–296. [Google Scholar] [CrossRef]
- Liu, J.; Kida, Y.; Teramoto, T.; Kobayashi, T. Simultaneous Compression and Amplification of a Laser Pulse in a Glass Plate. Opt. Express OE 2010, 18, 2495–2502. [Google Scholar] [CrossRef] [PubMed]
- Campillo, A.J. Small-Scale Self-Focusing. In Self-Focusing: Past and Present; Boyd, R.W., Lukishova, S.G., Shen, Y.R., Eds.; Topics in Applied Physics; Springer: New York, NY, USA, 2009; Volume 114, pp. 157–173. ISBN 978-0-387-32147-9. [Google Scholar]
- Weitenberg, J.; Vernaleken, A.; Schulte, J.; Ozawa, A.; Sartorius, T.; Pervak, V.; Hoffmann, H.-D.; Udem, T.; Russbüldt, P.; Hänsch, T.W. Multi-Pass-Cell-Based Nonlinear Pulse Compression to 115 Fs at 75 µJ Pulse Energy and 300 W Average Power. Opt. Express 2017, 25, 20502. [Google Scholar] [CrossRef] [PubMed]
- Spanner, M.; Ivanov, M.Y.; Kalosha, V.; Hermann, J.; Wiersma, D.A.; Pshenichnikov, M. Tunable Optimal Compression of Ultrabroadband Pulses by Cross-Phase Modulation. Opt. Lett. 2003, 28, 749. [Google Scholar] [CrossRef] [PubMed]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Susnjar, P.; Demidovich, A.; Kurdi, G.; Cinquegrana, P.; Nikolov, I.; Sigalotti, P.; Danailov, M.B. Four-Fold, Cross-Phase Modulation Driven UV Pulse Compression in a Thin Bulk Medium. Photonics 2024, 11, 520. https://doi.org/10.3390/photonics11060520
Susnjar P, Demidovich A, Kurdi G, Cinquegrana P, Nikolov I, Sigalotti P, Danailov MB. Four-Fold, Cross-Phase Modulation Driven UV Pulse Compression in a Thin Bulk Medium. Photonics. 2024; 11(6):520. https://doi.org/10.3390/photonics11060520
Chicago/Turabian StyleSusnjar, Peter, Alexander Demidovich, Gabor Kurdi, Paolo Cinquegrana, Ivaylo Nikolov, Paolo Sigalotti, and Miltcho B. Danailov. 2024. "Four-Fold, Cross-Phase Modulation Driven UV Pulse Compression in a Thin Bulk Medium" Photonics 11, no. 6: 520. https://doi.org/10.3390/photonics11060520
APA StyleSusnjar, P., Demidovich, A., Kurdi, G., Cinquegrana, P., Nikolov, I., Sigalotti, P., & Danailov, M. B. (2024). Four-Fold, Cross-Phase Modulation Driven UV Pulse Compression in a Thin Bulk Medium. Photonics, 11(6), 520. https://doi.org/10.3390/photonics11060520




