Generation and Dynamics of Multiple Pulses in an Ultrafast Fiber Laser with a Single-Mode Fiber–Graded-Index Multimode Fiber–Single-Mode Fiber-Based Saturable Absorber
Abstract
:1. Introduction
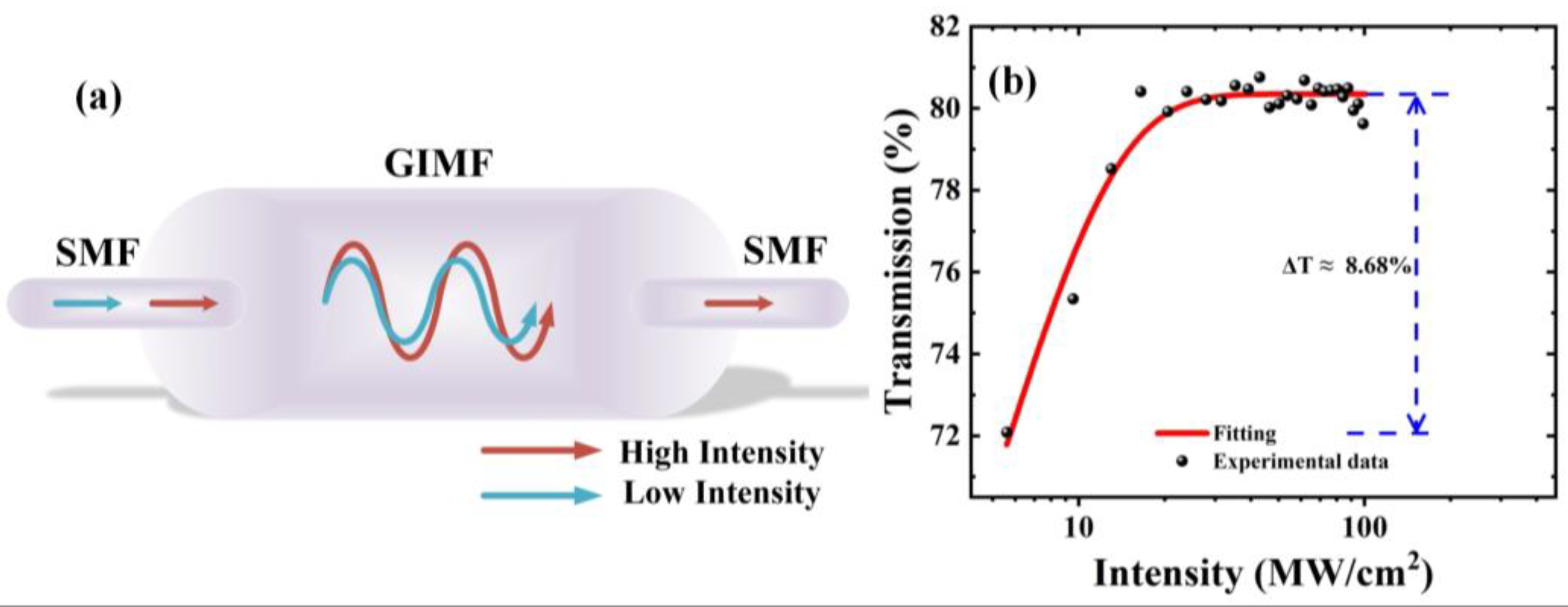
2. Fabrication and Principle
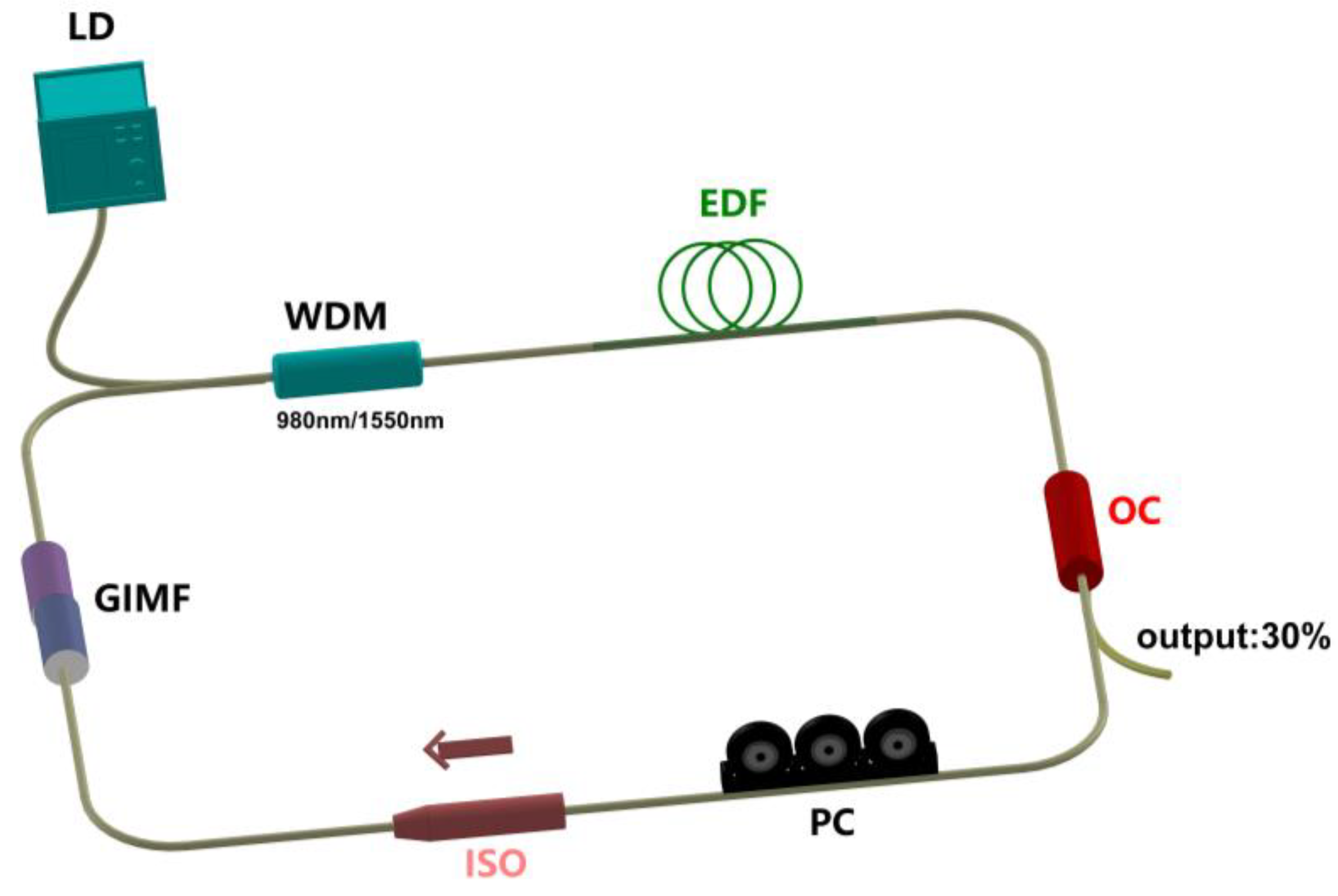
3. Experimental Configuration
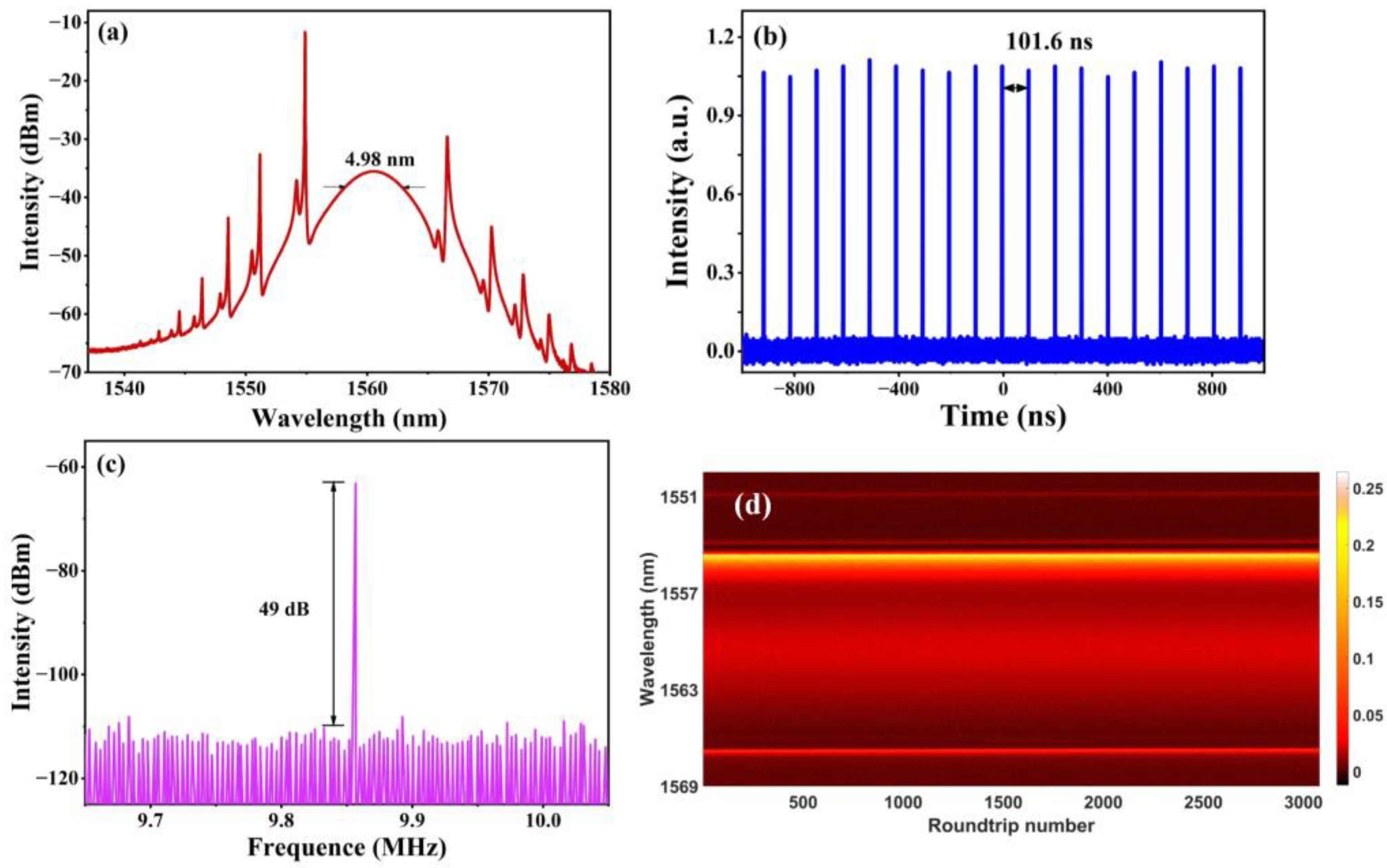
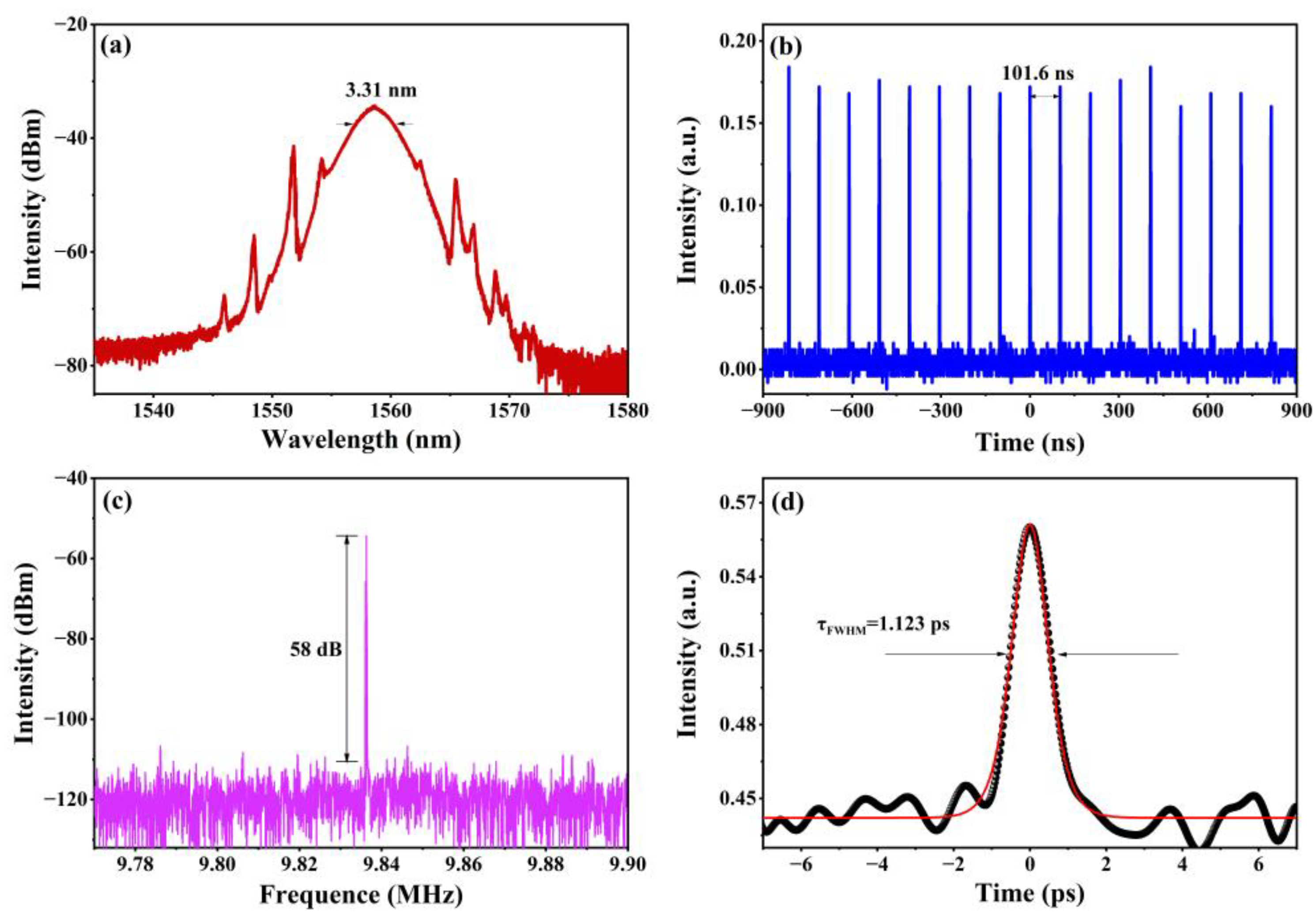
4. Experiments and Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ebrahim-Zadeh, M.; Sorokina, I.T. Mid-Infrared Coherent Sources and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Ramaswami, R.; Sivarajan, K.; Sasaki, G. Optical Networks: A Practical Perspective; Morgan Kaufmann: Cambridge, MA, USA, 2009. [Google Scholar]
- Mollenauer, L.F.; Gordon, J.P. Solitons in Optical Fibers: Fundamentals and Applications; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Mollenauer, L.F.; Mamyshev, P.V. Massive Wavelength-Division Multiplexing with Solitons. IEEE J. Quantum Electron. 1998, 34, 2089–2102. [Google Scholar] [CrossRef]
- Huang, J.; Yang, S. Investigation on Anisotropic Tribological Properties of Superhydrophobic/Superlipophilic Lead Bronze Surface Textured by Femtosecond Laser. Appl. Surf. Sci. 2022, 579, 152223. [Google Scholar] [CrossRef]
- Mehta, A.; Mohammed, W.; Johnson, E.G. Multimode Interference-Based Fiber-Optic Displacement Sensor. IEEE Photonics Technol. Lett. 2003, 15, 1129–1131. [Google Scholar] [CrossRef]
- Goda, K.; Jalali, B. Dispersive Fourier Transformation for Fast Continuous Single-Shot Measurements. Nat. Photonics 2013, 7, 102–112. [Google Scholar]
- Qi, Y.; Yang, S.; Wang, J.; Li, L.; Bai, Z.; Wang, Y.; Lv, Z. Recent Advance of Emerging Low-Dimensional Materials for Vector Soliton Generation in Fiber Lasers. Mater. Today Phys. 2022, 23, 100622. [Google Scholar]
- Chernysheva, M.A.; Krylov, A.A.; Kryukov, P.G.; Arutyunyan, N.R.; Pozharov, A.S.; Obraztsova, E.D.; Dianov, E.M. Thulium-Doped Mode-Locked All-Fiber Laser Based on NALM and Carbon Nanotube Saturable Absorber. Opt. Express 2012, 20, B124–B130. [Google Scholar] [CrossRef]
- Zhang, M.; Kelleher, E.J.R.; Torrisi, F.; Sun, Z.; Hasan, T.; Popa, D.; Wang, F.; Ferrari, A.C.; Popov, S.V.; Taylor, J.R. Tm-Doped Fiber Laser Mode-Locked by Graphene-Polymer Composite. Opt. Express 2012, 20, 25077–25084. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Shi, Z.; Shi, X.; Zhang, K.; Zhang, H. Recent Progress in Black Phosphorus and Black-Phosphorus-Analogue Materials: Properties, Synthesis and Applications. Nanoscale 2019, 11, 14491–14527. [Google Scholar]
- Wu, K.; Guo, C.; Wang, H.; Zhang, X.; Wang, J.; Chen, J. All-Optical Phase Shifter and Switch near 1550nm Using Tungsten Disulfide (WS 2) Deposited Tapered Fiber. Opt. Express 2017, 25, 17639–17649. [Google Scholar] [CrossRef]
- Yan, P.; Lin, R.; Ruan, S.; Liu, A.; Chen, H.; Zheng, Y.; Chen, S.; Guo, C.; Hu, J. A Practical Topological Insulator Saturable Absorber for Mode-Locked Fiber Laser. Sci. Rep. 2015, 5, 8690. [Google Scholar] [CrossRef]
- Liu, J.; Xu, J.; Wang, P. High Repetition-Rate Narrow Bandwidth SESAM Mode-Locked Yb-Doped Fiber Lasers. IEEE Photonics Technol. Lett. 2012, 24, 539–541. [Google Scholar] [CrossRef]
- Yan, P.; Liu, A.; Chen, Y.; Chen, H.; Ruan, S.; Guo, C.; Chen, S.; Li, I.L.; Yang, H.; Hu, J. Microfiber-Based WS 2-Film Saturable Absorber for Ultra-Fast Photonics. Opt. Mater. Express 2015, 5, 479–489. [Google Scholar] [CrossRef]
- Seredych, M.; Alhabeb, M.; Anasori, B.; Gogotsi, Y. High-Temperature Behaviors of MXenes. In Proceedings of the Electrochemical Society Meeting Abstracts 233; The Electrochemical Society, Inc.: Pennington, NJ, USA, 2018; p. 1136. [Google Scholar]
- Nazemosadat, E.; Mafi, A. Nonlinear Multimodal Interference and Saturable Absorption Using a Short Graded-Index Multimode Optical Fiber. JOSA B 2013, 30, 1357–1367. [Google Scholar] [CrossRef]
- Teğin, U.; Ortaç, B. All-Fiber All-Normal-Dispersion Femtosecond Laser with a Nonlinear Multimodal Interference-Based Saturable Absorber. Opt. Lett. 2018, 43, 1611–1614. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Wang, Z.; Li, C.; Tian, Y.; Xiao, Z.; Zhang, J.; Xu, S. Self-Starting Mode-Locked Tm-Doped Fiber Laser Using a Hybrid Structure of No Core-Graded Index Multimode Fiber as the Saturable Absorber. Opt. Laser Technol. 2019, 113, 317–321. [Google Scholar] [CrossRef]
- Zhu, T.; Wang, Z.; Wang, D.N.; Yang, F.; Li, L. Observation of Controllable Tightly and Loosely Bound Solitons with an All-Fiber Saturable Absorber. Photonics Res. 2019, 7, 61–68. [Google Scholar] [CrossRef]
- Jiang, H.; Li, H.; Hu, F.; Ren, X.; Li, C.; Xu, S. Mode-Locked Tm Fiber Laser with a Tapered GIMF SA Based on Nonlinear Multimode Interference Effect. IEEE Photonics Technol. Lett. 2020, 32, 503–506. [Google Scholar] [CrossRef]
- Li, X.; Wang, D.N.; Chen, J. Saturable Absorber Based on a Hybrid Structure of Graded-Index Multimode Fiber and Graphene for a Passive Mode-Locked Erbium-Doped Fiber Laser. JOSA B 2021, 38, 2112–2117. [Google Scholar] [CrossRef]
- Zhao, F.; Li, N.; Wang, H. Generation of a Noise-like Pulse from an Erbium-Doped Fiber Laser Based on Nonlinear Multimode Interference. Laser Phys. 2020, 30, 125102. [Google Scholar] [CrossRef]
- Cheng, P.; Han, M.; Li, Q.; Shu, X. Generation of Different Mode-Locked States in a Yb-Doped Fiber Laser Based on Nonlinear Multimode Interference. Opt. Express 2022, 30, 35911–35922. [Google Scholar] [CrossRef]
- Ren, X.; Li, H.; Zhang, Z.; Zhang, J.; Xu, S. Generation of Bound Solitons in a Mode-Locked Tm-Doped Fiber Laser Based on a Graded-Index Multimode Fiber Saturable Absorber. Opt. Laser Technol. 2022, 149, 107865. [Google Scholar] [CrossRef]
- Liu, M.; Qi, Y.; Yang, S.; Bai, Z.; Yan, B.; Ding, J.; Wang, Y.; Lu, Z. Switchable L-Band Dual-Wavelength Dark–Bright Pulse Pair Generation from an Er-Doped Mode-Locked Fiber Laser with SMF–GIMF–SMF as the Saturable Absorber. Appl. Phys. B 2022, 128, 190. [Google Scholar] [CrossRef]
- Bae, J.E.; Mateos, X.; Aguiló, M.; Díaz, F.; Vázquez de Aldana, J.R.; Romero, C.; Lee, H.; Rotermund, F. Transition of Pulsed Operation from Q-Switching to Continuous-Wave Mode-Locking in a Yb:KLuW Waveguide Laser. Opt. Express 2020, 28, 18027–18034. [Google Scholar] [CrossRef] [PubMed]
- Bae, J.E.; Mateos, X.; Aguiló, M.; Díaz, F.; Ajates, J.G.; Romero, C.; Vázquez de Aldana, J.R.; Rotermund, F. Multi-Gigahertz Mode-Locked Femtosecond Yb:KLuW Waveguide Lasers. Photon. Res. 2022, 10, 2584–2589. [Google Scholar] [CrossRef]
- Bae, J.E.; Calmano, T.; Kränkel, C.; Rotermund, F. Controllable Dynamic Single- and Dual-Channel Graphene Q-Switching in a Beam-Splitter-Type Channel Waveguide Laser. Laser Photonics Rev. 2022, 16, 2100501. [Google Scholar] [CrossRef]
- Liu, M.; Zhao, N.; Liu, H.; Zheng, X.-W.; Luo, A.-P.; Luo, Z.-C.; Xu, W.-C.; Zhao, C.-J.; Zhang, H.; Wen, S.-C. Dual-Wavelength Harmonically Mode-Locked Fiber Laser with Topological Insulator Saturable Absorber. IEEE Photonics Technol. Lett. 2014, 26, 983–986. [Google Scholar] [CrossRef]
- Wang, Y.; Mao, D.; Gan, X.; Han, L.; Ma, C.; Xi, T.; Zhang, Y.; Shang, W.; Hua, S.; Zhao, J. Harmonic Mode Locking of Bound-State Solitons Fiber Laser Based on MoS 2 Saturable Absorber. Opt. Express 2015, 23, 205–210. [Google Scholar] [CrossRef]
- Stratmann, M.; Pagel, T.; Mitschke, F. Experimental Observation of Temporal Soliton Molecules. Phys. Rev. Lett. 2005, 95, 143902. [Google Scholar] [CrossRef]
- Gattass, R.R.; Cerami, L.R.; Mazur, E. Micromachining of Bulk Glass with Bursts of Femtosecond Laser Pulses at Variable Repetition Rates. Opt. Express 2006, 14, 5279–5284. [Google Scholar] [CrossRef]
- Seong, N.H.; Kim, D.Y. Experimental Observation of Stable Bound Solitons in a Figure-Eight Fiber Laser. Opt. Lett. 2002, 27, 1321–1323. [Google Scholar] [CrossRef]
- Allison, S.W.; Gillies, G.T. Observations of and Applications for Self-Imaging in Optical Fibers. Appl. Opt. 1994, 33, 1802–1805. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, G.P. Invite Paper: Self-Imaging in Multimode Graded-Index Fibers and Its Impact on the Nonlinear Phenomena. Opt. Fiber Technol. 2019, 50, 309–316. [Google Scholar] [CrossRef]
- Zhu, X.; Schülzgen, A.; Li, H.; Li, L.; Han, L.; Moloney, J.V.; Peyghambarian, N. Detailed Investigation of Self-Imaging in Largecore Multimode Optical Fibers for Application in Fiber Lasers and Amplifiers. Opt. Express 2008, 16, 16632–16645. [Google Scholar] [CrossRef]
- Asawa, C.K.; Taylor, H.F. Propagation of Light Trapped within a Set of Lowest-Order Modes of Graded-Index Multimode Fiber Undergoing Bending. Appl. Opt. 2000, 39, 2029–2037. [Google Scholar] [CrossRef] [PubMed]
- Su, L.; Chiang, K.S.; Lu, C. Microbend-Induced Mode Coupling in a Graded-Index Multimode Fiber. Appl. Opt. 2005, 44, 7394–7402. [Google Scholar] [CrossRef] [PubMed]
- Renninger, W.H.; Wise, F.W. Optical Solitons in Graded-Index Multimode Fibres. Nat Commun 2013, 4, 1719. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.; Zhang, Q.; Zhang, Y.; Li, X.; Zhang, H.; Xia, W. All-Fiber Passively Mode-Locked Laser Using Nonlinear Multimode Interference of Step-Index Multimode Fiber. Photon. Res. 2018, 6, 1033. [Google Scholar] [CrossRef]
- Fu, S.; Sheng, Q.; Zhu, X.; Shi, W.; Yao, J.; Shi, G.; Norwood, R.A.; Peyghambarian, N. Passive Q-Switching of an All-Fiber Laser Induced by the Kerr Effect of Multimode Interference. Opt. Express 2015, 23, 17255–17262. [Google Scholar] [CrossRef]
- Dong, Z.; Lin, J.; Li, H.; Li, S.; Tao, R.; Gu, C.; Yao, P.; Xu, L. Generation of Mode-Locked Square-Shaped and Chair-like Pulse Based on Reverse Saturable Absorption Effect of Nonlinear Multimode Interference. Opt. Express 2019, 27, 27610–27617. [Google Scholar] [CrossRef]
- Tang, D.Y.; Zhao, L.M.; Zhao, B.; Liu, A.Q. Mechanism of Multisoliton Formation and Soliton Energy Quantization in Passively Mode-Locked Fiber Lasers. Phys. Rev. A 2005, 72, 043816. [Google Scholar] [CrossRef]
- Li, C.; Kong, C.; Wong, K.K.Y. High Energy Noise-Like Pulse Generation from a Mode-Locked Thulium-Doped Fiber Laser at 1.7 Μm. IEEE Photonics J. 2019, 11, 1–6. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhao, D.; Liu, R.; Ma, W.; Wang, T. Switchable Generation of a Sub-200 Fs Dissipative Soliton and a Noise-like Pulse in a Normal-Dispersion Tm-Doped Mode-Locked Fiber Laser. Appl. Opt. 2020, 59, 3575–3581. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Liang, X.; Hu, G.; Zheng, Z.; Lin, S.; Ouyang, D.; Wu, X.; Yan, P.; Ruan, S.; Sun, Z.; et al. 152 Fs Nanotube-Mode-Locked Thulium-Doped All-Fiber Laser. Sci. Rep. 2016, 6, 28885. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.M.; Tang, D.Y.; Cheng, T.H.; Lu, C. Nanosecond Square Pulse Generation in Fiber Lasers with Normal Dispersion. Opt. Commun. 2007, 272, 431–434. [Google Scholar] [CrossRef]
- Zaviyalov, A.; Grelu, P.; Lederer, F. Impact of Slow Gain Dynamics on Soliton Molecules in Mode-Locked Fiber Lasers. Opt. Lett. 2012, 37, 175–177. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Zeng, Q.; Yang, Y.; Du, G.; Ji, J.; Song, Y.; Wang, Z.; Wang, K. Generation and Dynamics of Multiple Pulses in an Ultrafast Fiber Laser with a Single-Mode Fiber–Graded-Index Multimode Fiber–Single-Mode Fiber-Based Saturable Absorber. Photonics 2024, 11, 52. https://doi.org/10.3390/photonics11010052
Yang Y, Zeng Q, Yang Y, Du G, Ji J, Song Y, Wang Z, Wang K. Generation and Dynamics of Multiple Pulses in an Ultrafast Fiber Laser with a Single-Mode Fiber–Graded-Index Multimode Fiber–Single-Mode Fiber-Based Saturable Absorber. Photonics. 2024; 11(1):52. https://doi.org/10.3390/photonics11010052
Chicago/Turabian StyleYang, Yatao, Qiong Zeng, Yanzhao Yang, Geguo Du, Jianhua Ji, Yufeng Song, Zhenhong Wang, and Ke Wang. 2024. "Generation and Dynamics of Multiple Pulses in an Ultrafast Fiber Laser with a Single-Mode Fiber–Graded-Index Multimode Fiber–Single-Mode Fiber-Based Saturable Absorber" Photonics 11, no. 1: 52. https://doi.org/10.3390/photonics11010052
APA StyleYang, Y., Zeng, Q., Yang, Y., Du, G., Ji, J., Song, Y., Wang, Z., & Wang, K. (2024). Generation and Dynamics of Multiple Pulses in an Ultrafast Fiber Laser with a Single-Mode Fiber–Graded-Index Multimode Fiber–Single-Mode Fiber-Based Saturable Absorber. Photonics, 11(1), 52. https://doi.org/10.3390/photonics11010052





