Increase in Modulation Speed of Silicon Photonics Modulator with Quantum-Well Slab Wings: New Insights from a Numerical Study
Abstract
:1. Introduction
2. Review of Carrier-Depletion Silicon Photonics Modulators
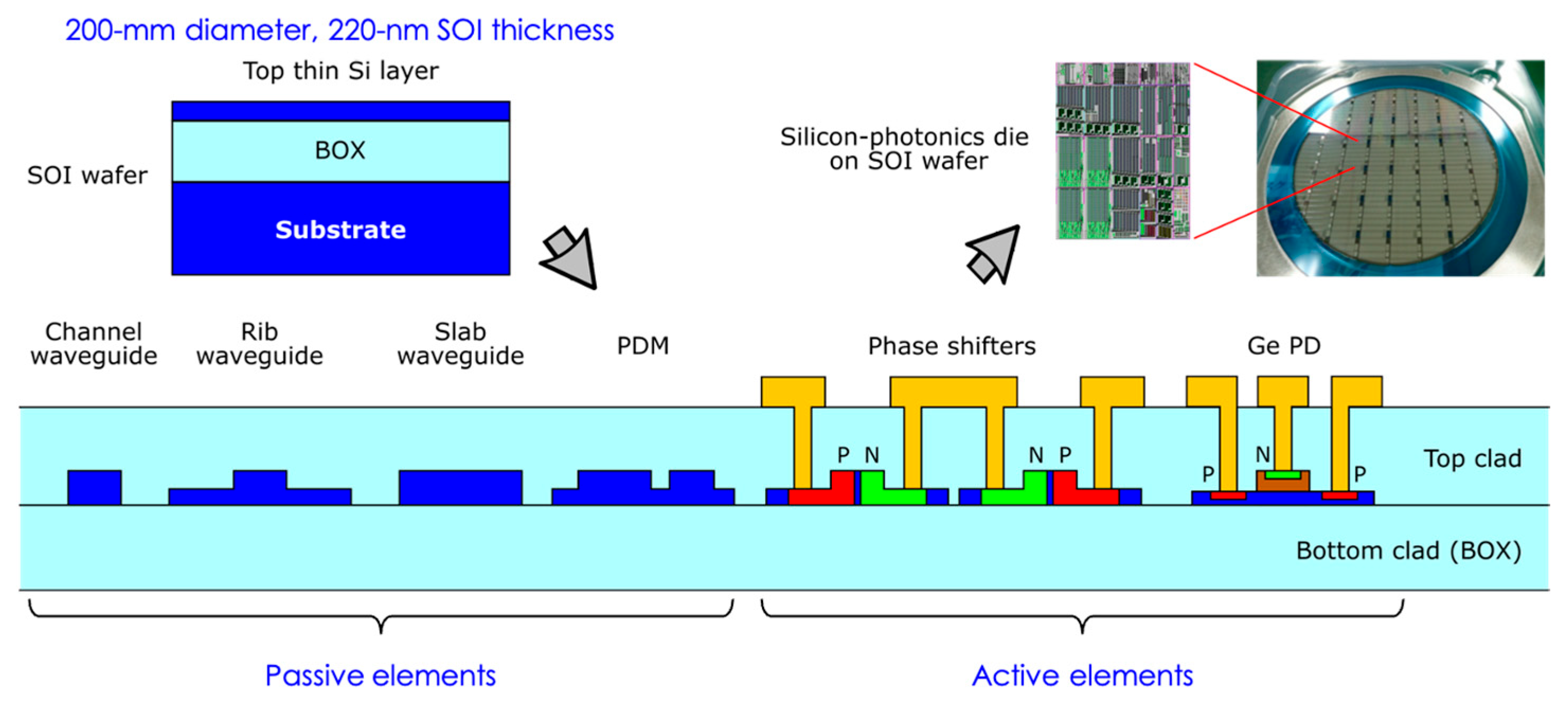
2.1. Design Considerations
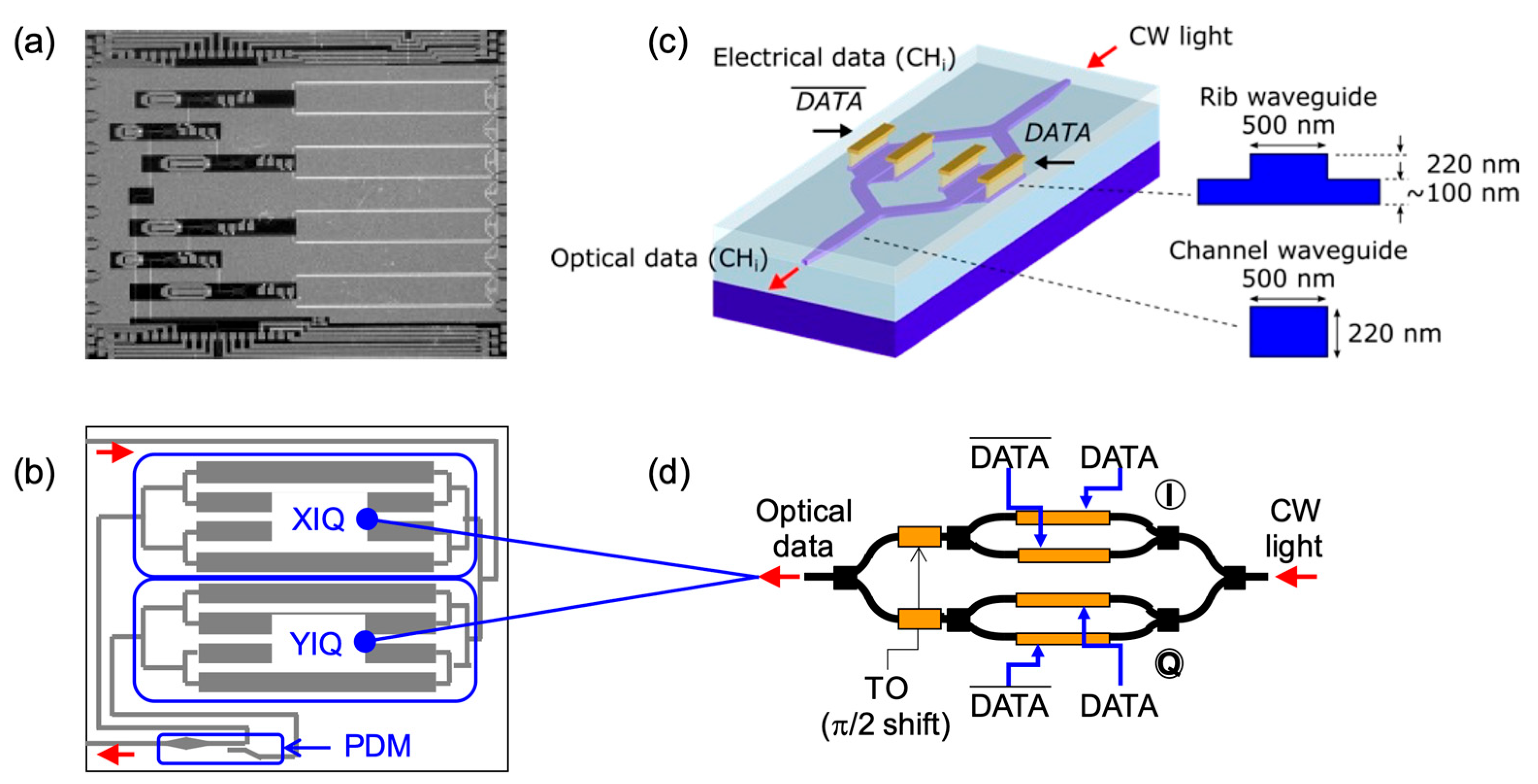
2.2. Fabrication Processes
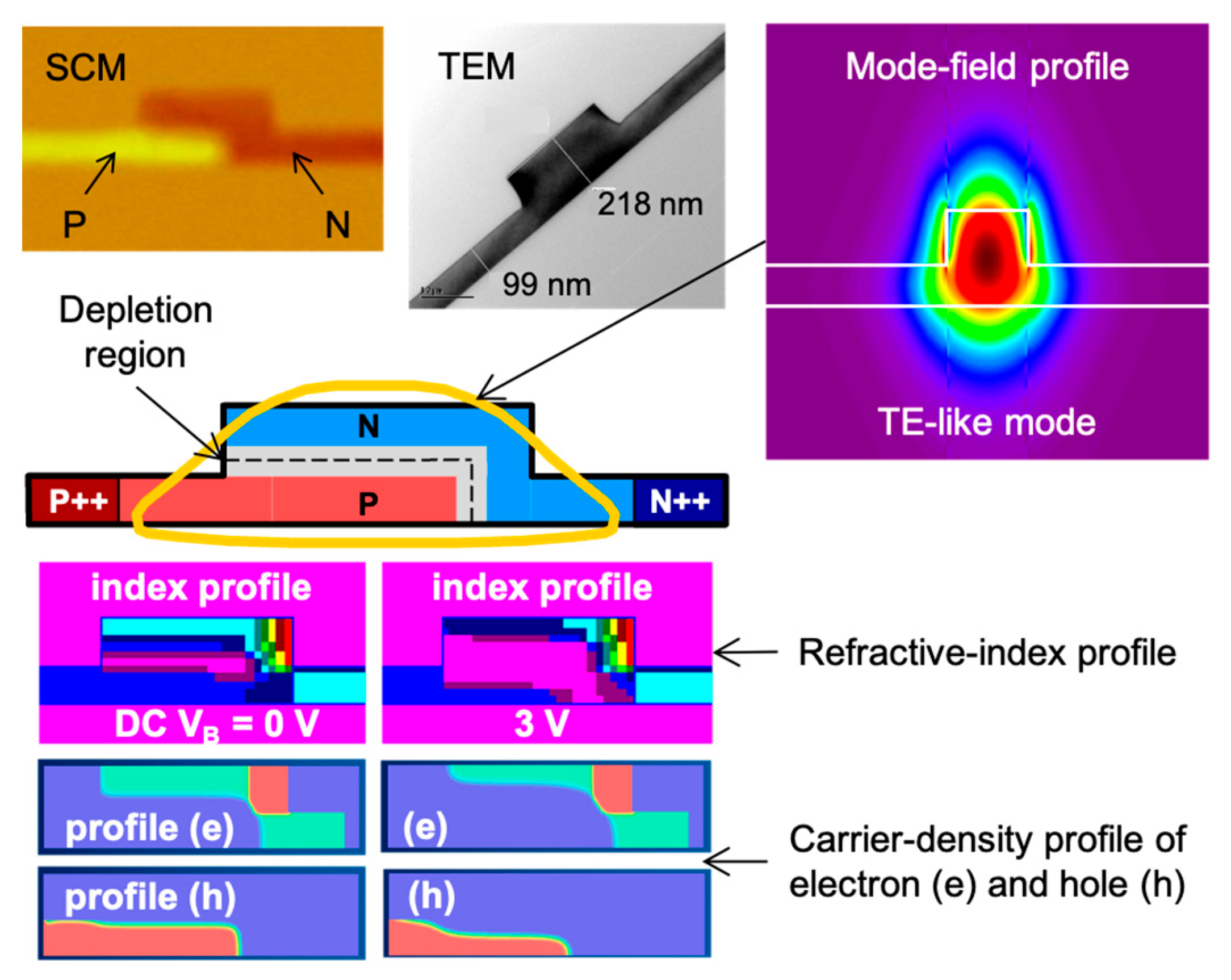
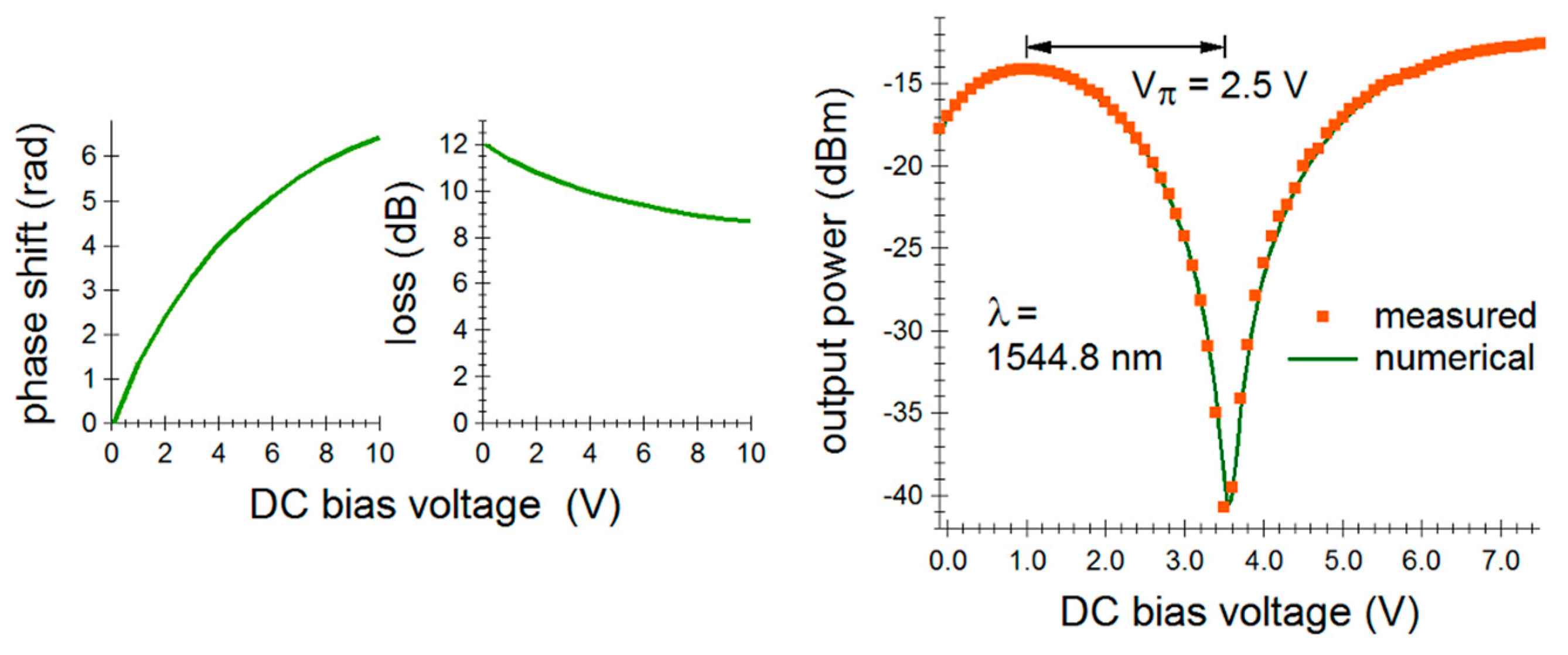
2.3. Fundamental Characteristics
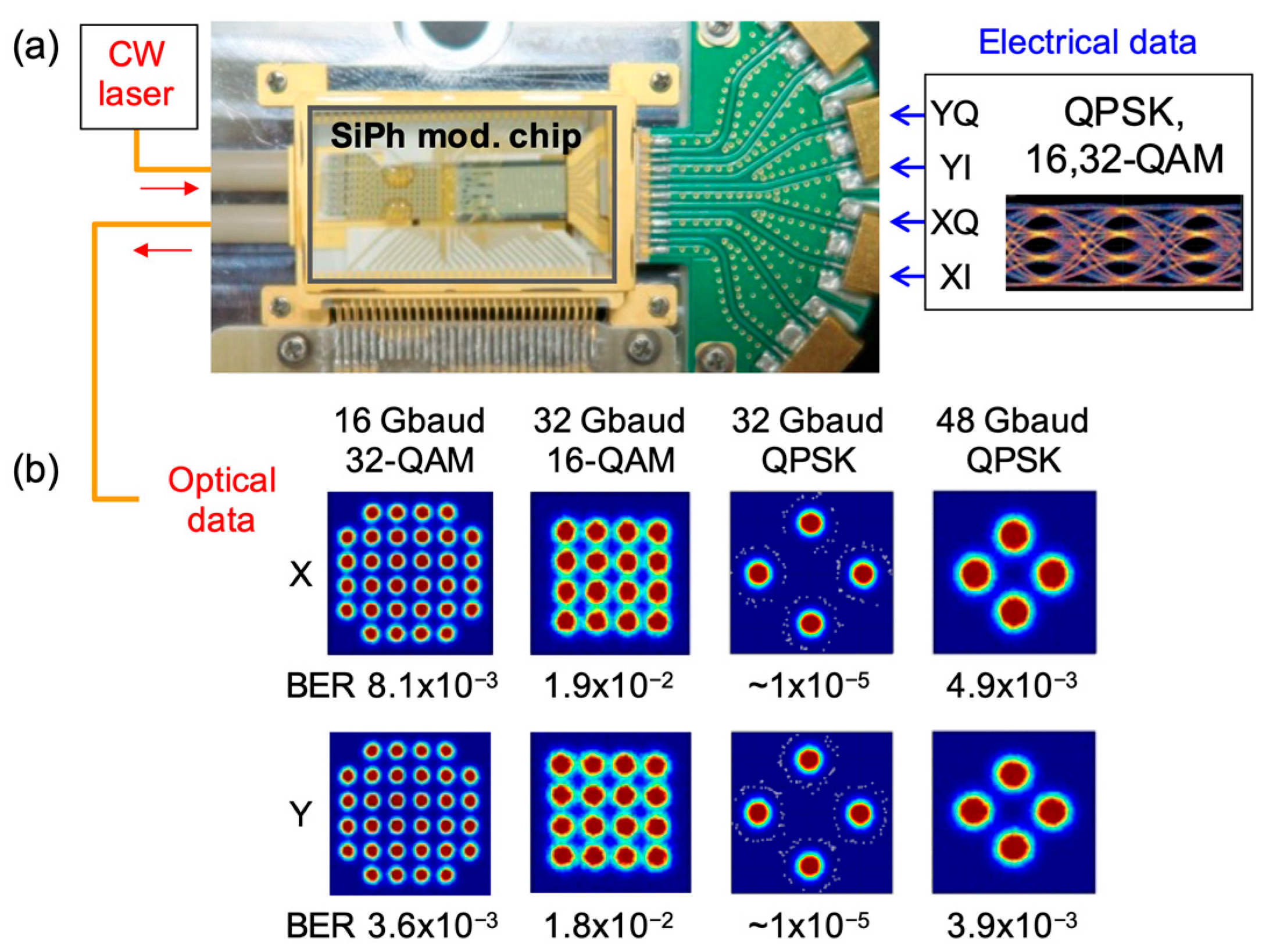
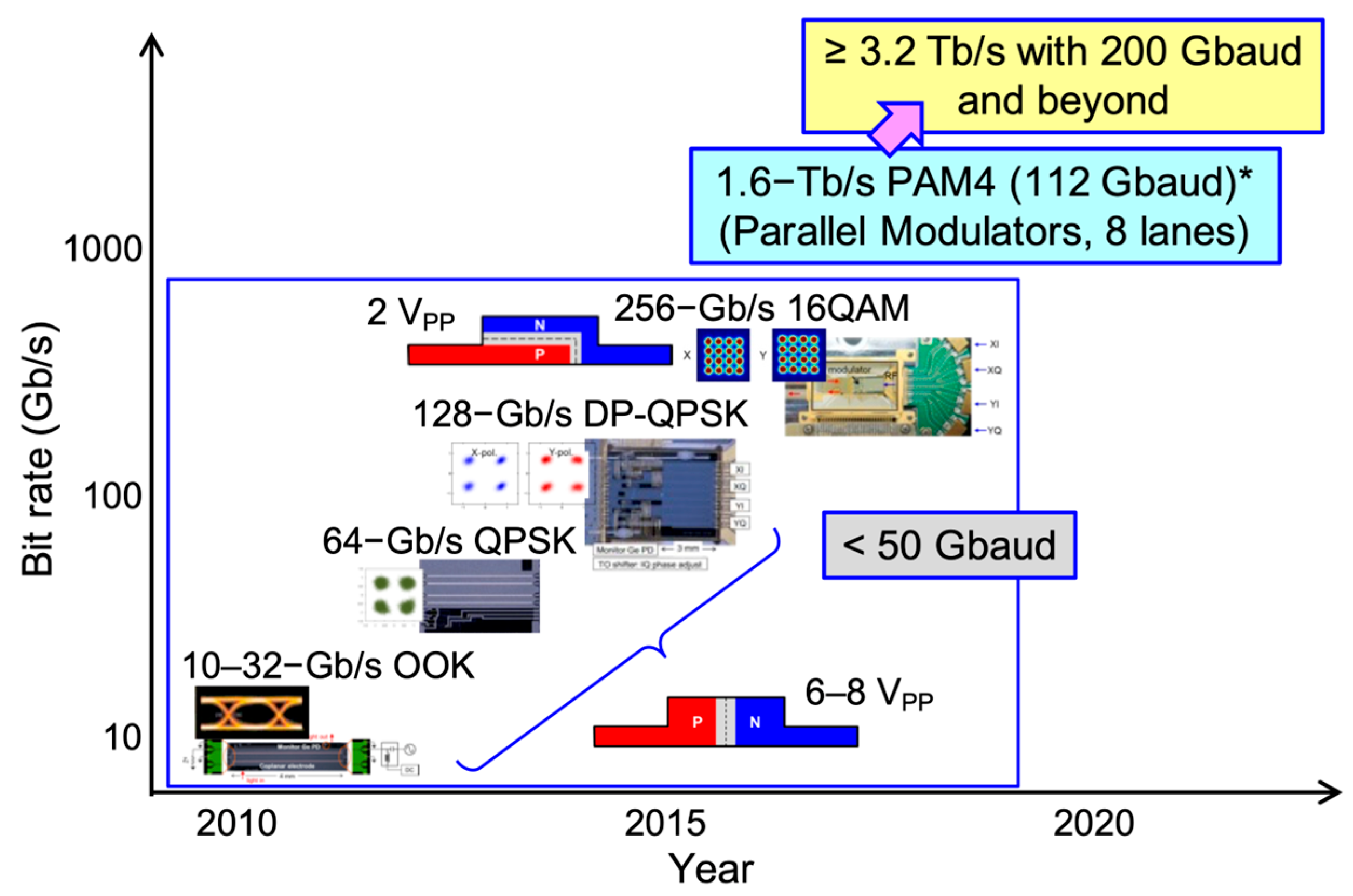
3. High-Speed Performance
3.1. Modulation Characteristics and Prospect
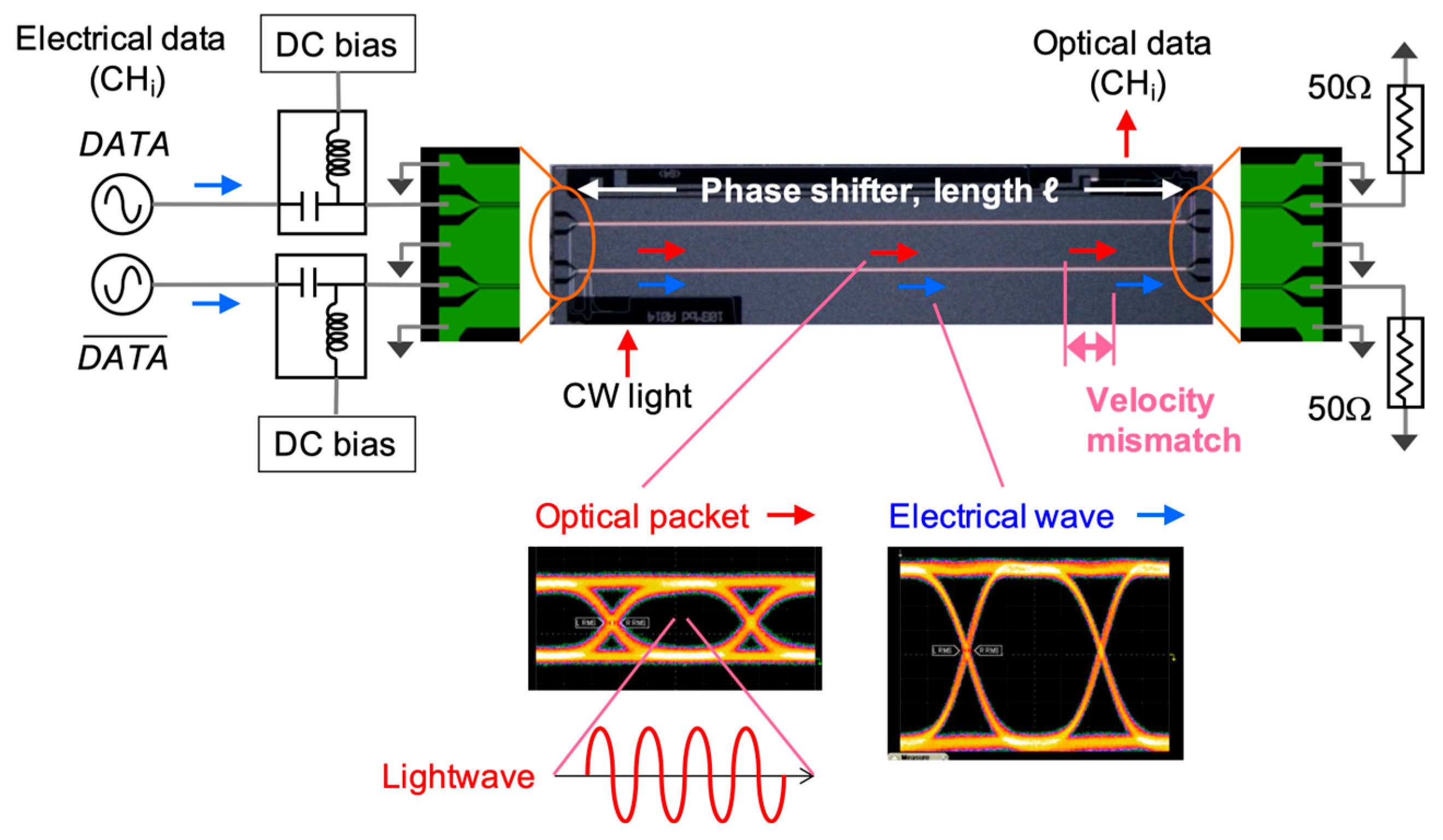
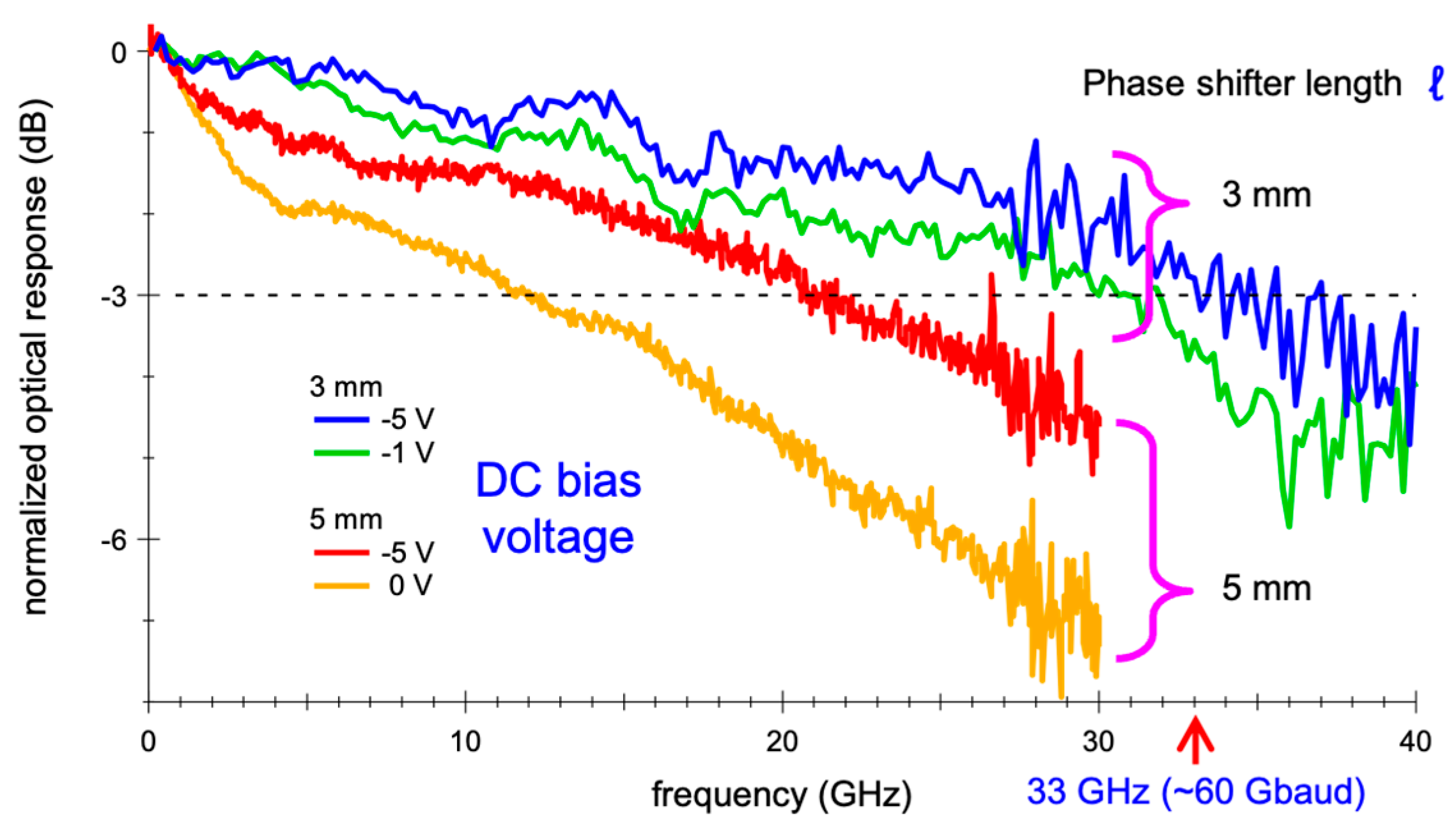
3.2. Limiting Factors
3.2.1. Transit Time
3.2.2. Velocity Mismatch
3.2.3. Attenuation of RF Electrical Wave
3.2.4. RC Coupling
3.3. Bandwidth–Loss Trade-Offs
4. Expansion of Modulation Bandwidth
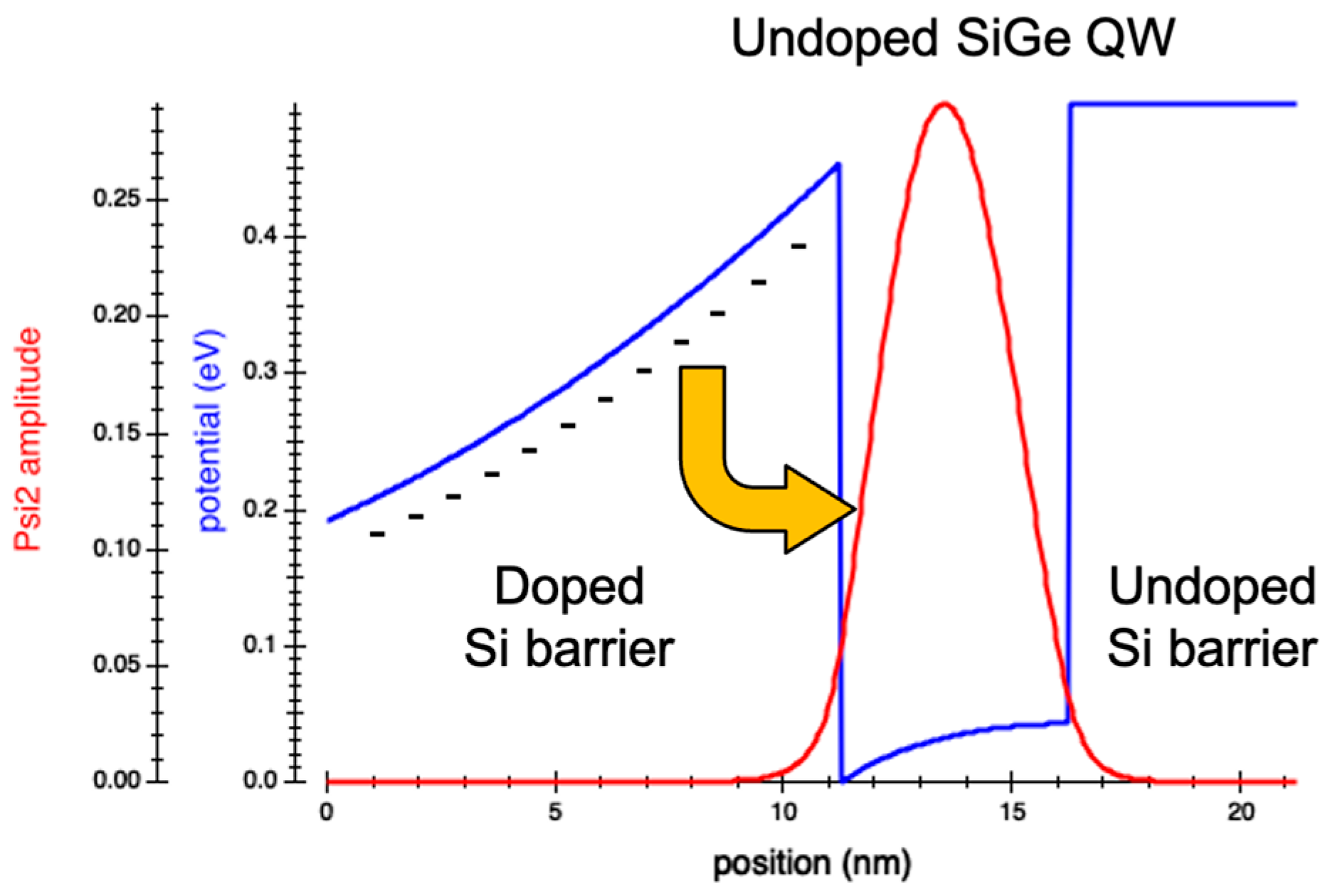
4.1. Design, Simulation Framework, and Material Parameters
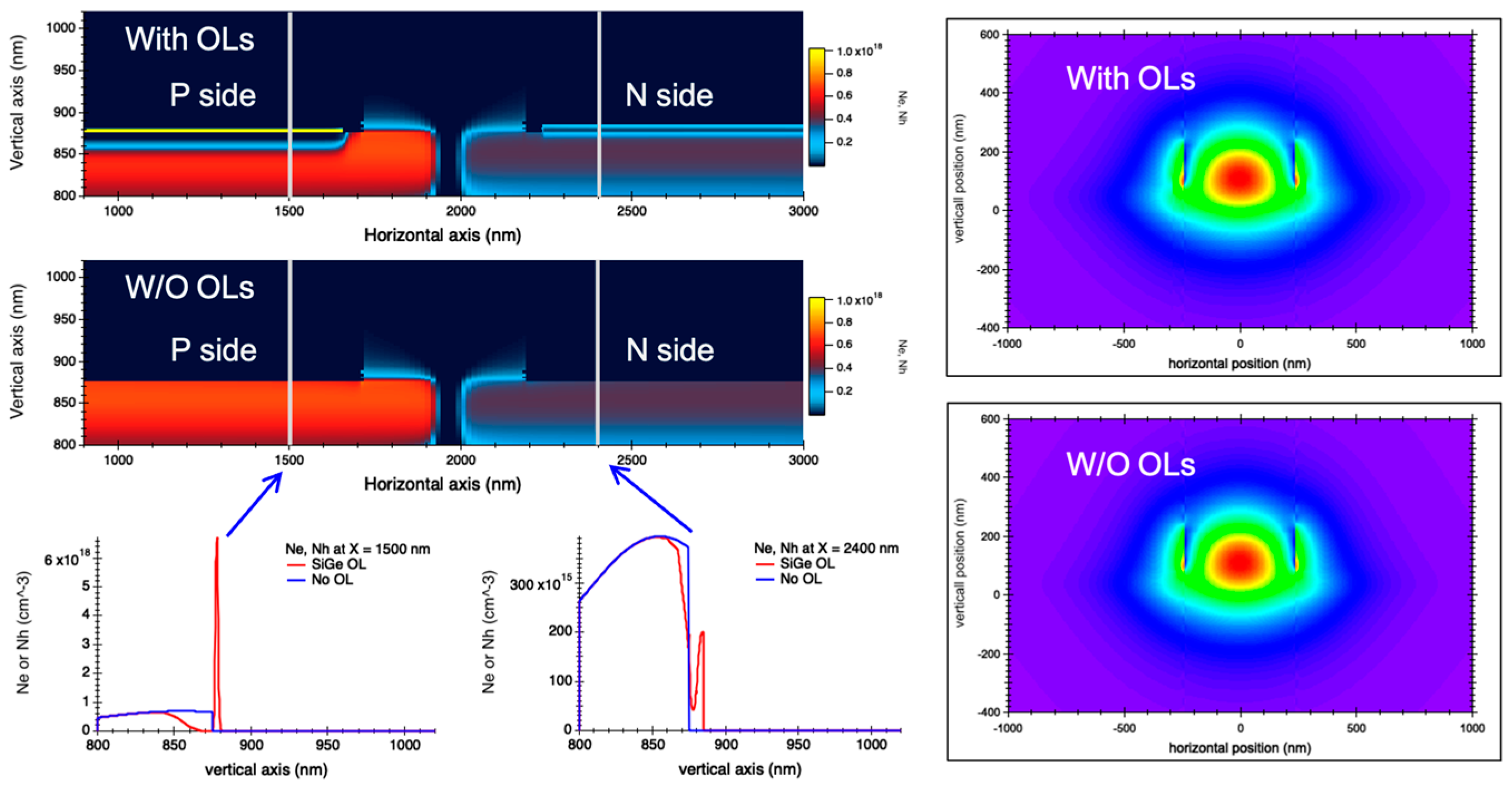
4.2. Simulation Results and Discussion
4.2.1. Carrier Distribution and Optical Loss
4.2.2. Series Electrical Resistance
4.2.3. Modulation Bandwidth
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gardes, F.Y.; Reed, G.T.; Emerson, N.G.; Png, C.E. A sub-micron depletion-type photonic modulator in Silicon on Insulator. Opt. Express 2005, 13, 8845–8854. [Google Scholar] [CrossRef]
- Pinguet, T.; Sadagopan, V.; Mekis, A.; Analui, B.; Kucharski, D.; Gloeckner, S. A 1550 nm, 10 Gbps optical modulator with integrated driver in 130 nm CMOS. In Proceedings of the 2007 4th IEEE International Conference on Group IV Photonics, Tokyo, Japan, 19–21 September 2007; pp. 1–3. [Google Scholar]
- Liao, L.; Liu, A.; Rubin, D.; Basak, J.; Chetrit, Y.; Nguyen, H.; Cohen, R.; Izhaky, N.; Paniccia, M. 40 Gbit/s silicon optical modulator for highspeed applications. Electron. Lett. 2007, 43, 1196–1197. [Google Scholar] [CrossRef]
- Marris-Morini, D.; Rasigade, G.; Vivien, L.; Cassan, E.; Laval, S.; Rivallin, P.; Lyan, P.; Fedeli, J.M. Recent progress in fast silicon modulators. In Proceedings of the 2008 5th IEEE International Conference on Group IV Photonics, Sorrento, Italy, 17–19 September 2008; pp. 1–3. [Google Scholar]
- Absil, P.; Croes, K.; Lesniewska, A.; De Heyn, P.; Ban, Y.; Snyder, B.; De Coster, J.; Fodor, F.; Simons, V.; Balakrishnan, S.; et al. Reliable 50 Gb/s Silicon Photonics platform for next-generation data center optical interconnects. In Proceedings of the 2017 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 2–6 December 2017; pp. 34.2.1–34.2.4. [Google Scholar]
- Giewont, K.; Hu, S.; Peng, B.; Rakowski, M.; Rauch, S.; Rosenberg, J.C.; Sahin, A.; Stobert, I.; Stricker, A.; Nummy, K.; et al. 300-mm Monolithic Silicon Photonics Foundry Technology. IEEE J. Sel. Top. Quant. Electron. 2019, 25, 1–11. [Google Scholar] [CrossRef]
- Fahrenkopf, N.M.; McDonough, C.; Leake, G.L.; Su, Z.; Timurdogan, E.; Coolbaugh, D.D. The AIM Photonics MPW: A Highly Accessible Cutting Edge Technology for Rapid Prototyping of Photonic Integrated Circuits. IEEE J. Sel. Top. Quant. Electron. 2019, 25, 1–6. [Google Scholar] [CrossRef]
- Siew, S.Y.; Li, B.; Gao, F.; Zheng, H.Y.; Zhang, W.; Guo, P.; Xie, S.W.; Song, A.; Dong, B.; Luo, L.W.; et al. Review of Silicon Photonics Technology and Platform Development. J. Light. Technol. 2021, 39, 4374–4389. [Google Scholar] [CrossRef]
- Ogawa, K. Integrated Silicon-Based Optical Modulators: 100/Gb/s and Beyond; SPIE Press: Bellingham, WA, USA, 2019. [Google Scholar]
- Ogawa, K.; Goi, K.; Tan, Y.T.; Liow, T.-Y.; Tu, X.; Fang, Q.; Lo, G.-Q.; Kwong, D.-L. Silicon Mach-Zehnder modulator of extinction ratio beyond 10 dB at 10.0–12.5 Gbps. Opt. Express 2011, 19, B26–B31. [Google Scholar] [CrossRef]
- Petousi, D.; Zimmermann, L.; Gajda, A.; Kroh, M.; Voigt, K.; Winzer, G.; Tillack, B.; Petermann, K. Analysis of Optical and Electrical Tradeoffs of Traveling-Wave Depletion-Type Si Mach–Zehnder Modulators for High-Speed Operation. IEEE J. Sel. Top. Quant. Electron. 2015, 21, 199–206. [Google Scholar] [CrossRef]
- Anderson, R.L. Germanium-Gallium Arsenide Heterojunctions. IBM J. Res. Dev. 1960, 4, 283–287. [Google Scholar] [CrossRef]
- Mimura, T.; Hiyamizu, S.; Fujii, T.; Nanbu, K. A New Field-Effect Transistor with Selectively Doped GaAs/n-AlxGa1-xAs Heterojunctions. Jpn. J. Appl. Phys. 1980, 19, L225–L227. [Google Scholar] [CrossRef]
- Hiyamizu, S.; Junji Saito, J.; Nanbu, K.; Ishikaw, T. Improved Electron Mobility Higher than 106 cm2/Vs in Selectively Doped GaAs/N-AlGaAs Heterostructures Grown by MBE. Jpn. J. Appl. Phys. 1983, 22, L609–L611. [Google Scholar] [CrossRef]
- Ando, T. Self-Consistent Results for a GaAs/AlxGa1-xAs Heterojunction. I. Subband Structure and Light-Scattering Spectra. J. Phys. Soc. Jpn. 1982, 51, 3898–3899. [Google Scholar] [CrossRef]
- Ando, T.; Fowler, A.B.; Stern, F. Electronic properties of two-dimensional systems. Rev. Mod. Phys. 1982, 54, 437–672. [Google Scholar]
- Ishikura, N.; Goi, K.; Zhu, H.; Illarionov, M.; Ishihara, H.; Oka, A.; Oda, T.; Masuko, K.; Ori, T.; Ogawa, K.; et al. Transmission characteristics of 32-Gbaud PDM IQ monolithic silicon modulator operating with 2-VPPD drive voltage. In Proceedings of the 42nd European Conference on Optical Communication (ECOC), Dusseldorf, Germany, 18–22 September 2016. [Google Scholar]
- Koyama, F.; Iga, K. Frequency chirping in external modulators. J. Light. Technol. 1988, 6, 87–93. [Google Scholar] [CrossRef]
- Han, J.; Seo, B.-J.; Han, Y.; Jalali, B.; Fetterman, H. Reduction of fiber chromatic dispersion effects in fiber-wireless and photonic time-stretching system using polymer modulators. J. Light. Technol. 2003, 21, 1504–1509. [Google Scholar]
- Goi, K.; Oda, K.; Kusaka, H.; Terada, Y.; Ogawa, K.; Liow, T.-Y.; Tu, X.; Lo, G.-Q.; Kwong, D.-L. 11-Gb/s 80-km transmission performance of zero-chirp silicon Mach-Zehnder modulator. Opt. Express 2012, 20, B350–B356. [Google Scholar] [CrossRef]
- Nedeljkovic, M.; Soref, R.; Mashanovich, G.Z. Free-carrier electrorefraction and electroabsorption modulation predictions for silicon over the 1–14-μm infrared wavelength range. IEEE Photonics J. 2011, 3, 1171–1180. [Google Scholar] [CrossRef]
- Goi, K.; Oka, A.; Kusaka, H.; Terada, Y.; Ogawa, K.; Liow, T.-Y.; Tu, X.; Lo, G.-Q.; Kwong, D.-L. Low-loss high-speed silicon IQ modulator for QPSK/DQPSK in C and L bands. Opt. Express 2014, 22, 10703–10709. [Google Scholar] [CrossRef]
- Goi, K.; Oda, K.; Mashiko, Y.; Ogawa, K.; Liow, T.-Y.; Tu, X.; Lo, G.-Q.; Kwong, D.-L. 128 Gb/s DP-QPSK Silicon Modulator Module Integrated with Driver Amplifiers. In Proceedings of the 2014 European Conference on Optical Communication (ECOC), Cannes, France, 21–25 September 2014. [Google Scholar]
- Li, X.; Gourikutty, S.B.N.; Wu, J.; Lim, T.G.; Guo, P.; Davies, J.C.; Koh, E.S.C.; Long, L.B.; Jong, M.C.; Li, C.; et al. 1.6 Tbps (224 Gbps/λ) Silicon Photonic Engine Fabricated with Advanced Electronic-Photonic FOWLP for Co-Packaged Optics and Linear Drive Applications. In Proceedings of the Optical Fiber Communication Conference, San Diego, CA, USA, 24–28 March 2024. [Google Scholar]
- Ostrovskis, A.; Szczerba, K.; Salgals, T.; Norberg, E.; Koenigsmann, M.; Sonkoly, J.; Rubuls, K.; Yun, H.; Krüger, B.; Piels, M.; et al. Heterogenous InP Electro-Absorption Modulator with Si Waveguides for Beyond 200 Gbps/λ Optical Interconnects. In Proceedings of the Optical Fiber Communication Conference, San Diego, CA, USA, 24–28 March 2024. [Google Scholar]
- St-Arnault, C.; Bernal, S.; Berikaa, E.; Wei, Z.; Gutiérrez-Castrejón, R.; Zhang, J.; Alam, S.; Nikic, A.; Krueger, B.; Pittalà, F.; et al. Net 1.6 Tbps (4×400Gbps/λ) O-Band IM/DD Transmission Over 2 km Using Uncooled DFB Lasers on the LAN-WDM grid and Sub-1V Drive TFLN Modulators. In Proceedings of the 2024 Optical Fiber Communications Conference and Exhibition, San Diego, CA, USA, 24–28 March 2024. [Google Scholar]
- Schwarzenberger, A.; Sarwar, S.; Eschenbaum, C.; Mertens, A.; Martens, M.; Kotz, A.; Fang, D.; Sherifaj, A.; Singer, S.; Kholeif, H.; et al. O-Band SOH Mach-Zehnder Modulator Operating at a PAM4 Line Rate of 384 Gbit/s with Sub-Volt Drive Voltage. In Proceedings of the 2024 Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 24–28 March 2024. [Google Scholar]
- Png, C.E.; Sun, M.J.; Lim, S.T.; Ang, T.Y.L.; Ogawa, K. Numerical modeling and analysis for high-efficiency carrier-depletion silicon rib-waveguide phase shifters. IEEE J. Sel. Top. Quantum Electron. 2016, 22, 3300208. [Google Scholar] [CrossRef]
- Rigrod, W.W.; Kaminow, I.P. Wide-band microwave light modulation. Proc. IEEE 1963, 51, 137–140. [Google Scholar] [CrossRef]
- Liu, J. Photonic Devices; Cambridge University Press: Cambridge, UK, 2005; pp. 274–279. [Google Scholar]
- Yang, Y.; Fang, Q.; Yu, M.; Tu, X.; Rusli, R.; Lo, G.-Q. High-efficiency Si optical modulator using Cu travelling-wave electrode. Opt. Express 2014, 22, 29978–29985. [Google Scholar] [CrossRef]
- Xu, H.; Li, X.; Xiao, X.; Li, Z.; Yu, Y.; Yu, J. Bandwidth performances analysis for high-speed silicon depletion-mode modulator. In Proceedings of the OFC 2014, San Francisco, CA, USA, 9–13 March 2014. [Google Scholar]
- Allam, J.; Baynes, N.d.B.; Cleaver, J.R.A.; Ogawa, K.; Mishima, T.; Ohbu, I. Monolithically-integrated optoelectronic circuit for ultrafast sampling of a dual-gate field-effect transistor. Opt. Quant. Electron. 1996, 28, 875–896. [Google Scholar] [CrossRef]
- Xiao, X.; Li, M.; Li, Z.; Wang, L.; Yang, Q.; Yu, S. Substrate removed silicon Mach-Zehnder modulator for high baud rate optical intensity modulations. In Proceedings of the 2016 Optical Fiber Communications Conference and Exhibition (OFC), Anaheim, CA, USA, 20–24 March 2016. [Google Scholar]
- People, R. Physics and applications of GexSi1-x/Si strained-layer heterostructures. IEEE J. Quantum Electron. 1986, 22, 1696–1710. [Google Scholar] [CrossRef]
- Van de Walle, C.G.; Martin, R.M. Theoretical calculations of heterojunction discontinuities in the Si/Ge system. Phys. Rev. B 1986, 34, 5621–5634. [Google Scholar] [CrossRef]
- Almeida, V.R.; Xu, Q.; Barrios, C.A.; Lipson, M. Guiding and confining light in void nanostructure. Opt. Lett. 2004, 29, 1209–1211. [Google Scholar] [CrossRef]
- Noumerov, B.V. A Method of Extrapolation of Perturbations. Mon. Not. R. Astron. Soc. 1924, 84, 592–602. [Google Scholar] [CrossRef]
- Quiroz González, J.L.M.; Thompson, D. Getting started with Numerov’s method. Comput. Phys. 1997, 11, 514–515. [Google Scholar] [CrossRef]
- Pillai, M.; Goglio, J.; Walker, T.G. Matrix Numerov method for solving Schrödinger’s equation. Am. J. Phys. 2012, 80, 1017–1019. [Google Scholar] [CrossRef]
- Cooney, P.J.; Kanter, E.P.; Vager, Z. Convenient numerical technique for solving the one-dimensional Schrödinger equation for bound states. Am. J. Phys. 1981, 49, 76–77. [Google Scholar] [CrossRef]
- Kim, Y.; Takenaka, M.; Osada, T.; Hata, M.; Takagi, S. Strain-induced enhancement of plasma dispersion effect and free-carrier absorption in SiGe optical modulators. Sci. Rep. 2014, 4, 4683. [Google Scholar] [CrossRef]
- Feynman, R.P. Space-Time Approach to Non-Relativistic Quantum Mechanics. Rev. Mod. Phys. 1948, 20, 367–387. [Google Scholar] [CrossRef]
- Doll, J.D.; Myers, L.E. Semiclassical Monte Carlo methods. J. Chem. Phys. 1979, 71, 2880–2883. [Google Scholar] [CrossRef]
- Voth, G.A. Calculation of equilibrium averages with Feynman-Hibbs effective classical potentials and similar variational approximations. Phys. Rev. A 1991, 44, 5302–5305. [Google Scholar] [CrossRef]
- Yang, L.; Watling, J.R.; Wilkins, R.C.W.; Boriçi, M.; Barker, J.R.; Asenov, A.; Roy, S. Si/SiGe heterostructure parameters for device simulations. Semicond. Sci. Technol. 2004, 19, 1174–1182. [Google Scholar] [CrossRef]
- Manku, T.; McGregor, J.M.; Nathan, A.; Roulston, D.J.; Noel, J.P.; Houghton, D.C. Drift hole mobility in strained and unstrained doped Si1−xGex alloys. IEEE Trans. Elect. Dev. 1993, 40, 1990–1996. [Google Scholar] [CrossRef]
- 3-Dimensional TCAD System Advance/TCAD. Available online: https://www.advancesoft.jp/products/semiconductor/advance-tcad/ (accessed on 2 May 2024). (In Japanese).
- Liow, T.-Y.; Ang, K.W.; Fang, Q.; Song, J.F.; Xiong, Y.Z.; Yu, M.B.; Lo, G.Q.; Kwong, D.L. Silicon Modulators and Germanium Photodetectors on SOI: Monolithic Integration, Compatibility, and Performance Optimization. IEEE J. Sel. Top. Quant. Electron. 2010, 16, 307–315. [Google Scholar] [CrossRef]
- LTspice. Available online: https://www.analog.com/en/resources/design-tools-and-calculators/ltspice-simulator.html (accessed on 7 May 2024).







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ogawa, K. Increase in Modulation Speed of Silicon Photonics Modulator with Quantum-Well Slab Wings: New Insights from a Numerical Study. Photonics 2024, 11, 535. https://doi.org/10.3390/photonics11060535
Ogawa K. Increase in Modulation Speed of Silicon Photonics Modulator with Quantum-Well Slab Wings: New Insights from a Numerical Study. Photonics. 2024; 11(6):535. https://doi.org/10.3390/photonics11060535
Chicago/Turabian StyleOgawa, Kensuke. 2024. "Increase in Modulation Speed of Silicon Photonics Modulator with Quantum-Well Slab Wings: New Insights from a Numerical Study" Photonics 11, no. 6: 535. https://doi.org/10.3390/photonics11060535
APA StyleOgawa, K. (2024). Increase in Modulation Speed of Silicon Photonics Modulator with Quantum-Well Slab Wings: New Insights from a Numerical Study. Photonics, 11(6), 535. https://doi.org/10.3390/photonics11060535




