Mathieu–Hill Equation Stability Analysis for Trapped Ions: Anharmonic Corrections for Nonlinear Electrodynamic Traps
Abstract
:1. Introduction
Structure of the Paper
2. Mathieu–Hill Equations
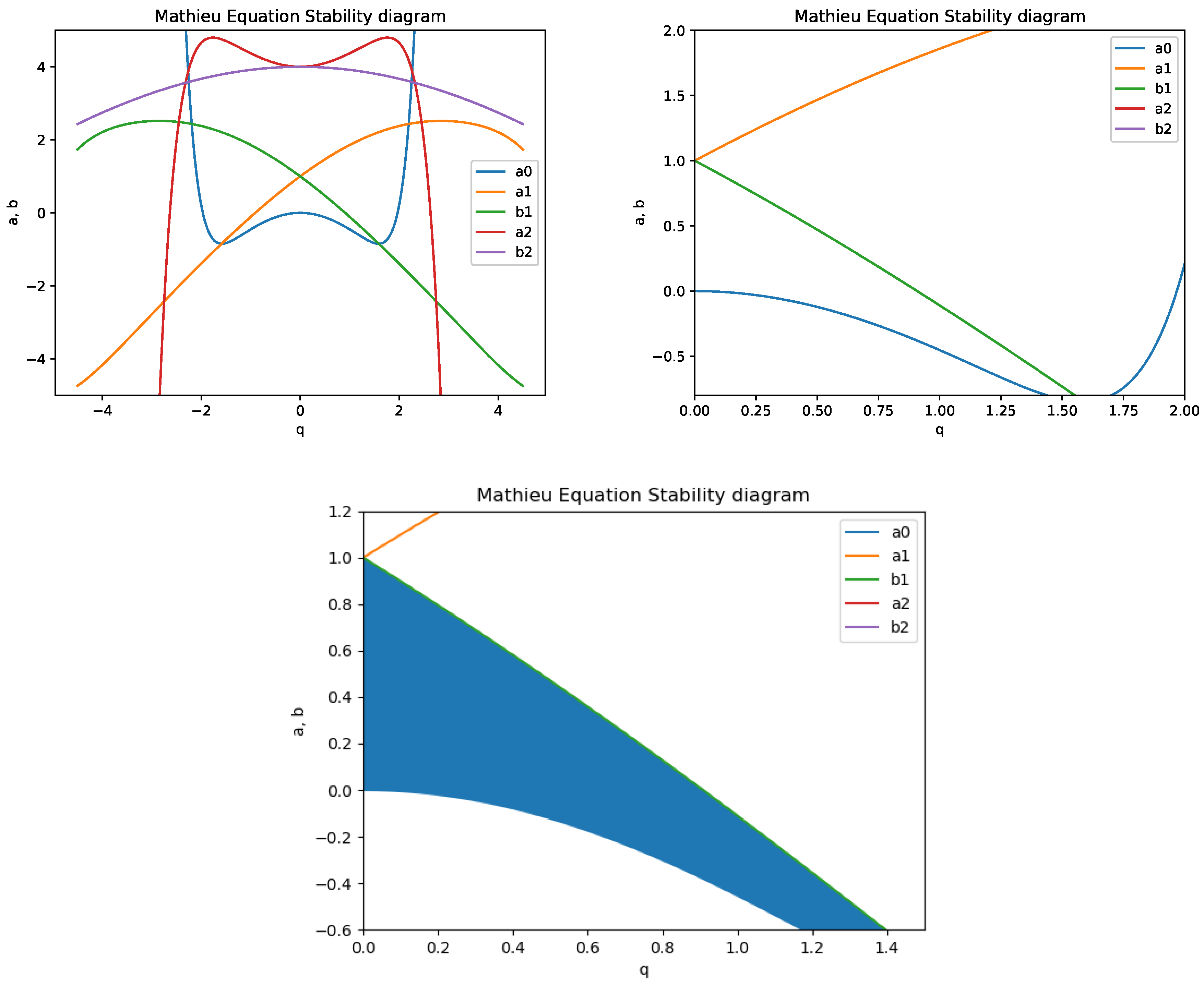
3. Stability of the Solutions of the Mathieu–Hill Equation for a Trapped Ion
The Kicked Damped Parametric Oscillator
4. Anharmonic Corrections for Electrodynamic (Paul) Traps: Perturbation Method Analysis
4.1. Solutions of the Mathieu Equation
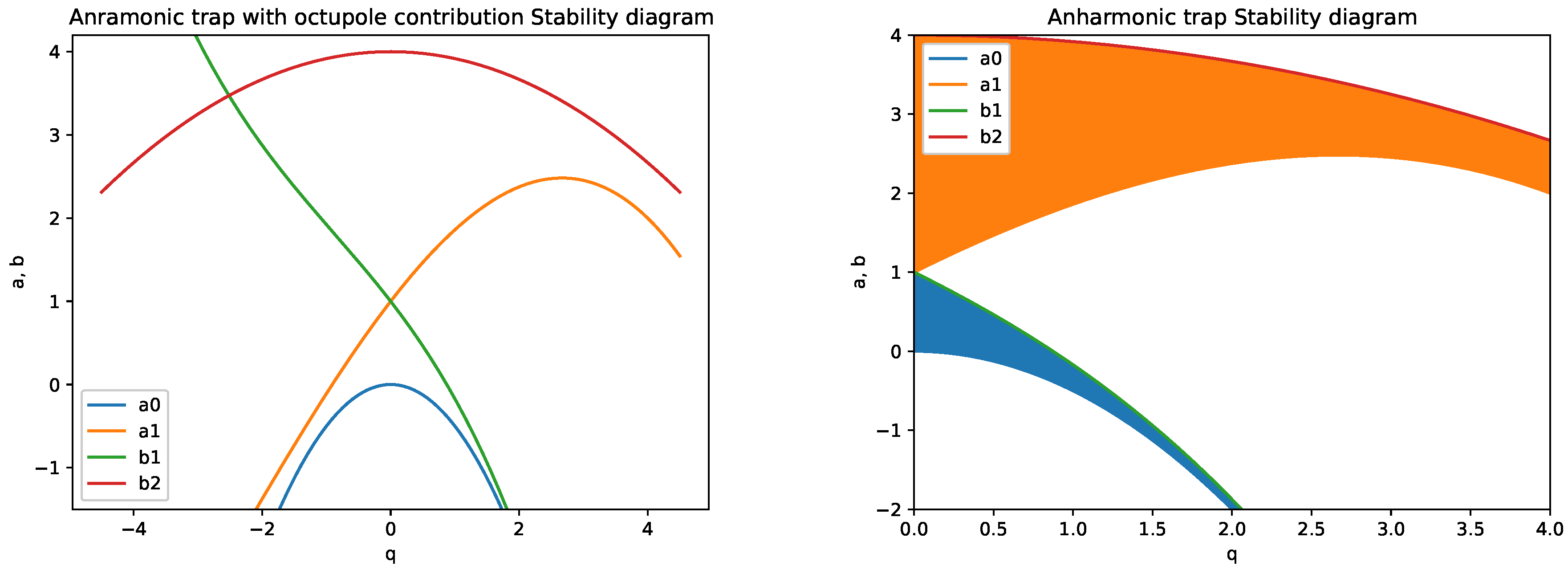
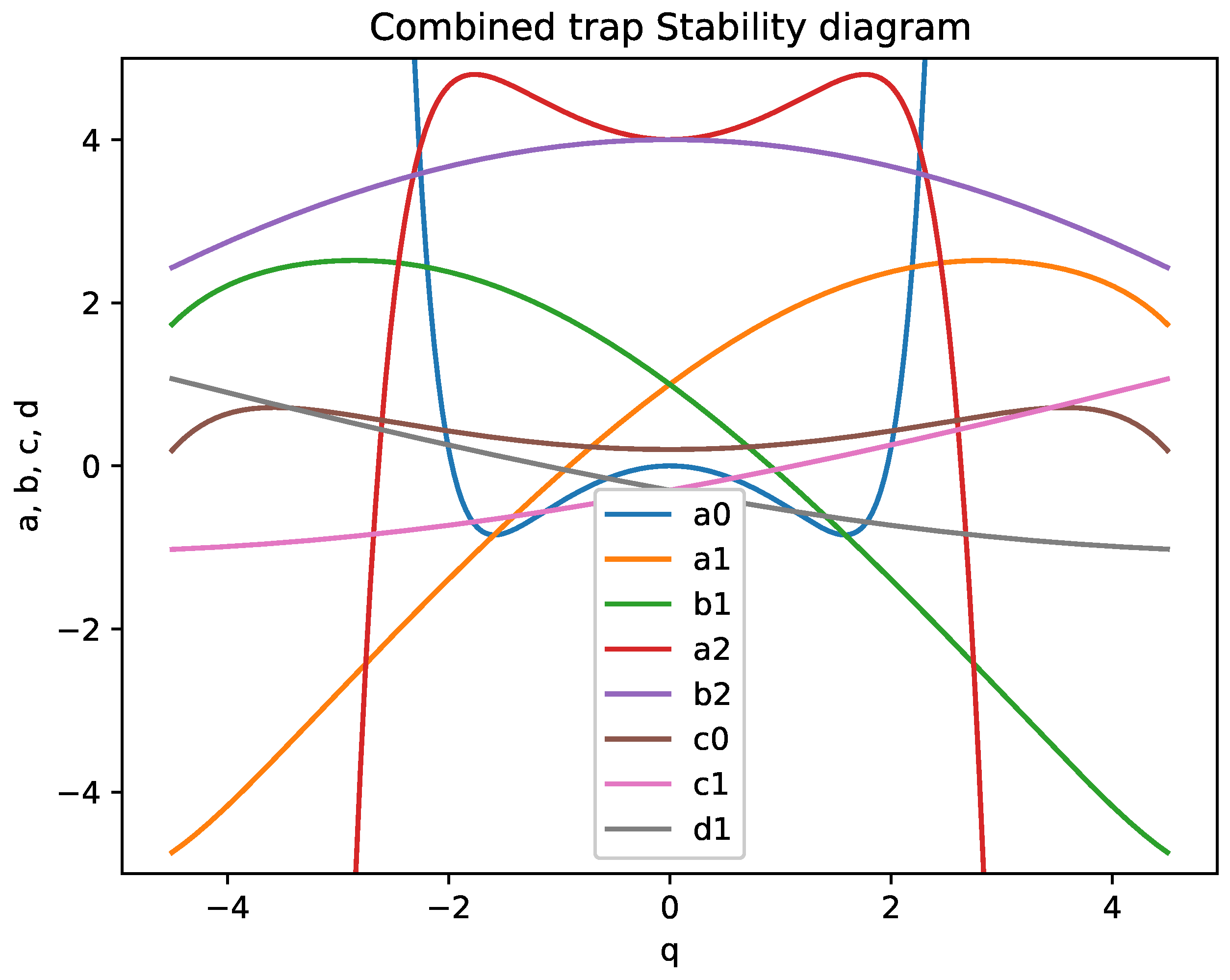
4.2. The Frontiers of the Stability Diagram for the Mathieu Equation with Nonlinear Term
5. Discussion
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| 2D | Two-Dimensional |
| 3D | Three-Dimensional |
| BSM | Beyond the Standard Model |
| COTS | Commercial Off-The-Shelf |
| DC | Direct Current |
| DE | Differential Equation |
| DO | Duffing Oscillator |
| DSAC | Deep Space Atomic Clock |
| GEO | Geostationary Orbit |
| HB | Harmonic Balance |
| HPM | Homotopy Perturbation Method |
| HO | Harmonic Oscillator |
| IT | Ion Trap |
| LDE | Linear Differential Equations |
| LIT | Linear Ion Trap |
| LPT | Linear Paul Trap |
| MOT | Magneto-Optical Trap |
| MS | Mass Spectrometry |
| NLDE | Nonlinear Differential Equations |
| NME | Nonlinear Mathieu Equation |
| ODE | Ordinary Differential Equation |
| QIP | Quantum Information Processing |
| QMS | Quadrupole Mass Spectrometer |
| PKL | Poincaré–Lighthill–Kuo |
| PO | Parametric Oscillator |
| QIT | Quadrupole Ion Trap |
| RF | Radiofrequency |
| RK | Runge–Kutta |
| SI | International System of Units |
| SNR | Signal-to-Noise Ratio |
| SQL | Standard Quantum Limit |
| STP | Standard Temperature and Pressure |
| UHV | Ultra-high Vacuum |
Appendix A. Hill’s Method to Find the Solution of the Mathieu Equation
Appendix A.1. Sträng’s Recursion Formula for △(0)
Appendix B. The Frontiers of the Stability Regions
Appendix C. Solving the Mathieu Equation: Perturbation Theory
Perturbation Theory
References
- Nayfeh, A.H.; Sanchez, N.E. Bifurcations in a forced softening duffing oscillator. Int. J. Nonlin. Mech. 1989, 24, 483–497. [Google Scholar] [CrossRef]
- Serov, V. Fourier Series, Fourier Transform and Their Applications to Mathematical Physics; Applied Mathematical Sciences; Springer: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Gadella, M.; Giacomini, H.; Lara, L. Periodic analytic approximate solutions for the Mathieu equation. Appl. Math. Comput. 2015, 271, 436–445. [Google Scholar] [CrossRef]
- Rand, R.H. CISM Course: Time-Periodic Systems. 5–9 September 2016. Available online: http://audiophile.tam.cornell.edu/randpdf/rand_mathieu_CISM.pdf (accessed on 22 May 2024).
- Krack, M.; Gross, J. Harmonic Balance for Nonlinear Vibration Problems; Schröder, J., Weigand, B., Eds.; Mathematical Engineering; Springer: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Mathieu, E. Mémoire sur le mouvement vibratoire d’une membrane de forme elliptique. J. Math. Pures Appl. 1868, 13, 137–203. [Google Scholar]
- Arfken, G.B.; Weber, H.J.; Harris, F.E. Mathematical Methods for Physicists, 7th ed.; Academic Press: Waltham, MA, USA, 2013; Chapter 32; pp. 1–29. Available online: https://booksite.elsevier.com/9780123846549/Chap_Mathieu.pdf (accessed on 11 May 2024).
- Daniel, D.J. Exact solutions of Mathieu’s equation. Prog. Theor. Exp. Phys. 2020, 2020, 043A01. [Google Scholar] [CrossRef]
- Brimacombe, C.; Corless, R.M.; Zamir, M. Computation and Applications of Mathieu Functions: A Historical Perspective. SIAM Rev. 2021, 63, 653–720. [Google Scholar] [CrossRef]
- Wilkinson, S.A.; Vogt, N.; Golubev, D.S.; Cole, J.H. Approximate solutions to Mathieu’s equation. Phys. E Low Dimens. Syst. Nanostruct. 2018, 100, 24–30. [Google Scholar] [CrossRef]
- Corless, R.M. An Hermite–Obreshkov method for 2nd-order linear initial-value problems for ODE. Numer. Algorithms 2024. [Google Scholar] [CrossRef]
- Butikov, E. Analytical expressions for stability regions in the Ince–Strutt diagram of Mathieu equation. Am. J. Phys. 2018, 86, 257–267. [Google Scholar] [CrossRef]
- Kovacic, I.; Rand, R.; Sah, S.M. Mathieu’s Equation and Its Generalizations: Overview of Stability Charts and Their Features. Appl. Mech. Rev. 2018, 70, 020802. [Google Scholar] [CrossRef]
- Nayfeh, A.H. Introduction to Perturbation Techniques; Wiley Classics Library, Wiley: Weinheim, Germany, 2011. [Google Scholar]
- Doroudi, A. Application of a Modified Homotopy Perturbation Method for Calculation of Secular Axial Frequencies in a Nonlinear Ion Trap with Hexapole, Octopole and Decapole Superpositions. J. Bioanal. Biomed. 2012, 4, 85–91. [Google Scholar] [CrossRef]
- Jazar, R.N. Perturbation Methods in Science and Engineering; Springer: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- El-Dib, Y.O. An innovative efficient approach to solving damped Mathieu–Duffing equation with the non-perturbative technique. Commun. Nonlinear Sci. Numer. Simul. 2024, 128, 107590. [Google Scholar] [CrossRef]
- Gadella, M.; Lara, L.P. A variational modification of the Harmonic Balance method to obtain approximate Floquet exponents. Math. Meth. Appl. Sci. 2023, 46, 8956–8974. [Google Scholar] [CrossRef]
- McLachlan, N.W. Theory and Application of Mathieu Functions; Dover Publications: New York, NY, USA, 1964; Volume 1233. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. (Eds.) Mathieu Functions; Appl. Math. Series; US Dept. of Commerce, National Bureau of Standards: Washington, DC, USA, 1972; Volume 55, Chapter 20; pp. 722–750.
- Major, F.G.; Gheorghe, V.N.; Werth, G. Charged Particle Traps: Physics and Techniques of Charged Particle Field Confinement; Springer Series on Atomic, Optical and Plasma Physics; Springer: Berlin/Heidelberg, Germany, 2005; Volume 37. [Google Scholar] [CrossRef]
- Morais, J.; Porter, R.M. Reduced-quaternionic Mathieu functions, time-dependent Moisil-Teodorescu operators, and the imaginary-time wave equation. Appl. Math. Comput. 2023, 438, 127588. [Google Scholar] [CrossRef]
- Orszag, M. Quantum Optics: Including Noise Reduction, Trapped Ions, Quantum Trajectories, and Decoherence, 3rd ed.; Springer: Cham, Switzerland, 2016. [Google Scholar] [CrossRef]
- Birkandan, T.; Hortaçsu, M. Examples of Heun and Mathieu functions as solutions of wave equations in curved spaces. J. Phys. A Math. Theor. 2007, 40, 1105–1116. [Google Scholar] [CrossRef]
- Quinn, T.; Perrine, R.P.; Richardson, D.C.; Barnes, R. A Symplectic Integrator for Hill’s Equations. Astron. J. 2010, 139, 803. [Google Scholar] [CrossRef]
- Knoop, M.; Madsen, N.; Thompson, R.C. (Eds.) Physics with Trapped Charged Particles: Lectures from the Les Houches Winter School; Imperial College Press & World Scientific: London, UK, 2014. [Google Scholar] [CrossRef]
- Knoop, M.; Madsen, N.; Thompson, R.C. (Eds.) Trapped Charged Particles: A Graduate Textbook with Problems and Solutions; Advanced Textbooks in Physics; World Scientific Europe: London, UK, 2016. [Google Scholar] [CrossRef]
- Vasil’ev, I.A.; Kushchenko, O.M.; Rudyi, S.S.; Rozhdestvenskii, Y.V. Effective Rotational Potential of a Molecular Ions in a Plane Radio-Frequency Trap. Tech. Phys. 2019, 64, 1379–1385. [Google Scholar] [CrossRef]
- Kajita, M. Ion Traps; IOP Publishing: Bristol, UK, 2022. [Google Scholar] [CrossRef]
- Vogel, M. Particle Confinement in Penning Traps: An Introduction, 2nd ed.; Babb, J., Bandrauk, A.D., Bartschat, K., Joachain, C.J., Keidar, M., Lambropoulos, P., Leuchs, G., Velikovich, A., Eds.; Springer Series on Atomic, Optical, and Plasma Physics; Springer: Cham, Switzerland, 2024; Volume 100. [Google Scholar] [CrossRef]
- Mihalcea, B.M.; Lynch, S. Investigations on Dynamical Stability in 3D Quadrupole Ion Traps. Appl. Sci. 2021, 11, 2938. [Google Scholar] [CrossRef]
- Mihalcea, B.M.; Filinov, V.S.; Syrovatka, R.A.; Vasilyak, L.M. The physics and applications of strongly coupled Coulomb systems (plasmas) levitated in electrodynamic traps. Phys. Rep. 2023, 1016, 1–103. [Google Scholar] [CrossRef]
- Paul, W. Electromagnetic traps for charged and neutral particles. Rev. Mod. Phys. 1990, 62, 531–540. [Google Scholar] [CrossRef]
- Baril, M.; Septier, A. Piégeage des ions dans un champ quadrupolaire tridimensionnel à haute fréquence. Rev. Phys. Appl. 1974, 9, 525–531. [Google Scholar] [CrossRef]
- Schulte, M.; Lörch, N.; Leroux, I.D.; Schmidt, P.O.; Hammerer, K. Quantum Algorithmic Readout in Multi-Ion Clocks. Phys. Rev. Lett. 2016, 116, 013002. [Google Scholar] [CrossRef] [PubMed]
- Keller, J.; Burgermeister, T.; Kalincev, D.; Didier, A.; Kulosa, A.P.; Nordmann, T.; Kiethe, J.; Mehlstäubler, T.E. Controlling systematic frequency uncertainties at the 10−19 level in linear Coulomb crystals. Phys. Rev. A 2019, 99, 013405. [Google Scholar] [CrossRef]
- Zhao, X.; Granot, O.; Douglas, D.J. Quadrupole Excitation of Ions in Linear Quadrupole Ion Traps with Added Octopole Fields. J. Am. Soc. Mass Spectrom. 2008, 19, 510–519. [Google Scholar] [CrossRef] [PubMed]
- Austin, D.E.; Hansen, B.J.; Peng, Y.; Zhang, Z. Multipole expansion in quadrupolar devices comprised of planar electrode arrays. Int. J. Mass Spectrom. 2010, 295, 153–158. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, X.; Feng, Y.; Shao, R.; Xiong, X.; Fang, X.; Deng, Y.; Xu, W. Characterization of geometry deviation effects on ion trap mass analysis: A comparison study. Int. J. Mass Spectrom. 2014, 370, 125–131. [Google Scholar] [CrossRef]
- Reece, M.P.; Huntley, A.P.; Moon, A.M.; Reilly, P.T.A. Digital Mass Analysis in a Linear Ion Trap without Auxiliary Waveforms. J. Am. Soc. Mass Spectrom. 2019, 31, 103–108. [Google Scholar] [CrossRef]
- Nolting, D.; Malek, R.; Makarov, A. Ion traps in modern mass spectrometry. Mass Spectrom. Rev. 2019, 38, 150–168. [Google Scholar] [CrossRef] [PubMed]
- Mandal, P.; Mukherjee, M. Non-degenerate dodecapole resonances in an asymmetric linear ion trap of round rod geometry. Int. J. Mass Spectrom. 2024, 498, 117217. [Google Scholar] [CrossRef]
- Kaur Kohli, R.; Van Berkel, G.J.; Davies, J.F. An Open Port Sampling Interface for the Chemical Characterization of Levitated Microparticles. Anal. Chem. 2022, 94, 3441–3445. [Google Scholar] [CrossRef]
- Harris, W.A.; Reilly, P.T.A.; Whitten, W.B. Detection of Chemical Warfare-Related Species on Complex Aerosol Particles Deposited on Surfaces Using an Ion Trap-Based Aerosol Mass Spectrometer. Anal. Chem. 2007, 79, 2354–2358. [Google Scholar] [CrossRef]
- Pan, Y.L.; Wang, C.; Hill, S.C.; Coleman, M.; Beresnev, L.A.; Santarpia, J.L. Trapping of individual airborne absorbing particles using a counterflow nozzle and photophoretic trap for continuous sampling and analysis. Appl. Phys. Lett. 2014, 104, 113507. [Google Scholar] [CrossRef]
- Fachinger, J.R.W.; Gallavardin, S.J.; Helleis, F.; Fachinger, F.; Drewnick, F.; Borrmann, S. The ion trap aerosol mass spectrometer: Field intercomparison with the ToF-AMS and the capability of differentiating organic compound classes via MS-MS. Atmos. Meas. Tech. 2017, 10, 1623–1637. [Google Scholar] [CrossRef]
- Rajagopal, V.; Stokes, C.; Ferzoco, A. A Linear Ion Trap with an Expanded Inscribed Diameter to Improve Optical Access for Fluorescence Spectroscopy. J. Am. Soc. Mass Spectrom. 2018, 29, 260–269. [Google Scholar] [CrossRef] [PubMed]
- Johnston, M.V.; Kerecman, D.E. Molecular Characterization of Atmospheric Organic Aerosol by Mass Spectrometry. Annu. Rev. Anal. Chem. 2019, 12, 247–274. [Google Scholar] [CrossRef] [PubMed]
- Snyder, D.T.; Szalwinski, L.J.; St. John, Z.; Cooks, R.G. Two-Dimensional Tandem Mass Spectrometry in a Single Scan on a Linear Quadrupole Ion Trap. Anal. Chem. 2019, 91, 13752–13762. [Google Scholar] [CrossRef] [PubMed]
- Newsome, G.A.; Rosen, E.P.; Kamens, R.M.; Glish, G.L. Real-time Detection and Tandem Mass Spectrometry of Secondary Organic Aerosols with a Quadrupole Ion Trap. ChemRxiv 2020. [Google Scholar] [CrossRef]
- Cho, H.; Kim, J.; Kwak, N.; Kwak, H.; Son, T.; Lee, D.; Park, K. Application of Single-Particle Mass Spectrometer to Obtain Chemical Signatures of Various Combustion Aerosols. Int. J. Environ. Res. Pub. Health 2021, 18, 11580. [Google Scholar] [CrossRef]
- Gonzalez, L.E.; Szalwinski, L.J.; Marsh, B.M.; Wells, J.M.; Cooks, R.G. Immediate and sensitive detection of sporulated Bacillus subtilis by microwave release and tandem mass spectrometry of dipicolinic acid. Analyst 2021, 146, 7104–7108. [Google Scholar] [CrossRef]
- Wineland, D.J.; Monroe, C.; Meekhof, D.M.; King, B.E.; Leibfried, D.; Itano, W.M.; Bergquist, J.C.; Berkeland, D.; Bollinger, J.J.; Miller, J. Quantum state manipulation of trapped atomic ions. Proc. R. Soc. Lond. A 1998, 454, 411–429. [Google Scholar] [CrossRef]
- Blaum, K.; Novikov, Y.N.; Werth, G. Penning traps as a versatile tool for precise experiments in fundamental physics. Contemp. Phys. 2010, 51, 149–175. [Google Scholar] [CrossRef]
- Wineland, D.J. Nobel Lecture: Superposition, entanglement, and raising Schrödinger’s cat. Rev. Mod. Phys. 2013, 85, 1103–1114. [Google Scholar] [CrossRef]
- Mihalcea, B.M. Squeezed coherent states of motion for ions confined in quadrupole and octupole ion traps. Ann. Phys. 2018, 388, 100–113. [Google Scholar] [CrossRef]
- Wan, Y.; Jördens, R.; Erickson, S.D.; Wu, J.J.; Bowler, R.; Tan, T.R.; Hou, P.Y.; Wineland, D.J.; Wilson, A.C.; Leibfried, D. Ion Transport and Reordering in a 2D Trap Array. Adv. Quantum Technol. 2020, 3, 2000028. [Google Scholar] [CrossRef]
- Mihalcea, B.M. Quasienergy operators and generalized squeezed states for systems of trapped ions. Ann. Phys. 2022, 442, 169826. [Google Scholar] [CrossRef]
- Häffner, H.; Roos, C.F.; Blatt, R. Quantum computing with trapped ions. Phys. Rep. 2008, 469, 155–203. [Google Scholar] [CrossRef]
- Pagano, G.; Hess, P.W.; Kaplan, H.B.; Tan, W.L.; Richerme, P.; Becker, P.; Kyprianidis, A.; Zhang, J.; Birckelbaw, E.; Hernandez, M.R.; et al. Cryogenic trapped-ion system for large scale quantum simulation. Quantum Sci. Technol. 2018, 4, 014004. [Google Scholar] [CrossRef]
- Bruzewicz, C.D.; Chiaverini, J.; McConnell, R.; Sage, J.M. Trapped-ion quantum computing: Progress and challenges. Appl. Phys. Rev. 2019, 6, 021314. [Google Scholar] [CrossRef]
- Mokhberi, A.; Hennrich, M.; Schmidt-Kaler, F. Chapter Four-Trapped Rydberg ions: A new platform for quantum information processing. In Advances in Atomic, Molecular, and Optical Physics; Dimauro, L.F., Perrin, H., Yelin, S.F., Eds.; Academic Press: Cambridge, MA, USA; Volume 69, pp. 233–306. [CrossRef]
- LaPierre, R. Introduction to Quantum Computing; The Materials Research Society Series; Springer: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- Reiter, F.; Sørensen, A.S.; Zoller, P.; Muschik, C.A. Dissipative quantum error correction and application to quantum sensing with trapped ions. Nat. Commun. 2017, 8, 1822. [Google Scholar] [CrossRef] [PubMed]
- Fountas, P.N.; Poggio, M.; Willitsch, S. Classical and quantum dynamics of a trapped ion coupled to a charged nanowire. New J. Phys. 2019, 21, 013030. [Google Scholar] [CrossRef]
- Wolf, F.; Schmidt, P.O. Quantum sensing of oscillating electric fields with trapped ions. Meas. Sens. 2021, 18, 100271. [Google Scholar] [CrossRef]
- Affolter, M.; Ge, W.; Bullock, B.; Burd, S.C.; Gilmore, K.A.; Lilieholm, J.F.; Carter, A.L.; Bollinger, J.J. Toward improved quantum simulations and sensing with trapped two-dimensional ion crystals via parametric amplification. Phys. Rev. A 2023, 107, 032425. [Google Scholar] [CrossRef]
- Sinclair, A. An Introduction to Trapped Ions, Scalability and Quantum Metrology. In Quantum Information and Coherence; Andersson, E., Öhberg, P., Eds.; Scottish Graduate Series; Springer: Berlin/Heidelberg, Germany, 2011; Volume 67, pp. 211–246. [Google Scholar] [CrossRef]
- Colombo, S.; Pedrozo-Peñafiel, E.; Adiyatullin, A.F.; Li, Z.; Mendez, E.; Shu, C.; Vuletić, V. Time-reversal-based quantum metrology with many-body entangled states. Nat. Phys. 2022, 18, 925–930. [Google Scholar] [CrossRef]
- Lee, D.; Watkins, J.; Frame, D.; Given, G.; He, R.; Li, N.; Lu, B.N.; Sarkar, A. Time fractals and discrete scale invariance with trapped ions. Phys. Rev. A 2019, 100, 011403. [Google Scholar] [CrossRef]
- Li, T.; Gong, Z.X.; Yin, Z.Q.; Quan, H.T.; Yin, X.; Zhang, P.; Duan, L.M.; Zhang, X. Space-Time Crystals of Trapped Ions. Phys. Rev. Lett. 2012, 109, 163001. [Google Scholar] [CrossRef] [PubMed]
- Vanier, J.; Tomescu, C. The Quantum Physics of Atomic Frequency Standards: Recent Developments; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar] [CrossRef]
- Ludlow, A.D.; Boyd, M.M.; Ye, J.; Peik, E.; Schmidt, P.O. Optical atomic clocks. Rev. Mod. Phys. 2015, 87, 637–701. [Google Scholar] [CrossRef]
- Nordmann, T.; Didier, A.; Doležal, M.; Balling, P.; Burgermeister, T.; Mehlstäubler, T.E. Sub-kelvin temperature management in ion traps for optical clocks. Rev. Sci. Instrum. 2020, 91, 111301. [Google Scholar] [CrossRef] [PubMed]
- Hausser, H.N.; Keller, J.; Nordmann, T.; Bhatt, N.M.; Kiethe, J.; Liu, H.; von Boehn, M.; Rahm, J.; Weyers, S.; Benkler, E.; et al. An 115In+–172Yb+ Coulomb crystal clock with 2.5 ×10 −18 systematic uncertainty. arXiv 2024, arXiv:2402.16807. [Google Scholar] [CrossRef]
- Barontini, G.; Blackburn, L.; Boyer, V.; Butuc-Mayer, F.; Calmet, X.; López-Urrutia, J.R.C.; Curtis, E.A.; Darquié, B.; Dunningham, J.; Fitch, N.J.; et al. Measuring the stability of fundamental constants with a network of clocks. EPJ Quant. Technol. 2022, 9, 12. [Google Scholar] [CrossRef]
- Tsai, Y.D.; Eby, J.; Safronova, M.S. Direct detection of ultralight dark matter bound to the Sun with space quantum sensors. Nat. Astron. 2023, 7, 113–121. [Google Scholar] [CrossRef]
- Safronova, M.S.; Budker, D.; DeMille, D.; Kimball, D.F.J.; Derevianko, A.; Clark, C.W. Search for new physics with atoms and molecules. Rev. Mod. Phys. 2018, 90, 025008. [Google Scholar] [CrossRef]
- Schkolnik, V.; Budker, D.; Fartmann, O.; Flambaum, V.; Hollberg, L.; Kalaydzhyan, T.; Kolkowitz, S.; Krutzik, M.; Ludlow, A.; Newbury, N.; et al. Optical atomic clock aboard an Earth-orbiting space station (OACESS): Enhancing searches for physics beyond the standard model in space. Quantum Sci. Technol. 2022, 8, 014003. [Google Scholar] [CrossRef]
- Derevianko, A.; Gibble, K.; Hollberg, L.; Newbury, N.R.; Oates, C.; Safronova, M.S.; Sinclair, L.C.; Yu, N. Fundamental physics with a state-of-the-art optical clock in space. Quantum Sci. Technol. 2022, 7, 044002. [Google Scholar] [CrossRef]
- McGrew, W.F.; Zhang, X.; Leopardi, H.; Fasano, R.J.; Nicolodi, D.; Beloy, K.; Yao, J.; Sherman, J.A.; Schäffer, S.A.; Savory, J.; et al. Towards the optical second: Verifying optical clocks at the SI limit. Optica 2019, 6, 448–454. [Google Scholar] [CrossRef]
- Shen, Q.; Guan, J.Y.; Ren, J.G.; Zeng, T.; Hou, L.; Li, M.; Cao, Y.; Han, J.J.; Lian, M.Z.; Chen, Y.W.; et al. Free-space dissemination of time and frequency with 10−19 instability over 113 km. Nature 2022, 610, 661–666. [Google Scholar] [CrossRef] [PubMed]
- Kim, M.E.; McGrew, W.F.; Nardelli, N.V.; Clements, E.R.; Hassan, Y.S.; Zhang, X.; Valencia, J.L.; Leopardi, H.; Hume, D.B.; Fortier, T.M.; et al. Improved interspecies optical clock comparisons through differential spectroscopy. Nat. Phys. 2023, 19, 25–29. [Google Scholar] [CrossRef]
- Peik, E. Optical Atomic Clocks. In Photonic Quantum Technologies; Benyoucef, M., Ed.; Wiley: Weinheim, Germany, 2023; Chapter 14; pp. 333–348. [Google Scholar] [CrossRef]
- Dimarcq, N.; Gertsvolf, M.; Mileti, G.; Bize, S.; Oates, C.W.; Peik, E.; Calonico, D.; Ido, T.; Tavella, P.; Meynadier, F.; et al. Roadmap towards the redefinition of the second. Metrologia 2024, 61, 012001. [Google Scholar] [CrossRef]
- Tomescu, C.; Giurgiu, L. Atomic Clocks and Time Keeping in Romania. Rom. Rep. Phys. 2018, 70, 205. Available online: https://rrp.nipne.ro/2018/AN70205.pdf (accessed on 11 May 2024).
- Itano, W.M.; Bergquist, J.C.; Bollinger, J.J.; Gilligan, J.M.; Heinzen, D.J.; Moore, F.L.; Raizen, M.G.; Wineland, D.J. Quantum projection noise: Population fluctuations in two-level systems. Phys. Rev. A 1993, 47, 3554–3570. [Google Scholar] [CrossRef]
- Wineland, D.J.; Bollinger, J.J.; Itano, W.M.; Heinzen, D.J. Squeezed atomic states and projection noise in spectroscopy. Phys. Rev. A 1994, 50, 67–88. [Google Scholar] [CrossRef]
- Wolf, F.; Shi, C.; Heip, J.C.; Gessner, M.; Pezzè, L.; Smerzi, A.; Schulte, M.; Hammerer, K.; Schmidt, P.O. Motional Fock states for quantum-enhanced amplitude and phase measurements with trapped ions. Nat. Commun. 2019, 10, 2929. [Google Scholar] [CrossRef]
- Spampinato, A.; Stacey, J.; Mulholland, S.; Robertson, B.I.; Klein, H.A.; Huang, G.; Barwood, G.P.; Gill, P. An ion trap design for a space-deployable strontium-ion optical clock. Proc. R. Soc. A 2024, 480, 20230593. [Google Scholar] [CrossRef]
- Zhiqiang, Z.; Arnold, K.J.; Kaewuam, R.; Barrett, M.D. 176Lu+ clock comparison at the 10−18 level via correlation spectroscopy. Sci. Adv. 2023, 9, eadg1971. [Google Scholar] [CrossRef] [PubMed]
- Caldwell, E.D.; Sinclair, L.C.; Deschenes, J.D.; Giorgetta, F.; Newbury, N.R. Application of quantum-limited optical time transfer to space-based optical clock comparisons and coherent networks. APL Photonics 2024, 9, 016112. [Google Scholar] [CrossRef]
- Joshi, M.K.; Satyajit, K.T.; Rao, P.M. Influence of a geometrical perturbation on the ion dynamics in a 3D Paul trap. Nucl. Instrum. Methods Phys. Res. A 2015, 800, 111–118. [Google Scholar] [CrossRef]
- Tian, Y.; Decker, T.K.; McClellan, J.S.; Wu, Q.; De la Cruz, A.; Hawkins, A.R.; Austin, D.E. Experimental Observation of the Effects of Translational and Rotational Electrode Misalignment on a Planar Linear Ion Trap Mass Spectrometer. J. Am. Soc. Mass. Spectrom. 2018, 29, 1376–1385. [Google Scholar] [CrossRef] [PubMed]
- Alheit, R.; Kleineidam, S.; Vedel, F.; Vedel, M.; Werth, G. Higher order non-linear resonances in a Paul trap. Int. J. Mass Spectrom. Ion Proc. 1996, 154, 155–169. [Google Scholar] [CrossRef]
- Takai, R.; Nakayama, K.; Saiki, W.; Ito, K.; Okamoto, H. Nonlinear Resonance Effects in a Linear Paul Trap. J. Phys. Soc. Japan 2007, 76, 014802. [Google Scholar] [CrossRef]
- Xiong, C.; Zhou, X.; Zhang, N.; Zhan, L.; Chen, Y.; Nie, Z. Nonlinear Ion Harmonics in the Paul Trap with Added Octopole Field: Theoretical Characterization and New Insight into Nonlinear Resonance Effect. J. Am. Soc. Mass Spectrom. 2016, 27, 344–351. [Google Scholar] [CrossRef]
- Marchenay, M.; Pedregosa-Gutierrez, J.; Knoop, M.; Houssin, M.; Champenois, C. An analytical approach to symmetry breaking in multipole RF-traps. Quantum Sci. Technol. 2021, 6, 024016. [Google Scholar] [CrossRef]
- Shaikh, F.A.; Ozakin, A. Stability analysis of ion motion in asymmetric planar ion traps. J. Appl. Phys. 2012, 112, 074904. [Google Scholar] [CrossRef]
- Wu, H.Y.; Xie, Y.; Wan, W.; Chen, L.; Zhou, F.; Feng, M. A complicated Duffing oscillator in the surface-electrode ion trap. Appl. Phys. B 2014, 114, 81–88. [Google Scholar] [CrossRef]
- Ghosh, I.; Saxena, V.; Krishnamachari, A. Resonance Curves and Jump Frequencies in a Dual-Frequency Paul Trap on Account of Octopole Field Imperfection. IEEE Trans. Plasma Sci. 2023, 51, 1924–1931. [Google Scholar] [CrossRef]
- Mihalcea, B.M.; Visan, G.T.; Giurgiu, L.C.; Radan, S. Optimization of ion trap geometries and of the signal to noise ratio for high resolution spectroscopy. J. Optoelectron. Adv. Mat. 2008, 10, 1994–1998. Available online: https://old.joam.inoe.ro/download.php?idu=1538 (accessed on 11 May 2024).
- Pedregosa, J.; Champenois, C.; Houssin, M.; Knoop, M. Anharmonic contributions in real RF linear quadrupole traps. Int. J. Mass Spectrom. 2010, 290, 100–105. [Google Scholar] [CrossRef]
- Home, J.P.; Hanneke, D.; Jost, J.D.; Leibfried, D.; Wineland, D.J. Normal modes of trapped ions in the presence of anharmonic trap potentials. New J. Phys. 2011, 13, 073026. [Google Scholar] [CrossRef]
- Lindvall, T.; Hanhijärvi, K.J.; Fordell, T.; Wallin, A.E. High-accuracy determination of Paul-trap stability parameters for electric-quadrupole-shift prediction. J. Appl. Phys. 2022, 132, 124401. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, B.; Zeng, M.; Hao, Y.; Ma, Z.; Zhang, H.; Guan, H.; Chen, Z.; Wang, M.; Gao, K. Liquid-Nitrogen-Cooled Ca+ Optical Clock with Systematic Uncertainty of 3 × 10−18. Phys. Rev. Appl. 2022, 17, 034041. [Google Scholar] [CrossRef]
- Leibrandt, D.R.; Porsev, S.G.; Cheung, C.; Safronova, M.S. Prospects of a thousand-ion Sn2+ Coulomb-crystal clock with sub-10−19 inaccuracy. arXiv 2022, arXiv:2205.15484. [Google Scholar] [CrossRef]
- Martínez-Lahuerta, V.J.; Eilers, S.; Mehlstäubler, T.E.; Schmidt, P.O.; Hammerer, K. Ab initio quantum theory of mass defect and time dilation in trapped-ion optical clocks. Phys. Rev. A 2022, 106, 032803. [Google Scholar] [CrossRef]
- Mehta, K.K.; Zhang, C.; Malinowski, M.; Nguyen, T.L.; Stadler, M.; Home, J.P. Integrated optical multi-ion quantum logic. Nature 2020, 586, 533–537. [Google Scholar] [CrossRef]
- Sutherland, R.T.; Yu, Q.; Beck, K.M.; Häffner, H. One- and two-qubit gate infidelities due to motional errors in trapped ions and electrons. Phys. Rev. A 2022, 105, 022437. [Google Scholar] [CrossRef]
- Fan, M.; Holliman, C.A.; Shi, X.; Zhang, H.; Straus, M.W.; Li, X.; Buechele, S.W.; Jayich, A.M. Optical Mass Spectrometry of Cold RaOH+ and RaOCH3+. Phys. Rev. Lett. 2021, 126, 023002. [Google Scholar] [CrossRef] [PubMed]
- Landau, A.; Eduardus.; Behar, D.; Wallach, E.R.; Pašteka, L.F.; Faraji, S.; Borschevsky, A.; Shagam, Y. Chiral molecule candidates for trapped ion spectroscopy by ab initio calculations: From state preparation to parity violation. J. Chem. Phys. 2023, 159, 114307. [Google Scholar] [CrossRef] [PubMed]
- Rajanbabu, N.; Marathe, A.; Chatterjee, A.; Menon, A.G. Multiple scales analysis of early and delayed boundary ejection in Paul traps. Int. J. Mass Spectrom. 2007, 261, 170–182. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, Z.; Jiang, Y.; Xiong, X.; Deng, Y.; Fang, X.; Xu, W. The coupling effects of hexapole and octopole fields in quadrupole ion traps: A theoretical study. J. Mass Spectrom. 2013, 48, 937–944. [Google Scholar] [CrossRef] [PubMed]
- Xiong, C.; Zhou, X.; Zhang, N.; Zhan, L.; Chen, Y.; Chen, S.; Nie, Z. A Theoretical Method for Characterizing Nonlinear Effects in Paul Traps with Added Octopole Field. J. Am. Soc. Mass Spectrom. 2015, 26, 1338–1348. [Google Scholar] [CrossRef] [PubMed]
- Moatimid, G.M.; Amer, T.S.; Amer, W.S. Dynamical analysis of a damped harmonic forced duffing oscillator with time delay. Sci. Rep. 2023, 13, 6507. [Google Scholar] [CrossRef] [PubMed]
- Kovacic, I.; Brenner, M.J. (Eds.) The Duffing Equation: Nonlinear Oscillations and their Behaviour; Theoretical, Computational, and Statistical Physics; Wiley: Chichester, UK, 2011. [Google Scholar] [CrossRef]
- Strogatz, S.H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering, 2nd ed.; Studies in Nonlinearity; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar] [CrossRef]
- Hasegawa, T.; Uehara, K. Dynamics of a single particle in a Paul trap in the presence of the damping force. Appl. Phys. B 1995, 61, 159–163. [Google Scholar] [CrossRef]
- Sevugarajan, S.; Menon, A.G. Frequency perturbation in nonlinear Paul traps: A simulation study of the effect of geometric aberration, space charge, dipolar excitation, and damping on ion axial secular frequency. Int. J. Mass Spectrom. 2000, 197, 263–278. [Google Scholar] [CrossRef]
- Sevugarajan, S.; Menon, A.G. Transition curves and iso-βu lines in nonlinear Paul traps. Int. J. Mass Spectrom. 2002, 218, 181–196. [Google Scholar] [CrossRef]
- Zhou, X.; Zhu, Z.; Xiong, C.; Chen, R.; Xu, W.; Qiao, H.; Peng, W.P.; Nie, Z.; Chen, Y. Characteristics of stability boundary and frequency in nonlinear ion trap mass spectrometer. J. Am. Soc. Mass Spectrom. 2010, 21, 1588–1595. [Google Scholar] [CrossRef] [PubMed]
- Ishizaki, R.; Sata, H.; Shoji, T. Chaos-Induced Diffusion in a Nonlinear Dissipative Mathieu Equation for a Charged Fine Particle in an AC Trap. J. Phys. Soc. Jpn. 2011, 80, 044001. [Google Scholar] [CrossRef]
- Brouwers, J.J.H. Asymptotic solutions for Mathieu instability under random parametric excitation and nonlinear damping. Phys. D 2011, 240, 990–1000. [Google Scholar] [CrossRef]
- Mihalcea, B.M.; Vişan, G.G. Nonlinear ion trap stability analysis. Phys. Scr. 2010, T140, 014057. [Google Scholar] [CrossRef]
- Rybin, V.; Rudyi, S.; Rozhdestvensky, Y. Nano- and microparticle nonlinear damping identification in quadrupole trap. Int. J. Non-Linear Mech. 2022, 147, 104227. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Balachandran, B. Applied Nonlinear Dynamics: Analytical, Computational, and Experimental Methods, 2nd ed.; Wiley Series in Nonlinear Science; Wiley-VCH: Weinheim, Germany, 2004. [Google Scholar] [CrossRef]
- Kyzioł, J.; Okniński, A. Duffing-type equations: Singular points of amplitude profiles and bifurcations. Acta Phys. Pol. B 2021, 52, 1239–1262. [Google Scholar] [CrossRef]
- El Fakkousy, I.; Zouhairi, B.; Benmalek, M.; Kharbach, J.; Rezzouk, A.; Ouazzani-Jamil, M. Classical and quantum integrability of the three-dimensional generalized trapped ion Hamiltonian. Chaos Solit. Fractals 2022, 161, 112361. [Google Scholar] [CrossRef]
- Mihalcea, B.M. Study of quasiclassical dynamics of trapped ions using the coherent state formalism and associated algebraic groups. Rom. J. Phys. 2017, 62, 113. Available online: https://www.nipne.ro/rjp/2017_62_5-6/RomJPhys.62.113.pdf (accessed on 11 May 2024).
- Rudyi, S.; Vasilyev, M.; Rybin, V.; Rozhdestvensky, Y. Stability problem in 3D multipole ion traps. Int. J. Mass Spectrom. 2022, 479, 116894. [Google Scholar] [CrossRef]
- Sträng, J.E. On the characteristic exponents of Floquet solutions to the Mathieu equation. Bull. Acad. R. Belg. 2005, 16, 269–287. [Google Scholar] [CrossRef]
- Rudyi, S.S.; Rybin, V.V.; Semynin, M.S.; Shcherbinin, D.P.; Rozhdestvensky, Y.V.; Ivanov, A.V. Period-doubling bifurcation in surface radio-frequency trap: Transition to chaos through Feigenbaum scenario. Chaos 2023, 33, 093133. [Google Scholar] [CrossRef] [PubMed]
- Hill, G.W. On the part of the motion of lunar perigee which is a function of the mean motions of the sun and moon. Acta Math. 1886, 8, 1–36. [Google Scholar] [CrossRef]
- Viswanath, D. The Lindstedt–Poincaré Technique as an Algorithm for Computing Periodic Orbits. SIAM Rev. 2001, 43, 478–495. [Google Scholar] [CrossRef]
- Magnus, W.; Winkler, S. Hill’s Equation; Interscience Tracts in Pure and Applied Mathematics; Wiley: New York, NY, USA, 1966; Volume 20. [Google Scholar] [CrossRef]
- Whittaker, E.T.; Watson, G.N. A Course of Modern Analysis, 5th ed.; Moll, V.H., Ed.; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar] [CrossRef]
- Wilson, E.; Holzer, B.J. Beam Dynamics. In Particle Physics Reference Library: Volume 3: Accelerators and Colliders; Myers, S., Schopper, H., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 15–50. [Google Scholar] [CrossRef]
- Rodriguez, A.; Collado, J. Periodic Solutions in Non-Homogeneous Hill Equation. Nonlinear Dyn. Syst. Theory 2020, 20, 78–91. Available online: https://www.e-ndst.kiev.ua/v20n1/7(71).pdf (accessed on 11 May 2024).
- Brillouin, L. A practical method for solving Hill’s equation. Quart. Appl. Math. 1948, 6, 167–178. [Google Scholar] [CrossRef]
- Moussa, R.A. Generalization of Ince’s Equation. J. Appl. Math. Phys. 2014, 2, 1171–1182. [Google Scholar] [CrossRef]
- Wolf, G. Mathieu Functions and Hill’s Equation. In NIST Handbook of Mathematical Functions; Olver, F.W.J., Lozier, D.W., Boisvert, R.F., Clark, C.W., Eds.; NIST & Cambridge University Press: New York, NY, USA, 2010; Chapter 28; pp. 651–681. [Google Scholar]
- Landa, H.; Drewsen, M.; Reznik, B.; Retzker, A. Modes of oscillation in radiofrequency Paul traps. New J. Phys. 2012, 14, 093023. [Google Scholar] [CrossRef]
- Ck Function. Available online: https://mathworld.wolfram.com/C-kFunction.html (accessed on 2 May 2024).
- Landa, H.; Drewsen, M.; Reznik, B.; Retzker, A. Classical and quantum modes of coupled Mathieu equations. J. Phys. A Math. Theor. 2012, 45, 455305. [Google Scholar] [CrossRef]
- Frenkel, D.; Portugal, R. Algebraic methods to compute Mathieu functions. J. Phys. A Math. Gen. 2001, 34, 3541–3551. [Google Scholar] [CrossRef]
- Wong, C.W. Introduction to Mathematical Physics: Methods and Concepts, 2nd ed.; Oxford University Press: Oxford, UK, 2013. [Google Scholar] [CrossRef]
- Gezerlis, A. Numerical Methods in Physics with Python, 2nd ed.; Cambridge University Press: Cambridge, UK, 2023. [Google Scholar] [CrossRef]
- Jones, T. Mathieu’s Equations and the Ideal RF-Paul Trap. Available online: http://einstein.drexel.edu/~tim/open/mat/mat.pdf (accessed on 21 May 2024).
- Weyl, H. Meromorphic Functions and Analytic Curves; Annals of Mathematics Studies, Princeton University Press—De Gruyter: Princeton, NJ, USA, 2016; Volume 12. [Google Scholar] [CrossRef]
- Meromorphic Function. Available online: https://mathworld.wolfram.com/MeromorphicFunction.html (accessed on 2 May 2024).
- Canosa, J. Numerical solution of Mathieu’s equation. J. Computat. Phys. 1971, 7, 255–272. [Google Scholar] [CrossRef]
- Bibby, M.M.; Peterson, A.F. Accurate Computation of Mathieu Functions; Balanis, C.A., Ed.; Synthesis Lectures on Computational Electromagnetics; Morgan & Claypool: San Rafael, CA, USA, 2014; Volume Lecture 32. [Google Scholar] [CrossRef]
- Gheorghe, V.N.; Giurgiu, L.; Stoican, O.; Cacicovschi, D.; Molnar, R.; Mihalcea, B. Ordered Structures in a Variable Length AC Trap. Acta Phys. Pol. A 1998, 93, 625–629. [Google Scholar] [CrossRef]
- Kotana, A.N.; Mohanty, A.K. Computation of Mathieu stability plot for an arbitrary toroidal ion trap mass analyser. Int. J. Mass Spectrom. 2017, 414, 13–22. [Google Scholar] [CrossRef]
- Wuerker, R.F.; Shelton, H.; Langmuir, R.V. Electrodynamic Containment of Charged Particles. J. Appl. Phys. 1959, 30, 342–349. [Google Scholar] [CrossRef]
- Dehmelt, H. Radiofrequency Spectroscopy of Stored Ions I: Storage. In Advances in Atomic and Molecular Physics; Academic Press: Cambridge, MA, USA, 1968; Volume 3, pp. 53–72. [Google Scholar] [CrossRef]
- March, R.E.; Todd, J.F.J. Quadrupole Ion Trap Mass Spectrometry, 2nd ed.; Winefordner, J.D., Ed.; Chemical Analysis; Wiley: Hoboken, NJ, USA, 2005; Volume 165. [Google Scholar] [CrossRef]
- Breslin, J.K.; Holmes, C.A.; Milburn, G.J. Quantum signatures of chaos in the dynamics of a trapped ion. Phys. Rev. A 1997, 56, 3022–3027. [Google Scholar] [CrossRef]
- Gardiner, S.A.; Cirac, J.I.; Zoller, P. Quantum Chaos in an Ion Trap: The Delta-Kicked Harmonic Oscillator. Phys. Rev. Lett. 1997, 79, 4790–4793. [Google Scholar] [CrossRef]
- Menicucci, N.C.; Milburn, G.J. Single trapped ion as a time-dependent harmonic oscillator. Phys. Rev. A 2007, 76, 052105. [Google Scholar] [CrossRef]
- Mihalcea, B.M. Semiclassical dynamics for an ion confined within a nonlinear electromagnetic trap. Phys. Scr. 2011, T143, 014018. [Google Scholar] [CrossRef]
- Mihalcea, B.M. Nonlinear harmonic boson oscillator. Phys. Scr. 2010, T140, 014056. [Google Scholar] [CrossRef]
- Gheorghe, V.N.; Mihalcea, B.M.; Gheorghe, A. Ion stability in laser fields and anharmonic RF potentials. In Proceedings of the 29th EGAS Conference Abstracts, Berlin, Germany, 16–20 June 1997; Kronfeldt, H.D., Ed.; European Physical Society: Berlin, Germany, 1997; p. 427. [Google Scholar]
- Pedregosa-Gutierrez, J.; Champenois, C.; Kamsap, M.R.; Hagel, G.; Houssin, M.; Knoop, M. Symmetry breaking in linear multipole traps. J. Mod. Opt. 2018, 65, 529–537. [Google Scholar] [CrossRef]
- Michaud, A.L.; Frank, A.J.; Ding, C.; Zhao, X.; Douglas, D.J. Ion Excitation in a Linear Quadrupole Ion Trap with an Added Octopole Field. J. Am. Soc. Mass Spectrom. 2005, 16, 835–849. [Google Scholar] [CrossRef]
- Benkhali, M.; Kharbach, J.; El Fakkousy, I.; Chatar, W.; Rezzouk, A.; Ouazzani-Jamil, M. Painlevé analysis and integrability of the trapped ionic system. Phys. Lett. A 2018, 382, 2515–2525. [Google Scholar] [CrossRef]
- Vasilyev, M.; Rudyi, S.; Rozhdestvensky, Y. Theoretical description of electric fields in three-dimensional multipole ion traps. Eur. J. Mass Spectrom. 2021, 27, 158–165. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Quist, H.; Peng, Y.; Hansen, B.J.; Wang, J.; Hawkins, A.R.; Austin, D.E. Effects of higher-order multipoles on the performance of a two-plate quadrupole ion trap mass analyzer. Int. J. Mass Spectrom. 2011, 299, 151–157. [Google Scholar] [CrossRef]
- Niranjan, M.; Prakash, A.; Rangwala, S.A. Analysis of Multipolar Linear Paul Traps for Ion–Atom Ultracold Collision Experiments. Atoms 2021, 9, 38. [Google Scholar] [CrossRef]
- Chimwal, D.; Kumar, S.; Joshi, Y.; Lal, A.A.; Nair, L.; Quint, W.; Vogel, M. Electrostatic anharmonicity in cylindrical Penning traps induced by radial holes to the trap center. Phys. Scr. 2024, 99, 055404. [Google Scholar] [CrossRef]
- Nötzold, M.; Hassan, S.Z.; Tauch, J.; Endres, E.; Wester, R.; Weidemüller, M. Thermometry in a Multipole Ion Trap. Appl. Sci. 2020, 10, 5264. [Google Scholar] [CrossRef]
- Poli, N.; Oates, C.W.; Gill, P.; Tino, G.M. Optical atomic clocks. Nuovo Cimento 2013, 36, 555–624. [Google Scholar] [CrossRef]
- Margolis, H.S. Frequency standards with trapped ions. In Ion Traps for Tomorrow’s Applications; Proc. Intl. School Phys. “Enrico Fermi”; IOS & Societa Italiana di Fisica: Amsterdam, The Netherlands; Bologna, Italy, 2015; Volume 189 “Ion Traps for Tomorrow’s Applications”. [Google Scholar] [CrossRef]
- Taylor, M.E. Introduction to Complex Analysis; Graduate Studies in Mathematics; American Mathematical Society: Providence, RI, USA, 2019; Volume 202. [Google Scholar] [CrossRef]
- Khan, H.; Shah, R.; Kumam, P.; Baleanu, D.; Arif, M. Laplace decomposition for solving nonlinear system of fractional order partial differential equations. Adv. Differ. Equ. 2020, 2020, 375. [Google Scholar] [CrossRef]
- Richards, D. Advanced Mathematical Methods with Maple; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Liu, C.S.; Chen, Y.W. A Simplified Lindstedt-Poincaré Method for Saving Computational Cost to Determine Higher Order Nonlinear Free Vibrations. Mathematics 2021, 9, 3070. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mihalcea, B.M. Mathieu–Hill Equation Stability Analysis for Trapped Ions: Anharmonic Corrections for Nonlinear Electrodynamic Traps. Photonics 2024, 11, 551. https://doi.org/10.3390/photonics11060551
Mihalcea BM. Mathieu–Hill Equation Stability Analysis for Trapped Ions: Anharmonic Corrections for Nonlinear Electrodynamic Traps. Photonics. 2024; 11(6):551. https://doi.org/10.3390/photonics11060551
Chicago/Turabian StyleMihalcea, Bogdan M. 2024. "Mathieu–Hill Equation Stability Analysis for Trapped Ions: Anharmonic Corrections for Nonlinear Electrodynamic Traps" Photonics 11, no. 6: 551. https://doi.org/10.3390/photonics11060551