Spatio-Temporal Dynamics of Pulses in Multimode Fibers
Abstract
1. Introduction
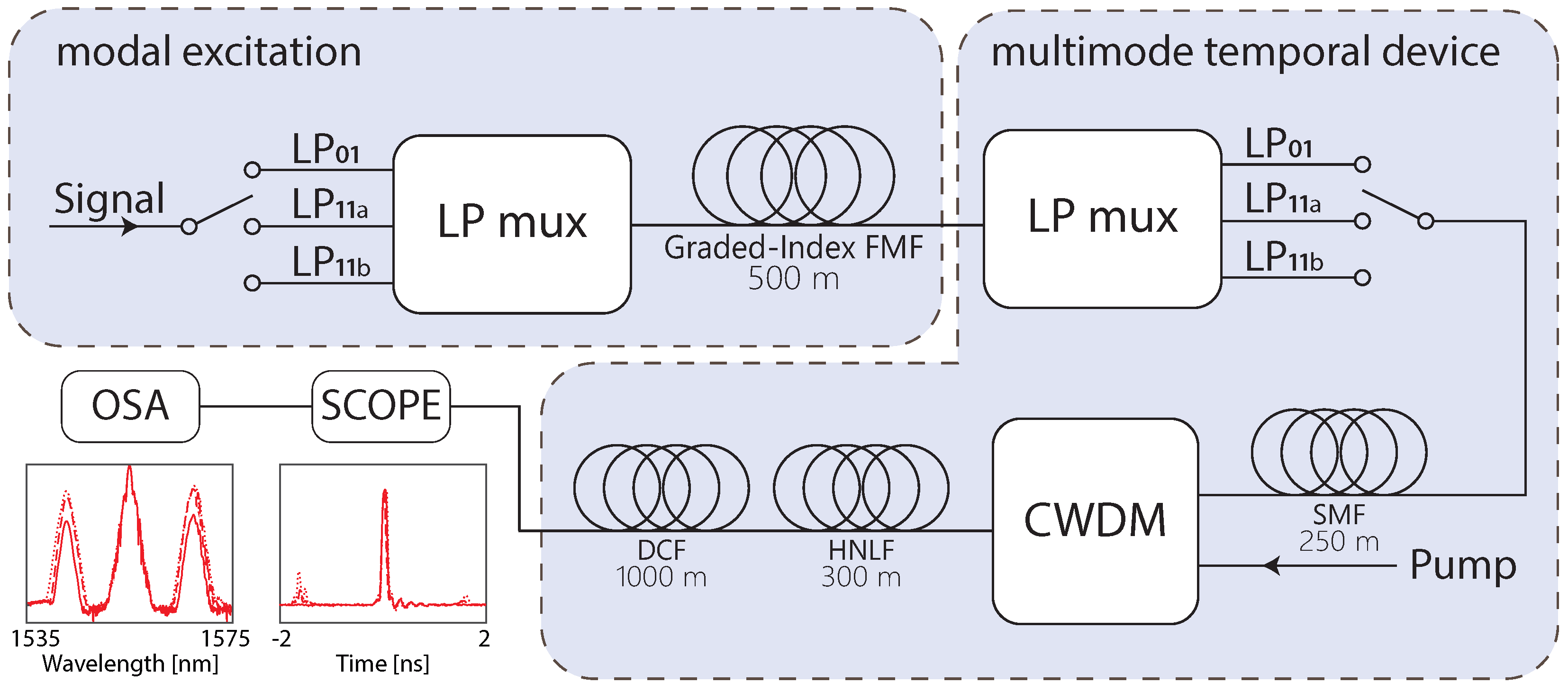
2. Methods
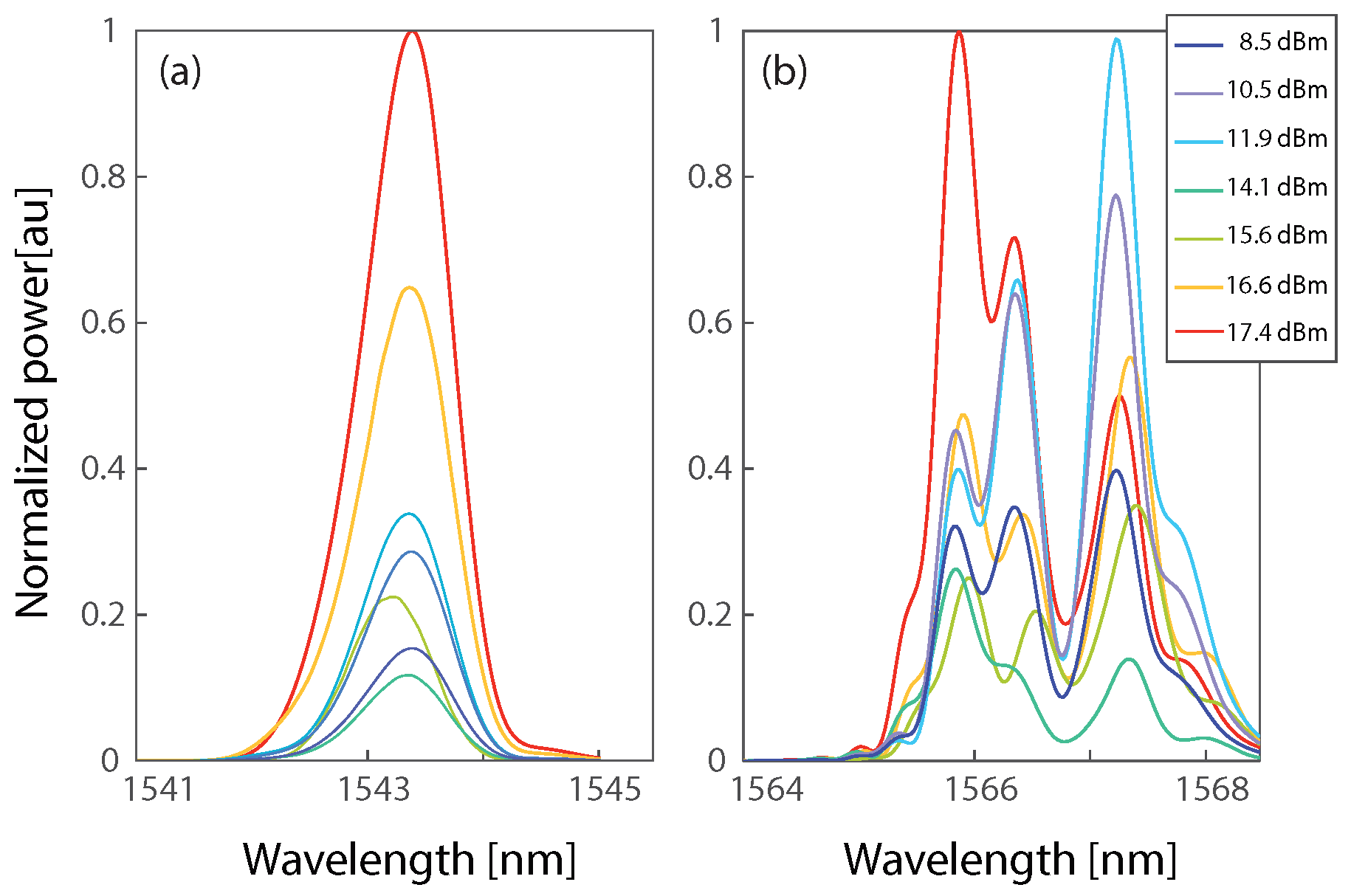
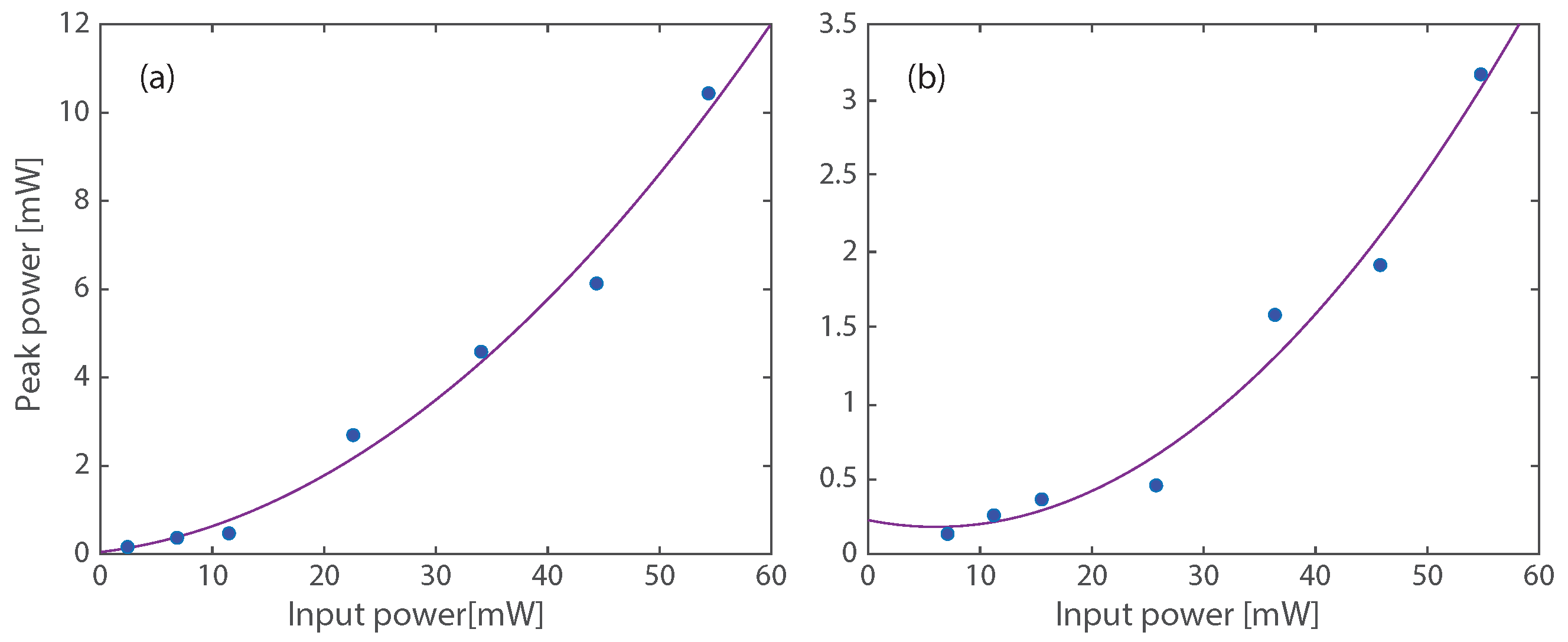
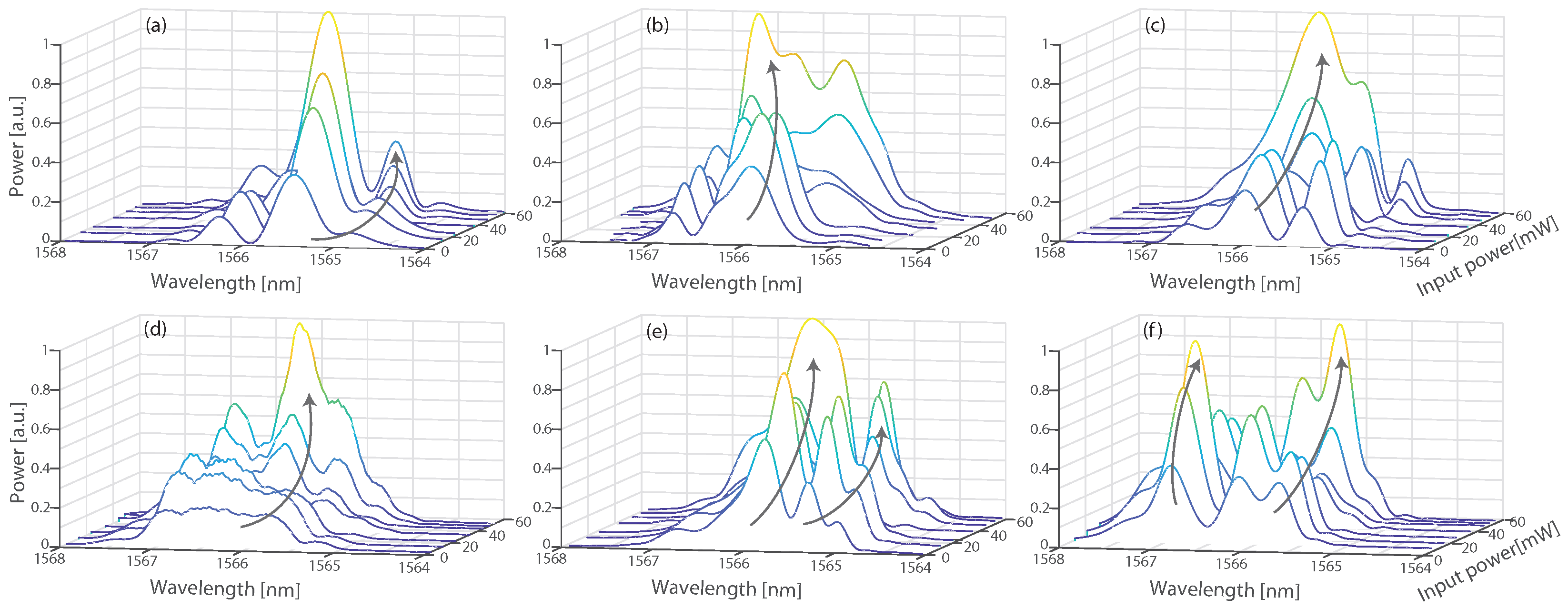
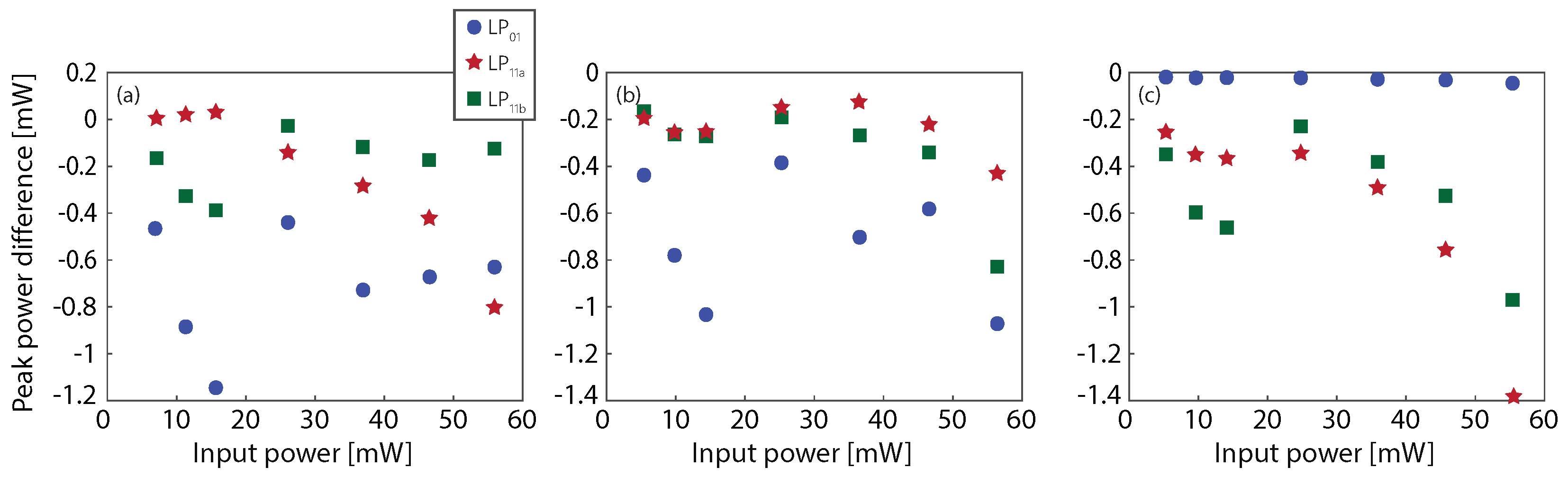
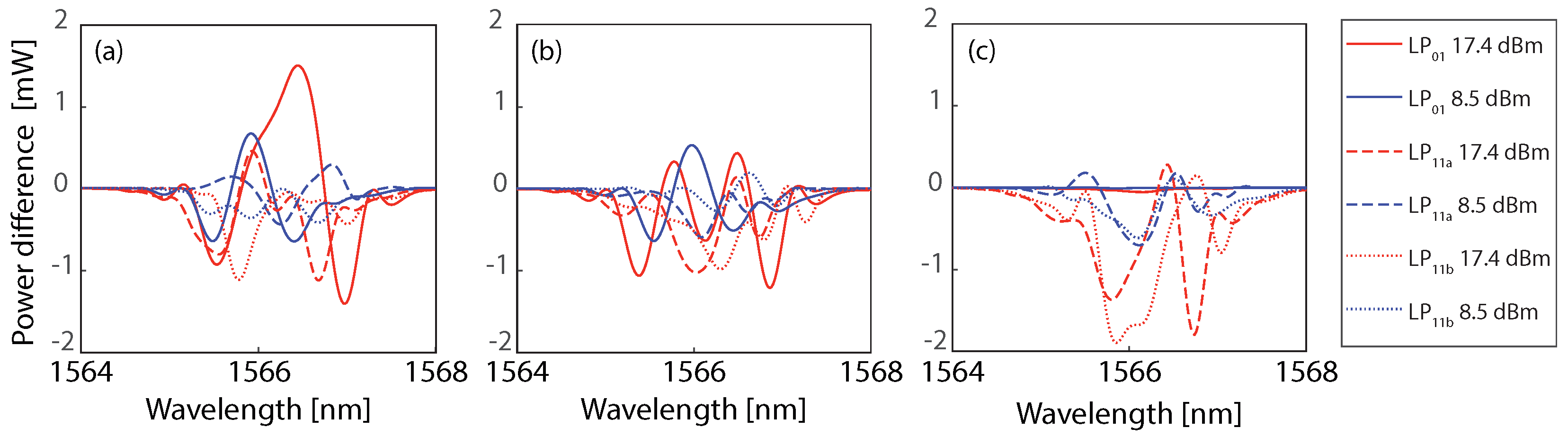
3. Results
4. Numerical Simulation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Krupa, K.; Tonello, A.; Barthélémy, A.; Mansuryan, T.; Couderc, V.; Millot, G.; Grelu, P.; Modotto, D.; Babin, S.A.; Wabnitz, S. Multimode nonlinear fiber optics, a spatiotemporal avenue. APL Photonics 2019, 4, 110901. [Google Scholar] [CrossRef]
- Goudreau, E.S.; Kupchak, C.; Sussman, B.J.; Boyd, R.W.; Lundeen, J.S. Theory of four-wave mixing of cylindrical vector beams in optical fibers. JOSA B 2020, 37, 1670–1682. [Google Scholar] [CrossRef]
- Ahsan, A.S.; Agrawal, G.P. Effect of an input beam’s shape and curvature on the nonlinear effects in graded-index fibers. JOSA B 2020, 37, 858–867. [Google Scholar] [CrossRef]
- Wright, L.G.; Ziegler, Z.M.; Lushnikov, P.M.; Zhu, Z.; Eftekhar, M.A.; Christodoulides, D.N.; Wise, F.W. Multimode nonlinear fiber optics: Massively parallel numerical solver, tutorial, and outlook. IEEE J. Sel. Top. Quantum Electron. 2017, 24, 1–16. [Google Scholar] [CrossRef]
- Kakkava, E.; Romito, M.; Conkey, D.B.; Loterie, D.; Stankovic, K.M.; Moser, C.; Psaltis, D. Selective femtosecond laser ablation via two-photon fluorescence imaging through a multimode fiber. Biomed. Opt. Express 2019, 10, 423–433. [Google Scholar] [CrossRef]
- Kakkava, E.; Rahmani, B.; Borhani, N.; Teğin, U.; Loterie, D.; Konstantinou, G.; Moser, C.; Psaltis, D. Imaging through multimode fibers using deep learning: The effects of intensity versus holographic recording of the speckle pattern. Opt. Fiber Technol. 2019, 52, 101985. [Google Scholar] [CrossRef]
- Xiong, W.; Redding, B.; Gertler, S.; Bromberg, Y.; Tagare, H.D.; Cao, H. Deep learning of ultrafast pulses with a multimode fiber. APL Photonics 2020, 5, 096106. [Google Scholar] [CrossRef]
- Kakkava, E.; Borhani, N.; Rahmani, B.; Teğin, U.; Moser, C.; Psaltis, D. Deep learning-based image classification through a multimode fiber in the presence of wavelength drift. Appl. Sci. 2020, 10, 3816. [Google Scholar] [CrossRef]
- Wright, L.G.; Christodoulides, D.N.; Wise, F.W. Controllable spatiotemporal nonlinear effects in multimode fibres. Nat. Photonics 2015, 9, 306–310. [Google Scholar] [CrossRef]
- Wright, L.G.; Sidorenko, P.; Pourbeyram, H.; Ziegler, Z.M.; Isichenko, A.; Malomed, B.A.; Menyuk, C.R.; Christodoulides, D.N.; Wise, F.W. Mechanisms of spatiotemporal mode-locking. Nat. Phys. 2020, 16, 565–570. [Google Scholar] [CrossRef]
- Ding, Y.; Xiao, X.; Wang, P.; Yang, C. Multiple-soliton in spatiotemporal mode-locked multimode fiber lasers. Opt. Express 2019, 27, 11435–11446. [Google Scholar] [CrossRef] [PubMed]
- Deliancourt, E.; Fabert, M.; Tonello, A.; Krupa, K.; Desfarges-Berthelemot, A.; Kermene, V.; Millot, G.; Barthélémy, A.; Wabnitz, S.; Couderc, V. Kerr beam self-cleaning on the LP 11 mode in graded-index multimode fibers. OSA Contin. 2019, 2, 1089–1096. [Google Scholar] [CrossRef]
- Krupa, K.; Tonello, A.; Shalaby, B.M.; Fabert, M.; Barthélémy, A.; Millot, G.; Wabnitz, S.; Couderc, V. Spatial beam self-cleaning in multimode fibres. Nat. Photonics 2017, 11, 237–241. [Google Scholar] [CrossRef]
- Wright, L.G.; Liu, Z.; Nolan, D.A.; Li, M.J.; Christodoulides, D.N.; Wise, F.W. Self-organized instability in graded-index multimode fibres. Nat. Photonics 2016, 10, 771–776. [Google Scholar] [CrossRef]
- Deng, Z.; Chen, Y.; Liu, J.; Zhao, C.; Fan, D. Graded-index breathing solitons from Airy pulses in multimode fibers. Opt. Express 2019, 27, 483–493. [Google Scholar] [CrossRef] [PubMed]
- Wright, L.G.; Renninger, W.H.; Christodoulides, D.N.; Wise, F.W. Spatiotemporal dynamics of multimode optical solitons. Opt. Express 2015, 23, 3492–3506. [Google Scholar] [CrossRef] [PubMed]
- Wright, L.G.; Christodoulides, D.N.; Wise, F.W. Spatiotemporal mode-locking in multimode fiber lasers. Science 2017, 358, 94–97. [Google Scholar] [CrossRef]
- Cao, B.; Gao, C.; Liu, K.; Xiao, X.; Yang, C.; Bao, C. Spatiotemporal mode-locking and dissipative solitons in multimode fiber lasers. Light Sci. Appl. 2023, 12, 260. [Google Scholar] [CrossRef]
- Li, L.; Leng, J.; Zhou, P.; Chen, J. Modulation instability induced by intermodal cross-phase modulation in step-index multimode fiber. Appl. Opt. 2019, 58, 4283–4287. [Google Scholar] [CrossRef]
- Dupiol, R.; Bendahmane, A.; Krupa, K.; Fatome, J.; Tonello, A.; Fabert, M.; Couderc, V.; Wabnitz, S.; Millot, G. Intermodal modulational instability in graded-index multimode optical fibers. Opt. Lett. 2017, 42, 3419–3422. [Google Scholar] [CrossRef]
- Hasegawa, A. Self-confinement of multimode optical pulse in a glass fiber. Opt. Lett. 1980, 5, 416–417. [Google Scholar] [CrossRef]
- Crosignani, B.; Cutolo, A.; Di Porto, P. Coupled-mode theory of nonlinear propagation in multimode and single-mode fibers: Envelope solitons and self-confinement. JOSA 1982, 72, 1136–1141. [Google Scholar] [CrossRef]
- Mecozzi, A.; Antonelli, C.; Shtaif, M. Soliton trapping in multimode fibers with random mode coupling. arXiv 2012, arXiv:1207.6506. [Google Scholar]
- Renninger, W.H.; Wise, F.W. Optical solitons in graded-index multimode fibres. Nat. Commun. 2013, 4, 1719. [Google Scholar] [CrossRef] [PubMed]
- Fontaine, N.K.; Ryf, R.; Chen, H.; Neilson, D.T.; Kim, K.; Carpenter, J. Laguerre-Gaussian mode sorter. Nat. Commun. 2019, 10, 1865. [Google Scholar] [CrossRef] [PubMed]
- Tarnowski, K.; Majchrowska, S.; Béjot, P.; Kibler, B. Numerical modelings of ultrashort pulse propagation and conical emission in multimode optical fibers. JOSA B 2021, 38, 732–742. [Google Scholar] [CrossRef]
- Kolner, B.H. Space-time duality and the theory of temporal imaging. IEEE J. Quantum Electron. 1994, 30, 1951–1963. [Google Scholar] [CrossRef]
- Foster, M.A.; Salem, R.; Geraghty, D.F.; Turner-Foster, A.C.; Lipson, M.; Gaeta, A.L. Silicon-chip-based ultrafast optical oscilloscope. Nature 2008, 456, 81–84. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Huang, S.W.; Li, Y.; Wong, C.W.; Wong, K.K. Panoramic-reconstruction temporal imaging for seamless measurements of slowly-evolved femtosecond pulse dynamics. Nat. Commun. 2017, 8, 61. [Google Scholar] [CrossRef]
- Li, B.; Azaña, J. Incoherent-light temporal stretching of high-speed intensity waveforms. Opt. Lett. 2014, 39, 4243–4246. [Google Scholar] [CrossRef]
- Bennett, C.; Scott, R.; Kolner, B. Temporal magnification and reversal of 100 Gb/s optical data with an up-conversion time microscope. Appl. Phys. Lett. 1994, 65, 2513–2515. [Google Scholar] [CrossRef]
- Meir, S.; Tamir, Y.; Duadi, H.; Cohen, E.; Fridman, M. Ultrafast Temporal SU (1, 1) Interferometer. Phys. Rev. Lett. 2023, 130, 253601. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Li, B.; Wong, K.K.Y. Ultrafast spectroscopy based on temporal focusing and its applications. IEEE J. Sel. Top. Quantum Electron. 2015, 22, 295–306. [Google Scholar] [CrossRef]
- Fernández-Ruiz, M.R.; Azaña, J. Temporal phase conjugation based on time-domain holography. Opt. Lett. 2015, 40, 127–130. [Google Scholar] [CrossRef] [PubMed]
- Klein, A.; Masri, G.; Duadi, H.; Sulimany, K.; Lib, O.; Steinberg, H.; Kolpakov, S.A.; Fridman, M. Ultrafast rogue wave patterns in fiber lasers. Optica 2018, 5, 774–778. [Google Scholar] [CrossRef]
- Klein, A.; Shahal, S.; Meir, S.; Duadi, H.; Sulimany, K.; Lib, O.; Steinberg, H.; Kolpakov, S.A.; Fridman, M. Ultrafast twin-peak rogue waves in a vector field. OSA Contin. 2019, 2, 3102–3106. [Google Scholar] [CrossRef]
- Feng, J.; Xu, W.; Li, S.; Liu, S. Analytic solutions of self-similar pulse based on Ginzburg-Landau equation with constant coefficients. Sci. China Ser. G Phys. Mech. Astron. 2008, 51, 299–306. [Google Scholar] [CrossRef]
- Nazemosadat, E.; Pourbeyram, H.; Mafi, A. Phase matching for spontaneous frequency conversion via four-wave mixing in graded-index multimode optical fibers. JOSA B 2016, 33, 144–150. [Google Scholar] [CrossRef]
- Mafi, A. Pulse propagation in a short nonlinear graded-index multimode optical fiber. J. Light. Technol. 2012, 30, 2803–2811. [Google Scholar] [CrossRef]
- Kolner, B.H.; Nazarathy, M. Temporal imaging with a time lens. Opt. Lett. 1989, 14, 630–632. [Google Scholar] [CrossRef]
- Meir, S.; Klein, A.; Duadi, H.; Cohen, E.; Fridman, M. Single-shot analysis of amplified correlated light. Opt. Express 2022, 30, 1773–1781. [Google Scholar] [CrossRef]
- Klein, A.; Shahal, S.; Masri, G.; Duadi, H.; Fridman, M. Four wave mixing-based time lens for orthogonal polarized input signals. IEEE Photonics J. 2017, 9, 1–7. [Google Scholar] [CrossRef]
- Klein, A.; Duadi, H.; Fridman, M. Full-stokes temporal imaging. Opt. Lett. 2018, 43, 1651–1653. [Google Scholar] [CrossRef]
- Klein, A.; Yaron, T.; Preter, E.; Duadi, H.; Fridman, M. Temporal depth imaging. Optica 2017, 4, 502–506. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tamir, Y.; Meir, S.; Duadi, H.; Fridman, M. Spatio-Temporal Dynamics of Pulses in Multimode Fibers. Photonics 2024, 11, 591. https://doi.org/10.3390/photonics11070591
Tamir Y, Meir S, Duadi H, Fridman M. Spatio-Temporal Dynamics of Pulses in Multimode Fibers. Photonics. 2024; 11(7):591. https://doi.org/10.3390/photonics11070591
Chicago/Turabian StyleTamir, Yuval, Sara Meir, Hamootal Duadi, and Moti Fridman. 2024. "Spatio-Temporal Dynamics of Pulses in Multimode Fibers" Photonics 11, no. 7: 591. https://doi.org/10.3390/photonics11070591
APA StyleTamir, Y., Meir, S., Duadi, H., & Fridman, M. (2024). Spatio-Temporal Dynamics of Pulses in Multimode Fibers. Photonics, 11(7), 591. https://doi.org/10.3390/photonics11070591




